Distributed Testing of Distance-k Colorings

Abstract

We study the distributed decision problem related to checking distance-k coloring, defined as color assignments to the nodes such that every pair of vertices at distance at most k must receive distinct colors. While checking the validity of a distance-k coloring only requires $\lceil k/2\rceil$ rounds in the Local model, and a single round in the Congest model when $k\le 2$, the task is extremely costly for higher k’s in Congest—there is a lower bound of $\varOmega (\varDelta ^{k/2})$ rounds in graphs with maximum degree $\varDelta$. We therefore explore the ability of checking distance-k coloring via distributed property testing. We consider several farness criteria for measuring the distance to a valid coloring, and we derive upper and lower bounds for each of them. In particular, we show that for one natural farness measure, significantly better algorithms are possible for testing distance-3 coloring than for testing distance-k coloring for $k \ge 4$.

Pierre Fraigniaud is partially supported by ANR Projects DESCARTES, QuDATA, and FREDDA; Magnús M. Halldórsson and Alexandre Nolin are partially supported by Icelandic Research Foundation grant 174484-051.

1 Introduction

We study problems related to checking whether a given distance-k coloring is proper, in the distributed Congest model. A valid (or proper) distance-k coloring of a graph $G=(V,E)$, for $k \ge 1$, is a coloring of each node v with integer $c_v$ so that any two nodes u, v of distance at most k are colored differently, i.e., $c_u \ne c_v$. This is equivalent to the usual vertex coloring of the graph $G^k = (V,E^k)$, where two nodes are adjacent if they are within distance k in G.

Classical distance-1 colorings have been extensively studied in distributed computing as a tool of breaking symmetry. Let us denote by n the number of nodes, by m the number of edges, and by $\varDelta$ the maximum degree of G. For the core problem of finding a $(\varDelta +1)$-coloring, there is a simple folklore $O(\log n)$-round randomized algorithm, and recent $\mathrm {polylog}(n)$-round deterministic algorithm by Bamberger, Kuhn and Maus [4] that works in Congest (leveraging the recent breakthrough of Rozhoň and Ghaffari [35]). The corresponding distance-2 coloring questions has recently been addressed in [25], where an $O(\log \varDelta \log n)$-round randomized algorithm is given that uses $\varDelta ^2+1$ colors, as well as a $\mathrm {polylog}(n)$-round deterministic algorithm that uses $(1+\epsilon )\varDelta ^2$ colors, for any $\epsilon > 0$. This opens the question about distance-k coloring problems, for $k \ge 3$, which appear considerably harder.

Why Distance-k Coloring? Distributed distance-k colorings are interesting for various reasons. They appear naturally when constant-round randomized algorithms are derandomized using the method of conditional expectation  [22]. They also appear in certain models of wireless models, where senders must be sufficiently separated, to limit interference. More abstractly, we can view distance-k coloring problems as a way of studying communication capacity constraints on nodes, where communication must go through intermediate relays. Given that distance-2 colorings can be efficiently computed, distance-3 colorings appear to lie at the frontier of what can be solved efficiently by distributed algorithms.

Deciding Distance-k Coloring. Given the apparently challenging task of finding an efficient distance-3 coloring, a natural question that arises is if we can at least check that a given coloring is valid. We can quickly dispose of that hope, as there is an easy reduction to Set Disjointness that shows that verifying a distance-k coloring requires $\varOmega (\varDelta ^{\lfloor (k-1)/2\rfloor })$ rounds in Congest. We provide a proof of this fact, for completeness, in Appendix A. Observe that the question is trivially answered in $\lceil k/2 \rceil$ rounds of the Local model.

Testing Distance-k Coloring. Distributed property testing is a relaxation of distributed decision, where we seek a Congest algorithm that can distinguish whether the given graph satisfies a given property (e.g., having a distance-k coloring), or is far from having such a property. The most common notion for this is $\epsilon$-farness in the sparse model, when the addition or deletion of up to $\epsilon \cdot m$ arbitrary edges to/from the graph $G=(V,E)$ does not result in the property being satisfied. This notion is renamed $\epsilon$-edge in this paper, so as to avoid confusion as we use alternative notions of being far to a valid coloring. Distributed algorithms testing a property (here distance-k coloring) are compared according to the error rate $\epsilon (r)$ they can tolerate if restricted to r rounds, or equivalently, the round complexity $r(\epsilon )$ to distinguish between legal instances and instances $\epsilon$-far from being legal.

1.1 Summary of Main Results

We consider several measures of distance from a valid coloring to define various notion of $\epsilon$-farness, deduce their relationship, and bound the efficiency of testing distance-k colorings in Congest under these measures. As examples of such measures, we consider $\epsilon$-edge, where deleting up to $\epsilon m$ edges cannot result in a valid distance-k coloring, and $\epsilon$-middle, where there exist more than $\epsilon m$ paths of length at most $k-2$ between two nodes with distinct neighbors of the same color. We present the following results:

• 1. An algorithm for any constant $k \ge 3$, with round complexity $O(1/\epsilon )$, for all our measures but $\epsilon$-middle. We provide a matching lower bound for any algorithm under two of our considered measures.

• 2. An improved algorithm for distance-3 colorings under the $\epsilon$-middle measure. The round complexity is $O(\epsilon ^{-3/2}m^{-1/2})$, for $\epsilon \ge m^{-1/3}$. We prove a matching lower bound, and as well as an $\widetilde{\varOmega }(\epsilon ^{-1})$ lower bound for distance-4. This shows that distance-4 is strictly harder than distance-3.

• 3. A communication complexity lower bound of $\tilde{\varOmega }(\epsilon ^{-1} (\epsilon m)^{-1})$, for any $k \ge 3$, under the $\epsilon$-edge measure.

The results suggest that distance-3 colorings are easier to test than for larger distances. This reinforces the role of distance-3 coloring on the frontier of what is computable efficiently in Congest.

1.2 Related Work

Property testing has an extensive history in the sequential setting  [23]. Distributed property testing was recently introduced by Brakerski and Patt-Shamir [6], and subsequently revisited and formalized more broadly by Censor-Hillel et al.  [8]. As in the centralized setting, different variants of farness can be considered, but most of the efforts on distributed property testing has been carried out in the sparse model, that is, the model of this paper, where farness is measured by the fraction of the number of edges that must be added or removed for satisfying the property under consideration. In this framework, most previous work has been dedicated to checking the absence of a specific graph pattern (e.g., a cycle $C_k$, or a clique $K_k$, for some $k\ge 3$) as a subgraph of the actual network  [12, 18, 20]. To our knowledge, this paper is the first to consider distributed testing proper distance-k coloring.

More generally, distributed property testing falls into the wide class of distributed decision problems, initially motivated by fault-tolerant distributed computing  [2, 3, 28]. Since these early works, there has been a large body of work on distributed decision, with a range of models—see [13] for a survey. The closest to ours are local decision  [15, 17], and local verification  [17, 19, 24, 31]. In both cases, the nodes perform a constant number of rounds of communication before reaching a decision. Distributed property testing is a relaxed version of randomized distributed local decision, as nodes are not bounded to detect illegal instances that are “close to be legal”. In distributed verification, every node is also supplied with a certificate string, and the collection of certificates is supposed to form a distributed proof that the instance is legal. Distributed property testing performs in absence of such certificates. Recently, distributed verification has been extended to distributed interactive proofs  [30, 33], involving interactions between the nodes and a powerful centralized oracle. Such mechanisms are obviously much more powerful than distributed property testing.

Overall, distributed property testing offers a tradeoff between simplicity (no need of certificates, nor of any interactions with an external entity), and efficiency (configurations that are “slightly” illegal may not be detected). It is thus an appealing lightweight alternative to complex mechanisms for distributed systems that can tolerate to be slightly faulty. This is typically the case of wireless systems, which are able to tolerate a certain level of interference, as long as these interferences do not exceed a certain threshold.

2 Model and Definitions

The input of our algorithms is a graph G, and a proposed coloring $C = (c_v)_{v\in V}$. Given an underlying distance metrics between solutions, we say that a solution is $\epsilon$-far from being correct (or valid, or legal) if it is of distance at least $\epsilon$ from any valid solution for G. We seek a Congest protocol running on G to distinguish valid solutions from $\epsilon$-far solutions. The protocol should have 1-sided error:

If C is valid, then, with probability 1, all nodes output “yes”.

If C is $\epsilon$-far from being valid, then, with probability at least 2/3, some node outputs “no”.

We explore different types of solution distances. In particular, we can divide them into two types: distance to a graph for which the given solution is valid, and distance to a valid solution for the given graph. We call two distinct nodes with the same color at distance at most k a bad pair, and call a path connecting a bad pair a bad path.

Definition 1

An n-node m-edge graph $G=(V,E)$ and a coloring of its vertices $(c_v)_{v\in V}$ are said to be

• $\epsilon$-edge, when deleting up to $\epsilon m$ arbitrary edges does not result in a valid distance-k coloring.

• $\epsilon$-disjoint, when there exist more than $\epsilon m$ distinct pairs of similarly colored vertices linked by edge-disjoint paths of length at most k.

• $\epsilon$-middle, when there exist more than $\epsilon m$ paths of length at most $k-2$ between two nodes with distinct neighbors of the same color.

• $\epsilon$-node, when recoloring up to $\epsilon n$ arbitrary vertices does not result in a valid distance-k coloring.

• $\epsilon$-conflict, when more than $\epsilon n$ vertices have the same color as one of their distance-k neighbors.

The $\epsilon$-edge measure is the classical one from property testing literature [6, 8, 18]. The $\epsilon$-disjoint measure is a variation that requires there to be many conflict pairs, not just one vertex that conflicts with many nodes (that might not conflict between themselves).

The $\epsilon$-middle measure has the appearance of being contrived, but actually captures the essence of the problem. In the first round, each node learns of the colors of all its neighbors. Thus, what we really need is to somehow connect the second node on a bad k-path to the second-to-last node, and see if the sets of colors in their neighborhoods intersect.

Fig. 1.

The relationships between our notions of distance from a valid solution as well as our upper and lower bounds on the costs of testing for them. For two notions of farness notion$_1$ and notion$_2$, an arrow from $\epsilon$-notion$_1$ to $\epsilon$-notion$_2$ indicates that a solution that is $\epsilon$-notion$_1$ is also $\varOmega (\epsilon )$-notion$_2$ away from a valid solution. Dashed lines indicate incomparability.

The last two definitions correspond to natural measures of invalidity of colorings. The $\epsilon$-conflict measure counts how many nodes are improperly colored (i.e., have a same-colored distance-$\le k$ neighbor), while $\epsilon$-node is more conservative, bounding the number of recolorings needed to turn the coloring into a valid one.

We say that a measure $\mu$ is more strict than measure $\mu '$ if $\mu (G,c) = O(\mu '(G,c))$, for all graphs G and colorings c. Thus, if (G, c) is $\epsilon$-far in terms of measure $\mu '$, then it is $O(\epsilon )$-far in terms of measure $\mu$ (but could be much less far).

It is easy to see that $\epsilon$-disjoint is more strict than $\epsilon$-edge, and $\epsilon$-node is more strict than $\epsilon$-conflict. It also holds that $\epsilon$-disjoint is more strict than $\epsilon$-conflict on sparse graphs, when $|E(G)| = O(|V(G)|)$. This is illustrated in Fig. 1, where solid arrows are drawn from a stricter measures to a less stricter one.

We can also verify that other pairs of measures can be arbitrarily divergent. The examples in Fig. 2 show that for any pair of measures connected by a dotted line in Fig. 1, there is a graph where one is constant and the other is O(1/n) (or O(1/m)), and vice versa. The same holds for the inverse direction of the solid edges.

Fig. 2.

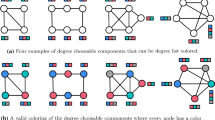
Three colored graphs showing the incomparability of some of the measures of Definition 1. A number indicates a node’s color, unnumbered nodes each receive a color unique to them. For each graph, the second line indicates values of $\epsilon$ for which the graph is (in order) $\epsilon$-disjoint, $\epsilon$-node, $\epsilon$-edge, $\epsilon$-conflict, and $\epsilon$-middle. The arrows between measure values are the same as those of Fig. 1

The property of $\epsilon$-edge and $\epsilon$-disjoint assignments that we shall use is that there is a set of at least $\epsilon m$ edges, each of which is the first edge of a bad path. For $\epsilon$-node or $\epsilon$-conflict assignment, it follows from the definition that there is a set of $\epsilon n$ nodes that have a same-colored node within distance at most k.

3 Preliminaries: Set Disjointness

The Set Disjointness problem is a two-party communication complexity decision problem where two players each receive a subset of an universe [N] and must decide whether their subsets are disjoint. This problem is known to require $\varOmega (N)$ communication – as large as the players’ inputs – to solve with bounded error by a randomized communication complexity protocol  [5, 29, 34]. Doing a reduction from Set Disjointness to a task in the Congest model has been a fruitful source of lower bounds  [1, 9, 10, 21, 27, 36].

In this paper, we will use slight variations of the original Set Disjointness problem. We consider a subset of the original problem, where the players have two additional promises: that their sets are of size at most s, and that their sets’ intersection is either empty or contains at least t elements, where s and t are two integer parameters.

Definition 2 (Gap Bounded Size Set Disjointness)

Let N, s, t be three integers such that $N\ge s \ge t > 0$, $\mathcal X=\mathcal Y=[N]$, and the players’ set of admissible inputs $\mathcal I_{s,t}\subseteq \mathcal X\times \mathcal Y$ be:

$$\begin{aligned} \mathcal I_{s,t}=\left\{ (X,Y):|X| \le s , |Y|\le s , |X \cap Y| \in \{0\}\cup [t,+\infty )\right\} \end{aligned}$$

The Gap Bounded Size Set Disjointness problem $\mathbf {DISJ}^N_{s,t}: \mathcal I_{s,t} \rightarrow \{0,1\}$ is defined as:

$$\mathbf {DISJ}^N_{s,t}(X,Y) = {\left\{ \begin{array}{ll} 1 &{} \text {if }X \cap Y = \emptyset ,\\ 0 &{} \text {otherwise}. \end{array}\right. }$$

The standard Set Disjointness problem corresponds to the choice of parameters $s=N,t=1$. A commonly studied variant bounds the size of the player’s sets but promises nothing about the intersection ($t=1$). This problem is known to have randomized communication complexity $\varTheta (s)$  [26]. Computing the intersection of the two sets also has randomized communication complexity only $\varTheta (s)$  [7]. Leaving the players’ sets unbounded ($s=N$) while keeping the promise on the intersection’s size also appears in the literature, referred to as the Gap Set Disjointness problem  [14, 32]. In both cases, the lower bound is a simple consequence of the lower bound for the standard Set Disjointness problem.

Let us denote by $R_\epsilon (f)$ the randomized communication complexity of a problem f with error at most $\epsilon$.

Lemma 1

For any constant $\epsilon \in (0,1/2)$, $R_{\epsilon }\left( \mathbf {DISJ}^N_{s,t}\right) \in \varOmega \left( \frac{s}{t}\right)$

Proof

Consider the $\mathbf {DISJ}^{N/t}_{s/t,1}$ Set Disjointness problem. This is known to require $\varOmega \left( s/t\right)$ communication as the standard Set Disjointness problem $\mathbf {DISJ}^{s/t}_{s/t,1}$ reduces to it (it is the same problem but on a subset of its input space). Now remark that $\mathbf {DISJ}^{N/t}_{s/t,1}$ reduces to $\mathbf {DISJ}^{N}_{s,t}$, as the players can construct a valid input to $\mathbf {DISJ}^{N}_{s,t}$ from a $\mathbf {DISJ}^{N/t}_{s/t,1}$ input by making t copies of each of their set elements, which concludes the proof.    $\square$

Our lower bounds on testing a distance-3 coloring use the $\mathbf {DISJ}^N_{s,t}$ problem with parameters $s\in \varTheta (m)$ and $t \in \varTheta (\epsilon m)$ (Theorem 3), $s\in \varTheta (m)$ and $t \in \varTheta (\epsilon m)$ (Theorem 4), and $s\in \varTheta (\sqrt{m/\epsilon })$ and $t=1$ (Theorem 5), while our lower bound on testing a distance-4 coloring (Theorem 6) uses parameters $s=m$ and $t=1$. Our lower bound on verifying a distance-k coloring for an arbitrary k (Theorem 7) uses parameters $s\in \varTheta (\varDelta ^{\lfloor (k-1)/2\rfloor })$ and $t=1$. Notice that the complexity of the Set Disjointness problem does not depend on N – the size of the universe – but only on s and t, the sizes of the input sets and their potential intersection.

4 Testing Distance-k Colorings

For all the measures previously introduced (Definition 1), we give upper and lower bounds on detecting being $\epsilon$-far from a solution. Our first result is a protocol for all measures except $\epsilon$-middle, and for any constant k (Theorem 1). This protocol is later shown to be tight for the $\epsilon$-node and $\epsilon$-conflict models, even for $k=3$. In the case $k=3$, we give a more efficient algorithm in the $\epsilon$-middle, $\epsilon$-edge and $\epsilon$-disjoint models (Theorem 2). We prove that the algorithm is optimal for the $\epsilon$-middle measure (Theorem 5) and also prove an non-matching lower bound for the $\epsilon$-far and $\epsilon$-disjoint measures (Theorem 3). For $k=4$, we prove an $\widetilde{\varOmega }(\epsilon ^{-1})$ lower bound in the $\epsilon$-middle model. This last lower bound is strictly higher than the complexity of the same problem when $k=3$, demonstrating that the complexity of the problem can keep increasing as we increase k beyond 3 not just when doing verification, but also property testing.

All the lower bounds use the Set Disjointness problem (Definition 2). For a graphical summary of the results of this section, see Fig. 1.

4.1 A General Algorithm for Any k

We first give an algorithm that works for all values of k and all our farness measures except $\epsilon$-middle. The basic building block of our algorithm is a subroutine has each node assign a random priority to its color, and has them then broadcast colors according to their assigned priorities. This idea of breaking symmetry by assigning random priorities to elements of interest has appeared previously in the literature  [11, 12, 16].

Theorem 1

There exists a randomized Congest algorithm running in $O\left( \frac{1}{\epsilon }\right)$ rounds for testing an $\epsilon$-edge distance-k coloring. By extension this also applies to $\epsilon$-disjoint, and a slight modification yields the same result for $\epsilon$-node and $\epsilon$-conflict.

Proof

Consider the following basic algorithm Bfs that runs for k rounds, which we then repeat to obtain success probability 2/3. The edges are independently assigned a random priority (such as a random value from $[|E|^3]$, with higher values receiving precedence). Nodes use the max of the priorities of their incident edges as their own priority. In the initial round, each node transmits its color (along with its ID) to all its neighbors, along with its priority. In each subsequent round, the algorithm transmits to each neighbor the color and priority of the two highest priority colors it received in the previous round. Effectively, the color from a highest priority node gets forwarded along a breadth-first-search tree. If at the end of round k, the algorithm has received a color (from another node) that matches its own, it outputs ‘invalid’; otherwise, it outputs ‘valid’.

In an $\epsilon$-edge graph, there are at least $\epsilon m$ edges that are the first edge of a bad path. If any of those edges receives the highest priority in a round of the basic algorithm, a color conflict gets detected. So with probability at least $\epsilon$, the basic algorithm detects an $\epsilon$-edge graph.

This basic algorithm is then repeated to increase the success probability to at least 2/3. It suffices to repeat it t times, where t satisfies $(1-\epsilon )^t \le 1/3$. The time complexity is then $t \cdot k$. Setting $t = \ln (3)/\epsilon$ achieves the desired result, yielding an $O(k/\epsilon )$-round algorithm.

We can simplify and adapt this algorithm for the $\epsilon$-conflict model: Each node picks a random priority. There are now $\epsilon n$ improperly colored nodes, and if any of them gets selected, the coloring will be found to be invalid. The rest of the argument is the same.    $\square$

4.2 A Better Running Time for $k=3$

Theorem 2

There exists a randomized Congest algorithm running in $O\left( \frac{1}{\epsilon \cdot \sqrt{\epsilon m}}\right)$ rounds for testing an $\epsilon$-middle distance-3 coloring. By extension, this also applies to the $\epsilon$-edge and $\epsilon$-disjoint measures.

Proof

Let the nodes follow the following simple algorithm Random: in the first round, each node informs its neighbors of its color and identifier, and in $k-2$ subsequent rounds, for each link a node has, it picks uniformly at random one of the (color,ID) pair it received from its neighbors in the previous round and sends it on this link. Any node that receives the same color twice but with a different ID, and such that it received the pairs in two (not necessarily distinct) rounds i and j such that $i+j \le k$, flags the coloring as invalid. This $(k-1)$-rounds protocol is repeated T times. Let us analyze the probability of success of this protocol when $k=3$.

Let $\sigma = 4\sqrt{m/\epsilon }$. We say that an edge uv is good if $\min (d(u),d(v)) \le \sigma$, and bad otherwise. In an $\epsilon$-middle graph, there is a set $\varPi$ of edges, each of which is on a 3-path between same-colored nodes, with $|\varPi |\ge \epsilon m$. Observe that if a, u, v, b is a path where a and b have the same color, then this will be detected if either u forwards the ID of a to v or v forwards the ID of b to u. The probability $\bar{p}_{P_e}$ of non-detection along a path $P_e$ with middle edge $e=(u,v) \in \varPi$ is therefore $(1-1/d(u))^T \cdot (1-1/d(v))^T\le e^{-T/\min (d(u),d(v))}$. We say that a path $P_e \in \varPi$ is good if e is good. Let $\varPi '\subseteq \varPi$ be the set of good paths. Let B be the set of nodes with degree at least $\sigma$. There are at most $\sqrt{\epsilon m}/2$ nodes in B, as otherwise the total number incidences on nodes in B would exceed 2m. Thus, there are at most $\left( {\begin{array}{c}|B|\\ 2\end{array}}\right) \le \epsilon m/8$ edges with both endpoints in B. Hence, there are at least $5\epsilon m/8$ good paths in $\varPi '$.

The probability that none of those good paths detect a conflict in the color assignment is:

$$\begin{aligned} \prod _{P \in \varPi '} \bar{p}_P \le \exp \left( \frac{-T\cdot |\varPi '|}{\sigma }\right) \le \exp \left( -\frac{5}{32}T\cdot \epsilon ^{3/2}m^{1/2}\right) \end{aligned}$$

Therefore, running the protocol for $T \in O(\epsilon ^{-3/2}m^{-1/2})$ is enough to solve the problem with probability at least 2/3.   $\square$

In particular, this protocol runs in constant time when $\epsilon \in \varOmega (m^{-1/3})$. We give a matching lower bound later in the paper (Theorem 5). This algorithm is also able to detect $\epsilon$-edge and $\epsilon$-disjoint graphs with the same running time because of the relationships that exist between the measures, however the lower bounds we have for these measures are weaker (Theorem 3) and do not match our upper bound.

4.3 Lower Bounds for $k \ge 3$

In this section, we prove lower bounds for the detection of $\epsilon$-disjoint colored graphs (Theorem 3), $\epsilon$-node colored graphs (Theorem 4) and $\epsilon$-middle colored graphs (Theorems 5 and 6) in the Congest model. By the relationships that exist between the separation measures of Definition 1, the lower bound on detecting an $\epsilon$-disjoint coloring also holds for $\epsilon$-edge colorings. Similarly, the lower bound on the detection of $\epsilon$-node colorings also holds for $\epsilon$-conflict colorings.

All lower bounds use the same following classical proof architecture: we take a two-party communication complexity problem f of communication complexity $R^{cc}(f)$, and show that the players can solve an instance f(x, y) of this problem by simulating a Congest algorithm for our testing task on a graph $G_{x,y}$ with color assignment $(c^{x,y}_v)_{v \in V}$. The vertices of $G_{x,y}$ are partitioned into two sets $V_A$ and $V_B$, and the edges are such that the colors and intraconnexions of $V_A$’s vertices only depend on x, and similarly with $V_B$’s vertices and y, while the interconnexions between a vertices of $V_A$ and $V_B$ are fixed and therefore independent of x and y. Let T be the number of rounds of a Congest algorithm for the Congest task, and C the number of edges between vertices of $V_A$ and $V_B$. Simulating the Congest algorithm in the two-party communication complexity model can be done in $T\cdot C \cdot \log (n)$ bits of communication. This last quantity has to exceed $R^{cc}(f)$, which yields that any Congest algorithm for our testing task requires at least $T\ge \frac{R^{cc}(f)}{C \cdot \log (n)}$ rounds.

Theorem 3

For $k\,{\ge }\,3$, testing whether a distance-k coloring is $\epsilon$-disjoint requires $\widetilde{\varOmega }\left( \frac{1}{\epsilon \cdot (\epsilon m)}\right)$ rounds in the Congest model.

Note that this lower bound matches neither our general upper bound (Theorem 1) nor our upper bound for $k=3$ (Theorem 2), leaving open the possibility of more efficient algorithms or stronger lower bounds.

For this lower bound, we consider graphs of the form presented in Fig. 3. We conjecture that our analysis is not tight, and that detecting whether such graphs are $\epsilon$-disjoint actually requires $\widetilde{\varOmega }(\epsilon ^{-3/2}m^{-1/2})$.

Fig. 3.

The graph we use for our lower bound. It consists of 4 layers, with the outer layers having $\left( \frac{1}{2} - \epsilon \right) m$ vertices and the inner layers $\sqrt{2 \epsilon m}$. There only exist edges between adjacent layers, and vertices in layers 1 and 4 have degree 1, while layers 2 and 3 form a biclique. Layers 1 and 2 are randomly connected together by $\left( \frac{1}{2} - \epsilon \right) m$ edges, as are layers 3 and 4.

Proof

Let m be an integer and $\epsilon \in \left[ \frac{1}{m},\frac{1}{2}\right)$. Set $N=m$, $s=\left( \frac{1}{2} - \epsilon \right) m$, $t=2 \epsilon m+3$, and consider an instance of $\mathbf {DISJ}^{N}_{s,t}$: a pair of sets (X, Y), $X,Y \subseteq [m]$. Let us consider the graph $G_{x,y}=(V,E)$ of Fig. 3. Its vertices V are partitioned into four layers $(V_i)_{i\in [4]}$. Let Alice possess the two leftmost layers ($V_A = V_1 \cup V_2$) and Bob possess the two rightmost layers ($V_B = V_3\cup V_4$). The inner layers are of size $|V_2|=|V_3| = \sqrt{2\epsilon m}$ and form a biclique (complete bipartite graph) of $2 \epsilon m$ edges, while the outer layers are of size $|V_1|=|V_4|=\left( \frac{1}{2} - \epsilon \right) m$. Let us first describe how the players color their vertices, before describing how they connect the outer layers to the inner layers.

Let all of Alice’s and Bob’s vertices be initially uncolored. For each element $x \in X\subseteq [m]$, Alice picks an arbitrary uncolored vertex of $V_1$ and colors it with x. Bob does the same with his input set Y and the layer $V_4$. Alice then colors her remaining uncolored vertices with distinct even numbers from $[m+1,2m]$, while Bob colors his remaining uncolored vertices with distinct odd numbers from $[m+1,2m]$.

Then, for each vertex $u\in V_1$, Alice connects it to a single vertex of $V_2$ picked uniformly at random. Bob similarly connects vertices of $V_4$ to vertices of $V_3$.

Let us now analyze the graph we constructed with respect to the Set Disjointness instance we started with. If $X \cap Y=\emptyset$, the way the players assigned colors ensures that the graph received a valid distance-3 coloring. If $|X\cap Y| \ge t$, however, there are t pairs $(u,v) \in V_1 \times V_4$ of distinct vertices that are at distance 3 and received the same color. For each pair, there is a single length-3 path connecting them, and the only way those paths can share an edge is by sharing an edge in $V_2 \times V_3$. Let us prove that with high probability, more than $\epsilon m$ of those paths are edge-disjoint, and therefore the graph is $\epsilon$-disjoint (see Definition 1).

Let S be an $\epsilon m$-sized subset of the $2 \epsilon m$ edges between $V_2$ and $V_3$. The probability that none of those edges are directly connected to two vertices in layers $V_1$ and $V_4$ that received the same color is at most $\left( 1-\frac{|S|}{2 \epsilon m}\right) ^{t} = 2^{-t}$. As there are $\left( {\begin{array}{c}2\epsilon m\\ \epsilon m\end{array}}\right) \le 2^{2 \epsilon m}$ such subsets S, the probability that less than $\epsilon m$ edges of $V_2 \times V_3$ are part of a length-3 path between similarly colored vertices of the outer layers is at most $2^{2\epsilon m - t} \le \frac{1}{8}$ for our choice of t.

Since the graph the players constructed is well-colored when they received disjoint sets, and $\epsilon$-disjoint with probability $\ge$ $7/8$ when they received intersecting sets, the players can solve the Set Disjointness problem with error at most 1/4 by simulating a Congest algorithm to detect an $\epsilon$-disjoint distance-3 coloring that makes an error at most 1/8. Since there are $2\epsilon m$ edges between Alice’s and Bob’s vertices, the number of rounds T of a Congest algorithm detecting an $\epsilon$-disjoint coloring with probability $\ge 7/8$ satisfies:

$$\begin{aligned} T \ge \frac{R^{cc}_{1/4}(\mathbf {DISJ}^m_{m/2,2 \epsilon m})}{2\epsilon m \log (m)} \in \widetilde{\varOmega }\left( \frac{1}{\epsilon \cdot (\epsilon m)}\right) \end{aligned}$$

   $\square$

Note that since a graph that is $\epsilon$-disjoint from a valid solution is also $\epsilon$-edge, the lower bound also applies to testing being $\epsilon$-edge. As corollary, we have that no constant-round algorithm can detect an $\epsilon$-disjoint coloring when $\epsilon \in o(m^{-1/2})$.

Theorem 4

For $k \ge 3$, testing whether a distance-k coloring is $\epsilon$-node requires $\widetilde{\varOmega }\left( \frac{1}{\epsilon }\right)$ rounds in the Congest model.

Fig. 4.

The graph we use for our lower bound for the $\epsilon$-node measure. It consists of two stars of degree $\left( \frac{n}{2} -1 \right)$, linked by their roots.

Proof sketch. We do another reduction from communication complexity, this time using the graph shown in Fig. 4, and Set Disjointness instances with sets of size up to $\varTheta (n)$ and intersection either empty or of size $\varOmega (\epsilon n)$. The lower bound follows from the communication complexity of this type of Set Disjointness instance and the single edge between Alice’s and Bob’s parts of the graph.    $\square$

Note that contrary to our previous theorem for detecting $\epsilon$-disjoint colored graphs (Theorem 3), this lower bound is tight with respect to our first algorithm (Theorem 1).

Theorem 5

For $k = 3$, testing whether a distance-k coloring is $\epsilon$-middle requires $\widetilde{\varOmega }\left( \frac{1}{\epsilon \cdot \sqrt{\epsilon m}}\right)$ rounds in the Congest model.

Note that this lower bound matches our upper bound for $k=3$ (Theorem 2). For this lower bound, we use graphs as depicted in Fig. 5.

Fig. 5.

The graph we use for our lower bound on testing for $\epsilon$-middle colorings (Theorem 5), showing that the algorithm Random is tight for this measure and $k=3$. It consists of a central biclique between two layers of size $\sqrt{\epsilon m}$, and each vertex of these layers is connected to $\sqrt{m/\epsilon }$ leaves in the outer layers.

Proof

Let $m \in \mathbb {N}$ and $\epsilon \in \left[ \frac{1}{m},\frac{1}{2}\right)$. Set $N=s=\frac{1-\epsilon }{2}\sqrt{m/\epsilon }$, $t=1$, and consider an instance of $\mathbf {DISJ}^{N}_{s,t}$: a pair (X, Y) of subsets of [N]. Consider the four layer graph $G_{x,y}=(V,E)$ of Fig. 5. The vertices $V_2$ and $V_3$ of layers 2 and 3 form a biclique. Every vertex of layer 2 is connected to s degree-1 vertices in layer 1, and layers 3 and 4 are similarly connected.

Let Alice possess as $V_A$ the vertices of layers 1 and 2 and Bob possess the rest. For any vertex $v\in V_2$, let $N_1(v) \subseteq V_1$ be the vertices of layer 1 connected to v, and similarly for any vertex $v\in V_3$, consider $N_4(v)$ the vertices of layer 4 connected to v.

For each $v\in V_2$, Alice colors the nodes of $N_1(v)$ with the elements of X as colors (without repetition, leaving uncolored nodes if necessary). Bob does the same with nodes of $N_4(v)$ for each $v \in V_3$. The coloring is then completed without creating any new distance-3 conflict, using odd large colors on Alice’s side and even large colors on Bob’s side.

If the players received disjoint sets, the resulting graph $G_{X,Y}$ is well-colored. If the sets’ intersect, however, the coloring is $\epsilon$-middle, because for each pair of vertices $(u,v) \in V_2 \times V_3$, there exists a pair of vertices $(u',v')\in N_1(u) \times N_4(v)$ that have the same color. Therefore, the players can solve their Set Disjointness instance by simulating a Congest algorithm for detection of $\epsilon$-middle colored graphs. Since $\epsilon m$ edges connect Alice’s and Bob’s parts of the graph, the number of rounds T of a Congest algorithm detecting an $\epsilon$-middle coloring with probability $\ge 2/3$ satisfies:

$$\begin{aligned} T \ge \frac{R^{cc}_{1/3}(\mathbf {DISJ}^N_{\frac{1-\epsilon }{2}\sqrt{m/\epsilon },1})}{\epsilon m \cdot \log (m)} \in \widetilde{\varOmega }\left( \frac{1}{\epsilon \sqrt{\epsilon m}}\right) \end{aligned}$$

   $\square$

Finally, we prove a lower bound on testing a distance-4 coloring in the $\epsilon$-middle model. The lower bound we obtain is strictly higher than our upper bound on the same task with distance-3, which shows that there is a clear gap between distance-3 and distance-4 colorings.

Theorem 6

Testing whether a distance-4 coloring is $\epsilon$-middle requires $\widetilde{\varOmega }\left( \frac{1}{\epsilon }\right)$ rounds in the Congest model.

Fig. 6.

The graph we use for our lower bound on testing for $\epsilon$-middle distance-4 colorings (Theorem 6).

Proof sketch. This lower bound is again proved by a reduction from communication complexity, this time using the graph depicted in Fig. 6, and Set Disjointness instances with sets of size up to $\varTheta (m)$ and no promise on the size of the intersection.    $\square$

5 Conclusion

In this work, we studied the testing and verification of distance-k colorings in the Congest model for $k\ge 3$ and several notions of distance from a valid solution. We showed that the testing of distance-3 colorings admits a significantly more efficient algorithm than distance-4 for one of our measures ($\epsilon$-middle), and gave indications that it might also be the case for the other edge- and path-based measures. The node-based measures show no such gap. Our work does not give a full picture how the complexity of the problem evolves as k increases in the edge- and path-based models. A first open question is finding the exact complexity of testing in the $\epsilon$-disjoint and $\epsilon$-edge model: we conjecture that this complexity matches that of our algorithm for these models, rather than that of our lower bound or something intermediate.

Another open question is what algorithm we can design in the $\epsilon$-middle model for arbitrary k, as the Bfs algorithm does not function in it. Even tackling the case $k=4$ is of interest, potentially to match our lower bound. Finally, the several measures we introduced to study this problem might be of independent interest. Are there other problems for which the same measures would make sense? A natural candidate here is testing edge-colorings.

A Verifying Distance-k Colorings in Bounded-Degree Graphs

1.1 A.1 A matching lower bound for the natural algorithm

In a graph of maximum degree $\varDelta$, the nodes can learn their distance-$\lceil k / 2 \rceil$ neighborhood in $O\left( \varDelta ^{\lceil k/2\rceil -1}\right)$ rounds in Congest. In particular, an invalid distance-k coloring can be detected with this number of rounds in Congest, since two nodes of distance at most k are both within a distance $\lceil k / 2 \rceil$ of some node. This protocol is actually close to optimal, as our next theorem shows.

Theorem 7

For $k \ge 3$, the verification of a distance-k coloring requires $\widetilde{\varOmega }\left( \varDelta ^{\lceil k/2\rceil -1}\right)$ rounds in the Congest model.

Fig. 7.

The graph we use for our lower bound. It consists of 2 complete $(\varDelta -1)$-ary trees of depth $\lceil k/2\rceil -1$ linked at their roots.

Proof sketch. The proof again relies on embedding a Set Disjointness instance in a graph (see Fig. 7). Here, a Set Disjointness instance with sets of size up to $\varTheta (\varDelta -^{\lceil k/2\rceil -1})$ and no promise on the intersection can be embedded, with a single edge connecting Alice’s and Bob’s parts of the graph.