Abstract
Accurate identification of electromechanical oscillations on power systems and determination of its stability condition is a fundamental process in order to carry out an appropriate control action to prevent the partial loss or complete blackout of the system. However, the non-linear characteristics of measured variables often lead to incorrect information about the development of the electromechanical oscillations, making wide-area monitoring a challenging task. In addition, significant amount of information in extra large power systems is produced, which has to be stored on local servers requiring large amounts of central processing unit (CPU) storage. For these reasons, algorithms for Big Data problems in power systems are required and the methods presented on this chapter introduce some potential solutions. In this context, different data-driving methods based on spectral analysis of linear operator are presented for the analysis of electromechanical oscillations from a spatio-temporal perspective. These algorithms have the ability to process spatio-temporal data simultaneously, making possible to characterize inter-area and global oscillations (from 0.1 Hz to 1.0 Hz). To validate the effectiveness of the proposed approaches, two test systems with different structural and generation capacities are analysed: the Mexican Interconnected (MI) system and the initial dynamic model of Continental Europe from ENTSO-E. First, data collected from a transient stability study on the MI system are used to illustrate the ability of data-driving methods to characterize modal oscillations on longitudinal systems; where several inter-area modes produce interactions of different electrical areas. Then, simulation results from the initial dynamic model of ENTSO-E are analysed to characterize the propagation of its global electromechanical modes across Europe, which have been denominated as the North-South and East-West modes with frequencies of approximately 0.15 Hz and 0.25 Hz, respectively. The second analysis include the interconnection of Turkey (TR) to Continental Europe in December 2010, which derived on the grow of size and complexity of the original system having as result a decrease in the frequency value for the East-West mode and the introduction of a third inter-area mode on the system. The chapter concludes comparing the results of the proposed approaches against conventional methods available in the literature.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Interconnections among different electrical power systems (EPS) offers significant technical, economic and environmental advantages. In the same way, energy exchange over distant regions provides flexibility in terms of maintaining the balance between generation and demand as result of the energy transfer condition [1, 2].
On the other hand, despite the advantages offered by these interconnections, there are several technical and economic limitations related to it. Particularly when the energy has to be transferred over long distances (generally over more than 100 km), which in power systems commonly represents spanning over one or more countries [3]. The interconnection of the EPS represents a complex problem for the system operators and is the main cause of low frequency oscillations when negative events such as trip of generation units, load variation or three-phase faults on transmission lines occur [4].
The presence of this type of oscillations, commonly referred as electromechanical oscillations, is a typical problem of interconnected systems around the world [3]. The electromechanical oscillations, which are the responsible of the low frequency oscillations can be classified as: local, inter-area and inter-continental oscillation modes, respectively [4]. These modes are characterized by its frequencies range, the number of participating and the location of generation units involved during the oscillatory process. Local modes oscillate between ~0.8 and 2 Hz and the participating machines are located in the same power station, which can accommodate up to 10 generation units. Inter-area modes range from ~0.25 to 0.7 Hz are characterized by oscillations between large groups of machines, which are located at different defined regions, especially when the interconnection in the system is weak. Intercontinental oscillation modes present a similar pattern as inter-area modes, however, the oscillation frequency is lower (between ~0.1 and 0.2 Hz) and involves large groups of machines during the oscillatory process, which are located on different countries [1, 2].
The effect and behaviour of low-frequency oscillations on interconnected power systems depends on different factors such as size of the areas conforming the interconnected system, the geographic distance between areas, the generation and power transfer capacity between the different areas, the demand of the loads, the synchronous machine type and the network topology. Identification of inter-area oscillations in large power systems represents an extra degree of complexity due to the processing capacity required from classical analysis tools, which are affected by the volume, speed and variety of the input data generated from numerical simulation based on models or monitoring systems [2, 5]. For these reasons, it is necessary to use new alternative approaches for the analysis of large dimensional power systems.
The recent development of wide area monitoring systems (WAMS) has open the opportunity to observe and track variables such as frequency and voltage magnitudes and angles of the voltage and current at strategic locations such as directly on the generation units, relevant loads and EPS compensation [6]. The fast recording (5–120 samples/s) achieved by phasor measurement units (PMUs), which is data including also the time stamp open new opportunities to develop tools for monitoring, analysis and control of electromechanical oscillations on EPS [7, 8]. However, is not straightforward to accomplish these tasks given the challenges related to these devices such as having partial observability of the system, the limitation for the detection and prediction of an instability condition in case of a disturbance and the capacity to process the data correlating the spatio-temporal information contained in the EPS.
The development and improvement of analytical tools [6,7,8] represents a difficult task due to the particular characteristics inherent within these datasets such as volume, variety and speed on which the data is generated, such as computer simulations or real measurement systems. These characteristics vary depending on the order (nodes, generators, among others), of the dynamic model of the EPS, the sampling and simulation time. Furthermore, the volume of data obtained from the measurement recordings varies depending on the number of PMUs placed in the network, as well as the sampling frequency and the window size collected. Therefore, one of the alternatives adopted in recent years to address this issue is the inclusion of data mining and data-driven techniques for evaluation of the security of the EPS, fault detection, as well as monitoring and analysis of electromechanical oscillations [8].
The aforementioned challenges motivate the development of algorithms with potential to process data that consider the spatio-temporal information available in the EPS. The proposed approach should include the ability to process volume, variety and speed within the data in order to capture the dynamic behaviour that occurs during an electromechanical oscillation. Similarly, the proposed methods should provide analytical information to understand the mechanism of propagation of the electromechanical oscillations. Upon this premise, this chapter presents different alternative approaches, to extract relevant modal characteristics of electromechanical oscillations that help to analyse this phenomenon on large interconnected electrical power systems.
2 Dynamic System Analysis Based on the Koopman Operator
The basis of the method referred as dynamic mode decomposition (DMD) is in fact the theory of the Koopman operator, which was introduced in 1931 for the analysis of Hamiltonian systems in discrete time [9]. DMD can be used as one algorithm for finding Koopman modes from spatio-temporal data. Each Koopman mode may be associated to a unique frequency and growth rate and interpreted as a nonlinear generalization of global eigenmodes of a linearized system. Based on the original definition of the Koopman operator in continuous time [10]:
Consider a continuous time dynamic system:
where \( \varvec{x} \in {\mathcal{M}} \) is the state within a manifold \( {\mathcal{M}} \) of dimension \( N \). The Koopman operator \( {\mathbf{\mathcal{K}}} \) is a linear operator of infinite dimension, which operates on all observable functions \( g:{\mathcal{M}} \to {\mathbb{C}} \) such that
it is established that the Koopman operator performs a transformation from the representation in state space that considers a non-linear dynamic of finite dimension, towards the Koopman representation that considers a linear dynamic of infinite dimension.
In this case, the \( f\left( \varvec{*} \right) \) term represents the dynamic of the system and the Koopman operator can be defined as a dynamic system in discrete time [11]. From (1), it can be induced a discrete system given by the flow map \( \varvec{F}:{\mathcal{M}} \to {\mathcal{M}} \) mapping the state \( \varvec{x}\left( {t_{0} } \right) \) to a future time \( \varvec{x}\left( {t_{0} + t} \right) \):
From the previous definition, the dynamic system is induced in discrete time as follows:
where the discrete time vector is defined as \( \varvec{x}_{k} = \varvec{x}\left( {kt} \right) \) and \( \varvec{F} \) represents the flow map in discrete time. The analogue operation for the discrete time Koopman operator \( {\mathbf{\mathcal{K}}} \) for the observable function \( g \) is based in the continuous time Eq. (2) and it is formulated using the following expression:
where \( \varvec{K} \) denote the discrete time Koopman operator. By considering the spectral decomposition of the Koopman operator as an eigenvalue problem it is possible to represent the dynamic solution of the system:
where \( \varvec{\varphi }_{k} \) are the Koopman’s eigenfunctions. Expanding these eigenfunctions \( \varvec{\varphi }_{k} \) based on the solution of the Koopman operator it is possible to represent the evolution of the dynamic of the system through expansion of the nonlinear observable functions \( g \) in terms of \( \varvec{\varphi }_{k} \):
where \( \varvec{v}_{k} \) is the mode kth associated to \( \varvec{\varphi }_{k} \). Considering the eigenvalue problem described on (6), with the definition (7) it is possible to represent the dynamic evolution of the system using the following equation:
This expression represents the solution of the operator \( \varvec{K} \) in terms of the modes \( \varvec{v}_{k} \) and the eigenvalues \( \lambda_{k} \) of the system by means of an infinity sum. The dimensional problem can be tackled with a finite sum of modes that approximate the spectral solution of Koopman.
In the following section, a methodology to approximate a linear Koopman operator using considerations such as the measurements of the system under investigation is provided.
2.1 Schematic Visualization of Finite Dimensional Approximation of the Koopman Operator
To approximate the operator of infinite dimension \( {\mathbf{\mathcal{K}}} \), in [12] is considered one restriction in the group of nonlinear observable functions \( \varvec{g} \) in the form of an invariant subspace defined as \( {\mathbb{R}}^{N} \), which includes eigenfunctions of the Koopman operator \( \varvec{K} \). With this restriction, the formation of a finite dimension operator \( \varvec{K} \) is induced and also the observation functions in the subspace \( {\mathbb{R}}^{N} \) are mapped.
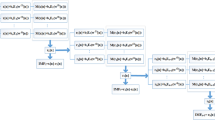
Figure 1a represents the transition of the flow map in state space \( \varvec{x} \) to the flow map of nonlinear observable functions \( \varvec{g} = \left[ {\begin{array}{*{20}c} {g_{1} } & {g_{2} } & {\begin{array}{*{20}c} \ldots & {g_{m} } \\ \end{array} } \\ \end{array} } \right]^{T} \) restricted by a finite subspace \( {\mathbb{R}}^{N} \) through the Koopman operator \( \varvec{K} \). The space \( {\mathbb{R}}^{N} \) can be interpreted as a delineation from which the mapping of the states of the system operate. On the other hand, Fig. 1b represents the sequence of the observation functions mapping \( \varvec{g}\left( {\varvec{x}_{k} } \right) = \varvec{y}_{k} \) conducted by the operator \( \varvec{K} \). In this case, the mapping of the operator \( \varvec{K} \) approximates the original trajectory on a linear space of infinite dimension. The mapping effect of the Koopman operator on dynamic systems has been numerically illustrated at Ref. [12].
Schematic visualization of the Koopman operator mapping in the invariant subspace \( {\mathbb{R}}^{N} \): a represents a linear space of finite dimension on which the operator K acts and b mapping equivalent of the observable functions \( \varvec{y} \) and the states \( \varvec{x} \) [12]
Transition of DMD model approximation to Koopman model [12]
Through this finite dimensional approximation, the DMD method was developed as an alternative to approximate the modes of the Koopman operator \( \varvec{K} \). The following section presents the relationship of the Koopman modal decomposition with the DMD model.
2.2 Dynamic Mode Decomposition (DMD) as Approximation to the Koopman Operator
As introduced on Sect. 2.1, DMD approach only requires the vector measurement of the states of the system, which is defined as \( \varvec{x}_{k} = \left[ {\begin{array}{*{20}c} {x_{1} \left( {t_{k} } \right)} & {x_{2} \left( {t_{k} } \right)} & \ldots & {x_{m} \left( {t_{k} } \right)} \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{m} , k = 1,2, \ldots , N \), to approximate the dynamic of the system by means of the linear operator \( \varvec{A} \in {\mathbb{R}}^{mxm} \):
In (9), the operator \( \varvec{A} \) represents the approximation of the DMD model to the finite dimensional operator \( \varvec{K} \) in discrete time through a noise-free process [13]. The assembling of the DMD model as an approximation to the Koopman model is shown on Fig. 2.
From Fig. 2 it can be observed that the Koopman model is put together from nonlinear observable functions \( \varvec{y}_{k} = g\left( {\varvec{x}_{k} } \right) \), from which the columns of the matrices \( \varvec{Y}_{1}^{N - 1} \) and \( \varvec{Y}_{2}^{N} \) are formed as follows:
where \( N \) is the total number of snapshots and \( m \) is the total number of observations or states respectively.
In this case, the columns of \( \varvec{y}_{k} \) corresponding to the spectral analysis of Koopman represent the transition in the physical space of the mapping to a space of observable functions. Within this space, a representation of the dynamic of the system using (8) can be created. Using this representation, the intrinsic properties of the dynamic of the system represented in (1) are meet. Moreover, the eigenfunctions define a change of coordinates that linearize the system and where the observable functions \( \varvec{y}_{k} \) define a lineal evolution of the characteristic space.
In contrast, the DMD model is developed from direct measurements of the state vector \( \varvec{x}_{k} \), from which the matrices \( \varvec{X}_{1}^{N - 1} \) and \( \varvec{X}_{2}^{N} \) are derived:
The relation between the models deduced with DMD and Koopman is based on the following two criteria:
-
1.
The spectral decomposition of the operator \( \varvec{A} \) through the eigenvalue problem:
$$ \varvec{AW} = \varvec{W}\lambda_{k} $$(14)where \( \lambda_{k} \) and \( \varvec{W} \) represent the eigenvalues and eigenvectors, respectively.
-
2.
From the spectral decomposition of \( \varvec{A} \), the Theorem from [9] is presented:
“Take \( \varphi_{k} \) as the eigenfunctions of \( \varvec{K} \) and eigenvalues \( \lambda_{k} \), and assume \( \varphi_{k} \in span\left\{ {g_{j} } \right\} \), such that
$$ \varphi_{k} \left( \varvec{x} \right) = w_{1} g_{1} \left( \varvec{x} \right) + w_{2} g_{2} \left( \varvec{x} \right) + \cdots + w_{m} g_{m} \left( x \right) $$(15)For some \( \varvec{W} = \left[ {\begin{array}{*{20}c} {w_{1} } & {w_{2} } & {\begin{array}{*{20}c} \ldots & {w_{m} } \\ \end{array} } \\ \end{array} } \right]^{T} \in {\mathbb{C}}^{m} \). If \( \varvec{W} \in R\left( \varvec{X} \right) \), where \( R \) is the rank of the matrix \( \varvec{X} \), then \( \varvec{W} \) is a left eigenvector of the operator \( \varvec{A} \) with eigenvalues \( \lambda_{k} \) such that \( \varvec{W}^{\varvec{*}} \varvec{A} = \lambda_{k} \varvec{W}^{\varvec{*}} \).”
In this case, the associated eigenvectors \( \varvec{W} \) to the operator \( \varvec{A} \) are used to approximate the Koopman eigenfunctions \( \varvec{\varphi }_{k} \) and the eigenvalues \( \lambda_{k} \) represent an approximation to the eigenvalues \( \lambda_{k} \) associated to the operator \( \varvec{K} \) by means of the DMD algorithm.
After the relation between the DMD and the Koopman models have been presented, in the next section the different forms to compute the operator \( \varvec{A} \) and the potential applications of the DMD method are introduced.
2.3 Standard Approximation of the Operator \( \varvec{A} \)
Taking the formulation depicted on [13, 14] as reference, the development of the approximation of the operator DMD in a general form is introduced. From (9) and with the help of the Krylov sequence [15]:
in this case, Eq. (16) shows the succession from \( \varvec{x}_{2} = \varvec{Ax}_{1} \), \( \varvec{x}_{3} = \varvec{Ax}_{2} = \varvec{A}\left( {\varvec{Ax}_{1} } \right) = \varvec{A}^{2} \varvec{x}_{1} \) to \( \varvec{x}_{k} = \varvec{Ax}_{k - 1} \).
This technique is based on Arnoldi’s method [15], which is related to the solution of a polynomial approximation problem. This technique assumes that the polynomial operator is invariant and the system measurements are linearly independent. With a sufficiently large number of snapshots it is considered that the last vector \( \varvec{x}_{N} \) can be represented as a linear combination of the previous snapshots [14], as indicated in the following expression:
From Eq. (19), a more compact form of the expansion of vector \( \varvec{x}_{N} \) by means of the coefficient vector \( \varvec{c} = \left[ {c_{1} c_{2} \ldots c_{N - 1} } \right]^{T} \in {\mathbb{R}}^{N - 1} \) is shown.
The expansion of the sequence \( \varvec{X}_{2}^{N} \) can be represented using the following equation:
and in matrix form using the companion matrix \( \varvec{S} \):
where the structure of the \( \varvec{S} \) matrix is shown in the following expression:
On the other hand, by approximating the sequence \( \varvec{X}_{2}^{N} \) using the operator \( \varvec{A} \) through \( \varvec{X}_{2}^{N} = \varvec{AX}_{1}^{N - 1} \) and taking (22) it can be shown that:
Conversely, two of the approximations for obtaining the companion matrix \( \varvec{S} \) are presented by means of the following algorithms [16]:
-
Pseudoinverse
The solution through pseudoinverse matrix, also known as the Moore–Penrose matrix, is a generalization of the inverse matrix and represents the best approximation of the solution to the mean square error corresponding to the following optimization problem:
The solution to this optimization problem focused on the Companion matrix is given by the following equation:
where \( \dag \) represents the Moore–Penrose matrix. With this expression, an approximation of the operator \( \varvec{A} \) is obtained through the Companion \( \varvec{S} \) matrix in an \( N - 1 \) dimension.
-
Orthogonal Projection Matrix
In this technique, the approximation of operator \( \varvec{A} \) is obtained from a low order model using a reduction technique such as proper orthogonal decomposition (POD). The basis of this technique is the singular value decomposition (SVD).
The SVD decomposition is based on a matrix representation \( \varvec{M} \in {\mathbb{R}}^{mxN} \) using two orthogonal unitary matrices \( \varvec{U} \in {\mathbb{R}}^{Nxm} \) and \( \varvec{V}^{\varvec{*}} \in {\mathbb{R}}^{NxN} \), which are denominated left and right singular vectors respectively, and a diagonal matrix \( \varvec{\varSigma}\in {\mathbb{R}}^{mxm} \), which contains the singular values of the matrix in descending order. It is possible to compute a reduced version of the SVD decomposition using the first \( r \) singular values of \( {\varvec{\Sigma}} \), where the dimension of \( \varvec{U} \), \( \varvec{V}^{\varvec{*}} \) and \( \varvec{\varSigma} \) is reduced to \( \widetilde{\varvec{U}} \in {\mathbb{R}}^{Nxr} \), \( \widetilde{\varvec{V}}^{*} \in {\mathbb{R}}^{rxr} \) and \( \widetilde{\varvec{\varSigma}} \in {\mathbb{R}}^{rxr} \).
From the SVD decomposition of the sequence \( \varvec{X}_{1}^{{\varvec{N} - 1}} \):
The approximation of the sequence \( \varvec{X}_{2}^{\varvec{N}} \) is posed through the operator \( \varvec{A} \) using the following equation:
As mentioned in [14], a representation of \( \varvec{A} \) is obtained in the base covered by the left singular vector’s modes of the sequence \( \varvec{X}_{1}^{{\varvec{N} - 1}} \) by means of the following expression
This approach seeks a reduced representation based on r dominant modes that capture the larger energy content in the dynamic of the system.
3 DMD Based Data-Driving Methods for Simultaneous Processing of Spatio-Temporal Data
Nowadays, the application of data-driven techniques in the modelling and control of physical systems is a field that has evolved rapidly due to the potential to work with measurements, either from historical data, numerical simulations or experimental data [12, 14]. DMD is one of the methods that has the potential to obtain the dynamics of complex and large systems. The DMD method was introduced by Schmid & Sesterhen for the analysis of dynamic fluids and was defined in [14] as a form to decompose complex flows into a representation based on coherent spatio-temporal structures. However, DMD has been widely used for the analysis of nonlinear dynamical systems, such as stock market [17], neuroscience [18], climate phenomena [19], thermodynamic process [20], foreground/background video separation [21] and more.
In the context of power system applications, DMD is one of the most recent post-processing tools for application on power system, where a large volume of data is collected from diverse monitoring systems (WAMS, SCADA, AMI), taking advantage of its ability to process simultaneously spatio-temporal data. Based on the pointed-out ability, DMD has been applied on ring-down modal identification analysis, [13, 22,23,24,25,26] state estimation and prediction and control [27], coherency identification [28,29,30,31], distortion harmonic identification [32], short-term electric load forecasting [33], voltage analysis [34] and various other power system applications [35].
In this chapter a comparison among DMD variants is carried out; its performance is evaluated through various experiments conducted on different power system scenarios with different interconnected system network. The effectiveness of the DMD based method is verified by comparing the results with conventional power system stability methods. The promising results suggest that the some of the DMD approach can be used as an efficient candidate for estimating the power system frequency and amplitude, damping rate, coherency groups identification on large interconnected power systems.
3.1 SVD Based DMD (SVD-DMD)
One form of interpreting the dynamic behaviour of a system can be obtained from the modal decomposition of the \( \widetilde{\varvec{S}} \) operator by taking the orthogonal projection matrix as a basis
where \( {\varvec{\Upsilon}}^{SVD} \) represents the matrix of the left eigenvectors, \( {\varvec{\Upsilon}}^{SVD - 1} \) is the matrix of the right eigenvectors and \( {\varvec{\Lambda}}^{SVD} \) is a diagonal matrix of eigenvectors and are defined by the following expressions:
With the modal decomposition of the operator \( \widetilde{\varvec{S}} \) the analytical solution to the problem of reconstructing data is presented:
where the structure \( {\varvec{\Phi}}^{SVD} \) represents the spatial term of the dynamic of the system and is defined as follows:
and the structure \( {\varvec{\Gamma}}^{SVD} \left( t \right) \) represents the temporal evolution of the modes of the system and is defined as [13]:
Figure 3 shows a schematic representation of the spatio-temporal structure associated to the dynamic of the system through the solution of the data reconstruction problem.
Spatio-temporal modal decomposition structure of data by SVD-DMD
In this case, the spatio-temporal structure shown on Fig. 3 displays the principal components, a spatial component \( \varvec{\phi} \), a temporal component \( \widetilde{\varvec{a}}_{\varvec{k}} \) and a weighting factor \( \lambda \). With these three components, the associated characteristics of the spatio-temporal structure of the dynamic of the system can be identified.
Identification of frequency and damping associate to mode \( \varvec{\phi}_{j}^{SVD} \) can be represented as follows [13]:
On the other hand, due to the spatial structure of the dynamic of the system associated to the modes of the system defined as \( \varvec{\phi}_{j}^{SVD} \) a participation factor related to each mode at instant \( t_{0} \) can be calculated using the normalized magnitude of each mode \( \left\| {\varvec{\phi}_{j}^{SVD} } \right\| \). Similarly, the existing groups can be visualized with a similar dynamic behaviour using the phase \( \angle\varvec{\phi}_{j}^{SVD} \).
One form of visualizing the participation factors for each state of the system is through the time structure associated with the expression (35). When the energy resulting from each temporal term defined on Eq. (38) is considered
the relation mode-state is defined as in the Ref. [13]:
where the term \( \alpha_{ij}^{SVD} \) is a measure of the participation factor of mode \( \varvec{\phi}_{j}^{SVD} \) in the states of the system.
It is important to note that the use of each variant depends on the characteristics of the dataset \( \varvec{X} \), whether \( m < N \) or \( m > N \), since the matrix structure in each case will be different. One of the application approaches to the \( \widetilde{\varvec{S}} \) variant allows a compact representation in the sense of the use of a certain amount of singular values, unlike the Companion \( \varvec{S} \) matrix, which focus its approximation on the number of available snapshots.
In the same way, in the modal identification approach, by means of the operator \( \widetilde{\varvec{S}} \) the modal analysis is based on the selection of the \( r \) singular values with the largest energy content considered in the SVD decomposition. In this case a full range matrix is assumed, i.e. \( r = m \); on the other hand, the operator \( \varvec{S} \) considers \( N - 1 \) modal components. This part represents an advantage in the selection and display of a certain number of modal components for on-line applications.
Recently, one of the trends in the search for a solution to the problem of calculating the approximation to operator \( \varvec{A} \) based on (15) is through the use of optimization methodologies. This approach aims to improve the extraction of the dominant modal characteristics associated with the dynamics of the system. Several DMD algorithms have been developed with the inclusion of optimization methodologies applied to different fields of knowledge, with different analysis approaches and different objectives. In the following section seven approximations to the operator \( \varvec{A} \) based on optimization methodologies are presented.
As discussed before, the conventional approaches for approximating the operator \( \varvec{A} \) are mainly based on a polynomial variant \( \varvec{S} \) and a reduced variant \( \widetilde{\varvec{S}} \), which is stablished on an orthogonal projection. From these matrices, several works have been developed on diverse applications and proposing DMD algorithms with optimization methodologies that have converge to different results [36,37,38].
In the following sections, three methodologies based on optimization within the DMD method are presented. The analytical solution to the data reconstruction problem of each methodology is presented, and as an additional point, the mathematical formulation to obtain the characteristics of frequency, damping, mode shape, modal energy and participation factors in three of the methodologies is presented in the subsequent sections.
3.2 Optimal Mode Decomposition (OMD)
This methodology introduced by Goulart et al. in [36, 39] is a variant of the DMD technique that works with projections in low rank matrices. The mathematical formulation is proposed by means of an objective function that aims to identify a low dimensional subspace in a large dimensional system in which the trajectories of the system are optimally characterized. The formulation of the objective function is expressed by the following formulation:
where the operator OMD \( \varvec{O} \) is defined as \( \varvec{O} = \varvec{LML}^{T} \), matrix \( \varvec{L} \) is a base of Stiefel type is defined as \( \varvec{L} \in {\mathbb{R}}^{rxr} |\varvec{L}^{\varvec{T}} \varvec{ L} = \varvec{I},\varvec{ }r \le m \) and \( r \) is the rank of the matrix, in this case, a full rank is assumed such that \( r = m \). The main objective is to maximize the base \( \varvec{L} \) through the following formulation:
This optimization problem is solved using the ascending gradient-based algorithm described in detail in [39].
Alternatively, the matrix \( \varvec{M} \) represents an approximation of the operator \( \widetilde{\varvec{S}} \) and is dependant of the base \( \varvec{L} \). The assembling of this matrix is based on the solution to the following equation:
This relationship is associated with the development of the optimization problem formulated in [36] where the dependence of the operator \( \varvec{M} \) with the orthogonal base \( \varvec{L} \) and the matrices \( \varvec{X}_{1}^{N - 1} \) y \( \varvec{X}_{2}^{N} \) is stressed. Comparing this approach as an analogue formulation of the DMD method, substituting the base \( \varvec{L} \) with \( \widetilde{\varvec{U}} \) on Eq. (44) and considering the orthogonal characteristics of \( \widetilde{\varvec{U}} \), it can be proved that:
After finding the solution to the optimization problem, the analytic solution to the problem of data reconstruction is presented with the following expression:
Equation (46) can be represented through mode decomposition of the operator \( \varvec{M} =\varvec{\varUpsilon}^{OMD} \widetilde{\varvec{\varLambda}}^{OMD}\varvec{\varUpsilon}^{OMD - 1} \), which result on the following equation:
From Eq. (56) a spatial component can be defined using the mode matrix \( {\varvec{\Phi}}^{OMD} \), which is defined as follows:
Similarly, a temporal component can be defined as \( \varvec{\varGamma}\left( t \right)^{OMD} \) and represents the temporal evolution of the modes, which can be defined as follows:
where the term \( \varvec{a}_{k}^{OMD} \) is defined through the relationship of \( \varvec{a}_{k}^{OMD} = \varvec{L}_{i}^{T} \varvec{x}_{j} \), \( \varvec{L}_{i}^{T} \) represent the columns of \( \varvec{L}^{T} \) and \( \varvec{x}_{\varvec{j}} \) are the rows of \( \varvec{X}_{1}^{N - 1} \).
The variable \( \varvec{\phi}_{j}^{OMD} \) is the participation factor of the jth mode at time \( t_{0} \) through the normalized magnitude of the same mode \( \left\| {\varvec{\phi}_{j}^{OMD} } \right\| \). Similarly, different groups existing in the time series that follow a similar dynamic behaviour can be observed with the phase \( \angle\varvec{\phi}_{j}^{OMD} \). Identification of particular characteristics such as frequency and damping associated to a particular mode \( \varvec{\phi}_{j}^{OMD} \) are defined by means of the following expressions [13]:
On the other hand, if we consider the energy extracted from each temporal term of Eq. (49) by means of the expression:
the relationship mode-state is defined:
where the term \( \alpha_{ij}^{OMD} \) is a measure of the participation factor of mode \( \varvec{\phi}_{j}^{OMD} \) on the states of the system.
3.3 Nuclear Norm Regularised DMD (NNR-DMD)
This methodology, originally presented in Ref. [37], presents a DMD algorithm based on the use of the nuclear norm regularised. The goal of the objective function is to determine a low-rank representation of the \( \widetilde{\varvec{S}} \) matrix that captures the dynamics inherent in the data sequence through the following objective function:
where the constant \( \mu \) represents a penalization term to the nuclear norm \( \left\| \cdot \right\|_{ *} \) in order to introduce a sparse methodology in the objective function.
The purpose of this formulation is to obtain an \( \widetilde{\varvec{S}}^{NNR} \) operator. By introducing the penalization term μ the problem becomes non-restrictive and the solution to the optimization problem is a system of equations obtained using the Split-Bregman method, which is described in detail in [37]. The solution of the S operator \( \widetilde{\varvec{S}}^{NNR} \) is shown below:
where the terms \( \mu \), \( \eta \), \( \varvec{H} \) and \( \varvec{B} \) are products resulting from the Split-Bregman method and the terms \( \widetilde{\varvec{U}} \), \( \widetilde{\varvec{\varSigma}} \) y \( \widetilde{\varvec{V}}^{*} \) are products of the SVD decomposition from Eq. (26). The solution of this iterative method is based on the Split-Bregman algorithm considering two different criteria: maximum number of iterations and an error criterion defined in Ref. [37].
By obtaining the solution to the optimization problem, the analytical solution to the data reconstruction problem is obtained by means of the following expression:
where part of Eq. (57) can be defined as spatial through the modal matrix \( {\varvec{\Phi}}^{NNR} \) defined by the following equation:
and where \( {\varvec{\Upsilon}}^{NNR} \) is calculated from the modal decomposition of the \( \widetilde{\varvec{S}}^{NNR} =\varvec{\varUpsilon}^{NNR} \widetilde{\varvec{\varLambda}}^{NNR}\varvec{\varUpsilon}^{NNR - 1} \) operator and the matrix \( \varvec{\varGamma}\left( t \right)^{NNR} \in {\mathbb{C}}^{mxN - 1} \) represents the temporal evolution of the modes and is defined as follows:
where the term \( \varvec{a}_{k}^{NNR} \) is described as \( \varvec{a}_{k}^{NNR} = \widetilde{\varvec{T}}_{\varvec{j}}^{NNR} \) and the term \( \widetilde{\varvec{T}}_{\varvec{j}}^{NNR} \) corresponds to the rows of the matrix \( \widetilde{\varvec{T}}^{NNR} \). The weight of the temporal structure corresponds to the element \( b_{\varvec{i}} \) of matrix \( \varvec{B}: = diag\left( \varvec{b} \right) \in {\mathbb{R}}^{mxm} \), which represents the weight in descending order of relevance associated to each mode \( \phi_{j}^{NNR} \) and is calculated using the sparse DMD approach. The mode frequency and damping rate is computed as:
On the other hand, the energy extracted from each temporal term is considered by means of the expression:
and the relation mode-state is defined as:
where the term \( \alpha_{ij}^{NNR} \) represents a measure of the participation factor of mode \( \varvec{\phi}_{j}^{NNR} \) on the states of the system.
3.4 Sparse-Promoting DMD (SP-DMD)
In the work developed in [38], a variant of the DMD algorithm is proposed. The alternative approach seeks to compensate the quality of the approximation in the formulation of the sequence of matrices and the number of modes used for the representation of the dynamic of the system. The process is carried out through exponential sequence of eigenvalues and eigenvectors based on a sparse methodology. In this case, the formulation of to the problem is based on finding the modal amplitude vector \( \varvec{b} \) such that weights the modal components in the most optimal form in the objective function \( \varvec{J}\left( \varvec{b} \right) \) described in the following equation:
where the terms \( \varvec{G},\varvec{ q},\varvec{ s} \) are defined by the following equations:
These terms correspond to the development of the problem presented in [38] and are based on the SVD decomposition presented in Eq. (26).
The algorithm for solving Eq. (65) is based on a sparse methodology by formulating a new objective function:
Previous equation represents a convex problem with the aim of finding a vector \( \varvec{b} \) and to determine the components that identify the modes with more influence on the system. The parameter \( \gamma \) has a direct impact on the number of components with a zero value that are obtained in the structure of vector \( \varvec{b} \). Thus, as the value of the parameter γ increases, the amount of zero components increases. The methodology proposes to solve this optimization problem is based on an ADMM method, and is presented in detail in the Ref. [38].
When the solution to the optimization problem is calculated, the analytical solution to the data reconstruction problem is obtained by means of the following expression:
From (70) a spatial term is decoupled using the modal matrix \( {\varvec{\Phi}}^{SP} \) defined in the following equation:
in this case, the modal matrices \( {\varvec{\Phi}}^{SP} = {\varvec{\Phi}}^{POD} \) are equivalent. Matrix \( \varvec{\varGamma}\left( t \right)^{SP} \) represents a temporal structure during the process of reconstructing the signal and is defined as follows:
where the term \( \varvec{a}_{k}^{SP} \) is defined as \( \varvec{a}_{k}^{SP} = \widetilde{\varvec{T}}_{j} \) and \( \widetilde{\varvec{T}}_{j} \) corresponds to the rows of the matrix \( \widetilde{\varvec{T}} \). The weight of this temporal structure corresponds to the element \( b_{\varvec{i}} \) from matrix \( \varvec{B}: = diag\left( \varvec{b} \right) \in {\mathbb{R}}^{mxm} \).
The identification of the frequency and damping characteristics associated to the mode \( \phi_{j}^{SP} \), following expressions (36) and (37), that is \( f_{j}^{SP} = f_{j}^{POD} \) y \( \zeta_{j}^{SP} = \zeta_{j}^{POD} \).
In this case, by considering the energy extracted from each temporal term by the expression:
The relation mode-state is defined:
where the term \( \alpha_{ij}^{SP} \) represents a measure of the degree of participation of \( \varvec{\phi}_{j}^{SP} \) mode in the system states.
3.5 Summary of Different DMD Approaches
Most of the DMD algorithms with optimization presented in this chapter consider the approximation of a low order operator as in the case of \( \widetilde{\varvec{S}} \), with the exception of the Optimal Mode Decomposition (OMD) approach.
In Sects. 3.2 and 3.3 the main objective is the calculation of the approximation to the operator \( \widetilde{\varvec{S}} \) directly. In the case of Sect. 3.4, the main objective is to obtain the vector of the amplitudes that adequately weights the modal components of the system. Different conditions are presented for the solution of the problem associated with the objective function of each section. In Sects. 3.3 and 3.4 regularization and penalty parameters are introduced for the formulation of non-restrictive optimization problems. In Sects. 3.3 and 3.4 a sparse parameter γ is introduced in the solution algorithm to identify the dominant modes of the system. In Sect. 3.3, two dimensionless parameters \( \mu \) and \( \eta \) are introduced which are part of the solution of the optimization problem.
On the other hand, the analytical solution to the problem of reconstructing signals by means of modal components presents a different vision on different sections presented. In the case of the alternatives selected for evaluation, two main components are presented: a parameter associated to the spatial structure, in this case the modal matrix \( {\varvec{\Phi}} \), and a parameter associated to the temporal structure \( \varvec{\varGamma}\left( t \right) \). In Sects. 3.3 and 3.4 the temporal structure \( \varvec{\varGamma}\left( t \right) \) is constructed using the Vandermonde \( \varvec{T} \) matrix and the amplitude matrix \( \varvec{B} \) calculated from the disperse-based method. In Sect. 3.2 the time structure \( {\varvec{\Gamma}}\left( {\text{t}} \right) \) is formulated from the modal decomposition of the operator \( \varvec{M} \) and the base \( \varvec{L} \).
4 Wide Area Monitoring of Inter-area Oscillations Modes in a Longitudinal Interconnected System
The identification of inter-area oscillations presents an extra degree of complexity in large interconnected systems due to the volume and variety of information collected. Conventional tools for stability analysis based on mathematical models are limited by their accuracy and updating of their parameters. Similarly, the algorithms proposed to monitor spatio-temporal data from a wide area monitoring system are limited by the processing capacity of large volume of data. Therefore, it is necessary to propose new alternatives for the analysis of large interconnected electrical systems.
4.1 Description of Mexican Interconnected System
The test system used in this section, approximates the Mexican Interconnected (MI) system, which is distributed in seven electrical areas. The MI system has a longitudinal configuration characterized by long transmission lines and remote generation sources. As a consequence, SVC are the support voltage devices to improve the dynamic stability and voltage considerations. The network configuration requires implementation of several supplementary control schemes to meet the performance requirements. The overall generating capacity in the MIS is about 75.91 GW comprising 22.87 GW to renewable energy and the rest correspond to fossil energy. The bulk transmission system consists of 58,588 km of prevailing 400/230 kV lines, which is complemented by a network of 161 and 69 kV sub-transmission lines. The average demand of the MI system increases annually at a rate of about 7.1%. The MI system is characterized by a longitudinal infrastructure transmission system, supported in long transmission lines that help to import generation from neighbours areas; exciting undamped or poorly damped power oscillations when there are high power transfers from the areas I, II, III and VI, VII systems to areas IV and V. Based on this, the system studies carry out in this research assume that dynamic model of the generators are represented by a two-axis dynamic model, [5, 13] controlled with a simple excitation system. The loads of the system are assumed to be constant and SVCs are modelled to provide voltage support when required due to long transmission lines helping to interconnect all areas in the system. Figure 4 shows a simplified representation of the MI system control areas and illustrates the dynamic interaction of the different electrical areas.
Illustration of slowest electromechanical modes on the MI system [40]
Only 45 major generators distributed along the MI system were considered in this study. The interaction of the different electrical areas is caused by the presence of inter-area modes, which are excited by disturbances on the specific localization of the system [5, 41]. The equivalent of MI system is characterized by three inter-area modes involving the participation of different areas of the system [41].
4.2 Power System Stability Analysis Using Conventional Tools
The scenario for study is a three-phase fault event between the LGV-PBD transmission line located in area V at north-east of the country. This perturbation, stimulates the onset of the three inter-area modes, illustrated in Fig. 4. The dynamic responses are measured at the generator terminals and the angles signals \( \Delta \delta_{i} \) are referenced to generator number 1 and collected. Figure 5 shows the transient responses of the referenced nodal angles \( \varvec{X}_{\Delta \delta } = \left[ {\begin{array}{*{20}c} {\Delta \delta_{1} } & {\Delta \delta_{2} } & \ldots & {\Delta \delta_{41} } & {\Delta \delta_{45} } \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{45x2000} \), corresponding to 20 s of simulation, with an integration step of \( \Delta t_{i} = 0.01 \;{\text{s}} \) and a sampling frequency \( f_{s} = 1/\Delta t_{i} \) of 100 Hz. The simulation was performed in Power System Toolbox (PST) open software [42]. From Fig. 5, the presence of inter-area oscillations can be clearly observed. In particular, a slow growing oscillation can be seen, suggesting an unstable condition of the system.
a Dynamic response of the referenced nodal angle signals from 45 generators [42] and b spectral decomposition of the corresponding signals \( \Delta \delta_{i} \) using the FFT
As a first approximation to the identification of the modal components associated with the oscillatory process observed in Fig. 5a; the fast Fourier transform (FFT) is applied to each of the signals \( \Delta \delta_{i} \), to estimate their spectral content. Figure 5b shows the magnitude of each spectral component associated with each signal from \( \Delta \delta_{i} \). Figure 5b shows three dominant frequencies obtained by the FFT: 0.39 Hz, 0.58 Hz and 0.782 Hz, respectively. The frequency components with the largest magnitude of the FFT are associated with the frequencies of 0.390 Hz and 0.781 Hz respectively. Generators #11 to 45 present a dominant frequency of 0.390 Hz. On the other hand, generators #1 to #10, #13 to #26 and #35 to #40 present a dominant frequency of 0.781 Hz. The results depicted on Fig. 5b suggest the presence of different coherent generators groups during the oscillatory process.
To gain more insight about the oscillation development on the MI system, a small signal stability analysis (SSSA) is performed. Figure 5b presents the frequency of the inter-area modes and their damping ratio coefficients resulted from the analysis.
From Fig. 5b, three modes of interest (0.385, 0.560 and 0.729 Hz) can be observed, which are indicated by red rectangular symbols. In particular, it can be seen that the 0.385 Hz mode has a damping coefficient of -0.0060, indicating the presence of an unstable electromechanical mode. The result agrees with the transient response depicted previously on Fig. 5a.
To visualize the separation mechanism and the interaction between electrical areas during an inter-area oscillation, mode shape is calculated using the right eigenvectors obtained from the decomposition by eigenvalues of the state matrix [42]. Figure 7 shows the mode-shape for the 3 modes of interest highlighted on Fig. 6.
Inter-area modes of MI system equivalent
Figures 7 shows the oscillation patterns involving different electrical areas of the system MI system under investigation. Figure 7a shows the oscillation pattern corresponding to the lowest frequency component and the interactions of the electric areas I, II and II against areas III, IV, VI and VII. While Fig. 7b depicts a different oscillation pattern, composed by the interaction of areas VII against IV and VI, respectively, which are located in the southeast of the country. Finally, Fig. 7c displays the interaction of areas IV against the area VI, involving a large number of hydraulic generators.
Mode shape of modes inter-area showing the major coherent groups: a mode shape of 0.385 Hz, b mode shape of 0.560 Hz and c mode shape of 0.729 Hz
Table 1 shows a descriptive synthesis of the inter-area oscillation modes identified in the system according to previous studies.
The three-phase fault in area V excites the three inter-area oscillation modes. Mode #1 is the more complex mode because it involves participation of all electrical areas of the system and presents a dominant participation during the unstable oscillation process. In the following section a complementary analysis is performed using a space-time processing technique that allows to obtain a spectral analysis from the processing of the data collected from the simulation.
4.3 Spectral Analysis Based on SVD-DMD
Now, from the space-time decomposition simulation data given by \( \varvec{X}_{\Delta \delta } \); the SVD-DMD described at Sect. 3.1 is applied. The nature of system behaviour can be found by examining the empirical Ritz values, λ and their associated magnitudes [13, 14]. Figures 9 shows a plot of the empirical Ritz values, λ and their associated energy obtained from the norm of the time-dependent coefficients, \( \left| {\left| {\widetilde{\varvec{a}}_{1}^{SVD} \left( t \right)} \right|} \right| \), in (35).
As seen in Fig. 8a all the empirical Ritz values are on the unit circle \( \lambda_{j} \) ≈ 1.0, indicating that the states of the dynamic system converge to a stable condition. Analysis of the relative energies in Fig. 8b, show that the modes with the largest energy contributions are those with frequencies of 0.384 Hz and 0.718 Hz, which are frequencies associated to the oscillation inter-area modes. The third identified mode with an approximate frequency of 0.515 Hz, represents the last inter-area mode and has a marginal impact during the oscillatory process.
Empirical Ritz values and their associated norms. a Empirical Ritz values estimated by SVD-DMD and b norm of dynamic modes and energy amplitudes associated with SVD-DMD modes
Table 2 compares the modes estimation resulting from the application of SVD-DMD against conventional eigenvalue analysis. The results of modal estimated of frequencies obtained with SVD-DMD are in good agreement with the estimation from SSSA, however SVD-DMD estimation damping ratio are underestimated for mode #27 and #31 respectively.
In both methods, SSSA and SVD-DMD the, mode #1 produces a slow unstable oscillatory condition, while mode #2 and #3 are very well damped.
Clusters of coherent generators can be identified from the spatial signatures of SVD-DMD, contained in the modal vector \( {\Re }\left\{ {\phi_{j}^{SVD} } \right\} \). Figure 9a shows score plot for the three dominant modes obtained using SVD-DMD described at Sect. 3.1. SVD-DMD technique identifies three groups of coherent generators that involve all geographical areas.
Two ways to visualize the inter-area mode interaction: a coherency identification and b factor participation
From (39), a spatial (temporal) contribution factor that measure the contribution of each sensor to each state, can be defined. The strength of spatial contributions from each sensor to the observed data can be characterized and visualized. Figure 9b depicts a 2-D representation of the participation measures in (39) as a function of the sensor locations. Examination of Fig. 9b shows that mode #27 is strongly observable at sensors number #11 to #45, although the sensors #25 to #33 present the highest participation factor in the system. This result has a strong relationship with the result depicted on Fig. 6.
4.4 Computational Effort and Time Window Simulation on Modal Parameter Estimation
Detailed simulations were conducted to assess the computational cost of SVD-DMD analysis for a study using a realistic dataset. Figure 10a shows the CPU time required to characterize the system behaviour for the scenario described before. Figure 10a shows a comparison of the CPU time for SVD-DMD analysis as a function of the size of the observation window. Previous results have illustrated that SVD-DMD is faster that Arnoldi-Koopman analysis for a similar sampling frequency [13, 43].
a CPU time as a function of the sampling window, b time window effect on modal frequency, c time window effect on modal damping ratio estimation
Based on the simulation results, it can be noted that the CPU time required by the SVD-DMD analysis is competitive in comparison with different modal estimation techniques [13]. In general, short time observation windows may degrade the quality of the estimation and result in various numerical problems, which is a common problem among other estimation techniques such as the Koopman mode analysis. Both observations are depicted at Fig. 10b, c respectively.
The following section presents a comparison of variants of the DMD technique in a larger interconnected continental system.
5 Wide-Area Monitoring of Global Oscillations Modes on Interconnected Continental System
As mentioned in previous sections, the presence of inter-area oscillations is a common problem around the world related to the interconnection of large and distant areas. This problem is more evident when groups of generators located on different geographical areas oscillate against each other. The objective in this section is to present a spectral analysis focused on identifying the modal characteristics associated with a disturbance taking place on an interconnected continental power system.
The following section presents a case study based on simulation data of an event in a given region of the European power system.
5.1 Description of the Power System from Continental Europe
The system under investigation is based on the studies carried out in the papers presented in [2, 44]. A representative schematic diagram of the test system is depicted on Fig. 11, where the selected regions are indicated; Spain (ES), Switzerland (CH), Germany (DE), Italy (IT) and Turkey (TK). The aforementioned countries have been selected based on the experience of the analysis described in [2, 44, 45] the level of detail in which these countries have been modelled.
Schematic illustration of ENTSO-E regions of continental Europe considered in this analysis [46]
Table 3 displays the distribution of generation units corresponding to each region.
Additionally, Table 4 shows the distribution of regions associated with each cluster identified in previous works [47].
In this subsection the exposure of the system to a three-phase fault of 100 sample/sec length in the region of France and applied at instant t = 6 s is presented. The fault leads to the disconnection of a 1.4 GW generation unit on its three phases. The simulation was performed in the professional software DIgSILENT PowerFactory 2018 SP1with a sampling frequency fs = 100 Hz according to the recommendation of the IEEE standard for synchrophasor measurements in SEP C37.118.1-2011 [48]. The response of the frequency signals is displayed on Fig. 12.
Frequency responses associate at each region CH, DE, IT, ES and TR to the loss of a large generator of 1.4 GW in France
Figure 12 shows the recording of 70 s of simulation at a frequency of 100 Hz, and it can be observed that the system converges to a new equilibrium point approximately from the instant t = 60 s. By considering the global set of the frequency signal response on each of the selected countries the data matrix \( \varvec{X} = \left[ {\begin{array}{*{20}c} {\varvec{CH}} & {\varvec{DE}} & {\varvec{IT}} & {\varvec{ES}} & {\varvec{TR}} \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{653x7000} \) is assembled. Figure 13 shows more clearly the oscillatory behaviour of the signals in the region of Turkey (TR) against the signals on the other regions. This behaviour in the dynamic response of the frequency signals suggests the presence of low frequency oscillation modes.
Spectral decomposition by FFT of data set \( \varvec{X} \)
5.2 Spectral Analysis Based on FFT Approach
The records from the WAMS system installed in the corresponding region of areas under investigation confirm the presence of two modes, which have frequency range of inter-area oscillation modes. These modes are the result of the power transfers between large geographical distances in continental Europe [2, 44]. Due to the structure of this network, two predominant low frequency global modes between 0.2 Hz (Global Mode #1) and 0.3 Hz (Global Mode #2) exist on the system. The interconnection with Turkey in December 2010 [45] increased the size and complexity of the original system, and as a consequence a new additional mode (Global Mode #3) of 0.15 Hz was incorporated.
As a first approach to identify the frequency components present in the system, the classical FFT tool is used. Figure 13 shows the calculation of the FFT applied to the 653 signals of the \( \varvec{X} \) data set:
Figure 13 illustrates the presence of three main low frequency components, in this case two of them corresponding to Global Modes #1 and #2. Figure 13 represents a first attempt to achieve modal identification on the response of frequency signals corresponding to the countries under analysis.
5.3 Spectral Analysis Based on Variants of DMD
One of the objectives in spectral analysis of PES is the identification of the dominant modes existing in the dynamics of the system. Figure 14 shows the result of the mode identification and their modal energy level calculated using Eqs. (38), (52), (62) and (70).
Dynamic modes and energy amplitudes associated with the DMD variant modes: a SVD-DMD \( \widetilde{E}_{k}^{SVD} \), b NNR-DMD \( \widetilde{E}_{k}^{NNR} \), c OMD \( \widetilde{E}_{k}^{OMD} \) and d SP-DMD \( \widetilde{E}_{k}^{SP} \)
Figure 14 shows the 653 dynamic modes associated with the spatial structure \( m \) of the DMD operator. It can also be noted from the results of the different DMD variants that only a reduced number of them present a significant contribution to the dynamic behaviour of the system. In the case of the approaches OMD and SVD-DMD, approximately 25 modes that have different level of energy are identified. On the other hand, the results corresponding to approaches such as SP-DMD and NNR-DMD identify 20 dominant modes.
The difference between the number of identified modes on the different approaches correspond to the analytical solution of the reconstruction of data. Unlike the SVD-DMD and OMD methods, which have a temporal structure dependent on the modal decomposition of the DMD operator, sparsity-based approaches identify dominant modes in the system and assign a weight equal to zero to the remaining modes. Figure 15 displays the evolution in time of the modes with largest energy content, which have been depicted on Fig. 14.
Comparison of coherency identification DMD variants: a SVD-DMD \( {\varvec{\Gamma}}^{SVD} \left( t \right) \), b NNR-DMD \( {\varvec{\Gamma}}^{NNR} \left( t \right) \), c OMD \( {\varvec{\Gamma}}^{OMD} \left( t \right) \) and d SP-DMD \( {\varvec{\Gamma}}^{SP} \left( t \right) \)
Figure 15 depicts the behaviour of the components \( \widetilde{\varvec{a}}_{k}^{NNR} \left( t \right) \) y \( \widetilde{\varvec{a}}_{k}^{SP} \left( t \right) \), which depend on the Vandermonde matrix \( \widetilde{\varvec{T}} \), while the components \( \widetilde{\varvec{a}}_{k}^{SVD} \left( t \right) \) and \( \widetilde{\varvec{a}}_{k}^{OMD} \left( t \right) \) are dependent of the right eigenvectors as result of the modal decomposition of the operators \( \widetilde{\varvec{S}}^{SVD} \) and \( \varvec{M} \) respectively.
In such a case, modes whose frequencies are approximate the same as Global Modes #2 and #3 are identified. Table 5 shows the mode number and its damping.
With the results presented in Table 5 it is possible to observe the temporal evolution of these modes on Fig. 16.
Comparison of temporal amplitudes associated to dominant dynamic modes (0.15 and 0.39 Hz): a SVD-DMD \( \widetilde{\varvec{a}}_{K}^{SVD} (t) \), b NNR-DMD \( \widetilde{\varvec{a}}_{\varvec{k}}^{NNR} \left( t \right) \), c OMD \( \widetilde{\varvec{a}}_{K}^{OMD} \left( t \right) \) and d SP-DMD \( \widetilde{\varvec{a}}_{k}^{SP} \left( t \right) \)
The temporal evolution of the modes corresponds to the oscillation that dissipates and reaches a new point of equilibrium, as shown in the response of the frequency signals in Fig. 16. In this case, the components \( \widetilde{\varvec{a}}_{k}^{NNR} \left( t \right) \) and \( \widetilde{\varvec{a}}_{k}^{SP} \left( t \right) \) show an oscillation of lower amplitude corresponding to the structure of the Vandermonde matrix, where it is observed that the component corresponding to the frequency of the Global mode of 0. 15 Hz presents an abrupt increase and fast settling. Unlike the components \( \widetilde{\varvec{a}}_{k}^{SVD} \left( t \right) \) and \( \widetilde{\varvec{a}}_{k}^{OMD} \left( t \right) \) that base their response on the modal decomposition of the operators \( \widetilde{\varvec{S}}^{SVD} \) and \( {\mathbf{M}} \), and that their oscillatory response has small amplitude and short oscillation time.
An important parameter in the modal analysis corresponds to the participation factors. Figure 17 shows the influence of the modes at each measurement point by means of the participation factors calculated from each different methodology.
Participation factors that relate the # of sensors and # of modes: a SVD-DMD \( \alpha_{ij}^{SVD} \), b NNR-DMD \( \alpha_{ij}^{NNR} \), c OMD \( \alpha_{ij}^{OMD} \) and d SP-DMD \( \alpha_{ij}^{SP} \)
As depicted on Fig. 17, the most influencing modes on the dynamic behaviour of the system, correspond to the modes identified first on the different variation of the analysis. The most susceptible areas are identified in a sensor range between #1 and #20, corresponding to the region of Switzerland (CH) and between the sensors #460 and #520, corresponding to Spain (ES) and Italy (IT) regions. Moreover, the modes with the largest impact are in a range between #1 and #20. In this case, the SP-DMD and the NNR-DMD restrict the participation factors to a limited number of modes, identifying more clearly the critical areas in the system. The dominant participation factors are located among generators #480 to #510 corresponding to TR.
On the other hand, from the data presented in Table 5; Figs. 18 shows the formation of clusters by grouping the modal components associated with inter-area frequencies by means of the \( {\Re }\left\{\varvec{\phi}\right\} \) structure.
Comparison of coherency identification DMD variants: a SVD-DMD, b NNR-DMD, c OMD \( \left( {\text{t}} \right) \) and d SP-DMD
As shown in Fig. 18, three main clusters are identified: \( c_{1} \), \( c_{2} \) and \( c_{3} \) as shown in Table 5. The distribution of the clusters corresponds to the response of the frequency signals observed in Fig. 18 where it is possible to identify three oscillation groups. In this case, a spatial distribution presenting three oscillation groups in the dynamic behaviour of the system is observed. However, the structure of the \( {\mathbf{M}} \) operator corresponding to the OMD variant presents a different spatial structure due to the searching space within the gradient methodology. The formulation described in the rest of the variants presents a similar structure due to the characteristics of the \( \widetilde{\varvec{S}} \) operator, which depends on the SVD decomposition.
One approach to evaluate the performance of the different algorithms presented here, is the computational time associated to the calculation of the DMD operator and include the reconstruction signal process for each DMD variant. Table 6 shows the processing times for the dataset \( \varvec{X} \).
In this case, the method with the slowest processing time corresponds to the NNR-DMD method that integrates the weighting methodology corresponding to the sparse DMD variant as a solution to the problem of signal reconstruction. The computational time is an important parameter related to the processing capacity that must be considered when analysing large systems. Additionally, with the development of online algorithms the processing time is an important feature for the development of new tools for real-time application.
6 Conclusions
In this chapter, four variants of the DMD method were described. These alternative algorithms are based on a polynomial variant \( \varvec{S} \) and a reduced orthogonal projection matrix \( \widetilde{\varvec{S}} \), that are used to approximate the Koopman operator \( \varvec{A} \). In this form, DMD algorithms with optimization methodologies and their respective application were shown.
It has been demonstrated that the processing time depends mostly on the volume of the dataset under analysis. The variant representing the shortest processing time corresponds to the algorithm SVD-DMD. While the NNR-DMD variant resulted on the slowest algorithm among the others due to the double optimization process that is required.
One of the advantages observed when using a method based on sparsity to assign weights is the clear visualization of dominant components. This means, that the modal amplitude matrix shows only a limited number of components that have the largest effect on the dynamic of the system. This effect can be reflected in the visualization process of the participation factors. Modes that affect sensitive areas on the system are easily identified. However, the parameter γ immerse on the optimization problem must be correctly calibrated.
Participation factors represent a quantitative measure that is used to display the most affected areas on the system, the impact of the dominant modes on the states of the system and their geographical location. It has been observed that as the dimension of the system increase, the identification of these areas becomes more challenging and restrictive, because a smaller number of the dominant modes are visible.
The temporal evolution of the oscillation modes associated with the low frequency components in the system dynamics is an initial approximation within the system dynamics and affects the duration of the transient event. The behaviour resulting from the effect of the Vandermonde matrix, depends on the weighting of the eigenvalues raised to an exponential depending on the number of snapshots considered in the modal analysis, so the oscillatory behaviour depends partly on the location of the identified number of modes. On the other hand, the behaviour observed in the SVD-DMD and OMD variants depends on the modal decomposition of the \( \widetilde{\varvec{S}} \) y \( {\mathbf{M}} \) operators, respectively. In this case, through these variants, the duration of the oscillatory effects associated with characteristic related to the dominant modes can be more easily visualized.
References
Electricity european network of transmission system (2019), https://docstore.entsoe.eu/Documents/Publications/Statistics/Factsheet/entsoe_sfs2018_web.pdf
F. Segundo Sevilla, P. Korba, K. Uhlen, Evaluation of the ENTSO-E initial dynamic model of continental Europe subject to parameter variations, in 2017 IEEE Power and Energy Society Innovative Smart Grid Technologies Conference (ISGT 2017), Arlington, VA, USA (2017)
P. Kundur, Transient stability, Power System Stability and Control (McGraw-Hill Inc., Mexico City, 1993), pp. 827–828
G. Rogers, Power System Oscillations (Kluwer Academic Publishers, New York, 2000)
J.G. Calderón-Guizar, M. Ramirez-González, R. Castellanos-Bustamante, Low frequency oscillations in large power grids, in 2017 IEEE XXIV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Cusco, Perú (2017)
Y. Zhang, Wide-area frequency monitoring network (FNET) architecture and applications. IEEE Trans. Smart Grid 1(2), 159–167 (2010)
J. Thambirajah, E. Barocio, N.F. Thornhill, Comparative review of methods for stability monitoring in electrical power systems and vibrating structures. IET Gener. Transm. Distrib. 4(10), 1086–1103 (2010)
Task Force on Identification of Electromechanical Mode. IEEE Power and Energy Society, NA June 2012 (2012), http://resourcecenter.ieee-pes.org/pes/product/technical-publications/PESTR15. Accessed 01 Marzo 2019
B. Koopman, Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 17(5), 315–318 (1931)
C.W. Rowley, I. Mezic, S. Bagheri, P. Schlatter, D.S. Henningson, Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009)
J.N. Kutz, J.L. Proctor, S.L. Brunton, Applied Koopman theory for partial differential equations and data-driven modeling of spatio-temporal systems. Hindawi Complex. 2018, 1–17 (2018)
N.J. Kutz, S.L. Brunton, B.W. Brunton, J.L. Proctor, Dynamic Mode Decomposition Data-Driven Modeling of Complex Systems (SIAM, Philadelphia, 2016)
E. Barocio, B.C. Pal, N.F. Thornhill, A.R. Messina, A dynamic mode decomposition framework for global power system oscillation analysis. IEEE Trans. Power Syst. 30(6), 2902–2912 (2015)
P.J. Schmid, Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010)
M. Hochbruck, C. Lubich, On Krylov subspace approximations to the matrix exponential operator. SIAM J. Numer. Anal. 24(5), 12–17 (1997)
K.K. Chen, J.H. Tu, C.W. Rowley, Variants of dynamic mode decomposition: boundary conditions, Koopman, and Fourier analysis. J. Nonlinear Sci. 1–28 (2011)
H. Jia-Chen, R. Sukesh, J.L. McCauley, G.H. Gunaratne, Using dynamic mode decomposition to extract cyclic behavior in the stock market. Phys. A: Stat. Mech. Appl. 448, 172–180 (2016)
B.W. Brunton, L. Johnson, J. Ojeman, J. Kutz, Extracting spatial-temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition. J. Neurosci. Methods 258, 1–15 (2016)
F.G. Georg, A. Gottwald, Detecting regime transitions in time series using dynamic mode decomposition. J. Stat. Phys. 1–23 (2019)
T. Grenga, J.F. MacArt, M.E. Mueller, Dynamic mode decomposition of a direct numerical simulation of a turbulent premixed planar jet flame: convergence of the modes. J. Combust. Theory Model. 22(4), 795–811 (2018)
J.N. Kutz, X. Fu, S.L. Brunton, N.B. Erichson, Multi-resolution dynamic mode decomposition for foreground/background separation and object tracking, in IEEE International Conference on Computer Vision Workshop, Santiago, Chile (2015)
N. Mohan, K. Soman, K.S. Sachin, A data-driven approach for estimating power system frequency and amplitude using Dynamic Mode Decomposition, in 2018 International Conference and Utility Exhibition on Green Energy for Sustainable Development (ICUE), Phuket, Tailandia (2018)
S. Mohapatra, T.J. Overbye, Fast modal identification, monitoring, and visualization for large-scale power systems using Dynamic Mode Decomposition, in 2016 Power Systems Computation Conference (PSCC), Genova, Italia (2016)
J.J. Ramos, J.N. Kutz, Dynamic mode decomposition and sparse measurements for characterization and monitoring of power system disturbances. Nonlinear Sci. (2019)
Y. Suski, A. Chakrabortty, Introduction to Koopman mode decomposition for data-based technology of power system nonlinear dynamics. IFAC Pap. OnLine 51(28), 327–332 (2018)
M.A. Hernandez, A.R. Messina, Nonlinear power system analysis using Koopman mode decomposition and perturbation theory. IEEE Trans. Power Syst. 33(5), 5124–5134 (2018)
M. Netto, L. Mili, A robust data-driven koopman kalman filter for power systems dynamic state estimation. IEEE Trans. Power Syst. 33(6), 7228–7237 (2018)
Y. Susuki, I. Mezic, Nonlinear Koopmnan modes and coherency identification of coupled swing dynamics. IEE Trans. Power Syst. 26(4), 1904–1984 (2011)
Y. Susuki, I. Mezic, F. Raak, T. Hikihara, Applied Koopman operator theory for power systems technology. IECE Nonlinear Theory Appl. 7(4), 430–459 (2016)
F. Raak, Y. Susuki, T. Hikihara, Data-driven partitioning of power networks via nonlinear koopman mode analysis. IEEE Trans. Power Syst. 48(30), 1–10 (2015)
M. Netto, Y. Susuki, L. Mili, Data-driven participation factors for nonlinear systems based on koopman mode decomposition. IEEE Control. Syst. Lett. 3(1), 198–203 (2018)
A. Saldaña, E. Barocio, A.R. Messina, J.J. Ramos, R.J. Segundo, G.A. Tinajero, Monitoring harmonic distortion in microgrids using dynamic mode decomposition, in IEEE Power & Energy Society General Meeting, Chicago, IL, USA (2017)
N. Mohan, K.P. Soman, S.S. Kumar, A data-driven strategy for short-term electric load forecasting using dynamic mode decomposition model. Appl. Energy 232(15), 229–244 (2018)
Y. Susuki, K. Sako, Data-based voltage analysis of power systems via delay embedding and extended dynamic mode decomposition. IFAC-Pap. OnLine 51(28), 221–226 (2018)
A. Alassaf, L. Fans, Dynamic mode decomposition in various power system applications, in North American Power Symposium (NAPS), Wichita, KS, USA (2019)
P.J. Goulart, A. Wynn, D. Pearson, Optimal mode decomposition for high dimensional systems, in IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI (2012)
S. Wang, X. Qing, Nuclear norm regularised dynamic mode decomposition. IET Signal. Process. 10(6), 626–632 (2016)
M.R. Jovanović, P.J. Schmid, J.W. Nichols, Sparsity promoting dynamic mode decomposition. Phys. Fluids 26(2), 0234103(1–22) (2014)
A. Wynn, D.S. Pearson, B. Ganapathisubramani, P.J. Goulart, Optimal mode decomposition for unsteady flows. J. Fluid Mech. 773(SN), 473–503 (2013)
Comisión Reguladora de Energía, 17 Diciembre 2019 (2019), https://www.gob.mx/, https://www.gob.mx/cre/documentos/reporte-de-confiabilidad-del-sistema-electrico-nacional-2016-2017. Accessed 17 Diciembre 2019
J. Ayon, E. Barocio, I. Cabrera, R. Betancourt, Identification of coherent areas using a power spectral density algorithm. Electr. Eng. 100(2), 1–11 (2017)
C. Joe, R. Graham, Power system toolbox, version 3.0, Ontario, Canada (1991–2008)
M.A. Hernandez, A.R. Messina, An observability-based approach to extract spatiotemporal patterns from power system Koopman mode analysis. Electr. Power Compon. Syst. 45(4), 355–365 (2016)
A. Semerow, S. Höhn, M. Luther, W. Sattinger, H. Abildgaard, A. Diaz Garcia, G. Giannuzzi, Dynamic study model for the interconnected power system of continental Europe in different simulation tools, in IEEE Eindhoven PowerTech, Eindhoven, Netherlands (2015)
ENTSO-E, Analysis of Continental Europe Inter-Area Oscillations on 1st December 2016 (2017)
European network of transmission system operators for electricity, 5 Junio 2019 (2019), https://docstore.entsoe.eu/Documents/Publications/Statistics/Factsheet/entsoe_sfs2018_web.pdf. Accessed 24 Diciembre 2019
E. Barocio, K. Petr, S. Walter, R. Felix, Segundo, Online coherency identification and stability condition for large interconnected power systems using an unsupervised data mining technique. IET Gener. Transm. Distrib. 13(15), 3323–3333 (2019)
IEEE, Standard for synchrophasor measurements for power systems. Revision of IEEE Std. C37.118–2005 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Barocio, E., Romero, J., Betancourt, R., Korba, P., Sevilla, F.R.S. (2021). Wide-Area Monitoring of Large Power Systems Based on Simultaneous Processing of Spatio-Temporal Data. In: Haes Alhelou, H., Abdelaziz, A.Y., Siano, P. (eds) Wide Area Power Systems Stability, Protection, and Security. Power Systems. Springer, Cham. https://doi.org/10.1007/978-3-030-54275-7_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-54275-7_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-54274-0
Online ISBN: 978-3-030-54275-7
eBook Packages: EnergyEnergy (R0)