Keywords

1 Introduction

In traditional electrical power systems, the generation of electrical energy is in charge of few large-capacity generation plants, basing their operation on synchronous machines, which are dispatched in a coordinated manner to supply all the demand of the system. With the technological advance and to improve the operation of the network, microgrids with distributed generation (DG) resources have been introduced to the system, this mostly at the distribution level to take advantage of the small local generation. The DG’s are mostly renewable generation sources and are of small capacity compared to the traditional plant. DG’s are strategically placed to distribute additional energy near the local load. The integration of the DG’s has been increased due to the advantages it presents, such as the environmental benefit due to the use of mainly renewable energy, allowing the primary network transmission capacity to be released. Besides, losses in transmission and distribution lines are reduced due to its location near the load, thereby improving network efficiency. DGs improve system reliability by reducing dependency on large plants and allowing continuity of service in the event of a failure in the main network.

However, DG presents some disadvantages that should be considered: the availability of the source determines its location; the intermittency of its primary source; power quality problems. Also, DG does not provide inertia to the system and the time constants of DG units are smaller than synchronous generators constants, making the power system weak and less tolerant of disturbances.

Although power systems are designed to be robust and tolerant of contingencies, they can become vulnerable to them, and even more so with the addition of DG. Simple events (i. e. the loss or operation output of an element) can occur up to severe events (as the loss of a group of elements), causing the activation of the system protections and leading to the disconnection and isolation of one or more generators and loads from the rest of the network. The afore is known as unintentional island formation; this, in turn, can lead to a partial or total collapse of the system. In many occasions, to safeguard the integrity of the system against severe disturbance, the disconnection of individual elements is performed to form an independent microgrid which can subsist. This action is known as intentional island formation. Under these conditions, the presence of DG’s enables island operation. The electric islanding phenomenon is one of DG’s main problems.

Unintentional island formation may trigger several problems in the network in terms of stability, security and energy quality. Since, in this scenario, the island may have a power deficit or excess accompanied by the dynamic response of synchronous generators, variations in both voltage and frequency are often found. For these reasons, it is necessary to estimate how generators will be grouped and to evaluate island conditions once the frequency cannot be recovered to operating values. Likewise, an islanding operation can cause risks both for the electricity companies and for consumers since the event that originated the island, may not be detected by the DG and it continues to function and in turn, feeds the event (as in the case of a failure). On the other hand, if generators are out of sync with the main network, the DG’s and the generators can be damaged if a reconnection with the primary system is attempted [1].

In an island condition, it is essential to take control actions to avoid disconnecting generators and subsequently, analyze controlled islanding to improve the performance of the power system after it suffers a severe disturbance. Several methods have been proposed to estimate generators clustering after a disturbance, and they meet its objective. However, some of them, to some extent, have disadvantages that cause estimating the generators clustering and hence controlled islanding become complex when power system topology or some parameters are unknown. The electric island phenomenon has been a subject of study for many years and has been mainly intended for the increase in distributed generation. That is why they have developed techniques for the detection and protection of electric islands. Among these, they are more distinguished in 2 main groups: remote and local methods (see Fig. 1).

Fig. 1
figure 1

Classification of islanding detection techniques

Full size image

The first group are remote techniques that consist of communication systems between elements of the electrical system, as well as connection points with the DG. For this, these techniques require advanced hardware and with it a higher price, which makes it not profitable to implement. In [2] they use distribution feeders as routes where they transmit a coded signal from a substation to the DG to monitor it when the signal is interrupted, they detect the island condition. Other of these techniques are based on the use of monitoring, control and data acquisition systems (SCADA) [3]. Voltage sensors are installed on the DG side and the measurements obtained are transmitted to the network and by monitoring them determine if the DG is connected or in an island condition. Under this same principle, techniques based on the use of PMU have been developed [4] to monitor the angular difference of the voltages between two points where an island can be formed. This difference is derived to obtain the frequency and determine a threshold in normal operation. If this threshold is exceeded, island formation is detected [5].

The second group consists of local techniques divided into two subgroups (see Fig. 1): passive and active methods. Passive methods are based on the monitoring of some network parameters such as frequency, voltage, phase changes, or harmonic distortion at the common connection points (PCC); precisely the point where the electric island can form. In turn, these techniques can be time- or frequency-domain based. Those that stand out in the time domain are those based on over-low voltage and over-low frequency detection [3]. Voltage or frequency are monitored where the island may occur or at the DG connection point. When an island condition occurs, due to power imbalances, the voltage and frequency values vary. Therefore, when these variables exceed a predetermined value, island formation is detected. They are low-cost methods, and generally, the DG’s converters have this protection system.

Likewise, another widely used technique that detects the formation of islands faster than the previous ones is the one based on the measurement of the rate of change of frequency (ROCOF) [6]. This technique uses the derivative of the frequency calculated from the voltage measurements at the susceptible point of island formation; it uses the principle that when a disturbance occurs the value of this derivative changes and when it is an island condition, it increases. Based on this, for each system, an adjustment value of this derivative is assigned in a stable state, and when it exceeds this value, island formation is detected.

Ref. [7] presents a time-domain technique based on the analysis of the ripple content of the voltage at the connection point between the DG, and the network. When an island condition occurs, this content increases considerably due to the commutation of the high inverter frequency. The island formation is determined by utilizing the level of undulation established in a stable state.

Among the most reported techniques in the frequency domain are those that monitor the content of harmonic distortion (THD) [8]. This method calculates the THD from the monitoring of the generator current. It is monitored by calculating an average for each cycle and evaluating the difference between each cycle, defining a threshold limit of difference. When this threshold is exceeded, the generator disconnection is detected, and island formation is recognized. The method is based on the commutation of the DG’s converters: when the DG has disconnected the THD level decreases. In [8], this methodology is used to test the correct operation of wind turbines. However, there are load variations in the system —many of them are non-linear— and affect the THD levels. Therefore, for complex systems, the selection of the threshold setting can become complicated.

Techniques have also been reported that use the wavelet transform to estimate the frequency components of the monitored signals. In [9], authors use local current and voltage measurements and, with the help of the wavelet transform, calculate the rate of change of the power defined in the frequency domain. When a value of change is exceeded, the island is identified.

The other group of local techniques are active methods. These techniques inject signals to change the amplitude, phase or frequency of the current or voltage waveforms in the CCP. When the DG is connected to the system, the injected distortions are absorbed by the power system. When the DG is disconnected, these distortions cause the network protections to activate and detect the island.

The most-reported methods are those based on the measurement of impedance [10]. These methodologies are based on the injection of frequency components into the output current of the DG inverter. The selection of these frequency components is aligned with the system so that it does not affect its THD level. With this modified current and measuring the voltage at the same point, it is possible to calculate the impedance. When an impedance variation is detected, an island operation is determined.

Ref. [11] presents another active technique based on the injection of currents in the dq frame. This technique uses the Park’s transform to refer the triphase signals to the dq reference frame in which \(i_d\) and \(i_q\) currents are injected at a specific frequency. When the power system operates under normal conditions, these currents do not cause effects on the electrical variables. However, when the island separation occurs, these current injections cause a deviation in the system frequency. By monitoring this frequency and determining a threshold, island formation is detected.

An additional methodology used is the active frequency drift technique (AFD) [12]. The injection of currents causes the frequency of the system in CCP to deviate from the established limits for the correct operation of installed protections in the DG. Under the same operating principle, other techniques were developed: the reactive power variation (RPV) is an active technique used for island detection that introduces reactive power variances to generate reactive power mismatches between the load and the inverter output, which in turn generates a frequency deviation from the voltage measured in CCP. Like the previous methodologies, the imbalance of this frequency is monitored, and if it exceeds the established range, the island is detected.

The methodologies mentioned above fulfil the objective of detecting the island formation; however, most of them do it so only at a specific point where the separation of the system is foreseen, or at the connection point of the DG. Besides, many of the techniques only consider the separation of the DG. I. e., they do not take into account the rest of the system, nor the synchronous machines that support the network. Some of the methodologies developed modify some parameters of the network that, if not correctly adjusted, can harm the power system operation and many more require much investment for its implementation. An important point to note about the presented techniques is that they only consider the formation of the island, but not the grouping of it.

Islanding detection in systems with DG penetration is a challenging task. This chapter aims to present a methodology that allows detecting island formation. However, it covers both the estimation of the generator’s clustering and the evaluation of its application on controlled islanding on a power system with distributed generation, using data obtained from phasor measurement units (PMUs) after a severe disturbance.

The chapter is organized as follows. Section 2 recalls some definitions of eigenvalue theory and participation factors. Section 3 presents and explains the method to detect islands. Further, on Sect. 4 the methodology performance is assessed. Finally, the conclusion is presented in Sect. 5.

2 Theoretical Foundation

In this section, some critical issues necessary to understand the proposed methodology will be introduced. In the following subsections, a brief exposition of the topic of eigenvalues and eigenvectors will be made, as well as their sensitivity, in order to reach the necessary foundation of the presented algorithm, which are the participation factors.

2.1 Eigenvalues and Eigenvectors

For a matrix \({\textit{\textbf{A}}}\in \mathcal {M}_n(\mathbb {C})\), the scalar \(\lambda \) is called the characteristic value or eigenvalue of \({\textit{\textbf{A}}}\) if there exists a nonzero vector \({\textit{\textbf{x}}}\) that satisfies the following:

$$\begin{aligned} {\textit{\textbf{A}}} {\textit{\textbf{x}}}_i= \lambda _i {\textit{\textbf{x}}}_i.\end{aligned}$$
(1)

The vector \({\textit{\textbf{x}}}_i\ne 0\in \mathbb {C}^n\) is known as the rigth eigenvector of \({\textit{\textbf{A}}}\) associated with the eigenvalue \( \lambda _i\), for \(i=1,2,\ldots ,n\) [13, 14]. This eigenvector has the form:

(2)

Similarly, the column vector \({\textit{\textbf{y}}}_j\in \mathbb {C}^n\) which satisfies

$$\begin{aligned} {\textit{\textbf{y}}}_j{\textit{\textbf{A}}}= \lambda _j {\textit{\textbf{y}}}_j \quad \text {for }j=1,2,...,n \end{aligned}$$
(3)

is called the left eigenvector of \({\textit{\textbf{A}}}\) associated with the eigenvalue \(\lambda _j\). \({\textit{\textbf{y}}}_j\) has the following form:

(4)

The set of eigenvalues of the matrix \({\textit{\textbf{A}}}\) can be found rearranging (1) as

$$\begin{aligned} ({\textit{\textbf{A}}}- \lambda {\textit{\textbf{I}}}){\textit{\textbf{x}}}=0.\end{aligned}$$
(5)

and solving for \(\lambda \) the polynomial \(\det ({\textit{\textbf{A}}}- \lambda {\textit{\textbf{I}}})=0\).

The left and right eigenvectors corresponding to the different eigenvalues are orthogonal. That is, for \(i\ne j\), we have:

$$\begin{aligned} {\textit{\textbf{y}}}_j {\textit{\textbf{x}}}_i=0.\end{aligned}$$
(6)

However, when the eigenvectors are associated to the same eigenvalue, we have:

$$\begin{aligned} {\textit{\textbf{y}}}_i {\textit{\textbf{x}}}_i=c,\end{aligned}$$
(7)

where c is a nonzero constant. If both eigenvectors are normalized, we have:

$$\begin{aligned} {\textit{\textbf{y}}}_i {\textit{\textbf{x}}}_i=1.\end{aligned}$$
(8)

In terms of matrices, the set of right eigevectors of \( {\textit{\textbf{A}}}\) can be expressed as

(9)

and the set of left eigenvectors as

(10)

Likewise, if \({\textit{\textbf{A}}}\) has distinct eigenvalues \((\lambda _1,\ldots , \lambda _p)\), \(1 \le p \le n\), there exist a matrix

(11)

such that (1) and (8) can be expressed as

$$\begin{aligned} {\textit{\textbf{A}}}{\textit{\textbf{X}}}&=\varvec{\Lambda }{\textit{\textbf{X}}},\end{aligned}$$
(12)
$$\begin{aligned} {\textit{\textbf{Y}}}{\textit{\textbf{X}}}&={\textit{\textbf{I}}}.\end{aligned}$$
(13)

From (12), the matrix \({\textit{\textbf{A}}}\) can be reduced to diagonal form [14] by

$$\begin{aligned} {\textit{\textbf{X}}}^{-1}{\textit{\textbf{A}}}{\textit{\textbf{X}}}=\varvec{\Lambda }.\end{aligned}$$
(14)

Eigenvalues and their respective eigenvectors provide relevant information about the dynamics of the matrix \({\textit{\textbf{A}}}\). I. e., the eigenvector measures the rate of change of the magnitude of the eigenvalues.

2.2 Eigenvalue Sensitivity

Once the eigenvalues and eigenvectors have been defined, the sensitivity of the eigenvalue will be explained briefly, since this is where the analysis of the participation factors is derived, which are the foundation of the work carried out.

The mathematical modelling of the dynamic behaviour of a physical system is referred to as a set of nonlinear differential equations. These equations require to be linearized at an operating point of the system to perform some dynamic studies in particular; obtaining a set of ordinary differential equations. The solution of such equations is governed by the eigenvalues of the system, algebraically related to the system parameters. Any variation in the system parameters will produce changes in the behaviour of the eigenvalues. These changes are dependent on the sensitivity of the eigenvalues to said parameters.

In particular, for an electric power system, the eigenvalues are a function of all the design and control parameters of the power system. A change in any of these parameters affects the performance of the system. Therefore, this will cause a change in the behaviour of the eigenvalue. The change magnitude depends on the sensitivity of the eigenvalues to the parameter. Moreover, it depends on the change of said parameter [15].

The eigenvalue problem associated with a matrix \({\textit{\textbf{A}}}\) is defined by the algebraic equation (1). A differential change in the elements of \({\textit{\textbf{A}}}\) directly generates a change in the eigenvalues.

To explain the sensitivity of the eigenvalues to the system parameters, assume a change in the elements of \({\textit{\textbf{A}}}\). For this, we take the partial derivative of (1) with respect to element \( a_{k,j}\) from \({\textit{\textbf{A}}}\), obtaining:

$$\begin{aligned} \frac{\partial {\textit{\textbf{A}}}}{\partial a_{k,j}}{\textit{\textbf{x}}}_i+ {\textit{\textbf{A}}}\frac{\partial {\textit{\textbf{x}}}_i}{\partial a_{k,j}}= \frac{\partial \lambda _i}{\partial a_{k,j}}{\textit{\textbf{x}}}_i+ \lambda _i\frac{\partial {\textit{\textbf{x}}}_i}{\partial a_{k,j}}.\end{aligned}$$
(15)

Multiplying on the left by \({\textit{\textbf{y}}}_i \) and noting that \({\textit{\textbf{y}}}_i{\textit{\textbf{x}}}_i=1\), (15) is simplified to:

$$\begin{aligned} {\textit{\textbf{y}}}_i\frac{\partial {\textit{\textbf{A}}}}{{\partial a_{k,j}}}{\textit{\textbf{x}}}_i=\frac{\partial _i \lambda }{\partial a_{k,j}}.\end{aligned}$$
(16)

Because

$$\begin{aligned} \frac{\partial {\textit{\textbf{A}}}}{\partial a_{k,j}} = {\left\{ \begin{array}{ll} 1 &{} \text {for the elements in the }k\text {-th row and }j\text {-th column,}\\ 0 &{} \text {otherwise;} \end{array}\right. } \end{aligned}$$
(17)

Eq. (16) can be written as

$$\begin{aligned} \frac{\partial \lambda _i}{\partial a_{k,j}}= y_{i,k} x_{j,i},\end{aligned}$$
(18)

i. e., the sensitivity of the eigenvalue \(\lambda _i\) with respect to the element \(a_{k,j}\) of \( {\textit{\textbf{A}}}\) is equal to the product of the element \(y_{i,k} \) of the left eigenvector and the element \(x_{j,i}\) from the right eigenvector [16].

2.3 Participation Factors

From the sensitivity of an eigenvalue concept, the participation matrix (\({\textit{\textbf{P}}}\in \mathcal {M}_n(\mathbb {C})\)) combines right and left eigenvectors as a measure of association between the variables of a matrix and its eigenvalues. Defined as

(19)

where

(20)

where \(x_{k,i}\) is the k, i-th element of the the matrix \({\textit{\textbf{X}}}\) (the k-th element of the right eigenvector \({\textit{\textbf{x}}}_i\)), and \(y_{i,k}\) is the i, k-th element of the matrix \({\textit{\textbf{Y}}}\) (the k-th element of the left eigenvector \({\textit{\textbf{y}}}_i\)).

The element \(p_{k,i}=x_{k,i}y_{i,k}\) is called a participation factor. If the eigenvectors are normalized, the sum of the participation factors associated with any eigenvalue is 1.

Taking up and analyzing (18), it is observed that the participation factor \(p_{k,i}\) is equal to the sensitivity of the eigenvalue \(\lambda _i\) with respect to the element \(a_{k,k}\) of \({\textit{\textbf{A}}}\).

$$\begin{aligned} p_{k,i}=\frac{\partial \lambda _i}{\partial a_{k,k}}.\end{aligned}$$
(21)

Therefore, the participation factors of \(\lambda _d\) will be all the elements of the diagonal of the sensitivity matrix of \(\lambda _d\); this is generated by calculating \(\partial \lambda _i\) with respect to all the elements of the matrix.

2.4 Covariance Matrix

A covariance matrix concentrates the variances and covariances of a set of variables with respect to the samples. The covariance matrix is widely used for multivariate statistical issues. Let us see in more detail what it is about.

Suppose a data set V of p variables with n samples. The variables are denoted by the set (\(v_1, v_2,\ldots , v_p\)). Therefore this data set can be viewed as a rectangular matrix \({\textit{\textbf{V}}}\in \mathcal {M}_{n,p}(\mathbb {R})\):

(22)

From this, the variance \(\sigma ^2\) of the variable v is defined as the average of the squared differences with respect to its mean, that is:

$$\begin{aligned} \sigma ^2_v=\frac{1}{n}\sum _{i=1}^n{(v_i-\overline{v})}^2.\end{aligned}$$
(23)

Similarly, given two variables v and w the covariance can be defined as:

$$\begin{aligned} \sigma _{vw}=\frac{1}{n}\sum _{i=1}^n{(v_i-\overline{v})(w_i-\overline{w})}.\end{aligned}$$
(24)

where \(\overline{\cdot \phantom {x}}\) denotes here the arithmetic mean of \(\mathbb {R}^n\).

In matrix notation, the covariance matrix \({\textit{\textbf{S}}}\in \mathcal {M}_{p}(\mathbb {R})\) is then expressed as:

(25)

where \(\sigma ^2_i\) is the variance of the variable \(v_i\), and \(\sigma _{ij}\) is the covariance between the variables \(v_i\) and \(v_j\). This matrix is square and symmetric and summarizes the variability of the data and the information related to the linear relationships between the variables. If the covariances are not equal to zero, this indicates that there is a linear relationship between these two variables [17].

3 Estimation Method of Generation Clustering and Islanding Condition in Power System

In this section, each of the steps of the proposed algorithm for the identification of generator clusters and the detection of islanding condition in an electrical power system will be explained in detail through the analysis of participation factors.

This algorithm is implemented in three stages: the first stage consists of data acquisition; the second stage, of data processing; while the last one consists of the calculation of the participation factors, the detection of the islanding condition, and the determination of the grouping of the machines. These stages are presented in the flow diagram shown in Fig. 2.

In the following sections, a detailed description of each of the algorithm stages is presented below.

Fig. 2
figure 2

Stages of the proposed algorithm

Full size image

3.1 First Stage: Data Acquisition

The first stage of the algorithm corresponds to the reading of the input signals as well as their processing. As seen in Fig. 2, this stage, in turn, has two steps: phasor measurement and data window sampling. Let us analyze each one.

3.1.1 Phasor Measurements

To perform transient stability analysis and obtain reliable results, an accurate model of the power system containing the information network connection and parameters of the elements that comprise it is necessary. Currently, having a realistic power system model represents a significant challenge due to constant changes in the network connection, the dynamics of the loads and the complex models of the transmission lines, and even more so today with the connection of DG [18].

The emergence and application of the wide-area measurement systems (WAMS) in power systems has facilitated the monitoring of the stability of the system since it provides information on its dynamics. They also allow monitoring the entire system at the same time, reducing computational time.

WAMS uses devices to collect data; these are known as PMUs. PMUs allow obtaining synchronized measurements at various points of the network, with high precision and speed. Therefore, it can be used for real-time applications. These devices calculate the current and voltage phasors of the location where they are installed and are synchronized with a global time reference, which makes it possible to compare the phasors measured at that point with the other phasors obtained from the PMUs installed in the different locations of the network.

For the present algorithm, the input data is obtained from the PMU devices of the WAMS. These signals come from the PMUs installed in the generation buses or buses above (Fig. 3), this because PMUs can generally be embedded into protection devices. However, as will be seen later, the measurement can be performed on any of the network buses.

Fig. 3
figure 3

Algorithm’s input data

Full size image

Usually, the network state estimation and the detection of events of the power system are based on measurements of voltages and currents in the buses of interest. This mainly to the difficulty of measuring the internal angle of the machines, which would be the most direct measurement of the dynamics of the system. The dynamics of the voltage phasor’s angle at the buses, obtained from the PMUs, represents the dynamics of the machine internal angle in terms of the behaviour that the system will have subjected to a disturbance. In addition to this measurement, there are less noise-contaminated signals [19].

Figure 4 shows the simulation of the voltage phasor angle at the machine terminals and the internal angle of the machine when the power system is subjected to a three-phase failure; Fig. 4a a stable case and Fig. 4b an unstable case are presented. As noted, the angle of the voltage phasor at machine terminals reflects the dynamic behaviour of the machine.

Fig. 4
figure 4

The behaviour of the machine angle (solid lines) and behaviour of the angle of the voltage phasor at machine terminals (dashed lines) in the event of a three-phase fault in the power system. a stable case. b unstable case

Full size image

The input signals are arranged in a vector:

$$\begin{aligned} {\textit{\textbf{s}}}_{\text {in}}=\begin{bmatrix} \delta _{\text {v}1}&\delta _{\text {v}2}&\cdots&\delta _{\text {v}n} \end{bmatrix},\end{aligned}$$
(26)

where \(\delta _{\text {v}i}\) represents the signals measured on the buses and n the number of buses measured. For an initial approach n is the number of generation buses.

Fig. 5
figure 5

Sliding data window

Full size image

3.1.2 Data Window

Once the phasor measurements are read in real-time, using a mobile data window, they are stored in a data matrix \({\textit{\textbf{A}}}\), made up of 32 samples per cycle, with a sampling frequency of 256 Hz, as seen in Fig. 5.

For each data window, a matrix \({\textit{\textbf{A}}}\in \mathcal {M}_{m,n}(\mathbb {R})\) is formed:

$$\begin{aligned} {\textit{\textbf{A}}}=\begin{bmatrix} \delta _{1,1} &{} \delta _{1,2} &{} \cdots &{} \delta _{1,n}\\ \delta _{2,1} &{} \delta _{2,2} &{} \cdots &{} \delta _{1,n}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ \delta _{m,1} &{} \delta _{m,2} &{} \cdots &{} \delta _{m,n} \end{bmatrix} \end{aligned}$$
(27)

consisting of m samples in each data window and n measured buses.

3.2 Second Stage: Data Processing

As mentioned in Sect. 3, the second stage consists of the processing of the data window generated in the previous step. Each of the procedures that comprise it is explained in detail below.

3.2.1 Covariance Matrix

The covariance matrix of the data matrix \({\textit{\textbf{A}}}\) obtained in the previous step is calculated to obtain the most synthesized information on the variability of the data.

The formation of this covariance matrix is crucial since it concentrates the mutual and proper relationship of the input variables, which in this case are the voltage angles of the buses measured. Likewise, a square symmetric matrix is obtained.

Once the measurement matrix is formed from the most recent sliding window, the covariance matrix of \({\textit{\textbf{A}}}\) is obtained, applying (24), from which the matrix \({\textit{\textbf{S}}}\in \mathcal {M}_n(\mathbb {R})\), where n represents the number of buses measured, is obtained:

(28)

This matrix is symmetric since \(\sigma _{ij} = \sigma _{ji}\).

3.2.2 Eigenvector Calculation

With the previous step, a square matrix was obtained, and its eigenvectors can already be calculated. The eigenvalues and eigenvectors of a matrix represent its dynamics since they contain information on the behaviour of the matrix.

To gain insight into (1) and (3) lets note that a matrix \({\textit{\textbf{A}}}\) can increase or decrease the magnitude of both left and right eigenvectors without changing their direction. The eigenvalue represents this rate of change of the magnitude of the eigenvector [20]. Thus, the covariance matrix eigenvalues indicate the variance of the variables in the direction of the eigenvectors.

In this proposed methodology, it is interesting to observe the behaviour of the eigenvalue that generates the maximum change in the eigenvectors. Therefore, the dominant eigenvalue \(\lambda _d\) (defined as the eigenvalue with the maximum magnitude) will be used. \(\lambda _d\) indicates the highest variance in the direction of the dominant eigenvector [21]. This eigenvalue represents the dynamics of the angles of the power system machines, as well as the voltage angles dynamics provided by the PMUs.

Therefore, it is proposed to calculate the eigenvectors according to (1) and (3) associated with the dominant eigenvalue. An important aspect here is that, as mentioned, the covariance matrix is a symmetric positive definite matrix; therefore, the left and right eigenvectors concerning the dominant eigenvalue are the same [14]:

3.3 Third Stage: Calculation of Participation Factors

The next and last step of the proposed algorithm is the calculation of the participation factors to measure the relative participation of the variables of the covariance matrix \({\textit{\textbf{S}}}\) associated with the dominant eigenvalue. Moreover, it is necessary to calculate the eigenvectors associated with the dominant eigenvalue in the previous step.

As we saw in Sect. 2.2 and Sect. 2.3, participation factors can be calculated in two ways: calculating the sensitivity matrix concerning the dominant eigenvalue (21) and taking the values of the diagonal or directly obtaining the eigenvectors of the covariance matrix \({\textit{\textbf{S}}}\) corresponding to \(\lambda _d\) and applying (20).

Taking the eigenvalue problem defined by (1):

$$\begin{aligned} {\textit{\textbf{S}}}{\textit{\textbf{x}}} = \lambda {\textit{\textbf{x}}}.\end{aligned}$$
(29)

Thus,

$$\begin{aligned} \left( {\textit{\textbf{S}}}{\textit{\textbf{x}}}\right) ^T&= \lambda {\textit{\textbf{x}}}^T,\\ {\textit{\textbf{x}}}^T {\textit{\textbf{S}}}^T&= \lambda {\textit{\textbf{x}}}^T.\end{aligned}$$

Since the covariance matrix \({\textit{\textbf{S}}}\in \mathcal {M}_n(\mathbb {R})\) is a symmetric matrix (\({\textit{\textbf{S}}}={\textit{\textbf{S}}}^T\)), then:

$$\begin{aligned} {\textit{\textbf{x}}}^T {\textit{\textbf{S}}} = \lambda {\textit{\textbf{x}}}^T,\end{aligned}$$
(30)

i. e., the right eigenvectors are also left eigenvectors of the covariance matrix \({\textit{\textbf{S}}}\).

Applying (20), and taking into account (30), the participation factors associated to \({\textit{\textbf{x}}}_d\)

$$\begin{aligned} {\textit{\textbf{p}}}_d = \begin{bmatrix} p_{d1} \\ p_{d2} \\ \vdots \\ p_{dn} \end{bmatrix} \end{aligned}$$
(31)

can be calculated as

$$\begin{aligned} p_{di} = x_{di}^2,\end{aligned}$$
(32)

where \({\textit{\textbf{x}}}_d\) is the eigenvector associated to the dominant eigenvalue \(\lambda _d({\textit{\textbf{S}}})\) and n is the number of acquired measurements. The element \(p_{di}\) is related to the participation of the \(\delta _i\) measurement into the system dynamics.

Where d refers to the column of the dominant eigenvector, n is the number of buses measured. As can be seen, each element of this vector corresponds to the participation factor of each of the measured angles (\(\delta _i\)). Therefore, the behaviour of the participation factors could be used to identify the island formation and the grouping mainly of generation buses, when this condition occurs.

The analysis of these participation factors also allows us to identify which machines or buses are the most sensitive concerning the disturbances present in a power system.

By analyzing how the participation factors of each generation bus change, it is possible to observe the grouping of buses that present a similar sensitivity factor, along with the buses with the highest sensitivity tend to separate themselves from the others.

4 Testing and Validation of the Proposed Methodology

This section will evaluate the capacity of the presented method to detect and recognize the grouping of system generators in an electrical island condition. This section presents a brief description of the two test systems used, the tests carried out, and the results obtained at the simulation level.

4.1 Test Systems

This section presents the characteristics of the systems used to carry out the corresponding tests to validate the proposed algorithm. For this, two test systems are modelled and simulated using DIgSILENT PowerFactory simulation software.

4.1.1 First Test System

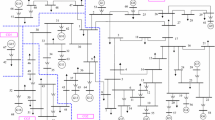
The first test system corresponds to the IEEE 39-bus system, also known as the New England system, consisting of 39 buses, ten synchronous generators, 19 loads with constant impedance, 34 lines and 12 transformers. The generators have AVR controls and governors. Also, each machine has a PSS stabilizer. Ref. [22] presents comprehensive information about the system.

The nominal frequency of the system is 60 Hz, and the voltage level of the network is 345 kV. Figure 6 shows the one-line diagram of this system.

Fig. 6
figure 6

Single-line diagram of the IEEE 39-bus power system

Full size image

4.1.2 Second Test System

The second test system corresponds to Anderson’s 9-bus test system, shown in Fig. 7. The original system consists of 3 synchronous machines with IEEE Type 1 exciters [23]. Generation buses have different voltage values, so they are connected to the system by means of 3 transformers, with a ring of the nominal voltage of 230 kV interconnected by six lines. Detailed data can be found in [24].

This classical 9-bus system was modified replacing the generator connected to bus four by a rural medium-voltage (MV) distribution network: a CIGRE benchmark introduced for DG integration studies (see Fig. 8). This benchmark is a modification from a German MV distribution network [25]. In Fig. 8, it is observed that the MV network is made up of several types of DG sources, so it provides a more realistic picture of DG penetration. The characteristics and parameters of the CIGRE network modelling are detailed in [26,27,28].

Fig. 7
figure 7

Anderson’s 9-bus modified test system

Full size image
Fig. 8
figure 8

Single-line diagram of MV distribution benchmark network

Full size image

The systems presented are those that will use to verify the functionality of the proposed methodology. The following sections show the test cases and the results obtained.

4.2 Tests and Results for the 39-Bus System

In order to evaluate the performance of the algorithm, three simulation scenarios for the first test system are analyzed (Table 1). In each situation, the islands were created by opening switches at a simulation time \(t=2\) s. It is worthy to note for simulation cases that because generator one is taken as a reference; its behaviour will not be so noticeable.

Table 1 Test cases in 39-bus system
Full size table
Table 2 Generator groups for Case 1
Full size table

4.2.1 Case 1

In Case 1, as observed in the Table 1, the formation of two groups was confirmed. That is, an island was formed by disconnecting the line that goes from bus 16 to bus 19, causing two groups of generators to run coherently, as shown in Table 2 and Fig. 9.

The methodology presented in Sect. 3 was applied to obtain and analyze the behaviour of the participation factors. For this case, since the measurements were made only on the generation bus, the method returns a vector with ten elements for each sampling window. Each element of this vector represents the behaviour of each synchronous machine for which the groupings are determined. Graphically, Fig. 10 shows the dynamics of the participation factors. It can be seen that the system is divided into two groups.

Fig. 9
figure 9

Islanding formation: Case 1 (the dotted lines represent the cut necessary to produce the two groups)

Full size image
Fig. 10
figure 10

Dynamics of the participation factors for Case 1

Full size image

As observed in Fig. 10, the dynamic behaviour of the participation factors with respect to time highlights the formation of the two groups or islands. At time \(t=2\) s, when the line is opened, the factors’ dynamics change, indicating a disturbance occurring in the power system. At a time \(t=500\) ms after the disturbance occurred, it is observed how the factors of each group converge to a single value.

Table 3 presents the numerical values of the partition factors at three different times: at time \(t_1=1\) s when the line is still closed; at time \(t_2=2.5\) s when the line had already been disconnected; and at time \(t_3=3\) s when the participation factors had already stabilized.

It is observed how numerically G5 and G4 present similar values at all times. Further, the fact that, before the line is opened, they have similar values, does not determine that they are going to be in the same group as G2 has a similar initial value. The above shows that the algorithm does determine a correct grouping, even though at the beginning, some generators have the same participation factor magnitude. Likewise, as mentioned in Sect. 2.3, the sum of the participation factors at every time instant is equal to 1, as can be corroborated in Table 3.

Table 3 Numerical values of the participation factors over time for Case 1
Full size table
Table 4 Generator groups for Case 2
Full size table

4.2.2 Case 2

For the second test case, the system was divided into three islands accordingly to a previous analysis [29]. However, a modification was made to the predefined grouping for the island of the previous case can be incorporated.

Table 4 shows the generators in each formed group. Additionally, Fig. 11 graphically shows the line openings made for the formation of the islands.

Accordingly, using the proposed methodology the dynamic behaviour of the generator was obtained, as shown in Fig. 12. It is observed that the algorithm detects the formation of the islands and the correct grouping of generators.

Further, Fig. 12 shows the grouping of the generators was readily determined before the 500 ms mark, as the island condition presented. Table 5 shows numerically the results obtained at specific points in time (\(t_1=1\) s, \(t_2=2.5\) s, and \(t_3=3\) s). It is verified numerically how the representative participation factors for each group of generators tend to converge to the same value.

Fig. 11
figure 11

Islanding formation: Case 2 (the dotted lines represent cuts necessary to produce the three groups)

Full size image
Fig. 12
figure 12

Dynamics of the participation factors for Case 2

Full size image
Table 5 Numerical values of the participation factors over time for Case 2
Full size table
Fig. 13
figure 13

Dynamics of the participation factors for Case 3

Full size image

4.2.3 Case 3

The purpose of the third case is to evaluate the performance of the method measuring not just the generation buses of the system. For this case, the same partition configuration was used as in the previous case (Fig. 11). The difference with Case 2 is that the measurements were acquired from the 39 buses of the system. Thirty-nine participation factors were computed (one for each bus). Figure 13 shows the obtained results. It can be seen after the island separation the participation factors display different behaviour than the previous cases. This because, for this case, the covariance matrix has 39 rows and 39 columns, i. e., there are more variables involved, and the covariance between them highlights this behaviour. However, the detection of the grouping was performed approximately 250 ms after the event occurred. After this time, it is seen how each island’s participation factors converge to the same value.

4.3 Tests and Results for the 9-Bus Extended System

In a follow-up with the tests to evaluate the presented method, this section presents the tests performed on the second system. The objective is to analyze the operation of the algorithm when the system has a mix of DG sources, where the majority are unconventional sources. The extensive use of converters for their connection makes the tests more interesting. There are two simulation cases, which are detailed below.

4.3.1 Case 1

For the first simulation scenario, the original 9-bus system is evaluated (Fig. 14). The literature shows that this system can be optimally divided into two islands [29]. In Fig. 15 is observed that the method determines the grouping correctly. Note that the magnitude of the participation factors associated with each generator before the event is in general very different to the magnitude shown after the event. Moreover, the factors associated to generator one and two tends to similar magnitudes. It is also confirmed that the sum of all the factors is equal to one every time instant.

Using measurements at the generators terminals (buses 1–3), the method correctly determines one island consisting of buses 3, 6, and 9; and a second island consisting of buses 1,2,4,5,7, and 8. For this case, a 3-by-3 covariance matrix was obtained at each sampling time.

Fig. 14
figure 14

Island formation for the unmodified Anderson’s 9-bus system (the dotted lines represent the cut necessary to produce the two islands)

Full size image
Fig. 15
figure 15

Dynamics of the participation factors of Case 1 for the 9-bus system

Full size image
Fig. 16
figure 16

Island formation: Case 2 (the dotted lines represent the cut necessary to produce the two islands)

Full size image

4.3.2 Case 2

For this case, the generation grouping of the extended system (including distributed generation sources) shown in Fig. 7 is evaluated.

The objective of this test is to asses how the method’s performance is affected by the presence of DG. For this scenario, bus 4, where the medium voltage network is connected (Fig. 8), is considered for the sake of analysis as a controlled-voltage bus. The system is divided as in the previous case (Fig. 16); however, now the measurements are acquired at the terminals of generators 2 and 3 (buses 2 and 3) and bus 4 (Fig. 16).

Figure 17 shows the behaviour of the participation factors. It can be observed that, as in the previous cases, the method correctly identifies the formation of the island and accurately groups the generation buses. Further, the method performance is not affected by the DGs connected to the system.

Fig. 17
figure 17

Dynamics of the participation factors of Case 2 for the 9-bus extended system

Full size image

As mentioned above, measurements can be acquired either on the generation buses or buses above. For this scenario, a second test was performed where measurements were taken after the transformer, as seen in Fig. 18. Figure 19 shows the dynamic behaviour of the participation factorsfor this measurement arrangement. The method performance is not altered. The grouping of the generation buses was correctly identified.

Fig. 18
figure 18

Island formation: Case 2 measuring data after transformers

Full size image
Fig. 19
figure 19

Dynamics of the participation factors of Case 2 for the 9-bus extended system measuring data after transformers

Full size image

5 Conclusion

Although many of the algorithms proposed in literature detect the formation of an electrical island, they are not capable of distinguishing the grouping dynamics of the generators. Further, many of them require a priori system configuration and analysis. The sweeping change in electrical power systems’ operational paradigm requires algorithms capable of adapting to new generation technologies such as photovoltaic, wind, and battery storage.

A significant challenge of islanding detections methodologies is the ability to detect and estimate the grouping of generators during and after an islanding condition. The analysis of the participation factors proved to be useful to identify the generator’s grouping since it does not need the modelling of the network and adapts to the dynamics of the operation of the power system. Both aggregated and individual DGs are grouped correctly in \(\sim \)250–500 ms. However, work is necessary to real-time track the formed generator’s groups dynamically.

It is worthy to note the advantage of using measurements at generator terminals as well as measurements non-generation buses on the network. This feature allowed the aggregation of DG presented in Fig. 19.