Dynamical Response of a Beam in a Centrifugal Field Using the Finite Element Method

Abstract

In this chapter, we propose a method of analyzing the motion equations in the case of a beam in rotation in plane, in order to determine the domain of instability without actually calculating the eigenvalues or to integrate the obtained equations of motion. This can ease the computational effort needed to solve such a problem. Some examples are studied in the paper.

1 Introduction

The first research in the field of elastic elements with a general rigid motion using numerical methods (especially Finite Element Method) has begun in the 1970s. The first studies were made for a single-beam one-dimensional finite element, using third-degree-shape functions. The complexity of the studied cases increased, and the method was developed for fifth-degree-shape polynomials. The method was used for a plane motion and for the three-dimensional rigid motion of a beam. In all these cases, a one-dimensional finite element was used [1,2,3,4,5]. The first model was a Bernoulli model. Other models, such as the Rayleigh model or Timoshenko model, were studied in [6,7,8,9,10,11]. Thereafter, the researchers developed two-dimensional and three-dimensional finite elements [12,13,14]. The developed models created new theoretical problems related to the methods of solving and qualitative analysis of such equations [15, 16]. To study a mechanical system with elastic elements which also involve a previous dynamical analysis, so we use of MBS (multibody models) models. In this paper, we propose to make a study, for a set of geometrical parameters, if the mechanical system is stable or not, in the case of a beam with a rotation around one of the ends. More elaborated models are made in [17,18,19].

In the study, an analysis is made of the motion equations in the case of a beam in rotation in plane, in order to determine the domain of instability without actually calculating the eigenvalues or to integrate the obtained equations of motion. This problem can be important in the engineering of the multibody with elastic elements.

2 One-Dimensional Finite Element

The problem of the study of a one-dimensional finite element in a centrifugal field was made by many researchers, for a general three-dimensional motion and for a plane motion [12, 14]. In the following, we will use the notation from [4, 5] in order to obtain the motion equations for a single element. We need this approach to apply our proposal concerning the study of such a system. Let’s consider a point M of beam and its displacements [δ(u, v, w)] that can be expressed in terms of nodal displacements at the ends as follows:

$$\left\{ \delta \right\} = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \left[ N \right]\,\left\{ {\delta_{e,L} } \right\} = \left[ N \right]\left\{ {\begin{array}{*{20}c} {\delta_{\_1} } \\ {\delta_{\_2} } \\ \end{array} } \right\}$$

(1)

where we have the vector of nodal displacements {δ_e}:

$$\left\{ {{\varvec{\updelta}}_{e,L} } \right\} = \left\{ {\begin{array}{*{20}c} {{\varvec{\updelta}}_{\_1} } \\ {{\varvec{\updelta}}_{\_2} } \\ \end{array} } \right\} = \left\{ {{\varvec{\updelta}}_{e} } \right\}$$

(2)

where {δ_e} is the displacement vector for e-th finite element in the local coordinate system, δ_{_1} and δ_{_2}, are, respectively, the displacement vectors of the nodes one and two.

Consider a finite element with a rotational motion around an axis. The nodal coordinates: the displacements of the beam ends in the three directions x, y, and z, the torsion angles at the end, the angles of rotation β and γ of the cross section at ends around the two y and z axes, and the curvatures of the neutral axis in the two xOz and xOy planes at both ends. If we consider the two ends, then the displacements at the ends, the rotations, and the curves are [20]:

$$\begin{aligned} \left\{ {f_{1} } \right\} & = \left\{ {\begin{array}{*{20}c} {u_{1} } \\ {v_{1} } \\ {w_{1} } \\ \end{array} } \right\};\quad \left\{ {f_{2} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{2} } \\ {v_{2} } \\ {w_{2} } \\ \end{array} } \right\};\quad \left\{ {\phi_{1} } \right\} = \left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ {\beta_{1} } \\ {\gamma_{1} } \\ \end{array} } \right\};\quad \left\{ {\phi_{2} } \right\} = \left\{ {\begin{array}{*{20}c} {\alpha_{2} } \\ {\beta_{2} } \\ {\gamma_{2} } \\ \end{array} } \right\}; \\ \left\{ {m_{1} } \right\} & = \left\{ {\begin{array}{*{20}c} {m_{xOz1} } \\ {m_{xOy1} } \\ \end{array} } \right\};\quad \left\{ {m_{2} } \right\} = \left\{ {\begin{array}{*{20}c} {m_{xOz2} } \\ {m_{xOy2} } \\ \end{array} } \right\} \\ \end{aligned}$$

(3)

where β₁, γ₁ and β₂, γ₂ are the slopes of the ends of the beam; α₁ and α₂ represent the torsion of the end sections; m_xOz1, m_xOy1 and m_xOz2, m_xOy2 are the curvatures in the corresponding plane.

If v and w are the displacements of a beam point on the directions Oy and Oz, respectively, we shall have the equations known from the continuum mechanics [12]:

$$\beta = - \frac{{{\text{d}}w}}{{{\text{d}}x}}\;{\text{and}}\;\gamma = \frac{{{\text{d}}v}}{{{\text{d}}x}}.$$

(4)

The matrix [N] contains shape functions. The lines of the matrix [N] correspond to the displacements u, v, and w. We have denoted as N(u), N(v), and N(w):

$$\varvec{N} = \left[ {\begin{array}{*{20}c} {N_{\left( u \right)} } \\ {N_{\left( v \right)} } \\ {N_{\left( w \right)} } \\ \end{array} } \right]$$

(5)

The displacements of the nodes at beam ends (left and right ends) have been named {δ_{_1}} and {δ_{_2}}.

For the rotations angles, we have:

$$\left\{ {\begin{array}{*{20}c} \alpha \\ \beta \\ \gamma \\ \end{array} } \right\} = \left[ {N^{*} } \right]\left\{ {\delta_{e} } \right\};\quad \left\{ {\begin{array}{*{20}c} {\dot{\alpha }} \\ {\dot{\beta }} \\ {\dot{\gamma }} \\ \end{array} } \right\} = \left[ {N^{*} } \right]\left\{ {\dot{\delta }_{e} } \right\};$$

(6)

where: $\left[ {N^{*} } \right] = \left[ {\begin{array}{*{20}c} {N_{\left( \alpha \right)}^{*} } \\ {N_{\left( \beta \right)}^{*} } \\ {N_{\left( \gamma \right)}^{*} } \\ \end{array} } \right]$. Can be noted that: $\left[ {N_{\left( \beta \right)}^{*} } \right] = \left[ {N_{w}^{\prime} } \right]$ and $\left[ {N_{\left( \gamma \right)}^{*} } \right] = \left[ {N_{v}^{\prime} } \right]$.

For axial displacements u linear interpolation polynomials are chosen:

$$u = N_{1} u_{1} + N_{2} u_{2}$$

(7)

with:

$$N_{1} = 1 - \xi ;\quad N_{1} = \xi ;\quad {\text{where:}}\;\xi = \frac{x}{L}$$

(8)

Let us consider now the transversal displacements v and w:

$$v = N_{3} v_{1} + N_{5} \gamma_{1} + N_{7} m_{xOz1} + N_{4} v_{2} + N_{6} \gamma_{2} + N_{8} m_{xOz2} ;$$

(9)

$$w = N_{3} w_{1} - N_{5} \beta - N_{7} m_{xOy1} + N_{4} w_{2} - N_{6} \beta_{2} - N_{8} m_{xOy2} ,$$

(10)

The interpolation polynomials will be chosen as:

$$\begin{aligned} N_{3} & = 1 - 10\zeta^{3} + 15\zeta^{4} - 6\zeta^{5} ;\quad N_{4} = 10\zeta^{3} - 15\zeta^{4} + 6\zeta^{5} ; \\ N_{5} & = l\left( {\zeta - 6\zeta^{3} + 8\zeta^{4} - 3\zeta^{5} } \right);\quad N_{6} = l\left( { - 4\zeta^{3} + 7\zeta^{4} - 3\zeta^{5} } \right); \\ N_{7} & = \frac{{l^{2} }}{2}\left( {\zeta^{2} - 3\zeta^{3} + 3\zeta^{4} - \zeta^{5} } \right);\quad N_{8} = \frac{{l^{2} }}{2}\left( {\zeta^{3} - 2\zeta^{4} + \zeta^{5} } \right). \\ \end{aligned}$$

(11)

The shape function matrix is:

$$\begin{aligned} & \left[ {\mathbf{N}} \right] = \left[ {\begin{array}{*{20}c} {N_{\left( u \right)} } \\ {N_{\left( v \right)} } \\ {N_{\left( w \right)} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {N_{1} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {N_{2} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {N_{3} } & 0 & 0 & 0 & {N_{5} } & 0 & 0 & {N_{7} } & 0 & {N_{4} } & 0 & 0 & 0 & {N_{6} } & 0 & 0 & {N_{8} } \\ 0 & 0 & {N_{3} } & 0 & { - N_{5} } & 0 & 0 & { - N_{7} } & 0 & 0 & 0 & {N_{4} } & 0 & { - N_{6} } & 0 & 0 & { - N_{8} } & 0 \\ \end{array} } \right] \\ \end{aligned}$$

(12)

The rotations of the beam ends can be obtained as:

$$\beta = - \frac{\text{d}}{{{\text{d}}x}}\left( {\left[ {N_{w} } \right]\left\{ {\delta_{e} } \right\}} \right) = - \left[ {N_{w}^{\prime} } \right]\left\{ {\delta_{e} } \right\};\quad \gamma = \frac{\text{d}}{{{\text{d}}x}}\left( {\left[ {N_{v} } \right]\left\{ {\delta_{e} } \right\}} \right) = \left[ {N_{v}^{\prime} } \right]\left\{ {\delta_{e} } \right\};$$

(13)

Let’s also note:

$$\begin{aligned} & \left[ {N^{*}} \right] = \left[ {\begin{array}{*{20}c} {N^{*}_{\left( \alpha \right)} } \\ {N^{*}_{\left( \beta \right)} } \\ {N^{*}_{\left( \gamma \right)} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {N_{1} } & 0 & 0 & 0 & 0 & 0 & 0 & {N_{2} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & { - N_{3}^{\prime} } & 0 & {N_{5}^{\prime} } & 0 & {N_{7}^{\prime} } & 0 & 0 & 0 & { - N_{4}^{\prime} } & 0 & {N_{6}^{\prime} } & 0 & {N_{8}^{\prime} } & 0 \\ 0 & {N_{3}^{\prime} } & 0 & 0 & 0 & {N_{5}^{\prime} } & 0 & {N_{7}^{\prime} } & 0 & {N_{4}^{\prime} } & 0 & 0 & 0 & {N_{6}^{\prime} } & 0 & {N_{8}^{\prime} } \\ \end{array} } \right] \\ \end{aligned}$$

(14)

$$\begin{aligned} & \left[ {N^{**}} \right] = \left[ {\begin{array}{*{20}c} {N^{**}_{(z)} } \\ {N^{**}_{(y)} } \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} 0 & 0 & { - N^{\prime\prime}_{3} } & 0 & {N^{\prime\prime}_{5} } & 0 & { - N^{\prime\prime}_{7} } & 0 & 0 & 0 & { - N^{\prime\prime}_{4} } & 0 & {N^{\prime\prime}_{6} } & 0 & { - N^{\prime\prime}_{8} } & 0 \\ 0 & {N^{\prime\prime}_{3} } & 0 & 0 & 0 & {N^{\prime\prime}_{5} } & 0 & {N^{\prime\prime}_{7} } & 0 & {N^{\prime\prime}} & 0 & 0 & 0 & {N^{\prime\prime}_{6} } & 0 & {N^{\prime\prime}} \\ \end{array} } \right] \\ \end{aligned}$$

(15)

So:

$$\left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \alpha \\ \beta \\ \gamma \\ {m_{xOz} } \\ {m_{xOy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} N \\ {N^{*} } \\ {N^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\delta_{1} } \\ {\delta_{2} } \\ \end{array} } \right\}$$

(16)

The internal energy stored in the beam shall be calculated. The internal energy due to bending is given by the relation:

$$\begin{aligned} E_{pi} & = \frac{1}{2}\int\limits_{0}^{L} {\left[ {EI_{y} \left( {\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}} \right)^{2} + EI_{z} \left( {\frac{{{\text{d}}^{2} v}}{{{\text{d}}x^{2} }}} \right)^{2} } \right]{\text{d}}x} \\ & = \frac{1}{2}\int\limits_{0}^{L} {\left[ {EI_{y} \beta^{{{\prime}2}} + EI_{z} \gamma^{{{\prime}2}} } \right]{\text{d}}x} \\ & = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {\int\limits_{0}^{L} {\left( {EI_{y} \left[ {N^{\prime\prime}_{(w)} } \right]^{T} \left[ {N^{\prime\prime}_{(w)} } \right] + EI_{z} \left[ {N^{\prime\prime}_{(v)} } \right]^{T} \left[ {N^{\prime\prime}_{(v)} } \right]} \right){\text{d}}x} } \right]\left\{ {\delta_{e} } \right\} \\ & = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {k_{eb} } \right]\left\{ {\delta_{e} } \right\} \\ \end{aligned}$$

(17)

where E is Young’s modulus, I_y and I_z represent the geometrical moment of inertia around the axis Oy and Oz.

The energy due to the tension/compression is:

$$\begin{aligned} E_{pa} & = \frac{1}{2}\int\limits_{0}^{L} {EA\left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)}^{2} {\text{d}}x = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \int\limits_{0}^{L} {\left( {\left[ {N^{\prime}_{u} } \right]^{T} \left[ {N^{\prime}_{u} } \right]EA{\text{d}}x} \right)} \left\{ {\delta_{e} } \right\} \\ & = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {k_{ea} } \right]\left\{ {\delta_{e} } \right\} \\ \end{aligned}$$

(18)

where A is the area of the cross section of the beam.

The axial load P in an axial section of the beam gives the energy if in a first approximation the axial deformations are neglected:

$$E_{a} = \frac{1}{2}\int\limits_{0}^{L} {P_{\text{tot}} \left[ {\left( {\frac{{{\text{d}}v}}{{{\text{d}}x}}} \right)^{2} + \left( {\frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)^{2} } \right]{\text{d}}x} = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {k_{e}^{G} } \right]\left\{ {\delta_{e} } \right\}$$

(19)

where P_tot represents the axial force in the beam cross section at distance x. The force components acting at the right beam end considered in the local coordinate system are represented by P_x, P_y = 0, P_z = 0. Beside these components, the value of P and the components of the inertia forces acting upon the portion of the beam between x and L are being determined.

The total internal energy is:

$$\begin{aligned} E_{p} & = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left( {\left[ {k_{eb} } \right] + \left[ {k_{ea} } \right] + \left[ {k_{et} } \right] + \left[ {k_{e}^{G} } \right]} \right)\left\{ {\delta_{e} } \right\} \\ & = \frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {k_{e} } \right]\left\{ {\delta_{e} } \right\} \\ \end{aligned}$$

(20)

The external work of distributed loads is:

$$\begin{aligned} W & = \int\limits_{0}^{L} {\left( {p_{x} u + p_{y} v + p_{z} w + m_{x} \alpha + m_{y} \beta + m_{z} \gamma } \right){\text{d}}x} \\ & = \int\limits_{0}^{L} {\left[ {\begin{array}{*{20}c} {p_{x} } & {p_{y} } & {p_{z} } & {m_{x} } & {m_{y} } & {m_{z} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} N \\ {N^{*} } \\ \end{array} } \right]\left\{ {\delta_{e} } \right\}{\text{d}}x} \\ & = \left\{ {q_{eL}^{*} } \right\}^{T} \left\{ {\delta_{e} } \right\}, \\ \end{aligned}$$

(21)

here the vector {q ^*_eL } contains the three components of the distributed loads and the three components of the distributed moments.

The external work of concentrated loads {q_eL} in the nodes is:

$$W^{c} = \left\{ {q_{eL} } \right\}^{T} \left\{ {\delta_{e} } \right\}$$

(22)

After deformation, the position vector of point M becomes M′ and it is expressed by:

$$\left\{ {r_{{M^{\prime},L}} } \right\} = \left\{ {r_{M,L} } \right\} + \left\{ \delta \right\} = \left\{ {r_{M,L} } \right\} + \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \left\{ {r_{o,L} } \right\} + \left\{ {\begin{array}{*{20}c} {x + u} \\ v \\ w \\ \end{array} } \right\},$$

(23)

or, with respect to the global coordinate system:

$$\begin{aligned} \left\{ {r_{{M^{\prime},G}} } \right\} & = \left\{ {r_{M,G} } \right\} + \left[ R \right]\left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \left\{ {r_{o,G} } \right\} + \left[ R \right]\left\{ {\begin{array}{*{20}c} x \\ 0 \\ 0 \\ \end{array} } \right\} + \left[ R \right]\left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} \\ & = \left\{ {r_{o,G} } \right\} + \left[ R \right]\left\{ {\begin{array}{*{20}c} x \\ 0 \\ 0 \\ \end{array} } \right\} + \left[ R \right]\left[ N \right]\left\{ {\delta_{e} } \right\} \\ \end{aligned}$$

(24)

where the matrix [R] expresses the change of the component of a vector from the local coordinate system Oxyz to the fixed (global) reference system O′XYZ. The velocity is obtained by differentiation:

$$v_{M,G} = \dot{r}_{{M^{\prime},G}} = \dot{r}_{o,G} + \dot{R}\left\{ {\begin{array}{*{20}c} x \\ 0 \\ 0 \\ \end{array} } \right\} + \dot{R}N\delta_{e} + RN\dot{\delta }_{e}$$

(25)

The kinetic energy expression is:

$$E_{c} = \frac{1}{2}\int\limits_{0}^{L} {\rho \left( {A\left\{ {\dot{r}_{{M^{\prime},G}} } \right\}^{T} \left\{ {\dot{r}_{{M^{\prime},G}} } \right\} + \left\{ {\omega^{\prime}_{L} } \right\}^{T} \left[ I \right]{\kern 1pt} {\kern 1pt} \left\{ {\omega^{\prime}_{L} } \right\}} \right){\text{d}}x}$$

(26)

where:

$$\left[ {\mathbf{I}} \right] = \left[ {\begin{array}{*{20}c} {I_{x} } & 0 & 0 \\ 0 & {I_{y} } & 0 \\ 0 & 0 & {I_{z} } \\ \end{array} } \right]$$

(27)

I_yy and I_zz represent moments of inertia of the beam cross section about coordinate axis Oy and Oz, respectively, of a reference system with its origin in the mass center of the element dm = ρAdx (ρ-density); I_xx is the inertia moment about the co-ordinate axis Ox. We have chosen y and z as principal directions of inertia I_yz = 0, we have:

$$\left\{ {\omega^{\prime}_{L} } \right\} = \left\{ {\begin{array}{*{20}c} {\omega_{1L} } \\ {\omega_{2L} } \\ {\omega_{3L} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\dot{\alpha }} \\ {\dot{\beta }} \\ {\dot{\gamma }} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\omega_{1L} } \\ {\omega_{2L} } \\ {\omega_{3L} } \\ \end{array} } \right\} + \left[ {N^{*} } \right]\left\{ {\delta_{e} } \right\}$$

(28)

here ω_1L, ω_2L, ω_3L are the components of the vector angular velocity refer to the local coordinate system.

The Lagrangian for one is:

$$L = E_{c} - E_{p} - E_{a} + W + W^{c} .$$

(29)

Applying the Lagrange’s equations [21,22,23,24]:

$$\frac{\text{d}}{{{\text{d}}t}}\left\{ {\frac{\partial L}{{\partial \dot{\delta }_{e} }}} \right\} - \left\{ {\frac{\partial L}{{\partial \delta_{e} }}} \right\} = 0.$$

(30)

the motion equations for a single element in a centrifugal field can be obtained in the form:

$$\begin{aligned} & \left( {\left[ {m_{11} } \right] + \left[ {m_{22} } \right]} \right)\left\{ {\ddot{\delta }_{e} } \right\} + 2\omega \left( {\left[ {m_{21} } \right] - \left[ {m_{12} } \right]} \right)\left\{ {\dot{\delta }_{e} } \right\} \\ & + \left[ {\left[ {k_{e} } \right] + \varepsilon \left( {\left[ {m_{21} } \right] - \left[ {m_{12} } \right]} \right) - \omega_{{}}^{2} \left( {\left[ {m_{11} } \right] + \left( {m_{22} } \right)} \right)} \right] \\ & = \left\{ {q_{e} } \right\} + \left\{ {q_{e}^{*} } \right\} - \left\{ {q_{e}^{i} \left( \varepsilon \right)} \right\} - \left\{ {q_{e}^{i} \left( {\omega^{2} } \right)} \right\} - \left[ {m_{Ee}^{i} } \right]\left[ I \right]\left\{ \varepsilon \right\}_{L} \\ & \quad - \left[ {m_{oe} } \right]\left[ R \right]^{T} \left\{ {\ddot{r}_{o} } \right\} \\ \end{aligned}$$

(31)

where:

$$\begin{aligned} \left[ {m_{oe}^{i} } \right] = \int\limits_{0}^{L} {\rho A\left[ N \right]}^{T} {\text{d}}x;\quad \left[ {m_{Ee}^{i} } \right] = \int\limits_{0}^{L} {\left[ N \right]^{*} } {\text{d}}x; & \quad \left[ {m_{ij} } \right] = \int\limits_{0}^{L} {\left[ {N_{i} } \right]}^{T} \left[ {N_{j} } \right]\rho A{\text{d}}x \\ & i,j = 1, 2, 3\\ \end{aligned}$$

$$\left\{ {q_{e}^{*} } \right\} = \int\limits_{0}^{{_{L} }} {\left[ {\begin{array}{*{20}c} {p_{x} } & {p_{y} } & {p_{z} } & {m_{x} } & {m_{y} } & {m_{z} } \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}c} N \\ {N^{*} } \\ \end{array} } \right\}{\text{d}}x$$

(32)

3 Eigenvalues and Domain of Stability

In the following, it was studied a beam that is in a centrifugal field, following how the eigenvalues of the system change according to the variation of the beam geometrical parameters. Considering a certain number of finite elements in which the structure is discretized, after assembling, the motion equations will be of the form:

$$\left[ M \right]\left\{ {\ddot{\Delta }} \right\} + \left[ C \right]\left\{ {\dot{\Delta }} \right\} + \left[ K \right]\left\{ \Delta \right\} = 0$$

(33)

The matrix [C] is skew-symmetric. If we note:

$$\left\{ X \right\} = \left\{ \Delta \right\};\quad \left\{ Y \right\} = \left\{ {\dot{\Delta }} \right\}$$

(34)

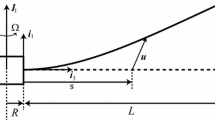
The beam is considered clamped to one end and has a rotation motion around this end with variable angular speed ω.

To perform the calculus, we used the soft MATLAB with its classical subroutines (Figs. 1 and 2).

Fig. 1

Eigen pulsations for a beam with L = 0.55 m (D variable and ω variable)

Fig. 2

Eigen pulsations for a beam with L = 0.55 m and L = 1 m (D variable and ω variable). The first eigenvalue

The motion equations become a linear differential system of the form:

$$\left\{ {\begin{array}{*{20}c} {\dot{X}} \\ {\dot{Y}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & E \\ { - \left[ M \right]^{ - 1} \left[ K \right]} & { - \left[ M \right]^{ - 1} \left[ C \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} X \\ Y \\ \end{array} } \right\}$$

(35)

In a previous paper, it has been shown that the skew-symmetric matrix [C] does not change the nature of the system matrix’s eigenvalues (35). The eigenvalues will be complex, without a real part (the Coriolis matrix doesn’t introduce damping in the system) (Figs. 3 and 4).

Fig. 3

Eigen pulsations for a beam with L = 0.55 … 0.1 m (D variable and ω variable). The first eigenvalue

Fig. 4

Eigen pulsations for a beam with L = 0.55 … 1 m (D variable and ω variable). The fifth eigenvalue

The problem arising in calculating a beam in a centrifugal field is the loss of stability, which happens from a mathematical point of view, when the stiffness matrix becomes negatively defined.

It is virtually impossible to determine analytical expressions to determine the geometric and mass field that ensures the stability of the beam in the centrifugal field. In this case, a numerical analysis can be made to determine the nature of the values.

The numerical calculus of eigenvalues and eigenvectors for a matrix is a difficult operation that consumes time resources. A simpler method is to determine whether the stiffened matrix is positively defined. For a set of defining values for the beam, it is determined whether the matrix is positively defined. If it is negatively defined then the beam enters into a field of instability. In the paper, the stiffness matrix was analyzed for different sets of beam length, diameter, and angular speeds with which the beam is rotated in a centrifugal field. Figures 5, 6 and 7 show these results. The areas in which we have instability are hatched in the figure.

Fig. 5

Domain of instability for D, ω, L variable

Fig. 6

Domain of instability for D, ω, L variable

Fig. 7

Domain of instability for D, ω, L variable

4 Conclusions

Operation of a machine element that can be modeled as a beam, being in a centrifugal field, can lead to instability phenomena, especially for the reason that the rotations can be found frequently in technical applications. For this reason, it is the question of determining the admissible values for geometric and mass elements. Because a theoretical approach is less useful in practical applications, only the numerical approach can provide useful results. In the paper, the motion equations obtained by other authors have been used, in a particular form, for the rotation of a beam around an axis. On the basis of these equations obtained via FEA, it is analyzed for some cases, the domain of values that the geometric and mass parameters can have. The results are presented in graphical form and the method used to determine areas of instability uses the calculation of the positivity of the stiffness matrix, a much easier operation than the calculation of its eigenvalues. Our application is inspired from the practical case of the rotor blade of helicopters, where the use of one-dimensional finite element has the advantage of simplicity and offers, in the same time, good results. Such kind of problems occurs often in the engineering practice where great operation speed and high loads can lead to instability.