Keywords

Mathematics Subject Classification (2010)

1 Introduction

Contact potentials are interactions supported on manifolds of lower dimension than the dimension of the overall space [1, 3, 11, 16]. Along the present manuscript, we shall consider the time independent one dimensional Schrödinger equation and contact potentials supported on isolated points (this is why we shall also use the term of point interactions to refer to them) or on lower dimensional varieties. The simplest case of a one dimensional contact potential is the Dirac delta interaction δ(x) supported at a point. In this case the Schrödinger equation comes from a one dimensional Hamiltonian of the form H = −d 2∕dx 2 + V (x), where V (x) accounts for the contact potential. This study is important in quantum mechanics and here are a few reasons:

  • Many of these models are exactly solvable and are very suitable to study scattering properties [2, 21, 31]. In particular, they are good toy models to study resonances and antibound states and their properties [4, 5].

  • They may serve to model point defects in materials, topological insulators [10, 28] and heterostructures, which may be represented by abrupt mass changes [20, 30].

  • In nanophysics: to mimic sharply peaked impurities inside quantum dots.

  • In scalar QFT on a line: used to show the influence of impurities and external singular backgrounds [33].

  • Point interactions of the type Dirac delta, δ(x) or δ ′(x), can be understood as perturbations of a free kinetic Schrödinger Hamiltonian, but they could be also combined with other type of interactions such as the harmonic oscillator, a constant electric field, the infinite square well, the conical oscillator, etc. [19, 22, 23, 27, 39].

  • Double δ-δ ′ barriers have been used to study the Casimir effect [8, 17, 24, 35].

  • Chains of periodic δ-δ ′ interactions have been considered in order to analyze a solvable Kronig-Penney model in solid state, where the behaviour of band spectrum has been thoroughly analyzed in order to obtain a better comprehension of dielectric and conducting phenomena [15, 25].

  • Although in principle we focused our attention in one dimensional non-relativistic problems, work has been done also in the study of contact potentials in higher dimensions [36], or as perturbations of the Dirac equation or the Salpeter Hamiltonian [18]. There is a wide range of problems in this field that will be studied in a near future.

In one dimension, it has been proven the existence of families depending on four real parameters of contact potentials at each point compatible with the self-adjointness of the Hamiltonian. There are some discussion on the physical meaning of these families that are obtained through the formalism of self-adjoint extensions of symmetric operators on Hilbert spaces.

Along this presentation, we shall consider the following forms for V (x):

  • V (x) = −aδ(x) + bδ ′(x), where a and b are real numbers with a > 0.

  • The Kronig-Penney model \(V(x)=\sum _{n=-\infty }^\infty (V_0\delta (x-na)+aV_1\delta ^{\prime }(x-na))\).

  • The radial potential V (r) = aδ(r − r′) + bδ ′(r − r′) with a and b real.

  • An application to nuclear physics, considering the previous radial potential plus a finite spherical well V 0[θ(r − R) − 1].

2 A δ-δ ′ Perturbation of the One Dimensional Free Hamiltonian

We start with the one dimensional Hamiltonian of the form

$$\displaystyle \begin{aligned} H=H_0+V(x)=\frac{p^2}{2m}-a\delta(x)+b\delta^{\prime}(x)\,, \text{ with }\, a>0\,, b\in\mathbb R\,, \end{aligned} $$
(1)

where H 0 = p 2∕(2m) and V (x) := −aδ(x) + bδ ′(x). Here, we need a definition of the potential V (x) such that the Hamiltonian H in (1) be self-adjoint. While a perturbation of the type − δ(x) is well defined on H 0, the point is to add the term containing the δ ′(x). There is not a unique definition for perturbation of this kind, but we need one compatible with the term on δ(x). This is sometimes called the local δ ′(x) and the interaction V (x) has to be defined via the self-adjoint extensions of symmetric (Hermitian) operators.

A self-adjoint determination of the Hamiltonian (1) can be provided through the theory of self-adjoint extensions of symmetric (Hermitian) operators with equal deficiency indices. First of all, we define the domain of the “free” operator H 0 = −d 2∕dx 2 as the Sobolev space \(W_2^2(\mathbb R\backslash \{0\})\) of absolutely continuous functions \(\psi (x): \mathbb R\backslash \{0\}\longmapsto \mathbb C\), on the real line excluded the origin, such that:

  1. (1)

    The first derivative ψ ′(x) is absolutely continuous on \(\mathbb R\backslash \{0\}\) (note that an absolutely continuous function admits derivative at almost all points);

  2. (2)

    Both ψ(x) and ψ ′′(x) are square integrable:

    $$\displaystyle \begin{aligned} \int_{-\infty}^\infty \{|\psi(x)|{}^2+|\psi^{\prime\prime}(x)|{}^2\}\,dx <\infty\,. \end{aligned} $$
    (2)
  3. (3)

    ψ(0) = ψ ′(0) = 0.

With this domain, H 0 is a symmetric operator with deficiency indices (2, 2), which means that it has a set of self-adjoint extensions depending on 4 real parameters. Note that Conditions (1) and (2) give the domain of the adjoint, \(H_0^\dagger \), of H 0. Self-adjoint extensions of H 0 have domains included in the domain of \(H_0^\dagger \) and are characterized by matching conditions at the origin. They have been classified in [9, 31]. In our case, we propose for V (x) = −a δ(x) + b δ ′(x) the following matching conditions:

$$\displaystyle \begin{aligned} \begin{pmatrix} \psi(0^+)\\ {} \psi^{\prime}(0^+) \end{pmatrix} = \begin{pmatrix} \displaystyle\frac{\hbar^2+mb}{\hbar^2-mb} & 0\\ {} \displaystyle\frac{-2\hbar^2 am}{\hbar^4-m^2b^2} & \displaystyle\frac{\hbar^2-mb}{\hbar^2+mb}\end{pmatrix} \begin{pmatrix} \psi(0^-)\\ {} \psi^{\prime}(0^-) \end{pmatrix} \,, \end{aligned} $$
(3)

where f(0+) and f(0−) are the right and left limits, respectively, of the function f(x) at the origin. The corresponding Schrödinger equation for H = H 0 + V (x) is

$$\displaystyle \begin{aligned} -\frac{\hbar^2}{2m}\,\psi^{\prime\prime}(x) -a\,\delta(x)\psi(x)+ b\,\delta^{\prime}(x)\,\psi(x) =E\,\psi(x)\,. \end{aligned} $$
(4)

Since neither the functions ψ(x) in the domain of H nor their first derivatives are continuous at the origin, we need to give a determination of the products δ(x)ψ(x) and δ ′(x) ψ(x) that replace the usual ones and that were somehow compatible with (3). Following [31], we propose

$$\displaystyle \begin{aligned} &\;\, \delta(x)\psi(x) := \frac{\psi(0^+)+\psi(0^-)}{2}\,\delta(x)\,, {} \end{aligned} $$
(5)
$$\displaystyle \begin{aligned} &\delta^{\prime}(x)\,\psi(x):= \frac{\psi(0^+)+\psi(0^-)}{2}\,\delta^{\prime}(x)-\frac{\psi^{\prime}(0^+)+\psi^{\prime}(0^-)}{2}\,\delta(x)\,. {} \end{aligned} $$
(6)

Some conclusions will be presented next. This includes bound states and scattering coefficients.

2.1 Bound States and Scattering Coefficients

It is well known that the Hamiltonian (1) has a bound state for b = 0, since − a is negative. When b≠0, it is easy to prove that a bound state must exist. Furthermore, we can find its energy and its wave function by solving the Schrödinger equation (4). Note that outside the origin, this is the Schrödinger equation for the free particle, so its solution should be of the form

$$\displaystyle \begin{aligned} \psi(x)=\alpha\,e^{\kappa x}\,\theta(-x) +\beta\,e^{-\kappa x}\,\theta(x)\,,\quad \kappa=\sqrt{-2mE/\hbar^2}\,, \end{aligned} $$
(7)

with E < 0, θ(x) is the Heaviside step function, α = ψ(0−) and β = ψ(0+). In addition, the function ψ(x) in (7) must belong to the domain of the Hamiltonian (1), so that it must satisfy the matching conditions (3). Taking into account (3), the final form of (7) is

$$\displaystyle \begin{aligned} \psi(x)=\frac{\sqrt{ma}\,\hbar}{\hbar^4+m^2b^2} [(\hbar^2-mb)\,e^{\kappa x}\,\theta(-x) +(\hbar^2+mb)\,e^{-\kappa x}\,\theta(x)]\,. \end{aligned} $$
(8)

Note that the function (8) is square integrable and, therefore, represents the wave function for the unique bound state of the system. Then, we plug (8) into the Schrödinger equation (4), which after some algebra gives the energy value for the unique bound state,

$$\displaystyle \begin{aligned} E= -\frac 12\, \frac{ma^2\hbar^6}{(\hbar^4+b^2m^2)^2}\,. \end{aligned} $$
(9)

It is a simple task to obtain the scattering coefficients. Assume that a monochromatic wave e ikx, \(k=\sqrt {2mE}/\hbar ^2\), E ≥ 0, comes from the left to the right. After scattering with the potential V (x), the resulting wave function has different forms on the regiones x < 0 or x > 0, which are given by

$$\displaystyle \begin{aligned} \mathrm{for}\; x<0:\ \psi(x)=e^{ikx} +R\, e^{-ikx}\,; \quad \mathrm{for}\; x>0: \ \psi(x)= T\,e^{ikx}, \end{aligned} $$
(10)

where R and T are the reflection and transmission coefficients, respectively. These coefficients are easily obtained by using matching conditions (3), where we now choose ħ = 1 for simplicity:

(11)

so that,

$$\displaystyle \begin{aligned} R(k)= \frac{-(am+2mbki)}{am+(1+m^2b^2)ki}\,, \qquad T(k)= \frac{(1-m^2b^2)ki}{am+(1+m^2b^2)ki}\,, \end{aligned} $$
(12)

where i is the imaginary unit. Note that |R(k)|2 + |T(k)|2 = 1. At the exceptional values b = ±1∕m, there is no transmission. This case will not be treated in the sequel, but it was carefully considered in [24, 34].

3 The Dirac δ-δ ′ Comb

The correspondence between boundary conditions and surface interactions in quantum field theory was established by Symanzik some time ago [38]. One the most interesting examples of these surface interactions is given by the Casimir effect [14]. It was in [34] where an interpretation of the Casimir effect using a δ-δ ′ type of potential was proposed. The idea in [34] was mimicking the plates in the Casimir effect as two point interactions, so that the Hamiltonian becomes

$$\displaystyle \begin{aligned} H=H_0+V(x)= -\frac{\hbar^2}{2m}\,\frac{d^2}{dx^2} +a_1\, \delta(x+q) + b_1\,\delta^{\prime}(x+q) +a_2\,\delta(x-q) + b_2\,\delta^{\prime}(x-q)\,,\end{aligned} $$
(13)

where q > 0 and the meaning of H 0 and V (x) is obvious.

A generalization of the Hamiltonian (13) is given by the Dirac δ-δ ′ comb. This is a modification of the Kronig-Penney model, which is an exactly solvable periodic potential, used in Solid State Physics, which describes electron motion in a periodic array of rectangular barriers. The most obvious generalization of the Kronig-Penney model is to replace the rectangular barriers by Dirac deltas of the same amplitude, something that can be obtained by a formal limit procedure. Now, the one dimensional Hamiltonian H = H 0 + V (x) is given by a periodic potential of the form \(V(x)=V_0 \sum _{n=-\infty }^\infty \delta (x-na)\), with V 0 > 0 and a > 0.

Inspired in the above mentioned analysis of the Casimir effect, we propose the study of the Dirac δ-δ ′ comb, in which the potential takes the form:

$$\displaystyle \begin{aligned} V_1(x)=\sum_{n=-\infty}^\infty (V_0\,\delta(x-na)+a\,V_1\,\delta^{\prime}(x-na))\,, \quad a,V_0>0\,,\; V_1\in\mathbb R\,. \end{aligned} $$
(14)

so that it is a second generalization of the Kronig-Penney model. From the point of view of physics, this chain may model a periodic array of charges and dipoles. The objective is to solve the one dimensional Schrödinger equation using (14) as potential.

Now, we operate on a neighbourhood of the origin, see Fig. 1. If we call ψ I(x) and ψ II(x) to the wave functions in the region I (left) and II (right), respectively, they have the following form (\(k=\frac {\sqrt {2mE}}{\hbar }>0\)):

$$\displaystyle \begin{aligned} &\qquad \quad \, \psi_I(x)= A_I\,e^{ikx} +B_1\,e^{-ikx}\,, \quad \psi_{II}(x) =A_{II}\,e^{ikx} +B_{II}\,e^{-ikx}\,, \\ &\psi^{\prime}_I(x) = ik \,A_I\,e^{ikx} -ik\,B_1\,e^{-ikx}\,,\quad \psi^{\prime}_{II}(x) = ik\, A_{II}\,e^{ikx} - ik\, B_{II}\,e^{-ikx}\,. \end{aligned} $$
(15)

Equations (15) can be written in simplified matrix form as

$$\displaystyle \begin{gathered}{} {\boldsymbol \psi}_J(x) := \begin{pmatrix} \psi_J(x) \\ {} \psi^{\prime}_J(x) \end{pmatrix} = \mathbb K\mathbb M_x \begin{pmatrix}{c} A_J\\ {} B_J \end{pmatrix} \,, \quad J=I,II\,, \end{gathered} $$
(16)

with

$$\displaystyle \begin{gathered} {} \mathbb K= \begin{pmatrix} 1 & 1 \\ {} ik & -ik \end{pmatrix} \,, \qquad \mathbb M_x = \begin{pmatrix} e^{ikx} & 0 \\ {} 0 & e^{-ikx} \end{pmatrix} \,. \end{gathered} $$
(17)
Fig. 1
figure 1

Periodic potential (14) near the origin

Full size image

In order to include the perturbation of the form δ-δ ′ at the origin, we have to use the matching conditions, as before. The resulting equation has the form \(\boldsymbol \psi _{II}(0^+) = \mathbb T_U\,\boldsymbol \psi _I(0^-)\), with

$$\displaystyle \begin{aligned} \mathbb T_U =\begin{pmatrix} \displaystyle\frac{1+U_1}{1-U_1} & 0 \\ {} \displaystyle \frac{2U_0/a}{1- U_1^2} & \displaystyle \frac{1-U_1}{1+U_1}\end{pmatrix} \,, \qquad U_0=\frac{maV_0}{\hbar^2}\,, \quad U_1=\frac{maV_1}{\hbar^2}\,. \end{aligned} $$
(18)

Again, (18) is valid provided that V 1≠ ±ħ 2∕(ma), otherwise the origin becomes opaque. After some algebra, we finally arrive to the following relation between the coefficients of the wave function to both sides of the origin:

$$\displaystyle \begin{aligned} \begin{pmatrix} A_{II}\\ {} B_{II} \end{pmatrix} = \mathbb K^{-1} \mathbb T_U \mathbb K \; \begin{pmatrix} A_I\\ {} B_I \end{pmatrix} \,. \end{aligned} $$
(19)

Then, we use the periodicity properties of the potential in order to obtain the wave function over all the real line \(\mathbb R\) and some other properties. First of all, the Floquet-Bloch theorem imposes the following condition (x ∈ (−a, a)):

$$\displaystyle \begin{aligned} \psi(x+a) =e^{iqa}\,\psi(x) \Longrightarrow \psi^{\prime}(x+a) =e^{iqa}\,\psi^{\prime}(x)\,, \end{aligned} $$
(20)

where q is a constant called the quasi-momentum and it is a characteristic of the periodic potential given, and a is the distance between the nodes or points supporting the contact potential. We may write relation (20) in matrix form, which for x ∈ (−a, 0) is

$$\displaystyle \begin{aligned} \boldsymbol\psi_{II}(x+a) =e^{iqa}\,\boldsymbol \psi_I(x) \Longrightarrow \mathbb K \mathbb M_x \mathbb M_a \;\begin{pmatrix} A_{II}\\ {} B_{II} \end{pmatrix} = e^{iqa}\,\mathbb K \mathbb M_x \; \begin{pmatrix} A_I\\ {} B_I \end{pmatrix}\,. \end{aligned} $$
(21)

From (17), the matrices \(\mathbb M_x\) and \(\mathbb K\) are invertible, so that (21) implies that

$$\displaystyle \begin{aligned}{}[\mathbb M_a \mathbb K^{-1} \mathbb T_U\mathbb K -e^{iqa}\,\mathbb I] \begin{pmatrix} A_I\\ {} B_I \end{pmatrix} =\mathbf{0} \Leftrightarrow \det [\mathbb T_U -e^{iqa}\,\mathbb K\mathbb M_a^{-1} \mathbb K^{-1}] =0\,, \end{aligned} $$
(22)

where \(\mathbb I\) is the 2 × 2 identity matrix. The cancellation of the determinant in (22) has some important consequences. With the definitions \(\widetilde q=aq\) and \(\widetilde k = ka\), Eq. (22) gives

$$\displaystyle \begin{aligned} \cos\widetilde q =f(U_1) \left[ \cos\widetilde k +U_0\,g(U_1)\,\frac{\sin \widetilde k}{\widetilde k} \right]\,, \ f(U_1) = \frac{1+U_1^2}{1-U_1^2}, \ g(U_1) =\frac{1}{1+U_1^2}, \end{aligned} $$
(23)

and U 0 and U 1 are as in (18). The first equation in (23) is often known as the secular band equation and determines the dispersion relation in each energy band \(\tilde {k}=\tilde {k}_n(q)\). It is an even function of U 1, or equivalently, of aV 1 the coefficient of δ ′. The main interest of the dispersion relation comes from the fact that that it provides the band spectrum of the Hamiltonian (14). The case U 1 = 0, i. e., no δ ′ term is present, has been previously studied. If U 1≠0, the δ ′ term appears and the structure of the band spectrum changes drastically and must be obtained numerically. The graphical results can be seen in Fig. 2.

Fig. 2
figure 2

Band structure for different values of U 0. From left to right U 0 = 0.1, U 0 = 1, U 0 = 10 and U 0 = 30. In all the cases, the band structure of the standard Dirac comb corresponds to U 1 = 0

Full size image

3.1 A Two Species Dirac δ-δ ′ Comb

Let us now consider a Hamiltonian of the form H = H 0 + V 1(x) + V 2(x), where H 0 = −ħ 2∕(2m) d 2∕dx 2, V 1(x) is as in (14) and V 2(x) is given by

$$\displaystyle \begin{aligned} V_2(x)= \sum_{n=-\infty}^\infty \left( W_0\,\delta(x-na-b) +a\,W_1\, \delta^{\prime}(x-na-b) \right), \ a>0, W_0,W_1\in\mathbb R. \end{aligned}$$

We called this model the two species Dirac δ-δ ′ comb in comparison with the model discussed just above in relation to the Hamiltonian with periodic potential V 1(x). The objective is again to study the band spectrum. Now, the discussion is quite similar to the precedent one, albeit a bit more complicated, but it is carried out under the same premises. We arrive to a band secular equation of the form

$$\displaystyle \begin{aligned} \cos (qa)= F(k;a,b,W_0,W_1,U_0,U_1)\,, \end{aligned} $$
(24)

where the explicit form of the function F is rather complicated and has been obtained in [25]. A numerical analysis gives the behaviour of the band spectrum. There are interesting differences in the behaviour of band spectrum as compared with this band spectrum for the one species Dirac δ-δ ′ comb. Now the band shape is completely deformed and, for certain values of the parameters U 1 and W w, the band shape is the reverse of what is for the one species comb. See details in [25]. This effect is particularly notorious for high values of |U 1| and |W 1|. In addition, there are critical values of the parameters, typically U 1 = ±1 and W 1 = ±1, for which impenetrable barriers appear.

4 Hyperspherical δ-δ ′

One of the most obvious generalizations of the Dirac δ-δ ′ potentials is a homogeneous d-th dimensional potential supported on a hull sphere of radius r 0. Due to the symmetry of this model, this potential would be equivalent to a one dimensional contact potential at the point r = r 0 > 0 plus an impenetrable barrier at the origin. Let us pose the problem from the very beginning and consider the d-th dimensional Hamiltonian of the form [35]

$$\displaystyle \begin{aligned} H:= -\frac{\hbar^2}{2m}\,\widehat {\boldsymbol\Delta}_d+\widehat V(\mathbf x)\,, \end{aligned} $$
(25)

with

$$\displaystyle \begin{aligned} \widehat V(\mathbf x) = a\,\delta( x- x_0) + b\,\delta^{\prime}( x- x_0),\quad x=|\mathbf x| . \end{aligned} $$
(26)

Here it is convenient to introduce the following dimensionless quantities:

$$\displaystyle \begin{aligned} \mathfrak h:= \frac{2}{mc^2}\,H\, \quad w_0:= \frac{2a}{\hbar c}\,,\quad w_1:= \frac{bm}{\hbar^2}\,,\quad r:= \frac{mc}{\hbar}\,|\mathbf x|\,, \end{aligned} $$
(27)

where c is the speed of light in the vacuum. After (27), the new Hamiltonian reads:

$$\displaystyle \begin{aligned} \mathfrak h= -\Delta_d+w_0\,\delta(r-r_0) +2w_1\,\delta^{\prime}(r-r_0) = -\Delta_d+V(r)\,. \end{aligned} $$
(28)

Here, Δd is the d-dimensional Laplace operator, which expressed in hyperspherical coordinates, (r, Ωd := {θ 1, θ 2, …, θ d−2, ϕ}) reads:

$$\displaystyle \begin{aligned} \Delta_d=\frac{1}{r^{d-1}}\,\frac{\partial}{\partial\,r} \left(r^{d-1}\,\frac{1}{r^{d-1}} \right) + \frac{\Delta_{S^{d-1}}}{r^2}\,, \end{aligned} $$
(29)

\(\Delta _{S^{d-1}}\) being the Laplace-Beltrami operator on functions defined on the hull hypersphere S d−1 with dimension d − 1. This operator satisfies the identity \(\Delta _{S^{d-1}}=-\mathbf L^2_d\), where L d is the generalized d-dimensional angular momentum operator.

The eigenvalue equation for \(\mathfrak h\) is separable, so that there are factorizable solutions of the form ψ λℓ(r, Ωd) = R λℓ(r) Y ℓ( Ωd), where R λℓ(r) is the radial wave function and Y ℓ( Ωd) are the hyperspherical harmonics. These are eigenfunctions of the Laplace-Beltrami operator \(\Delta _{S^{d-1}}\) with eigenvalues χ(d, ℓ) = −ℓ(ℓ + d − 2) [29]. The radial wave function is given by

$$\displaystyle \begin{aligned} \left[-\frac{d^2}{dr^2} - \frac{d-1}{r}\,\frac{d}{dr} + \frac{\ell(\ell+d-2)}{r^2} +V(r) \right] R_{\lambda\ell}(r) = \lambda\,R_{\lambda\ell}(r)\,, \end{aligned} $$
(30)

where V (r) was defined in (28).

Next, we introduce the reduced radial function,

$$\displaystyle \begin{aligned} u_{\lambda\ell}(r):= r^{\frac{d-1}{2}}\,R_{\lambda\ell}(r)\,. \end{aligned} $$
(31)

The effect of this change of indeterminate is to remove the term with the first derivative in (30). The resulting equation is

$$\displaystyle \begin{aligned} ({h}_0 + V(r))\,u_{\lambda\ell}(r) =\lambda_\ell\, u_{\lambda\ell}(r)\,, \end{aligned} $$
(32)

where,

$$\displaystyle \begin{aligned} h_0 = -\frac{d^2}{dr^2} + \frac{(d+2\ell-3)(d+2\ell-1)}{4r^2} \,. \end{aligned} $$
(33)

In order to define the potential V (r) using the theory of self-adjoint extensions of symmetric operators, we need to define a domain for h 0, in which h 0 be symmetric with equal deficiency indices (2, 2). Then, the domain \(\mathcal D(h_0)\) is the space of functions \(\varphi (r)\in L^2(\mathbb R^+)\) with the following properties:

  1. 1.

    Any \(\varphi (r)\in \mathcal D(h_0)\) is in the Sobolev space \(W^2_2(\mathbb R^+)\) of absolutely continuous functions with absolutely continuous first derivative and which second derivative is in \(L^2(\mathbb R^+)\).

  2. 2.

    They vanish at the origin, φ(0) = 0.

  3. 3.

    At the point r = r 0, they satisfy the property: φ(r 0) = φ′(r 0) = 0.

The domain \(\mathcal D(h_0^\dagger )\) of the adjoint, \(H_0^\dagger \), of h 0 is the space verifying some changes in the above conditions: in Condition (1), we replace \(W^2_2(\mathbb R^+)\) by \(W^2_2(\mathbb R^+\backslash \{r_0\})\), which is the space satisfying the same properties, except that its functions and their first derivatives have finite jumps at r 0 and, then, Condition (3) is not fulfilled. The domain \(\mathcal D(h_0+V(r))\) that makes the operator h 0 + V (r) self-adjoint is the space of all functions φ(r) in \(\mathcal D(h_0^\dagger )\) satisfying the following matching conditions at r 0:

$$\displaystyle \begin{aligned} \begin{pmatrix} \varphi(r_0^+) \\ {} \varphi'(r_0^+) \end{pmatrix} = \begin{pmatrix}\alpha & 0 \\ {} \beta & \alpha^{-1} \end{pmatrix} \begin{pmatrix} \varphi(r_0^-) \\ {} \varphi'(r_0^-) \end{pmatrix}\,, \end{aligned} $$
(34)

where \(\varphi (r_0^\pm )\) are the right (+) and left (−) limits of φ(r) at r = r 0. Also,

$$\displaystyle \begin{aligned} \alpha= \frac{1+w_1}{1-w_1}\,,\qquad \beta= \frac{w_0}{1-w_1^2}\,. \end{aligned} $$
(35)

These matching conditions determine the boundary conditions that should be verified by the radial wave functions R λℓ(r). In fact, (31) and (34) give:

$$\displaystyle \begin{aligned} \begin{pmatrix} R_{\lambda\ell}(r_0^+) \\ {} R^{\prime}_{\lambda\ell}(r_0^+) \end{pmatrix} = \begin{pmatrix}\alpha & 0 \\ {} \widetilde\beta & \alpha^{-1} \end{pmatrix} \begin{pmatrix} R_{\lambda\ell}(r_0^-) \\ {} R^{\prime}_{\lambda\ell}(r_0^-) \end{pmatrix}\,, \end{aligned} $$
(36)

with

$$\displaystyle \begin{aligned} \widetilde \beta := \beta-\frac{(\alpha^2-1)(d-1)}{2\alpha r_0} = \frac{\widetilde w_0}{1-w_1^2}\,, \quad \widetilde w_0 = \frac{2(1-d)w_1}{r_0}+w_0\,. \end{aligned} $$
(37)

These matching conditions are well defined, except at the exceptional values w 1 = ±1. These two cases have to be treated separately, see [24, 31].

4.1 Bound States

Here, we present some results concerning the existence of bound states for the model under consideration. The eigenvalue equation for bound states is (30) with λ < 0. Then, it is convenient to use the parameter κ > 0 with λ = −κ 2. The general solution of (30) is

$$\displaystyle \begin{aligned} R_{\kappa\ell}(r)= \begin{cases} A_1\,\mathcal I_\ell(\kappa r) +B_1\, \mathcal K_\ell(\kappa r) & \text{if } r\in(0,r_0)\,, \\ {} A_2\,\mathcal I_\ell(\kappa r) +B_2\, \mathcal K_\ell(\kappa r) & \text{if } r\in(r_0,\infty)\,. \end{cases} \end{aligned} $$
(38)

Then, R κℓ(r) can be written in terms of modified hyperspherical Bessel functions of the first (I ℓ(z)) and second (K ℓ(z)) kind, respectively, where,

$$\displaystyle \begin{aligned} \mathcal I_\ell(\kappa r) = \frac{1}{(\kappa r)^\nu}\,I_{\ell+\nu}(\kappa\nu)\,,\quad \mathcal K_\ell(\kappa\nu) = \frac{1}{(\kappa r)^\nu}\, K_{\ell+\nu}(\kappa\nu)\,, \quad \nu:= \frac{d-2}{2}\,. \end{aligned}$$

The form of the solution in terms of the functions u κℓ(r) defined in (31) comes straightforwardly from (38). The square integrability condition of the radial wave function for bound states imposes that A 2 = 0. Furthermore, the term multiplied by B 1 is not square integrable, except for zero angular momentum in two and three dimensions. In three dimensions, the condition u κℓ(0) = 0 implies that B 1 = 0. There are other type of arguments that show that in two dimensions, we also have B 1 = 0 [26]. After these considerations, (36) can be written as

$$\displaystyle \begin{aligned} B_2 \begin{pmatrix} \mathcal K_\ell(\kappa r_0)\\ {} \kappa\, \mathcal K^{\prime}_\ell(\kappa r_0) \end{pmatrix} = A_1 \begin{pmatrix} \alpha & 0 \\ {} \widetilde \beta & \alpha^{-1} \end{pmatrix} \begin{pmatrix} \mathcal I_\ell(\kappa r_0)\\ {} \kappa\, \mathcal I^{\prime}_\ell(\kappa r_0) \end{pmatrix} \,. \end{aligned} $$
(39)

If we divide the identity obtained with the lower component of (39) with that found with the first component, we get the following expression called the secular equation:

$$\displaystyle \begin{aligned} \alpha\,\frac{d}{dr}\,\log \mathcal K_\ell(\kappa r) |{}_{r=r_0} = \widetilde\beta +\alpha^{-1} \,\frac{d}{dr} \log \mathcal I_\ell(\kappa r)|{}_{r=r_0}. \end{aligned} $$
(40)

Solutions for κ > 0 of (40) give the energies for the bound states of the model under consideration. If we denote by y 0 = κr 0, (40) takes the form

$$\displaystyle \begin{aligned} F(y_0)=-y_0 \left(\frac{I_{\nu+\ell-1}(y_0)}{I_{\nu+\ell}(y_0)} + \frac{\alpha K_{\nu+\ell-1}(y_0)}{K_{\nu+\ell}(y_0)} \right)-(\alpha-\alpha^{-1})\ell =2\nu(\alpha-\alpha^{-1}) +\widetilde \beta r_0\,. \end{aligned}$$

Observe that the right hand side is independent on the energy and the angular momentum. This equation cannot be solved analytically. However, it may be used to obtain some properties concerning the number of bound states, \(N_\ell ^d=n_\ell ^d\,\mathrm {deg}(d,\ell )\), that exist for given values of d and ℓ. Here \(n_\ell ^d\) is the number of negative energy eigenvalues and deg(d, ℓ) the degeneracy associated with ℓ in d dimensions. We listed here below these results without proofs that may be found in [26]:

  1. 1.

    In the d-dimensional quantum system described by the Hamiltonian (28), the number \(n_\ell ^d\) defined above is at most one. This is, \(n_\ell ^d\in \{0,1\}\).

  2. 2.

    The d-dimensional quantum system described by the Hamiltonian (28) admits bound states with angular momentum ℓ if and only if

    $$\displaystyle \begin{gathered}{} \ell_{\mathrm{max}} \ne L_{\mathrm{max}}\,, \quad \mathrm{and} \quad \ell\in\{0,1,\dots,\ell_{\mathrm{max}}\}\,, \quad \ell_{\mathrm{max}}>-1\,, \end{gathered} $$
    (41)

    with

    $$\displaystyle \begin{gathered} {} \ell_{\mathrm{max}} := \lfloor L_{\mathrm{max}}\rfloor\,, \quad L_{\mathrm{max}} := \frac{w_1-r_0 w_0/2}{w_1^2+1} + \frac{2-d}{2}\,, \end{gathered} $$
    (42)

    where ⌊A⌋ denotes the integer part of the real number A. In addition, if \(\lambda _\ell =-\kappa _\ell ^2\) is the energy of the bound state with angular momentum ℓ, the following inequality holds:

    $$\displaystyle \begin{aligned} \lambda_\ell <\lambda_{\ell+1}<0\,,\qquad \ell\in\{0,1,\dots, \ell_{\mathrm{max}}-1\}\,. \end{aligned} $$
    (43)
  3. 3.

    The quantum Hamiltonian (28) admits a bound state for any ω 0 > 0, only if d = 2 and ℓ = 0.

5 An Application to Nuclear Physics

The δ-δ ′ is an approximation that serves to obtain interesting results concerning realistic models in physics. Next, we want to introduce one of these examples coming from nuclear physics. Let us consider a model for atomic nuclei based on a mean field potential with volume, surface and spin orbits parts, for which the Hamiltonian is given by

$$\displaystyle \begin{aligned} H(\mathbf r) = -\frac{\hbar^2}{2\mu}\, \nabla_{\mathbf r}^2 + U_0(r) +U_{SO}(r) (\mathbf L \cdot \mathbf S) +U_q(r)\,, \end{aligned} $$
(44)

where r = |r|, μ is the reduced mass and the terms U 0(r), U SO(r) and U q(r) have their origin in the Wood-Saxon potential:

$$\displaystyle \begin{aligned} U_0(r) &= -V_0\,f(r):= -V_0\,\frac{1}{1+e^{(r-R)/a}}\,, {} \end{aligned} $$
(45)
$$\displaystyle \begin{aligned} U_{SO}(r) &= \frac{V_{SO}}{\hbar^2}\, f'(r) = - \frac{V_{SO}}{a\hbar^2}\, \frac{e^{(r-R)/a}}{(1+e^{(r-R)/a})^2}\,,{} \end{aligned} $$
(46)
$$\displaystyle \begin{aligned} U_q(r) &= V_q\,fi^{\prime\prime}(r) = -\frac{V_q}{a^2} \frac{e^{(r-R)/a}\,(1-e^{(r-R)/a})}{(1+e^{(r-R)/a})^3}\,. {} \end{aligned} $$
(47)

Here, V 0, V SO and V q are positive constants, R is the nuclear radius and a is the thickness of the nuclear surface.

The kinetic term in (44) can be written in terms of the orbital angular momentum L as

$$\displaystyle \begin{aligned} -\frac{\hbar^2}{2\mu}\, \nabla_{\mathbf r}^2 = -\frac{\hbar^2}{2\mu}\, \left[\frac{1}{r^2}\,\frac{\partial}{\partial r} \left(r^2\,\frac{\partial}{\partial r} \right) - \frac{\mathbf L^2/\hbar^2}{r^2} \right]. \end{aligned} $$
(48)

Then, there exist factorizable solutions for the Schrödinger equation associated to (48). This factorization is of the form,

$$\displaystyle \begin{aligned} \psi(\mathbf r)= \frac{u_{n\ell j}(r)}{r}\,\mathcal Y_{\ell jm}(\theta,\phi)\,, \end{aligned} $$
(49)

where the angular part, satisfies the following relations:

$$\displaystyle \begin{aligned} \mathbf L^2\, \mathcal Y_{\ell jm}(\theta,\phi) =\hbar^2\,\ell(\ell+1)\,\mathcal Y_{\ell jm}(\theta,\phi)\,, \end{aligned} $$
(50)

and

$$\displaystyle \begin{aligned} (\mathbf L \cdot \mathbf S)\mathcal Y_{\ell jm}(\theta,\phi) =\hbar^2\xi_{\ell,j}\mathcal Y_{\ell jm}(\theta,\phi), \ \mathrm{with} \ \xi_{\ell,j} := \begin{cases} \frac{\ell}{2} & \text{for } j=\ell+\frac 12, \\ {} -\frac{\ell+1}{2} & \text{for } j=\ell-\frac 12. \end{cases} \end{aligned}$$

Note that \(\ell \in \mathbb N\cup \{0\}\). The functions denoted as \(\mathcal Y_{\ell jm}(\theta ,\phi )\) are linear combination of spherical harmonics \(Y_{\ell }^m(\theta ,\phi )\), which are simultaneous eigenfunctions of the operators L 2, S 2 and J 2 = (L + S)2. The radial part of the three dimensional Schrödinger equation has the form

$$\displaystyle \begin{aligned} H(r) \,u_{n\ell j}(r) = E_{n\ell j}\, u_{n\ell j}(r)\,, \end{aligned} $$
(51)

where,

$$\displaystyle \begin{aligned} H(r) = -\frac{\hbar^2}{2\mu} \left[ \frac{d^2}{dr^2} -\frac{\ell(\ell+1)}{r^2} \right] -V_0\,f(r) +V_{SO}\, \xi_{\ell,j} \,f'(r) +V_q\,fi^{\prime\prime}(r)\,. \end{aligned} $$
(52)

Our approximation can be obtained by taking the limit a → 0+ in the potential terms. This limit makes proper mathematical meaning in a distributional sense. From this point of view, we have that (r ≥ 0)

$$\displaystyle \begin{aligned} \lim_{a\to 0^+} U_0(r) &= V_0[\theta(r-R)-1]\,, {} \end{aligned} $$
(53)
$$\displaystyle \begin{aligned} \lim_{a\to 0^+} V_{SO}(r) &=-V_{SO}\, \xi_{\ell,j} \,\delta(r-R) \,, {} \end{aligned} $$
(54)
$$\displaystyle \begin{aligned} \lim_{a\to 0^+} U_q(r) &= -V_q\, \delta^{\prime}(r-R)\,, {} \end{aligned} $$
(55)

where θ(x) in (53) is the Heaviside step function. After this limit procedure, we finally obtain our model, which is given by the following radial Hamiltonian with contact potential:

$$\displaystyle \begin{aligned} H_c = -\frac{\hbar^2}{2\mu} \left[ \frac{d^2}{dr^2} -\frac{\ell(\ell+1)}{r^2} \right] + V_0[\theta(r-R)-1] - V_{SO} \xi_{\ell,j} \delta(r-R) -V_q \delta^{\prime}(r-R). \end{aligned} $$
(56)

The advantage of the Hamiltonian in (56) over that in (48) is that the Schrödinger equation, H s(r) u nℓj(r) = E nℓj u nℓj, associated to the former can be exactly solved for all values of ℓ and j. If we use, α := (2μ∕ħ 2)V SO ξ ℓ,j and β = (2μ∕ħ 2)V q, this Schrödinger equation becomes, were we omit the subindices in u(r) for simplicity:

$$\displaystyle \begin{aligned} \frac{d^2u(r)}{dr^2} +&\Bigg\{ \frac{2\mu E}{\hbar^2} -\frac{2\mu V_0}{\hbar^2} \,[\theta(r-R)-1] \\ &\qquad \qquad \quad +\alpha\,\delta(r-R) +\beta\,\delta^{\prime}(r-R) -\frac{\ell(\ell+1)}{r^2} \Bigg\} u(r)=0\,. \end{aligned} $$

Square integrable solutions inside the nucleus are

$$\displaystyle \begin{aligned} u_{\ell}(r)= A_\ell\,\sqrt{\gamma r}\,J_{\ell+\frac 12}(\gamma r)\,, \qquad \gamma=\frac{\sqrt{2\mu(V_0+E)}}{\hbar}\,, \qquad r\in [0,R)\,, \end{aligned} $$
(57)

and outside the nucleus,

$$\displaystyle \begin{aligned} u_{\ell}=D_\ell \,\sqrt{\kappa r}\,K_{\ell+\frac 12}(\kappa r)\,, \qquad \kappa =\frac{\sqrt{2\mu|E|}}{\hbar}\,, \qquad r\in(R,\infty)\,. \end{aligned} $$
(58)

Then, we impose the condition that the above solution be in the domain of the Hamiltonian (52). To do it, we need to find a relation between the coefficients A ℓ and D ℓ such that (57) and (58) verify the precise matching relations at r = R so that (52) be self-adjoint. These relations are

$$\displaystyle \begin{aligned} \begin{pmatrix} u_{\ell}(R^+) \\ {} u^{\prime}_{\ell}(R^+) \end{pmatrix} = \begin{pmatrix} \displaystyle\frac{2-\beta}{2-\beta} & 0 \\ {} \displaystyle\frac{4\alpha}{4-\beta^2} & \displaystyle\frac{2-\beta}{2+\beta}\end{pmatrix}\begin{pmatrix} u_{\ell}(R^-) \\ {} u^{\prime}_{\ell}(R^-) \end{pmatrix} . \end{aligned} $$
(59)

This gives a system of two equations, which permits to find a relation which is independent of the coefficients A ℓ and D ℓ and is

$$\displaystyle \begin{aligned} \varphi(\chi):=\frac{\chi\,J_{\ell+3/2}(\chi)}{J_{\ell+1/2}(\chi)} = \frac{(2+\beta)^2}{(2-\beta)^2}\,\frac{\sigma\,K_{\ell+3/2}(\sigma)}{K_{\ell+1/2}(\sigma)} - \frac{8\beta(\ell+1)}{(2-\beta)^2} + \frac{w_0}{(2-b)^2}=:\phi(\sigma), \end{aligned} $$
(60)

with

$$\displaystyle \begin{gathered}{} \chi:= v_0 \sqrt{1-\varepsilon}\,,\quad \sigma:= v_0\sqrt\epsilon\,, \quad \epsilon:= \frac{|E|}{V_0}\in (0,1)\,, \end{gathered} $$
(61)
$$\displaystyle \begin{gathered} {} v_0= \sqrt{\frac{2\mu R^2 V_0}{\hbar^2}}>0\,,\qquad w_0=\frac{8\mu V_{SO}\,\xi_{\ell,j}\,R}{\hbar^2}\,. \end{gathered} $$
(62)

Equation (60) if often called the secular equation. It is useful in order to obtain results concerning bound states. These results have been derived and proven in [26]. Here, we listed some of which we consider the most interesting:

  1. 1.

    If for any value \(\ell \in \mathbb {N}_0\) such that ℓ ≤ ℓ max the following inequality holds

    $$\displaystyle \begin{aligned} w_0> -\left((\beta -2)^2+2 \ell\left(\beta ^2+4\right)\right), \end{aligned} $$
    (63)

    there exists one, and only one, energy level with relative energy

    $$\displaystyle \begin{aligned} \varepsilon_s \in \left(1- \frac{j^2_{\ell+1/2,s}}{v_0^2} , 1- \frac{j^2_{\ell +3/2,s-1}}{v_0^2} \right)\subset (0,1), \qquad s\in \mathbb{N}. \end{aligned} $$
    (64)

    For \(w_0 \in \mathbb {R}\) the final number of bound states, N ℓ = (2ℓ + 1)n ℓ, is determined by

    $$\displaystyle \begin{aligned} n_{\ell}= M + m_1-m_2, \end{aligned} $$
    (65)

    where M is

    $$\displaystyle \begin{aligned} M=\min\{s\in \mathbb{N}_0 \,| \, j_{\ell+1/2,s+1}> v_0\}, \end{aligned} $$
    (66)

    and, using the functions φ(χ) and ϕ(σ) defined in (60), we obtain

    $$\displaystyle \begin{aligned} m_1=\displaystyle\begin{cases} 1 &\text{if} \ \varphi(v_0)> \phi(0^+), \\ {} 0 &\text{if} \ \varphi(v_0)< \phi(0^+) \ \ \text{or} \ \ v_0= j_{\ell+1/2,M} , \end{cases} \ m_2=\displaystyle\begin{cases} 1 &\text{if} \ 0> \phi(v_0), \\ {} 0 &\text{if} \ 0< \phi(v_0). \end{cases} \end{aligned}$$
  2. 2.

    The quantum system governed by the Hamiltonian (56) does not admit bound states with angular momentum \(\ell >\ell _{\max }\), where

    $$\displaystyle \begin{aligned} \ell_{max}:=\max\{\ell\in\mathbb{N}_0 \ | \ j_{\ell+1/2,1} < v_0 \ \text{or} \ \varphi(v_0)>\phi(0^+)\}. \end{aligned}$$

    If there exist \(s_0 \in \mathbb {N}\) and \(\ell _0 \in \mathbb {N}_0\) such that \(v_0= j_{\ell _0+1/2,s_0}\) the second condition in the previous set cannot be evaluated. Nonetheless, it is not necessary since the existence of at least one bound state for ℓ 0 is guaranteed.

  3. 3.

    If there exist bound states with relative energies \(\varepsilon _{n\ell _j}, \varepsilon _{(n+1)\ell _j}, \varepsilon _{n(\ell +1)_j}\) for \(n,\ell \in \mathbb {N}_0\) the following inequalities hold:

    $$\displaystyle \begin{aligned} (a)\ \varepsilon_{n\ell_j}>\varepsilon_{(n+1)\ell_j} , \ \ (b)\ \varepsilon_{n\ell_{j}}>\varepsilon_{n(\ell+1)_{j}}, \ \ (c)\ \varepsilon_{n\ell_{\ell + 1/2}}>\varepsilon_{n\ell_{\ell - 1/2}}. \end{aligned}$$

    Notice that the second inequality only applies for j = ℓ + 1∕2.

  4. 4.

    There are two special cases, in which β = ±2. Now, the contact potential at r = R becomes opaque in the sense that the transmission coefficient is equal to zero. Here, we expect the existence of bound states alone, without resonances or scattering states. This specific problem has been discussed in [26], where the proposed nuclear model is tested with experimental and numerical data in the double magic nuclei 132Sn and 208Pb with an additional neutron.

5.1 Resonances

Apart from bound states, we may analyze scattering states or the possibility of the existence of resonances or even antibound states. Here, we briefly discuss the existence of resonances, which are unstable quantum states [12, 13]. Contrary to the case of bound states, wave functions (usually called Gamow functions) for unstable quantum states are not square integrable. Moreover, in the coordinate representation, they show an asymptotically exponential grow at the infinity. In our case, this have the following consequence: Although for consistency reasons, we should keep the expression (57) for the wave function inside the nucleus (r < R), we should use the complete solution for the Schrödinger equation outside the nucleus, i.e., in the region r > R. This is

$$\displaystyle \begin{aligned} u_\ell(r)= \sqrt{\kappa r} \left(C_\ell\,H^{(1)}_{\ell +\frac 12} (\kappa r) +D_\ell\, H^{(2)}_{\ell +\frac 12} (\kappa r) \right)\,, \quad \kappa:= \frac{\sqrt{2\mu E}}{\hbar}\,, \quad E>0\,, \end{aligned} $$
(67)

where H (i)(κr) are the Hänkel functions of first (1) and second (2) kind, respectively, and C ℓ and D ℓ are coefficients depending solely on κ. In the search for resonances, the knowledge of the asymptotic forms of the Hänkel functions for large values of r is essential. These are:

$$\displaystyle \begin{aligned} H^{(1)}_{\ell +\frac 12} (\kappa r) \approx \sqrt{\frac{2}{\pi\kappa r}}\; e^{-i(\kappa r-(\ell+1)\pi/2)}\,, \quad H^{(2)}_{\ell +\frac 12} (\kappa r) \approx \sqrt{\frac{2}{\pi\kappa r}}\; e^{i(\kappa r-(\ell+1)\pi/2)}\,.\end{aligned} $$
(68)

These asymptotic forms show that \(H^{(1)}_{\ell +\frac 12} (\kappa r)\) is an outgoing wave function while \(H^{(2)}_{\ell +\frac 12} (\kappa r)\) is an incoming wave function. Resonances are determined by the often called purely outgoing boundary conditions, which assumes that only the outgoing wave function survives. This implies that D ℓ(κ) = 0, and this is a transcendental equation for which the solutions coincide with the resonance poles of the S-matrix [13]. The determination of D ℓ comes after the use of the matching conditions (59) and the expression (57) for the wave function inside the nucleus, where without lack of generality we may choose A ℓ = 1. This gives D ℓ(κ) = 0. The latter is a complicated transcendental equation, which depends on Hänkel and Bessel functions with different indices, see [26]. The solutions of this equation should be classified in three categories:

  1. 1.

    Simple solutions on the positive imaginary axis correspond to bound states.

  2. 2.

    Simple solutions on the negative imaginary axis correspond to virtual states also called antibound states.

  3. 3.

    Pairs of solutions on the lower half plane, symmetrically located with respect to the imaginary axis that correspond to resonances. Both members of each pair determine the same resonance and must have the same multiplicity. Usually, this multiplicity is one, although models with resonance poles with multiplicity two have been constructed [7, 32].

This model shows resonance poles. Due to the complexity of the relation D ℓ(κ) = 0 these resonances can only be obtained numerically in most of cases. It is important to remark that the imaginary part of the resonance poles is always negative. This implies that the asymptotic form on r of the first expression in (68) is exponentially growing, as previously noted.

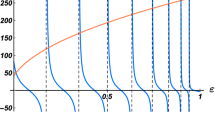
General arguments [37] show that the number of resonance poles should be infinite. In order to give an idea on how these poles look like, we show a few in Fig. 3. Resonance poles lie at the intersection of two curves. Here, we have chosen the following values of the parameters: ℓ = 0, v 0 = 5, w 0 = 10 and β = 1. Observe that resonance poles are rather close to the real axis, so that their imaginary part is rather small. Since the mean life of an unstable quantum state is related with the inverse of the imaginary part of its resonance pole, this means that the unstable states corresponding to the poles shown in Fig. 3 are rather stable. Some other cases with ℓ = 1, 2, 3, 4 have been also considered and we have seen a similar pattern for resonance poles [26]. Exact analytical results were also obtained.

Fig. 3
figure 3

Resonance poles are located at the intersection of curves below the real axis. here, ℓ = 0, v 0 = 5, w 0 = 10 and β = 1

Full size image

5.2 A Comment on the Self-adjointness of the Hamiltonian (56)

Take the Hamiltonian H c(r) in (56) and fix for simplicity ħ 2∕2μ = 1, which shall not alter our results. Then, write H c(r) = H ℓ + V (r), with

$$\displaystyle \begin{aligned} H_\ell:= -\frac{d^2}{dr^2} +\frac{\ell(\ell+1)}{r^2}+V_0[\theta(r-R)-1]\,,\;\; V(r)= a\delta(r-R)+b\delta^{\prime}(r-R)\,.\end{aligned} $$
(69)

We study the cases ℓ = 0 and ℓ≠0 separately. Let us discuss ℓ = 0, first. To begin with, take H r := −d 2∕dr 2 with domain, \(\mathcal D_c\), the subspace of functions f(r) ∈ L 2[0, ∞) such that: (1) f(r) is absolutely continuous with absolutely continuous first derivative; (2) The second derivative fi ′′(r) ∈ L 2[0, ∞) is square integrable; (3) For all functions f(r) in this domain, either f(0) + cf′(0) = 0 for some fixed real number c or f′(0) = 0. Each of these choices gives a self-adjoint determination of H r.

Next, define the subdomain \(\mathcal D_c(H_r)\) of all \(f(r)\in \mathcal D_c\) such that f(R) = f′(R) = 0. Choosing \(\mathcal D_c(H_r)\) as domain of H r, we conclude that H r is symmetric (Hermitian) with deficiency indices (2, 2). When H r is define on this domain, then the domain of the adjoint of H r, \(\mathcal D_c(H_r^\dagger )\), is the space of functions f(r) fulfilling conditions 1 and 2 above with one modification: they and their first derivatives have arbitrary although finite jumps at r = R. Self-adjoint extensions of H r are given by imposing the functions \(f(r)\in \mathcal D_c(H_r^\dagger )\) the matching conditions (59) at r = R. The exceptional cases β = ±2 also give respective self-adjoint extensions. These extensions determine self-adjoint operators of the form − d 2∕dr 2 + aδ(r − R) + bδ ′(r − R). Since the term V 0[θ(r − R) − 1) is bounded, adding it does not change anything.

Let us consider now the case ℓ≠0. In this case, we do not need to establish boundary conditions at the origin of the type f(0) = cf′(0), since the Hamiltonian H ℓ in (69) with ℓ≠0 is already essentially self-adjoint when its domain is the Schwartz space of functions supported on \(\mathbb R^+\equiv [0,\infty )\), \(S(\mathbb R^+)\), for which we always have that f(0) = f′(0) = 0. In this case − d 2∕dr 2 + ℓ(ℓ + 1)∕r 2 is essentially self-adjoint on the mentioned domain [6] and the same condition for H ℓ comes trivially, since V 0[θ(r − R) − 1 is bounded.

Then for any ℓ≠0, let us define a domain \(\mathcal D_{\ell ,0}\) of functions \(f(r)\in L^2(\mathbb R^+)\) fulfilling the following conditions:

  1. 1.

    f(r) and f′(r) are absolutely continuous;

  2. 2.

    The function − fi ′′(r) = [ℓ(ℓ + 1)∕r 2]f(r) belongs to \(L^2(\mathbb R^+)\);

  3. 3.

    f(0) = 0;

  4. 4.

    f(R) = f′(R) = 0.

The conclusion is that H ℓ on \(\mathcal D_{\ell ,0}\) is symmetric with deficiency indices (2, 2).

In order to add to H ℓ the perturbation V (r) = aδ(r − R) + bδ ′(r − R), we define the domain of the adjoint of H ℓ on \(\mathcal D_{\ell ,0}\) as the subspace of \(L^2(\mathbb R^+)\) satisfying the above conditions 1, 2 and 3 and replacing 4 by: 4′ f(r) and f′(r) have finite discontinuities at r = R. Then, imposing the matching conditions (59) to these functions, we obtain the domain in which H c(r) = H ℓ + V (r) is self-adjoint for any value of a and b. For ℓ≠0, the subindex c is irrelevant. This completes our discussion on the self-adjoint of the Hamiltonian.

6 Concluding Remarks

Contact potentials are quite interesting in quantum mechanics because they provide of simple models to analyze the behaviour of quantum systems. Along this presentation, we were concerned with perturbations of the type aδ(x − x 0) + bδ ′(x − x 0) either in one dimension or in arbitrary dimensions with spherical symmetry, so that the model could be projected to a one dimensional one. This is what we call δ-δ ′ interactions.

In the first place, we have introduced a very simple one-dimensional model with a unique δ-δ ′ interaction on the free Hamiltonian. This interaction can be easily studied and serves as a basis for more complicated models. The contact interaction can be mathematically well defined using the theory of self-adjoint extensions of symmetric operators with equal deficiency indices. The possible existence of a bound state is investigated and scattering coefficients are determined.

This is used for the construction of a sort of Kronig-Pennery model in which rectangular barriers are replaced by δ-δ ′ interactions with identical coefficients, so that the resulting potential is periodic. The behaviour of the energy bands can be studied in terms of the variations of the coefficients of the delta and the delta prime. We have also considered an hybrid potential with two types of δ-δ ′ interactions. The study of the energy bands requires powerful numerical estimations and the use of the software Mathematica. A detailed description of this model, which could be interesting in Condensed Matter, can be just briefly summarized in this short review and has been published in [25].

Spherically symmetric models in quantum mechanics are often studied as one dimensional models with an infinite barrier at the origin, after separation of radial and angular variables. This is also the case of the δ-δ ′ interactions supported on hull spheres of arbitrary dimensions. Here, we have determined matching conditions that make the Hamiltonian with this type of interaction self-adjoint and have obtained some results concerning the number of bound states. These results depend on the dimension as well as the angular momentum.

Finally, we have used one type of δ-δ ′ interaction as an approximation of a mean field potential of wide use in nuclear physics. The objective is double. In one side, we have obtained results concerning the existence and number of bound states in the considered model in terms of the given parameters. For two exceptional cases, the model shows no transmission through the δ-δ ′ barrier, so that the number of bound states is infinite. Otherwise this number is finite. Outside the exceptional cases, the model shows resonances that are manifested as pairs of poles of the analytic continuation to the complex plane of the S-matrix, S(k), in the momentum representation. These resonance poles can be obtained numerically as solutions of a transcendental equation. There is an infinite in number, so that in Fig. 2, we have depicted some resonance poles with the lowest real part. We have also discussed the construction of a self-adjoint Hamiltonian for such purpose.