Morse Theory, Stratifications and Sheaves

Abstract

After the local topological structure of stratified spaces was determined by R. Thom (Bull. Amer. Math. Soc., 75 (1969), 240–284) and J. Mather (Notes on topological stability, lecture notes, Harvard University, 1970) it became possible (see Kashiwara and Schapira, Sheaves on Manifolds, Grundlehren der math. Wiss. 292, Springer Verlag Berlin, Heidelberg, 1990; Goresky and MacPherson, Stratified Morse Theory, Ergebnisse Math. 14, Springer Verlag, Berlin, Heidelberg, 1988; Schürmann, Topology of Singular Spaces and Constructible Sheaves, Monografie Matematyczne 63, Birkhäuser Verlag, Basel, 2003) to analyze constructible sheaves on a stratified space using Morse theory. Although the detailed proofs are formidable, the statements and main ideas are simple and intuitive. This article is a survey of the constructions and results surrounding this circle of ideas.

5.1 Introduction

The stratified Morse theory of [29, 31] and the theory of constructible sheaves in [44] are two sides of the same coin. These books contain many parallel and overlapping results of a body of material that was developed in the 1980s. A brief outline applying Morse theory to constructible sheaves appears in Appendix 6.A of [31] and a complete and parallel development of the two theories is presented in [70]. In this article we provide a rapid and hopefully intuitive view of this circle of ideas.

In many situations the “nondegeneracy” conditions of Morse theory may be relaxed, which leads to a rich theory involving the topology of singular spaces, sheaves and maps, some of which we describe in Sects. 5.3.2, 5.11.1, 5.11.2, 5.12 below.

The author is grateful to Vidit Nanda and to an anonymous referee for many helpful corrections and suggestions on an earlier version of this paper. Some of the diagrams in this paper were typeset using Paul Taylor’s diagrams.sty package.

5.2 Preliminaries

A pair of topological spaces (A, B) means that B ⊂ A. A product of pairs (A, B) × (X, Y ) is the pair (A × X, A × Y ∪ B × X). If Z = X ∪ _B A is obtained by attaching a space A along a subspace B using two inclusions B → A and B → X, by abuse of notation we write simply Z = X ∪ (A, B). If $f:X \to {\mathbb R}$ is a continuous mapping and $a \in {\mathbb R}$ define

$$\displaystyle \begin{aligned} X_{\le a} = \left\{ x \in X|\ f(x) \le a \right\}\end{aligned} $$

and similarly for X _<a, X _>a, etc. For $a<b \in {\mathbb R}$, Morse theory addresses the question of how to obtain X _≤b from X _≤a by attaching a topological space A along a subspace B ⊂ A using an embedding B → X _≤a. In this case the pair (A, B) is said to be Morse data for f over the interval [a, b] and the excision isomorphism implies that H _i(X _≤b, X _≤a)≅H _i(A, B). One possible answer, of course, is the pair

$$\displaystyle \begin{aligned} (X_{[ab]},X_b) = (f^{-1}([a,b]), f^{-1}(b))\end{aligned} $$

which we refer to as coarse Morse data . One objective in Morse theory is to find explicit Morse data (A, B) that is as simple as possible.

5.3 Review of Smooth Morse theory

5.3.1 Manifolds

Let M be a smooth n-dimensional manifold and $f:M \to {\mathbb R}$ a smooth proper Morse function , that is, a function with isolated critical points (meaning df(p) = 0) and nondegenerate Hessian matrix (in local coordinates)

$$\displaystyle \begin{aligned} H(f)(p) = \left( \frac{\partial^2 f(p)}{\partial x_i \partial x_j}\right)\end{aligned} $$

at each critical point p. The Morse index λ at such a critical point p is the dimension of the greatest subspace on which H(f)(p) is negative definite. The zeroth theorem in Morse theory says: if $[a,b]\subset {\mathbb R}$ contains no critical values then M _≤a is diffeomorphic (as a manifold with boundary) to M _≤b. The first fundamental theorem of Morse theory says that (D ^λ, ∂D ^λ) × D ^n−λ is Morse data for f at p:

Theorem 5.3.1

If p ∈ M is a nondegenerate critical point with isolated critical value v = f(p) (meaning that no other critical points have critical value v) then for any 𝜖 > 0 sufficiently small, the smooth manifold with boundary M _≤v+𝜖 is homeomorphic to the adjunction space

$$\displaystyle \begin{aligned} M_{\le v-\epsilon} \bigcup (D^{\lambda} \times D^{n-\lambda}, \partial D^{\lambda} \times D^{n-\lambda}) \end{aligned} $$

(5.1)

where λ is the Morse index of f at the critical point p, and where D ^λ denotes the (unit) disk of dimension λ and boundary sphere ∂D ^λ.

An immediate consequence is that for any local coefficient system E → M (see Sect. 5.6.1) of finitely generated abelian groups,

$$\displaystyle \begin{aligned}H_i(M_{\le v+\epsilon}, M_{\le v-\epsilon};E) \cong \begin{cases} E_p & i = \lambda\\ 0 & \text{otherwise} \end{cases}\end{aligned}$$

where E _p denotes the stalk of E at the critical point p. There are two additional facts:

• The adjunction is local near the critical point p. Thus, if there are several critical points with the same critical value v and various but possibly different Morse indices λ ₁, λ ₂, ⋯ then by choosing 𝜖 sufficiently small the various embeddings $\partial D^{\lambda _i}$ can be chosen disjoint and the pairs $(D^{\lambda _i}, \partial D^{\lambda _i})$ may be adjoined independently.

• By “straightening the angle” [59] p. 34, [71] where the attaching occurs, the homeomorphism (5.1) may be realized as a diffeomorphism of manifolds with boundary.

5.3.2 Perfect Morse-Bott Functions

Morse theory may also be applied to smooth functions $f:M \to {\mathbb R}$ with minimally degenerate critical points. A nondegenerate critical submanifold V ⊂ M is a submanifold such that df(x)|T _x V = 0 for all x ∈ V , and the Hessian H(f)(x) is nondegenerate on the normal space T _V,x M = T _x M∕T _x V . A choice of Riemannian metric yields a decomposition $T_VM = E^{+} \bigoplus E^-$ into positive/negative eigenbundles. The rank of E ⁻ is the Morse index of the restriction f|W to a normal slice W through V  so it is referred to as the Morse index of f on V .

A Morse-Bott function is one whose critical points consist of nondegenerate critical submanifolds. Bott’s extension of Morse’s theorem is:

Theorem 5.3.2

With $f:M \to {\mathbb R}$ smooth and proper as above, if the critical value v is isolated and corresponds to a single connected critical submanifold V  then for sufficiently small 𝜖 > 0 the space M _≤v+𝜖 is homotopy equivalent to the space obtained from M _≤v−𝜖 by attaching the disk bundle D(E ⁻) of E ⁻ along its boundary sphere bundle S(E ⁻) = ∂D(E ⁻).

If S ¹ = {e ^iθ} acts by Hamiltonian diffeomorphisms on a symplectic manifold (M, ω) with resulting vector field Y  corresponding to ∂∕∂θ, then the moment map ¹ $\mu :M \to {\mathbb R}$ is a Morse-Bott function [4].

Let R be a commutative (coefficient) ring. A Morse-Bott function $f:M \to {\mathbb R}$ is perfect (for R) if the connecting homomorphisms for the long exact sequences involving H _i(M _≤v+𝜖, M _≤v−𝜖;R) vanish. If f is R-perfect and if the negative bundles E ⁻ of the critical submanifolds are also R-orientable then the Thom isomorphism gives a non-canonical decomposition

$$\displaystyle \begin{aligned} H^i(M;R) \cong \textstyle{\bigoplus_V} H^{i-\lambda_V}(V;R)\end{aligned} $$

(5.2)

where the sum is taken over all critical submanifolds V  and where λ _V is the corresponding Morse index of f on V .

This exceptional situation of a perfect Morse function, as described in [10], arises when $R = \mathbb Q$ and $M \subset {\mathbb C}\mathbb P^N$ is a nonsingular complex projective variety that is preserved by an algebraic action of ${\mathbb C}^*$, in which case the action of $S^1 \subset {\mathbb C}^{*}$ is Hamiltonian with respect to the canonical symplectic form² on M. Then the vector bundles E ^±→ V  arise geometrically: let V ⊂ M be a connected component of the fixed point set and let

$$\displaystyle \begin{aligned} V^- &= \left\{ x \in M|\ \lim_{t\to \infty} t.x \in V \right\}\\ V^+ &= \left\{x\in M|\ \lim_{t\to 0} t.x \in V \right\}.\end{aligned} $$

(5.3)

Theorem 5.3.3 ([10])

The projection V ⁺ → V  (resp. V ⁻→ V ) has the natural structure of an algebraic bundle of affine spaces that is diffeomorphic to the bundle E ⁺ → V  (resp. E ⁻→ V ) and the moment map $\mu :M \to {\mathbb R}$ is a perfect Morse-Bott function.

Equation (5.2) (equivalent to the perfection of the Morse function) then follows from the Bialynicki-Birula decomposition M =∐_V V ⁻ and the Weil conjectures (proved by Grothendieck and Deligne) which describe cohomology by counting points of these varieties mod p. See also Sect. 5.11.1 below.

5.4 Stratified Spaces

A stratification of a closed subset W ⊂ M is a locally finite decomposition into (disjoint) smooth locally closed submanifolds, called strata, $W = \coprod X_i$ such that the closure of each stratum is a union of strata of smaller dimension. A stratified mapping W → W′ between stratified spaces is a continuous mapping that takes strata to strata and is smooth on each stratum. It is a stratified homeomorphism if it has an inverse that is also a stratified mapping.

Write X < Y  if X≠Y  are strata of W with $X \subset \overline {Y}$. The pair X < Y  is said to satisfy Whitney’s conditions at a point x ∈ X if the following holds:

• suppose y _i ∈ Y  and x _i ∈ X are sequences that converge to the same point x ∈ X; suppose the secant lines $\overline {x_i,y_i}$ converge to some limiting line ℓ ⊂ T _x M and suppose the tangent planes $T_{y_i}Y$ converge to some limiting plane τ ⊂ T _x M. Then (A) T _x X ⊂ τ and (B) ℓ ⊂ τ.

Convergence of these lines and planes may be taken in the appropriate bundle of Grassmannians over M or equivalently, they may be taken with respect to some, and hence any, local coordinate system on M containing x. Condition (B) implies condition (A). A stratification of a space W is said to be a Whitney stratification if Whitney’s conditions hold at every point x with respect to every pair of strata X < Y .

If M is a (real) analytic manifold and W ₁, ⋯ , W _r are analytic, semi-analytic or sub-analytic subsets then there exists a Whitney stratification of M so that each W _j and each multi-intersection of the {W _j} are unions of strata, cf. [20, 25, 35,36,37, 51, 57].

The Whitney conditions are a sort of “no-wiggle” condition as points in Y  approach points in X but they imply the fundamental structure theorem of the Thom-Mather theory of Whitney stratified spaces: the space W is topologically locally trivial along each stratum X of W and each point in X has a basis of basic neighborhoods, all of which are stratified-homeomorphic. We make this statement precise in Sects. 5.4.1, 5.4.2.

5.4.1 Normal Slice and Link

Recall that submanifolds S, N ⊂ M of a smooth manifold M are transverse if T _p S + T _p N = T _p M for each point p ∈ S ∩ N, in which case the intersection is a smooth submanifold P = S ∩ N and we write $P=S \pitchfork N$. If W, W′⊂ M are Whitney stratified subsets, and if each stratum of W is transverse to each stratum of W′ then the intersection $W \pitchfork W'$ is Whitney stratified with strata of the form $S \pitchfork S'$ where S (resp. S′) run through the strata of W (resp. W′).

Let S be a stratum of dimension s in a Whitney stratified (closed) subset W ⊂ M of some smooth n dimensional manifold M. Fix p ∈ S and let T ⊂ M be a smooth submanifold (or germ of a submanifold) such that $S \pitchfork T = \{p\}$. This implies, by Whitney’s condition B that for every stratum R > S, the transversality condition $R\pitchfork T$ also holds at points in R that are sufficiently close to p ∈ S.

Let B _𝜖(p) be the (closed) ball of radius 𝜖 > 0 (with respect to some Riemannian metric on M) centered at p ∈ S. Whitney’s condition B implies that for sufficiently small 𝜖 > 0,

• the boundary sphere ∂B _𝜖(p) is transverse to every stratum of W and of T ∩ W and the same holds for all 0 < 𝜖′≤ 𝜖.

Define the normal slice,

$$\displaystyle \begin{aligned} (N_{\epsilon}(p), \partial N_{\epsilon}(p)) = T \cap W \cap (B_{\epsilon}(p), \partial B_{\epsilon}(p))\end{aligned} $$

(5.4)

with its induced stratification. Its boundary

$$\displaystyle \begin{aligned} L_S(p) = \partial N_{\epsilon}(p) = T \cap W \cap \partial B_{\epsilon}(p)\end{aligned} $$

(5.5)

is called the link of the stratum S at p. These objects are related by a local statement (Theorem 5.4.1) and a global statement (Sect. 5.4.4) below.

Theorem 5.4.1 ([31, §7])

The normal slice is stratified-homeomorphic to the cone over the link, that is, there exists a stratum preserving homeomorphism, smooth on each stratum,

$$\displaystyle \begin{aligned} N_{\epsilon}(p) \cong c\left(\partial N_{\epsilon}(p)\right)\end{aligned}$$

which takes the cone point to the point p. Suppose p, p′∈ S lie in the same connected component of the stratum S ⊂ W. Suppose N _𝜖(p) and $N^{\prime }_{\epsilon '}(p')$ are normal slices at p, p′ taken with respect to different choices of submanifold T, T′, different Riemannian metrics on M and different values 𝜖, 𝜖′. If 𝜖, 𝜖′ > 0 satisfy (*) above then there is a stratified homeomorphism

$$\displaystyle \begin{aligned}(N_{\epsilon}(p), \partial N_{\epsilon}(p)) \cong (N^{\prime}_{\epsilon'}(p'),\partial N^{\prime}_{\epsilon'}(p')).\end{aligned}$$

Moveover, there is a stratum preserving homeomorphism of pairs

$$\displaystyle \begin{aligned} (U_p, \partial U_p) &=(B_{\epsilon}(p), \partial B_{\epsilon}(p))\cap W \\ &\cong \left(B_{\epsilon}(p)\cap S,\partial B_{\epsilon}(p) \cap S\right)\times \left(N_{\epsilon}(p), \partial N_{\epsilon}(p)\right)\\ &\cong (D^s, \partial D^s) \times (c(\partial N_{\epsilon}(p)), \partial N_{\epsilon}(p)).\end{aligned} $$

(5.6)

where $s = \dim (S)$ and D ^s denotes the closed unit disk.

5.4.2 Basic Neighborhood

The homeomorphism (5.6) implies that the intersection L _p = ∂B _𝜖(p) ∩ W (the link of p in W) is homeomorphic to the s-fold suspension of L _S(p) = ∂N _𝜖(p) and that the whole closed neighborhood $\overline {U}_p = B_{\epsilon }(p) \cap W$ is homeomorphic to the product $\overline {U}_p \cong D^s \times N_{\epsilon }(p) \cong D^s \times c(L_S(p))$.

5.4.3 Deformation Arguments

Theorems 5.4.1, 5.5.1, 5.5.2, 5.5.3, 5.8.1, 5.9.1 (below) and many others like these are proven in [31]. The proofs involve deforming, in a smooth stratum preserving way, one subset, for example $\mathcal S_0=N_{\epsilon }(p)$, into another subset, say, $\mathcal S_1=N^{\prime }_{\epsilon '}(p')$. Although these sets are complicated, they arise from very simple pictures Y ₀, Y ₁ respectively, usually in ${\mathbb R}^2$. Theorem 5.4.2 [31, Theorems 4.3, 4.4] below says that a deformation {Y _t} of the simple “picture” gives rise to a corresponding deformation $\{\mathcal S_t\}$ of the (more complicated) set. For example, Theorem 5.5.2 below corresponds to moving the point (𝜖, δ) into the point (𝜖′, δ′) within the set of allowable possible choices.

Theorem 5.4.2 (Moving the wall)

Let W ⊂ M be a Whitney stratified set and let $\phi :M \to {\mathbb R}^2$ be a smooth mapping so that ϕ|W is proper. Let $Y \subset {\mathbb R}^2 \times {\mathbb R}$ be a closed Whitney stratified subset so that the projection $\pi :Y \to {\mathbb R}$ to the second factor is a submersion (everywhere surjective differential) on each stratum. Considering the second factor ${\mathbb R}$ to be a parameter space, let Y _t = π ⁻¹(t).

Suppose the restriction f|S to each stratum S of W is transverse to each stratum of Y _t , for all $t\in {\mathbb R}$ . Then there is a stratified homeomorphism

$$\displaystyle \begin{aligned} W \cap \phi^{-1}(Y_0) \cong W\cap \phi^{-1}(Y_1)\end{aligned}$$

This is little more than a restatement of Thom’s first isotopy lemma (see Theorem 5.5.1 below) and in fact the target space ${\mathbb R}^2$ may be replaced by an arbitrary smooth manifold. A similar result holds for pairs of spaces [31, §4.4]. A illustrative example in [31, §4.5] shows that Morse data for a Morse function on a smooth manifold is a product of cells. Cohomological (rather than homeomorphism) deformation arguments, applicable to a wide range of sheaves and spaces, are proven in [44, Theorem 2.7.2], [43, Theorem 1.4.3].

5.4.4 Control Data and Canonical Retraction

Let W ⊂ M be a closed Whitney stratified subset. The local structure of W near a point in a stratum S, as described in Theorem 5.4.1, is actually a consequence of the existence (due to R. Thom [77] and J. Mather [56]) of a global system of control data: a collection {(π _S, ρ _S) : T _S(𝜖) → S × [0, 𝜖)} of data for each stratum S, where T _S(𝜖) is a tubular neighborhood of S in M, ρ _S is a tubular “distance” function vanishing exactly on S, where (π _S, ρ _S) is a submersion when restricted to each stratum R > S and where π _S π _R = π _S and ρ _S π _R = ρ _S whenever both sides of these equations are defined.

It follows (after much work, see [56, 77]) that each fiber $\pi _S^{-1}(x)$ is stratified-homeomorphic to the normal slice N _𝜖(p)≅c(∂N _𝜖(p)) and the whole tubular neighborhood is stratified-homeomorphic to the mapping cylinder,

by homeomorphisms which (by a choice of a family of lines [26]) may be chosen to be compatible among strata.

Suppose Z ⊂ W is a closed union of strata and let T _Z(2𝜖) =⋃_S T _S(2𝜖) be the union of the tubular neighborhoods of strata S ⊂ Z and similarly for T _Z(𝜖). Then the projections and mapping cylinder structures may be assembled into a stratum preserving deformation retraction [27, §7], unique up to stratum preserving isotopy, T _Z(2𝜖) → T _Z(2𝜖) whose restriction

$$\displaystyle \begin{aligned} r_Z: T_Z(\epsilon) \to Z\end{aligned} $$

(5.7)

retracts T _Z(𝜖) to Z and agrees with the tubular projections: if x ∈ T _S(𝜖) −∪_R<S T _R(2𝜖) then r _Z(x) = π _S(x) ∈ S. If a point x is in the region

$$\displaystyle \begin{aligned} T_S(\epsilon) \cap \left(T_R(2\epsilon) - T_R(\epsilon)\right)\end{aligned}$$

then r _Z(x) = r _Z(π _S(x)) and r _Z|S shrinks towards R along the mapping cylinder lines (Fig. 5.1). So, for all y ∈ S there exists y′∈ S with r _Z(y′) = y and

$$\displaystyle \begin{aligned}r_Z^{-1}(y) \cong \pi_S^{-1}(y') \cong \pi_S^{-1}(y)\end{aligned}$$

Fig. 5.1

Tubular neighborhoods and retraction for R < S

5.5 Stratified Morse Theory

5.5.1 Conormal Vectors

Let M be a smooth manifold and let W ⊂ M be a Whitney stratified (closed) subset. Let X be a stratum of W and let p ∈ X.

A cotangent vector $\xi \in T_p^*M$ is said to be conormal to X if its restriction vanishes: ξ|T _p X = 0. The collection of all conormal vectors to X in M is denoted $T^*_XM$. It is a smooth conical Lagrangian locally closed submanifold of T ^∗ M.

If $f:M \to {\mathbb R}$ is smooth, its restriction f|X to X is a Morse function if and only if the graph of df is transverse to $T^*_XM$ in T ^∗ M (see, for example, [44, p. 311], [70, p. 286]).

A subspace τ ⊂ T _p M will be said to be a limit of tangent spaces from W if there is a stratum Y > X (Y ≠X) and a sequence of points y _i ∈ Y , y _i → p such that the tangent spaces $T_{y_i}Y$ converge to τ. A conormal vector $\xi \in T^*_XM$ at p is nondegenerate if ξ(τ)≠0 for every limit τ ⊂ T _p M of tangent spaces from larger strata Y > X. The set of nondegenerate conormal vectors is denoted Λ_X. Evidently,

$$\displaystyle \begin{aligned}\Lambda_X = T^*_XM - \bigcup_{Y>X} \overline{T^*_YM}\end{aligned}$$

where the union is over all strata Y > X (including the case Y = M − W because $T^*_MM$ is the zero section, and elements of Λ_X are necessarily nonzero).

5.5.2 Morse Functions

Let $f:M \to {\mathbb R}$ be a smooth function and let $\lambda = df(p) \in T^*_pM$. A critical point of f|W is a point p ∈ X in some stratum X such that df(p)|T _p X = 0, that is, $\lambda \in T^*_XM$. (In particular, every zero dimensional stratum is a critical point.) The value v = f(p) is said to be an isolated critical value of f|W if no other critical point q ∈ W of f|W has v = f(q). We say that f is a Morse function for W (cf. [50]) if

• its restriction to W is proper

• f|X has isolated nondegenerate critical points for each stratum X,

• at each critical point p ∈ X the covector λ = df(p) ∈ Λ_X is nondegenerate, that is, df(p)(τ)≠0 for every limit of tangent spaces τ ⊂ T _p M from larger strata Y > X.

In the case of a 1-dimensional target, Thom’s First Isotopy Lemma [56, 77], becomes the zeroth theorem of SMT, which says:

Theorem 5.5.1

Let $f:M \to {\mathbb R}$ be a smooth proper function, let W ⊂ M be a Whitney stratified closed subset and suppose that $[a,b] \subset {\mathbb R}$ contains no critical values of the restriction of f to any stratum of W. Then W _≤a is homeomorphic to W _≤b by a stratum preserving homeomorphism that is smooth on each stratum.

5.5.3 Normal Morse Data

Suppose that $f:M \to {\mathbb R}$ is a smooth proper mapping that is Morse on W ⊂ M as above. Suppose S is a stratum of W of dimension s and p is a (nondegenerate) critical point of f|S. Let (N _𝜖(p), ∂N _𝜖(p)) be a normal slice (5.4) to the stratum at p with 𝜖 > 0 chosen sufficiently small so as to satisfy (*) in Sect. 5.4.1. Set v = f(p). The nondegeneracy of the conormal vector ξ = df(p) implies there exists δ > 0 so that

• f|N _𝜖(p) has no critical points on any stratum of N _𝜖(p) ∩ f ⁻¹[v − δ, v + δ] other than {p}, and the same holds for all δ′≤ δ.

In this case we write 0 < δ ≪ 𝜖. The set of possible choices for 𝜖, δ will be an open region in the (𝜖, δ) plane as in Fig. 5.2:

Fig. 5.2

δ ≪ 𝜖 region

The normal Morse data for f at p is defined to be the coarse Morse data of the normal slice, that is, the pair

$$\displaystyle \begin{aligned}\left( N_{\epsilon}(p)_{[v-\delta,v+\delta]}, N_{\epsilon}(p)_{v-\delta}\right) = N_{\epsilon}(p) \cap \left(f^{-1}[v-\delta,v+\delta],\ f^{-1}(v-\delta)\right) \end{aligned}$$

Theorem 5.5.2 ([31, Theorem 3.6.2])

Suppose the stratum S is connected, p′∈ S is a nondegenerate critical point of a second function $f':M \to {\mathbb R}$ with ξ′ = df′(p′) ∈ Λ _S and suppose that ξ, ξ′ are in the same connected component of Λ _S . Then there is a stratified homeomorphism between the normal Morse data for f at p and normal Morse data for f′ at p′.

5.5.4 Main Theorem

With $p\in S \subset W \subset M \to {\mathbb R}$ as in Sect. 5.5.2 above, let λ denote the Morse index of f|S at the critical point p. Define the tangential Morse data to be the pair (D ^λ, ∂D ^λ) × D ^s−λ, see Eq. (5.1). The main theorem [31, Theorem 3.7] in stratified Morse theory says that Morse data at an isolated critical point is the product of the tangential Morse data with the normal Morse data. The proof involves repeated application of Theorem 5.4.2 to provide a sequence of stratum preserving deformations.

Theorem 5.5.3

Suppose $[a,b] \subset {\mathbb R}$ contains a single (isolated) critical value v ∈ (a, b) of f|W corresponding to a nondegenerate critical point p ∈ S. Suppose 0 ≤ δ ≪ 𝜖 are chosen as in (*) Sect. 5.4.1 and (**) Sect. 5.5.3 above so that the normal Morse data is well defined. Then there is a homeomorphism between the space W _≤b and the space obtained from W _≤a by attaching the pair

$$\displaystyle \begin{aligned} \left(D^{\lambda}, \partial D^{\lambda} \right) \times D^{s-\lambda} \times \left( N_{\epsilon}(p)_{[v-\delta,v+\delta]}, N_{\epsilon}(p)_{v-\delta}\right).\end{aligned}$$

Hence H _i(W _≤b, W _≤a)≅H _i−λ(N _𝜖(p)_{[v−δ,v+δ]}, N _𝜖(p)_≤v−δ) for all i.

5.5.5 Illustration

Figure 5.3 illustrates Theorem 5.5.3. The stratified space W is like three pages of a book glued along the spine with two “pages” going up and one “page” going down. The critical value is v = 0. The Morse function is the height function and the height − δ cuts the stratified space W along the red horizontal slice. The normal slice is a “Y”. The tangential and normal Morse data and their product is shown in the second row of the diagram with the red region marking the subspace.

Fig. 5.3

Normal Morse data × Tangential Morse data = Total Morse data. Glue along the red subspace

To obtain W _≤δ from W _≤−δ, attach the Morse data long the red subspace. In order to do this, it is necessary to deform the Morse data, stretching it so that the red vertical “ends” of the Morse data become horizontal, so they can be lined up with f ⁻¹(−δ). This simple example illustrates the complexity of the deformation arguments, which take about 50 pages in [31].

5.5.6 Existence of Morse Functions

If M is an analytic manifold and W ⊂ M is a subanalytically Whitney stratified subanalytic set then the collection of Morse functions is open and dense in the space of smooth mappings $M \to {\mathbb R}$ that are proper on W, in the Whitney C ^∞ topology, cf. [64, 67].

5.6 Recollections on Sheaves

5.6.1 Presheaves and Sheaves

A presheaf S of abelian groups on a topological space X is a contravariant functor from the category of open subsets of X (and inclusions) to the category of abelian groups (and homomorphisms). Elements of S(U) are called “sections” over the open set U ⊂ X.

A presheaf S is a sheaf if it is “locally defined”, that is, if the following condition holds. Let {U _α}_{α ∈ I} be a (possibly infinite) collection of open subsets of X and set U = ∪_{α ∈ I} U _α. Suppose that s _α ∈ S(U _α) are sections such that s _α|U _α ∩ U _β = s _β|U _α ∩ U _β for all α, β ∈ I. Then there is a unique section s ∈ S(U) so that s|U _α = s _α for all α ∈ I.

For any presheaf S the stalk at x ∈ X is the direct limit $S_x = \underset {x \in U}\lim S(U)$. There is a unique topology on the leaf space LS =⋃_{x ∈ U} S _x so that each stalk has the discrete topology and so that the projection π : LS → X is locally (near each point in LS) a homeomorphism. If U ⊂ X is open define the group of sections

$$\displaystyle \begin{aligned} \Gamma(U, LS) = \left\{ s: U \to LS|\ s\text{ is continuous and } \pi\circ s = Id\right\}.\end{aligned}$$

The restriction homomorphisms S(U) → S _x (x ∈ U) determine a canonical homomorphism

$$\displaystyle \begin{aligned}\phi_U:S(U) \to \Gamma(U,LS).\end{aligned}$$

The presheaf S is a sheaf if and only if ϕ _U is an isomorphism for all open sets U ⊂ X, in which case the group of sections is commonly denoted

$$\displaystyle \begin{aligned} \Gamma(U,S) = S(U) = \Gamma(U,LS)\end{aligned}$$

If S is a presheaf then the functor U↦ Γ(U, LS) is a sheaf and so this gives a canonical sheafification operation which identifies the category of sheaves as a full subcategory of the category of presheaves. A local coefficient system is a locally trivial sheaf LS → X.

5.6.2 Čech Cohomology

Let $\mathcal U = \{U_{\alpha }\}_{\alpha \in I}$ be a collection of open sets that cover X. A Čech q-cochain σ assigns to each ordered collection {U ₀, U ₁, ⋯ , U _q} of elements of $\mathcal U$ with nonempty intersection, an element

$$\displaystyle \begin{aligned} \sigma(U_0, U_1, \cdots, U_q) \in \Gamma(U_0\cap U_1\cap \cdots \cap U_q,S)\end{aligned}$$

that is antisymmetric: for any permutation π,

$$\displaystyle \begin{aligned} \sigma(U_{\pi(0)}, U_{\pi(1)}, \cdots, U_{\pi(q)}) = \mathrm{sign}(\pi)\sigma(U_0,\cdots, U_q).\end{aligned}$$

(The sign corresponds to a choice of orientation of the associated simplex in the nerve of the covering $\mathcal U$). The group of Čech q-cochains for the cover $\mathcal U$ is denoted $\check {C}^q_{\mathcal U}(X;S)$. The coboundary operator $d^q:\check {C}^q_{\mathcal U} \to \check {C}^{q+1}_{\mathcal U}$ is defined as follows. Let (U ₀, U ₁, ⋯ , U _q+1) be an ordered collection of elements of $\mathcal U$ and set V = U ₀ ∩ U ₁ ∩⋯ ∩ U _q+1. Then

$$\displaystyle \begin{aligned}(d^q \sigma)(U_0, U_1,\cdots, U_{q+1}) = \sum_{j=0}^{q+1} (-1)^j \sigma(U_0,\cdots, \widehat{U}_j,\cdots, U_{q+1})|V\end{aligned}$$

(where |V  denotes the restriction to V  and $\widehat {U}_j$ means “omit U _j”). Then d ^q+1 ∘ d ^q = 0. Define

$$\displaystyle \begin{aligned}\check{H}^q_{\mathcal U}(X;S) = \ker (d^q)/ \text{Im} (d^{q-1}).\end{aligned}$$

Note that $\check {H}^0_{\mathcal U}(X;S) = \Gamma (X,S)$. The Čech cohomology $\check {H}^q(X;S)$ is defined to be the limit over all open coverings of $\check {H}^q_{\mathcal U}(X;S)$ but typically fewer open sets suffice:

Theorem 5.6.1

Suppose the open cover $\mathcal U$ has the property that H ^q(U _J;S) = 0 for all q > 0 and for every J ⊂ I, where U _J = ∩_{j ∈ J} U _j . Then for all q ≥ 0 the natural homomorphism is an isomorphism:

5.6.3 Resolutions

The second way to construct the cohomology of a sheaf is with a resolution. Recall that a sheaf I on X is flabby if Γ(X, I) → Γ(U, I) is surjective for every open set U ⊂ X. It is soft if Γ(X, I) → Γ(K, I) is surjective for every closed set K ⊂ X. It is injective if: for every morphism f : S → I and for every injection g : S → T there exists a morphism h : T → I so that f = h ∘ g. An injective (resp. flabby, resp. soft) resolution of S is an exact sequence

$$\displaystyle \begin{aligned} 0 \to S \to I^0 \to I^1 \to I^2 \to \cdots\end{aligned} $$

(5.8)

where I ^j are injective (resp. flabby, resp. soft) sheaves.³ (A sequence of sheaves is exact if and only if it is exact on the stalks.) For the following see, for example, [7, §4].

Theorem 5.6.2

Suppose S is a sheaf on a locally compact, paracompact Hausdorff topological space X. Let (5.8) be an injective (resp. flabby, resp. soft) resolution of S. Then the Čech cohomology $\check {H}^*(X;S)$ coincides with the cohomology of the complex of global sections,

$$\displaystyle \begin{aligned} \Gamma (X, I^0) \to \Gamma(X, I^1) \to \Gamma(X, I^2) \to \cdots\end{aligned}$$

and is therefore independent of the choice of resolution I ^•.

5.6.4 Chains and Cochains

In many cases the central object of study is the resolution itself. For example, if M is a smooth manifold then the complex of differential forms is a fine (hence flabby) resolution of the constant sheaf ${\mathbb R}$:

$$\displaystyle \begin{aligned} 0 \to {\mathbb R} \to \boldsymbol{\Omega}^0 \to \boldsymbol{\Omega}^1 \to \boldsymbol{\Omega}^2 \to \cdots\end{aligned}$$

because the Poincaré lemma says that it is exact on stalks. Therefore $H^i(X;{\mathbb R})$ is isomorphic to the cohomology of the complex Γ(X, Ω ^•) =  Γ(X, Ω ^•) of global sections, a theorem of G. deRham. More generally let X be a topological space and let R be a commutative ring. If U ⊂ X is an open set then the complex of singular chains (C _r(U;R), ∂ _r) consists of finite formal sums (with coefficients in R) of singular simplices whose image is contained in U. Its dual is the complex of singular cochains $(C^r(U;R) = \operatorname {\mathrm {Hom}}(C_r(U;R),R), d^r = \partial _r^*)$ which evidently form a complex of sheaves C ^• on X by allowing U to vary over all open subsets of X. It is a flabby resolution of the constant sheaf and the cohomology of the complex of global sections is the singular cohomology of X.

Unfortunately the singular chains C _r(U;R) do not form a sheaf because restriction maps are not defined for V ⊂ U. Borel and Moore [11] solved this problem by dualizing again. If R is a field define

$$\displaystyle \begin{aligned} \omega^{-r}_{BM}= \omega_r^{BM}(U;R) = \mathrm{Hom}_R(\Gamma_c(U, {\mathbf{C}}^r),R)\end{aligned}$$

where Γ_c denotes sections with compact support.⁴

Theorem 5.6.3 ([11])

The Borel-Moore complex of chains $\omega ^{-r}_{BM}(U)$ form an injective complex (see Sect. 5.6.6) of sheaves ${\mathbf \omega }^{\bullet }_{BM}$ whose stalk cohomology (see Sect. 5.6.6) is the local homology: $H^{-r}_{x}(\mathbf \omega ^{\bullet }_{BM}) \cong H_r(X,X-x;R)$.

5.6.5 PL Chains

A more concrete description (see [30]) of the Borel-Moore sheaf of chains exists if the space X has a piecewise linear (or subanalytic or o-minimal) structure. Let R be a commutative ring. Suppose X is a simplicial complex, U ⊂ X is an open subset and T is a locally finite triangulation of U. Define $C_i^T(U;R)$ to be the group of T-simplicial chains in U, that is, finite sums $\xi = \sum a_j \sigma _j$ where a _j ∈ R and σ _j ⊂ U is a (closed) i dimensional simplex, with the usual boundary operator. If T′ refines T there is a canonical inclusion $C_i^{T}(U;R) \to C_i^{T'}(U;R)$. Set $C_i^{PL}(U;R) = \underset {\longrightarrow }{\lim } C_i^T(U;R)$. If V ⊂ U are open and if T is a locally finite triangulation of U there exists a locally finite triangulation T′ of V  so that every simplex of T′ is contained in a single simplex of T so we obtain restriction maps $C_i^{PL}(U;R) \to C_i^{PL}(V:R)$ and therefore a soft sheaf ${\mathbf {C}}_i^{PL}$ on X of “locally finite chains” or “infinite chains” on X. The complex of soft sheaves $\omega ^{\bullet }_{PL}$ with $\omega ^{-i}_{PL} = {\mathbf {C}}_i^{PL}$ and d = ∂ (the differential increases degree) is quasi-isomorphic to the Borel-Moore complex.

5.6.6 Complexes of Sheaves

A (bounded below) complex of sheaves (of abelian groups)

on a topological space X is a collection {S ⁱ} ($i \in {\mathbb Z}$) which vanish for i sufficiently small, and satisfy d ∘ d = 0. For each x ∈ X there is a resulting complex of stalks, $\cdots \to S^0_x \to S^1_x \to \cdots$ whose cohomology $H^i(S^{\bullet }_x)$ is called the stalk cohomology of the complex S ^•. Since sheaves form an abelian category we may form the cohomology of the sequence S ^• in the category of sheaves. Thus, the i-th cohomology sheaf of S ^• is

$$\displaystyle \begin{aligned} {\mathbf H}^{\mathbf i}(S^{\bullet}) = \mathbf{ker}(d^i)/\mathbf{Im}(d^{i-1})\end{aligned}$$

and its stalk coincides with the stalk cohomology, that is, ${\mathbf H}^{\mathbf i}_x(S^{\bullet }) = H^i(S^{\bullet }_x)$. A morphism S ^• → T ^• of complexes of sheaves is a collection of sheaf morphisms S ^r toT ^r that commute with the differentials. It is said to be a quasi-isomorphism if it induces isomorphisms H ^r(S ^•) →H ^r(T ^•) for all r, which is the same as saying that it induces an isomorphism on stalk cohomology $\mathbf H^r_x(S{{ }^{\bullet }}) \cong \mathbf H^r_x(T{{ }^{\bullet }})$ for all r and for all x ∈ X. If each T ^r is injective (resp. flabby, resp. soft) then such a quasi-isomorphism is said to be an injective (resp. flabby, resp. soft) resolution of S ^•.

To find such a resolution, first choose injective (resp. flabby, resp. soft) resolutions of each S ^j so that these fit together into a commuting double complex with horizontal and vertical differentials d _h, d _v respectively,

Define the associated single complex J ^• by adding along diagonals,

$$\displaystyle \begin{aligned} J^r = \bigoplus_{p+q=r}I^{pq}\ \text{ with } d(c_{pq})= (d_h + (-1)^pd_v)c_{pq}\end{aligned}$$

for c _pq ∈ I ^pq. Then d ∘ d = 0 and the homomorphism S ^• → J ^• is a quasi-isomorphism, hence an injective (resp. flabby, resp. soft) resolution of S ^•.

5.6.7 Cohomology

Let S ^• be a complex of sheaves on a topological space X. The total cohomology

$$\displaystyle \begin{aligned} H^r(X; S^{\bullet}) = H^r(\Gamma(X, J^{\bullet}))\end{aligned}$$

is defined to be the cohomology of the complex of global sections of any injective, flabby or soft resolution J ^• of S ^•. It is independent of the resolution and, more generally, the following fact from homological algebra is messy but straight forward. It is the main technical tool for establishing cohomology isomorphisms because it reduces such questions to isomorphisms on stalk cohomology.

Theorem 5.6.4

Let S ^• be a complex of sheaves and let I ^pq be a double complex of injective resolutions as above. Then this double complex determines a spectral sequence with

$$\displaystyle \begin{aligned} E_2^{pq} = H^p(X; \mathbf H^q(S{{}^{\bullet}})) \implies H^{p+q}(X;S{{}^{\bullet}}).\end{aligned}$$

Consequently a quasi-isomorphism S ^• → T ^• induces an isomorphism

$$\displaystyle \begin{aligned}H^r(U;S{{}^{\bullet}}) \to H^r(U;T{{}^{\bullet}})\end{aligned}$$

for any open subset U ⊂ X and for all r.

5.7 Derived Category and Constructible Sheaves

5.7.1 Construction of the Derived Category

Good general references for derived categories are [23, 24]; a quick summary is in [30]. Grothendieck recognized (see Theorem 5.6.4) that for most purposes, quasi-isomorphic (complexes of) sheaves behave alike, so there should be a category in which such sheaves become isomorphic. This dream was realized by Jean-Louis Verdier ([79, 80], who added enough morphisms to the category of sheaves so that every quasi-isomorphism acquired an inverse. An object in the (bounded) derived category

$$\displaystyle \begin{aligned}D^b(X) = D^b(Sh_X)\end{aligned}$$

of sheaves on X is a complex of sheaves A ^•, bounded from below (A ^j = 0 for j ≪ 0), whose cohomology sheaves are also bounded from above H ^j(A ^•) = 0 for j ≫ 0). A morphism A ^• → B ^• is an equivalence class of diagrams

where $C^{{ }^{\bullet }} \to A{{ }^{\bullet }}$ is a quasi-isomorphism, and where two such morphisms $A{{ }^{\bullet }} \leftarrow C_1^{\bullet } \to B{{ }^{\bullet }}$ and $A{{ }^{\bullet }} \leftarrow C_2^{\bullet } \to B{{ }^{\bullet }}$ are considered to be equivalent if there exists a diagram that is commutative up to chain homotopy:

5.7.2 Derived Functor

If A ^• → B ^• is a quasi-isomorphism of complexes of sheaves and if each B ^j is injective then there exists an inverse up to homotopy, B ^• → A ^•. In fact, the homotopy category of (bounded below) complexes of injective sheaves is equivalent to the derived category (see [24, §III.5]). Moreover, there is a canonical functorial construction of an injective resolution of any complex of sheaves, due to Godement. Accordingly, if T is a left exact functor from the category of sheaves $\mathcal {S}h_X$ to some abelian category $\mathcal A$, Verdier defines its right derived functor RT(S ^•) = T(J ^•) where S ^• → J ^• is the Godement injective resolution. This procedure passes to the derived category producing a right derived functor

$$\displaystyle \begin{aligned} RT: D^b(\mathcal{S}h_X) \to D^b(\mathcal A).\end{aligned}$$

It is possible to replace the injective resolution J ^• with any T-acyclic or T-adapted resolution, see [23, §4.3] or [24, §III.6.3]. For the functor T =  Γ of global sections, and for the functors T = f _∗, f _! (push forward, push forward with proper support, see below), fine sheaves and soft sheaves are T-acyclic.

5.7.3 Derived Push Forward

If f : X → Y  is a continuous map and S is a sheaf on X then its push forward is denoted f _∗(S). If A ^• is a complex of sheaves on X the derived functor is Rf _∗(A ^•) = f _∗(J ^•) where A ^• → J ^• is an injective, flabby or soft resolution of A ^• and there is a canonical isomorphism

$$\displaystyle \begin{aligned} H^i(X;A{{}^{\bullet}}) \cong H^i(Y; Rf_*(A{{}^{\bullet}}))\end{aligned} $$

(5.9)

for all i, which is to say that the cohomology of X may be computed locally on Y . In many applications this isomorphism replaces arguments involving the Leray-Serre spectral sequence, illustrating the power and convenience of the derived category.

If f is proper, the stalk cohomology of the derived push forward is $H^i_y(Rf_*(A{{ }^{\bullet }})) = H^i(f^{-1}(y);A{{ }^{\bullet }})$ and the cohomology sheaf H ⁱ(Rf _∗(A ^•)) is classically denoted R ⁱ f _∗(A ^•). The push forward with proper support and its derived functor are denoted f _! and Rf _! respectively.

5.7.4 Mapping Cone

The following construction works in any Abelian category $\mathcal A$ but we are mostly concerned with the category of sheaves on some space. The mapping!cone C ^• = C ^•(ϕ) of a morphism ϕ : A ^• → B ^• of complexes is the complex $C^r = A^{r+1} \bigoplus B^r$ with differential d _C(a, b) = (d _A(a), (−1)^deg(a) ϕ(a) + d _B(b)). It is the total complex of the double complex

with morphisms β : B ^• → C ^• and γ : C ^• → A[1]^• where A[1]^j = A ^j+1. Denote this by:

Lemma 5.7.1

If ϕ is injective then there is a natural quasi-isomorphism

$$\displaystyle \begin{aligned}\operatorname{\mathrm{coker}}(\phi) \cong C{{}^{\bullet}}(\phi).\end{aligned}$$

If ϕ is surjective then there is a natural quasi-isomorphism

$$\displaystyle \begin{aligned}C{{}^{\bullet}}(\phi) \cong\ker(\phi)[1].\end{aligned}$$

There are natural quasi-isomorphisms A ^•[1]≅C ^•(β) and B ^•[1]≅C ^•(γ) so that any side of this triangle determines the third element up to quasi-isomorphism. This triangle determines a long exact sequence on cohomology

$$\displaystyle \begin{aligned} \cdots\to {\mathbf{H}}^{r-1}(B{{}^{\bullet}}) \to {\mathbf{H}}^{r-1}(C{{}^{\bullet}}) \to {\mathbf{H}}^r(A{{}^{\bullet}}) \to {\mathbf{H}}^r(B{{}^{\bullet}}) \to {\mathbf{H}}^r(C{{}^{\bullet}}) \to \cdots.\end{aligned}$$

A triangle of morphisms of complexes

is said to be a distinguished triangle if it is homotopy equivalent to a triangle

5.7.5 Restriction to Subspaces

There are two ways to restrict a sheaf S on a topological space X to a closed subspace i _Z : Z → X. The ordinary restriction $S|Z=i_Z^*S$ is the sheaf whose leaf space (Sect. 5.6.1) is π ⁻¹(Z) where π : LS → X is the leaf space of S. Let j : U = X − Z → X be the inclusion. Then there is a distinguished triangle:

The long exact cohomology sequence is that of the pair

$$\displaystyle \begin{aligned}H^r(X,Z;A{{}^{\bullet}}) = H^r(X;Rj_!j^* A{{}^{\bullet}}).\end{aligned}$$

The second type of restriction, denoted $i_Z^!S$, is the restriction to Z of the presheaf with sections supported in Z, that is

$$\displaystyle \begin{aligned} i_Z^!(S) = i_Z^*(S_Z) \text{ where } \Gamma(V, S_Z) = \left\{ s \in \Gamma(V,S)|\ \text{supp}(s) \subset Z \right\}.\end{aligned}$$

The group of global sections is

$$\displaystyle \begin{aligned} \Gamma(Z, i_Z^!(S)) = \underset{\overrightarrow{V \supset Z}}{\lim}\Gamma_Z(V,S)\end{aligned}$$

(the limit is over open sets V ⊂ X containing Z). The functor $i_Z^!$ is a right adjoint to the pushforward with compact support (i _Z)_!. For any A ^• ∈ D ^b(X) there is a distinguished triangle,

(5.10)

which gives the long exact sequence for the pair:

$$\displaystyle \begin{aligned}H^r(X,X-Z;A{{}^{\bullet}})\cong H^r(X; Ri_{Z*}i_Z^!A{{}^{\bullet}}).\end{aligned}$$

The object $i_Z^{!}A{{ }^{\bullet }}$ is denoted R Γ_Z A ^• in [44].

5.7.6 Constructible Sheaves

Let X be a Whitney stratified space. A complex of sheaves A ^• on X is said to be (cohomologically) constructible with respect to this stratification if each of the cohomology sheaves H ^r(A ^•) is locally constant on each stratum of X and its stalk is finite dimensional at each point. The constant sheaf, the sheaf of singular cochains, and the Borel-Moore sheaf of chains are constructible. If we do not specify a stratification, a complex of sheaves on X is said to be constructible if it is (cohomologically) constructible with respect to some Whitney stratification. If X is real or complex algebraic, analytic, or subanalytic then the relevant stratification is assumed to be algebraic, analytic, etc. The constructible derived category $D^b_c(X)$ is the corresponding full subcategory of the derived category.

Lemma 5.7.2

Suppose A ^• is a complex of sheaves, constructible with respect to some Whitney stratification of X. Let x ∈ X and let U _x be a basic neighborhood as described in Sect. 5.4.2 . Then there is a canonical isomorphism

$$\displaystyle \begin{aligned} H^r(U_x;A{{}^{\bullet}}) \cong {\mathbf{H}}^r_x(A{{}^{\bullet}})\end{aligned}$$

between the sheaf cohomology of U _x and the stalk cohomology of A ^•.

The stratified homeomorphism $\overline {U}_x \cong D^s \times N_{\epsilon }(x)$ of Eq. (5.6) and the constructibility hypothesis imply that H ^r(U _x;A ^•)≅H ^r(N _𝜖(x);A ^•). But the normal slice is a cone and the cohomology sheaves H ^r(A ^•) are locally constant along the cone lines. So there is a one parameter family of shrinking maps θ _t : N _𝜖(x) → N _𝜖(x) (with θ ₁ the identity and θ ₀ the map to the cone point) inducing quasi-isomorphisms $\theta _t^*(A{{ }^{\bullet }}) \to A{{ }^{\bullet }}$ for all t > 0. Therefore its cohomology H ^r(N _𝜖(x)) coincides with ${\mathbf {H}}^r_x(A{{ }^{\bullet }})$. The local topological triviality of a stratification gives the following fact, crucial for many arguments involving constructible sheaves because it produces a constructible sheaf on a larger set than it started with:

Lemma 5.7.3

Suppose X is Whitney stratified and Σ ⊂ X is a closed union of strata with complement U = X − Σ and inclusion j : U → X. Let A ^• be a complexes of sheaves on U that is constructible with respect to the (induced) stratification of U. Then the complexes Rj _∗(A ^•) and Rj _!(A ^•) on X are constructible with respect to the given stratification of X.

5.7.7 Verdier Duality

Let X be a Whitney stratified space as above. The sheaf $\omega ^{\bullet }_X$ of Borel-Moore chains is a dualizing complex and the dual of a complex of sheaves $A{{ }^{\bullet }} \in D^b_c(X)$ is defined to be the sheaf

$$\displaystyle \begin{aligned} \mathbb D_X(A{{}^{\bullet}}) = {\mathbf{RHom}}^{\bullet}(A{{}^{\bullet}}, \omega_X^{\bullet}).\end{aligned}$$

(See [11, 23, 79, 80, §5.16], [39, §6], [44, §3], [21, §3].) The operation RHom may be replaced by Hom if an injective model⁵ is used for $\omega _X^{\bullet }$. The dual of the constant sheaf is $\omega _X^{\bullet }$. There is a canonical double duality isomorphism $\mathbb D_X(\mathbb D_X(A{{ }^{\bullet }})) \cong A{{ }^{\bullet }}$ in $D^b_c(X)$. If f : X → Y  then duality switches Rf _∗ and Rf _!. It also switches f ^∗ with f ^! which may be taken to give a definition of f ^!, that is,

$$\displaystyle \begin{aligned} f^!(A{{}^{\bullet}}) = \mathbb D_X(f^*(\mathbb D_Y(A{{}^{\bullet}}))\end{aligned}$$

which agrees with the operation i ^! of Sect. 5.7.5 for closed embeddings i : Z → W and agrees with j ^∗ = j ^! for open embeddings j : U → W.

5.8 Morse Theory of Constructible Sheaves

5.8.1 Basic Result

Throughout this section we fix a Whitney stratified closed subset W ⊂ M and a complex of sheaves A ^• on W that is (cohomologically) constructible with respect to this stratification. Since the homeomorphism in Theorem 5.5.3 is stratum preserving, the same deformation argument as in Lemma 5.7.2 gives the following.

Theorem 5.8.1

Let $f:M \to {\mathbb R}$ be a smooth function and suppose f|W is proper. Suppose X ⊂ W is a stratum and that x ₀ ∈ X is a nondegenerate critical point of f with isolated critical value v = f(x ₀) ∈ (a, b) and Morse index λ. Suppose there are no more critical values of f|W in the interval [a, b]. Choose 0 < δ ≪ 𝜖 as in (*) and (**) and let N = N _𝜖(x ₀) be the normal slice. Then there is a natural isomorphism of Morse groups

$$\displaystyle \begin{aligned} H^r(W_{\le b},W_{\le a}; A{{}^{\bullet}}) \cong H^{r-\lambda} \left(N_{[v-\delta,v+\delta]}, N_{v-\delta};A{{}^{\bullet}}|N \right).\end{aligned}$$

5.8.2 Sheaf Theoretic Expression

Kashiwara and Schapira [44, §5.1, §5.4] and Schürmann [70] prefer a sheaf-theoretic expression for the Morse group. Let

$$\displaystyle \begin{aligned} x_0 \in X \subset W \subset M \overset{f}{\longrightarrow} {\mathbb R}\end{aligned}$$

as in Theorem 5.8.1 above and suppose f(x ₀) = 0 is an isolated critical value of f|W. Let $A{{ }^{\bullet }}\in D^b_c(W)$ be a constructible complex of sheaves. Set

$$\displaystyle \begin{aligned} Z = \left\{ x \in W| f(x)\ge 0\right\}\end{aligned}$$

with inclusion i : Z → W and let $S_Z^{\bullet }=i_Z^!A{{ }^{\bullet }}=R\Gamma _ZA{{ }^{\bullet }}$ denote the sheaf obtained from A ^• with sections supported in Z, cf. Sect. 5.7.5. Let U = B _𝜖(x ₀) ∩ W be a basic neighborhood of the critical point x ₀. If a < 0 < b and [a, b] contains no critical values other than 0 then for 0 < δ ≪ 𝜖 Thom’s first isotopy lemma (Theorem 5.5.1 above) gives isomorphisms of the Morse groups:

$$\displaystyle \begin{aligned} H^r(W_{\le b}, W_{\le a}; A{{}^{\bullet}}) &\cong H^r(U_{\le \delta}, U_{\le -\delta}; A{{}^{\bullet}})\\ &\cong H^r(U_{\le \delta}, U_{<0}; A{{}^{\bullet}})\\ &\cong H^r(U_{\le \delta}; i_Z^!A{{}^{\bullet}})\\ &\cong {\mathbf{H}}^{\mathbf r}_{x_0}(i_Z^!A{{}^{\bullet}}) = {\mathbf{H}}^{\mathbf r}_{x_0}(R\Gamma_ZA{{}^{\bullet}}) \end{aligned} $$

since the stalk cohomology is the limit as 𝜖, δ → 0, but changing 𝜖, δ does not change the cohomology provided 0 < δ ≪ 𝜖 remain in the region shown in Fig. 5.2, that is, they satisfy (*) Sect. 5.4.1 and (**) of Sect. 5.5.3. If we apply the main theorem in stratified Morse theory, this Morse group is identified with

$$\displaystyle \begin{aligned}\mathbf{ H}^{\mathbf{r-\lambda}}_{x_0}(i_{Z \cap N}^!(A{{}^{\bullet}}|N))\end{aligned}$$

where N = T ∩ W ∩ B _𝜖(p) denotes the normal slice to the stratum X. Except for the shift λ (which comes from the tangential Morse data), this expression depends only on the (nondegenerate) covector ξ = df(x ₀) ∈ Λ_X, cf. Theorem 5.5.2. In Sect. 5.8.3 we arrange that λ = 0.

5.8.3 Characteristic Cycle

Let A ^• be a constructible complex of sheaves on a Whitney stratified subset W ⊂ M. From the preceding paragraph, for each stratum X of W, for each point x ₀ ∈ X and for each nondegenerate conormal vector ξ ∈ Λ_X at x ₀ there is a collection of Morse groups

$$\displaystyle \begin{aligned}H^r(\xi;A{{}^{\bullet}}):=H^r(N_{\le \delta}, N_{<0}; A{{}^{\bullet}}|N) \cong H^r_{x_0}(i^!_{Z\cap N}(A{{}^{\bullet}}|N)) \cong H^r_{x_0}(i^!_Z(A{{}^{\bullet}}))\end{aligned}$$

that measures the local change in cohomology for any smooth function $\phi :M \to {\mathbb R}$ chosen so that

• ϕ(x ₀) = 0

• $d\phi (x_0)|T_{x_0}X=0$,

• dϕ(x ₀) = ξ ∈ Λ_X is nondegenerate

• ϕ|X has a local nondegenerate minimum at x ₀

If ξ varies within a single connected component Λ_α of Λ_X the Morse group H ^r(ξ, A ^•) does not change, nor does the Euler characteristic

$$\displaystyle \begin{aligned} \chi(\xi;A{{}^{\bullet}}) = \sum_{r \ge 0} (-1)^r \text{rank}(H^r(\xi;A{{}^{\bullet}}) \otimes \mathbb Q).\end{aligned} $$

(5.11)

Kashiwara’s idea [42] is to use these coefficients to create a Lagrangian cycle. (cf. [44, §IX], [70, §5.2].)

Each $T^*_XM$ is a smooth Langrangian submanifold of T ^∗ M and the union $\bigcup _XT^*_XM$ is closed by Whitney’s condition A. However, the closure $\overline {T^*_XM}$ could be wild unless we assume, as we do for the rest of this article, that W is a subanalytic subset of an orientable real analytic manifold M Then an orientation of M induces an orientation on $T^*_XM$ (cf. [69, §2]) and the set of nondegenerate conormal vectors $\Lambda _X \subset T^*_XM$ breaks into finitely many connected components Λ_α. Define the characteristic cycle

$$\displaystyle \begin{aligned} CC(A{{}^{\bullet}}) = \sum_X \sum_{\alpha} m_{\alpha}\left[\overline{\Lambda_{\alpha}}\right]\end{aligned} $$

(5.12)

where the first sum is over strata X, the second sum is over connected components Λ_α of Λ_X, where $m_{\alpha } = \chi (\xi ;A{{ }^{\bullet }})\in {\mathbb Z}$ for any ξ ∈ Λ_α, and where Λ_α is oriented as above.

Theorem 5.8.2 ([42])

If A ^• is cohomologically constructible then CC(A ^•) is well defined and is a Borel-Moore Lagrangian cycle in $H_n^{BM}(T^*M)$ supported on $T^*_WM=\bigcup _XT^*_XM$.

For any triangulation of CC(A ^•) the interior of each n-dimensional simplex will be contained in a connected component Λ_α of the nondegenerate covectors of some stratum X, and so the above prescription will define a simplicial chain (with infinite support) in T ^∗ M. Kashiwara’s theorem is that its homological boundary vanishes, cf. the discussion [70, §5.0.1].

The characteristic cycle construction is natural with respect to push forward, pullback and Verdier duality [44, §9.4]. The characteristic cycle has many applications in the theory of $\mathcal D$-modules [55], the Gauss-Manin connection [46] and representation theory [69, 75].

5.8.4 Euler Characteristic

Let A ^• be a complex of sheaves of k-vector spaces (where k is a field) that is constructible with respect to a Whitney stratification (with connected strata) of a closed subanalytic subset W ⊂ M. The Euler characteristic of the stalk cohomology at a point x ∈ W is

$$\displaystyle \begin{aligned} \chi_x(A{{}^{\bullet}}) = \sum_{j\ge 0}(-1)^j \dim H^j_x(A{{}^{\bullet}}).\end{aligned} $$

(5.13)

It is independent of the point x as it varies within a single connected component of a single stratum, which is to say that it is a constructible function.

The Euler characteristic with compact support is additive. Therefore, if the cohomology with compact support $H_c^r(W;A{{ }^{\bullet }})$ is finite dimensional for all r then the Euler characteristic with compact support

$$\displaystyle \begin{aligned} \chi_c(W;A{{}^{\bullet}}) = \sum_{r \ge 0}(-1)^r\dim H_c^r(W;A{{}^{\bullet}}) = \sum_X \chi_c(X)\chi_x(A{{}^{\bullet}}) \end{aligned} $$

(5.14)

is defined and finite, where the sum is over the strata of W and x ∈ X. Kashiwara’s index theorem [41] says that if W is compact then the Euler characteristic is the intersection product of the zero section with the characteristic cycle:

$$\displaystyle \begin{aligned} \chi(W;A{{}^{\bullet}}) = \chi_c(W;A{{}^{\bullet}}) = T^*_MM \cap CC(A{{}^{\bullet}}).\end{aligned}$$

5.9 Complex Stratified Morse Theory

5.9.1 Levi Form

Let M be a complex n dimensional manifold and let $f:M \to {\mathbb R}$ be a smooth function. The E. E. Levi form at x ∈ M is the Hermitian form

$$\displaystyle \begin{aligned}L_f(x)=\partial \bar\partial f(x) = \left( \frac{\partial^2f(x)}{\partial z_i\partial \bar z_j} \right)\end{aligned}$$

defined on the tangent space T _x M. The associated quadratic form satisfies

$$\displaystyle \begin{aligned}L_f(x)(v) = \sum_{i,j} \frac{\partial^2 f} {\partial z_i \partial \bar z_j} v_i \bar v_j = \frac{1}{4}(H_f(x)(v) + H_f(x)(iv))\end{aligned}$$

where

$$\displaystyle \begin{aligned}H_f(x)(v) = \sum_{i,j} \frac{\partial^2f(x)}{\partial x_i \partial x_j}v_iv_j\end{aligned}$$

is the quadratic form associated to the Hessian of f at x by forgetting the complex structure on M. If N ⊂ M is a complex submanifold containing x then L _f(x)|N = L _f|N(x) but the same does not hold for H _f unless df(x) = 0.

Now suppose that df(x) = 0 and that H _f(x) is nondegenerate. Let λ _x(f) be the Morse index of f at x, that is, the (real) dimension of the largest (real) subspace of T _x M on which H _f is negative definite. Let σ _x(f) the complex dimension of the largest complex subspace on which L _f is negative definite and let ν _x(f) be the nullity of L _f. An exercise (see [31, §4.A.2], [5, p. 311]) gives:

$$\displaystyle \begin{aligned} \lambda_x(f) &\ge \sigma_x(f) + \nu_x(f)\\ \lambda_x(-f) &\ge \sigma_x(-f) + \nu_x(f). \end{aligned} $$

If $f:{\mathbb C}^N \to {\mathbb R}$ is the distance from a codimension r linear subspace of ${\mathbb C}^N$ and $M \subset {\mathbb C}^N$ is a submanifold of complex dimension n and if f|M has a nondegenerate critical point at x ∈ M then the Morse index λ of f|M at x satisfies n ≥ λ ≥ n − r.

5.9.2 Local Structure of Complex Varieties

Throughout this chapter, W ⊂ M denotes a complex analytic subvariety of a complex analytic variety, together with a complex analytic stratification with connected strata of W. If X is a stratum of W and p ∈ X then there is a canonical isomorphism of real vector spaces

$$\displaystyle \begin{aligned} T_p^*(X)= \mathrm{Hom}_{{\mathbb R}}(T_pX, {\mathbb R}) \cong \mathrm{Hom}_{{\mathbb C}}(T_pX,{\mathbb C}).\end{aligned} $$

(5.15)

In this case, a theorem of B. Teissier [76] states that the set of degenerate covectors (that is, $\xi \in T^*_XM$ such that ξ(τ) = 0 for some limit τ of tangent spaces from some larger stratum Y > X) form a proper complex analytic (conical) subvariety of the conormal space $T^*_{X,p}M$ of complex codimension ≥ 1. So its complement Λ_X,p is connected and the normal Morse data (Sect. 5.5.3) is independent (up to stratum preserving homeomorphism) of the choice of covector ξ ∈ Λ_X.

By choosing local coordinates near p ∈ M, replacing M by ${\mathbb C}^m$, any $\xi \in T_p^*(M)$ may be realized as the differential of a complex linear function $\pi :{\mathbb C}^m \to {\mathbb C}$, or equivalently, using (5.15) as the differential of a real linear function $\phi = Re(\pi ):{\mathbb C}^m \to {\mathbb R}$. By choosing an analytic submanifold T transversal to X with $T \pitchfork X = \{p\}$ we may also arrange (locally) that the normal slice $N=T\pitchfork W$ to the stratum X is a closed complex analytic subvariety of ${\mathbb C}^m$, Whitney stratified with strata T ∩ Y  where Y ≥ X runs through strata of W. It has a zero dimensional stratum T ∩ X = {p} = {0}, and we may assume that π(0) = 0.

5.9.3 Complex Link

Assume as above that $N \subset {\mathbb C}^m$, {p} = {0}⊂ N is a zero dimensional stratum, that $\pi :{\mathbb C}^m \to {\mathbb C}$ is linear and ξ = dπ(0) ∈ Λ_X is a nondegenerate covector. Let r(z) denote the square of the distance in ${\mathbb C}^m$ from the origin. As in Sect. 5.5.3 there is an open region $0 < \delta \ll \epsilon \subset {\mathbb R}^2$ such that for any pair (δ, 𝜖) in this region the following holds:

• ∂B _𝜖(0) is transverse to each stratum of N

• for each stratum Y ∩ T of N (where Y > X) the restriction π|(Y ∩ T) has no critial points with critical values in the disk D _δ(0) except for the case {0} = X ∩ T

• for each stratum Y ∩ T of N and for any point z ∈ Y ∩ T ∩ ∂B _𝜖(0) such that |π(z)|≤ δ, the complex linear map

  $$\displaystyle \begin{aligned} (dr(z), d\pi(z)):T_z(Y \cap T) \to {\mathbb C}^2\end{aligned}$$

  has rank 2. (Such points z do not exist if $\dim (Y \cap T) <2$.)

With this data, identify $\delta = \delta + 0i \in {\mathbb C}$ and define the complex link

$$\displaystyle \begin{aligned} \mathcal L = \pi^{-1}(\delta) \cap N \cap B_{\epsilon}(0),\ \partial\mathcal L = \pi^{-1}(\delta) \cap N \cap \partial B_{\epsilon}(0).\end{aligned} $$

(5.16)

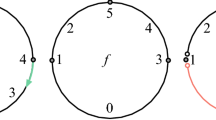
It is a single fiber of the (stratified) fiber bundle over the circle S ¹ = ∂D _δ,

$$\displaystyle \begin{aligned} \mathcal E =\pi^{-1}(\delta e^{i \theta}) \cap N \cap B_{\epsilon}(0),\ \partial\mathcal E = \pi^{-1}(\delta e^{i \theta}) \cap N \cap \partial B_{\epsilon}(0)\end{aligned}$$

$$\displaystyle \begin{aligned}(\mathcal E, \partial \mathcal E) \to S^1=\partial D_{\delta} = \{ \delta e^{i\theta}|\ 0 \le \theta \le 2\pi\} \end{aligned}$$

and the boundary $\partial \mathcal E$ is a trivial bundle over S ¹ = ∂D _δ. See Fig. 5.4.

Fig. 5.4

Normal slice with complex link, 𝜖-ball and δ-disk

Theorem 5.9.1 ([31])

The bundle $\mathcal E$ is stratified-homeomorphic to the mapping cylinder of a (stratified) monodromy homeomorphism

$$\displaystyle \begin{aligned} \mu: (\mathcal L, \partial \mathcal L) \to (\mathcal L, \partial \mathcal L)\end{aligned}$$

that is the identity on $\partial \mathcal L$ and is well defined up to stratum preserving isotopy. The link L _X(p) (Eq. (5.5)) is homeomorphic to the “cylinder with caps”,

$$\displaystyle \begin{aligned} L_X(p) \cong \mathcal E \cup_{\partial \mathcal E} \left(\partial \mathcal L \times D_{\delta}\right).\end{aligned} $$

(5.17)

5.9.4 First Consequences

Let $f:W \to {\mathbb R}$ be a Morse function with a nondegenerate critical point p ∈ X ⊂ W. Let $\mathcal L$ be the complex link of the stratum X. Since the set Λ_X of nondegenerate covectors is connected, the complex link is independent (up to stratum preserving homeomorphism) of the covector ξ ∈ Λ_X that is used in its definition and we may take ξ = df(p). Let $A{{ }^{\bullet }} \in D^b_c(W)$ be a constructible complex of sheaves.

Theorem 5.9.2

The normal Morse data for f at the critical point p ∈ X ⊂ W has the homotopy type of the pair

$$\displaystyle \begin{aligned} \left( \mathit{\text{cone}}(\mathcal L), \mathcal L\right).\end{aligned}$$

The Morse group H ^r(ξ, A ^•) at p is:

$$\displaystyle \begin{aligned} H^r(N,N_{<0};A{{}^{\bullet}}) \cong H^r(N_{\epsilon}(p), \mathcal L; A{{}^{\bullet}})= {\mathbf H}^r_{p}(R\Gamma_ZA{{}^{\bullet}}) \end{aligned}$$

where $Z = \left \{z\in N|\ f(z) \ge 0\right \}$ , cf. Sect. 5.8.2 and N _𝜖(p) = N ∩ B _𝜖(p).

5.10 Complex Morse Theory of Sheaves

5.10.1 The Braid Diagram

Throughout this section we fix a constructible complex of sheaves $A{{ }^{\bullet }} \in D^b_c(W)$ and x ∈ X. The homeomorphisms described in the preceding section are stratum preserving so they induce isomorphisms on cohomology with coefficients in A ^• and they allow us to interpret these cohomology groups,

$$\displaystyle \begin{aligned} H^r(N-x; A{{}^{\bullet}}) &\cong H^r(L_X(x);A{{}^{\bullet}}) & H^r(N,N-x;A{{}^{\bullet}}) &\cong H^r(i_x^!A{{}^{\bullet}})\\ H^r(N;A{{}^{\bullet}}) &\cong H^r(i_x^*A{{}^{\bullet}}) &H^r(N,N_{<0};A{{}^{\bullet}}) &\cong H^r(\xi;A{{}^{\bullet}}) \\ H^r(N_{<0};A{{}^{\bullet}}) &\cong H^r(\mathcal L; A{{}^{\bullet}})& H^{r+1}(N-x, N_{<0};A{{}^{\bullet}})&\cong H^{r}(\mathcal L,\partial\mathcal L; A{{}^{\bullet}}) \end{aligned} $$

By (5.17) the “variation” map $I-\mu : H^r(\mathcal L;A{{ }^{\bullet }}) \to H^r(\mathcal L, \partial \mathcal L; A{{ }^{\bullet }})$ may be identified with the connecting homomorphism in the third row of this display, that is, the long exact sequence for the pair (N − x, N _<0), cf. [28]. As in [31, p. 215] the long exact sequences for the triple of spaces

$$\displaystyle \begin{aligned} N_{<0} \subset N-\{x\} \subset N\end{aligned}$$

may be assembled into a braid diagram with exact sinusoidal rows (Fig. 5.5). (cf. [70, §6.1] where the same sequences are considered separately):

Fig. 5.5

Braid diagram

5.10.2 Euler Characteristics and the Characteristic Cycle

The results in Sects. 5.8.3 and 5.8.4 become simpler in the presence of a complex structure. Let W be a complex analytic variety with a fixed analytic Whitney stratification with connected strata. Let $A{{ }^{\bullet }} \in D^b_c(W)$. The Euler characteristics of the normal Morse data (5.11), of the complex link (5.16), and of the stalk cohomology (5.13) are constructible functions (that is, constant on strata). For a stratum X of W we denote these values by

$$\displaystyle \begin{aligned} m_X(A{{}^{\bullet}}), \chi(\mathcal L, A{{}^{\bullet}}), \chi_x(A{{}^{\bullet}}) = m_X(A{{}^{\bullet}}) + \chi(\mathcal L, A{{}^{\bullet}})\end{aligned}$$

respectively (where x ∈ X). Equation (5.14) becomes⁶ the sum over strata,

$$\displaystyle \begin{aligned} \chi(W;A{{}^{\bullet}}) = \sum_X\chi(X)\chi_x(A{{}^{\bullet}}) = \chi_c(W;A{{}^{\bullet}})\end{aligned}$$

(where x ∈ X) assuming the cohomology H ^∗(W;A ^•) is finite dimensional.

The characteristic cycle (5.12) of A ^• is the sum over all strata X ⊂ W:

$$\displaystyle \begin{aligned} CC(A{{}^{\bullet}}) = \sum_X m_X(A{{}^{\bullet}}) \left[ \overline{T^*_XM}\right]. \end{aligned}$$

Euler characteristics of the normal Morse data and of the stalk cohomology at a point p ∈ W are related by a formula of [15], the sum over strata X such that $\overline {X} \ni p$:

$$\displaystyle \begin{aligned} \chi_x(A{{}^{\bullet}}) = \sum_{X}(-1)^{\dim_{{\mathbb C}}X} m_X(A{{}^{\bullet}}) \mathbf{Eu}_p(\overline{X}).\end{aligned}$$

Here, $\mathbf {Eu}_p(\overline {X})$ is MacPherson’s local Euler obstruction [53] and the sign $(-1)^{\dim _{{\mathbb C}}X}$ arises due to choice of orientations, cf. [70, §5.0.3].

When $A{{ }^{\bullet }} = \mathbb Q$ this formula can be inverted, so as to express Eu _p(W) as a linear combination of the various $m_X(\mathbb Q)$ by considering $\mathbf {Eu}_Y(\overline {X})=\mathbf {Eu}_y(\overline {X})$ (where y ∈ Y ) to be a square matrix of integers indexed by strata Y < X (say, with respect to a total ordering of the strata that respects the natural ordering). It is lower triangular, of determinant 1, so it has an inverse that is also a lower triangular matrix of integers with 1s on the diagonal.

5.10.3 Vanishing Conditions

The braid diagram, together with induction and the estimates in Sect. 5.9.1, may be used to prove many vanishing theorems and Lefschetz-type theorems in sheaf cohomology, see [28, 31, 34, 42, 70]. The following serve as illustrations. To avoid issues of torsion and injective resolutions of R-modules, from now on we assume that all sheaves are sheaves of vector spaces over a field k (usually $k = \mathbb Q$). Using the convex function distance² from the point {x} below, and induction, one finds the following two results (cf. [3]) which may be proven together (since the statement for one becomes the inductive step for the other):

Theorem 5.10.1

Suppose $A{{ }^{\bullet }}\in D^b_c(W)$ is a complex of sheaves of k-vector spaces on a complex analytic set W such that for each stratum X and for each point x ∈ X, with i _x : {x}→ W, the stalk cohomology vanishes:

$$\displaystyle \begin{aligned}H^r(i_x^*A{{}^{\bullet}}) = 0 \mathit{\text{ whenever }}\ r > \mathrm{codim}_{{\mathbb C}}(X).\end{aligned} $$

(5.18)

Then $H^r(\mathcal L; A{{ }^{\bullet }}) = 0$ for all $r > \ell = \dim _{{\mathbb C}}(\mathcal L)$ . If the Verdier dual $\mathbb D_W(A{{ }^{\bullet }})$ satisfies (5.18), or equivalently, (if W has pure (complex) dimension n and)

$$\displaystyle \begin{aligned} H^r(i_x^!A{{}^{\bullet}}) = 0 \mathit{\text{ whenever }}\ r < n+\dim_{{\mathbb C}}(X),\end{aligned} $$

(5.19)

then $H^r(\mathcal L, \partial \mathcal L; A{{ }^{\bullet }}) = 0$ for all r < ℓ.

Theorem 5.10.2

Let W be a Stein space or an affine complex algebraic variety of dimension n and let $A{{ }^{\bullet }}\in D^b_c(W)$ be a complex of sheaves on W that satisfies (5.18). Then H ^r(W;A ^•) = 0 for all r > n. Let W be a projective variety and let H be a hyperplane that is transverse to each stratum of some Whitney stratification of W. Let A ^• be a complex of sheaves on W that satisfies (5.19). Then H ^r(W, W ∩ H;A ^•) = 0 for all r < n.

5.10.4 Homotopy Version

Homotopy versions of these statements follow from the same induction, by replacing Theorem 5.10.1 with Theorem 5.10.3 below, see [31].

Theorem 5.10.3

The complex link $\mathcal L$ of a point x in a stratum X of a complex analytically stratified complex analytic set W ⊂ M has the homotopy type of a CW complex of dimension $\le \ell = \dim _{{\mathbb C}}(\mathcal L) = \operatorname {\mathrm {codim}}_W(X)-1$ . Moreover $\mathcal L$ may be obtained from $\partial \mathcal L$ by attaching cells of dimension ≥ ℓ.

Consequently, a Stein space or affine complex algebraic variety of dimension n has the homotopy type of a CW complex with cells of dimension ≤ n. Partially weakening the hypotheses in Theorems 5.10.1, 5.10.2, or 5.10.3 will result in a partial weakening of the conclusions, so Grothendieck’s conjectures [33] on rectifiable homotopical depth and their homological analogues may be proven this way, see [34] and [70, §6.0].

5.10.5 Perverse Sheaves

The standard reference for this section is [8] but a great survey is [16]. See also [44, 48]. Suppose W ⊂ M is an algebraic variety of pure dimension n. A complex of sheaves A ^• on W is said to be (middle) perverse if it satisfies both (5.18) and (5.19) with respect to some⁷algebraic stratification of W. It is an intersection complex (IC) if it satisfies the stronger conditions, obtained by replacing >  with ≥ and <  with ≤ in (5.18) and (5.19). An IC sheaf on W is determined by its restriction E to the top stratum, which is (isomorphic to) a local coefficient system [30] so we may denote it unambiguously by IC _W(E).

The category $\mathcal P(W)$ of perverse sheaves is the full subcategory of $D^b_c(W)$ whose objects are perverse. It is an Abelian, Artinian and Noetherian subcategory and is preserved under Verdier duality. The simple perverse sheaves are the shifted IC sheaves, $IC_V(E_V)[\dim (V)]$ of irreducible subvarieties V ⊂ W and irreducible local systems E _V defined on the nonsingular part of V . Using the braid diagram and induction it is easy to show [44, Thm. 10.3.12] that:

Theorem 5.10.4

A constructible complex A ^• on W is perverse if and only if for every stratum X of W, for every x ∈ W and for every nondegenerate covector $\xi \in T_X^*M$ at x, the Morse groups H ^r(ξ, A ^•) = 0 vanish unless $r = \operatorname {\mathrm {codim}}(X)$.

Consequently, Morse theory applied to perverse sheaves reduces to the familiar situation in which the nonzero Morse groups live in a single degree.

The Abelian category of perverse sheaves was first discovered in conjunction with the Kazhdan-Lusztig conjecture [47, Conj. 1.5] whose proof (cf. [9, 14]) involved the Riemann-Hilbert correspondence which we state here without explaining the terms, cf. [12]. Let M be a complex analytic manifold and $\mathcal D_M$ its sheaf of differential operators. Let $D^b_{rh}(\mathcal D_M)$ be the derived category of (coherent sheaves of) modules over $\mathcal D_M$ whose cohomology sheaves are holonomic with regular singularities. Then the de Rham functor defines an equivalence [40, 58] of derived categories $D^b_{rh}(\mathcal D_M) \to D^b_c(M)$ which commutes with direct images, inverse images and duality, and it restricts to an equivalence between the abelian category of holonomic modules with regular singularities and the abelian category of perverse sheaves on M.

5.10.6 Further Properties

In this section W is a complex projective algebraic variety and “sheaf” means sheaf of $\mathbb Q$-vector spaces or ${\mathbb C}$-vector spaces, but the theory extends to $\mathbb Q_{\ell }$-sheaves on schemes over any field. Properties of perverse sheaves are most conveniently expressed by introducing Deligne’s degree shift which is assumed throughout [8] and which we shall use in this paragraph, replacing IC _W with $IC_W[\dim (W)]$ so that Verdier duality is symmetric about degree 0. Hence, if i : V ⊂ W is a (closed) subvariety and $\mathcal L$ is a local system on the nonsingular part of V  then $Ri_*IC_V(\mathcal L)$ is perverse on W and more generally (using this degree shift), i ^∗, i ^! and Ri _∗ = Ri _! take perverse sheaves to perverse sheaves. The conditions (5.18) and (5.19) that A ^• should be a perverse sheaf are that for all x ∈ W (with i _x : {x}→ W) and for all $r \in {\mathbb Z}$ the following holds:

$$\displaystyle \begin{aligned} \dim \{ x \in W| \ H^r(i_x^*A{{}^{\bullet}}) \ne 0 \} & \le -r\\ \dim \{ x\in W| \ H^r(i_x^!A{{}^{\bullet}}) \ne 0 \} & \le r. \end{aligned} $$

The perverse cohomology functors ${ }^p\mathcal H^j:D^b_c(W) \to \mathcal P(W)$ take distinguished triangles to long exact sequences (of perverse sheaves), commute with Verdier duality, and identify perverse sheaves⁸as those complexes $A{{ }^{\bullet }} \in D^b_c(W)$ such that ${ }^p\mathcal H^r(A{{ }^{\bullet }}) = 0$ for all r≠0.

If f : W → Y  is a proper algebraic map, the decomposition theorem with coefficients in $\mathbb Q$ [8, §5.4] says:

Theorem 5.10.5

There is a decomposition in $D^b_c(Y)$,

$$\displaystyle \begin{aligned} Rf_*(IC_W) \cong \bigoplus_{i \in {\mathbb Z}} {}^p\mathcal H^i(Rf_*(IC_W)[-i],\end{aligned} $$

(5.20)

and a hard Lefschetz morphism $\eta :{ }^p\mathcal H^i(Rf_*(IC_W)) \to { }^p\mathcal H^{i+2}(Rf_*(IC_W))$ which induces isomorphisms of perverse sheaves,

$$\displaystyle \begin{aligned} \eta^r: {}^p\mathcal H^{-r}(Rf_*(IC_W)) \to {}^p\mathcal H^{r}(Rf_*(IC_W))\end{aligned}$$

for all r ≥ 1. There is a stratification Y =∐_β Y _β with local systems E _β on Y _β and a further decomposition

$$\displaystyle \begin{aligned}^p\mathcal H^i(Rf_*(IC_W)) \cong \textstyle{\bigoplus_{\beta}} IC(\overline{Y_{\beta}}; E_{\beta})\end{aligned}$$

of each factor in (5.20) into a direct sum of IC sheaves of subvarieties.

This is one of the deepest and most useful results in mathematics, with many applications to algebraic geometry, representation theory, combinatorics, number theory, automorphic forms and other areas of mathematics. See, for example, [16, 38, 52, 60, 61, 63, 72].

5.11 Perfect Morse Functions and Fixed Point Theorems

5.11.1 Torus Actions

The Morse-Bott theory (Sect. 5.3.2) of critical points for smooth manifolds also has various extensions to singular spaces. Suppose the torus $T = {\mathbb C}^*$ acts algebraically on a (possibly singular) normal projective algebraic variety W with resulting moment map $\mu :W \to {\mathbb R}$ as in Sect. 5.3.2. Let W ^T =∐_r V _r denote the fixed point components of the torus action and define $V_r^{\pm }$ as in (5.3) with inclusions

(5.21)

On each V _r there is a complex of sheaves,

$$\displaystyle \begin{aligned} IC_r^{!*} = (j_r^+)^!(h_r^+)^*(IC_W) \cong (j_r^-)^*(h_r^-)^!(IC_W)\end{aligned}$$

representing cohomology with closed supports in the directions flowing into V _r and with compact supports in the directions flowing away from V _r. (The isomorphism is proven in [6] and [32]). In [49] F. Kirwan uses the decomposition theorem (Theorem 5.10.5) to prove the following.

Theorem 5.11.1 ([49])

The moment map μ is a perfect Morse Bott function and it induces a decomposition for all i, expressing the intersection cohomology of W as a sum of locally defined cohomology groups of the fixed point components:

$$\displaystyle \begin{aligned} IH^i(W) \cong \bigoplus_r H^i(V_r;IC_r^{!*}).\end{aligned} $$

(5.22)

The result also generalizes to actions of a torus $T = ({\mathbb C}^*)^m$. In [6] the sheaf $IC_r^{!*}$ is shown to be a direct sum of IC sheaves of subvarieties of V _r.

5.11.2 Hyperbolic Lefschetz Numbers

The time $t = 1 \in {\mathbb C}^*$ map of a ${\mathbb C}^*$ action (see Sects. 5.11.1, 5.3.2 above) is an example of a map with hyperbolic fixed points. For general hyperbolic maps the full decomposition (5.22) may fail but the Lefschetz number can still be expressed as a sum of explicit local contributions.

Let f : W → W be a subanalytic self map defined on a subanalytically stratified subanalytic set W. A connected component V  of the fixed point set of f is said to be hyperbolic⁹ if there is a neighborhood U ⊂ W of V  and a subanalytic mapping $r=(r_1,r_2):U \to {\mathbb R}_{\ge 0} \times {\mathbb R}_{\ge 0}$ so that r ⁻¹(0) = V  and so that r ₁(f(x)) ≥ r ₁(x) and r ₂(f(x)) ≤ r ₂(x) for all x ∈ U. Hyperbolic behavior of f : W → W is illustrated in Fig. 5.6. (Flow lines connecting r(x) and r(f(x)) do not exist in general).

Fig. 5.6

Behavior near a hyperbolic fixed point

Let V ⁺ = r ⁻¹(Y ) and V ⁻ = r ⁻¹(X) where X, Y  denote the X and Y  axes in ${\mathbb R}_{\ge 0} \times {\mathbb R}_{\ge 0}$ with inclusions j ^±, h ^± as in (5.21). If $A{{ }^{\bullet }} \in D^b_c(W)$ define

$$\displaystyle \begin{aligned}A^{!*} = (j^+)^!(h^+)^*A{{}^{\bullet}}\ \text{ and }\ A^{*!} = (j^-)^*(h^-)^!A{{}^{\bullet}}.\end{aligned}$$

A morphism Φ : f ^∗(A ^•) → A ^• is called a lift of f to $A{{ }^{\bullet }} \in D^b_c(W)$. Such a lift induces a homomorphism Φ_∗ : H ⁱ(W;A ^•) → H ⁱ(W;A ^•) and defines the Lefschetz number

If V ⊂ W is a hyperbolic component of the fixed point set then Φ also induces self maps $\Phi _V^{!*}$ on H ⁱ(V ;A ^!∗) and $\Phi _V^{*!}$ on H ⁱ(V ;A ^∗!) and in [32] it is proven that associated local Lefschetz numbers $\text{Lef}(\Phi _V^{!*}; A^{!*})$ and $\text{Lef}(\Phi _V^{*!};A^{*!})$ are equal.

Theorem 5.11.2 ([32])

Given f : W → W, $A{{ }^{\bullet }} \in D^b_c(W)$ and Φ : f ^∗(A ^•) → A ^• as above. Suppose that W is compact and that all connected components of the fixed point set are hyperbolic. Then the global Lef(f, A ^•) is the sum over connected components of the fixed point set of the local Lefschetz numbers:

$$\displaystyle \begin{aligned} \mathrm{Lef}(f, A{{}^{\bullet}}) = \sum_V \mathrm{Lef}(\Phi_V^{!*}; A^{!*}) = \sum_V \mathrm{Lef}(\Phi_V^{*!}; A^{*!}).\end{aligned}$$

Moreover, each local Lefschetz number $\mathrm {Lef}(\Phi ^{!*}_V)$ is the Euler characteristic of a constructible function Lef( Φ_x, A ^!∗) for x ∈ V  (see Sect. 5.8.4 above). Let $V = \coprod V_r$ be a stratification of the fixed point component V  so that the pointwise Lefschetz number Lef( Φ_x, A ^!∗) is constant on each stratum V _r, and call it L _r( Φ;A ^!∗). If V  is compact then (cf. [32, §11.1]),

$$\displaystyle \begin{aligned}\text{Lef}(\Phi_V^{!*};A^{!*}) = \sum_r \chi_c(V_r) L_r(\Phi;A^{!*}).\end{aligned}$$

5.12 Specialization

5.12.1 Specialization by Retraction

The geometry described in Sect. 5.9.3 and Fig. 5.4, associated to a nondegenerate covector ξ = dπ(0) extends with very few modifications to much more general situations. Let X ⊂ M be a complex (n + 1) dimensional analytic subvariety of some complex analytic manifold M and let $f:X \to {\mathbb C}$ be a proper complex analytic mapping. Such a mapping can be stratified with complex analytic strata, which in the target space ${\mathbb C}$ consists of discrete points. We wish to understand the local behavior of f near one such stratum which we may take to be $0 \in {\mathbb C}$. The central fiber X ₀ = f ⁻¹(0) is a closed union of strata and X _t = f ⁻¹(t) is called “the” nearby fiber if t≠0 is sufficiently small (see below). Let

$$\displaystyle \begin{aligned} r_0:T_{X_0}(\epsilon) \to X_0\end{aligned}$$

denote the canonical retraction (Sect. 5.4.4) of a neighborhood $T_{X_0}$ of X ₀, whose fiber at x ∈ X ₀ is stratified-homeomorphic to the normal slice N _𝜖(x) at x through the stratum S ⊂ X ₀ containing x.

As in Sect. 5.9.3 there is an open region, 0 < δ ≪ 𝜖 in the (δ, 𝜖) plane so that if (δ, 𝜖) lies in this region and if $t\in {\mathbb C}^*$, 0 < |t|≤ δ then the pre-image X _t = f ⁻¹(t) is contained in $T_{X_0}(\epsilon )$ and is transverse to ∂T _S(𝜖) for each stratum S ⊂ X ₀. The specialization map ψ : X _t → X ₀ is the restriction ψ = r ₀|X _t. The fiber ψ ⁻¹(x) of the specialization map is therefore the Milnor fiber of f, that is, the intersection of the normal slice N(x) with a ball B _𝜖(x) and with the nearby fiber X _t. Its (real) dimension is 2c where c denotes the complex codimension in X ₀ of the stratum S containing x. (So the codimension of S in X is c + 1. If the differential df(x) is a nondegenerate covector then the fiber ψ ⁻¹(x) is the complex link $\mathcal L$ in X of the stratum S, cf. Sect. 5.9.3). The monodromy μ : X _t → X _t is a stratum preserving homeomorphism and ψ ∘ μ = ψ.

5.12.2 Nearby Cycles

With $f:X \to {\mathbb C}$ and $t\in {\mathbb C}^*$ as above, and i _t : X _t → X, let $A{{ }^{\bullet }}\in D^b_c(X)$. The sheaf

$$\displaystyle \begin{aligned} \psi_f(A{{}^{\bullet}})=R\psi_*i_t^*A{{}^{\bullet}}=R\psi_*(A{{}^{\bullet}}|X_t) \in D_b(X_0)\end{aligned}$$

is called the sheaf of nearby cycles on X ₀. Its isomorphism class in $D^b_c(X_0)$ is independent of the choice of t (provided |t| < δ as above). Its cohomology is H ^r(X ₀;ψ _f(A ^•))≅H ^r(X _t;A ^•|X _t), cf. Eq. (5.9). The stalk cohomology of ψ _f(A ^•) at a point x ∈ X ₀ is the cohomology of the Milnor fiber, as described above. The monodromy passes to a morphism μ : ψ _f(A ^•) → ψ _f(A ^•). This sheaf may also be constructed [19] without choosing $t\in {\mathbb C}^*$: let

$$\displaystyle \begin{aligned}\tilde U = U \times_{f,e}{\mathbb C} \to U = X-X_0 = f^{-1}({\mathbb C} - \{0\})\end{aligned}$$

be the infinite cyclic cover obtained by pulling back $U \to {\mathbb C}^*$ under the map $e:{\mathbb C} \to {\mathbb C}^{*}$, $e(z) = \exp (2 \pi i z)$ as in the following diagram,

Then ψ _f(A ^•) = j ^∗ Ri _∗ Rπ _∗ π ^∗(A ^•|U).

As in Sect. 5.9.1 the index estimates for (a Morse perturbation of the) distance from x and induction show that ψ ⁻¹(x) has the homotopy type of a CW complex of dimension ≤ c, where c denotes the codimension (in X ₀) of the stratum containing x. Moreover, if A ^• is a complex of sheaves on X that satisfies (5.18) of Sect. 5.10.3 then the same argument implies that ψ _f(A ^•) also satisfies (5.18). Since the pushforward under a proper mapping commutes with Verdier duality, this proves (see [28, 31, §6.A], [44, §10], [8, §4.4], [13, Thm. 1.2]) that specialization takes constructible sheaves to constructible sheaves and preserves perverse sheaves (using Deligne’s degree shift):

Theorem 5.12.1

Suppose f : X → C is a proper complex algebraic map to a curve C. Let p ∈ C be a point and X _p = f ⁻¹(p) be the “central fiber”. Let ψ : X _t → X _p be the specialization map, for t ∈ C sufficiently close to p. Let A ^• be a perverse sheaf on X. Then A ^•|X _t is perverse on X _t and Rψ _∗(A ^•|X _t) = ψ _f(A ^•) is perverse on X _p.

If $D_{\delta }\subset {\mathbb C}$ is a sufficiently small disk about $0\in {\mathbb C}$ then for all i,

$$\displaystyle \begin{aligned} H^i(f^{-1}(D_{\delta}); A{{}^{\bullet}}) \cong H^i(X_0;A{{}^{\bullet}})\end{aligned}$$

for any $A{{ }^{\bullet }} \in D^b_c(X)$. The local invariant cycle theorem [8, §6.2.9], a corollary of Theorem 5.10.5, says that every monodromy-invariant class in IH ⁱ(X _t) extends to a class in IH ⁱ(f ⁻¹(D _δ)):

Theorem 5.12.2

The natural homomorphism to the invariant classes

$$\displaystyle \begin{aligned}H^i(X_0; IC_X|X_0) \to IH^i(X_t)^{\pi_1}=H^i(X_0; \psi_f(IC_X))^{\pi_1}\end{aligned}$$

is surjective, where $\pi _1\cong {\mathbb Z}$ is the monodromy action.

5.12.3 Vanishing Cycles

There is a canonical morphism A ^•|X ₀ → ψ _∗(A ^•) that arises from the restriction of sheaves for the inclusion $X_t\subset T_{X_0}(\epsilon )$. The sheaf of vanishing cycles ϕ _f(A ^•) is the third term in the resulting distinguished triangle:

(5.23)

Let $Z = \left \{x \in X|\ Re(f(x)) \ge 0 \right \}$ with inclusion i _Z : Z → X and j : X ₀ → Z. The sheaf of vanishing cycles is $\phi _f(A{{ }^{\bullet }}) \cong j^* i_Z^!A{{ }^{\bullet }}$ and its stalk cohomology $\mathbf {H^r}_{x}(i_Z^!A{{ }^{\bullet }})$ at x ∈ X ₀ is the local Morse group (with degree shift of 1) for the function $Re(f):X \to {\mathbb R}$, even though the covector ξ = df(x) may be degenerate. (If x ₀ ∈ X ₀ is a 0-dimensional stratum and if df(x ₀) is a nondegenerate covector then this is exactly the Morse group for Re(f) at x ₀ and the exact sequence on cohomology from (5.23) may be found in the braid diagram Sect. 5.10.1.) The action of the monodromy μ : X _t → X _t extends to a morphism μ : ϕ _f(A ^•) → ϕ _f(A ^•) and the variation map I − μ extends naturally to a morphism

$$\displaystyle \begin{aligned} \mathrm{var}:\phi_f(A{{}^{\bullet}}) \to \psi_f(A{{}^{\bullet}}).\end{aligned}$$

If A ^• is a perverse sheaf then so are ψ _f(A ^•) and ϕ _f(A ^•).

In particular if $X={\mathbb C}$ is stratified with a single stratum at $0\in {\mathbb C}$ and if A ^• is constructible and perverse with respect to this stratification then V = ψ _f(A ^•) and W = ϕ _f(A ^•) are (quasi-isomorphic to) vector spaces in degree zero with the following result (cf. [54, §6], [22, 81, §4]):

Theorem 5.12.3

The category of perverse sheaves on $({\mathbb C}, \{0\})$ is equivalent to the category of diagrams

where I + αβ and I + βα are invertible.

Vanishing cycles may be used to give quiver-like descriptions of the category of perverse sheaves in many other situations [54]. Oscillatory integrals and exponential sums may be estimated using vanishing cycles [1, 2, 17, 18, 45, 66, 68, 78]. The Fourier transform has a sheaf theoretic analog, the geometric Fourier transform [13, 44, 48] that is constructed using vanishing cycles and has many applications to representation theory and symplectic geometry (see for example [61, 62]). Mixed Hodge structures are constructed on the cohomology of vanishing cycles [65, 73, 74]. Morse theory and structure of the singularities plays a key role in the analysis of each of these fascinating applications.