Using “Enhanced Quantization” to Bound the Cosmological Constant, (for a Bound-on Graviton Mass), by Comparing Two Action Integrals (One Being from General Relativity) at the Start of Inflation

Abstract

The first result from 2018 is looking at two action integrals and also a Lagrangian multiplier as a constraint equation (on cosmological expansion). In doing so, with Padmanabhan’s version version of an inflaton, we then have a bound upon the cosmological constant. For the record, this is in fidelity with the author’s publication, in JHEPGC, entitled “Using ‘Enhanced Quantization’ to Bound the Cosmological Constant, and Computing Quantum Number n for Production of 100 Relic Mini Black Holes in a Spherical Region of Emergent Space-Time” which was in 2018. And was the genesis of the two integral comparison idea. The second result from 2018 is to use the inflaton results and conflate them with John Klauder’s action principle for a way to have the idea of a potential well, generalized by Klauder, with a wall of space-time in the pre-Planckian regime to ask what bounds the cosmological constant prior to inflation, and get an upper bound on the mass of a graviton. The third result from 2018 and the first cited reference is a redo of a multiverse version of the Penrose cyclic conformal cosmology to show how this mass of a heavy graviton inconsistent from cycle to cycle. The fourth result from 2020 is to ask if we can, using an idea from a publication by Diosi, in the Dice 2018 physics conference use a high energy comparison of Planck Length, and a De Broglie wavelength, to find out if we can extract from our estimate of Planck mass a statement as to entropy of the early universe, and the fifth result from 2020 is to comment upon a comparison of the power of the entropy result so obtained with the number of e foldings arising in inflation. This last question we view as essential for answering if there is a foundation of inflation which is linked to quantum gravity. We wish to avoid the anthropic principle in setting initial conditions for the massive graviton, which is why we referenced the modification of the Penrose CCC theory in part of our manuscript.

1 Basic Idea, Can Two First Integrals Give Equivalent Information? This Is Due to the First Reference

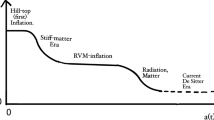
We use a construction for a mass of a graviton from Beckwith (2018). Instead of Hamber’s (Beckwith 2018; Hamber 2009) first integral, we use what John Klauder wrote in Klauder (2015) to form a first integral in Beckwith (2018) so as to make a 1 to 1 equivalence with the first integral of general relativity (Dalarsson and Dalarsson 2005; Weinberg 1972). As in Beckwith (2018) we have a 1 to 1 relationship between two first action integrals. We avoid starting with a cosmic singularity, and use the cosmic bounce, as given in Rovelli and Vidotto (2015). In doing so, from Beckwith (2017, 2018) we use a barrier between interior and exterior space-time, to set up a cosmological constant. Our goal is to set up arguments which have no connection to the anthropic principle (Barrow and Tipler 1988) which the author regards as crackpot science of the worst sort. Having a clean break from the anthropic principle is a main goal of our enterprise.

1.1 This Is Our Argument for the GR First Integral: From Beckwith (2018)

The first integral used in Beckwith (2018) is also in a first integral (Padmanabhan 2005) of the form given by Eq. (3.1), having a Ricci scalar (Padmanabhan 2006). Also, the curvature ℵ is small. Therefore

$$ {\displaystyle \begin{array}{c}{S}_1=\frac{1}{2\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^4x\cdot \left(\Re -2\Lambda \right)\\ {}\&-g=-\det {g}_{uv}\\ {}\&\Re =6\cdot \left(\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2+\frac{\aleph }{a^2}\right)\end{array}} $$

(3.1)

Also, $\delta {g}_{tt}\approx {a}_{\mathrm{min}}^2\phi$ (Beckwith 2016; Giovannini 2008) uses inflaton, ϕ (Padmanabhan 2006). Which if we abide by Beckwith (2018) and Padmanabhan (2006)) we have

$$ a(t)={a}_{\mathrm{min}}\cdot {t}^{\gamma } $$

(3.2)

Padmanabhan, in (2006), states Eq. (3.2) above leads to the Beckwith (2018) and Padmanabhan (2006)) inflaton.

$$ \phi \approx \sqrt{\frac{\gamma }{4\pi G}}\cdot \ln \left\{\sqrt{\frac{8\pi {GV}_0}{\gamma \cdot \left(3\gamma -1\right)}}\cdot t\right\} $$

(3.3)

Here a_min is a minimum value of the scale factor (Beckwith 2018; Camara et al. 2004) which may have an electromagnetic contribution as given in Camara et al. (2004).

2 Next from Klauder Details Which Are Used to Give More Q.M. Structure

Note (Beckwith 2018) we are using a restricted quantum action principle (Klauder 2015) S₂, Eq. (3.4), when we assume for simplicity that Λ is a constant.

$$ {\displaystyle \begin{array}{c}{S}_2={\int}_0^T\mathrm{d}t\cdot \left[p(t)\dot{q}(t)-{H}_N\left(p(t),q(t)\right)\right]\\ {}\approx {S}_1=\frac{1}{2\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^4x\cdot \left(\Re -2\Lambda \right)\end{array}} $$

(3.4)

Hence

$$ \Lambda \approx \frac{-\left[p\left(\tilde{t}\right)\dot{q}\left(\tilde{t}\right)-{H}_N\left(p\left(\tilde{t}\right),q\left(\tilde{t}\right)\right)\right]}{\frac{1}{\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^3x}+\frac{\frac{1}{2\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^3x\cdot {\left.\left(\Re =6\cdot \left(\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2+\frac{\aleph }{a^2}\right)\right)\right|}_{t=\tilde{t}}}{\frac{1}{2\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^3x} $$

(3.5)

3 Filling in the Details of the Above Using Details from Klauder (2015) with Explanations

First

• (a) That S₂ ≈ S₁ from pre-Planckian to Planckian space-time when we avoid the cosmic singularity (Beckwith 2018). We ask that our model be consistent with the cosmology associated with a cosmic bounce, instead of a traditional singularity (Beckwith 2017)

• (b) Also curvature ℵ will be a small part of Ricci scalar ℜ (Novello n.d.)

$$ \Re =6\cdot \left(\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2+\frac{\aleph }{a^2}\right)\sim 6\cdot \left(\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2\right) $$

(3.6)

Furthermore, assume that there is a barrier between the pre-Planckian and Planckian physics regimes, so that we have a quantum mechanical potential well, using Beckwith (2017) which has Klauder’s (2015) notation that N represents the strength of the wall.

$$ {\displaystyle \begin{array}{c}\frac{p_0^2}{2}=\frac{p_0^2(N)}{2}+N;\kern1em \mathrm{for}\;0<N\le \infty \\ {}q={q}_0\pm {p}_0t\\ {}{V}_N(x)=0;\kern1em \mathrm{for}\;0<x<1\\ {}{V}_N(x)=N;\kern1em \mathrm{otherwise}\\ {}{H}_N\left(p(t),q(t)\right)=\frac{p_0^2}{2}+\frac{{\left(\mathrm{\hslash}-\pi \right)}^2}{2}+N;\kern1em \mathrm{for}\;0<N\le \infty \end{array}} $$

(3.7)

We set q = q₀ ± p₀t~ϕ and assume small time steps, and the scale factor is given by Camara et al. (2004)

4 Why This Is Linked to Gravity/Massive Gravitons

Klauder’s program is to isolate a regime of space-time for a canonical quantization of a classical system. That is, what we did is to utilize the ideas of Klauder (2015) to make the identification of Eq. (3.7) which when combined with enhanced quantization of the, as given in Eq. (3.3). That is, assume$\sqrt{-g}$ is a constant. And this is for extremely small-time intervals (in the boundary between pre-Planckian to Planckian physical boundary regime). As given by Giovannini (2008) in his comprehensive review of cosmological production of gravitons and early universe entropy. This approximation is why ${g}_{tt}\sim \delta {g}_{tt}\approx {a}_{\mathrm{min}}^2\phi$_.

If so, the mass of a graviton is referred to, as given by Novello (n.d.). We can then write a bound, based upon the early universe conditions so set forth, as a way to ascertain a bound to the effective heavy graviton (Beckwith 2014, 2018; Novello n.d.)

$$ {m}_{\mathrm{g}}^2={\left(\frac{\mathrm{\hslash}\cdot \sqrt{\Lambda}}{c}\right)}^2\approx \frac{{\mathrm{\hslash}}^2}{c^2}{\left[\frac{-\left[\frac{V_0}{3\gamma -1}+2N+\frac{\gamma \cdot \left(3\gamma -1\right)}{8\pi G\cdot {\tilde{t}}^2}\right]}{\frac{1}{\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^3x}+{\left.\left(6\cdot \left(\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2\right)\right)\right|}_{t=\tilde{t}}\right]}_{\tilde{t}=t\left(\mathrm{Planck}\right)} $$

(3.8)

Our next step is to review the input of parameters which may affect Eq. (3.10). To do so we consider a multi universe generalization of the CCC as given below. This is done specifically to kill off references to the anthropic principle as far as Eq. (3.8) (Barrow and Tipler 1988).

5 Reviewing Multiverse Generalization of the CCC of Penrose, and How This Relates to Beckwith’s (2018) Conclusions

We are extending Penrose’s suggestion of cyclic universes, black hole evaporation, and the embedding structure our universe is contained within. The following is largely taken from Beckwith (2014, 2018) and Penrose (2011) and has relevance to the final part of the conclusion. That there are no fewer than N(Penrose style ccc) universes undergoing Penrose “infinite expansion” (Penrose) (Beckwith 2014, 2018; Penrose 2011) contained in a mega universe structure. Furthermore, each of the N(Penrose style ccc) universes has black hole evaporation, with the Hawking radiation from decaying black holes. If each of the N(Penrose style ccc) universes is defined by a partition function, called ${\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}$, then there exist an information ensemble of mixed minimum information correlated as about 10⁷ − 10⁸ bits of information per partition function in the set ${\left.{\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}\right|}_{\mathrm{before}}$, so minimum information is conserved between a set of partition functions per universe

$$ {\left.{\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}\right|}_{\mathrm{before}}\equiv {\left.{\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}\right|}_{\mathrm{after}} $$

(3.9)

However, there is non-uniqueness of information put into each partition function ${\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}$. Furthermore, Hawking radiation from the black holes is collated via a strange attractor collection in the mega universe structure to form a new big bang for each of the N (Penrose CCC style) universes represented by ${\left\{{\Xi}_i\right\}}_{i\equiv N}^{i\equiv 1}$. The n_f value will be using Ng (2008) S_entropy~n_f (Beckwith 2014, 2018; Ng 2008). This assumes an energy expression as given by Beckwith (2014, 2018) and Poplawski (2011) and as by Beckwith (2018) will be an energy conservation equation before and right after the big bang, for the structure of our local universe, so formed in our modified CCC argument. Then the following holds (Beckwith 2014, 2018; Penrose 2011),

Claim 3.1

$$ \frac{1}{N}\cdot \sum \limits_{j=1}^N{\left.{\Xi}_j\right|}_{j\hbox{-} \mathrm{before}\hbox{-} \mathrm{nucleation}\hbox{-} \mathrm{regime}}\underset{\mathrm{vacuum}\hbox{-} \mathrm{nucleation}\hbox{-} \mathrm{tranfer}}{\to }{\left.{\Xi}_i\right|}_{i\hbox{-} \mathrm{fixed}\hbox{-} \mathrm{after}\hbox{-} \mathrm{nucleation}\hbox{-} \mathrm{regime}} $$

(3.10)

And

$$ {\left.{\Xi}_j\right|}_{j\hbox{-} \mathrm{before}\hbox{-} \mathrm{nucleation}\hbox{-} \mathrm{regime}}\approx \sum \limits_{k=1}^{\operatorname{Max}}{\left.{\tilde{\Xi}}_k\right|}_{\mathrm{black}\hbox{-} \mathrm{holes}\hbox{-} j\mathrm{th}\hbox{-} \mathrm{universe}} $$

For N (Penrose style ccc) number of universes, with each Ξ_j|_{j ‐ before ‐ nucleation ‐ regime} for j = 1 to N(Penrose style ccc) (Beckwith 2014, 2018; Penrose 2011) being the partition function of each universe just before the blend into the RHS of Eq. (3.11) above for our present universe. Also, each of the independent universes given by Ξ_j|_{j ‐ before ‐ nucleation ‐ regime} is constructed by the absorption of black holes taking in energy. I.e., (Penrose) (Beckwith 2014, 2018; Penrose 2011). Furthermore, Eq. (3.11) uses the idea of Dye (1965) in terms of general ergodic mixing.

This is after we make the following identification, i.e., look at the formation of a nontrivial gravitational measure as a new big bang for each of the N universes as by n(E_i)⋅ the density of states at a given energy E_i for a partition function (Beckwith 2014, 2018; Poplawski 2011).

Claim 3.2

$$ {\left\{{\Xi}_i\right\}}_{i\equiv 1}^{i\equiv N}\propto {\left\{{\int}_0^{\infty}\mathrm{d}{E}_i\cdot n\left({E}_i\right)\cdot {\mathrm{e}}^{-{E}_i}\right\}}_{i\equiv 1}^{i\equiv N} $$

(3.11)

What is done in Claim 3.1 and Claim 3.2 is to come up with a protocol as to how a multi-dimensional representation of black hole physics enables continual mixing of space-time (Hawkings n.d.) largely as a way to avoid the anthropic principle (Barrow and Tipler 1988), as to a preferred set of initial conditions.

Claim 3.1 which uses Claim 3.2 is important. The idea here is to use what is known as CCC cosmology (Beckwith 2014, 2018; Penrose 2011), which can be thought of as the following. First. Have a big bang (initial expansion) for the universe. After redshift z = 10, a billion years ago, SMBH formation starts. Matter-energy is vacuumed up by the SMBHs, which at a much later date than today (present era) gather up all the matter-energy of the universe and recycle it in a cyclic conformal translation. As given, by the transformations alluded to in Eqs. (3.12) and (3.13) below. So we can thereby understand the change in CCC space-time geometry.

Note that the main methodology in the Penrose proposal (Beckwith 2014, 2018; Penrose 2011) has been evaluating a change in the metric g_ab by a conformal mapping $\hat{\Omega}$ to

$$ {\hat{g}}_{ab}={\hat{\Omega}}^2{g}_{ab} $$

(3.12)

Penrose’s suggestion has been to utilize the following (Beckwith 2014, 2018; Penrose 2011)

$$ \hat{\Omega}\underset{ccc}{\to }{\hat{\Omega}}^{-1} $$

(3.13)

In fall into cosmic black hopes has been the main mechanism which will be useful for the recycling apparent in Eq. (3.14) above with ℏ kept constant from cycle to cycle as represented by Beckwith (2014, 2018)

$$ {\mathrm{\hslash}}_{\mathrm{old}\hbox{-} \mathrm{cosmology}\hbox{-} \mathrm{cycle}}={\mathrm{\hslash}}_{\mathrm{present}\hbox{-} \mathrm{cosmology}\hbox{-} \mathrm{cycle}} $$

(3.14)

We claim that Eq. (3.14) with Eq. (3.8) and Eq. (3.10) above gives a uniform mass to a graviton, per cycle, if Equation (3.14) holds we have the ability to make gravitons keep a constant non zero mass from cycle to cycle of the CCC paradigm. The idea is to keep consistency in physical law during each cycle of CCC dynamics. If the laws of laws of physics remain invariant , then graviton mass will not be altered. This also involves the physics of Ng (2008), Poplawski (2011), and Hawkings (n.d.). In doing so, from Beckwith (2018) consider the dynamics of the scale factor a(t), which is nearly zero, in the pre-Planckian regime of space-time. i.e., as to how a(t) changes and evolves, we look at the treatment given in Roos (2003) as well as Dye (1965). In addition by Beckwith (2018) and Hamber (2009).

$$ {\displaystyle \begin{array}{c}\int \mathrm{d}t\sqrt{g_{tt}}{V}_3(t)={V}_4(t)\sim 8{\pi}^2{r}^4/3\\ {}\&{V}_3(t)=2{\pi}^2a{(t)}^3/3\\ {}\&{k}_2=9{\left(2{\pi}^2\right)}^{2/3}\end{array}} $$

(3.15)

These are volume elements of the Hamber (2009) first integral. i.e., see Ambjorn et al. (2010), Karabulut (2006), Spiegel (1980). A Lagrangian multiplier is a constraint of how a “minimal surface” is obtained by constraining a physical process so as to use Ambjorn et al. (2010), Karabulut (2006), and Spiegel (1980). In the case of Karabulut (2006), the minimization process is if a(t) a scale factor as defined by Dye (1965) and g_tt a time component of a metric tensor. Here, the subscripts 3 and 4 in the volume refer to 3- and 4-dimensional spatial dimensions, and this will lead to, via Hamber (2009), a first integral as defined by Beckwith (2018) and Hamber (2009), in the form, if G is the gravitational constant,

$$ {S}_1=\frac{1}{24\pi G}\cdot \left(\int \mathrm{d}t\sqrt{g_{tt}}\left(\frac{g_{tt}{\dot{V}}_3^2}{V_3(t)}+{k}_2{V}_3^{1/3}(t)-\lambda {V}_3(t)\right)\right) $$

(3.16)

This should be compared against the Padmanabhan first integral (Barrow and Tipler 1988; Padmanabhan 2005), with the third entry of Eq. (3.3) having a Ricci scalar defined via Weinberg (1972) and usually the curvature ℵ (Weinberg 1972) set as extremely small, with the general relativity version of from Beckwith (2018) of Eq. (3.1). Note that our write-up actually uses all this and aligns it with the ideas of the Klauder enhanced quantization (Klauder 2015) for what we think is a better extension of the same idea. In order to obtain maximum results, we will be stating that the following will be assumed to be equivalent, i.e., in the spirit of Beckwith (2018)

$$ \sqrt{g_{tt}}\left(\lambda {V}_3(t)\right)\sim \frac{1}{2\kappa}\int \sqrt{-g}\cdot {\mathrm{d}}^3x\cdot \left(2\Lambda \right) $$

(3.17)

So, from Beckwith (2018), a relationship of the Lagrangian multiplier:

$$ \lambda \sim \frac{1}{\kappa}\sqrt{\frac{-g}{\left(\delta {g}_{tt}\approx {a}_{\mathrm{min}}^2\phi \right)}}\cdot \Lambda $$

(3.18)

We are obtaining the exact same physics, as in Beckwith (2018) for when we appeal to Eq. (3.8) as a bound to the enhanced quantization, hence we have extended our basic idea via use of Beckwith (2018) and Klauder (2015). To conclude with this mini section, this is included in as a way to set up a statistical averaging procedure as to avoid the anthropic principle. After having said this, if our Eq. (3.11) has successfully set up a program to avoid the anthropic principle (Barrow and Tipler 1988), we can relate this to massive gravitons, next and early universe entropy.

6 Why This Is Linked to Gravity/Massive Gravitons, and Possibly Early Universe Entropy

Klauder’s program (Klauder 2015) is to embed via Eq. (3.8) as a quantum mechanical well for a pre-Planckian system for inflaton physics as given in Beckwith (2018) where we go to the idea as given in Klauder’s treatment of the action integral as of page 87 of Klauder (2015) where Klauder talks of the weak correspondence principle, where an enhanced classical Hamiltonian is given 1–1 correspondence with quantum effects, in a non-vanishing fashion. If so, by Novello (Camara et al. 2004) and Eq. (3.8) we have then for early universe conditions, that we will be leading up to using an algorithm for massive gravitons, as we were working with in Beckwith (2018) with the result that we write, for a Plank time value is to go back to our Eq. (3.8) which we subsequently turn into Eq. (3.11) where we use the convention for scale factors as given in Camara et.al. (Giovannini 2008) so that we have a tentative value of the cosmological constant and then by extension the graviton mass via Novello (Camara et al. 2004) of Eq. (3.11). The long and short of it is to tie this value of the cosmological constant, and the production of gravitons due to early universe conditions, to a relationship between De Broglie wavelength, Planck length, and if the velocity v gets to a partial value close to the speed of light, that, we have, say by using Landau and Lifshitz (2005) as given in DICE 2018 and also part of the JHEPGC publication for quantum systems, if we have instead of a velocity much smaller than the speed of light, a situation where the particle moves very quickly (a fraction of the speed of light) that instead of the slow massive particle postulated in Landau and Lifshitz (2005)

$$ {\displaystyle \begin{array}{l}{\lambda}_{\mathrm{De}\hbox{-} \mathrm{Broglie}}\approx \frac{2\pi \mathrm{\hslash}}{m_gv}\cdot \sqrt{1-\frac{v^2}{c^2}}\cong {\mathrm{\ell}}_{\mathrm{Planck}}\approx \sqrt{\frac{\mathrm{\hslash}G}{c^3}}\\ {}\Rightarrow \mathrm{if}\;v\left(\mathrm{particle}\right)\to c-{\xi}^{+};\mathrm{then}\\ {}\varepsilon \left(\mathrm{energy}\hbox{-} \mathrm{particle}\right)\approx {E}_{\mathrm{Planck}}\left(\mathrm{Planck}\hbox{-} \mathrm{energy}\right)\end{array}} $$

(3.19)

Let us start with a specified value of mass of a graviton, say of the order of 10–62 g and also the application of the Ng “infinite quantum statistic” counting algorithm with S (entropy) being equivalent to the number of generated gravitons, which we call n. We will then use the construction of cyclic conformal cosmology (ccc) given by Penrose (2011) so that

$$ {\displaystyle \begin{array}{l}\mathrm{If}\;c\equiv 1,{m}_{\mathrm{g}}\approx {10}^{-62}\;\mathrm{g}\\ {}{E}_{\mathrm{Planck}}\left(\mathrm{Planck}\hbox{-} \mathrm{energy}\right)\cong 2.18\times {10}^{-5}\;\mathrm{g}\\ {}\cong \left({m}_{\mathrm{g}}\approx {10}^{-62}\;\mathrm{g}\right)\times N\left(\mathrm{entropy}\hbox{-} \mathrm{number}\right)\\ {}\Rightarrow N\left(\mathrm{entropy}\hbox{-} \mathrm{number}\right)\cong {10}^{58}\equiv {10}^{\mathrm{\mathbb{N}}},\mathrm{and}\therefore \mathrm{\mathbb{N}}\cong 58\end{array}} $$

(3.20)

7 Can This Tie in with Early Universe e Folds? That Is, from Chongchitnan (n.d.) e Folds Are Between 55 and 60

E folds in cosmology are a way of delineating if we have enough expansion of the universe in line with inflation. As seen in Chongchitnan (n.d.), we can have

$$ \mathrm{\mathbb{N}}\left(\mathrm{e}\hbox{-} \mathrm{fold},\cos \mathrm{mol}\right)\approx -\int \mathrm{d}t\cdot H\left(\cos \mathrm{mol}\right) $$

(3.21)

where H(cosmol) is a value of the Friedman equation, and if we use the idea that the potential energy, V, of initial inflation is initially over shadowed by the contributions of the Friedman equation, H, at the onset of inflation. Then

$$ \mathrm{\mathbb{N}}\left(\mathrm{e}\hbox{-} \mathrm{fold},\mathrm{cosmol}\right)\approx 55-60 $$

(3.22)

What we wish to explore is if Eq. (3.22) is consistent with Eq. (3.23) and what the consequences will be of this identification

$$ N\left(\mathrm{entropy}\hbox{-} \mathrm{number}\right)\cong {10}^{58}\equiv {10}^{\mathrm{\mathbb{N}}},\mathrm{and}\therefore \mathrm{\mathbb{N}}\cong 58 $$

(3.23)

Doing so may involve use of the Corda article, as given in Corda (2018).

8 Conclusion, Does Our Bound as to the Graviton Mass, and Its Input Variables Due to Klauder Enhanced Quantization Argue in Favor of a Quantum Gravity Linkage to e Folds and Inflation? This Needs to Be Determined Next

We argue that we may have inputs into the building of a bound to the mass of a graviton if a multiverse may contribute to the construction of the graviton mass. That is the input side of the phenomena used for getting a bound to the massive graviton, and the use of the Novello (Camara et al. 2004) supposition of a linkage between massive gravity and an allowed cosmological constant. An output version of this phenomena after we create a necessary condition for massive gravity is in the issue raised by Eq. (3.8). And also the intriguing possibility of more overlap between Eqs. (3.22) and (3.23). If there is an overlap of these two Eqs. (3.22) and (3.23), which raises the intriguing question of if a mass of a graviton, i.e., a quantum gravity lodestone is in fidelity with the e folds of cosmology, then we have the distinct possibility of quantum gravity having at least a partial linkage to e fold inflationary cosmology. If this is not true, then tensor-scalar version of gravity and other models need a very hard look over. And while we are on the subject, Appendix A, as given below is yet another datum which needs experimental vetting. All these together would be needed to be confirmed via experimental gravitational data sets. A side note which is to consider is, if this happens, does it in any way have linkage to the idea of forming symmetries in space-time which could lead to SU(n) type group thinking? See Dyson (1966) as the gold standard. We can only go there though if we understand the physical input phenomena as to the creation of a burst of inflationary energies later, and if we have quantifiable data sets to come up with readily understood models. With falsifiable input parameters. This is our hope and our aspiration as of the twenty-first century as far as gravitational experimental science.

Finally what if there are many micro black holes created almost at the start of the Universe? What would this do in terms of GW generation? See Appendix B, as a future works project which may add more context as far as the varying mechanisms as far as GW, and our project is so delineated. This is in terms of entropy, itself and is a much smaller contribution of entropy than what is already delineated. But if we develop GW physics as an experimental science, this too may be something not to ignore and will involve the physics of Chongchitnan (n.d.), Corda (2018), and Dyson (1966) fully.

Appendices

Appendix A: Infinite Quantum Statistics as Given by Jack Ng

Jack Ng changes conventional statistics: he outlines how to get S ≈ N, which with additional arguments we refine to be S ≈  < n> (where <n> is graviton density). Begin with a partition function (Beckwith 2014, 2018; Ng 2008)

$$ {Z}_N\sim \left(\frac{1}{N!}\right)\cdot {\left(\frac{V}{\lambda^3}\right)}^N $$

(3.24)

This, according to Ng, leads to entropy of the limiting value of, if S = (log[Z_N])

$$ S\approx N\cdot \left(\log \left[V/N{\lambda}^3\right]+5/2\right)\underset{\mathrm{Ng}\hbox{-} \operatorname{inf}\;\mathrm{inite}\hbox{-} \mathrm{Quantum}\hbox{-} \mathrm{Statistics}}{\to }N\cdot \left(\log \left[V/{\lambda}^3\right]+5/2\right)\approx N $$

(3.25)

Appendix B: Micro Black Hole, at the Start of the Universe and Their Contribution to Early Universe GW Generation Via an Entropy Count

This is in partial fidelity to Beckwith (2018) and may be added as a factor in future entropy contributions as a secondary effect which may affect future analysis of this phenomenon. We begin first with what would transpire for micro black holes, at the start of the space-time regime. That is the first level of analysis we have done in the main document purports to create graviton type disturbances at or before the electroweak regime of space-time. The addition of entropy so given here is meant to be included, pending an evaluation as to how many primordial black holes may be considered to be created. If the number is large (many micro black holes), then what we have below will significantly add to entropy. Or it may not be a decisive factor. The analysis is included for this document as a secondary effect for entropy generation. The idea would be that we would have, for a quantum level, n, specified for a black hole, due to what Corda developed the following temperature distribution which would ALSO add into more entropy. We include it in as a future works project. The first term below comes from Dyson (1966) and is linkable to a way to also, in addition to the mechanism so brought up a way to also add more early universe entropy, which is linkable to gravitons.

$$ {\displaystyle \begin{array}{l}{T}_{\mathrm{H}}={m}_D\cdot {\left(\frac{m_D\cdot \left(n+2\right)}{m_{bh}\cdot 8\cdot \Gamma \left(\frac{n+3}{2}\right)}\right)}^{\left(1/n+1\right)}\cdot \left(\frac{n+1}{4\sqrt{\pi }}\right)\\ {}{m}_D\doteq 1\;\mathrm{TeV}\equiv {10}^{12}\kern0.37em \mathrm{eV}=1.783\times {10}^{-30}\;\mathrm{g}\\ {}{m}_{bh}\doteq 1.22\times {10}^{21}\;\mathrm{TeV}=2.175\times {10}^{-9}\ \mathrm{g}\\ {}{T}_{\mathrm{H}}\propto 1\;\mathrm{TeV}\cdot {\left(\frac{\left(n+2\right)}{1.22\times {10}^{21}\cdot 8\cdot \Gamma \left(\frac{n+3}{2}\right)}\right)}^{\left(1/n+1\right)}\cdot \left(\frac{n+1}{4\sqrt{\pi }}\right)\end{array}} $$

(3.26)

We look at the initial state of created gravitons, and use the physics given in Hawking (1974) with the specified Hawking temperature, as the main physics phenomenon of interest to our analysis. We then can, if we have this Hawkings temperature, as given in Eq. (3.7) consider the question of first, if the black holes have classical or quantum behavior as well as Γ being a gamma function, i.e., look at what is given in Beckwith (2018), in its conclusion which we will cite here. That is, the idea is based upon the formation of a finite number of black holes, which decay. Quoting Beckwith (2018) we have that we will be looking at the following:

Quote, Beckwith (2018)

“Our physics is simplified if we change Planck length to be scaled as 1 and we look at a ‘unit’ evaluated space-time volume.” Then we can set n of Eq. (3.26) equal to zero initially and obtain the following from Corda (2018) and Beckwith (2018)

$$ {\displaystyle \begin{array}{l}16\pi \left(\frac{{\tilde{n}}_{\mathrm{qm}}}{4\times {10}^4}\right)\cdot \left|\sqrt{1-\left(\frac{{\tilde{n}}_{\mathrm{qm}}-1}{{\tilde{n}}_{\mathrm{qm}}}\right)}\right|\approx {10}^6\\ {}{m}_{bh}\approx {10}^2\times {m}_{\mathrm{planck}}\left(4-\dim \right)\\ {}\Delta {V}_{\mathrm{total}}\simeq {10}^2\times \Delta {V}_{{\tilde{n}}_{\mathrm{qm}}-1\to {\tilde{n}}_{\mathrm{qm}}}\approx {10}^2\times 16\pi \left(\frac{{\tilde{n}}_{\mathrm{qm}}}{4\times {10}^4}\right)\cdot \left|\sqrt{1-\left(\frac{{\tilde{n}}_{\mathrm{qm}}-1}{{\tilde{n}}_{\mathrm{qm}}}\right)}\right|\approx {10}^8\end{array}} $$

(3.27)

This puts a serious restriction on the number of allowed quantization levels ${\tilde{n}}_{\mathrm{qm}}$, but it also means that within this horizon space we may be seeing mini black holes created which could release gravitons. We will then discuss what may be pertinent to characterizing if the black holes are behaving classically or quantum mechanically. Note, if n in Eqs. (3.26) and (3.31) is set equal to zero, we have that if we literally interpreted Eq. (3.26), with n equal zero (4 dimensions) with a 10² plank mass (in four dimensions) black hole, that we would have

$$ {T}_{\mathrm{H}}\propto 1\;\mathrm{TeV}\cdot \left(\frac{1}{1.22\times {10}^{21}\cdot 2\cdot \sqrt{\pi }}\right)\cdot \left(\frac{1}{4\sqrt{\pi }}\right) $$

(3.28)

Noticeably we have a set of reality problems to attend to. Hawking radiation and the Ng (2008) paradigm alter our process so that we obtain the following results as given in Eq. (3.29) for Hawking blackbody style results.

Diosi (2019) and Calmet (n.d.) will add further refinement as to the physics of Eq. (3.29) and hopefully alter them to reflect more of the known observational physics, since Eq. (3.29) is a greatly over simplified version of the gravitational physics input into observational gravitational astronomy. We hope in doing so we obtain data sets as to confirm or falsify our hypothesis as given in this document.

$$ {\displaystyle \begin{array}{l}{T}_{\mathrm{H}}\left(\mathrm{normal}-4\dim \right)=\frac{\mathrm{\hslash}{c}^3}{8\pi {Gm}_{bh}{k}_{\mathrm{B}}}=6.17\times {10}^{-8}\;\mathrm{K}-\mathrm{if}\;{m}_{bh}=1-\mathrm{solar}\hbox{-} \mathrm{mass}\\ {}{T}_{\mathrm{H}}\left(\mathrm{normal}-4\dim \right)=\frac{\mathrm{\hslash}{c}^3}{8\pi {Gm}_{bh}{k}_{\mathrm{B}}}\simeq 6.17\times {10}^{28}\;\mathrm{K}-\mathrm{if}\;{m}_{bh}={10}^2\times {m}_{\mathrm{planck}}\left(4-\dim \right)\\ {}{T}_{\mathrm{H}}\left(\mathrm{normal}-4\dim \right)=\frac{6.17\times {10}^{28}}{11,604}\;\mathrm{eV}-\mathrm{if}\;{m}_{bh}={10}^2\times {m}_{\mathrm{planck}}\left(4-\dim \right)\\ {}{T}_{\mathrm{H}}\left(\mathrm{normal}-4\dim \right)=5.317\times {10}^{12}\;\mathrm{TeV}-\mathrm{if}\;{m}_{bh}={10}^2\times {m}_{\mathrm{planck}}\left(4-\dim \right)\end{array}} $$

(3.29)

The sun is 9.8 times 10³⁷ Planck masses, so this means that the Hawkings temperature of a 10² times four-dimensional Planck mass black hole, as postulated here would be then about 10³⁶ times higher, 1 eV in Kelvin is 11,604 K, hence if we have only n = 0 we really would prefer not to use Eq. (3.28). Hence, using Eq. (3.29). we can then go to Hawking (1974) for entropy, i.e., we have then that

$$ {\displaystyle \begin{array}{l}{S}_{bh}=\frac{1+n}{2+n}\cdot \frac{m_{bh}}{T_{bh}}=\frac{1+n}{2+n}\cdot \frac{10^2\times {m}_{\mathrm{planck}}\left(4-\dim \right)}{5.317\times {10}^{12}\;\mathrm{TeV}}\approx \frac{1+n}{2+n}\cdot \frac{10^2\times 1.22\times {10}^{16}\;\mathrm{TeV}}{5.317\times {10}^{12}\;\mathrm{TeV}}\\ {}{S}_{bh}\approx \frac{1+n}{4+2n}\cdot {10}^4\underset{n\to 0}{\to }{10}^3\end{array}} $$

(3.30)

That is, if we had 10² black holes, of mass about 10² times a four-dimensional black hole, we probably would be looking at an initial entropy of about 10⁵. Then using Kolb and Turner (1991), we would see

$$ s\left(\mathrm{entropy}\hbox{-} \mathrm{density}\right)=\frac{2{\pi}^2}{45}{g}_{\ast}\cdot {\left({T}_{\mathrm{universe}}/{T}_{\mathrm{Planck}}\right)}^2 $$

(3.31)

This postulates that relic, initially formed black holes would be formed, say in a one-meter radius ball about 10⁻²⁷ s, after the onset of inflation and that we would see the rapid decay of these micro-sized black holes in less than 10⁻²⁷ s.

End of quote from Beckwith (2018)

This construction above, with suitable work later on, will be useful in removing the anthropic principle from serious consideration in cosmology (Barrow and Tipler 1988) Once again, the relevance to the analysis given in the main text is heavily flavored as to precisely how many primordial black holes are created. If it is just 10², the number of primordial black holes, then this is a very minor addition to the entropy. If the number of primordial black holes is significantly higher, then the contribution is different and then alters the calculations in potentially significant ways. See Ruutu et al. (1996) as to another model of what may transpire as yet another effect if there are many primordial black holes, creating early universe turbulence which may contribute (the turbulence) to entropy generation, i.e., in a cosmological scale replicating (Ruutu et al. 1996) and cosmic string representations of black holes (t’Hooft n.d.) in the early universe.