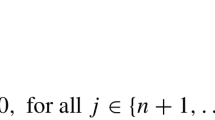Structural Properties of Pareto Fronts: The Occurrence of Dents in Classical and Parametric Multiobjective Optimization Problems

Abstract

This contribution deals with the occurrence of “dents” in Pareto fronts of continuous and adequately smooth multiobjective optimization problems. After giving a formal definition of this notion, a system of equations is derived that characterizes points on the boundary of the dent. This can be used to obtain information about the structure of the Pareto front without computing the entire Pareto set. Furthermore, the evolution of dents in parametric multiobjective optimization problems is studied using results from bifurcation theory. Theory and computations are illustrated by several examples, whose construction is described as well.

M. Dellnitz—This contribution is dedicated to Michael on the occasion of his 60th birthday. He really is one of its authors, although at the time of publication he does not know it has been written.

1 Introduction

In many fields of research and industrial applications optimization plays an important role. In a variety of these not only one but several objectives are required to be optimal at the same time. For instance, in manufacturing cost has to be minimized, but at the same time also quality is desired to be maximized – at least to a certain degree. The development of theory and algorithms for the determination of solutions that are as good as possible with respect to all objectives is the task of multiobjective optimization. Mathematically, a continuous multiobjective optimization problem is given as

$$\begin{aligned} \min _x \{F(x): x\in S\subseteq \mathbb {R}^n\}, \end{aligned}$$

where F is defined as the vector of the objective functions $f_1,\ldots , f_k$, $k\ge 2$, which each map from $\mathbb {R}^n$ to $\mathbb {R}$, and S denotes the feasible region. The example mentioned above already illustrates that the several objectives typically contradict each other and thus do not have identical optima. Consequently, the solution of a multiobjective optimization problem is given by the set of optimal compromises of the objectives, the so-called Pareto set. In the case of minimization problems the Pareto set is given by the set of solutions in which the value of any objective function can only be decreased at the cost of increasing another one.

To obtain solutions that lie within the Pareto set many algorithms have been developed. There are essentially two different types: algorithms that allow for the computation of only one or a few Pareto points, and algorithms that approximate the entire Pareto set. In the first case often a priori information, such as a specific weighting or some kind of ordering of the objectives, is required. Examples for those methods are the ‘weighted sums method’, the ‘$\varepsilon$-constraint-method’ and the ‘lexicographic ordering’ (see [8, 20]). Over the past years algorithms that are able to approximate the entire Pareto set have been developed (see e. g. [2, 4, 5, 11, 19, 22, 23, 30]). For the computations of Pareto sets in the examples given in this work set-oriented, numerical methods which are implemented in the software package GAIO have been used (see [24]).

Motivated by the fact that in the case of nonconvex objective functions it is not possible to compute all Pareto optimal solutions by the weighted sums method, in this chapter the occurrence of dents in Pareto fronts is studied (restricted to continuous and adequately smooth multiobjective optimization problems). In [3], Das and Dennis give a trigonometric argument why – in the case of two objectives – the weighted sums method cannot be used to compute points in the nonconvex part, as they call the subset of the Pareto front that contains no global optima of the weighted sum of the objectives for every weight vector. It is an interesting task to find out if a Pareto front contains nonconvex parts. If one assumes that the Pareto front is connected, then every nonconvex part contains a region in which the Pareto front ‘bends inside the feasible region’. This part of the Pareto front will be called a dent. In Sect. 3 a formal definition of a dent is given (see also [28]).

It will be shown that at the border of a dent (seen as a subset of the Pareto front) typically the Hessian of the weighted sum of the objectives is singular. These points will be called dent border points and the corresponding preimages on the Pareto set will be called dent border preimages.

In the case of parametric multiobjective optimization problems naturally the question comes up, how dents evolve under the variation of the external parameter. This question is addressed in Sect. 4. Making use of results from bifurcation theory, it is proven that under certain assumptions dent border preimages are turning points of the Kuhn-Tucker equations

$$H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=\sum _{i=1}^k \alpha _i^\star \nabla _x f_i(x,\lambda )=0,$$

where $\alpha ^\star$ ist the weight vector corresponding to the dent border preimage. Several examples of parametric multiobjective optimization problems in which the Pareto front contains dents will be given at the end of Sect. 4.

Fig. 1.

Typical shape of a Pareto front for a convex problem (left figure) and possible shape in a nonconvex problem (right figure). The shaded regions represent the image of the feasible set.

2 Theoretical Background

In this section the theoretical background from multiobjective optimization, parametric multiobjective optimization and bifurcation theory needed within the context of this chapter is summarized.

2.1 Multiobjective Optimization

A continuous (constrained) multiobjective optimization problem (MOP) is given by

$$\begin{aligned} \begin{aligned} \min _x \{F(x): x\in S\subseteq \mathbb {R}^n\}, \end{aligned} \end{aligned}$$

(MOP)

where F is defined as the vector of the objective functions $f_1,\ldots , f_k$, $k\ge 2$, which each map from $\mathbb {R}^n$ to $\mathbb {R}$, i. e.

$$ F: \mathbb {R}^n \rightarrow \mathbb {R}^k, \;F(x)=(f_1(x),\ldots , f_k(x)).$$

The feasible set S is given as

$$S=\{x\in \mathbb {R}^n: h(x)=0,\, g(x)\le 0\}$$

with equality constraints $h:\mathbb {R}^n\rightarrow \mathbb {R}^m, \, m\le n$ and inequality constraints $g:\mathbb {R}^n\rightarrow \mathbb {R}^q$. The MOP is called unconstrained MOP, if $S=\mathbb {R}^n$. In all the following considerations it is assumed that $F=(f_1,\ldots ,f_k)$ consists of at least continuous objective functions.

It has to be explained what is meant by ‘$\min$’ in the problem (MOP), as a vector-valued function has to be minimized. The following definition which introduces an appropriate partial order on $\mathbb {R}^k$ allows comparisons of vectors (cf. [6]).

Definition 1

Let u, v be two vectors in $\mathbb {R}^k$. Then the vector u is less than v (denoted by $u<_p v$) if

$$\begin{aligned} u_i < v_i\quad \text {for all }i\in \{1,\ldots ,k\}. \end{aligned}$$

In an analogous way, the relation $\le _p$ is defined. The vector u is said to dominate the vector v if

$$ u\le _p v \;\text {and} \; u_i<v_i \; \text {for at least one}\; i\in \{1,\ldots ,k\}.$$

Using the relation $\le _p$ we define what a solution of (MOP) is.

Definition 2

A point $x^\star \in \mathbb {R}^n$ is called globally Pareto optimal for (MOP) (or a global Pareto point of (MOP)) if there exists no $x\in S\subseteq \mathbb {R}^n$ with

$$ F(x)\le _p F(x^\star )\; \text {and }f_j(x)<f_j(x^\star )\text { for at least one }j\in \{1,\ldots ,k\}. $$

If this property is only valid inside a neighborhood $U(x^\star )\subset S \subseteq \mathbb {R}^n$, then $x^\star$ is called locally Pareto optimal (or a local Pareto point).

The set of all Pareto points is the Pareto set. Following [10], the set of the function values of all Pareto points is called the Pareto front.

In the literature, one can find several different names for Pareto optimal solutions. Examples are ‘efficient solutions’ [9, 25], ‘noninferior solutions’ [10], ‘nondominated points’ [17], ‘vector minimum points’ [1], and ‘admissible points’ [15]. Especially the image of a Pareto optimal solution often is denoted as an efficient point.

The following classical result which goes back to Kuhn and Tucker [18] provides a necessary condition for Pareto optimality. The version of the theorem written down here can be found in [16], which itself is a reformulated version of the one given in [14].

Theorem 1

(Kuhn and Tucker, 1951 [18])  

Let $x^\star$ be a Pareto optimal solution of (MOP). It is assumed that $\nabla h_i(x^\star ), i=1,\ldots , m$ and $\nabla g_j(x^\star )$ for $j\in \{J:g_J(x^\star )=0\}$ (the active constraints) are linearly independent. Then there exist vectors $\alpha \in \mathbb {R}^k$ with $\alpha _i\ge 0$ for $i=1,\ldots , k$ and $\sum _{i=1}^{k}\alpha _i = 1$, $\gamma \in \mathbb {R}^m$ and $\delta \in \mathbb {R}^q$ with $\delta _j\ge 0$ for $j=1,\ldots , q$ such that

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{k}\alpha _i\nabla f_i(x^\star )+\sum _{j=1}^{m}\gamma _j\nabla h_j(x^\star ) +\sum _{l=1}^{q}\delta _l\nabla g_l(x^\star )&= 0 \\ \delta _j\cdot g_j(x^\star )&= 0,\;\forall j=1,\ldots ,q.\\ \end{aligned} \end{aligned}$$

(1)

Following [20], points $x^\star \in \mathbb {R}^n$ that satisfy the Kuhn-Tucker condition (1) are called substationary points. Given a Pareto point $x^\star$ the vector of multipliers $\alpha$ is called the weight vector corresponding to $x^\star$.

Obviously the condition in the Kuhn-Tucker theorem is not sufficient for Pareto optimality in general. In the case of convex¹ objective functions, convex inequality constraints and affine² equality constraints, it is proven that for $\alpha >0$ the Kuhn-Tucker conditions are also sufficient [14]. However, numerical methods often make use of this criterion.

An intuitive, classical approach to solve a multiobjective optimization problem is the weighted sums method, also called the ‘weighting method’, which goes back to Gass and Saaty [12] and Zadeh [29]. It is a very popular approach which makes use of the intuitive idea of converting the multiobjective optimization problem into a single objective one. For this, the objective functions are summed up, each multiplied with an individual weight. More precisely, k weights $\alpha _i$ are chosen such that $\alpha _i \ge 0$ for $i=1,\ldots , k$ and $\sum _{i=1}^k \alpha _i=1$ and the problem

$$\begin{aligned} \begin{aligned} \min _x g_\alpha (x)\\ \text {s. t.}\; x\in S\subseteq \mathbb {R}^n,\\ \end{aligned} \end{aligned}$$

(2)

with $g_\alpha (x) = \sum _{i=1}^k\alpha _i f_i(x)$ is considered.

Varying the weights $\alpha _i$, different Pareto points can be obtained by solving (2) – in the case of convex objective functions even all Pareto points can be computed in this way. The reason for this is that the shape of the Pareto front is also convex in such a situation. Moreover, the optimization of the weighted sums results in different points on the Pareto front for different weight vectors.

In contrast to this, for nonconvex objective functions the Pareto front can contain nonconvex parts as illustrated in Fig. 1 on the right. Here, the nonconvex part is defined to be a subset of the Pareto front that contains no global optima of the weighted sum of the objectives for every weight vector. Pareto points, which are mapped into the nonconvex part of the Pareto front, can have the same weight vector as other Pareto points whose weighted sum has a smaller value (cf. Fig. 2), as they are only local minima or saddle points of $g_\alpha (x)$.

In [3], Das and Dennis give a trigonometric argument, why – in the case of two objectives – the weighted sums method cannot be used to compute points in the nonconvex part.

It is an interesting question to find out if a Pareto front contains nonconvex parts. If one assumes that the Pareto front is connected, then any nonconvex part contains a region in which the Pareto front ‘curves inside the image of the feasible region’. This part of the Pareto front will be called a ‘dent’. In Sect. 3 the formal definition of a dent is given and an approach which allows the numerical computation of dents in Pareto fronts is presented.

Fig. 2.

Schematic illustration of the weighted sums approach

2.2 Parametric Multiobjective Optimization Problems

An unconstrained (one-) parametric multiobjective optimization problem is given as

$$\begin{aligned} \begin{aligned} \min _x \{F(x,\lambda ): x\in \mathbb {R}^n, \lambda \in [\lambda _\mathrm {start},\lambda _\mathrm {end}]\subseteq \mathbb {R}\}, \end{aligned} \end{aligned}$$

(ParMOP)

where F is defined as the vector of the objective functions, i. e.

$$ F: \mathbb {R}^n\times [\lambda _\mathrm {start},\lambda _\mathrm {end}] \rightarrow \mathbb {R}^k, \;F(x,\lambda )=(f_1(x,\lambda ),\ldots , f_k(x,\lambda )).$$

The solution set of (ParMOP) is a $\lambda$-dependent family of Pareto sets.

Every point in this family satisfies the necessary condition of Kuhn and Tucker with respect to the x-variables. As (ParMOP) is an unconstrained multiobjective optimization problem, Theorem 1 reduces to the fact that there exist multipliers $\alpha _1,\ldots ,\alpha _k \in \mathbb {R}_{+,0}$ such that

$$\begin{aligned} H_\mathrm {KT}(x, \alpha , \lambda ) = \left( \begin{array}{c} \sum \nolimits _{i=1}^{k}\alpha _i\nabla _x f_i(x,\lambda ) \\ \sum \nolimits _{i=1}^{k}\alpha _i-1 \end{array} \right) =0, \end{aligned}$$

(3)

where $(x,\lambda )$ is a solution of (ParMOP).

Definition 3

If $x\in \mathbb {R}^n$ satisfies the Kuhn-Tucker condition (3) for a specific value of $\lambda$, then it is called – as in the non-parametric case – a substationary point. The set of all substationary points for the respective value of $\lambda$ is denoted by $S_{\lambda }$.

2.3 Bifurcation Theory

Bifurcation theory analyzes the behavior of solutions of parameter-dependent systems of equations when they become singular under variation of the parameter. In the context of this work it becomes applicable when considering solutions of the Kuhn–Tucker–Eq. (3) for the parametric, unconstrained case.

It will be shown in Sect. 3 that in a dent border point a zero eigenvalue of the Hessian of $g_\alpha$ occurs, where $g_\alpha (x,\lambda ) = \sum _{i=1}^k \alpha _i f_i(x,\lambda )$. The Hessian of $g_\alpha$ equals $\frac{\partial }{\partial x}H_\mathrm {KT}^\alpha$, as $H_\mathrm {KT}^\alpha (x,\lambda )=\nabla _x g_\alpha (x,\lambda )$. Thus, the implicit function theorem is not applicable to the Kuhn-Tucker equations (with respect to x) in a dent border point. Whenever the Jacobian with respect to x of a parametric system of equations is singular, the structure of the solution set may change. One possibility is that the system of equations has no solution before the singularity occurs, and two solutions afterwards (here, “before” and “afterwards” have to be understood in terms of the values of $\lambda$). In this case, the solution curve “turns” at the point $(x^\star ,\lambda ^\star )$, where the Jacobian with respect to x is singular. More formally, such a turning point – which sometimes is also called saddle-node bifurcation or fold in the literature – is defined as follows:

Definition 4

(Turning point (see [21])) 

Consider the solutions of a nonlinear system of equations $H(x,\lambda )=0$, where $H:\mathbb {R}^N\times \mathbb {R}\rightarrow \mathbb {R}^N$. Assume that $(x^\star ,\lambda ^\star )$ is such a solution which satisfies

• (i) there exists $\phi ^\star \in \mathbb {R}^N\backslash \{0\}$ with $\ker \left( \frac{\partial }{\partial x}H(x^\star ,\lambda ^\star )\right) = \mathrm {span }\{\phi ^\star \}$,

• (ii) $\frac{\partial }{\partial \lambda }H(x^\star ,\lambda ^\star )\notin \mathrm {im }\frac{\partial }{\partial x}H(x^\star ,\lambda ^\star )$.

Then, $(x^\star , \lambda ^\star )$ is called a turning point.

Let $\psi ^\star$ be a left eigenvector of the zero eigenvalue of $\frac{\partial }{\partial x}H(x^\star ,\lambda ^\star )$, i. e.

$$\psi ^\star \frac{\partial }{\partial x}H(x^\star ,\lambda ^\star ) = 0.$$

If in addition to (i) and (ii) $\psi ^\star \left( \frac{\partial ^2}{\partial x^2}H(x^\star ,\lambda ^\star )\phi ^\star \phi ^\star \right) \ne 0$, then the point $(x^\star , \lambda ^\star )$ is called a simple turning point.

In Fig. 3 an example of an equation whose solution curve includes a turning point is sketched. As one can observe, the solution curve turns in the point (0, 0).

Fig. 3.

For the equation $H(x,\lambda )=x^2-\lambda =0$, $H:\mathbb {R}\times \mathbb {R} \rightarrow \mathbb {R}$, a turning point occurs in the point (0, 0)

3 Dents in Non-parametric Pareto Fronts

In Fig. 1 it has already been illustrated that the Pareto front may curve inside the image of the feasible region in the case of nonconvex objective functions. As already mentioned in Sect. 2 Pareto points whose images lie in such a dent cannot be computed by using the weighted sums method. The reason is that two or more Pareto points satisfy the Kuhn-Tucker equations with the same weight vector $\alpha$ while the weighted sum $\sum _{i=1}^k\alpha _i f_i(x)$ cannot be minimal for all these solutions. The following definition gives a mathematical description of a dent.

Definition 5

(Dent point, Dent preimage) 

Let $P\subseteq S$ be the Pareto set of a multiobjective optimization problem $\min _{x\in S} F(x)$ with $F:\mathbb {R}^n\rightarrow \mathbb {R}^k$, $F(x)=\left( f_1(x),\ldots ,f_k(x)\right) ^T$ and $f_i$ at least twice continuously differentiable $\forall \, i=1,\ldots , k$. For $\alpha _i\in [0,1]$ with $\sum _{i=0}^k\alpha _i=1$ define $g_\alpha :\mathbb {R}^n\rightarrow \mathbb {R}$ by

$$\begin{aligned} g_\alpha (x)=\sum _{i=1}^k \alpha _i f_i(x). \end{aligned}$$

A point $x^\star \in P$ is called a dent preimage if it is a saddle point of $g_\alpha$. The corresponding point $y^\star =F(x^\star )$ on the Pareto front is called a dent point.

Definition 6

(Dent, dent border, complete dent)  

Let $P\subseteq S$ be the Pareto set of an at least twice continuously differentiable multiobjective optimization problem $\min _{x\in S} F:\mathbb {R}^n\rightarrow \mathbb {R}^k$ and let $PF=F(P)$ be the Pareto front. Let $y^\star \in PF$ be a dent point. Then, the connected component of dent points which includes $y^\star$ is called a dent corresponding to $y^\star$, denoted by $D_{y^\star }$:

$$\begin{aligned} \begin{aligned} D_{y^\star }=\left\{ y \in PF\;|\; \exists \delta \ge 0 \;\text {and}\;\exists c:[0,\delta ]\rightarrow PF, c\;\text {continuous, with} \; c(0)=y^\star , \right. \\ \left. c(\delta )=y,\; \text {and}\;c(s) \;\text {is a dent point}\;\forall \;s\in [0,\delta ]\right\} . \end{aligned} \end{aligned}$$

A dent $D_{y^\star }$ is called complete, if

$$\partial PF \cap \overline{D_{y^\star }}=\emptyset ,$$

where $\partial PF$ is the boundary of the Pareto front PF as a subset of $\partial F(S)$ (with the induced topology from $\mathbb {R}^k$).

The boundary $\partial D_{y^\star }$ of a complete dent $D_{y^\star }$ (seen as a subset of PF) is called dent border and a boundary point $y_b\in \partial D_{y^\star }$ is called a dent border point. A point $x_b \in P$ with $F(x_b)=y_b$ is called a dent border preimage of $y_b$.

Remark 1

In [16] dents have been studied from a differential geometric point of view. In this book it has been shown that – under certain geometrical assumptions on the multiobjective optimization problem – saddle points of $g_\alpha$ occur if and only if the corresponding point on the Pareto front has at least one negative principal curvature.

In [16] it has already been considered what happens during the transition from a minimizer $x_1$ of $g_{\alpha _1}$ to a saddle point $x_2$ of $g_{\alpha _2}$ on a connected Pareto front i. e. during the transition of non-dent preimages to dent preimages ($\alpha _1$ and $\alpha _2$ denote the weight vectors corresponding to $x_1$ and $x_2$, respectively):

Assume that the non-dent preimage $x_1$ can be connected to the dent preimage $x_2$ by a continuous curve $\gamma :[0,1]\rightarrow P\subseteq S$ with $\gamma (\tau )=\left( x(\tau ),\alpha (\tau )\right)$, $\gamma (0)= (x_1,\alpha _1)$ and $\gamma (1)= (x_2,\alpha _2)$. To each curve point $\gamma (\tau )$ the n-tuple of eigenvalues of $\frac{\partial ^2}{\partial x^2}g_{\alpha }(x)$, denoted by $\left( e_1(\tau ),\ldots , e_n(\tau )\right) ^T$, is assigned, where $\alpha$ again is the corresponding weight vector to x. This leads to another continuous curve $\tilde{\gamma }:\tau \mapsto \left( e_1(\tau ),\ldots , e_n(\tau )\right) ^T$ corresponding to $\gamma$. As $x_1$ is a minimizer of $g_{\alpha _1}$, $\tilde{\gamma }(0)>0$. In the saddle point $x_2$ of $g_{\alpha _2}$, there exists an index $i\in \{1,\ldots ,n\}$ such that $e_i(1)<0$. Because of the continuity of $\tilde{\gamma }$ there must exist $\bar{\tau }\in [0,1]$ with $e_i(\bar{\tau })=0$.

To sum up, in dent border points a zero-eigenvalue of the Hessian of $g_\alpha$ occurs.

Definition 7

(Simple dent border point/preimage) 

Let $P\subseteq S$ be the Pareto set of an at least twice continuously differentiable multiobjective optimization problem $F:\mathbb {R}^n\rightarrow \mathbb {R}^k$ and let $PF=F(P)$ be the Pareto front. Let $y_b^\star \in PF$ be a dent border point and let $x_b^\star \in P$ be a dent border preimage of $y_b^\star$.

Then, $y_b^\star$ is called a simple dent border point if the zero eigenvalue of the Hessian $g_\alpha ''(x_b^\star )$ is simple. In this case, $x_b^\star$ is called a simple dent border preimage.

Fig. 4.

Pareto front and dent points (black) for Example 1

Example 1

(Computation of dents) 

Consider the bi-objective optimization problem defined by the two objectives

$$\begin{aligned} f_1(x,\lambda ) = \frac{1}{2}(\sqrt{1+(x_1+x_2)^2}+ \sqrt{1+(x_1-x_2)^2}+x_1-x_2)+\lambda \cdot e^{-(x_1-x_2)^2}\\ f_2(x,\lambda ) = \frac{1}{2}(\sqrt{1+(x_1+x_2)^2}+ \sqrt{1+(x_1-x_2)^2}-x_1+x_2)+\lambda \cdot e^{-(x_1-x_2)^2} \end{aligned}$$

with a fixed value $\lambda =0.6$ and $x=(x_1,x_2)$. Then, the Pareto set can be approximated e. g. by use of the set-oriented techniques.

The algorithm returns a set of boxes that covers the Pareto set. Within these boxes, a number of test points is evaluated, the best of which are in the following considered as the Pareto set. By solving the Kuhn-Tucker equations of $F=(f_1,f_2)$ for each of these points, the corresponding weight vectors $\alpha \in \mathbb {R}^k$ can be computed. Then, the eigenvalues of the Hessians of the weighted sums of the objectives are determined. All points x, in which both eigenvalues $>0$ and eigenvalues $<0$ exist, are dent preimages. The Pareto front and the resulting dent points for this example are visualized in Fig. 4.

4 Evolution of Dents in Parameter-Dependent Pareto Fronts

In the previous section dents in Pareto fronts have been defined motivated by the fact that these points cannot be computed by the weighted sums method . Also, dent border points have been defined. When considering parametric multiobjective optimization problems, naturally the question arises, how dents and especially dent border points evolve. The Kuhn-Tucker Eq. (3) provide a necessary condition for Pareto optimality. Within this section this parametric system of equations will be analyzed in order to obtain results about the local behavior of parameter-dependent Pareto fronts.

Solutions of parametric systems of equations have already been widely studied in bifurcation theory. The first part of this section deals with the study of properties of dent border points. It will be proven that under certain assumptions dent border preimages are turning points of the Kuhn-Tucker equations. In the second part of this section, several numerical examples for parametric multiobjective optimization problems in which dents occur are given.

Within this section it is assumed that the objective functions are at least twice continuously differentiable. Only points $x\in P_\lambda$ are considered for which the corresponding weight vector $\alpha$ is an element of $(0,1)^k$. Define $H_\mathrm {KT}^\alpha :\mathbb {R}^n\times \mathbb {R}\rightarrow \mathbb {R}^n$ by

$$H_\mathrm {KT}^\alpha (x,\lambda )=\sum _{i=1}^k \alpha _i \nabla _x f_i(x,\lambda ).$$

4.1 Properties of Dent Border Points

First, it will be shown that dent border preimages can be characterized as certain turning points of the Kuhn-Tucker equations

Proposition 1

Let $P_\lambda \subseteq S_\lambda$ be the Pareto set of a parametric multiobjective optimization problem $\min F:\mathbb {R}^n\times \mathbb {R}\rightarrow \mathbb {R}^k$ with $F(x,\lambda )=\left( f_1(x,\lambda ),\ldots , f_k(x,\lambda )\right) ^T$. Let $x^\star \in P_{\lambda ^\star }$ be a simple dent border preimage. Let $\alpha ^\star$ denote the weight vector corresponding to $x^\star$ and assume that the Jacobian ${H_\mathrm {KT}^{\alpha ^\star }}'(x,\lambda )$ has full rank.

Then, $(x^\star ,\lambda ^\star )$ is a turning point of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$ with respect to $\lambda$.

Proof. It has been shown in [16] (see also Sect. 3) that dent border preimages $x^\star$ are solutions of the Kuhn-Tucker equations $H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star )=0$ in which $\frac{\partial ^2}{\partial x^2}g_{\alpha ^\star }(x^\star ,\lambda ^\star )$ is singular. Thus, there exists an eigenvector $\phi ^\star$ of $\frac{\partial ^2}{\partial x^2}g_{\alpha ^\star }(x^\star ,\lambda ^\star )$ with

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x^2}g_{\alpha ^\star }(x^\star ,\lambda ^\star )\right) \phi ^\star =0. \end{aligned}$$

(4)

From the assumption that the dent border preimage is simple, i. e. exactly one eigenvalue of $\frac{\partial ^2}{\partial x^2}g_{\alpha ^\star }(x^\star ,\lambda ^\star )$ equals zero (cf. Definition 7), it directly follows that

$$\begin{aligned} \dim \ker \left( \frac{\partial ^2}{\partial x^2}g_{\alpha ^\star }(x^\star ,\lambda ^\star )\right) =1. \end{aligned}$$

(5)

As $H_\mathrm {KT}^{\alpha }(x,\lambda )=\nabla _x g_{\alpha } (x,\lambda )$, and thus

$$ \frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha }(x,\lambda ) = \frac{\partial }{\partial x}\left( \nabla _x g_{\alpha } (x,\lambda )\right) = \frac{\partial ^2}{\partial x^2}g_{\alpha }(x,\lambda ),$$

(4) is equivalent to

$$ \frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star ) \varphi ^\star = 0 $$

and (5) is the same as

$$\dim \ker \left( \frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star ) \right) =1.$$

Thus, property (i) of Definition 4 is proven for $H(x,\lambda )= H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$.

Property (ii) of Definition 4 directly follows from the assumption that the Jacobian ${H_\mathrm {KT}^{\alpha ^\star }}'(x,\lambda )$ has full rank, i. e. rank n: if the vector $\frac{\partial }{\partial \lambda }H\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star )$ were in the image of the $n\times n$-matrix $\frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star )$, then the rank of the Jacobian ${H_\mathrm {KT}^{\alpha ^\star }}'(x,\lambda )$ were $n-1$, in contradiction to the assumption. Thus, it has to be true that $\left( \frac{\partial }{\partial \lambda }H_\mathrm {KT}^{\alpha ^\star } (x^\star ,\lambda ^\star )\right) \notin \;\mathrm {im }\frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star ).$

To sum up, both properties given in Definition 4 are satisfied, and thus $(x^\star ,\lambda ^\star )$ is a turning point of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$ with respect to $\lambda$.    $\square$

Remark 2

Using the notation of the proof of Proposition 1 one observes that the matrix $\frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }$ is symmetric, as it is the Hessian of the weighted sums function $g_\alpha$. Thus, $\psi ^\star =\left( \phi ^\star \right) ^T$ is a left eigenvector of $\frac{\partial }{\partial x}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star )$. It follows that, if additionally to (i) and (ii) of Definition 4

$$(\phi ^\star )^T\left( \frac{\partial ^2}{\partial x^2}H_\mathrm {KT}^{\alpha ^\star }(x^\star ,\lambda ^\star )\right) \phi ^\star \phi ^\star \ne 0,$$

then $(x^\star ,\lambda ^\star )$ is a simple turning point of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$ with respect to $\lambda$.

To sum up, a dent border preimage can be obtained by solving the system of equations

$$\begin{aligned} H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )&= 0\nonumber \\ \frac{\partial }{\partial x} H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )\cdot \phi&= 0\\ l^T \phi - 1&=0\nonumber \end{aligned}$$

(6)

with an arbitrary but fixed vector $l\in \mathbb {R}^n$ which satisfies $l^T\phi ^\star \ne 0$ and has non-zero entries, and $x,\phi \in \mathbb {R}^n$, $\lambda \in \mathbb {R}$. In the literature, this system of equations is also called the extended system of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$ (cf. [21]).

Remark 3

A family of dent border preimages can be obtained by solving

$$\begin{aligned} \nabla _x g_\alpha (x,\lambda )&= 0\nonumber \\ \sum _{i=1}^k \alpha _i -1&=0\nonumber \\ \frac{\partial ^2}{\partial x^2} g_\alpha (x,\lambda )\cdot \phi&= 0\\ l^T \phi - 1&=0\nonumber \end{aligned}$$

(7)

with an arbitrary fixed vector $l\in \mathbb {R}^n$ which satisfies $l^T\phi ^\star \ne 0$ and has non-zero entries, $x,\phi \in \mathbb {R}^n$, $\lambda \in \mathbb {R}$ and $\alpha \in \mathbb {R}^k$ with $\alpha _i>0\;\forall i=1,\ldots , k$.

4.2 Numerical Examples

In the following, several new examples for parametric multiobjective optimization problems are presented and its construction is motivated. The examples all have in common that the corresponding Pareto fronts contain dents for specific values of the external parameter $\lambda$. Moreover, under the variation of $\lambda$, dents originate or vanish (cf. Examples 2 and 4), or dents double or merge (cf. Example 3).

Example 2

We again consider the bi-objective optimization problem defined by the two objectives

$$\begin{aligned} f_1(x_1,x_2,\lambda )= & {} \frac{1}{2}(\sqrt{1+(x_1+x_2)^2}+\sqrt{1+(x_1-x_2)^2}+x_1-x_2)+ \lambda \cdot e^{-(x_1-x_2)^2}\\ f_2(x_1,x_2,\lambda )= & {} \frac{1}{2}(\sqrt{1+(x_1+x_2)^2}+\sqrt{1+(x_1-x_2)^2}-x_1+x_2)+ \lambda \cdot e^{-(x_1-x_2)^2} \end{aligned}$$

which we have already seen in Example 1.

Before we are going to examine this example numerically, it is worthwhile to note that it can be understood geometrically and/or analytically. To see the picture, we can use the vectors $q = (1, 1)^T$ and $q^\perp = (1, -1)^T$ as a basis of $\mathbb {R}^2$ and new coordinates $u_1 = x_1+x_2$ and $u_2 = x_1- x_2$, so that for $x = (x_1, x_2)^T$ we have $x = \nicefrac 12 \cdot (u_1\cdot q + u_2 \cdot q^\perp )$. Then we can write the objective as

$$\begin{aligned} F(u_1, u_2, \lambda )&= \left( \frac{1}{2}\cdot \left( \sqrt{1+u_1^2}+\sqrt{1+u_2^2}\right) + \lambda \cdot e^{-u_2^2} \right) \cdot q + u_2\cdot q^\perp \\&= \underbrace{\frac{1}{2}\cdot \sqrt{1+u_1^2} \cdot q}_{=:F^1(u_1)} + \underbrace{ \left( \frac{1}{2} \cdot \sqrt{1+u_2^2}+\lambda \cdot e^{-u_2^2}\right) \cdot q + u_2\cdot q^\perp }_{=:F^2(u_2, \lambda )} \end{aligned}$$

This means the $q^\perp$-component of $F(u_1, u_2, \lambda )$ is simply $u_2\cdot q^\perp$, while the q-component is a sum of three terms, two of which are functions of $u_2$ only, and only one of which depends on $\lambda$. Now an easy computation shows that the q-component of $F^2$ is a convex function for $\lambda < \nicefrac 14$ and that it has a non-convex part around $u_2 =0$ for $\lambda > \nicefrac 14$. This is the reason for the generation of a dent in the Pareto front. To see this, observe that the image of $F^2$ determines the form of the boundary of the image of F, as the $F_1$ term adds a component in positive q-direction only, i.e. a component that moves the image “further inside” the positive quadrant of $\mathbb {R}^2$, and has its minimum for $u_1 = 0$. Thus by adjusting the value of $\lambda$, we can control whether the boundary of the image of F is given by a convex function, that is, whether the Pareto front has a dent or not.

Fig. 5.

Visualization of some Pareto sets and the solution curve of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=0$ (black) for the dent border preimage $x^\star$ (red) for Example 2

In Fig. 5 the Pareto sets of these two objectives for $(x_1,x_2)\in [-1.3,1.3]^2$ are plotted for different values of the external parameter $\lambda$: for $\lambda = 0$ (green), $\lambda = 0.2$ (gray), $\lambda = 0.4$ (light blue), $\lambda = 0.6$ (cyan), and for $\lambda = 0.8$ (magenta). We see that they are all part of the line given by $u_1 = 0$.

In the same figure, an example for a $\lambda$-dependent solution path of the Kuhn-Tucker equations with a fixed weight vector $\alpha ^\star \approx (0.25,0.75)$ which corresponds to the dent border preimage $(x_1^\star ,x_2^\star ) \approx (-0.28,0.28)$ of the dent border point $(y_1^\star ,y_2^\star ) \approx (1.23,1.79)$, located on the Pareto front for $\lambda ^\star =0.6$, is visualized for $\lambda \in [0,1]$ (black paths). The paths have been computed with the help of the software package AUTO2000 [7]. As one can observe, $y^\star$ is indeed a simple turning point of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )$ with respect to $\lambda$. Figure 6 shows the same results in objective space. Here one clearly observes that the Pareto front does not have a dent for $\lambda < 0.25$ and does have a dent for $\lambda > 0.25$.

Fig. 6.

Visualization of some Pareto fronts and the image of the solution curve of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=0$ (black) for a dent border point $y^\star$ (red) for Example 2

In Fig. 7 the entire curve of dent border points in objective space is plotted. To compute this $\lambda$-dependent solution curve (red), again the software package AUTO2000 has been used. One can observe that the point $(y_1^\star ,y_2^\star ,\lambda ^\star )=(1.25,1.25,0.25)$ (with the corresponding weight vector $\alpha ^\star =(0.5,0.5)$), marked by a black dot, is specific: in this point a dent originates, i. e. for $\lambda <\lambda ^\star$ the Pareto front contains no dent whereas for $\lambda >\lambda ^\star$ a dent is contained in the Pareto front.

Fig. 7.

Some Pareto fronts, the curve of dent border points (red) and the point in which the dent originates (black dot) for Example 2

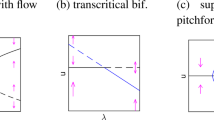
In Fig. 8 the solutions of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=0$ with $\alpha ^\star =(0.5,0.5)$, i. e. the $\lambda$-dependent path containing the specific point in which a non-dent point changes into a dent point, are visualized for $\lambda \in [0,1]$. One can observe that a pitchfork bifurcation³ occurs in this point. Figure 9 shows the same results in objective space.

Fig. 8.

Visualization of some Pareto sets and the $\lambda$-dependent solution curve of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=0$ with $\alpha ^\star =(0.5,0.5)$ (black) for Example 2

Fig. 9.

Visualization of some Pareto fronts and the image of the solution curve of $H_\mathrm {KT}^{\alpha ^\star }(x,\lambda )=0$ with $\alpha ^\star =(0.5,0.5)$ (black) for Example 2

Example 3

Consider the bi-objective optimization problem defined by the two objectives

$$\begin{aligned} f_1(x_1,x_2,\lambda )= & {} \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+ e^{-(x_2-\lambda )^2}+ e^{-(x_2+\lambda )^2}-x_2\\ f_2(x_1,x_2,\lambda )= & {} \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+ e^{-(x_2-\lambda )^2}+ e^{-(x_2+\lambda )^2}+x_2. \end{aligned}$$

Using the same notation as in Example 2, we can write the objective as

$$\begin{aligned} F(x_1, x_2, \lambda )&= \sqrt{1+x_1^2}\cdot q + \underbrace{\left( \sqrt{1+x_2^2}+e^{-(x_2-\lambda )^2}+e^{-(x_2+\lambda )^2}\right) \cdot q + x_2\cdot q^\perp }_{=:F^2(x_2, \lambda )} \end{aligned}$$

and apply a similar analysis. Here the q-component of $F^2$ is non-convex for every $\lambda$ (in fact, for $\lambda = 0$ we have the same situation as for $\lambda = 1$ in Example 2), and a variation of $\lambda$ results in the movement of the “peaks” of the exponential terms. Thus we obtain, for $|\lambda |$ sufficiently large, two separate non-convex parts of the q-component of $F^2$, while there is only one non-convex part for $\lambda = 0$. Correspondingly, one dent in the Pareto front for $\lambda = 0$ will split into two dents for a larger value of $\lambda$.

In Fig. 10 the Pareto fronts which result from the minimization of these two objectives are plotted for different values of $\lambda$. As one can observe the Pareto front contains one dent for $\lambda =0.4$, for example. Under the variation of $\lambda$ it changes into two dents (cp. for instance $\lambda =0.8$). In between, there is a specific point in which the dent splits up into two dents, which is given by $(x_1,x_2,\lambda )\approx (0,0,0.5716)$ with the corresponding weight vector $\alpha ^\star =(0.5,0.5)$. In Fig. 11 the solutions of the Kuhn-Tucker equations for the fixed weight vector $\alpha ^\star =(0.5,0.5)$ are sketched. One can observe that in the point where the dent splits up into two dents a pitchfork bifurcation occurs.

Fig. 10.

Pareto fronts for the multiobjective optimization problem given in Example 3 for different values of $\lambda$

Fig. 11.

Pareto fronts and solutions of the Kuhn-Tucker equations for $\alpha ^\star =(0.5,0.5)$ in $(f_1,f_2,\lambda )$-space for Example 3

Example 4

Consider the three-objective optimization problem defined by the following three objectives

$$\begin{aligned} f_1(x_1,x_2,x_3,\lambda )= & {} \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+\sqrt{1+x_3^2}+\lambda \cdot e^{-(x_2^2+x_3^2)}+\sqrt{2}x_2\\ f_2(x_1,x_2,x_3,\lambda )= & {} \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+\sqrt{1+x_3^2}+\lambda \cdot e^{-(x_2^2+x_3^2)}-\frac{\sqrt{2}}{2}x_2+\sqrt{\frac{3}{2}}x_3\\ f_3(x_1,x_2,x_3,\lambda )= & {} \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+\sqrt{1+x_3^2}+\lambda \cdot e^{-(x_2^2+x_3^2)}-\frac{\sqrt{2}}{2}x_2-\sqrt{\frac{3}{2}}x_3. \end{aligned}$$

In this case, the analysis is somewhat more complicated. Using the vector $q = (1, 1, 1)^T$, we can write

$$\begin{aligned} F(x_1, x_2, x_3, \lambda ) =&\left( \sqrt{1+x_1^2}+\sqrt{1+x_2^2}+\sqrt{1+x_3^2}+\lambda \cdot e^{-(x_2^2+x_3^2)} -\frac{\sqrt{2}}{3}\cdot x_2 \right) \cdot q \\&+ \underbrace{\begin{pmatrix} \frac{8}{3\sqrt{2}} &{} 0 \\ -\frac{4}{3\sqrt{2}} &{} \sqrt{\frac{3}{2}} \\ -\frac{4}{3\sqrt{2}} &{} -\sqrt{\frac{3}{2}} \\ \end{pmatrix}}_{=:q^\perp } \cdot \begin{pmatrix} x_2 \\ x_3 \end{pmatrix} \end{aligned}$$

where, similarly to Examples 2 and 3, the matrix $q^\perp$ spans the orthogonal complement to q. Thus we see that again the q-component of F consists of a convex function independent of $\lambda$ and a $\lambda$-dependent non-convex term that introduces a dent into the Pareto front for sufficiently large values of $\lambda$.

Figure 12 shows the Pareto fronts which result when minimizing these three objectives for $x\in [-2,2]^3$ for different values of $\lambda$. One can observe that under the variation of $\lambda$ a dent originates.

Fig. 12.

Pareto fronts for the multiobjective optimization problem given in Example 4 for different values of the parameter $\lambda$

Remark 4

It has been observed in Examples 2 and 3 that pitchfork bifurcations occur in those points where – under the variation of $\lambda$ – a dent originates in the Pareto front $PF_\lambda$, or a dent splits up into two dents, respectively. Pitchfork bifurcations typically occur if the system of equations $H(x,\lambda )=0$, in our case $H_{\mathrm {KT}}^{\alpha ^\star }(x,\lambda )=0$, includes a symmetry of the form

$$\begin{aligned} \begin{aligned} H(Sx,\lambda )=SH(x,\lambda ), \end{aligned} \end{aligned}$$

(Z2)

where S is a suitable symmetry matrix with $S\ne \mathbbm {1}$ and $S^2= \mathbbm {1}$ (cf. [26]).

In the examples mentioned above, indeed symmetries occur. The Kuhn-Tucker equations of the objective functions given in Example 2 have a $\mathbb {Z}_2$-symmetry for $\alpha ^\star =(0.5,0.5)$. In this case, possible symmetry matrices are given as

$$S_1=\begin{pmatrix}0&{}1 \\ 1&{}0\end{pmatrix} \text { and } S_2=\begin{pmatrix}-1&{}0 \\ 0&{}-1\end{pmatrix}.$$

The Kuhn-Tucker equations of the objective functions given in Example 3 satisfy the symmetry condition (Z2) with

$$S_1=\begin{pmatrix}1&{}0\\ 0&{}-1\end{pmatrix} \text { if } \alpha ^\star = (0.5, 0.5),\text { and }$$

$$S_2=\begin{pmatrix}-1&{}0\\ 0&{}1\end{pmatrix} \text { independent of the weight vector } \alpha .$$

The Kuhn-Tucker equations for the objective functions given in Example 4 also satisfy the symmetry condition (Z2) with

$$S = \begin{pmatrix}-1&{}0&{}0 \\ 0&{}1&{}0\\ 0&{}0&{}1 \end{pmatrix}$$

for arbitrary weight vectors $\alpha ^\star$.

5 Conclusion and Outlook

In this work the occurrence of dents in Pareto fronts has been studied. A formal definition of a dent has been introduced. Points at the border of a (complete) dent have a significant property. In these points a zero eigenvalue of the Hessian of the weighted sum of the objectives occurs. Thus, dent border points are solutions of a certain system of equations. Given a sufficiently smooth multiobjective optimization problem it is possible to find out if dent border points, and thus also possibly dents, occur in the Pareto front by solving this system of equations. Consequently, information about the geometry of the Pareto front can be obtained without computing the entire Pareto set. This information can for example serve as a criterion for the choice of the algorithm one wants to use for solving the multiobjective optimization problem.

Based on theoretical results from bifurcation theory, parameter-dependencies in multiobjective optimization problems have been studied in this chapter. It has been proven that dent border points are turning points of the Kuhn-Tucker equations with a fixed weight vector corresponding to the dent border point.

Several examples for parametric multiobjective optimization problems have been constructed in which dents occur. It is still an open question what happens if a dent originates or vanishes under the variation of the external parameter. The examples given at the end of Sect. 4 lead to the conjecture that in this case pitchfork bifurcations of the Kuhn-Tucker equations occur. However, the theoretical analysis of this statement has to be addressed in future work.