Keywords

1 Introduction

Beliefs have become an important field of research in mathematics education (Philipp 2007). They are research objects of their own, but they are also used as background variables to explain psychological or behavioural aspects of the teaching and learning of mathematics—especially with regard to mathematics performance. One important question is the relationship between performance and self-assessment. Nearly every international large-scale study is combined with some scales to measure students’ mathematical self-assessment mostly to predict and to explain their performance (OECD 2005; OECD 2013). Research has shown that the relationship among self-concept, self-efficacy, and mathematics performance is strong and that mathematics self-concept and self-efficacy are in general powerful predictors to students’ mathematics performance (Multon et al. 1991). The aim of the study presented here is to extend the application of scales related to mathematics self-concept and self-efficacy from lower secondary schools to upper secondary schools and universities. New scales have been developed to cover the mathematical content and skills of the transition phase from school to university. This paper presents the results of a first application of these scales in the context of a two-week bridging course that was designed to repeat secondary school mathematics. All participants of this course had to take part in a mathematics pre-test and a post-test and both tests were combined with a context questionnaire including the new scales. The research questions are as follows: (1) Do the new scales possess satisfactory psychometric properties? (2) Can these scales reveal group differences concerning relevant co-variates? (3) How are these scales related to each other and to other attributes of the students (e.g. performance, mathematics self-concept, and mathematics anxiety)? (4) Are these scales good predictors for the students’ performance? (5) Can the scales be used to detect belief changes between the pre-test and the post-test and—if so—how are these changes related to the change of the students’ general mathematics self-concept and mathematics performance?

2 Theoretical Background

There are two different ways to conceptualise students’ mathematical self-assessment. The first one is related to a person’s mathematics self-concept, measured by general statements like “I have always believed that mathematics is one of my best subjects” (Marsh 1990). The second approach is called mathematics self-efficacy. It was introduced by Bandura’s idea of measuring a person’s self-assessment by his level of confidence about feeling able to solve specific problems that are relevant to the domain of interest (Bandura 1977, 1986). Bandura defined self-efficacy beliefs as “people’s judgments of their capabilities to organise and execute courses of action required to attain designated types of performances” (Bandura 1986, p. 391). Related to this idea, Shavelson et al. (1976) invented a hierarchical model starting with the “general self-concept” on the most abstract level, going down on different steps like the “academic self-concept” and the “mathematical academic self-concept”, and finally arriving at the “evaluation of behaviour in specific situations” that is very close to Bandura’s concept of self-efficacy. Two theoretical claims of this hierarchical model are most relevant to our study: (1) the higher and more abstract the level, the more stable the associated concept and (2) the lower and less abstract the level is, the more the associated concept can be represented by several different dimensions (Shavelson et al. 1976, pp. 412–414). The second claim was the reason to use a multidimensional model consisting of five scales related to different aspects of mathematics instead of a one-dimensional scale. The first claim culminated in the fifth research question mentioned above, namely whether and how changes in mathematics self-efficacy are related to changes in mathematics self-concept and performance—in particular, whether a different degree of stability is recognisable concerning these three aspects. An examination of the students’ mathematics anxiety was added to the questionnaire as the “emotional counterpart” of the mathematics self-concept: according to Hannula’s distinction between mathematics affects as states and traits, mathematics anxiety as a trait is stable and typically highly negatively correlated to mathematics performance and self-concept (Hannula et al. 2019).

3 Self-efficacy, Self-concepts, and Anxiety

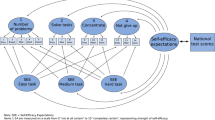
The new scales are based on the PISA self-efficacy scale used in 2003 and 2012 (OECD 2005, pp. 291–294, OECD 2014, pp. 322–323). The PISA scale is short and closely related to tasks typically used at lower secondary schools. But there were three obstacles to adopt this scale to university courses without changes: (1) the PISA scale was designed to measure mathematics self-efficacy only on lower secondary school level; (2) an exploratory factor analysis of this scale indicated that it cannot be considered as one-dimensional, but as multidimensional with respect to mathematical subdomains: algebra, elementary geometry, and applied mathematics/word problems (Girnat 2018); (3) Shavelson et al.’s model mentioned above is based on different subdomains on the more basic and less abstract levels. Insofar, the idea was to invent a bundle of self-efficacy scales that are (a) as short as possible, (b) related additionally to upper secondary school mathematics, and (c) multidimensional with respect to its different subdomains. To match the demands, it was necessary to define subdomains of upper secondary mathematics in a similar manner the re-analysis of the PISA scale suggested (Girnat 2018). To do so, some subdomains could remain, some had to be changed: algebra and applied mathematics are also relevant to upper secondary schools. These subdomains could remain and even some of the items of the PISA scale could be reused (indicated by “PISA”). Elementary geometry was replaced by analytic geometry; and calculus and probability theory were introduced as new subdomains. Since every subdomain should be represented by a scale that could stand for its own, four items per subdomain ought to be regarded as the minimum. Hence, the solution contains 20 items organised in five scales to represent a multidimensional model of mathematics self-efficacy (Table 18.1). The items were introduced with the following question: “How confident do you feel about having to do the following mathematics tasks (using a simple, non-graphing calculator)?”

Table 18.1 The items of the five mathematics self-efficacy scales
Full size table

The items on mathematics anxiety were directly reused from the PISA study in 2012 (OECD 2014, p. 323). The mathematics self-concept has to be adapted from the PISA scale (OECD 2014, p. 323), since some items with a direct reference to school contexts had to be removed or reformulated to be applicable at university level.

4 A Performance Test for a Bridging Course

The primary focus of this paper is the scales described above. Since they were used in the context of a bridging course that was evaluated by a mathematics performance test with a pre-/post-test design, it is also necessary to describe the bridging course and the performance tests. The teaching and learning of mathematics at university level have become a prominent part of mathematics education in recent years—especially the discrepancy between the requests of university mathematics and the skills students have achieved at school (Di Martino and Gregorio 2018). There are several proposals how to deal with this challenge. One of them is a bridging course to enable first-year students to university mathematics. In 2013, the University of Hildesheim decided to establish a voluntary bridging course for all courses of study including a substantial amount of mathematics (Hamann etal. 2014): computer science, business informatics, and elementary and secondary education with mathematics as a major. Although there are different views on which mathematical skills first-year students should possess, it is common sense that the skills students should have learnt at secondary schools are regarded as crucial for being successful at university (Nicholas et al. 2015). The department of mathematics decided to restrict the content to the following topics, since the bridging course had to be limited to 2 weeks and a preceding study had shown that the students demanded a special need of algebra, arithmetic, functions, graphs, and calculus and their applications in real-world situations (Kreuzkam 2013). These five topics have become the core area of the bridging course and the items of the test had to match these circumstances. The bridging course took place in October 2018. 312 students attended the course; 271 of them took part in the pre-test, 224 in the post-test, and 194 in both tests. The participants were distributed as shown in Table 18.2.

Table 18.2 Properties and sub-groups of the sample
Full size table

The labels “basic level” and “advanced level” refer to a characteristic of the German school system: students have to choose in grade 10 if they want to be taught in mathematics on a basic or on an advanced level during grade 11 and 12.

5 Psychometric Properties of the Scales and the Test

The psychometric properties of the scales and the performance test are reported now. The reliabilities of the scales were estimated by Cronbach’s alpha (Cronbach 1951). Since we will later use confirmatory factor analyses (CFA) and structural equation modelling (SEM), the typical fit indices used within this paradigm are reported additionally (Beaujean 2014, pp. 153–166). All calculations were done using R (R Core Team 2018) and the R package “lavaan” (Rosseel 2012) with a DWLS estimator (Beaujean 2014, pp. 92–113).

Table 18.3 contains the values of the pre-test (the values of the post-test are quite similar and are omitted to save space). According to the usual criteria, all scales have good properties. For the performance test, a unidimensional Rasch model was used to obtain a scale that expresses the “overall” mathematics performance of the participants (Linden 2016). The analysis was done using the R package “TAM” (Robitzsch et al. 2018). The Rasch model had an excellent EAP reliability (0.904).

Table 18.3 Reliability and fit indices of the scales in the pre-test
Full size table

6 Results

The results are presented in four steps: (1) correlations between all scales; (2) group differences with respect to background variables mentioned in Table 18.2; (3) Table 18.3 shows the changes between the pre-test and the post-test; (4) linear models to explain students’ mathematics performance and beliefs. The asterisks stand for the usual significance levels: * for p < 0.05, ** for p < 0.01, and *** for p < 0.001.

Correlations

Table 18.4 shows the latent correlations (Beaujean 2014, pp. 100–103) between the performance test, the scales of the context questionnaire, and the final school exam mark with respect to the data of the pre-test—estimated using a structural equation model with good fit indices (RMSEA 0.013, CFI 1.000, SRMR 0.052). The correlations are mostly as expected: there are substantial correlations between the five scales of the multidimensional self-efficacy model, but they are not that high that they could not be empirically differentiated. This is different in case of the mathematics self-concept (matcon) and mathematics anxiety (matanx). This finding supports the hypothesis that both scales are (positive and negative) indicators of the same underlying concept (Hannula et al. 2019, mentioned above).

Table 18.4 Latent correlation between all scales (pre-test)
Full size table

Group Differences

The focus of the analysis is now set to mean differences related to different sub-groups of the sample. Here, we omit the co-variate “choice of the study course”, since there are no significant differences observable. This is very surprising, since the most relevant study to this topic (Betz and Hackett 1983) indicates that mathematics self-efficacy is a good predictor for the students’ choices of their study courses. The reason may be the fact that the possibilities to choose a study course is rather limited at the University of Hildesheim and, therefore, remarkable differences cannot occur. To make the differences on different scales comparable, we report the differences in terms of Cohen’s d (Cohen 1988), i.e. the mean of one group (the “reference group”) is set to zero and the mean of the other group is given as the difference to zero on a standardised metric. Cohen’s d is usually interpreted as follows (Cohen 1988): d = 0.2 indicates a small effect, d = 0.5 a medium effect, and d = 0.8 a strong effect (Table 18.5).

Table 18.5 Mean differences between sub-groups of the sample (pre-test)
Full size table

There is no significant gender difference concerning the performance test (d = −0.120), but the situation is quite diverse with respect to the different self-efficacy scales. There is a small to medium difference (d = 0.339*) in favour to the female group in case of analytic geometry; and there is nearly a large (d = −0.678***) difference to the detriment of the female group in case of applied mathematics. Both cases are remarkable aberration in perception compared to the measured (insignificant) performance difference.

Differences Between Pre-test and Post-test

Now, we compare the results of the pre-test and the post-test. The two tests were connected using the linking method according to Stocking and Lord (1983). Again, the differences are expressed in terms of Cohen’s d (Table 18.6).

Table 18.6 Mean differences between pre-test and post-test
Full size table

The difference concerning the performance tests is huge (d = 0.978***). However, it is remarkable that this successful development is reflected very diversely with respect to the beliefs and emotions measured by the scales of the context questionnaires: both mathematics self-concept (d = 0.144) and mathematics anxiety (d = −0.105) did not change significantly. That may be an evidence for the conjecture that these beliefs (or emotions, respectively) belong to the set of central beliefs within a beliefs system that do not change rapidly—especially not on the basis of a relatively short experience of a two-week bridging course (Philipp 2007, p. 260). Therefore, they seem to be no good indicators for detecting short-term changes. It is exactly the opposite concerning the scales of mathematics self-efficacy: these scales reflect the achievement change almost in the same size that is observed in the performance tests.

Linear Models

Finally, we come back to the pre-test. We suspected that the scales of the context questionnaire may be good predictors for the students’ performance. We analyse this hypothesis using linear models (Searle and Gruber 2016) that include scales of the questionnaire as predictors (independent variables) and the results of the pre-test as the dependent variable to explain. The model was defined in two steps (Table 18.7): firstly, all variables were used as predictors (model above the line, RMSEA 0.36, CFI 0.963, SRMR 0.53); then, all insignificant predictors were removed leading to the result that only one predictor has a significant and substantial explorative value: the self-efficacy concerning algebra (model below the line, RMSEA 0.32, CFI 0.976, SRMR 0.43). We used b i to denote the unstandardised regression coefficients, SE(b i) for their standard errors, and β i for the standardised regression coefficients.

Table 18.7 Linear models explaining students’ mathematics performance (pre-test)
Full size table

Since we already observed that the mathematics self-concept scale has different properties than the self-efficacy scales, we analyse the relationship between these concepts, defining linear models in the same way as above, but now using the mathematics self-concept as depending variable (Table 18.8).

Table 18.8 Linear models explaining students’ mathematics self-concept (pre-test)
Full size table

The result is remarkable. The self-concept is explained by only two significant predictors: the self-efficacy concerning applied mathematics and calculus. That may be an explanation why the mathematics self-concept acts in different way than the self-efficacy scales: it is mostly determined by two self-efficacy scales that are irrelevant for explaining the students’ performance (Table 18.7).

7 Conclusion

The first application of the new scales on mathematics self-efficacy in the context of a bridging course shows the following results: firstly, the five scales of this model (related to algebra, applied mathematics, calculus, analytic geometry, and probability) are short and easy to apply, have good statistical properties, and are substantially, but not too highly correlated, so that they describe different facets of interrelated concepts. Secondly, they allow analysing group differences in details. For example, the self-concept did not allow detecting gender differences; the self-efficacy scales, on the contrary, showed a large difference specifically related to applied mathematics and—not having a similar large counterpart in mathematics performance—suggesting that this difference is “exaggerated”. Thirdly, the scales are useful tools to describe and to explain changes related to beliefs and to mathematics performance. Whereas the mathematics self-concept is more stable and obviously a part of a student’s central beliefs system, the scales of self-efficacy are more peripheral, so that they are appropriate to detect short-term changes as shown by the analyse of the two-week bridging course. Lastly, the self-efficacy scales can explain a considerable amount of both students’ mathematics performance and self-concept, revealing that the self-concept is mostly determined by the students’ self-efficacy related to applied mathematics and to calculus, whereas their performance could be explained best by their algebraic self-efficacy. Insofar, the scales of self-efficacy can clarify relationships between different mathematically relevant beliefs and concepts.

All results have to be understood against to the background that the two-week bridging course was the first and very limited opportunity to apply and to test the scales. This fact induces some limitations: until now, there is no information about the marks and the drop out of the participants during their upcoming academic courses; there are also no data about the long-term effects on the participants’ performance, beliefs, and emotions; and there was no possibility to control the tasks given during the bridging course. Especially the latter would be desirable to check if the predominant role of the algebraic self-efficacy as a predictor of the students’ performance is a general fact or if this role is limited to the specific content of the bridging course at Hildesheim.