Abstract
This chapter contains the translation of the paper:
-
M. Sce, Sui sistemi di equazioni differenziali a derivate parziali inerenti alle algebre reali, (Italian) Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat. (8) 18 (1955), 32–38 as well as some comments and historical remarks.
Access provided by Autonomous University of Puebla. Download chapter PDF
This chapter contains the translation of the paper:
-
M. Sce, Sui sistemi di equazioni differenziali a derivate parziali inerenti alle algebre reali, (Italian) Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat. (8) 18 (1955), 32–38.
Article by Michele Sce, presented during the meeting of 11 December 1954 by B. Segre, member of the Academy.
In this Note, after some preliminaries in algebra and analysis, we classify systems of partial differential equations which give monogenicity conditions in algebras. These systems are elliptic for primitive algebras, parabolic with algebras with radical; the proof of this latter fact is based on a characterization, maybe unknown, of semisimple algebras via their determinant. Among hyperbolic systems, we highlight the one obtained from a regular algebra, and which has as characteristic hypersurface the cone of zero divisors of the algebra itself.
From these systems we deduce some partial differential equations of order equal to the order of the algebra which are of the same type of those satisfied by all monogenic functions. I hope that a further study of these equations would eventually lead me to solve, at least for monogenic functions in regular algebras, some problems analogous to the Cauchy problem.
1. Let \(\mathscr A\) be an associative algebra over the real, with unit, and let U = (u 1, …, u n) be a basis. The algebras of matrices \(\mathscr A'\) (\(\mathscr A''\)) which gives the first (second) regular representation of \(\mathscr A\) are such that for every x in \(\mathscr A\) and X′ (X″) in \(\mathscr A'\) (\(\mathscr A''\)) one has
the determinant of X′, (X″) is also called left (right) determinant of x.Footnote 1
The element y = y 1u 1 + ⋯ + y nu n = ηu −1 in \(\mathscr A\) is said to be left (right) monogenic function of x = x 1u 1 + ⋯ + x nu n if y i are functions derivable with respect to x k and such that Footnote 2
By setting
one gets a system of n linear differential equations of the first order:
whose coefficients are the constants of multiplication in the algebra. By setting [Editors’ Note: ∥a ij∥ denotes the matrix with entries a ij]
(3.3) can be written in a more compact form as:
the determinant |C| of the matrix
\(C_k=\|c_{ki}^j\|\) (for i, j = 1, …, n), obtained from Ω by substituting z k instead of \(\dfrac {\partial }{\partial x_k}\), is called characteristic form of the system. The system itself is called elliptic or parabolic if the characteristic equation
does not have real solutions different from the trivial solution (0, …, 0) or, by means of a change of variables, it can be reduced to an equation depending on less than n variables;Footnote 3in the other cases the system is called hyperbolic and, in particular, totally hyperbolic if the matrix C is diagonalizable and its characteristic polynomial has real roots whatever are the z k’s.Footnote 4
Finally, a hypersurface φ(x 1, …, x n) = 0 in the Euclidean space of n-tuples (x 1, …, x n) is called characteristic if the directional cosines of its normal
satisfy the characteristic equation (3.6).Footnote 5
2. Let us multiply the matrix (3.5) on the right by the n-vector u −1; in force of (3.2), one has:

and, setting z = z 1u 1 + ⋯ + z nu n, we deduce
A comparison with (3.1) shows that C −1 is the matrix corresponding to z in the first regular representation of \(\mathscr A\);Footnote 6 thus the characteristic form of system (3.3) coincides with the left determinant of an element in \(\mathscr A\).
Since the determinants of elements in \(\mathscr A\) are invariant with respect to change of basis in the algebra, one has also that the characteristic form of the system expressing the monogenicity is invariant with respect to changes of basis in the algebra.Footnote 7
Primitive algebras have no zero divisors and so the determinants of their nonzero elements are always nonzero; and conversely. Based on the preceding arguments and on n. 1, this is equivalent to claim that system (3.3) is elliptic for primitive algebras and only for those.
3. We will prove that the system (3.3) is parabolic for algebras not semi-simple and only for them, by proving that an algebra is semi-simple if and only if, with respect to any basis, the determinant of the elements depends on all their coordinates.
Let us assume the \(\mathscr A\) is semi-simple and that the determinant of the elements does not depend on all their coordinates. \(\mathscr A\) is direct sum of simple algebras \(\mathscr A_i\) and so the determinant of the elements in \(\mathscr A\) is the product of the determinants of the elements in \(\mathscr A_i\); thus some algebra \(\mathscr A_i\) is such that the determinant of its elements x =∑ix iu i, y =∑iy iu i does not depend, for example, on the coefficients of the units u m, …, u n but it depends on the coefficients of all the other units. Then also the determinant of
does not depend on x m, …, x n;y m, …, y n; it turns out that all the products of units appearing in the second sum can be expressible as linear combinations of u m, …, u n, namely
must hold. The relations (3.7) allow to say that the set having basis u m, …, u n is a proper ideal of \(\mathscr A_i\); this contradicts the assumption that \(\mathscr A_i\) is simple and shows the necessity of the condition.
Let now \(\mathscr A\) an algebra not semi-simple, that is, it has a nonzero radical \(\mathscr R\). Let U 1, …, U m, …, U n, (1 < m < n) be a basis for \(\mathscr A'\) such that U m, …, U n is a basis for the image \(\mathscr R'\) of \(\mathscr R\) in the first regular representation of \(\mathscr A\); then the trace of any element X′ =∑ix iU i in \(\mathscr A'\) does not depend on x m, …, x n since the matrices U m, …, U n—which are elements of \(\mathscr R'\) are nilpotent. Since
only the coefficients of the first sum—among which x m, …, x n do not appear—can give a nonzero contribution to the trace of X′ 2 in fact \(\mathscr R'\) is an ideal of \(\mathscr A'\) and so a relation similar to (3.7) holds. Reasoning in this way we can prove that the traces of X′, X′ 2, …, X′ n do not depend on x m, …, x n. Using the recurrence formulas—which can be easily obtainedFootnote 8—expressing the coefficients of the characteristic equation of a matrix via the traces of a matrix and its powers, one gets that each coefficient of the characteristic equation of X′ does not depend on x m, …, x n. This is true, in particular, for the determinant of x and so the theorem is proved.
4. The system (3.3) is completely hyperbolic for the algebras of n-real numbers and only for them.
Let u 1, …, u n, \(u_i^2=u_i\), u iu k = 0, (i ≠ k), be the basis of n-real numbers; the matrix (3.5) turns out to be real and diagonal,so that the system (3.3) is totally hyperbolic.
Conversely, let us assume that the system (3.3) is totally hyperbolic, that is, C is diagonalizable and its characteristic roots are real. If C i is diagonal and all the z k except z i, z j are zero, the matrix z iC i + z jC j is diagonal only if C j is diagonal; it follows that, when i and j vary, a matrix which reduces a C k to the diagonal form must reduce to the diagonal form all the other C k. Thus the matrices C k are pairwise commuting;Footnote 9 and since their transpose correspond to the units of \(\mathscr A\) in the first regular representation, \(\mathscr A\) is commutative. On the other hand, since the system (3.3) is not parabolic, \(\mathscr A\) is semi-simple (n. 3); a semi-simple algebra which is commutative is direct sum of the real field and of the algebra of complex numbers, and both can be repeated a certain number of times.Footnote 10 However, if \(\mathscr A\) would have as a component the algebra of complex numbers, some C k would have complex characteristic roots; thus \(\mathscr A\) cannot be anything but the direct sum of the real field taken n times.
5. Let e 11, e 12, …, e nn with e ije jk = e ik, e ije lk = 0, (i ≠ l) the basis of a regular algebra \(\mathscr M_n\) of order n 2; the matrices of order n 2 elements of \(\mathscr {M}^{\prime }_n\) are direct sums of n matrices equal to ∥x ik∥, of order n, in \(\mathscr M_n\). Thus φ(x ik) = 0 is a characteristic hypersurface of system (3.3) if:
Since \(\dfrac {\partial |x_{ik}|}{\partial x_{ik}}\) is the adjoint of X ik in ∥x ik∥, one has
and the cone |x ik| = 0 of zero divisors of \(\mathscr M_n\) satisfies (3.8); thus the cone of zero divisors of a regular algebra \(\mathscr M_n\) counted n − 1 times, is a characteristic hypersurface of system (3.3).
Let us now consider the algebra \(\mathscr A\) of order 2n 2 direct product of the algebra of complex numbers and the regular algebra \(\mathscr M_n\). The elements of \(\mathscr A'\) with respect to e ik, ie ik are matrices of order 2n 2 direct sums of n matrices of order 2n,

where A, B are arbitrary elements of \(\mathscr M_n\). Denoting again by X jℓ the adjoint of x jℓ (where j, ℓ = 1, 2, …, 2n, a simple computation shows that—for i, k = 1, …, n—one has:
thus the equation \(|x_{j\ell }|{ }^{2n^2-1}=0\)—in the complex case—represents a characteristic hypersurface of system (3.3). However, it should be noted that, in the real field, |x jℓ| = 0 represents a cone (with vertex at the origin) of dimension 2(n 2 − 1) which certainly does not give a characteristic hypersurface.
Analogous remarks can be made in the case of an algebra direct product of the algebra of quaternions with a regular algebra.
6. Let A = ∥a ik∥ be a matrix of order n whose elements belong to an integral domain \(\mathscr D\) with unit, but which is not a principal ideal ring. If A has maximal rank, its first column cannot be zero; thus, multiplying A on the left by a suitable matrix, we can assume that the element (1, 1) is nonzero. Let us still denote by A the matrix obtained in this way, and let us multiply it by the nonsingular matrix

one obtains

Since also the first column of A 1 must be nonzero, we can act on A 1 as we did on A; iterating the procedure, we show that every nonsingular matrix in \(\mathscr D\) can be reduced in triangular form T, multiplying it on the left by a suitable nonsingular matrix.
As it can be seen from (3.9), the first two elements on the principal diagonal of T are two minors of order 1 and 2 respectively, the first one contained in the second; reasoning by induction one finds that—by selecting a sequence of nonzero minors α 1, α 2, …, α n = |A| of all the orders from 1 to n, each of which contained in the following (complete chain)—the elements on the principal diagonal of T are
Footnote 11The degree of the i-th element in the sequence (3.10) in the elements of A is clearly \(\sum _{k=1}^{i-2} k2^{i-2-k}+i\); since
we can conclude that the i-th element of the sequence (3.10) is of degree 2i−1 in the elements of A.
Let us consider the extension \(\mathscr F\) of the field of the real numbers by means of the operators \(\dfrac {\partial }{\partial x_1}, \ldots , \dfrac {\partial }{\partial x_n}\); defining formally, as usual, the operations of sums and product, \(\mathscr F\) turns out to be a ring with unit. The set of operators \(\mathscr F\) has no zero divisors; thus, if we assume that all the functions to which we apply elements of \(\mathscr F\) have finite derivatives, continuous up to the order m, we can say that all the elements of order not greater than m behave like elements in an integral domain.
Thus, if we suppose that the y i elements of η in (3.4) possess finite derivatives, continuous up to order 2n−1, we can apply to the matrix Ω the considerations made above, this gives for the element y n of η a partial differential equation of order at most 2n−1. An analogous result can be obtained for the other y i; but, in general, the equations obtained for the various y i are different. To obtain a differential equation satisfied by all the y i’s, one needs to multiply between them the n complete chains, assuming that the operators which are their elements commute (namely, that the functions have derivatives finite and continuous up to the order of the equation); taking into account that the n-chains have all the same last element, which does not have to be necessarily repeated in the product, one has that the single components of a monogenic function satisfy a same partial differential equation of order at most n(2n−1 − (n − 1)).
7. The procedure illustrated in the preceding section, is maybe of some interest; however, an equation satisfied by all the y i’s can be easily be obtained by multiplying (3.4) on the left by the matrix Ω ∗ adjoint of Ω. So we have that the components of a monogenic function satisfy an equation of order at most n.Footnote 12
The characteristic form of the equation coincides with the characteristic form of the system; thus the equations satisfied by the components of the monogenic functions are of the same kind of system (3.3) and the characteristic hypersurfaces of the system are the same of those of the equation.
Since, as we have seen in n. 5, the elements of the first regular representation of an algebra simple of order kn 2 are composed by n matrices and Ω, as we observed in the note 6, can be considered an element of the first regular representation, one has that the single components of a monogenic function in a simple algebra of order kn 2 satisfy an equation of order at most kn.
It is easy to extend the result to semisimple algebras.
3.1 Comments and Historical Remarks
In the paper translated in this chapter, Sce discusses the problem of characterising an algebra according to the properties of the system satisfied by the monogenic functions in that algebra see [8]. In his papers, he always has a special taste for algebraic questions, see also his paper [9], and in fact inspired by this problem, he also proves a new property of semi-simple algebras. Moreover, he also shows that each function, which is a component of a monogenic function, satisfies a suitable system of differential equations with order equal to the order of the algebra. Also this paper is an interesting combination of properties exquisitely algebraic in nature and analytical properties of functions.
Most of the properties of the algebras considered in this chapter are given in Chap. 2. The reader may refer to the books of Albert [1, 2] and of Scorza [10] which were also used by Sce.
Remark 3.1
In the paper we consider in this chapter, Sce makes use of the Italian term “algebra primitiva”, i.e., primitive algebra, that we keep in the translation. In more modern terms, one should translate the term as division algebra. In fact, as one can read in various old sources, see e.g. [11,12,13], a primitive algebra is an algebra which does not contain zero divisors. Such an algebra is semi-simple and also simple.
Another important definition is the following:
Definition 3.1
Let \(\mathscr A_1,\ldots , \mathscr A_m\) be algebras over a field F. We say that \(\mathscr A\) is the direct sum of \(\mathscr A_1,\ldots , \mathscr A_m\) and we write
if v i v j = 0 for \(v_i\in \mathscr A_i\), i ≠ j and the order of \(\mathscr A\) is the sum of the orders of \(\mathscr A_i\), i = 1, …, m.
Example 3.1
An instance of algebra which is a direct sum used in this chapter is the algebra of n-real numbers \(\mathbb R^n=\mathbb R\oplus \cdots \oplus \mathbb R\) in which all the various copies of \(\mathbb R\) are generated by u i (the unit of \(\mathbb R\)) for i = 1, …, n, and are such that u iu j = 0 when i ≠ j.
An algebra is said to be decomposable if it can be written as sum of its (nontrivial) subalgebras, indecomposable if this is not possible.
These notions about the algebras are useful to characterise the systems of differential equations associated with the various notions of monogenicity. To provide concrete examples, we consider the monogenicity conditions in Chap. 1, for increasing dimension of the algebras considered.
Example 3.2
Let us start by considering second order algebras. We begin with the real algebra of complex numbers, which is clearly a division algebra. Then

so that \(|C|=x_1^2+x_2^2\) and the system is, as it is well known, elliptic.
Again in dimension 2, we can consider the algebra of dual numbers and the left monogenicity condition, see (2.32), which are associated with the matrix

so that \(|C|=x_1^2\) and the system is parabolic, which is consistent with the fact that the algebra of dual numbers is not semi-simple.
Example 3.3
In the case of hyperbolic numbers, the monogenicity is expressed by the matrix

We have that \(|C|=x_1^2-x_2^2\). Moreover, the matrix is real symmetric with eigenvalues x 1 ± x 2, thus the system is completely hyperbolic. According to the result proven in n. 4 the algebra of hyperbolic numbers is, up to a suitable isomorphism, the algebra \(\mathbb R^2\). To see this fact, let us set
Then e, e † are two idempotents such that e e † = e † e = 0. The change of coordinates
allows to write x = x 1u 1 + x 2u 2 = z 1e + z 2e † = z. At this point we can identify the element z = z 1e + z 2e †with the pair \((z_1,z_2)\in \mathbb R^2\). We note that given two elements z = z 1e + z 2e †, \(z'=z^{\prime }_1\mathsf e+z^{\prime }_2\mathsf e^\dagger \) their sum and product are given by
which, at level of pairs, corresponds to the sum and multiplication componentwise. In this new basis, the monogenicity condition (left or right) of a function w = w(z) rewrites as

which leads to
that is
Example 3.4
As an example of third order algebra, we consider the ternions. The matrix C is in this case

and \(|C|=x_1x_2^2\). The matrix is lower triangular, with eigenvalues equal to the diagonal elements. Easy arguments show that C can be diagonalized over the real and so the system is completely hyperbolic. We note that by multiplying Ω by its adjoint Ω ∗ we get that the components y ℓ, ℓ = 1, 2, 3 of a monogenic function y 1e 1 + y 2e 2 + y 3e 3 satisfy the equation
Example 3.5
Let us now consider two cases of four dimensional algebras. First we look at the case of the algebra of quaternions which is a division algebra. Thus we expect an elliptic system. And in fact the left monogenicity condition is associated with the matrix

We have that \(|C|=(x_1^2+x_2^2+x_3^2+x_4^2)^2\) which vanishes only at (0, 0, 0, 0). In the case of the algebra of bicomplex numbers, we have:

and
The determinant |C| can vanish also for (x 1, x 2, −x 2, x 1) and (x 1, x 2, x 2, −x 1) with x 1x 2 ≠ 0. Thus the system is parabolic and it is possible to construct a change of basis for which the determinant of new matrix C associated with the monogenicity condition do not depend on all the four variables.
Remark 3.2
The work of Sce discussed in this chapter was, unfortunately, completely forgotten despite its relations with physical problems, see [3,4,5]. In the works of Krasnov, see e.g. [6, 7], the author discusses various properties of PDEs in algebras. In particular, in section 7.5 of [6] he considers ellipticity properties of the solutions of a generalized Cauchy–Riemann operator, i.e. monogenic functions, according to the type of algebras considered. In particular, it is shown that an operator is elliptic if and only if the algebra is a division algebra. He also widely discusses the case of the Riccati equation. Among various results, he shows that
Proposition 3.1 (Proposition 2.1, [6])
Any n-dimensional polynomial differential system x′ = P(x) with deg P = m can be embedded into a Riccati equation considered in an algebra \(\mathscr A\) of dimension ≥ n.
Notes
- 1.
See G. Scorza, Corpi numerici e algebre, Messina (1921), Part II, n. 184 and 185.
- 2.
See B. Segre, Forme differenziali e loro integrali, (Roma, 1951), Ch. IV, n. 90. The indices of the infinite sums, unless otherwise stated, always run from 1 to n. Later we will always refer to left monogenicity, since analogous results can be obtained in a similar way for right monogenicity.
- 3.
See R. Courant, D. Hilbert, Methoden der Mathematischen Physik, Band II (Berlin, 1937), Kap. III, § 4, n.2.
- 4.
A definition equivalent to ours can be found, for systems of quasi-linear equations, in R. Courant, K. O. Friedrichs, Supersonic flow and shock waves, Interscience Publishers, Inc., New York, N. Y., 1948, Chapt. II, n. 32; sometimes, as in R. Courant, P. Lax, On nonlinear partial differential equations with two independent variables, Comm. Pure Appl. Math., 2 (1949), 255–273, pp. 255–273, n.2, totally hyperbolic systems are called hyperbolic.
- 5.
See Courant-Friedrichs, cited in (4).
- 6.
In particular, Ω −1 corresponds to \(\omega =\sum _k \dfrac {\partial }{\partial x_k}u_k\) considered as an element in \(\mathscr A\) and the transpose of the C k’s in (3.5) correspond to the units in \(\mathscr A\).
- 7.
On the contrary, monogenicity conditions depend on the basis of the algebra; see M. Sce, Monogeneità e totale derivabilità nelle agebre reali e complesse, Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat., (8) 16 (1954), 30–35, Nota I, n. 1.
- 8.
When a matrix is in canonic form, these formulas reduce to those of symmetric functions.
- 9.
See M. Sce, Su alcune proprietà delle matrici permutabili e diagonalizzabili, Rivista di Parma, vol. 1, (1950), pp. 363–374, n.5.
- 10.
See Scorza cited in (1), part II, n. 292.
- 11.
Obviously for particular matrices one can obtain much more; for example, if
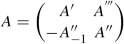
is a symmetric matrix of the fourth order one has:
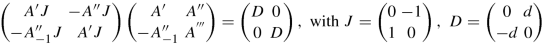
where d is the pfaffian of A. Another example is given by the elemnts in the algebra which is the first regular representation of quaternions; these matrices multiplied by the transposed give the scalar matrix |q|I 4 (where |q| is the norm of the quaternion q).
- 12.
Sometimes, by multiplying Ω on the left by matrices different from Ω ∗, we obtain equations of lesser order; for example, in the case of quaternions multiplying Ω by its transpose one obtains the scalar matrix ΔI n (Δ is the laplacian in four variables).
References
Albert, A.A.: Structure of Algebras, Vol. XXIV. American Mathematical Society Colloqium Publications, New York (1939)
Albert, A.A.: Modern Higher Algebra. The University of Chicago Science Series, Chicago (1937)
Courant, R., Friedrichs, K.O.: Supersonic Flow and Shock Waves. Interscience Publishers, New York, NY (1948)
Courant, R., Hilbert, D.: Methoden der Mathematischen Physik. Band II, Berlin (1937)
Courant, R., Lax, P.: On nonlinear partial differential equations with two independent variables. Comm. Pure Appl. Math. 2, 255–273 (1949)
Krasnov, Y.: Differential equations in algebras. Hypercomplex Analysis, pp. 187–205. Trends Math. Birkhäuser Verlag, Basel (2009)
Krasnov, Y.: Properties of ODEs and PDEs in algebras. Complex Anal. Oper. Theory 7, 623–634 (2013)
Sce, M.: Monogeneità e totale derivabilità nelle agebre reali e complesse. Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat., (8) 16, 30–35 (1954). See also this volume, Chap. 2
Sce, M.: Su alcune proprietà delle matrici permutabili e diagonalizzabili. Rivista di Parma 1, 363–374(1950)
Scorza, G.: Corpi numerici e algebre. Messina (1921)
Scorza, G.: La teoria delle algebre e sue applicazioni. Atti 1o Congresso dell’Un. Mat. Ital., 40–57 (1937) (available on line)
Segre, B.: Forme differenziali e loro integrali. Roma (1951)
Wedderburn, J.H.M.: A type of primitive algebra. Trans. Am. Math. Soc., 15, 162–166 (1914)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Colombo, F., Sabadini, I., Struppa, D.C. (2020). On Systems of Partial Differential Equations Related to Real Algebras. In: Michele Sce's Works in Hypercomplex Analysis. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-50216-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-50216-4_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-50215-7
Online ISBN: 978-3-030-50216-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)