Keywords

1 Introduction

At nowadays, one of the effective methods for solving the boundary value problems of the mechanics of a deformable body is to reduce them to solving integral equations, most often singular ones. Since the exact solution of these equations is rarely possible, the actual problem is the creation of numerical methods for their solution. The presence in the singular part of kernels with fixed singularities makes it difficult to solve r integral equations. In the monograph [1], as well as in articles [2,3,4] where exact solutions of singular integral equations are found, it is proved that the presence of fixed singularities affects the asymptotic behavior of the solution near the ends of the integration segments. Despite this, in many cases the real asymptotic of the unknown functions is either not taken into account Therefore, the convergence of these numerical methods is quite slow. Articles [5,6,7,8] show that the methods based on the use of special quadrature formulas for singular integrals and taking into account the real asymptotic of the solution are most effective in the sense of convergence. Such method for an integral equation with two fixed singularities, to which the contact problem of torsional vibrations of a cylinder on an elastic half space reduces is proposed in this article.

2 Statement of the Problem and Its Reduction to a Singular Integral Equation

Let an elastic cylinder \( 0 \le r < r_{0} ,0 \le z < a,0 \le \varphi < 2\pi \) locate on the elastic half-space \( 0 \le r < + \infty , \) \( - \infty < z \le 0, \, 0 \le \,{\upvarphi }\, < 2\,\uppi \) (Fig. 1) and coupled to it. A round rigid plate of the same radius as the cylinder and the thickness \( d \) is connected to the upper end of the cylinder. A torsion moment \( Me^{{ - i\,\upomega\,t}} \), harmoniously dependent on time, is exerted to the plate. The factor \( e^{{ - i\,\upomega\,t}} \) that determines the dependence on time is omitted farther. Under such conditions, an axisymmetric torsional deformation is realized in the cylinder and half-space and only angular displacements \( w_{j} \left( {r,z} \right), \, j = 1,2 \) is nonzero. They are determined from the equations

Fig. 1.
figure 1

The elastic cylinder coupled with half space

Full size image
$$ \frac{{\partial^{2} w_{j} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial w_{j} }}{\partial r} - \frac{{w_{j}^{2} }}{{r^{2} }} + \frac{{\partial^{2} w_{j} }}{{\partial z^{2} }} +\upkappa_{2j}^{2} w_{j} = 0;\upkappa_{2j}^{2} = \frac{{\uprho_{j}^{2}\upomega^{2} }}{{G_{j}^{2} }},\;\;j = 1,2; $$
(1)

where \( w_{1} \left( {r,z} \right) \) is displacement in cylinder, \( w_{2} \left( {r,z} \right) \) is displacement in half space, \( \uprho_{1} ,\,G_{1} \) are shear modulus and density of the cylinder, \( \uprho_{2} ,\,G_{2} \) are shear modulus and density of the half space. In the area of contact between the cylinder and the half-space, the following equations are satisfied:

$$ \uptau_{{{\upvarphi }\,z}}^{\left( 1 \right)} \left( {r, +0} \right) = q\left( r \right),\,\uptau_{{{\upvarphi }\,z}}^{\left( 2 \right)} \left( {r, - 0} \right) = q\left( r \right), \, 0 \le r < r_{0} $$
(2)

where \( q\left( r \right) \) is unknown stresses in the contact area. Also in the contact area, the condition of continuity of displacements is fulfilled

$$ w_{1} \left( {r, +0} \right) = w_{2} \left( {r, - 0} \right),\,\,\,0 \le r < r_{0} . $$
(3)

The surface of the half-space outside the contact area is considered unloaded

$$ \uptau_{{z\,{\upvarphi }}}^{\left( 2 \right)} \left( {r, - 0} \right) = 0,\,\,\,r > r_{0} . $$
(4)

On the upper end of the cylinder, the conditions of couple to the plate is satisfied

$$ w_{1} \left( {r,a} \right) =\uptheta_{0} r,\,0 \le r \le r_{0} . $$
(5)

where \( \uptheta_{0} \) is unknown plate rotation angle, It is determined from the equation

$$ - \omega^{2} j_{0}\uptheta_{0} = M - M_{R} , \, j_{0} = \,\uppi\,r_{0}^{4} d\uprho_{0} /2 $$
(6)

where \( j_{0} \) is the moment of inertia of the plate, \( M_{R} \) is the moment of the reaction forces. There \( \uprho_{0} \) is density of the plate. The lateral surface of the cylinder is not loaded:

$$ \uptau_{{r{\varphi }}}^{\left( 1 \right)} \left( {r_{0} ,z} \right) = 0,\,\,0 < z < a. $$
(7)

Angular displacement in a cylinder is the solution of the boundary value problem (1), (2), (5), (7) and it equal

$$ w_{1} \left( {r,z} \right) = - \int\limits_{0}^{{r_{0} }} {\upeta\frac{{q\left(\upeta \right)}}{{G_{1} }}F_{1} \left( {\upeta,r,z} \right)} d\upeta +\uptheta_{0} r\frac{{\cos\upkappa_{21} z}}{{\cos a\,\upkappa_{21} }}. $$
(8)
$$ F_{1} \left( {\upeta,r,z} \right) = \frac{2}{a}\sum\limits_{k = 1}^{\infty } {\left[ {g_{k}^{1} \left( {\upeta,r} \right)\left. { + \frac{{K_{2} \left( {q_{k1} r_{0} } \right)}}{{I_{2} \left( {q_{k1} r_{0} } \right)}}I_{1} \left( {q_{k1}\upeta} \right)I_{1} \left( {q_{k1} r} \right)} \right] \cdot \,\cos \,\uplambda_{k} z,} \right.} $$
$$ g_{k}^{1} \left( {\upeta,r} \right) = \left\{ {\begin{array}{*{20}c} {I_{1} \left( {q_{k1} r} \right)K_{1} \left( {q_{k1}\upeta} \right),\,\,\,r <\upeta;} \\ {I_{1} \left( {q_{k1}\upeta} \right)K_{1} \left( {q_{k1} r} \right),\,\,\,r >\upeta,} \\ \end{array} \, } \right. \, \quad\uplambda_{k} = \frac{{\uppi\left( {2k - 1} \right)}}{2a};\,\,q_{k1} = \sqrt {\uplambda_{k}^{2} -\upeta_{21}^{2} } . $$

Angular displacement in half-space is the solution of boundary value problem (1), (2) (4), and it equal to

$$ w_{2} \left( {\upeta,r} \right) = \int\limits_{0}^{{r_{0} }} {\upeta\frac{{q\left(\upeta \right)}}{{G_{2} }}} \int\limits_{0}^{ + \infty } {\frac{{\upbeta\,e^{{q_{2} \left(\upbeta \right)z}} }}{{q_{2} \left(\upbeta \right)}}J_{1} \left( {\upbeta\,r} \right)} J_{1} \left( {\upbeta\,\upeta} \right)d\upbeta\,d\upeta, \, q_{2} \left(\upbeta \right)a = \sqrt {\upbeta^{2} -\upkappa_{22}^{2} } $$
(9)

Now it is necessary to find the unknown contact stresses \( q\left( r \right) \) for the final determination of the displacement in the cylinder and the half-space For this purpose, the integral equation was obtained by substitution (8), (9) in (3). This integral equation can be transformed into a second-kind integral equation [9] for a new unknown function. This function is related to contact stresses by the next formulas

$$ {\upvarphi }\left( x \right) = \int\limits_{x}^{{r_{0} }} {\upeta\frac{{q\left(\upeta \right)}}{{\sqrt {\upeta^{2} - x^{2} } }}d\upeta} , \, q\left(\upeta \right) = - \frac{2}{\uppi}\frac{\partial }{{\partial\upeta}}\int\limits_{\upeta}^{{r_{0} }} {\frac{{{\upvarphi }\left( x \right)dx}}{{\sqrt {x^{2} -\upeta^{2} } }}} . $$
(10)

As a result of the transformations detailed in [9] and the extraction of the singular component, this equation takes the following form:

$$ \begin{aligned} & \left( {1 + c} \right)g\left(\upzeta \right) + \frac{1}{\uppi}\int\limits_{ - 1}^{1} {g\left(\uptau \right)\left[ {\frac{1}{{2 -\uptau -\upzeta}} + \frac{1}{{2 +\uptau +\upzeta}}} \right.} - \frac{15}{4}\ln \left( {2 +\uptau +\upzeta} \right) - \\ \, & \quad \quad \, \left. { - \frac{15}{4}\ln \left( {2 +\uptau +\upzeta} \right) + R\left( {\uptau,\upzeta} \right)} \right]d\tau = \frac{{2\uptheta_{0}\upzeta}}{{\cos \left( {\upgamma\,\upkappa_{0} } \right)}},\,\,\, - 1 <\upzeta < 1. \\ \end{aligned} $$
(11)

When deriving Eq. (11) the next notation was taken: \( x = r_{0}\uptau,\,\,\,y = r_{0}\upzeta,\,\, \), \( {\upvarphi }\left( {r_{0}\uptau} \right) = r_{0} G_{1} g\left(\uptau \right),\,\upgamma = {a \mathord{\left/ {\vphantom {a {r_{0} }}} \right. \kern-0pt} {r_{0} }},\,\,\,\upkappa_{0} =\upkappa_{21} r_{0} ,\,\,\,c = {{G_{1} } \mathord{\left/ {\vphantom {{G_{1} } {G_{2} }}} \right. \kern-0pt} {G_{2} }} \).

3 The Numerical Solution of Integral Equation

For construction an efficient numerical method of solving Eq. (11), we need to find out the asymptotic of the unknown function \( g\left(\uptau \right) \) for \( \uptau \to \pm 1 \). This defines the following form of solution:

$$ g\left(\uptau \right) = \left( {1 -\uptau^{2} } \right)^{\upsigma}\uppsi\left(\uptau \right),\;\upsigma = \frac{1}{\uppi}\arcsin \frac{1}{c + 1}, $$
(12)

where \( \uppsi\left(\uptau \right) \) is a function that satisfies the Holder conditions.

Quadrature formulas for singular integrals are based on the approximation of the function by the following interpolation polynomial:

$$ \uppsi\left(\uptau \right) \approx\Psi _{n} \left(\uptau \right) = \sum\limits_{m = 1}^{n} {\uppsi_{m} \frac{{P_{n}^{{\upsigma,\upsigma}} \left(\uptau \right)}}{{\left[ {P_{n}^{{\upsigma,\upsigma}} \left( {\uptau_{m} } \right)} \right]^{\prime } \left( {\uptau -\uptau_{m} } \right)}}} , $$
(13)

where \( \uppsi_{m} =\uppsi\left( {\uptau_{m} } \right) \), \( P_{n}^{{\upsigma,\upsigma}} \left(\uptau \right) \) are Jacobi polynomials and \( \tau_{m} \) are roots of these polynomials. As a result, we obtain the quadrature formulas by the method described in detail in the article [5]

$$ \int\limits_{ - 1}^{1} {\frac{{\left( {1 -\uptau^{2} } \right)^{\upsigma} \psi \left(\uptau \right)}}{{2 \pm\uptau \pm \zeta }}} d\uptau = \sum\limits_{m = 1}^{n} {\uppsi_{m} \frac{{A_{m}^{{\upsigma \upsigma }} \left[ {P_{n}^{{\upsigma \upsigma }} (\uptau_{m} )} \right]^{\prime } + ( \mp 1)^{n + 1} B_{n} \left( {\frac{{1 \pm {\varsigma }}}{2}} \right)}}{{\left( {P_{n}^{{\upsigma \upsigma }} (\uptau_{m} )} \right)^{\prime } (2 \pm\uptau_{m} \pm {\varsigma })}}} , $$
(14)
$$ B_{n} (Y) = \frac{{\Gamma \left( {1 + \sigma + n} \right)}}{{2^{{ - 2\upsigma}} n!}}\left[ {\sum\limits_{j = 0}^{ + \infty } {C_{nj} Y^{{\upsigma + j}} } } \right.\left. { + \sum\limits_{j = 0}^{ + \infty } {B_{nj} Y^{j} } } \right], $$
$$ C_{nj} = \frac{{( - 1)^{j}\Gamma \left( { -\upsigma - n} \right)\Gamma \left( {1 +\upsigma + n + j} \right)}}{{j!\Gamma \left( {1 +\upsigma + n + j} \right)}},B_{nj} = \frac{{( - 1)^{j}\Gamma \left( {\upsigma - j} \right)\Gamma \left( {1 + n + j} \right)}}{{j!\varGamma \left( {1 + 2\upsigma + n - j} \right)}}, $$

where \( A_{m}^{{\upsigma \upsigma }} \) are coefficients of the Gauss – Jacobi quadrature formula [10].

Similar formulas for integrals with a logarithmic singularity are obtained by the same method [5:

$$ \int\limits_{ - 1}^{1} {(1 -\uptau^{2} )^{\upsigma}\uppsi(\uptau)} { \ln }(2 \pm\uptau \pm\upzeta)d\uptau. = \sum\limits_{m = 1}^{n} {A_{m}^{{\upsigma \upsigma }}\uppsi_{m} \sum\limits_{j = 0}^{n - 1} {\frac{{P_{j}^{{\upsigma \upsigma }} (\uptau_{m} )}}{{( \mp 1)^{j}\upsigma_{j}^{2} }}h_{j} \left( {\frac{{1 \pm\upzeta}}{2}} \right).} } $$
(15)

The functions \( h_{j} \left( Y \right) \) are represented by series similar to these in formula (17).

Then in Eq. (11) the quadrature formulas (15), (17) are applied to the singular integrals, and to the regular ones the Gauss - Jacobi quadrature formulas [12] and as collocation points are taken \( \upzeta =\uptau_{k} ,\;_{{}} k = 1,2, \ldots ,n \). The result of these actions is a system of linear algebraic equations for \( \uppsi_{m} ,m = 1,2, \ldots ,n \). To the resulting system it is necessary to add the equation of motion of the plate (6). After solving the system, from formulas (10), (12), (13) we obtain formulas for the approximate calculation of the contact stresses.

$$ s(\upzeta) = \frac{{q(r_{0}\upzeta)}}{{G_{1} }} =\upzeta(1 -\upzeta^{2} )^{{\upsigma - \frac{1}{2}}} \sum\limits_{m = 1}^{n} {\Psi _{m} A_{m}^{{\upsigma \upsigma }} W_{m} (\zeta )} $$
(16)

Here functions \( W_{m} (\upzeta) \) are represented through hypergeometric functions very cumbersomely.

4 Results of Numerical Analysis and Conclusions

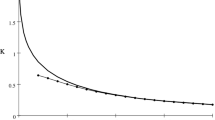
The cylinder of radius \( r_{0} = 0,2\;m \) of aluminum coupled to a cast iron base is considered, as an example. The plate adhered to the upper end of the cylinder is steel and has a thickness of \( d = 0,02\;m \). The plate is loaded by the moment with amplitude of \( M = 1000\;n \cdot m \). The frequency of oscillation changes so that the dimensionless wave number \( \upkappa_{0} =\upkappa_{2} r_{0} = \,\upomega\,r_{0} \sqrt {{{\uprho_{1} } \mathord{\left/ {\vphantom {{\uprho_{1} } {G_{1} }}} \right. \kern-0pt} {G_{1} }}} \) is in the range \( 0 \le\upkappa_{0} \le 10 \) (Fig. 2).

Fig. 2.
figure 2

The contact stresses for other values of frequency and relative height of cylinder

Full size image

The calculations showed that to obtain the values of contact stresses and the angle of rotation with a relative error of less than for the numerical solution of the integral Eq. (11) in the formula (13), it suffices to use 10–15 interpolation points.

Using formula (18), the influence of the frequency and the ratio of the dimensions of the cylinder on the values of contact stresses is studied. The results of these studies are shown in the figures. The graphs in these figures correspond to the following values of the ratio of the height of the cylinder to its radius 1−\( \gamma = 1, \) 2−\( \gamma = 2, \) 3−\( \gamma = 3, \) 4−\( \gamma = 4. \) The following conclusions can be drawn based on the analysis of the results of the calculations. The proposed method for numerically solving a singular integral equation with a fixed singularity with a small volume of calculations allows us to obtain results with high accuracy. This is explained by the fact that the solution takes into account the real asymptotic of unknown functions, and use special quadrature formulas are derived for singular integrals. At torsion of a cylinder which is coupled with an elastic foundation, the highest values of contact stress are observed under static loading \( \kappa_{0} = 0 \). In the same case, with an increase in the relative length of the cylinder, the absolute values of the contact stress increase. Monotonic increase in the absolute values of contact stresses is observed when approaching the boundary of the contact region in the considered frequency range \( 0 \le\upkappa_{0} \le 10 \).