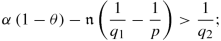Abstract
In this monograph we address some topics related to the well-posedness problem (in the sense of Hadamard) of nonlocal partial differential equations, which, in the context of mathematical physics, are also often referred to as fractional in time parabolic equations. These are known to possess solutions that exhibit anomalous behaviors.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
In this monograph we address some topics related to the well-posedness problem (in the sense of Hadamard) of nonlocal partial differential equations, which, in the context of mathematical physics, are also often referred to as fractional in time parabolic equations. These are known to possess solutions that exhibit anomalous behaviors [27, 28].
The nonlocal in time problem may be formulated roughly as follows. Consider an evolving nonlinear system, either described in terms of a partial or ordinary nonlocal differential equation, containing possibly some fractional kinetics. In brief, fractional kinetic equations occur often in the description of transport dynamics in complex systems which are governed by anomalous diffusion and/or non-exponential relaxation patterns. These equations are generally derived asymptotically from basic random walk models by various approaches in probability theory (see Appendix C). Given a time interval 0 < t ≤ T, and an initial state u 0, the goal is to determine whether the corresponding initial-boundary value problem (or initial-exterior value problem) can be solved globally and uniquely for any time T > 0. More precisely, the problem readsFootnote 1 for 0 < α ≤ 1,
Here \(\mathcal {X}\) stands for an appropriate physical domain and f is a nonlinear, possibly time-dependent source, that is generally of arbitrary growth in the unknown function u. The precise assumptions regarding the operator A and the space \(\mathcal {X}\) shall be stated precisely in Chap. 2. More concrete examples of operators and spaces \( \mathcal {X}\) that enter in our framework will be given in Sect. 2.3. Finally, we shall introduce the classes of admissible nonlinearities f in Sect. 3.1. A preliminary discussion regarding the nonlinearity f will be done in Sect. 1.2.
1.1 Historical Remarks
This is a classical problem in the theory of differential equations for α = 1 and the scientific literature on its global solvability is quite large when α = 1. We refer for instance to the book of Henry [19], Arendt et al. [5], Engel and Nagel [17] and Cholewa and Dlotko [10] for an introduction to this topic. There has been intensive research in this area for the ordinary problem when \(\alpha \in \left ( 0,1\right ) \) and A = 0 in the last two decades (see Agarwal et al. [1], Kilbas et al. [21], Kiryakova [22]). The survey paper [1] collects a sufficiently large number of results established up to 2008, that give sufficient conditions for the (local) solvability of the ordinary problem subject also to local, nonlocal and integral initial conditions. Multivalued versions of these problems, that include fractional-in-time ordinary differential inclusions, are also considered. In the specific context of partial differential equations for (1.0.1), when A is an unbounded operator and \(\alpha \in \left ( 0,1\right ) \), there has been only little success to address the global solvability problem in a satisfactory manner in view of the many applications that this important area holds (see Appendix C).
In this monograph, it is our main goal to focus on this latter, more difficult cases and aim to place this theory on solid footing by devising a unified approach and by giving a complete solution to the above global solvability problem as well as the global regularity problem. However, one still has to recall some pertinent literature and describe any attempts at giving a successful solution to the solvability problem, in various special cases for the nonlocal problem (1.0.1). The nonautonomous problem (\( f=f\left ( t\right ) \)) with a second-order differential (possibly quasilinear) operator A in divergence form and a Riemann-Liouville fractional derivative \(D_{t}^{\alpha }\) has been considered by Bazhlekova [6]. Among the most important results of [6] are maximal regularity results based on two distinct approaches; one that is based on the \(L^{p}\left ( L^{q}\right ) \)-regularity for the corresponding linear problem and, another that exploits the theory of sums of accretive operators in a Hilbert space setting. We should point out that one distinctive disadvantage of considering a parabolic equation with a Riemann-Liouville fractional derivative is that it needs to consider unpleasant initial conditions that are generally nonlocal in nature (see also [7]). The nonautonomous problem (1.0.1) (\(f=f\left ( t\right ) \)) when A is roughly the Laplacian, but with a Caputo-like derivative \(\partial _{t}^{\alpha }\), is also considered by Eidelman and Kochubei [16]. They construct a fundamental solution and then investigate its various asymptotic properties. The latter become important, for instance, to establish the optimal (namely, polynomial) decay properties of solutions to problem (1.0.1), when A = Δ and f = 0 (see Kemppainen et al. [20] and Vergara and Zacher [35]). Mostly for the same operator but with a semilinear \( f=f\left ( u\right ) \), the problem of blow-up in finite time of some solutions and some criteria of stability-instability are developed further in Vergara and Zacher [36], whereas some a priori bounds for some related singular evolutionary partial integro-differential equations are given in Vergara and Zacher [34]. Besides, a more general approach to the nonautonomous problem (\(f=f\left ( t\right ) \)), that is based instead on sesquilinear forms \(a\left ( t,\cdot ,\cdot \right ) ,\) to which a certain diffusion operator A can be associated with, is also used by Zacher [40] to prove existence and uniqueness of weak solutions in an appropriate regularity solution class. In addition, Zacher [41] provides interior H ölder regularity estimates for (1.0.1) in the case when A = Δ and \(f=f\left ( t\right ) \), in the spirit of the classical De Giorgi-Nash regularity theorem.
Some further progress for the abstract problem (1.0.1) has also been made by Clement et al. [11], assuming \(f=f\left ( u\right ) \) and \(\alpha \in \left ( 0,2\right ) ,\) and by analyzing (1.0.1) in continuous spaces \( BUC_{1-\mu }\left ( \left [ 0,T\right ] ;Y\right ) ,\) \(\mu \in \left ( 0,1\right ) \). This approach allows solutions to have a prescribed singularity at the origin in the sense that \(t^{1-\mu }\left \Vert u\left ( t\right ) \right \Vert { }_{Y}\rightarrow 0,\) as t → 0+. The local existence of smooth solutions is established via maximal regularity results for the linear equation associated with (1.0.1), by assuming that α + μ > 1, for \(\mu \in \left ( 0,1\right ) \) and \(\alpha \in \left ( 0,2\right ) \). However, these results rely too heavily on interpolation results and abstract conditions on \(\left ( A,f\right ) \) (see [11, Theorem 13 and (46)-(47)]) that renders their application to specific situations difficult, if not impossible. This is valid especially in those instances when the diffusion operator A turns out to be of “fractional” type. Indeed, due to the well recognized role of fractional operators in the presence of anomalous transport behaviors in some physical phenomena (see Appendix C), it is clearly important to investigate the global solvability and regularity problems for (1.0.1) in those cases. This is for instance, the case of fractional Laplace operators \(\left ( -\Delta \right ) _{\mathcal {X}}^{s},\) \(s\in \left ( 0,1\right ) \) (see Sect. 2.3 ), which as we shall see, turn out to have quite different properties than the classical Laplacian. In particular, such operators are known to generally lack, with the exception of some special cases, an explicit characterization in terms of (Sobolev) function spaces for any fractional powers \(Y_{\theta }:=D(\left ( -A\right ) ^{\theta }),\) \(\theta \in \left ( 0,1\right ) \). For this reason, the application of the results of [11] seems then best suited in those situations when A is a “local” operator, say a second-order quasilinear operator in divergence form (see the example of [11, Section 9]). Unfortunately, this is also the point taken by Andrade, Carvalho et al. [13] and Guswanto and Suzuki [18], who establish a local theory of mild solutions for problem (1.0.1), when \( f=f\left ( u\right ) \) and A is a sectorial (nonpositive) operator, using the concept of the so-called θ-regular maps (see also Neto [14, Chapter 3]). The latter means that the nonlinearity f is locally Lipschitz as a mapping from Y 1+θ to \(Y_{\gamma \left ( \theta \right ) },\) for some \(\gamma \left ( \theta \right ) \in \left ( 0,1\right ) \), a choice which turns out to be useful in the treatment of the problem (1.0.1) with nonlinearities of critical and subcritical polynomial growth. Here criticality is meant in the sense that there exist some critical exponent q, given by some well-known continuous embedding results in Sobolev theory, that controls the polynomial growth of the function \(f\left ( u\right ) \) as \(\left \vert u\right \vert \rightarrow \infty \). However, these techniques also suffer from several drawbacks: first, they are not well suited to deal with nonlinearities that are also x-dependent (\(f=f\left ( x,u\right ) \)), and secondly, such Lipschitz conditions lack any transparency and simplicity since once again they strongly rely on the explicit characterization of Y θ in terms of known Sobolev spaces. Indeed, most of the applications of these techniques seem to be found only in the case of classical operators, such as, when A = Δ (cf. [13, 18] ). Notably, other works by Liu and Liu [25, 26], Ouahab [29], Zhang and Liu [42], Wang and Zhou [37] and Wang et al. [38] (and the references there in), have obtained similar comparable results on the local existence of mild solutions, but with conditions on the nonlinearity which are also too strong; namely, by assuming either that \( f=f\left ( u\right ) \) is a globally Lipschitz function, or locally Lipschitz with a sufficiently small Lipschitz constant and/or a sufficiently small growth as a function of u. In the case when A is related to a fractional operator, in particular, \(A=\left ( -\Delta \right ) _{\mathcal {X}}^{s},\) \( s\in \left ( 0,1\right ) \), for a compact Riemannian manifold \(\mathcal {X}\) (without boundary), some local existence results for (1.0.1) with \( f=f\left ( u\right ) \) assuming some polynomial growth, are also contained in the lecture notes by Taylor [33]. Hölder continuity for the problem (1.0.1) assuming \(f=f\left ( t\right ) \) and an operator A that is related to the fractional Laplacian, has been established by Allen, Caffarelli et al. [3], when \(\partial _{t}^{\alpha }\) is meant as a (one-sided) nonlocal derivative in the sense of Marchaud.Footnote 2 Some related nonlocal ordinary differential equations associated with a Marchaud type of fractional derivative are also investigated in [8] and [24] , with the latter also providing an extensive comparison between the Marchaud, Riemann-Liouville and Caputo fractional derivatives, respectively. Further applications of the framework from [24] to nonlinear time fractional PDEs are also given in [23]. Most recently, the case 1 < α < 2 is further investigated in [4], where the existence of weak and strong (energy-like) solutions in various settings are among the central results. The work in [4] offers a new and fresh alternative from the contribution in [11] in the sense that the assumptions imposed on the operator A, as well as the nonlinearity f, are once again more natural and transparent than the conditions imposed by [11]. It is worth emphasizing that fractional kinetic equations typically exhibit a variety of behaviors which are completely different from the classical case, while in fact solutions of fractional equations can sometimes be “arbitrarily” complicated, as shown in [9, 15].
1.2 On Overview of Main Results and Applications
But none of these theories address the global regularity problem for the full semilinear problem (1.0.1) in a meaningful way for practical applications. Furthermore, these theories are far from being applicable to reaction–diffusion systems with vectorial quantities \(u\in \mathbb {R}^{m}\), m > 1, which contain some fractional kinetics, but which draw their breath from important applications in biology, chemistry and finance. This is particularly relevant in the context of biological systems where the mechanism is necessarily more involved and complex due to a richer structure associated to the corresponding couplings under consideration (especially when different nonlocal derivatives \(\partial _{t}^{\alpha _{i}},\) with α i ∈ (0, 1], \(i\in \left \{ 1,\ldots ,m\right \} \) are involved). As a matter of fact, understanding the connections between the right fractional parameter in concrete biological settings, also in relation to the environment, seem to be an important topic in optimization, see e.g. [32]. Interesting applications also arise in neuroscience and in neural networks, see e.g. [31]. As one knows, there is an extensive literature on the topic of reaction–diffusion systems when \(\partial _{t}^{\alpha _{i}}\equiv \partial _{t},\) for all \(i\in \left \{ 1,\ldots ,m\right \} \) (see, for instance, Yagi [39]). Although, the techniques and methodologies developed in this monograph for the scalar equation (1.0.1) shall prove quite useful, the problem of global solvability and regularity for m-systems needs to be addressed directly and independently. The main tools are borrowed essentially from the methodology that deals with the scalar equation. But let us first mention our unified approach and the type of results one can obtain for the scalar equation (1.0.1), in a successful manner that also covers the existing theory for (1.0.1) when α = 1 and/or A is a uniformly elliptic (second-order) operator. Although we cannot give a complete review of the literature for the problem (1.0.1) when α = 1 and A = Δ, the lecture notes of Rothe [30] give a good account of the main developments concerning the global existence of solutions for semilinear parabolic equations in that case.
The present work is concerned with some fundamental questions for the initial-boundary (or initial-exterior) value problem (1.0.1), namely,
-
the global existence of non-regular (mild) solutions;
-
the existence of sufficiently smooth (strong) solutions, for which the nonlocal equation is satisfied pointwise in time;
-
the global regularity problem, to establish sufficient conditions and uniform a priori bounds in such a way that each non-regular solution becomes a global smooth solution on \(\left ( 0,\infty \right ) \), and
-
what happens to any global solution of (1.0.1) as α → 1?
These aspects are studied in a unified framework for the scalar equation (1.0.1) in a first part, and then for general nonlocal reaction–diffusion m-systems, and some of their applications, in the second part. Of course, in this part only some non-trivial examples, which are motivated by applications in mathematical biology and chemistry, will be investigated thoroughly. But the general setting developed here allows to derive similar results for other important nonlocal reaction–diffusion m-systems which can be handled by the same techniques.
In our unified framework, the essential assumption about the semigroup \( S\left ( t\right ) \), associated with the diffusion operator A, is an ultracontractivity estimate of the form
for 1 ≤ p ≤ q ≤∞, and some positive constant \(C=C\left ( p,q, \mathcal {X}\right ) >0\). The constant β A > 0 is assumed independent of p, q; it plays the role of capturing the degree of “smoothness” of the fundamental solution associated with the diffusion operator A. For symmetric semigroups, it is well-known that (1.2.1) is also connected to optimal Sobolev inequalities (see, for instance, Davies [12]). For instance, when A = Δ is subject to classical boundary conditions and \( \mathcal {X}\subset \mathbb {R}^{N}\) is a smooth bounded domain, it holds β A = N∕2, while for \(A=\left ( -\Delta \right ) _{\mathcal {X}}^{s},\) \( s\in \left ( 0,1\right ) \), we have β A = N∕2s. Condition (1.2.1) constitutes the main assumption upon which our general theory is built on. Indeed, it allows to consider a general family of diffusion operators, including the classical ones as well as ones of “fractional” type, in addition to other non-standard examples of diffusion. We refer the reader to Sect. 2.3 for many examples of operators that are covered by our framework. Next, our main assumption on the nonlinearity \(f=f\left ( x,t,u\right ) \) is quite transparent and easy to verify in applications; in addition to other basic conditions (which imply that f is locally Lipschitz as a function of u, with the same c, Q; see (F4)), it is simply measurable and satisfies (as \(\left \vert u\right \vert \rightarrow \infty \)) a growth condition of the form
for some (nonnegative) integrable functionFootnote 3 \( c\in L_{q_{1},q_{2}}\), 1 ≤ q 1, q 2 ≤∞. Of course, the real-valued (positive) function Q generally captures the growth of the nonlinearity as \(\left \vert u\right \vert \rightarrow \infty \). In some cases, we will allow it to behave polynomially in the sense that
In this monograph, we look for complete results regarding the solvability of problem (1.0.1) in such a way that also the case α = 1 is automatically included. To this end, let us define a number \(W=W\left ( \alpha ,f,p_{0},q_{1},q_{2},Q\right ) \in \mathbb {R}\), by

as the essential range for problem (1.0.1) for which (at least local) well-posedness can be established. Theorem 3.1.4 establishes the existence of (locally-defined) mild solutions for (1.0.1) for non-regular initial data \(u_{0}\in L^{p_{0}}\left ( \mathcal {X}\right ) ,\) 1 ≤ p 0 ≤∞, in the following cases:
-
(i)
W ≤ α, under the assumptions (1.2.2)–(1.2.3) for some γ ∈ [1, ∞) and p 0 ∈ [1, ∞).
-
(ii)
When
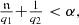 p
0 = ∞ and Q is an arbitrary positive function.
p
0 = ∞ and Q is an arbitrary positive function.
The critical case, defined by the equality W = α in case (i), is included; this range turns out to be also optimal in the sense that for some \(p_{0}\in \left [ 1,\infty \right ] \) and γ ≥ 1 that satisfy W > α, there are no locally-defined mild solutions for certain initial data \(u_{0}\in L^{p_{0}}\left ( \mathcal {X} \right ) \) (see Chap. 5, Remark 5.0.2). In the above cases (i)–(ii), Theorem 3.1.10 proves the existence of mild solutions on a maximal interval of existence \(\left ( 0,T_{\max }\right ) \), such that (non-regular) mild solutions are always locally bounded, namely, \(u\in L^{\infty }\left ( (0,T_{\max });L^{\infty }\left ( \mathcal {X}\right ) \right ) \). As usual the time \(T_{\max }>0\) is such that, either \(T_{\max }=\infty \) or \(T_{\max }<\infty \) with \(\left \Vert u\left ( t\right ) \right \Vert { }_{L^{\infty }\left ( \mathcal {X}\right ) }\rightarrow \infty \) as \( t\rightarrow T_{\max }^{-}\). In other words, knowledge of the a priori bound \(u\in L^{\infty }\left ( (0,T);L^{\infty }\left ( \mathcal {X}\right ) \right ) \) , for any (fixed) time T > 0, is essential for both the global solvability problem and the global regularity problem, as we shall see in what follows. It is worth stressing out that we recover the essential range for local solvability in the case when β A = N∕2 and α = 1 (see Rothe [30]).
A major development in the monograph is a unified theory of strong solutions that contains the case α = 1 as a particular case. Denote by A p the generator of the semigroup \(S\left ( t\right ) \) on \(L^{p}(\mathcal {X})\) so that A 2 ≡ A. Our next goal is to show that any maximally-defined mild solution can become, under natural conditions, a strong bounded solution on \(\left ( 0,T_{\max }\right ) \); the latter is by definition a sufficiently smooth solution of the abstract equation (1.0.1 ) in some Banach space. In particular, Theorem 3.2.2 proves the aforementioned statement in the space \(L^{p}(\mathcal {X}),\) 1 ≤ p ≤∞, for an initial datum \(u_{0}\in D\left ( A_{p}\right ) ,\) \(p\in \left ( \beta _{A},\infty \right ) \cap \left ( 1,\infty \right ) \), under either one of the following two alternatives:
-
(a)
if p ≥ q 1, assume f satisfies (1.2.2) and a locally Lipschitz-Hölder condition (see (F4)–(F5)) with q 2 ∈ (1∕α, ∞] and \(\theta \in \left ( \beta _{A}/p,1\right ) \) satisfying
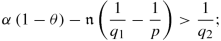
-
(b)
if p ≤ q 1, assume f satisfies (1.2.2) and a locally Lipschitz-Hölder condition (see (F4)–(F5)) with q 2 ∈ (1∕α, ∞] and \(\theta \in \left ( \beta _{A}/p,1\right ) \) satisfying
$$\displaystyle \begin{aligned} \alpha \left( 1-\theta \right) >\frac{1}{q_{2}}. \end{aligned}$$
The conditions (F4)–(F5) are generally satisfied in practical applications, as it can be observed in the context of specific examples, and there are situations when (F5) can be even entirely dropped, especially when \(f=f\left ( x,u\right ) \). Besides, we show in Theorem 3.2.6 that every bounded (maximally-defined) mild solution constructed in case (ii), becomes indeed a strong solution on \( \left ( 0,T_{\max }\right ) \). The techniques exploited in Sect. 3.2 provide several important developments among which we can mention the fact that the same a priori bound \(u\in L^{\infty }\left ( (0,T);L^{\infty }\left ( \mathcal {X}\right ) \right ) \), for the maximal strong solution, suffices for its global regularity. We refer the reader to Sect. 3.2 for further details and more precise statements of the above regularity results. Finally, in Sect. 3.3 we obtain some results on the differentiability properties of strong solutions in the case \( \alpha \in \left ( 0,1\right ) \) (the case α = 1 is well known, see e.g., [17, 19]). Such results are necessary in order to estimate the error in numerical approximations of the solution of (1.0.1 ). They turn out to be also important in existence proofs of certain energy inequalities that are used to derive the long term behavior for such solutions as time goes to infinity (see, for instance, the discussion in Sect. 3.4).
Perhaps then the next important point is the construction of uniform a priori bounds that imply the aforementioned bound in \(u\in L^{\infty }\left ( (0,T);L^{\infty }\left ( \mathcal {X}\right ) \right ) \), which is necessary to completely solve the global regularity problem. This problem may be formulated roughly as follows. Restricting to a smooth initial datum \( u_{0}\in D\left ( A_{p}\right ) ,\) consider the corresponding (unique) strong solution of (1.0.1) whose existence is assured by one of the previous statements. The main idea is to take a weak bound of the form \(u\in L^{r_{1}}\left ( (0,T);L^{r_{2}}\left ( \mathcal {X}\right ) \right ) \), that is known to be satisfied a priori for some 1 ≤ r 1, r 2 ≤∞, and to convert this information into an explicit bound for the strong solution in \(L^{\infty }\left ( (0,T);L^{\infty }\left ( \mathcal {X}\right ) \right ) \), for any T > 0. This goal will be achieved by two essentially different methods. On one hand, we shall employ and extend a “feedback” argument used by Rothe [30] in the case β A = N∕2 and α = 1, to provide such a statement in Theorem 3.4.1. This method has the advantage that it employs only elementary inequalities and bootstrapping arguments involving only space and time integrals. The second method we use to derive such a priori estimates is based on an iterative Moser procedure that was exploited by Alikakos [2] once again in the case β A = N∕2 and α = 1. We extend this procedure in our general setting when α ∈ (0, 1] and A is a “properly-behaved” diffusion operator that covers many of the examples we have in mind (see Sect. 2.3); one advantage of this scheme is that the estimates remain uniform as the order α of the fractional in time derivative \(\partial _{t}^{\alpha }\) approaches 1. Although, the precise statements of these global estimates are somewhat more complicated to state here, we refer the reader to Sect. 3.4 for the corresponding results. Furthermore, taking into account the above developments, we do mention that we can finally address the important issue of convergence as α → 1 for problem (1.0.1) under quite natural conditions on \(\left ( A,f\right ) \). The statement of Theorem 3.5.1 (in Sect. 3.5) shows in particular that for nonlinearities that satisfy \(f\left ( x,t,u\right ) u\leq c_{0}\left ( x,t\right ) \left ( 1+u^{2}\right ) \), for some c 0 ∈ L ∞,∞, any globally bounded mild solution u = u α of the abstract problem (1.0.1) converges in the sense that
to a bounded mild solution u 1 of problem (1.0.1) in the case when α = 1. Finally, one further important application of these results is that they guarantee the global solvability and regularity of solutions to a fractional in time Fischer-KPP like equation (see Sect. 3.7), for a large class of interesting diffusion operators A, as well as the aforementioned convergence result (1.2.4) holds.
1.3 Results on Nonlocal Reaction–Diffusion Systems
The setting in the first part of the monograph, which deals solely with the scalar equation (1.0.1), can be extended and applied to reaction–diffusion systems for an unknown vectorial quantity \(u=\left ( u_{1},\ldots ,u_{m}\right ) \in \mathbb {R}^{m}\), \(m\in \mathbb {N}\). Let d i = 0 for i = 1, …, r and d i > 0 for i = r + 1, …, m. We also allow the case r = 0 to occur so that all d i > 0 for i = 1, …, m. Next, let \(D=diag\left ( d_{1},\ldots ,d_{m}\right ) \) be the diagonal matrix of diffusion coefficients and assume that \(u_{0}=\left ( u_{01},\ldots ,u_{0m}\right ) \left ( x\right ) \in \mathbb {R}^{m},\) for \(x\in \mathcal {X},\) models the initial data. Let \(f=\left ( f_{1},\ldots ,f_{m}\right ) \left ( x,t,u_{1},\ldots ,u_{m}\right ) \) be a nonlinear function that models possible interactions between the various quantities u i (i = 1, …, m). After that we can set the diagonal (matrix) operator \(A=diag\left ( A_{1},\ldots ,A_{m}\right ) ,\) where each A i is a proper diffusion operator, and then introduce the following notation \( \partial _{t}^{\alpha }u=\left ( \partial _{t}^{\alpha _{1}}u_{1},\ldots ,\partial _{t}^{\alpha _{m}}u_{m}\right ) \in \mathbb {R}^{m}\), where each nonlocal derivative \(\partial _{t}^{\alpha _{i}}u_{i}\in \mathbb {R }\) is understood in the generalized sense of Caputo (see Sect. 2.1) for \(\alpha _{i}\in \left ( 0,1\right ) ,\) whereas for α i = 1, \( \partial _{t}^{1}=\partial _{t}=d/dt.\)
Consider then the following nonlocal reaction–diffusion system
Of course, the above framework allows a general study of (1.3.1) when diffusion can be also completely ignored in some of the components of u. In this case, we are looking for sufficiently general conditions on \(\left ( A,f\right ) \) such that it possesses maximally-defined bounded (mild) solutions as well as strong solutions. For \(u_{0}\in L^{\infty }\left ( \mathcal {X},\mathbb {R}^{m}\right ) \), Theorem 4.1.2 proves the existence of (maximal) bounded mild solutions under natural assumptions on f and analogous conditions on the operators A i, as in the scalar case (1.0.1). The conditions on the nonlinearity roughly imply that f is locally Lipschitz-Hölder in bounded subsets B of \(\mathcal {X}\times \lbrack 0,\infty )\times \mathbb {R}^{m}\) (see (SF1)–(SF2)). For more regular initial data u 0, Theorem 4.1.3 even shows the existence of (maximal) unique strong solutions; these are sufficiently smooth solutions satisfying (1.3.1) pointwise in time on the maximal interval of existence. In Chap. 4, we shall introduce the classes of diagonal matrix operators A and matrix diffusion coefficients D, and give the class of admissible nonlinearities that enter in the framework of the system (1.3.1).
As it was pointed out at the beginning of the introduction, the issues of global solvability and regularity for (1.3.1) must be instead addressed independently for problems that are suggested by a practical application. To this end, our main focus now turns onto some nonlocal systems that arise in population dynamics (see Sect. 4.2) and nuclear dynamics (see Sect. 4.3). The first one is a nonlocal model of Volterra–Lotka type and consists of a coupled system for two nonlocal partial differential equations, with the “nonlocality” being expressed in both space and time, in one of the equations. The second systems consists of a coupled system similar to the first one, but one of the components satisfies instead a nonlocal ordinary differential equation (namely, diffusion is totally ignored for that component). The results developed for the scalar equation (1.0.1) in the first part of the monograph, are crucial to the investigation of global solvability and global regularity for these specialized systems. They allow to prove sharper results by applying the corresponding theorems in the first part, to the diffusion equations for each individual component u i of u, and by treating the other remaining components u j, j ≠ i, in the nonlinearity f i, as part of a special “weight” function \(c\left ( x,t\right ) \). The advantage of this approach is that only very little information, such as some a priori \(L_{q_{1},q_{2}}\)-bound is required for \( c\left ( x,t\right ) \), to deduce global information on that component u i . Then these arguments can be repeated for each component of u, one by one, until the entire range of \(i\in \left \{ 1,\ldots ,m\right \} \) is exhausted. We refer the reader to Chap. 4 for the precise statements of these results and further details.
Finally, as we said above, the coverage of particular cases of nonlocal reaction–diffusion systems in this monograph is necessarily limited. But their successful treatment proves to be considerable progress in this area especially when such feats do not seem to have been attempted before. Nevertheless, we emphasize that other (more complicated) nonlocal systems can be included and treated within the above framework; we hope that their investigation might be of interest for other researchers in this area.
The content of this monograph is as follows. In Chap. 2 we make a complete study in the context of linear nonhomogeneous equations. Chapters 3 and 4 are devoted to the main results related to the global solvability and global regularity problems for the scalar equation (1.0.1) and reaction–diffusion system (1.3.1), respectively. Chapter 5 is devoted to some open problems and future directions of research. Three different appendices are included. Appendix A includes a number of supportive technical tools. Appendix B contains a complete discussion of the properties of the regional fractional Laplace operator in a bounded domain. Appendix C gives a full account of the physical literature on fractional kinetic equations and several applications involving evolution equations of single and distributed fractional order in time and/or in space.
References
R.P. Agarwal, M. Benchohra, S. Hamani, A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Appl. Math. 109(3), 973–1033 (2010)
N.D. Alikakos, L p bounds of solutions of reaction-diffusion equations. Commun. Partial Differ. Equ. 4(8), 827–868 (1979)
M. Allen, L. Caffarelli, A. Vasseur, A parabolic problem with a fractional time derivative. Arch. Ration. Mech. Anal. 221(2), 603–630 (2016)
E. Alvarez, C.G. Gal, V. Keyantuo, M. Warma, Well-posedness results for a class of semi-linear super-diffusive equations. Nonlinear Anal. 181, 24–61 (2019)
W. Arendt, C.J.K. Batty, M. Hieber, F. Neubrander, Vector-Valued Laplace Transforms and Cauchy Problems. Monographs in Mathematics, vol. 96, 2nd edn. (Birkhäuser/Springer Basel AG, Basel, 2011)
E.G. Bajlekova, Fractional Evolution Equations in Banach Spaces. Technische Universiteit Eindhoven Eindhoven, The Netherlands, 2001
E. Bazhlekova, Strict L p solutions for nonautonomous fractional evolution equations. Math. Balkanica (N.S.) 26(1–2), 25–34 (2012)
A. Bernardis, F.J. Martin-Reyes, P.R. Stinga, J.L. Torrea, Maximum principles, extension problem and inversion for nonlocal one-sided equations. J. Differ. Equ. 260, 6333–6362 (2016)
C. Bucur, Local density of Caputo-stationary functions in the space of smooth functions. ESAIM Control Optim. Calc. Var. 23(4), 1361–1380 (2017)
J.W. Cholewa, T. Dlotko, Global Attractors in Abstract Parabolic Problems. London Mathematical Society Lecture Note Series, vol. 278 (Cambridge University Press, Cambridge, 2000)
Ph. Clément, S-O. Londen, G. Simonett, Quasilinear evolutionary equations and continuous interpolation spaces. J. Differ. Equ. 196(2), 418–447 (2004)
E.B. Davies, Heat Kernels and Spectral Theory. Cambridge Tracts in Mathematics, vol. 92 (Cambridge University Press, Cambridge, 1990)
B. de Andrade, A.N. Carvalho, P.M. Carvalho-Neto, P. Marí n Rubio, Semilinear fractional differential equations: global solutions, critical nonlinearities and comparison results. Topol. Methods Nonlinear Anal. 45(2), 439–467 (2015)
P.M. de Carvalho Neto, Fractional Differential Equations: A Novel Study of Local and Global Solutions in Banach Spaces. PhD thesis, Universidade de São Paulo, 2013
S. Dipierro, O. Savin, E. Valdinoci, All functions are locally s-harmonic up to a small error. J. Eur. Math. Soc. 19(4), 957–966 (2017)
S.D. Eidelman, A.N. Kochubei, Cauchy problem for fractional diffusion equations. J. Differ. Equ. 199(2), 211–255 (2004)
K.-J. Engel, R. Nagel, One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194 (Springer, New York, 2000). With contributions by S. Brendle, M. Campiti, T. Hahn, G. Metafune, G. Nickel, D. Pallara, C. Perazzoli, A. Rhandi, S. Romanelli and R. Schnaubelt
B.H. Guswanto, T. Suzuki, Existence and uniqueness of mild solutions for fractional semilinear differential equations. Electron. J. Differ. Equ. 168, 16 (2015)
D. Henry, Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics, vol. 840 (Springer, Berlin/New York, 1981)
J. Kemppainen, J. Siljander, V. Vergara, R. Zacher, Decay estimates for time-fractional and other non-local in time subdiffusion equations in ℝd. Math. Ann. 366(3–4), 941–979 (2016)
A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204 (Elsevier Science B.V., Amsterdam, 2006)
V. Kiryakova, Generalized Fractional Calculus and Applications. Pitman Research Notes in Mathematics Series, vol. 301 (Longman Scientific & Technical, Harlow); copublished in the United States with John Wiley & Sons, Inc., New York, 1994
J.-G. Li, L. Liu, Some compactness criteria for weak solutions of time fractional PDEs. SIAM J. Math. Anal. 50, 3693–3995 (2018)
J.-G. Li, L. Liu, A generalized definition of caputo derivatives and its application to fractional ODEs. SIAM J. Math. Anal. 50, 2867–2900 (2018)
X. Liu, Z. Liu, Existence results for fractional semilinear differential inclusions in Banach spaces. J. Appl. Math. Comput. 42(1–2), 171–182 (2013)
X. Liu, Z. Liu, On the ‘bang-bang’ principle for a class of fractional semilinear evolution inclusions. Proc. R. Soc. Edinb. Sect. A 144(2), 333–349 (2014)
F. Mainardi, Fractional calculus: some basic problems in continuum and statistical mechanics, in Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996). CISM Courses and Lectures, vol. 378 (Springer, Vienna, 1997), pp. 291–348
B.B. Mandelbrot, J.W. Van Ness, Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437 (1968)
A. Ouahab, Fractional semilinear differential inclusions. Comput. Math. Appl. 64(10), 3235–3252 (2012)
F. Rothe, Global Solutions of Reaction-Diffusion Systems. Lecture Notes in Mathematics, vol. 1072 (Springer, Berlin, 1984)
F. Santamaria, S. Wils, E. De Schutter, G.J. Augustine, Anomalous diffusion in purkinje cell dendrites caused by spines. Neuron 52(4), 635–648 (2006)
J. Sprekels, E. Valdinoci, A new type of identification problems: optimizing the fractional order in a nonlocal evolution equation. SIAM J. Control Optim. 55(1), 70–93 (2017)
M. Taylor, Remarks on fractional diffusion equations. Preprint. http://mtaylor.web.unc.edu/files/2018/04/fdif.pdf
V. Vergara, R. Zacher, A priori bounds for degenerate and singular evolutionary partial integro-differential equations. Nonlinear Anal. 73(11), 3572–3585 (2010)
V. Vergara, R. Zacher, Optimal decay estimates for time-fractional and other nonlocal subdiffusion equations via energy methods. SIAM J. Math. Anal. 47(1), 210–239 (2015)
V. Vergara, R. Zacher, Stability, instability, and blowup for time fractional and other nonlocal in time semilinear subdiffusion equations. J. Evol. Equ. 17(1), 599–626 (2017)
J.R. Wang, Y. Zhou, Existence and controllability results for fractional semilinear differential inclusions. Nonlinear Anal. Real World Appl. 12(6), 3642–3653 (2011)
R.-N. Wang, D.-H. Chen, T.-J. Xiao, Abstract fractional Cauchy problems with almost sectorial operators. J. Differ. Equ. 252(1), 202–235 (2012)
A. Yagi, Abstract Parabolic Evolution Equations and Their Applications. Springer Monographs in Mathematics (Springer, Berlin, 2010)
R. Zacher, Weak solutions of abstract evolutionary integro-differential equations in Hilbert spaces. Funkcial. Ekvac. 52(1), 1–18 (2009)
R. Zacher, A De Giorgi–Nash type theorem for time fractional diffusion equations. Math. Ann. 356(1), 99–146 (2013)
Z. Zhang, B. Liu, Existence results of nondensely defined fractional evolution differential inclusions. J. Appl. Math. 2012, 19 (2012). Art. ID 316850
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
G. Gal, C., Warma, M. (2020). Introduction. In: Fractional-in-Time Semilinear Parabolic Equations and Applications. Mathématiques et Applications, vol 84. Springer, Cham. https://doi.org/10.1007/978-3-030-45043-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-45043-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45042-7
Online ISBN: 978-3-030-45043-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





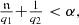 p
0 = ∞ and Q is an arbitrary positive function.
p
0 = ∞ and Q is an arbitrary positive function.