Abstract
We formally introduce a novel, yet ubiquitous, category of norms: norms of instrumentality. Norms of this category describe which actions are obligatory, or prohibited, as instruments for certain purposes. We propose the Logic of Agency and Norms (\(\mathsf {LAN}\)) that enables reasoning about actions, instrumentality, and normative principles in a multi-agent setting. Leveraging \(\mathsf {LAN}\), we formalize norms of instrumentality and compare them to two prevalent norm categories: norms to be and norms to do. Last, we pose principles relating the three categories and evaluate their validity vis-à-vis notions of deliberative acting. On a technical note, the logic will be shown decidable via the finite model property.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Agency logic
- Action constants
- Action logic
- Andersonian reduction
- Decidability
- Deontic logic
- Norms of instrumentality
1 Introduction
The formal analysis of normative reasoning, roughly starting with the introduction of deontic logic in the 1950s [21], has been guided by the conviction that action and agency are pivotal components of normative reasoning [8, 22]. In relation to this, an important development took place in the 1970s: the introduction of Propositional Dynamic Logic (\(\mathsf {PDL}\)) [10]. Modal logics of \(\mathsf {PDL}\) focus on the analysis of complex actions (or programs) and their relation to results. The framework was soon adapted to deontic reasoning [17] and it continues to receive attention to the present day [20]. The emphasis on action and agency in normative reasoning led to the distinction between two categories of norms: norms to be and norms to do [1, 8]. Norms of the former category address states of affairs, without making reference to how such states of affairs are obtained by the agent. The latter category normatively prescribes actions to agents, yet, without specifying the possible outcomes that might be produced by the action.
However, there is a third category of norms merging both approaches, which, to the best of our knowledge, has not been formally investigated. These norms prescribe a specific normative relation between an action and a goal, with the action serving as an instrument to achieve the goal. We will refer to such norms as norms of instrumentality. Consider the following example:
Although it is neither prohibited to use nonpublic information, nor is it prohibited to acquire financial profit on the stock market, it is in fact prohibited to use such information as an instrument to attain the latter.
The above principle is known as the law on ‘insider trading’ and belongs to this third category. Prohibitions of the form expressed above articulate which actions cannot be employed as instruments for achieving particular goals. Despite the ubiquity of normative constraints on instrumentality in legal, social, and ethical systems (e.g. protocols, rules of games, fairness constraints, etc.), an investigation of their philosophical ramifications in formal logic is absent. This work aims to provide the formal foundations for the analysis of norms of instrumentality.
In [1], a formal investigation of the first two norm categories is provided. The formalism employed there brings together Anderson’s reduction of norms of the first class [2] and Meyer’s reduction of norms of the second class [17] in a single system of modal logic called \(\mathsf {PDeL}\) (i.e. deontic \(\mathsf {PDL}\)). The first is a reduction of deontic operators to alethic formulae containing violation constants (e.g. a result A is obligatory when \(\lnot A\) strictly implies a violation). The second reduces deontic operators to formulae using action modalities and violation constants (e.g. an action \(\varDelta \) is obligatory when not performing \(\varDelta \) strictly implies a violation).
In [4], a third reduction is discussed, where action modalities of \(\mathsf {PDL}\) are reduced to alethic formulae containing action constants. The resulting logic facilitates reasoning about agent-dependent actions within the object language and formally captures different notions of instrumentality (in a non-normative setting). Decidability of this logic was left as an open problem.
The current work brings together the three reductions found in [1] and [4], and introduces a Logic of Agency and Norms called \(\mathsf {LAN}\) (Sect. 3). The resulting logic extends previous approaches by permitting us to reason with agent-dependent actions, as well as agent-dependent obligations and prohibitions, in multi-agent settings. The language of \(\mathsf {LAN}\) will enable us to formally investigate the three norm categories; we will pose principles describing relations between the three categories and evaluate their validity vis-à-vis different notions of deliberative acting (Sect. 4). Last, we prove the decidability of \(\mathsf {LAN}\) in Appendix A of the paper.
2 A Benchmark Example
In order to understand the distinct nature of the three kinds of norms, we provide an example protocol serving as a benchmark in developing our formal framework. In Sect. 5, we formalize and analyze the protocol using our developed logic.
A Hospital Health and Safety Protocol. The Health and Safety Committee of a public hospital in Vienna recently established a new set of guidelines to govern and redirect the behaviour of surgeons and nurses in the assistance and treatment of its patients. In particular, motivated by the increased awareness of the dangers of accidental self-inflicted wounds, caused by using sharp tools during surgery, the committee has proposed a new policy: that is, limiting the use of scalpels in surgery to surgeons and prohibiting assisting nurses the use of such instruments in the operation room. The protocol is summed up accordingly:
-
P1
A surgeon is obliged to use the prescribed scalpel to bring about a necessary incision during surgery.
-
P2
Assisting nurses are not allowed to use scalpels during surgery when the situation is not dire.Footnote 1
-
P3
Nurses and surgeons alike have the obligations to (i) promote the health of their patients and (ii) preserve hygiene safety in the operation room.
First, we observe that the norm expressed by P1 is a norm belonging to the third, novel, category of norms of instrumentality; that is, it describes a norm that specifically relates an action as an instrument to a particular outcome. P2 is a prohibition subsumed under norms to do, and holds independent of the instrument’s intended purpose. P3 is an obligation pertaining to norms to be, and holds independent of the instruments used to obtain (i) and (ii).
To stress the irreducibility of norms of instrumentality to norms to be and norms to do, consider the following: although a surgeon might be obliged to use a scalpel to ensure a required incision, it does not follow that she has the obligation to use scalpels independent of their intended purpose (some outcomes obtained by using scalpels could be prohibited), nor does it mean that she has the obligation to bring about the incision by any means necessary (some means could be prohibited). In fact, in case of P1, the surgeon has only the obligation to ensure the required incision by means of using the scalpel.Footnote 2
To continue, the committee makes two assumptions in drafting the protocol:
-
T1
The protocol resolves all normative issues in surgical situations by offering rules of conduct that ultimately provide ways out of any possible conflict.
-
T2
The protocol assumes that the choices described, and suggested, to the agents can be consistently performed together.
The committee is aware that sub-ideal situations can occur (e.g. whenever an employee (in)voluntarily violates an initial rule). Given T1, the committee provides the following principle which activates whenever P3 cannot be satisfied:
-
E1
In case of failing to preserve hygiene standards during surgery (e.g., in the case of self-inflicted wounds) the employee in question is obliged to immediately leave the operation room and call the safety-emergency number.
The purpose of the above rule is to ensure that damage in sub-ideal scenarios is controlled. Principle E1 prescribes measures to be taken in case of failure to comply with other prescriptions. As can be seen, there is a close connection between principle E1 and what is called contrary-to-duty reasoning; that is, reasoning about secondary norms that arise from violating primary norms. We come back to this point during the formalization of the example in Sect. 5.
Last, the committee desires that the above protocol is captured in a logical system, enabling them (i) to analyse the consistency of the protocol and (ii) to reason with the protocol whenever critical circumstances occur. As can be observed, the logical language must contain agents, actions, results and violations, in order to facilitate the formal distinction between the three norm categories.
3 Deontic Logic of Actions, Agency and Norms
In what follows, we introduce the language, semantics and axiomatization of our Logic of Agency and Norms, henceforth, \(\mathsf {LAN}\) (the logic will be a deontic extension of the machinery provided in [4]). As motivated in the introduction, we will employ a reductionist approach to norms via violation constants (following [17]) and to actions via action constants (following [4]). In order to reason with actions in a normative setting, we use a Boolean algebra of actions. The language of \(\mathsf {LAN}\) will depend on this algebra of actions, which will enable us to talk about complex, compound actions as formulae in the object language.
Definition 1
(Algebra of Actions \(Act_{\mathsf {LAN}}\)). Let \(Act=\{\delta _1,..., \delta _n\}\) be a set of atomic action-types and let \(\delta _{i} \in Act\). The language \(Act_{\mathsf {LAN}}\) of complex action-types \(\varDelta \) is given via the following BNF grammar:
The operations \(\cup \) and — represent disjunction and complement (resp.), allowing us to generate complex expressions such as ‘closing-the-door or opening-the-window’ and ‘not closing-the-window’. The conjunction operator & over actions is defined as \( \varDelta _1 \& \varDelta _2 := \overline{\overline{\varDelta _1}\cup \overline{\varDelta _2}}\). Let \(Agt= \{\alpha _1, \ldots ,\alpha _n\}\) be a set of agent labels; we say \(\varDelta ^{\alpha _i}\) is an agent-dependent action-type iff \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\).
We let \(Var=\{p_1,p_2, \dots \}\) be a countable set of propositional variables, and for any \(\alpha _i\in Agt\), we let \(Wit^{\alpha _i}=\{\mathfrak {d}^{\alpha _i}_1,...,\mathfrak {d}^{\alpha _i}_n\}\) be the set of propositional constants that witness the performance of atomic action-types \(\delta _1\), ..., \(\delta _n\) by \(\alpha _i\) (this is made formally precise in Definition 3). Let Wit be the union \(\bigcup _{\alpha _i\in Agt}Wit^{\alpha _i}\) and note that \(|Wit^{\alpha _i}|=|Act|=n\), for some \(n \in \mathbb {N}\). Also, we take \(\mathfrak {v}^{\alpha _i}\) to be a propositional constant witnessing a norm violation for agent \(\alpha _i\) and let \(Vio = \{\mathfrak {v}^{\alpha _i}\ | \ \alpha _i\in Agt\ \}\) be the set of all agential violation constants. Last, we let \(Atoms = Var \ {\cup } \ Wit \ {\cup } \ Vio\).Footnote 3
Definition 2
(The Language \(\mathcal {L}_{\mathsf {LAN}}\)). \(\mathcal {L}_{\mathsf {LAN}}\) is given by the following BNF:
where \(p_i\in Var\), \(\alpha _j\in Agt\), \(\mathfrak {v}^{\alpha _j}\in Vio\) and \(\mathfrak {d}^{\alpha _j}_i\in Wit\).
In short, the operators \(\wedge \), \(\vee \) and \(\equiv \) are defined in the usual way. Formulae of the form \(\Box \phi \) and \([\mathsf {N}]\phi \) express, respectively, ‘in all possible successor (future) states \(\phi \) holds’ and ‘in the actual successor (future) state \(\phi \) holds’. We take  and \(\langle \mathsf {N}\rangle \) as the duals of \(\Box \) and \([\mathsf {N}]\), respectively. Last, we take \(\mathfrak {d}_i^{\alpha _j}\) and \(\mathfrak {v}^{\alpha _j}\) to stand for ‘agent \(\alpha _j\) has performed action \(\delta _i\)’ and ‘agent \(\alpha _j\) has violated a norm’, respectively.
and \(\langle \mathsf {N}\rangle \) as the duals of \(\Box \) and \([\mathsf {N}]\), respectively. Last, we take \(\mathfrak {d}_i^{\alpha _j}\) and \(\mathfrak {v}^{\alpha _j}\) to stand for ‘agent \(\alpha _j\) has performed action \(\delta _i\)’ and ‘agent \(\alpha _j\) has violated a norm’, respectively.
Following [4], we define a translation that maps agent-dependent action-types to formulae of \(\mathcal {L}_{\mathsf {LAN}}\), enabling us to reason with actions inside the logic:
Definition 3
(Translation t between \(Act_{\mathsf {LAN}}\) and \(\mathcal {L}_{\mathsf {LAN}}\) ).
-
For any \(\delta _i\in Act\) and \(\alpha _j\in Agt\), \(t(\delta _i^{\alpha _j})=\mathfrak {d}_i^{\alpha _j}\), with \(\mathfrak {d}_i^{\alpha _j}\in \mathcal {L}_{\mathsf {LAN}}\).
-
For any \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\), \(t(\overline{\varDelta ^{\alpha _i}})=\lnot t(\varDelta ^{\alpha _i})\).
-
For any \(\varDelta ,\varGamma \in Act_{\mathsf {LAN}}\) and \(\alpha _i,\alpha _j\in Agt\), \(t(\varDelta ^{\alpha _i}\cup \varGamma ^{\alpha _j})= t(\varDelta ^{\alpha _i})\vee t(\varGamma ^{\alpha _j})\).
Consequently, from the above we can derive \( t(\varDelta ^{\alpha _i} \& \varGamma ^{\alpha _i}) = t(\varDelta ^{\alpha _i}) \wedge t(\varGamma ^{\alpha _i})\).Footnote 4
To demonstrate the potential of \(\mathcal {L}_{\mathsf {LAN}}\), we present below the agency operators for would, could and will, as introduced in [4]. These operators will play a central role in determining an agent’s compliance with the formalized example protocol in Sect. 5. We leave the introduction of normative operators to Sect. 4.
-
(1)
For any \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\), \([\varDelta ^{\alpha _i}]^{would}\phi :=\square (t(\varDelta ^{\alpha _i})\rightarrow \phi )\)
-
(2)
For any \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\),
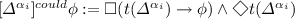
-
(3)
For any \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\), \([\varDelta ^{\alpha _i}]^{will}\phi :=\square (t(\varDelta ^{\alpha _i})\rightarrow \phi )\wedge \langle \mathsf {N}\rangle t(\varDelta ^{\alpha _i})\)
The above operators capture different relations between actions and results obtained at successor states. The first notion is interpreted as ‘currently, by performing the action \(\varDelta \), agent \(\alpha _i\) would bring about \(\phi \)’ (i.e. \(\varDelta \) suffices for guaranteeing \(\phi \)). This definition, however, does not ensure that the agent can in fact perform \(\varDelta \). The second definition extends the first by adding a notion of ability to it, reading ‘currently, by performing action \(\varDelta \), agent \(\alpha _i\) would bring about \(\phi \) and agent \(\alpha _i\) could currently perform \(\varDelta \)’. The third notion connects the actual course of events with the possible actions available to the agent, stating that ‘currently, by performing \(\varDelta \), agent \(\alpha _i\) would bring about \(\phi \) and agent \(\alpha _i\) will actually execute \(\varDelta \)’. (Note that (3) implies (2), and (2) implies (1) within the logic \(\mathsf {LAN}\); see Definition 4).
The logic \(\mathsf {LAN}\) is specified through a Hilbert-axiomatization presented in Definition 4. The axioms A1, A2, A4 and R1 specify that both \(\Box \) and \([\mathsf {N}]\) behave as normal modal operators. In addition, we make a few minimal assumptions for our logic: Axiom A3 ensures that every state has at most one actual successor. Axiom A4 guarantees that every actual future is also a possible future. Axiom A5 expresses that any list of available actions performable by different agents can be consistently performed together. Axiom A5 corresponds to clause T2 from the example of Sect. 2, and is an adaptation of the independence of agents principle (a pivotal condition for multi-agent \(\mathsf {STIT}\) logics; see [3, Ch. 7]). Last, for our deontic setting we adopt a weak contingency axiom with respect to agent-dependent norm violations. This condition, captured by axiom A6, ensures that no agent \(\alpha _i\) can end up in a state at which norm violations cannot be avoided; i.e. if there is a violation possible, there is also a successor state in which the violation is avoided. This axiom corresponds to requirement T1 made in Sect. 2. For a discussion of the contingency axiom A6 we refer to [2, 18].
Definition 4
(Axiomatization of \(\mathsf {LAN}\) ).
-
A0
All propositional tautologies
-
A1
\(\Box (\phi \rightarrow \psi )\rightarrow (\square \phi \rightarrow \square \psi )\)
-
A2
\( [\mathsf {N}](\phi \rightarrow \psi )\rightarrow ( [\mathsf {N}]\phi \rightarrow [\mathsf {N}]\psi )\)
-
A3
\(\langle \mathsf {N}\rangle \phi \rightarrow [\mathsf {N}]\phi \)
-
A4
\(\square \phi \rightarrow [\mathsf {N}]\phi \)
-
A5
For distinct \(\alpha _1,...,\alpha _n{\in } Agt\) and not necessarily distinct \(\varDelta _1,...,\varDelta _n{\in } Act_{\mathsf {LAN}}\),
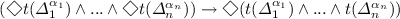
-
A6
For any \(\alpha _j\in Agt\),
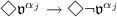
-
R0
Modus Ponens: \(\vdash _{\mathsf {LAN}} \phi \) and \(\vdash _{\mathsf {LAN}}\phi \rightarrow \psi \) imply \(\vdash _{\mathsf {LAN}}\psi \)
-
R1
Necessitation: \(\vdash _{\mathsf {LAN}}\phi \) implies \(\vdash _{\mathsf {LAN}}\square \phi \)
A derivation of \(\phi \) in \(\mathsf {LAN}\) from a set \(\varSigma \), written \(\varSigma \vdash _{\mathsf {LAN}}\phi \), is defined in the usual way (See [5, Def. 4.4]). When \(\varSigma = \emptyset \), we say \(\phi \) is a theorem, and write \(\vdash _{\mathsf {LAN}}\phi \).
The corresponding relational frames for \(\mathsf {LAN}\) are those of [4], modified to a deontic setting using violation constants:
Definition 5
(Relational \(\mathsf {LAN}\) Frames and Models). An \(\mathsf {LAN}\)-frame is a tuple \(F =( W,\{W_{\mathfrak {d}_i^{\alpha _j}}:\mathfrak {d}_i^{\alpha _j}\in \mathcal {L}_{\mathsf {LAN}} \}, \{W_{\mathfrak {v}^{\alpha _j}} : \mathfrak {v}^{\alpha _j}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_\mathsf {N})\), such that:
-
\(\blacktriangleright \) W is a non-empty set of worlds \(w,v,u, \ldots \) such that:
-
(R1) For each \(\mathfrak {d}_i^{\alpha _j}\in Wit\), \(W_{\mathfrak {d}_i^{\alpha _j}}\subseteq W\).
-
(R2) For each \(\mathfrak {v}^{\alpha _j}\in Vio\), \(W_{\mathfrak {v}^{\alpha _j}}\subseteq W\).
-
-
\(\blacktriangleright \) \(R,R_\mathsf {N}\subseteq W\times W\) are binary relations between worlds in W such that:
-
(R3) For all \(w,u,v \in W\), if \(wR_{\mathsf {N}}u\) and \(wR_{\mathsf {N}}v\), then \(u=v\).
-
(R4) For all \(w,v\in W\), if \(w R_{\mathsf {N}} v\), then wRv.
-
(R5) For all \(w\in W\) and for all \(1\le i, j, \le n\), if there are (not necessarily distinct) action-types \(\varDelta _1,...,\varDelta _n\) such that for \(1\le i \le n\) there is a world \(u_i\in W\), for which \(wR u_i\) and \(u_i \in W_{t(\varDelta _i^{\alpha _i})}\), then there is a world \(v\in W\) such that wRv and \(v\in W_{t(\varDelta _1^{\alpha _1})} \cap ...\cap W_{t(\varDelta _n^{\alpha _n})}\).\(^{\dag }\)
-
(R6) For all \(w\in W\) and all \(\alpha _j\in Agt\), if there exists a \(v\in W\) such that wRv and \(v \in W_{\mathfrak {v}^{\alpha _j}}\), then there is a world \(u\in W\) for which wRu and \(u \in W {-} W_{\mathfrak {v}^{\alpha _j}}\).
-
\((\dag )\) For an arbitrary \(\varDelta ^{\alpha _i}\), s.t. \(\varDelta \in Act_{\mathsf {LAN}}\) and \(\alpha _i\in Agt\), we define \(W_{t(\varDelta ^{\alpha _i})}\) using the following recursive clauses: \(W_{t(\delta _i^{\alpha _i})} = W_{\mathfrak {d}^{\alpha _i}_i}\), \(W_{t(\overline{\varDelta ^{\alpha _i}})} = W {-} W_{t(\varDelta ^{\alpha _i})}\) and \(W_{t(\varDelta ^{\alpha _i} \cup \varGamma ^{\alpha _j})} = W_{t(\varDelta ^{\alpha _i})} \cup W_{t(\varGamma ^{\alpha _j})}\).
-
An \(\mathsf {LAN}\)-model is a tuple \(M=(F, V)\) where F is an \(\mathsf {LAN}\)-frame and V is a valuation function mapping propositional atoms to subsets of W, that is \(V: Atoms\mapsto \mathcal {P}(W)\), for which the following two restrictions hold:
-
\(\blacktriangleright \) \(V(\mathfrak {d}_i^{\alpha _j})= W_{\mathfrak {d}_i^{\alpha _j}}\), for any \(\mathfrak {d}_i^{\alpha _j}\in \mathcal {L}_{\mathsf {LAN}}\).
-
\(\blacktriangleright \) \(V(\mathfrak {v}^{\alpha _j})= W_{\mathfrak {v}^{\alpha _j}}\), for any \(\mathfrak {v}^{\alpha _j}\in \mathcal {L}_{\mathsf {LAN}}\).
Let \(C^{\mathsf {LAN}}_f\) be the class of \(\mathsf {LAN}\)-frames. (NB. One can easily show that \(C^{\mathsf {LAN}}_f \ne \emptyset \).)
The relation R represents transitions between successive states. Whereas transitions represented by R capture possible transitions from the current state, the relation \(R_\mathsf {N}\) represents the actual transition from the current state. The only restrictions imposed are: there is at most one actual future (R3) and the actual future must be one of the possible futures (R4) (cf. A3 and A4 of Definition 4, resp.). The concept of ‘actual future’ is taken as state-dependent, which enables reasoning about states that would lie in the actual future of a counterfactual state (e.g., ‘although it is Monday, if it would have been Thursday today, then it would actually be Friday tomorrow’; see [4]). Next, condition (R5) ensures that any combination of actions performed by distinct agents is consistent (cf. A5 of Definition 4). Condition (R6) enforces that, if there is a possible future in which a norm violation occurs for some agent, then there is also an alternative future available in which a norm violation is avoided for that agent (cf. A6 of Definition 4).
The semantics of \(\mathcal {L}_{\mathsf {LAN}}\) is defined accordingly:
Definition 6
(Semantics for \(\mathcal {L}_{\mathsf {LAN}}\)). Let M be an \(\mathsf {LAN}\)-model and \(w\in W\) of M. The satisfaction of a formula \(\phi \in \mathcal {L}_{\mathsf {LAN}}\) in M at w is inductively defined as:
The semantic clauses for the dual operators  and \(\langle \mathsf {N}\rangle \), as well as global truth, validity and semantic entailment are defined as usual (see [5]).
and \(\langle \mathsf {N}\rangle \), as well as global truth, validity and semantic entailment are defined as usual (see [5]).
(NB. propositional constants for actions and violations maintain their semantic interpretation in all models over a frame. See [4] for a discussion.)
The adequacy of \(\mathsf {LAN}\) is directly obtained through a slight modification of the soundness and completeness proofs for the logic of actions and expectations presented in [4] (i.e. we substitute expectation constants for violation constants).
Theorem 1
(Adequacy [4]). For all \(\phi \in \mathcal {L}_{\mathsf {LAN}}\), we have that \(\phi \) is an \(\mathsf {LAN}\) theorem if and only if \(\phi \) is valid with respect to the frame class \(C^{\mathsf {LAN}}_f\).
Furthermore, the logic \(\mathsf {LAN}\) is decidable and has the finite model property:
Theorem 2
(Finite Model Property). \(\mathsf {LAN}\) has the finite (tree) model property (FMP), i.e. every satisfiable formula is satisfiable on a finite, treelike model.
Proof
The proof is presented in Appendix A at the end of this paper.
Corollary 1
(Decidability). The satisfiability problem of \(\mathsf {LAN}\) is decidable.
As a closing comment, we observe that the decidability of \(\mathsf {LAN}\) obtained here, implies decidability of the logic of actions and expectations, left as an open problem in [4] (this can be affirmed through a quick comparison of the axiomatizations).
4 Norms, Ability and Deliberation in \(\mathsf {LAN}\)
The logic \(\mathsf {LAN}\) allows us to reason about both actions and results. We can distinguish three different types of normative statements: normative statements about (1) results, (2) actions, and (3) actions in relation to results. We refer to the first two categories as norms to be and norms to do, respectively, and to the third category as norms of instrumentality. The last category articulates which actions must or must not be employed as instruments for obtaining particular goals (see [4, 23] for a discussion of different notions of instrumentality). In this section, we demonstrate the expressive power of \(\mathsf {LAN}\) through formalizing the aforementioned three categories, and use our formalization to investigate the dependencies between the different norm types. With this, we take a first step towards a formal analysis of norms of instrumentality. In the following section, we apply the attained notions to a formal analysis of our case study.
Before moving to our formal investigation, we need to establish some desiderata concerning the three norm-types and their interdependencies. First, we notice that according to [1], it is generally agreed upon that the categories of norms to be and norms to do cannot be completely reduced to one another. In Sect. 2 we discussed principle P1 of the protocol and argued that, in the case of obligations, norms of instrumentality are neither an instance of the former nor the latter category and, consequently, must be regarded as a category proper (the ‘insider trading’ example from Sect. 1 demonstrates the case for prohibitions). Still, we can identify several reasonable principles expressing certain interdependencies between the three categories:
-
D1
If a result is prohibited, then it will be prohibited regardless of the action used in obtaining it (i.e. prohibited given any action).
-
D2
If an action is prohibited, then its performance is prohibited irrespective of its outcome (i.e. prohibited given any outcome).
-
D3
If it is obligatory to perform a certain action to obtain a particular result (instrumentality), then it must be prohibited to not perform the action, as well as prohibited to not bring about the result.
In addition to the above, we will consider two pivotal principles from the realm of normative agency and investigate their effect on the three norm categories. The first is expressed as the no vacuously satisfied norms principle which states that all norms should be violable (see D4 below). This desideratum imposes a deliberate component on all norms (cf. Anderson’s contingency principles [2, 18] and Belnap and Horty’s notion of deliberative agency [3, 15]). As a second principle, we adopt a generalized variant of the ‘ought implies can’ principle—accredited to Immanuel Kant [16, A548/B576]—to which we will refer as the norm implies can principle. We will make a further distinction within the principle by considering two interpretations of the term ‘can’ (cf. [7] and [23] for different notions of ability). First, we take ‘can’ to denote ‘possible’ (D5 below). Second, we interpret ‘can’ as the stronger agentive notion of ‘ability’ (D6 below).
-
D4
Norms must be violable: If X is prohibited (obligatory), then (the negation of) X must be possible.
-
D5
Norms must be satisfiable: If X is obligatory (prohibited), then (the negation of) X must be possible.
-
D6
Norms must be agentively satisfiable: If X is obligatory (prohibited), then the agent must have the ability to guarantee (the negation of) X.
(NB. Where X can be substituted for a result or an action.)
Clauses D5 and D6 express, respectively, the weak and strong norm implies can principle. We emphasize that for prohibitions (obligations), in order to fulfill (defy) its duty, an agent must ensure the opposite of what is forbidden (obligatory). In the following sections, we will see that the D1–D3 break down when we consider them together with the above deliberation constraints on norms D4–D6.
4.1 Norms to Be
In what follows, we will use the symbol \(\mathsf {F}\) to refer to what is forbidden and we will use \(\mathsf {O}\) to denote what is obligatory. Adapting Anderson’s deontic reduction [2], we formally define the first category of norms to be (i.e. forbidden to be and ought to be, respectively) in accordance with principle D4 as follows:

We interpret \(\mathsf {F}[\top ^{\alpha _i}]\phi \) as ‘\(\phi \) is forbidden to become the case for agent \(\alpha _i\), iff (i) every possible transition to \(\phi \) would mean a norm violation for agent \(\alpha _i\) and (ii) \(\phi \) is possible’ and we read \(\mathsf {O}[\top ^{\alpha _i}]\phi \) as ‘\(\phi \) ought to become the case for agent \(\alpha _i\), iff (i) every possible transition to \(\lnot \phi \) would mean a norm violation for agent \(\alpha _i\) and (ii) \(\lnot \phi \) is possible’. The first conjunct (i) of F1 and O1 corresponds to Anderson’s reduction (referred to as the reduction clause), whereas the second conjunct (ii) captures that the norm can be violated (referred to as the violation clause of principle D4). We take \(\top ^{\alpha _i}\) to represent \(\alpha _i\)’s vacuously satisfied action: that is, \(\top ^{\alpha _i} := (\delta _{1} \cup \overline{\delta _{1}})^{\alpha _i}\) (cf. the universal action [17]). We take \( \bot ^{\alpha _i} := (\delta _{1} \& \overline{\delta _{1}})^{\alpha _i}\) to denote the impossible action, used in definitions F1\(^\prime \) and O1\(^\prime \) below.
We may extend the above formalizations to define norms to be in accordance with the more stringent principle D6. We write \(\mathsf {F}^{\prime }\) and \(\mathsf {O}^{\prime }\) to indicate what is forbidden and what is obligatory, respectively, within this paradigm:Footnote 5

The norms \(\mathsf {F}^{\prime }[\top ^{\alpha _i}]\phi \) and \(\mathsf {O}^{\prime }[\top ^{\alpha _i}]\phi \) are similar to \(\mathsf {F}[\top ^{\alpha _i}]\phi \) and \(\mathsf {O}[\top ^{\alpha _i}]\phi \) in that they contain a reduction clause and a violation clause. However, in addition they also contain a norm implies ability clause. This additional third clause expresses that (iii) ‘there exists an action available to the agent that would serve as a suitable instrument for satisfying the norm’ (cf. the ‘would’ operator, Sect. 3).
Principle D4 is explicitly satisfied by definition F1, O1, \(\text {F1}^{\prime }\), and \(\text {O1}^{\prime }\), whereas the latter two also explicitly satisfy D6. What is more, in \(\mathsf {LAN}\) we derive that all four definitions satisfy D5 too. This result is obtained through the following reasoning: Suppose \(\mathsf {F}[\top ^{\alpha _i}]\phi \). By definition,  holds. Through basic \(\mathsf {LAN}\) reasoning and the reduction clause,
holds. Through basic \(\mathsf {LAN}\) reasoning and the reduction clause,  holds and, by applying axiom A6, we obtain
holds and, by applying axiom A6, we obtain  . Last, from \(\mathsf {LAN}\) reasoning and the reduction clause we can derive
. Last, from \(\mathsf {LAN}\) reasoning and the reduction clause we can derive  . Similar arguments can be given for the remaining norms. Hence, we obtain the following \(\mathsf {LAN}\) theorem:
. Similar arguments can be given for the remaining norms. Hence, we obtain the following \(\mathsf {LAN}\) theorem:

In other words, in \(\mathsf {LAN}\) we derive that norms to be range over contingent state-of-affairs; i.e. the norms can be both satisfied and violated. We refer to this result as the contingency property of norms (cf. [2, 18]).
4.2 Norms to Do
With respect to the second category of norms to do, we adopt Meyer’s reduction [17] to the \(\mathsf {LAN}\) setting and formally define our forbidden to do and ought to do operators, respectively, as follows:

We read \(\mathsf {F}[\varDelta ^{\alpha _i}]\top \) as ‘the performance of \(\varDelta \) is forbidden for agent \(\alpha _i\), iff (i) every possible performance of \(\varDelta \) would mean a norm violation for agent \(\alpha _i\) and (ii) \(\varDelta \) can be performed by \(\alpha _i\)’ and we interpret \(\mathsf {O}[\varDelta ^{\alpha _i}]\top \) as ‘\(\varDelta \) ought to be performed by agent \(\alpha _i\), iff (i) every possible performance of \(\overline{\varDelta }\) would mean a norm violation for agent \(\alpha _i\) and (ii) \(\overline{\varDelta }\) can be performed by \(\alpha _i\)’. We take \(\top \) to represent the vacuously satisfied result; that is, we say that the norm applies independent of its result. The reduction clause (i) of F2 and O2 corresponds to Meyer’s deontic reduction, whereas clause (ii) captures the norm’s deliberative nature by requiring the possibility of norm violation.
The above, together with axiom A6, implies that also norms to do have the desired contingency characteristics; i.e. the following is an \(\mathsf {LAN}\) theorem:

However, the distinction between D5 and D6 breaks down for norms to do: the implied contingency clause in these norms directly incorporates the notion of ability. This is due to our interpretation of actions, which corresponds to the use of actions in \(\mathsf {PDeL}\) [1, 17]; i.e. when an agent has an action at its disposal this means that it has the ability to guarantee its performance. Hence, in the current framework these two notions equate.
4.3 Norms of Instrumentality
So far, the first two categories have been formally defined on the basis of their converged interpretation in the literature (e.g., [1, 8]) and extended with deliberative clauses. How should we formally capture the third, novel category of norms of instrumentality? The above analyses would suggest a definition comprising at least a reduction clause and a violation clause. However, with respect to norms of instrumentality this twofold reading does not suffice.
Let us first consider the obligations belonging to norms of instrumentality. First, recall that we take as instruments those actions that are suitable for serving a particular purpose. Hence, for an agent to be committed to such an obligation, we require that the prescribed action is in fact an instrument for bringing about the desired result; i.e. the action would guarantee the envisaged outcome. Observe that, given this reading, the strong norm implies can principle is immediately satisfied: i.e. the agent must be able to produce the desired result through the desired action. Hence, for the third category, we opt for a formalization that directly incorporates the agential notion of would (cf. Sect. 3). Second, we need to identify what it means for an agent to violate an obligation of the third category: If an agent \(\alpha _i\) has the obligation to employ \(\varDelta \) (as an instrument) to obtain \(\phi \), then \(\alpha _i\) violates this obligation whenever either \(\alpha _i\) does not perform \(\varDelta \) (independent of whether \(\alpha _i\) produced \(\phi \)) or \(\alpha _i\) does not bring about \(\phi \) (independent of whether \(\alpha _i\) performed \(\varDelta \)). On the basis of the above two observations, we thus say that ‘an agent \(\alpha _i\) has the obligation to employ \(\varDelta \) as an instrument to obtain \(\phi \) iff (i) performing \(\overline{\varDelta }\) or bringing about \(\lnot \phi \) would lead to a norm violation for agent \(\alpha _i\), (ii) such a norm violation is possible through \(\lnot \phi \) or \(\overline{\varDelta }\), and (iii) the performance of \(\varDelta \) by \(\alpha _i\) would ensure \(\phi \) (i.e. \(\varDelta \) is a \(\phi \)-instrument for \(\alpha _i\)).’ We formally define this norm as follows:

Notice that, in the three conjuncts of definition O3 we recognize: (i) the reduction clause, (ii) the violation clause, and (iii) the ability clause, respectively. Moreover, as with F1, O1, F1\(^\prime \), and O1\(^\prime \) we stipulate that \(\phi \) must be free of action constants from Wit (in both O3 and F3).
Should we give a similar reading for prohibitions of this category? The answer is not straightforward. Let us reconsider the example from Sect. 1: ‘it is prohibited to use non-public information as an instrument to attain financial profit on the stock market’. We say that an agent \(\alpha _i\) violates this prohibition whenever \(\alpha _i\) uses non-public information and consequently attains financial profit from it. However, should we additionally require that \(\alpha _i\) is only subject to this prohibition whenever \(\alpha _i\) has the strict ability to guarantee financial profit through using non-public information? The answer seems to be negative: we also desire to include cases in which \(\alpha _i\) accidentally obtains financial profit on the stock market through using non-public information.Footnote 6 Nevertheless, in adopting the strong norm implies can principle we still require that the agent must have the ability to avoid violating the prohibition in question, thus satisfying its duty. Putting the above together, we say that ‘agent \(\alpha _i\) is prohibited to employ action \(\varDelta \) as an instrument for the purpose \(\phi \), iff (i) in every case in which \(\varDelta \) has been performed and \(\phi \) has been successfully ensured, a norm violation has occurred, (ii) the norm can in fact be violated and, most importantly, (iii) either \(\alpha _i\) has the ability to avoid performing \(\varDelta \) or there is an action to \(\alpha _i\)’s disposal that is a suitable instrument for avoiding \(\phi \).’ Formally, this is expressed accordingly:

The first two conjuncts of F3 correspond to the reduction and violation clause, respectively. The additional third conjunct explicitly stipulates the ability and instrumentality relations which enable the agent in question to fulfil its duty.
Let us discuss the interaction between the proposed definitions of norms of instrumentality and the list of desiderata presented at the beginning of this section. First, we observe that the second conjunct of F3, ensuring the prohibition’s deliberative nature, invalidates principles D1 and D2. That is, an \(\mathsf {LAN}\)-model can be constructed to show the following are satisfiable for some \(\varDelta ^{\alpha _i}\) and \(\phi \):
The inconsistency of F3 with principles D1 and D2 can be understood as follows: a prohibition to bring about a result (action) should not imply that the result (action) must be avoided given any action (result), but only relative to those actions (results) possible. In other words, impossible combinations of actions and results are not forbidden because they are inviolable. Observe that D1 and D2 can be salvaged by abandoning principles D4, D5 and D6.
Second, as for the other two norm categories, definitions O3 and F3 imply the desired \(\mathsf {LAN}\) theorem concerning the contingency of instrumentality norms:

Third, as stated by principle D3, when an agent \(\alpha _i\) has the obligation to ensure \(\phi \), but only specifically through performing \(\varDelta \), we would like to be able to derive that for \(\alpha _i\) the state of affairs \(\lnot \phi \), as well as the performance of \(\overline{\varDelta }\), is prohibited. However, this principle only holds in our context when we forgo the weak norm implies can principle. In other words, by omitting the violation clause (ii) (and therefore the implied contingency property) of definitions F1, F1\(^\prime \), F2, and O3, we obtain the following \(\mathsf {LAN}\) theorems, satisfying principle D3:
That in the present setting definition O3 is incompatible with principle D3, follows from the observation that impossible combinations of actions and states of affairs cannot be violated and, thus, will not classify as deliberative norms.
As a final remark, we believe that clause (iii) is pivotal for norms of instrumentality: That is, we do not want to commit agents to a cause whose outcome is merely accidental (i.e. uncontrollable). This would be too stringent. Instead, we desire that the envisaged outcome is a proper consequence of the agent’s behaviour. In other words, when the agent has also the ability to fulfill its duty—i.e. guarantee that the action under consideration leads to the desired outcome—only then the agent can be demanded to ensure the outcome by performing the action. This claim is in line with principle D6, the strong, agentive reading of norm implies can where ‘can’ denotes ‘ability’ or ‘choice’ (cf. [3, 7, 15]). Given such a clause, our definitions avoid the overburdening of an agent by not committing the agent to a cause it cannot effectively fulfill. The following \(\mathsf {LAN}\) theorems capture the strong norm implies can reading of O3 and F3:
In conclusion, the final definitions—i.e. F1, \(\text {F1}^{\prime }\), F2, F3, O1, \(\text {O1}^{\prime }\), O2 and O3—are based on (i) Anderson’s and Meyer’s reduction, (ii) the no vacuously satisfied norms principle (of which the weak norm implies can principle was a logical consequence in \(\mathsf {LAN}\)), and (iii) the strong norm implies can (i.e. ability) principle for norms of instrumentality. We saw that, by adopting principles enforcing minimal deliberative criteria on norms (i.e. D4 and D5), we canceled basic dependencies between the three categories (i.e. D1, D2 and D3). In Table 1 we gathered some \(\mathsf {LAN}\) theorems that bear significance to the present analysis. For example, in losing the norm implies can principle altogether, we obtain interdependencies such as \(V1{-}V3\) of Table 1 first column. That \(\mathsf {O}[\varDelta ^{\alpha _i}]\phi \) implies \(\mathsf {O}[\varDelta ^{\alpha _i}]\top \) with complete clauses (V2) is (in part) due to the ability clause, which ensures the violation clause necessary for the implied norm to do. The dependencies described by V4 and V5 are invariant to deliberation. Last, V6–V8 express some dependencies between combinations of norms. Still, further investigation of the proposed definitions and interdependencies is required. The present analysis establishes a first step towards such an investigation by exhibiting the expressive power of the logic \(\mathsf {LAN}\). Let us now formally address our case study.
5 The Benchmark Example Revisited
In what follows, we apply our formal machinery to the example of Sect. 2. We formalize the protocol in \(\mathsf {LAN}\) by making use of definitions F1–F3 and O1–O3, and apply it to two concrete situations where an agent must invoke the protocol to make a decision. Our formalization will be used to demonstrate that the protocol is insufficient relative to its assumed aims (i.e. T1 and T2 of Sect. 2). We close by discussing the source of the aforementioned failure, arguing how the protocol and corresponding logic could be extended to repair such deficiencies.
For the formalization of the protocol, we take \(\texttt {sur}\) and \(\texttt {nur}\) to denote the agents ‘surgeon’ and ‘nurse’, respectively. The action language consists of the atoms \(\texttt {scalp}\), \(\texttt {leave}\) and \(\texttt {call}\), respectively describing ‘using a scalpel’, ‘leaving the operation room’ and ‘calling the safety-emergency number’. Let \(\texttt {incis}\), \(\texttt {operation}\), \(\texttt {dire}\), \(\texttt {health}\), \(\texttt {safety\_nur}\) and \(\texttt {safety\_sur}\) be propositional atoms denoting ‘the incision is made’, ‘the situation is an operation’, ‘the situation is dire’, ‘the patient’s health is promoted’, ‘hygiene safety is promoted from the nurse’s perspective’ and ‘hygiene safety is promoted from the surgeon’s perspective’, respectively. Consider the following possible formalization of the protocol:
-
P1.
\((\texttt {operation} \wedge \mathsf {O}[\top ^{\texttt {sur}}]\texttt {incis}) \rightarrow \mathsf {O}[\texttt {scalp}^{\texttt {sur}}] \texttt {incis}\)
-
P2.
\((\texttt {operation}\wedge \lnot \texttt {dire}) \rightarrow \mathsf {F}[\texttt {scalp}^{\texttt {nur}}] \top \)
-
P3.
\(\mathsf {O}[\top ^{\texttt {nur}}] \texttt {health} \wedge \mathsf {O}[\top ^{\texttt {nur}}]\texttt {safety\_nur}\) and
\(\mathsf {O}[\top ^{\texttt {sur}}] \texttt {health} \wedge \mathsf {O}[\top ^{\texttt {sur}}]\texttt {safety\_sur}\)
-
E1.
\(\lnot \texttt {safety\_nur} \rightarrow (\mathsf {O}[\texttt {leave}^{\texttt {nur}}]\top \wedge \mathsf {O}[\texttt {call}^{\texttt {nur}}]\top )\) and
\(\lnot \texttt {safety\_sur} \rightarrow (\mathsf {O}[\texttt {leave}^{\texttt {sur}}]\top \wedge \mathsf {O}[\texttt {call}^{\texttt {sur}}]\top ) \)
As an example of how to interpret the formulae above, we read P2 as: ‘if there is an operation and the situation is not dire, then the nurse is prohibited to use the scalpel (irrespective of its outcome)’. We are currently interested in whether the protocol is consistent, and whether it can provide agents with sufficient tools to solve normative issues (in situations relevant to our example). Concerning the former, consistency will be shown via the construction of a model for P1–P3 and E1 (below). Regarding the latter, let us consider some possible situations.
Situation 1. In the operation room Anna, the head-surgeon, and a nurse named Bill are performing a tonsillectomy on a patient (i.e. the patient’s tonsils are to be removed). Anna must make a final highly demanding dissection, involving both hands, when she realizes that another crucial incision had to be made using the harmonic scalpel (a scalpel that simultaneously cauterizes tissue). Since Anna is preoccupied and unable to do it, she appeals in this dire situation to Bill, asking whether he could make the other necessary incision with the harmonic scalpel, thus ensuring the patient’s health. The situation is formalized accordingly:

Bill is aware of the new protocol: he knows he is not allowed to use scalpels in regular situations but remembers his duty to the patient’s health too. What should Bill do? The protocol tells Bill that he has the obligation to promote the patient’s health (i.e. \(\mathsf {O}[\top ^{\texttt {nur}}] \texttt {health}\), follows from P3). Since the surgical situation is dire (i) principle P2 does not apply. What is more, since using the scalpel to make the incision is Bill’s only way to promote the patient’s health—by (ii)–(iv)—Bill in fact has the obligation to make the incision with the scalpel; that is, the following is valid:
Consequently, Bill is not prohibited from using the scalpel (i.e. \(\lnot \mathsf {F}[\texttt {scalp}^{\texttt {nur}}]\top \) follows from definition O3, \(\mathsf {LAN}\) reasoning and V5).
Furthermore, to see whether Bill complies with the protocol when he actually brings about the incision with the scalpel—i.e. (v) \([\texttt {scalp}^{\texttt {nur}}]^{will} \texttt {incis}\)—consider the corresponding \(\mathsf {LAN}\)-model in Fig. 1. Namely, the model shows that Bill’s behaviour (v), together with the formalized protocol P1–P3 and E1 and the present situation (i)–(iv), can be consistently represented together with Bill’s actual norm compliance; i.e. (vi) \(\langle \mathsf {N}\rangle \lnot \mathfrak {v}^{\texttt {nur}}\). For that reason, Bill’s decision to make the incision using the scalpel preserves the state of compliance (nevertheless, as expected, it can still be the case that, due to some other action of Bill’s, a violation is generated). (See [12] for a discussion of protocol consistency, compliance and model checking.) Conversely, if Bill actually decides to not use the scalpel, a norm violation will be inevitable; that is, the following is valid:
Last, we note that Fig. 1 also shows the consistency of the formalized protocol.
Situation 2. Let us continue the above example: right before Bill performs the procedure involving the scalpel, Bill accidentally hits his own arm with the harmonic scalpel and inflicts a painful wound. Bill and Anna know, since Bill has now violated his obligation (P3) to preserve the required hygiene safety, that he is obliged (E1) to immediately leave the operation room and call the safety-emergency number for assistance. However, Anna observes that the necessary incision still has to be made in order to secure the agent’s health, so she concludes that Bill must stay and assist her immediately without further ado. The situation is formalized accordingly:

First, we observe that given E1 and (vii) , Bill has the obligation to leave (i.e. \(\mathsf {O}[\texttt {leave}^{\texttt {nur}}]\top \)). However, through (viii), the act of leaving would imply that Bill violates his obligation to preserve the patient’s health (i.e. \(\mathsf {O}[\top ^{\texttt {nur}}]\texttt {health}\)). In fact, the current situation and the formalized protocol are inconsistent; namely, (vii)–(viii), together with P1–P3 and E1, would render in \(\mathsf {LAN}\) that Bill has an obligation to leave and to not leave (i.e. \( \mathsf {O}[\texttt {leave}^{\texttt {nur}} \& \overline{\texttt {leave}}^{\texttt {nur}}]\top \)). This inconsistency depends on the assumption T1 (cf. (R6) of Definition 5), which is the committee’s assumption that there is a way out to every possible dilemma. In conclusion, the formalism tells us that the protocol is current inadequate.
The source of the conflict that arises in the second situation above relates to Chisholm’s Paradox [9] and the issue of contrary-to-duty (CTD) reasoning. Principle E1, in fact, can be seen as a contrary-to-duty obligation and the present system suffers from the similar problem of detachment as the initial paradox does. In brief, a contrary-to-duty obligation is a specific obligation that comes into force whenever a primary obligation has been violated. What is more, their purpose is to (partially) restore compliance with the norm system (e.g. [11]). They are often referred to as secondary obligations, to denote the fact that they depend upon the possibility of violating primary obligations (cf. [9, 19]). Such a violation is always possible when employing norms F1–F3, O1–O3, \(\text {F1}^{\prime }\), and \(\text {O1}^{\prime }\) with \(\mathsf {LAN}\) due to the contingency requirements addressed in Sect. 4. An extension of our formalism to adequately account for such reasoning, is outside the scope of this paper, and so, we leave this to future work.
6 Conclusion
In this work, we provided the sound and complete logic \(\mathsf {LAN}\) that brings together Anderson’s reduction of norms to be and Meyer’s reduction of norms to do. We introduced a new category of norms—norms of instrumentality—and analyzed its relationships with the former two classes vis-à-vis different notions of deliberative action. The technical contribution of this work consists in proving the finite model property and decidability of \(\mathsf {LAN}\). Since the non-normative logic presented in [4] is an instance of \(\mathsf {LAN}\), we also answered the open problem for that logic’s decidability. These results show that \(\mathsf {LAN}\) has the potential to be employed in automated reasoning with norms relating agency, actions and results.
In comparing the present logic with state of the art frameworks, we see three possible directions for future work. First, as mentioned in Sect. 5, a natural way to extend our framework would be to incorporate normative reasoning about sub-ideal scenarios, involving a notion of contrary-to-duty norms that are primarily designed to bring the agent back into a state of compliance with the system. We aim to address this issue and analyze its relation to the three norm categories.
Second, our current analysis omitted consideration of permissions. The behaviour of permissions in relation to the three norm categories is not immediately clear. For example, although the notion of a weak permission appears equivalent to the dual of an unconditional obligation in the form of O1 or O2 , the concept of strong permission seems to require explicit formulations in permissive form (cf. [13]). Moreover, as argued in [13, 14], the traditional way of representing permissions as duals of obligations is an over-simplification that cannot adequately model many real-life scenarios. We plan to extend our formalism to incorporate such permissions.
Last, since the logic \(\mathsf {LAN}\) encompasses the Andersonian reductions analysed in [17], but uses a third reduction using action constants, we plan to devote future work to investigating the logic’s relation to the deontic action logic \(\mathsf {PDeL}\).
Notes
- 1.
Notice that principle P2 incorporates a form of defeasible reasoning through explicit exception, for the present analysis of norms of instrumentality, the above will suffice.
- 2.
Notice that in the present example, we use a material tool to exemplify instruments. However, we stress that the notion of instrumentality is more general and refers to all actions serving goals; e.g. ‘opening the window’ is an instrument for ‘changing the room’s temperature’ [22]. Following Von Wright [23], an action is a classified \(\phi \)-instrument—where \(\phi \) is the purpose—whenever the action serves the purpose of \(\phi \). Consequently, although in the above example reference is made to a ‘scalpel’ (i.e. a tool) the instrument under consideration—serving the purpose of ‘the incision being made’—is in fact the action ‘using the scalpel (for the purpose of incision)’. See [4] for a philosophical discussion on different notions of instrumentality.
- 3.
Following [1], to avoid paradoxes \(\mathfrak {v}^{\alpha _i}\) is read as ‘norm violation’ instead of ‘sanction’.
- 4.
We note in passing that one could define other action operators of \(\mathsf {PDL}\) within the reduced logic \(\mathsf {LAN}\); for example ‘composition’ as \([\varDelta ^{\alpha _i} ; \varGamma ^{\alpha _i}]\phi := [\varDelta ^{\alpha _i}][\varGamma ^{\alpha _i}]\phi \).
- 5.
Notice, since \(Act_{\mathsf {LAN}}\) represents a Boolean algebra of actions built over a finite number of actions types from Act, there are only finitely many equivalence classes \([\![ \varDelta ^{\alpha _i} ]\!]~:=~\{\varGamma ^{\alpha _i} \ | \ \vdash _{\mathsf {LAN}} t(\varGamma ^{\alpha _i}) \equiv t(\varDelta ^{\alpha _i}) \}\) of equivalent actions. We let \([\![ Act^{*}_{\mathsf {LAN}} ]\!]\) in F1\(^\prime \) and O1\(^\prime \) represent the set of all such equivalence classes minus the class \([\![ \bot ^{\alpha _i} ]\!]\) of all impossible actions. Additionally, since obligatory or forbidden results are central to norms to be, as opposed to obligatory or forbidden actions, we impose the following restriction on F1, O1, F1\(^\prime \) and O1\(^\prime \): the formula \(\phi \) is free of action constants from Wit. Without this restriction, norms to do could be seen as instances of norms to be—i.e. norms to bring about the witness of a performed action as a result—thus contradicting the observations made in [1] about the irreducibility of the two.
- 6.
The assumption avoids risk by forbidding acts that possibly produce violations; e.g. ‘it is forbidden to injure someone with a sharp tool, independent of the ability to guarantee the injury’. However, one could consider inclusion of instrumentality clauses for prohibitions when analyzing responsibility. We leave this for future work.
References
d’Altan, P., Meyer, J.J., Wieringa, R.J.: An integrated framework for ought-to-be and ought-to-do constraints. Artif. Intell. Law 4(2), 77–111 (1996)
Anderson, A.R., Moore, O.K.: The formal analysis of normative concepts. Am. Sociol. Rev. 22(1), 9–17 (1957)
Belnap, N., Perloff, M., Xu, M.: Facing the Future. Agents and Choices in our Indeterminist World. Oxford University Press, Oxford (2001)
van Berkel, K., Pascucci, M.: Notions of instrumentality in agency logic. In: Miller, T., Oren, N., Sakurai, Y., Noda, I., Savarimuthu, B.T.R., Cao Son, T. (eds.) PRIMA 2018. LNCS (LNAI), vol. 11224, pp. 403–419. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03098-8_25
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Broersen, J.: Deontic epistemic stit logic distinguishing modes of mens rea. J. Appl. Logic 9(2), 137–152 (2011)
Brown, M.A.: On the logic of ability. J. Philos. Logic 17(1), 1–26 (1988)
Castañeda, H.N.: On the semantics of the ought-to-do. In: Davidson, D., Harman, G. (eds.) Semantics of Natural Language. Synthese Library, vol. 40, pp. 675–694. Springer, Dordrecht (1972). https://doi.org/10.1007/978-94-010-2557-7_21
Chisholm, R.: Contrary-to-duty imperatives and deontic logic. Analysis 24, 33–36 (1963)
Fischer, M., Ladner, R.: Propositional dynamic logic of regular programs. J. Comput. Syst. Sci. 18(2), 194–211 (1979)
Governatori, G.: Practical normative reasoning with defeasible deontic logic. In: d’Amato, C., Theobald, M. (eds.) Reasoning Web 2018. LNCS, vol. 11078, pp. 1–25. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00338-8_1
Governatori, G., Hashmi, M.: No time for compliance. In: 19th International Enterprise Distributed Object Computing Conference, pp. 9–18. IEEE (2015)
Governatori, G., Olivieri, F., Rotolo, A., Scannapieco, S.: Computing strong and weak permissions in defeasible logic. J. Philos. Logic 42(6), 799–829 (2013). https://doi.org/10.1007/s10992-013-9295-1
Hansson, S.O.: The varieties of permission. In: Gabbay, D., Horty, J., Parent, X., van der Meyden, R., van der Torre, L. (eds.) Handbook of Deontic Logic and Normative Systems, pp. 195–240. College Publications, London (2013)
Horty, J.: Agency and Deontic Logic. Oxford University Press, Oxford (2001)
Kant, I.: Critique of Pure Reason. Cambridge University Press, Cambridge (2000)
Meyer, J.J.C.: A different approach to deontic logic: deontic logic viewed as a variant of dynamic logic. Notre Dame J. Formal Logic 29(1), 109–136 (1988)
Pascucci, M.: Anderson’s restriction of deontic modalities to contingent propositions. Theoria 83(4), 440–470 (2017)
Prakken, H., Sergot, M.: Dyadic deontic logic and contrary-to-duty obligations. In: Nute, D. (ed.) Defeasible Deontic Logic, pp. 223–262. Springer, Dordrecht (1997). https://doi.org/10.1007/978-94-015-8851-5_10
Prisacariu, C., Schneider, G.: A dynamic deontic logic for complex contracts. J. Logic Algebraic Program. 81(4), 458–490 (2012)
von Wright, G.H.: Deontic logic. Mind 60(237), 1–15 (1951)
von Wright, G.H.: An Essay in Deontic Logic and the General Theory of Action. North Holland Publishing Company, Amsterdam (1968)
von Wright, G.H.: The Varieties of Goodness. Routledge & Kegan Paul, London and Henley (1972). fourth impression
Acknowledgments
Work funded by projects: FWF I2982, FWF W1255-N23, FWF Y544-N2, and WWTF MA16-028.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Finite Model Property and Decidability
A Finite Model Property and Decidability
In this appendix, we provide the main technical contribution of this paper: we show that \(\mathsf {LAN}\) is decidable (Corollary 1), via proving the finite model property (FMP) for the logic (Theorem 2). Our strategy is, accordingly: first, we show that every satisfiable formula is satisfiable on a treelike model (Lemma 1). Second, we show that the depth of the treelike model can be bounded (Lemma 2). Last, we prove that the breadth of the model can be bounded (Lemma 3).
Lemma 1
Every formula \(\phi \in \mathcal {L}_{\mathsf {LAN}}\) satisfiable on a \(\mathsf {LAN}\)-model, is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model.
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a \(\mathsf {LAN}\)-model with \(w \in W\) and assume \(M, w \models \phi \) (i.e. \(\phi \) is satisfiable). To show that \(\phi \) is satisfiable at the root of a treelike model we evoke an unraveling procedure similar to the one in [5, Ch. 2.1]. We define the treelike model \(M^t\) as follows:
-
\(W^t \subseteq \bigcup _{n \in \mathbb {N}} W^{n}\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(wRw_{1}\), \( w_{1}Rw_{2}\), ..., \(w_{n-1}Rw_{n}\);
-
For each \(\alpha _{i} \in Agt\) and each \(\mathfrak {d}^{\alpha _{i}}_{j} \in Wit^{\alpha _{i}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^t \subseteq W^t\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(w_{n} \in W_{\mathfrak {d}^{\alpha _{i}}_{j}}\);
-
For each \(\alpha _{i} \in Agt\), \(W_{\mathfrak {v}^{\alpha _i}}^t \subseteq W^t\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(w_{n} \in W_{\mathfrak {v}^{\alpha _i}}\);
-
For all \(\varvec{w}, \varvec{u} \in W^t\), \(\varvec{w}R^t\varvec{u}\) iff \(\varvec{w} = (w,w_{1},{...},w_{n})\), \(\varvec{u} = (w,w_{1}{...},w_{n},w_{n+1})\), and \(w_{n}Rw_{n+1}\);
-
For all \(\varvec{w}, \varvec{u} \in W^t\), \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\) iff \(\varvec{w} = (w,w_{1},{...},w_{n})\), \(\varvec{u} = (w,w_{1}{...},w_{n},w_{n+1})\), and \(w_{n}R_{\mathsf {N}}w_{n+1}\);
-
For all \(\varvec{w} \in W^t\), \(\varvec{w} = (w,w_{1},{...},w_{n}) \in V^t(p)\) iff \(w_{n} \in V(p)\).
The model \(M^t\) is clearly treelike. Further, Prop. 2.14 and 2.15 of [5] imply:
-
(1)
For any formula \(\psi \in \mathcal {L}_{\mathsf {LAN}}\), each \(u \in W\), and each \(\varvec{u} \in W^t\) of the form
$$\begin{aligned} (w, w_{1}, {...}, u), \text { we have that } M,u \models \psi \text { iff } M^t,\varvec{u} \models \psi . \end{aligned}$$
This result, together with the assumption \(M, w \models \phi \), implies \(M^t, (w) \models \phi \), where (w) is the root of the treelike model \(M^t\). To complete the proof, we must argue that \(M^t\) is a \(\mathsf {LAN}\)-model, i.e., it satisfies conditions (R3)–(R6) of Definition 5:
(R3) Let \(\varvec{w}, \varvec{u}, \varvec{v} \in W^t\) and suppose \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\) and \(\varvec{w}R_{\mathsf {N}}^t\varvec{v}\). By definition of \(R_{\mathsf {N}}^t\) we get (i) \(\varvec{w}\) is a sequence of the form \((w,w_{1},{...},w_{n})\), (ii) \(\varvec{u}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1})\), (iii) \(\varvec{v}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1}')\), (iv) \(w_{n}R_{\mathsf {N}}w_{n+1}\), and (v) \(w_{n}R_{\mathsf {N}}w_{n+1}'\). Since the original model M satisfies (R3), it follows from (iv) and (v) that \(w_{n+1} = w_{n+1}'\), which, together with (ii) and (iii), implies \(\varvec{u} = \varvec{v}\).
(R4) Let \(\varvec{w}, \varvec{u} \in W^t\) and assume \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\). By definition of \(R_{\mathsf {N}}^t\) we get (i) \(\varvec{w}\) is a sequence of the form \((w,w_{1},{...},w_{n})\), (ii) \(\varvec{u}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1})\), and (iii) \(w_{n}R_{\mathsf {N}}w_{n+1}\). Since the original model M satisfies (R4), it follows from (iii) that \(w_{n}Rw_{n+1}\), which, together with (i) and (ii), implies \(\varvec{w}R^t\varvec{u}\).
(R5) Let \(\varvec{w} \in W^t\) and \(Agt = \{\alpha _{1}, ..., \alpha _{n}\}\). Suppose there are (not necessarily distinct) action-types \(\varDelta _{1}, {...}, \varDelta _{n} \in Act_{\mathsf {LAN}}\) s.t. for \(1 \le i \le n\) there exist \(\varvec{u}_{i} \in W^t\) s.t. \(\varvec{w}R^t\varvec{u}_{i}\) and \(\varvec{u}_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{t}\). It follows that \(\varvec{w}\) is of the form \((w,w_{1},{...},w_{n})\) and each \(\varvec{u}_{i}\) is of the form \((w,w_{1},{...},w_{n},u_{i})\) with \(w_{n}Ru_{i}\). The model M satisfies condition (R5), and hence there exists a world \(v \in W\) s.t. \(w_{n}Rv\) and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\). By definition of \(M^t\), we have \(\varvec{v} = (w,w_{1},{...},w_{n},v) \in W^t\), implying that \(\varvec{w}R^{t}\varvec{v}\) and \(\varvec{v} \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{t} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{t}\).
(R6) Let \(\varvec{w} \in W^t\) and \(\alpha _{i} \in Agt\). Assume there is a \(\varvec{v} \in W^t\) s.t. \(\varvec{w}R^t\varvec{v}\) and \(\varvec{v} \in W_{\mathfrak {v}^{\alpha _i}}^{t}\). This implies \(\varvec{w} = (w,w_{1},{...},w_{n})\) and \(\varvec{v} = (w,w_{1},{...},w_{n},v)\) with \(w_{n}Rv\). Since M satisfies (R6), there is a u s.t. \(w_{n}Ru\) and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\). By definition of \(M^t\), there is a \(\varvec{u} = (w,w_{1},{...},w_{n},u) \in W^t\) s.t. \(\varvec{w}R^t\varvec{u}\) and \(\varvec{u} \in W^{t} - W_{\mathfrak {v}^{\alpha _i}}^{t}\).
For the second transformation we define the following auxiliary concepts:
Definition 7
(Degree \(deg(\cdot )\)). The modal degree is recursively defined as:
-
\(deg(p) = deg(\mathfrak {d}^{\alpha _{i}}_{j}) = deg(\mathfrak {v}^{\alpha _i}) = 0\);
-
\(deg(\lnot \phi ) = \deg (\phi )\);
-
\(deg(\phi \rightarrow \psi ) = max\{\deg (\phi ),deg(\psi )\}\);
-
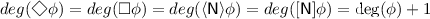 .
.
Definition 8
(Height \(height(\cdot )\) and Depth). Let M be a treelike model. We define the height of a node w in M recursively as follows:
-
\(height(w) = 0\), if w is the root of M;
-
\(height(w) = height(u) + 1\), if uRw in M.
The depth of M is the maximum height among all the worlds in M.
Lemma 2
Every formula \(\phi \) satisfiable at the root of a treelike \(\mathsf {LAN}\)-model, is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth (specifically, with a depth equal to \(deg(\phi )\)).
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a treelike \(\mathsf {LAN}\)-model with root \(w\in W\) and assume \(M, w \models \phi \). We first construct a treelike model \(M^d\) of finite depth by restricting the depth of \(M^d \) to \(deg(\phi )\) and argue that \(\phi \) is satisfiable at the root w of \(M^{d}\). We define \(M^d\) as follows:
-
For all \(w \in W\), \(w \in W^{d}\) iff \(height(w) \le deg(\phi )\);
-
For all \(\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^{d} = W_{\mathfrak {d}^{\alpha _{i}}_{j}} \cap W^{d}\);
-
For all \(\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {v}^{\alpha _i}}^{d} = W_{\mathfrak {v}^{\alpha _i}} \cap W^{d}\);
-
\(R^{d} = R \cap (W^{d} \times W^{d})\);
-
\(R_{\mathsf {N}}^{d} = R_{\mathsf {N}} \cap (W^d \times W^{d})\);
-
For all \(p \in Var\), \(V^{d}(p) = V(p) \cap W^{d}\).
The model \(M^d\) is treelike with finite depth. Further, Lem. 2.33 in [5] gives us:
From (2) we conclude that \(M^{d},w \models \phi \). Last, we show that \(M^{d}\) is a \(\mathsf {LAN}\)-model:
(R3) Let \(w,u,v \in W^{d}\) and assume \(wR_{\mathsf {N}}^{d}u\) and \(wR_{\mathsf {N}}^{d}v\). By definition of \(M^{d}\), we know that \(w,u,v \in W\) and that \(wR_{\mathsf {N}}u\) and \(wR_{\mathsf {N}}v\). Since the original model M satisfies property (R3), we have that \(u = v\).
(R4) Let \(w,u \in W^{d}\) and assume \(wR_{\mathsf {N}}^{d}u\). By definition of \(M^{d}\), we get \(w,u \in W\) and \(wR_{\mathsf {N}}u\). Since M satisfies property (R4), it follows that wRu. By the fact that \(w,u \in W^{d}\) and the definition of \(M^{d}\), we obtain \(wR^{d}u\).
(R5) Let \(w \in W^{d}\) and \(Agt = \{\alpha _{1}, ..., \alpha _{n}\}\). Suppose there are (not necessarily distinct) complex action-types \(\varDelta _{1}, {...}, \varDelta _{n} \in Act_{\mathsf {LAN}}\) s.t. for \(1 \le i \le n\) there exist \(u_{i} \in W^{d}\) s.t. \(wR^{d}u_{i}\) and \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{d}\). By definition of \(M^{d}\), it follows that \(wRu_{i}\) holds for each \(i \in \{1, {...}, n\}\) with \(height(u_{i}) \le deg(\phi )\). Since M satisfies (R5), we know there exists a \(v \in W\) s.t. wRv and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\). We know \(v \in W^{d}\) since \(height(v) = height(u_{i}) \le deg(\phi )\), which implies \(wR^{d}v\) and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{d} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{d}\) by definition of \(M^{d}\).
(R6) Let \(w \in W^{d}\) and \(\alpha _{i} \in Agt\). Assume there exists a \(v \in W^{d}\) s.t. \(wR^{d}v\) and \(v \in W_{\mathfrak {v}^{\alpha _i}}^{d}\). By definition of \(M^{d}\), we know that wRv holds with \(height(v) \le deg(\phi )\). Since M satisfies (R6), we know there exists a \(u \in W\) s.t. wRu and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\). Since \(height(u) = height(v) \le deg(\phi )\), it follows that \(u \in W^{d}\), \(wR^{d}u\), and \(u \in W^{d} - W_{\mathfrak {v}^{\alpha _i}}^{d}\).
Lemma 3
Every formula \(\phi \) satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth equal to \(deg(\phi )\), is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth and finite branching (i.e., \(\phi \) is satisfiable on a finite model).
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a treelike \(\mathsf {LAN}\)-model with depth equal to \(deg(\phi )\) with root \(w\in W\) and assume \(M, w \models \phi \). Let \(Var(\phi )\) be the set of propositional variables occurring in \(\phi \). We define the set Atoms as \(Var(\phi ) \cup Wit \cup \{\mathfrak {v}^{\alpha _i}: \alpha _{i} \in Agt\}\). By Prop. 2.29 in [5], we know there are only a finite number of modal formulae (up to logical equivalence) built from the finite set Atoms with degree less than or equal to \(deg(\phi )\). We use \(\varTheta \) to denote this collection of (equivalence classes of) formulae.
Using \(\varTheta \), we first provide a selection procedure, similar to Thm. 2.34 of [5], to construct a finite model \(M^f\) and show that the root of this model satisfies \(\phi \). Last, we show that \(M^f\) is indeed a \(\mathsf {LAN}\)-model. We construct \(M^f\) as follows:
-
\(W^{f}\) is the set obtained from the selection procedure (below);
-
For all \(\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^{f} = W_{\mathfrak {d}^{\alpha _{i}}_{j}} \cap W^{f}\);
-
For all \(\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {v}^{\alpha _i}}^{f} = W_{\mathfrak {v}^{\alpha _i}} \cap W^{f}\);
-
\(R^{f} = R \cap (W^{f} \times W^{f})\);
-
\(R_{\mathsf {N}}^{f} = R_{\mathsf {N}} \cap (W^{f} \times W^{f})\);
-
For all \(p \in Var\), \(V^{f}(p) = V(p) \cap W^{f}\).
Selection Procedure. We build our domain \(W^{f}\) by selecting a sequence of states \(S_{0}, S_{1}, ..., S_{deg(\phi )}\) up to a height of \(deg(\phi )\), where \(S_{0} = \{w\}\). Each subscript i of \(S_{i}\) represents that the states contained in the associated set are at a height of i in the original model M. Suppose that the sets \(S_{0}\), \(S_{1}\), ..., \(S_{i}\) have already been chosen; we now explain how to select the set \(S_{i+1}\) with \(i+1 \le deg(\phi )\). For each formula \(\psi \in \varTheta \) equivalent to a formula of the form  or \(\langle \mathsf {N}\rangle \chi \) with \(deg(\psi ) \le deg(\phi ) - i\) s.t. \(M,u \models \psi \) for some \(u \in S_{i} \subseteq W\), we choose a \(v \in W\) s.t. uRv (or, \(uR_{\mathsf {N}}v\), depending on the modality in \(\psi \)) and \(M,v \models \chi \). We define the domain \(W^{f} = S_{0} \cup S_{1} \cup {...} \cup S_{deg(\phi )}\).
or \(\langle \mathsf {N}\rangle \chi \) with \(deg(\psi ) \le deg(\phi ) - i\) s.t. \(M,u \models \psi \) for some \(u \in S_{i} \subseteq W\), we choose a \(v \in W\) s.t. uRv (or, \(uR_{\mathsf {N}}v\), depending on the modality in \(\psi \)) and \(M,v \models \chi \). We define the domain \(W^{f} = S_{0} \cup S_{1} \cup {...} \cup S_{deg(\phi )}\).
The next statement is a consequence of this selection procedure [5, pp. 76–77]:
-
(3)
For any formula \(\psi \in \varTheta \) s.t. \(deg(\psi ) \le deg(\phi )\) and any world \(u \in W^{f}\) s.t.
$$\begin{aligned} height(u) \le deg(\phi ) - \deg (\psi ), M,u \models \psi \text { iff }M^{f},u \models \psi . \end{aligned}$$
From (3), together with \(M,w\models \phi \), \(\phi \in \varTheta \), \(deg(\phi ) \le deg(\phi )\), \(w \in W^{f}\!\), and \(height(w) \le deg(\phi )\), we infer \(M^{f},w \models \phi \). We show that \(M^{f}\) is an \(\mathsf {LAN}\)-model:
(R3) Let \(w, u, v \in W^{f}\) and assume \(wR_{\mathsf {N}}^{f}u\) and \(wR_{\mathsf {N}}^{f}v\). By definition of \(M^{f}\), \(wR_{\mathsf {N}}u\) and \(wR_{\mathsf {N}}v\) hold. Since the model M satisfies (R3), we obtain \(u=v\).
(R4) Let \(w, u \in W^{f}\) and assume \(wR_{\mathsf {N}}^{f}u\). By definition of \(M^{f}\), \(wR_{\mathsf {N}}u\) must hold. Since the original model M satisfies (R4), we have wRu, and because \(R^{f}\) is the set R restricted to \(W^{f}\), which contains w and u, we infer \(wR^{f}u\).
(R5) Let \(w \in W^{f}\) and let \(Agt = \{\alpha _{1}, {...}, \alpha _{n}\}\). Suppose there are (not necessarily distinct) complex action-types \(\varDelta _{1}, ..., \varDelta _{n}\in Act_{\mathsf {LAN}}\) s.t. for all \(1 \le i \le n\) there exists a \(u_{i} \in W^{f}\) s.t. \(wR^{f}u_{i}\) and \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{f}\). By definition of \(M^{f}\), this implies \(wRu_{i}\), \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}\), and \(height(u_{i}) \le deg(\phi )\) for each \(i \in \{1, {...}, n\}\). Since M satisfies (R5), we know that there exists a v such that wRv and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\), i.e.,  . Observe that because \(height(w) + 1 = height(u_{i}) \le deg(\phi )\) that \(1 \le deg(\phi )\), implying that
. Observe that because \(height(w) + 1 = height(u_{i}) \le deg(\phi )\) that \(1 \le deg(\phi )\), implying that  , because \(deg(\bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})) = 0\). Consequently, by the selection procedure a \(v' \in W\) such that \(wRv'\) and \(M, v' \models \bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})\) must have been selected and placed in \(S_{height(v')}\). Hence, there exists a \(v' \in W^{f}\) s.t. \(wR^{f}v'\) and \(v' \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{f} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{f}\).
, because \(deg(\bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})) = 0\). Consequently, by the selection procedure a \(v' \in W\) such that \(wRv'\) and \(M, v' \models \bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})\) must have been selected and placed in \(S_{height(v')}\). Hence, there exists a \(v' \in W^{f}\) s.t. \(wR^{f}v'\) and \(v' \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{f} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{f}\).
(R6) Let \(w \in W^{f}\), \(\alpha _{i}\in Agt\), and assume there is a \(v \in W^{f}\) s.t. \(wR^{f}v\) and \(v \in W_{\mathfrak {v}^{\alpha _i}}^{f}\). By definition of \(M^{f}\) we infer wRv and \(v \in W_{\mathfrak {v}^{\alpha _i}}\) with \(height(v) \le deg(\phi )\); hence, there exists a \(u \in W\) s.t. wRu and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\) with \(height(u) \le deg(\phi )\). It follows that  . Since \(height(w) = height(v) + 1 \le deg(\phi )\), we know that \(1 \le deg(\phi )\), and so,
. Since \(height(w) = height(v) + 1 \le deg(\phi )\), we know that \(1 \le deg(\phi )\), and so,  . By the selection procedure, a \(u' \in W\) s.t. \(wRu'\) and \(u' \in W - W_{\mathfrak {v}^{\alpha _i}}\) must have been chosen and placed in \(S_{height(u)}\); hence, \(u' \in W^{f}\), \(wR^{f}u'\), and \(u' \in W^{f} - W_{\mathfrak {v}^{\alpha _i}}^{f}\).
. By the selection procedure, a \(u' \in W\) s.t. \(wRu'\) and \(u' \in W - W_{\mathfrak {v}^{\alpha _i}}\) must have been chosen and placed in \(S_{height(u)}\); hence, \(u' \in W^{f}\), \(wR^{f}u'\), and \(u' \in W^{f} - W_{\mathfrak {v}^{\alpha _i}}^{f}\).
Theorem 2. \(\mathsf {LAN}\) has the finite (tree) model property, i.e., every satsifiable formula is satisfiable on a finite, treelike model.
Proof
Follows from Lemmas 1, 2, and 3.
Corollary 1. The satisfiability problem of \(\mathsf {LAN}\) is decidable.
Proof
By [5, Thm. 6.15], we know that if a normal modal logic is finitely axiomatizable and has the FMP, then it is decidable, which is the case for \(\mathsf {LAN}\).
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
van Berkel, K., Lyon, T., Olivieri, F. (2020). A Decidable Multi-agent Logic for Reasoning About Actions, Instruments, and Norms. In: Dastani, M., Dong, H., van der Torre, L. (eds) Logic and Argumentation. CLAR 2020. Lecture Notes in Computer Science(), vol 12061. Springer, Cham. https://doi.org/10.1007/978-3-030-44638-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-44638-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-44637-6
Online ISBN: 978-3-030-44638-3
eBook Packages: Computer ScienceComputer Science (R0)




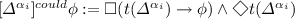
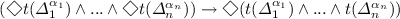
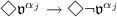

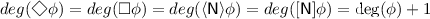 .
.