1 Introduction

The Wigner transport equation is a full quantum transport model able to capture the relevant physics in next generation of quantum semiconductor devices. It is well known that the pure state Wigner equation is an equivalent phase-space reformulation of the Schrödinger equation. At the same time the Wigner equation can be augmented by a Boltzmann-like collision operator accounting for the process of decoherence. However, this equation has represented a numerically daunting task and it has raised more problems than solutions.

In literature, we find a range of proposed techniques to tackle this problem. Deterministic solvers, based on finite difference method (FDM) for time-dependent Wigner simulations, has been introduced for the first time in the mid 1980s (see [2] for a review). In order to tackle the oscillatory components introduced by the Wigner kernel and the diffusion term, recently more sophisticated solvers have been developed [1, 4, 6, 7, 13, 14, 16].

In alternative particle Monte Carlo (MC) techniques can be introduced (see [12] for a review). In this paper, we have focused in the so called Signed Monte Carlo method [11] , where the Wigner potential is treated as a scattering source which determines the electron-potential interaction, and consequently new particles with different signs are stochastically added to the system. Recently this method has been also be understood in terms of the Markov jump process theory [8,9,10, 15], producing a class of new stochastic algorithms. In this paper a thorough validation of one of these algorithms will be presented in the already traditional benchmark experiment of a double well potential barrier.

2 The Wigner Function Formalism

The Wigner formulation of quantum mechanics offers a description of the electron state in terms of a phase-space function f w(x, k, t), where is the particle position, the wave vector (and ħk the momentum). The Wigner equation has the form

$$\displaystyle \begin{aligned} \frac{\partial f_w}{\partial t} + \frac{\hbar}{m^{*}} k \cdot \nabla_{x}f_w = \mathcal{Q}(f_w) {} \end{aligned} $$
(1)

which includes the quantum evolution term

$$\displaystyle \begin{aligned} \mathcal{Q}(f_w) = \int V_w(x, k - k') f_w(x,k') \, dk' {} \end{aligned} $$
(2)

where V w is the Wigner potential

$$\displaystyle \begin{aligned} V_w(x,k) = \frac{1}{i\hbar (2\pi)^d} \int dx' \, e^{-i k \cdot x'} \left[ V\left(x + \frac{x'}{2} \right) - V\left(x - \frac{x'}{2}\right) \right] {} \end{aligned} $$
(3)

and V (x) the potential energy. The Wigner potential is a non-local potential operator which is responsible of the quantum transport, is real-valued, and anti-symmetric with respect to k. The solution f w is real valued, but not necessarily nonnegative, and it can therefore not be interpreted as a probability density, but as a quasi-distribution of particles. It is related to the solution of the Schrödinger equation ψ(x, t) via the Wigner-Weyl transform [5] and, under some restrictions on ψ , the function f w satisfies

$$\displaystyle \begin{aligned} n(x,t) = \int \, f_w(x,k) \, dk = |\psi(x,t)|{}^2 \ge 0 {} \end{aligned} $$
(4)

where n is the mean density.

3 The Signed Particle Monte Carlo Method

Among MC solution techniques, we have considered the so called Signed particle Monte Carlo approach [11]. This technique is based on the observation that the quantum evolution term (2) looks like the Gain term of a collisional operator in which the Loss term is missing. But the Wigner potential (3) is not always positive and cannot be considered a scattering term. For this reason, it can be separated into a positive and negative parts \(V^+_w, V^-_w\) such that

$$\displaystyle \begin{aligned} V_w = V^+_w - V^-_w, \quad V^+_w, V^-_w \ge 0 \quad . {} \end{aligned} $$
(5)

In this way, we can define an integrated scattering probability per unit time as

$$\displaystyle \begin{aligned} \gamma(x) = \int dk' \, V^+_w(x, k - k') = \int dk' \, V^-_w(x, k - k') {} \end{aligned} $$
(6)

and rewrite the quantum evolution term as the difference between Gain and Loss terms, i.e.

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{Q}(f_w) = \int dk' w(k',k) f_w(x,k') - \gamma(x) f_w(x,k) {} \end{array} \end{aligned} $$
(7)
$$\displaystyle \begin{aligned} \begin{array}{rcl} w(k',k) = V_w^+(x, k - k') - V_w^-(x, k - k') + \gamma(x) \delta(k - k'). {} \end{array} \end{aligned} $$
(8)

The term w(k′, k) defines a new scattering mechanism whose effect is the production of pair of signed particles. An initial parent particle with sign u evolves on a free-flight trajectory and, according to a generation rate given by the function γ(x), two new signed particles, one positive and one negative, are generated with one momentum state generated with a probability equal to \(V^+_w(x,k)/\gamma (x)\). The main drawback of such technique is the exponential grow of the particle number.

To limit this number, a cancellation procedure must be introduced in such a way, if the total number of particles exceeds a certain bound N canc, then pairs of particles with similar positions and wave vectors, but with opposite signs, are removed from the system. Recently, the previous creation process has been understood in terms of the Markov jump process theory, providing that functionals of the solution of the Wigner equation (1) are expressed in terms of the particle system [15].

Moreover a time-splitting scheme has been introduced in [9] in order to separate the transport (i.e. movement in the position space) and the generation process, as follows

  1. 1.

    Transport step

    All particles (x i(t), k i(t), u i(t)) move according to

    $$\displaystyle \begin{aligned} x_i \rightarrow x_i + \varDelta t \frac{\hbar}{m^{*}}k_i {} \end{aligned} $$
    (9)

    The components u i and k i do not change.

  2. 2.

    Generation step

    According to probabilistic rules (to be determined below), all particles create new particles that are added to the system.

  3. 3.

    Cancellation step

    If the total number of particles exceeds a certain bound,

    $$\displaystyle \begin{aligned} N > N_{canc} {} \end{aligned} $$
    (10)

    then pairs of particles with similar positions and wave-vectors, but with opposite signs,are removed from the system.

In the following, we shall introduce a cutoff c > 0 which assures finiteness of the integrals (6) with respect to the wave vector. The generation step is based on a majorant \(\hat {V}_w(x,k)\) of the Wigner potential (3)

$$\displaystyle \begin{aligned} |V_w(x,k)| \le \hat{V}_w(x,k) \quad \forall x,k {} \end{aligned} $$
(11)

and the creation rate

$$\displaystyle \begin{aligned} \hat{\gamma}(x,k) = \frac{1}{2} \int_{-c}^{c} \hat{V}_w(x,k) \, dk . {} \end{aligned} $$
(12)

The splitting time step Δt is assumed to satisfy

$$\displaystyle \begin{aligned} \varDelta t < \left[ \mbox{sup}_x \hat{\gamma}(x,c) \right]^{-1} . {} \end{aligned} $$
(13)

This is the generation algorithm:

  1. s0.

    For each j-th particle

  2. s1.

    Let be r ∈ U[0, 1]

    $$\displaystyle \begin{aligned} \mbox{if} \quad r < 1 - \hat{\gamma}(x_j , c)\varDelta t {} \end{aligned} $$
    (14)

    do not create anything, next particle GOTO s0.

  3. s2.

    Otherwise generate a random parameter \(\tilde {k}\) uniformly on the interval [−c, c].

  4. s3.

    Let be r ∈ U[0, 1]

    $$\displaystyle \begin{aligned} \mbox{if} \quad r < 1 - \frac{ | V_w(x_j ,\tilde{k}) | } {\hat{V}_w(x_j ,\tilde{k})} {} \end{aligned} $$
    (15)

    do not create anything, next particle GOTO 2.0

  5. s4.

    Otherwise generate a couple of particle

    $$\displaystyle \begin{aligned} (x_j, k_j + \tilde{k}, \tilde{u}) \quad , \quad (x_j, k_j - \tilde{k}, -\tilde{u}) \quad , \quad \tilde{u}= u_j \, \mbox{sign} \left[ \frac{V_w(x_j ,\tilde{k})} {\hat{V}_w(x_j ,\tilde{k})} \right] {} \end{aligned} $$
    (16)

    next particle GOTO s0.

4 The Double Potential Barrier Benchmark

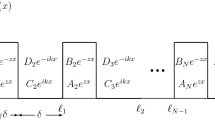
Let us introduce the double barrier, which is symmetric with respect to the y-axis, the height is a (in eV), the centers in ±|d|, and the amplitude b (see Fig. 1). The well potential length is

$$\displaystyle \begin{aligned} b_w = 2 \left(|d| -\frac{b}{2} \right) \quad . {} \end{aligned} $$
(17)
Fig. 1
figure 1

The double barrier

Full size image

In the double barrier case we have:

$$\displaystyle \begin{aligned} \begin{array}{rcl} V_w(x,k) = \frac{4a}{\hbar \pi k} \sin{}(2kx) \, \sin{}(kb) \, \cos{}( 2k |d| ) {} \end{array} \end{aligned} $$
(18)
$$\displaystyle \begin{aligned} \hat{V}_w(x,k) = \frac{4ab}{\hbar \pi} \quad , \quad \hat{\gamma}(x,c) = \frac{4ab}{\hbar \pi} c \quad , \quad \varDelta t < \frac{\hbar \pi}{4ab c} {} \end{aligned} $$
(19)

and we have considered a double barrier with the following parameters:

$$\displaystyle \begin{aligned} b = 2.2 \, \mbox{nm}, \quad |d| = 5.1 \, \mbox{nm}, \quad b_w = 8 \, \mbox{nm}. {} \end{aligned} $$
(20)

If the barrier height a goes to infinity, the Schrödinger equation gives a well known analytic solution (see Appendix) where, the lowest energy eigenstate with l = 1 is

$$\displaystyle \begin{aligned} E_1 = \frac{\pi^2 \hbar^2}{2 m^{*} b_w^2} = 1.8361 \,10^{-2} \mbox{eV} {} \end{aligned} $$
(21)

and the corresponding eigenfunction ψ(x, t) is shown in (35). According to Eq. (4), we have (for the infinite well)

$$\displaystyle \begin{aligned} n(x,t) = |\psi(x,t)|{}^2 = \frac{2 C^2}{b_w} \, \cos^2 \left( \frac{\pi x}{b_w} \right) \, . {} \end{aligned} $$
(22)

The previous solution does not depend on time, consequently if the system is prepared initially in this state, then it will remain in it throughout.

Our goal is to study how the our Wigner MC scheme, for large values of the barrier height, approaches to the Schrödinger one in the case of infinite well.

In particular we want to reproduce the density solution (22) for the lowest energy eigenstate. To achieve that, we have to use the right initial condition for the Wigner equation. Since, for pure state, Schrödinger and Wigner equations are equivalent, we have taken as initial condition the Wigner function corresponding to the Schrödinger one in the lowest energy state [3].

In the x-space we have considered an uniform mesh [−20, 20] (nm) with N x = 200 grid-points; also in the k-space we have an uniform mesh [−7.78, 7.78] (nm−1) with N k = 256. We have chosen absorption boundary conditions, i.e. if a particle is out of the mesh then it is erased. The cutoff has been fixed c =  7.68 nm−1, the initial particle number is N ini = 160,000, the cancellation parameter N canc =  480,000.

We plot in Fig. 2 the density (4) at the simulation times of 20 fsec, obtained with a = 0.3, 0.6, 1.2, 2.4, 4.8 eV, and compared with the solution (22). The penetration into the barrier decreases as the height a increases, while the MC solution approaches to the Schrödinger one.

Fig. 2
figure 2

The particle density (4) versus position a t = 20 fs, for same values of the barrier height a and the corresponding Schrödinger solution for an infinite barrier

Full size image

Due to the limitation on the time step Δt (19), the higher the barrier height a, the smaller the time step will be. Consequently a huge CPU consumption is measured, as shown in Table 1, which limits de facto the convergence of the MC solution to the analytic one. The results presented have been obtained using an AMD Phenom II X6 1090T 3.2 GHz and 8 Gb RAM.

Table 1 CPU and particle number at the final simulation time 20 fs
Full size table

5 Conclusions

The Wigner equation has been solved by using the Signed particle Monte Carlo method, where new pair of particles characterized by a sign are created randomly and added to the system. This creation mechanism has been recently understood in terms of the Markov jump process, producing a class of new stochastic algorithms [9]. One of these algorithms has been implemented and applied to the double potential barrier benchmark, and compared to the corresponding analytic solution of the Schrödinger equation for the infinite well. The results show that the MC data, for large values of the barrier height, converges to the analytic solution of the infinite well, but the accuracy is limited by a huge computational effort.