Dynamic Compartmental Models for Large Multi-objective Landscapes and Performance Estimation

Abstract

Dynamic Compartmental Models are linear models inspired by epidemiology models to study Multi- and Many-Objective Evolutionary Algorithms dynamics. So far they have been tested on small MNK-Landscapes problems with 20 variables and used as a tool for algorithm analysis, algorithm comparison, and algorithm configuration assuming that the Pareto optimal set is known. In this paper, we introduce a new set of features based only on when non-dominated solutions are found in the population, relaxing the assumption that the Pareto optimal set is known in order to use Dynamic Compartment Models on larger problems. We also propose an auxiliary model to estimate the hypervolume from the features of population dynamics that measures the changes of new non-dominated solutions in the population. The new features are tested by studying the population changes on the Adaptive $\epsilon$-Sampling $\epsilon$-Hood while solving 30 instances of a 3 objective, 100 variables MNK-landscape problem. We also discuss the behavior of the auxiliary model and the quality of its hypervolume estimations.

1 Introduction

Dynamic Compartmental Models (DCMs) [8, 9] are linear compartmental models that track population dynamics in Multi- and Many-Objective Evolutionary Algorithm (MOEAs). They are based on epidemiology models, mainly the SIR model [4]. In the SIR model, a population of individuals is broken in groups assigned each to a compartment of the model in accordance to their health status, which changes as time progresses. This is captured by the model equations and parameters. Similarly, the goal of a DCM is to capture the changes of the population focusing on the dominance relationship between individuals. Each group or compartment represents how many are in a particular state of domination. The interaction between compartments and the rates of interaction is captured by the equations that defined the model and its parameters. How membership to a compartment is defined represents a feature on the population, and different sets of features allow to explore the same algorithm, problem, and configuration from other perspectives.

Two and three compartments DCMs have been successfully used to study and explain in detail the dynamics of multi-objective evolutionary algorithms. DCMs do not provide a direct estimation of performance of an algorithm expressed in terms of well known performance estimators such as hypervolume, generational distance, inverse generational distance, and others. To associate dynamics to performance, DCMs require that at least one of the compartments relates to some rate of improvement of the algorithm, from which a known performance metric can be correlated or estimated. Previous works using DCMs have focused on problems where the Pareto optimal set is known and have therefore used features associated to rates of improvement of the algorithm that require knowledge of whether a solution is Pareto optimal or not. Although DCMs on these problems have served to gain knowledge about the working principles of multi- and many-objective evolutionary algorithms, in order to use DCMs on real world scenarios, where the set of Pareto optimal solutions is unknown, new sets of features and ways to estimate measures of performance from features of population dynamics are required.

From this standpoint, in this work, we introduce new features focusing on when non-dominated solutions appear in the population to define the compartments of the model. In particular, we define a three compartments DCM where the population is divided into (1) new non-dominated solutions, (2) non-dominated but not new solutions, and (3) dominated solutions. The goal of these features is to keep track of how many new solutions appear in each generation, which serves to estimate the rate of progress of the algorithm. These features are useful whether the problem is enumerable or not. In addition, we propose an additional model to estimate a performance metric, the hypervolume achieved by an algorithm, from the features of population dynamics, i.e. new non-dominated solutions. An effective way to estimate performance from features of dynamics opens new venues to apply DCMs beyond algorithm analysis and understanding.

The paper is organized as follows. Section 2 describes in more detail the DCMs, the proposed new feature set and how to relate them to performance. Section 3 covers the experimental results to test the new features with the DCMs and the HV model. Section 4 concentrates on the proposed model for estimation of performance, and analyzes it on more configurations. Finally, in Sect. 5 we resume the work done and propose some future directions to expand it.

2 Methodology

2.1 Dynamic Compartmental Models for Multi-objective Evolutionary Algorithms

Dynamic Compartmental Models (DCM) are mathematical models that simulate how individuals in different compartments in a population interact and affect the instantaneous composition of the compartments. Here, the assumptions are that the population can be divided into compartments and that every individual in the same compartment has the same characteristics. The rates of interaction between compartments are known as the parameters of the model.

Fig. 1.

A Three compartment DCM

Linear compartmental models of up to three compartments have been used to study the population dynamics of evolutionary multi-objective algorithms using the Pareto dominance status of the individuals as criteria to define the compartments. Figure 1 illustrates a three compartments DCM, which can be described by the following equations,

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{t+1} &{}= (1-(\alpha + \beta )) x_t + \bar{\alpha } y_t + \bar{\beta } z_t \\ y_{t+1} &{}= \alpha x_t + (1-(\bar{\alpha }+\gamma )) y_t + \bar{\gamma } z_t \\ z_{t+1} &{}= \beta x_t + \gamma y_t + (1-(\bar{\beta }+\bar{\gamma })) z_t \\ P &{}= x_t + y_t + z_t, \end{array}\right. } \end{aligned}$$

(1)

where $x_{t}$, $y_{t}$ and $z_{t}$ are variables associated to the number of individuals in the compartments at time (generation) t and $\alpha$, $\beta$, $\gamma$, $\bar{\alpha }$, $\bar{\beta }$, and $\bar{\gamma }$ are the interaction rates between compartments.

Each compartment size at time $t+1$ depends on its size and the size of all other compartments at time t modified by some constant, i.e a parameter of the model. From the system of Eq.  (1) and its graphical representation on Fig. 1, we see that any change in one compartment will be distributed into the other ones, therefore the total number of individuals remains constant. This models the dynamics of an evolutionary algorithm with a fixed population size throughout the generations. It is important to note that the model tracks changes between compartments, not specific individuals.

The parameter values of the model are estimated (learned) from the data generated by the algorithm which dynamics we want to capture. The selected algorithm is run tracking on each generation the features (compartments sizes) we choose for our model. The output data relevant to these features is used to fit the model’s parameters. Thus, the parameters of the model are linked to a particular algorithm set with a given configuration on a problem instance or a subclass of problems. If the algorithm, its configuration or the problem changes, parameters naturally will change too.

DCMs have been successfully used to study and explain in detail the dynamics of multi- and many-objective evolutionary algorithms, gaining knowledge about the working principles of the various approaches to design these algorithms [8, 9]. DCMs were used, for example, to study how multi- and many-objective evolutionary algorithms are able to continue discovering Pareto optimal solutions once their population is full of them in order to achieve a high resolution of the Pareto optimal set (POS). To answer this question the study was conducted on problems where the POS could be enumerated [9], defining the three compartments so that the population was divided into (1) newly discovered Pareto optimal solutions, (2) non-dominated but not new Pareto optimal solutions, and (3) dominated solutions. The union of the first two compartments is the set of non-dominated solutions in the population. Verifying that a non-dominated solution is also a Pareto optimal solution and that it has been seen by the algorithm for the first time in the current generation allows dividing non-dominated solutions into the two first compartments mentioned above. Of course, this can be done if and only if the POS is known.

As mentioned before, DCMs directly do not estimate the performance of an algorithm in terms of well known and commonly used estimators such as hypervolume, generational distance, inverse generational distance, and others. However, to associate the dynamics to performance is possible to have a feature set where at least one of them can carry information about the rate of improvement of the algorithm, which then can be correlated or used to estimate a more common performance metric. In [8, 9] the first compartment referred above, i.e. the number of new Pareto optimal solutions in the population, provides the rate of discovery of Pareto optimal solutions and gives a rate of improvement of the algorithm. Thus, in these works, this feature was correlated to performance. Namely, it was shown that the accumulation of newly discovered Pareto optimal solutions is highly correlated to the hypervolume. In other words, it is possible to look at this feature to decide with high confidence what algorithm (or algorithm configuration) is better than others.

DCMs can also be used to predict future behavior and performance of the algorithm. That is, running the DCM for additional generations for which the actual algorithm has not been yet run can be estimated with high confidence, for example, whether increasing the fitness evaluation budget for a giving algorithm may translate into improved performance. This is quite relevant to application domains where fitness is computationally expensive, such as simulation-based optimization.

Another important potential use of DCMs is for algorithm configuration and algorithm selection [9]. For example, let us assume we want to configure population size for a given budget of fitness evaluations. A common approach is to run the algorithm several times, each time with a different combination of population size and number of generations. Another alternative is to run the algorithms in a sample of configurations, learn DCMs for each one of them, and infer new models for intermediate configurations by interpolation of the models’ parameters.

Initial explorations of the application of DCMs are promising. However, the above studies have been done on small landscapes and using a feature that requires knowledge of the Pareto optimal set. In order to use DCMs in real-world scenarios, dynamics should relate to performance using features that correlate to a rate of improvement of the algorithm but do not require to know whether a solution is optimal or not.

In the next sections, we introduce a set of features that can be used for such purpose together with a method to estimate performance from one of them.

2.2 The NDNew-NDOld-DOM Feature Set

To explore DCMs in large problems, we define three compartments so that the population is divided into (1) new non-dominated solutions, (2) non-dominated but not new solutions, and (3) dominated solutions. These compartments or features are called for short Non-Dominated New, Non-Dominated Old, and Dominated. A solution is counted as Non-Dominated New at generation t only if it is a non-dominated solution in the population but did not appear in any previous generation from 0 to $t-1$. A solution is counted as Non-Dominated Old at generation t if it is a non-dominated solution and has also appeared in a previous generation. A solution is counted as Dominated at generation t if it is a dominated solution in the population. A more compact explanation can be seen in Table 1. While this set of features does not offer directly a way to measure performance, it still gives an idea of the progress of the search, since we expect to see the number of New Non-Dominated solutions to go down when the algorithm is converging.

It is important to mention that when we count a Non-Dominated solution at generation t, it is non-dominated relative to the population at that generation. It may be that at a future generation that solution becomes dominated. We could maintain an updated list of solutions non-dominated so far and check non-dominated solutions in the current population against it before counting it. However, this could add substantial computational overhead and it is not clear whether this could add any extra value to the feature. As it is defined now, it still serves the purpose of showing us from the algorithm perspective if the search is still moving, i.e. it has not stagnated.

Table 1. Proposed features. $\mathcal {F}_1$: first front containing all the non-dominated solutions. t: current generation. P: whole population including $\mathcal {F}_1$.

2.3 Performance Metrics and Features

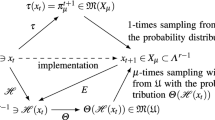
The new features of dynamics do not provide a direct measure of the algorithm performance from the model. One solution to this issue is creating an auxiliary model that takes in some of the features and an initial evaluation of a performance metric to estimate this value at any generation. In this work, we estimate the hypervolume indicator (HV) [11], more specifically the hypervolume calculated over the Non-Dominated set of all solutions in the population at generation t and previous ones. The reference point is set to (0,0,0). Figure 2 illustrates the model learning process of population dynamics and performance features from some sampled configurations. We try a model of the form $HV_{t+1} = HV_t + \mu \times \textit{some feature } / t$.

Fig. 2.

Scheme of the model learning process of population dynamics and performance features from some sampled configurations.

We used Grammatical Evolution, a tool from Genetic Programming, that searches for expressions instead of programs. To evaluate which expression gives the best model, we use the mean square error between the model and our reference data, namely the number of found NDNew, NDOld and DOM solutions in generation t and the corresponding hypervolume HV for generation $t+1$. The first step is defining a grammar than can derive in the type of expression we need, in this case, $\mu \times \textit{some feature}/t$, which we will refer to as $\varDelta \text {HV}_t$, and is presented in Fig. 3.

Fig. 3.

BNF Grammar used to search for an expression that relates the hypervolume to the features.

This grammar can generate expressions such as $0.833 \times \text {NDNew}/{\text {NDOld}}$ or $-5 \times \text {NDOld} \times t$. To implement this part we used gramEvol [10] a library available in the R language. After some tries with this library the suggested expression for the model was:

$$\begin{aligned} \text {HV}_{t+1} = \text {HV}_{t} + \frac{\mu \times \text {NDNew}_t}{t+1}, \end{aligned}$$

(2)

The model can be interpreted as the HV will grow on generation $t+1$ proportionally to how many New Non-Dominated solutions were found at generation t times a constant $\mu$ and inversely to the next generation number. This makes sense as the impact of finding solutions at the beginning will surely make the hypervolume value jump, while at the end we can think that these newly found solutions probably fill in gaps having very little effect.

3 Experimental Results

3.1 Test Problem and Experiment Settings

Testing these new features requires generating some data by running an MOEA with different configurations on a given problem. The MOEA we selected is the Adaptive $\epsilon$-Sampling $\epsilon$-Hood (A$\epsilon$S$\epsilon$H), a Many-objective Optimization Evolutionary Algorithm that can also handle Multi-objective problems. Its approach is Pareto dominance relaxation in the form of $\epsilon$-dominance to determine which solutions are kept and how parents are selected for the next generation [1]. The crossover is two-point with rate $pc=1$, bit flip mutation with rate $pm = 1/N$, the reference neighborhood size is set to 20 individuals and the $\epsilon$-dominance function is additive ($f' = f + \epsilon$).

The chosen problem is the combinatorial multi-objective problem generator MNK-Landscapes [2]. Its parameters are the number of objectives M, number of variables N and K, a value that allows setting the ruggedness by determining the number of epistatic interactions between variables. This is, it determines how much other variables affect the fitness contribution of a given variable. In MNK-Landscapes terms, an M = 3, N = 100 and K = 5 problem is a 3 objective, 100 variables one where each variable fitness contribution will be affected by other 5 variables values defined as part of the problem. We generated 30 landscapes or sub-classes of an M = 3, N = 100 and K = 5 problem, each time the epistatic interactions are determined at random when the problem is created.

The data for the models is then generated by running A$\epsilon$S$\epsilon$H on each of the 30 landscapes, with different configurations, i.e, population sizes ranging from 3000 to 10500, with increments of 2500. On each configuration, the maximum number of Function Evaluations (FE) allowed was of 600000, which determined the maximum number of generations to run the algorithm (FE = Population Size $\times$ $t_{max}$). In this section, results will be shown for models that only have seen data until 400000 FE, and in the next one, we will present results with other FE limits.

Lastly, when we talk about the models’ estimation we want to emphasize that for our DCMs we give only one measured value, the ones obtained from generation 0, i.e. the initial population. Here is also where we measure the first hypervolume value used to start the HV model. From there, both models use the estimation they generated for generation t to calculate the following one in $t+1$, and so on, until the required number of generations $t_{max}$ is met.

3.2 Fitting of the Models

The fitting process, was done with the Levenberg-Marquardt Non-Linear Least Squares algorithm [6, 7] using the R language implementation [3]. The input for this process is the feature data from the algorithms and the system of equations (1), obtaining the parameters for some configurations with different population sizes, (3000, 5500, 8000, 10500) and varying the FE limits, (300000, 400000, 500000, 600000).

We took some considerations while doing the fitting process. Instead of using the feature data from each landscape’s data, we take the average value of the features at each generation, including the HV value. This, at least for the DCM had a more significant impact on producing better estimations.

Cross-validation was also introduced, so the obtained parameters are not a product of over-fitting to our generated data and would generalize better in the presence of new and unseen data. We choose k-fold cross-validation and apply it during DCMs and HV model fitting process. In k-fold cross-validation, the dataset is split into k subsets of equal size, each subset is used only once as a test set and $k-1$ times as part of the training set. For our data, we have 30 runs of the algorithm, corresponding each one to a different landscape. To ensure an 80/20 split between training and testing data, we select $k = 5$, a common recommendation for this method as suggested in [5]. So each fold is composed of one subset of 6 landscapes worth of test data, and the remaining 4 subsets, provide 24 landscapes worth of training data. The score obtained on each set is measured by the goodness of fit or $R^2$, a value between 0 and 1 that indicates how much of the variance present in the data is explained by the model.

Under cross-validation, the fitting process per configuration is done only with the data from the training set, and the resulting parameters estimation ability is measured on the test set, repeated for each fold. We report in Table 2 the average $R^2$ of the 5 scores obtained for the training and test datasets for all population sizes and considering only 400000 FE available. Since at the end of the process we also have 5 sets of parameters, we take the average and keep the result as the best parameters found for that configuration and number of FE.

From the table, we can see that the $R^2$ is overall higher than 0.64 for the features NDOld, DOM and HV for both training and testing sets, while the NDNew feature has a lower score when compared to the other features. To understand better this situation, we can refer to Figs. 4, 5, 6 and 7 that show the NDNew-NDOld-DOM feature measured values and the DCM estimation for all the considered population sizes. In these plots, we are using the obtained best parameters and creating the estimations considering all available landscapes.

Table 2. $R^2$ values obtaining during the model training and testing. Obtained doing k-fold cross-validation with $k=5$. Considering only 400000 FE.

From a first look at the figures, we can see that the model estimation (red points), goes through the middle of the measured data (black points) since the fitting was done on the average values for the features. Not doing so, produced overestimations after the hump in the feature NDNew graph, which translated into a poor HV estimation as the other model depends on this value. The lower $R^2$ in this feature, when compared to the other two, could be attributed to the higher overall variance present as appreciated in the figure. An understandable situation, since the number of newly found non-dominated solutions, can change very quickly.

It is also interesting to notice how this simple model can adapt to different configurations, for larger population sizes the number of generations diminishes and the fitted model can keep up with the different rates of change in each case.

Fig. 4.

Non-Dominated New, Non-Dominated Old and Dominated Solutions DCM’s estimation vs Measured data for a configuration with Pop. Size 3000 and 400000 FE.

Fig. 5.

Non-Dominated New, Non-Dominated Old and Dominated Solutions DCM’s estimation vs Measured data for a configuration with Pop. Size 5500 and 400000 FE.

Fig. 6.

Non-Dominated New, Non-Dominated Old and Dominated Solutions DCM’s estimation vs Measured data for a configuration with Pop. Size 8000 and 400000 FE.

Now we move to the HV model results, in Fig. 8 we show the estimation against measured values for all sampled population sizes. As can be seen, the model seems to follow the change of the hypervolume until a certain point from which there is a tendency to overestimate in all configurations. Looking aside from the overestimation in the last few generations, it seems to follow the overall tendency of the hypervolume, which growth seems correlated to the NDNew feature.

Fig. 7.

Non-Dominated New, Non-Dominated Old and Dominated Solutions DCM’s estimation vs Measured data for a configuration with Pop. Size 10500 and 400000 FE.

4 Discussion

In the last section, we discussed how to create and fit both, the Dynamic Compartmental Model and the HV model. Here we want to explore how well they can to follow the trend in the performance data. We will look at the estimated accumulated HV at the end of a run for different population sizes and the maximum number of Function Evaluations allowed. As mentioned before, the hypervolume at each generation is calculated over all non-dominated solutions found until that generation t, therefore we refer to it as accumulated HV. In Figs. 9, 10, 11 and 12 we have two box plots per population size, the one in red represents the measured data (M) for all 30 landscapes while the one in blue is the HV model estimation (E) for the same 30 landscapes with each figure showing results considering 300000, 400000, 500000 and 600000 FE.

Looking at the big picture, we notice that for every variation of the FE the measured data indicates a downward trend. That is, even though we keep adding more FE so the largest population sizes could benefit with more time to get a better convergence, this does not translate into a better overall final HV. Thus, in this particular problem, it seems that a population size of 3000 is enough to ensure a good final hypervolume. If we look now at the model estimation, we notice a clear overestimation for all population sizes, though it maintains the ordering, replicating the trend seen in the data. This is particularly important if we want to use the models for any analysis and to distinguish which configurations perform better than others.

Fig. 8.

HV model estimation vs Measured data for sampled configurations with Pop. Size [3000,5500,8000,10500] and 400000 FE.

If we focus on the plot of the NDNew feature on Figs. 4, 5, 6 and 7, we see that our DCM learned the mean of the data and this still produces overestimation as can be checked in the plot against the measured data in Fig. 8. In fact, for all the variations in FE, the DCM keeps going through the mean and still ends in an overestimation when used by our current HV model.

From the formulation, it seems that we are on the right track and there is a connection between newly discovered solutions appearance rate and the growth of the HV, but our parameter $\mu$, or even the current generation number do not seem enough to keep this estimation closer to the measured values. In particular, it is important to tell the model that the weight of newly found solutions varies depending on what stage we are in the algorithm’s run. In the beginning, it is not strange to see the HV grow quicker with each newly found solution, while by the end we expect these solutions to fill gaps on a set of non-dominated solutions that form a good approximation set for this problem.

Even with the current formulation, it is still interesting to see how a simple feature such as the number of newly discovered non-dominated solutions per generation can carry enough information that can be translated into what kind of trend we can expect of a performance metric such as the hypervolume. More so if we remember that for all the estimations done with the models, they only start with one piece of measured data, and from there is purely the captured dynamics and behavior of the algorithm that guides the process.

Fig. 9.

Comparison between the final HV for all landscapes on 300000 FE.

Fig. 10.

Comparison between the final HV for all landscapes on 400000 FE.

Fig. 11.

Comparison between the final HV for all landscapes on 500000 FE.

Fig. 12.

Comparison between the final HV for all landscapes on 600000 FE.

5 Conclusions and Future Work

In this work we proposed a new set of features that allows Dynamic Compartmental Models to be used on larger multi-objective problems where the Pareto optimal set is not known or cannot be obtained through enumeration, removing the assumption that the Pareto optimal set is known made by previously proposed feature sets. Parting from the knowledge that features that capture the rate of improvement of an algorithm can be correlated to a performance metric, we presented and tested a possible auxiliary model that can estimate and capture the general trend of the hypervolume metric. We designed a simple HV model that can estimate, with good results, the value of the HV at the next generation from the HV value at the current generation, the number of newly found non-dominated solutions, the current generation and a parameter.

We tested DCM and HV models on several instances of the same class of problem, and showed in terms of goodness of fit score and visually the estimations produced by them. We verified that the DCM with the new set of features successfully learns the mean of the data, similarly to when it is used with other sets of features reported in the past. On the other hand, the HV model had a tendency for overestimation but still keeping the ordering when applied on different configurations. This allows selecting among them just by looking at the values of HV estimated by the model.

For future work, we want to revise the formulation to explore control mechanisms to discriminate between the algorithm’s initial and final stages, so the HV estimation can be smoother and closer to the measured values. We also plan to introduce interpolation of the parameters and use it for selecting configurations, exploiting the relationship between a set of parameters and the configuration and algorithm from which it was obtained.