Keywords

1 Introduction

CP is an original method, which can complement the predictions of conventional machine learning algorithms by measuring their confidence [4] in order to help to determine how accurate the prediction is, and to suggest good decision-making process consequently. References [4] and [5] proposed ICP to solve the computational ineffectiveness problem of CP.

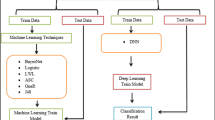
This work uses a regression CP [1] built on neural networks (NNs). An adjusted CP was needed so as to apply CP to NNs, which is called generalized regression neural network conformal prediction (GRNN-CP). In the case of regression, CPs give a sufficient level of confidence compared to conventional techniques We used the National Cancer Institute (NCI) at the National Institutes of Health (NIH). As the largest publicly available cancer dataset [3], this database provides de-identified information on cancer statistics of the United States population, thus facilitating large-scale outcome analysis. We apply machine learning techniques to this dataset to analyze data specific to lung cancer, with the goal of evaluating the predictive power of these techniques. Lung cancer was chosen as it ranks as a leading cause of cancer-related death, with dismal 5-year survival rates. The goal of identifying survivability given a specific medical diagnosis is of great importance in improving care and providing information to patients and clinicians. Given a dataset of lung cancer patients with certain information such as age, tumor size, Radiation, and Surgery applied, the question is whether patient survival can be computationally predicted with any accuracy. Although survival time analysis may be considered clinically relevant to evaluate patient prognosis, doctors have struggled to estimate the diagnosis of lung cancer patients. In a recent study, physician consultants predicted a survival time median of 25.7 months, while physician registrars and residents predicted survival times of 21.4 and 21.5 months, respectively, for patients on average with 11.7 months actual survival [6]. The study found that only ∼60% of patients whose physicians estimated survival time >3 months survived this long. Another study found that physicians correctly predicted survival time to the month 10% of the time, to 3 months 59% of the time, and to 4 months 71% of the time, and tended to overestimate short term survival times but underestimate long term survival times [7, 10, 11]. Applying a correlational methodology via machine learning to predict survivability could help to improve such predictions.

In this study, patients diagnosed with lung cancer during the years 2006–2011 were selected in order to be able to predict their survival time. Some supervised learning methods were employed to classify patients based on survival time as a function of crucial attributes and, thus, help illustrate the predictive value of the several methods. The dataset in this study emphasizes on dimensions available at or near the time of diagnosis, which represents a more positive set of survival predictors

1.1 Producing Confidence Information

Machine learning may be used to produce accepted confidence of information, e.g., the Bayesian framework and ‘probably approximately correct’ (PAC theory) [5, 8]. This experiment will focus on the robustness of prediction intervals for a future independent observation to examine the dilemma of constructing prediction intervals in a regression phase. An improvement of a prediction interval over a point estimate is that it takes into account the variation of the future observation around the point estimate [6].

An expected failure might occur for the confidence levels to attribute the percentage of expected errors. The next section explains the framework then investigates, via a simulation study, the performance of these prediction intervals in terms of the prediction intervals robustness and their possible uses

1.2 The CP Framework

In this section, we describe the idea behind CP, and a more detailed description is provided by [1]. The interest here is in predicting the label of an example xl + g, based on a set of training examples \( \{ (x1,y1), \ldots ,(xl,yl)\} \), where each xi ∈ qd is the vector of attributes: for example, i and yi ∈ R is the label of that example. The only assumption made is that all (xi, yi), \( i = 1,2, \ldots ,n \) have been produced from the probability distribution. The main aim of CP [6, 2] is to presume that each probable label \( \hat{y} \) is presented in the form of the example xl + g, to check the possibility to generate the prediction rule:

$$ \left\{ {\left( {x1,y1} \right), \ldots ,\left( {xl,yl} \right),\left( {xl + g,\hat{y}} \right)} \right\} $$
(1)

This rule maps every input pattern xi to a predicted label yi:

$$ D\left\{ {\left( {x1,y1} \right), \ldots ,\left( {xl,yl} \right),\left( {xl + g,\hat{y}} \right)} \right\} $$
(2)

The nonconformity total of every set (xi, yi): \( y = 1, \ldots ,l,l + g \) later estimated as the degree of contention between the prediction and the actual label yi; it may be noted that, in the case of the pair (xl + g, y), the actual label is replaced by the assumed label y. The function used for measuring this degree of contention is referred to as the nonconformity measure of the CP. A change in the assumed label \( {\hat{\text{y}}} \) affects all predictions. Following this, the nonconformity score xl + g is compared to the nonconformity results of remaining examples to ascertain how rare the pair (xl + g, y) is, regarding the nonconformity measure used by the following function:

$$ \hat{y}i = D\left\{ {x1,y1), \ldots ,\left( {xl,yl} \right),\left( {xl + g,\hat{y}} \right)} \right\}) $$
(3)

The main weakness of the prime CP technique is that, given its inspirational quality, all its computations require repeating each new test example for every assumed label. This makes it computationally incompetent. CP is tightly efficient [6], and maybe merged with any traditional regression technique.

CP splits the training set (of size l) into two smaller sets; the convenient training set with m < l examples, and the calibration set with q: = l − m examples. Then, it uses the convenient training set for training, and the calibration set for calculating the probability distribution of each possible label y for (x1, y1), . . ., (xm, ym) to generate the prediction rule, where the nonconformity of each example in the calibration set is i = 1, …, q, and the confidence level to be calculated as 1 − o which provide the minimum and maximum \( \hat{y} \)

CP algorithm requires a critical parameter that is the number q, of training examples to be allocated to the calibration set, while the nonconformity scores used by the CP to create its prediction intervals. This number is critical and should only relate to a small portion of the training set, where removing these examples causes a significant decrease in the predictive capability of the NN, and accordingly, to broader prediction intervals.

1.3 GRNN-CP Framework

The GRNN created by [5] is an estimation method for function regression that has been applied to engineering and science applications. GRNN is useful since it could employ a few training samples to converge to the underlying function of the data available. GRNN also is a useful tool to perform predictions and comparisons of system performance in practice. The standard GRNN in Fig. 1 can be used with a rapid training procedure due to the single training parameter σ. Finally, it does not require an exact topology definition such as the MLP, or basis function centers and weights, such as the RBF.

Fig. 1.
figure 1

(adapted from [9])

General GRNN architecture

Full size image

Employing CP with GRNN has the advantage of enabling much better control of the smoothness of the approximation so that the regression surface adapts to the local properties of the occurring in that area concedes a predicted output value data. In order to use CP in conjunction with some traditional algorithms, a nonconformity measure first needs to be defined.

As previously discussed, a nonconformity measure is a function measuring the contention between the actual label yi and prediction yi’ produced by the prediction rule described by [6] of the underlying algorithm for the example xi. Regression meanwhile, can be readily defined as the absolute difference Between the two. This section describes the GRNN in CP shown in (4)

$$ {\text{D}}({\text{x}},{\text{x}}) = \sum\nolimits_{{}}^{\text{P}} {({\text{x}} - {\text{x}}/\upsigma)^{2} } $$
(4)

where yi is the ith case actual output value, D(x, xi) is calculated from (5), and n is the total number of cases in the dataset j = 1

$$ {\text{D}}({\text{x}},{\text{x}}) = \sum\nolimits_{{}}^{\text{P}} {({\text{x}} - {\text{x}}/\upsigma)^{2} } $$
(5)

(GRNN CP) algorithm, and defines a normalized nonconformity measure, which has the effect of producing tighter prediction intervals by taking into account the expected accuracy of GRNN.

The GRNN predicts continuous outputs. GRNN nodes require two main functions to calculate the difference between all sets of input pattern vectors and estimate the probability density function of the input variables. Euclidean distance is used to calculate the difference between input vectors between data values in attribute space. Weighting the calculated distance of any point by the probability of other points, where x is the input vector, xi is the ith case vector, xj is the jth data value in the input vector, xij is the jth data value in the ith case vector, and σj is the smoothing factor (Parzen’s window) for the jth variable [6]. The error measurement of the mean square error (MSE) used in this work. The MSE measures the average of the square amount by which the estimator differs from the quantity to be estimated. While finding the error, the calculation mentioned earlier will frequently be running with different smoothing factors (sigmas) [8]. Training stops when either a threshold minimum square error value reached, or the test set square error concluded. Since the aim is to produce a level of confidence information, we employ GRNN here to complement predictions with probabilistic texture. The purpose of the global parameter σ is to regulate the smoothness of the regression surface. However, as discussed previously, because the data density can vary in different regions, different values of σ may be needed for different patterns xi. Allocating an individual σ i for each ith pattern in (5) and combining with (6) produces the standard GRNN as follows:

The smoothness parameter was arbitrarily chosen to σ = 0.1. As explained earlier in Sect. 3, CP splits the training set \( \left\{ {\left( {x1,y1} \right), \ldots ,\left( {xl,yl} \right)} \right\} \) into two subsets: the convenient training set: \( \left\{ {\left( {x1,y1} \right), \ldots ,\left( {xm,ym} \right)} \right\} \), and the calibration set:

$$ \left\{ {\left( {xm + 1,ym + 1} \right), \ldots ,\left( {xm + q,ym + q} \right)} \right\}. $$
$$ \upalpha{\text{i}} = \left| {{\text{yi}} - {\hat{\text{y}}\text{i}}} \right| $$
(6)

The GRNN-CP continues as follows:

Sort the nonconformity scores in descending order achieving the following order

$$ \upalpha\left( {{\text{m}} + 1} \right), \ldots ,\upalpha\left( {{\text{m}} + {\text{q}}} \right) $$
(7)

For each new test example \( xl + g \): supply the input pattern \( xl + g \) to the trained GRNN to get the prediction \( \hat{y}l + g \) and output the prediction interval

$$ \left( {{\hat{\text{y}}\text{l}} + {\text{g}} -\upalpha\left( {{\text{m}} + {\text{s}}} \right),{\hat{\text{y}}\text{l}} + {\text{g}} +\upalpha\left( {{\text{m}} + {\text{s}}} \right)} \right) $$
(8)

where \( {\text{s}} = {\text{o}}\left( {{\text{q}} + 1} \right) \).

2 Experimental Evaluation

The suggested approach has been examined on the NCI [9] dataset as Table 1 shows, dataset contains 683 instances with nine integers valued attributes for each instance. Prior to conducting the experiments in this section, datasets were normalized to the range between [−1, 1]. A random split has been conducted into k folds, and the trials were repeated k epochs, each using one k fold was tested, and the other k − 1 folds to be the training set. Trial and error decided the number of hidden neurons, through a fold cross-validation process, with the GRNN predictor on stochastic sequences, which were different from those that evaluated the GRNN- CP. The GRNN was applied to both calibration and test samples.

Fig. 2.
figure 2

Survival rate prediction with GRNN

Full size image
Table 1. Data attributes. AJCC [9]:
Full size table

The performance of the point predictions of the method used in this section, comparing its predictions to the estimated values, can estimate a model trained on the training set. These values are determined by periodically adjusted various model parameters. The fulfillment of the model was evaluated in terms of its root mean squared error (RMSE), see Fig. 2.

Measures, since we would like to have as many precise predictions as possible, given high confidence levels. The validation data across the Age, Stage, Grade, and Tumor Size groupings. Each frame has multiple lines showing the decrease in survival probability for each value, e.g., Stage, etc. The bulk of the curves is below the 50% survivability rate.

Since 50% of the validation patients survive less than 15 months, the standard deviation of residuals is higher than the survival time of half the population; any guess ∼15 months would have a similar result. Most of this deviation originates from the most extended surviving patients, which turned out to be the most difficult to predict. In contrast, the RMSE for patients in the validation set with survival time ≤35 months, compared to the ensemble prediction, is 11 months.

The comparison of the results to those in previous work or to clinical estimates is non-trivial. Much of the previous work differs from the approach here primarily through logistic regression into categorical survival times. 81% of those the model predicted results to live longer than 3 months.

The RMSE value is not the only factor to consider, however, favorable RMSE value, does not certainly monitor that RMSE correlates to relevance. The resulted values show that the prediction intervals produced by the method developed in this chapter are quite tight. The median widths obtained using nonconformity measures are 76.4% and 49.2% of the label range of the two datasets correspondingly, while the best widths achieved using the nonconformity degree are 72.5%, and 42.1% of the label range.

3 Conclusion

A new prediction system has been constructed in this paper. The proposed algorithm is based on using CP to find the most reliable prediction regressions using GRNN, to achieve low errors and more reliable predictions as the results show. The tests performed on the proposed training algorithm show that the right level of accuracy may be achieved when compared to other models.

A moderately considerable correlation was recognized between the measured and predicted values using the hybrid GRNN-CP method. The proposed algorithm produces prediction intervals to achieve a fitting confidence level. In terms of point predictions, the performed correlation coefficient between the predicted and the actual values was convenient; For example, 89% confidence level covers 21.5% of the data, while for the 91% confidence level, it covers 16.9%. It is worth mentioning that the prediction intervals produced by the proposed method are not only well-calibrated, and therefore highly stable, but they are also tight enough to be useful in patients’ trials. Besides, GRNN-CP made progress in terms of prediction interval tightness over the average regression measure, but it still could be developed by reaching more tightness when it comes to prediction regression. Also, other regression methods could be implemented and examined with CP, taking into attention that adding extended datasets with more records could enhance prediction confidence. The models excel when dealing with low to moderate survival time instances, which is the large majority of the data, although there were challenges with both the data and the models, such as the non-linearity of outcomes. As the models struggle to predict patient survival time exceeding 35+ months, logistic regression may be preferred. The cause could be having too many less weighty criteria or too few rules, or that the inexperienced volume of data is needed. Moreover, the more complex models may be insignificantly more precise than the linear regression but maybe more difficult to decipher. Whether or not the increment in performance is worth the extended complexity should be investigated in future.

Future work could also reassess the data optimization and inputs.