Surfaces

Abstract

This chapter contains a partial classification of real algebraic surfaces. Some of the results presented here are classical, others are more recent: we have tried to provide a panorama without attempting to be exhaustive, the selection criteria being the author’s personal preferences. This chapter provides a review of the geometry of real and complex surfaces: our leitmotif is an attempt to describe as far as possible the topological types and deformation classes of real algebraic surfaces, and whether each family of surfaces thus described contains any totally algebraic elements.

This chapter contains a partial classification of real algebraic surfaces. Some of the results presented here are classical, others are more recent: we have tried to provide a panorama without attempting to be exhaustive, the selection criteria being the author’s personal preferences. This chapter provides a review of the geometry of real and complex surfaces: our leitmotif is an attempt to describe as far as possible the topological types and deformation classes of real algebraic surfaces, and whether each family of surfaces thus described contains any totally algebraic elements.

In an ideal world we would find, as for algebraically closed base fields, a discrete invariant (i.e. a multi-integer) classifying the possible topological types of real varieties, plus, for each value attained by this discrete invariant, a continuous subinvariant, called a moduli space.¹ A perfect classification would establish a bijection between irreducible moduli spaces and possible values of the multi-integral invariant.

The first natural integral invariant is the dimension. In dimension 1 the topological classification, established by Klein, was described in Section 3.5: we now review it as motivation for higher dimensional theory. Any non singular projective $\mathbb {R}$-curve $(X,{\sigma })$ is associated to a triplet of integers (g, s, a) where $g:=g(X)$ is the genus of the orientable compact surface X, $s:=s(X,{\sigma })$ is the number of connected components of $X(\mathbb {R})$ and $a:=a(X,{\sigma })$ is the binary invariant determined by $a:=2-\#\pi _0(X\setminus ~X(\mathbb {R}))$. These invariants must satisfy the following conditions.

• 1. If $a=0$—i.e., if the curve is separating (Definition 3.5.1) then $1\leqslant s\leqslant g+1$ and $g-s\equiv 1 \mod 2$.

• 2. If $a=1$ then $0\leqslant s\leqslant g$.

We can give a discrete topological classification of $\mathbb {R}$-curves as follows: for any triplet of integers² (g, s, a), $a\in \{0,1\}$, satisfying the above conditions, there is a non singular projective $\mathbb {R}$-curve $(X,{\sigma })$ realising it, or in other words such that $g(X)=g$, $s(X,{\sigma })=s$ and $a(X,{\sigma })=a$. A refined topological classification of $\mathbb {R}$-curves follows because two $\mathbb {R}$-curves $(X,{\sigma })$ and $(Y,\tau )$ are deformation equivalent if and only if they have the same triplets: $(g(X),s(X),a(X))=(g(Y),s(Y),a(Y))$. See [Gab00] for more details.

From dimension 2 onwards it frequently becomes difficult to give such a precise classification, even for special classes of surfaces. We generally start our investigations by classifying real loci up to homeomorphism, as in Section 4.2. Even when we manage to identify a suitable multi-integer for the classification of a particular type of surface and endow the corresponding moduli space with a natural structure, it is not usually clear whether the number of irreducible components of this moduli space is finite. When it is finite, it is often difficult to calculate the number of its irreducible or connected components.

In this chapter we will list

• 1. All known classifications of real loci of $\mathbb {R}$-surfaces.

• 2. All known classifications of $\mathbb {R}$-surfaces up to isomorphism.

• 3. The cases in which the “quasi-simplicity” problem- a real version of the Def$=$Diff problem, see Question 4.3.29—is solved.

FormalPara Example 4.0.1

In this chapter we will study various “classes” of $\mathbb {R}$-surfaces: the word “class” is deliberately vague. For example, we will classify topological types of

• Geometrically rational $\mathbb {R}$-surfaces (Definition 4.4.1): the “class” is then a $\mathbb {C}$-birational equivalence class;

• Rational $\mathbb {R}$-surfaces (Definition 4.4.1): the “class” is then an $\mathbb {R}$-birational equivalence class;

• Real Enriques surfaces, (Definition 4.5.13) resp. real K3 surfaces (Definition 4.5.3): in this case we consider that $\mathbb {R}$-surfaces $(X,{\sigma })$ and $(Y,\tau )$ belong to the same class if and only if the complex surfaces X and Y belong to the unique irreducible family of complex deformations (Definition 4.3.25) of Enriques surfaces, resp. K3 surfaces;

• Real elliptic surfaces (Definition 4.6.1): the $\mathbb {R}$-surfaces $(X,{\sigma })$ and $(Y,\tau )$ belong to the same “class” if the complex surfaces X and Y belong to one of the irreducible families (of which there are an infinite number) of complex deformations of elliptic surfaces.

• Real Jacobian elliptic surfaces of irregularity zero and fixed holomorphic Euler characteristic: in this case the “class” is once again a unique irreducible family of complex Jacobian elliptic surfaces.

4.1 Curves and Divisors on Complex Surfaces

Section 2.6 of Chapter 2 deals with divisors on varieties of arbitrary dimension. Recall in particular that on a non singular irreducible complex variety X there is a one-to-one correspondance between Cartier divisors and Weil divisors and the linear equivalence groups $\mathrm{{Cl}}(X)$ and ${\text {CaCl}}(X)$ are isomorphic. To any divisor D on X represented by $(U_i,f_i)_i$ we associate a line bundle $\mathcal {O}_X(D)$ defined by $\mathcal {O}_X(D)|_{U_i}=f_i^{-1}\mathcal {O}_X|_{U_i}$ as in Definition 2.6.11. If the variety X is quasi-projective and non singular then the map $D\mapsto \mathcal {O}_X(D)$ induces an isomorphism

$$ \mathrm{{Cl}}(X)\simeq \mathrm{{Pic}}(X)\;, $$

as in Corollary 2.6.17.

On a surface, prime divisors are just irreducible curves and divisors are linear combinations of irreducible curves with integral coefficients. When this linear combination has positive coefficients the divisor is said to be effective. Many authors consider that a curve on a surface is simply an effective divisor on this surface: this recalls our plane curves of Section 1.6 which were allowed to be reducible  or non-reduced. Recall that as in Definition 2.6.26 the canonical divisor $K_X$ of a complex surface X is a³ divisor associated to the canonical bundle $\mathcal {K}_X=\det \Omega _X$. In particular, we have that $\mathcal {O}_X(K_X)=\bigwedge ^2\Omega _X=\Omega _X^2$. On an $\mathbb {R}$-surface $(X,{\sigma })$ the canonical bundle is an $\mathbb {R}$-bundle, ${{}^{\sigma }}\mathcal {K}_X=\mathcal {K}_X$. Recall that by the Cartan–Serre theorem D.1.3 the $\mathbb {C}$-vector spaces $H^i(X,\mathcal {F})$ of the cohomology of a coherent sheaf $\mathcal {F}$ are finite dimensional.

Definition 4.1.1

Let X be  a non singular complex projective surface, or more generally a compact Kähler surface.

• 1. The geometric genus of X is defined to be $p_g(X) :=\dim H^2(X,\mathcal {O}_X)$.

• 2. The irregularity of X is defined to be $q(X):=\dim H^1(X,\mathcal {O}_X)$.

• 3. The holomorphic Euler characteristic of X is defined to be

  $$ \chi (\mathcal {O}_X)=1-q(X)+p_g(X)\;. $$

• 4. The Hodge numbers of X are defined by $h^{a,b}(X):=\dim H^{b}(X,\Omega _X^a)$.

Proposition 4.1.2

Let X be a compact Kähler surface. We have the following identities.

• 1. $p_g(X)=\dim H^0(X,\mathcal {K}_X)=h^{2,0}(X)=h^{0,2}(X)$;

• 2. $q(X)=h^{1,0}(X)=h^{0,1}(X)=h^{3,0}(X)=h^{0,3}(X)$.

Proof

We refer to Appendix D for the proofs. By Hodge symmetry we have that $h^{p,q}=h^{q,p}$. As $H^0(X,\mathcal {K}_X)=H^{0}(X,\Omega _X^2)$ we have that $h^{2,0}(X)=\dim H^0(X,\mathcal {K}_X)$. We could also have used Serre duality, which gives us $H^2(X,\mathcal {O}_X)=H^0(X,\mathcal {K}_X)$. We complete the proof using Poincaré duality with complex coefficients which gives us $b_k=b_{4-k}$. As this duality is compatible with the Hodge decomposition we get that $h^{p,q}=h^{2-p,2-q}$.    $\square$

Definition 4.1.3

Let X be a  non singular irreducible complex projective surface. For any $m\geqslant 1$ the number $P_m(X) :=\dim H^0(X,\mathcal {K}_X^{\otimes m})$ is called the mth plurigenus of X: in particular, $P_1(X)=p_g(X)$. The canonical dimension ${\kappa }(X)$, also called the Kodaira dimension, is defined to be the Iitaka dimension of the canonical divisor

$$ {\kappa }(X) :=\left\{ \begin{array}{cc} -\infty &{}\text { if } P_m(X)=0 \text { for any } m\geqslant 1\;;\\ k \geqslant 0 &{}\text { the smallest integer such that the sequence } \bigl \{\frac{P_m(X)}{m^k}\bigr \}_m \text { is bounded.}\\ \end{array} \right. $$

If $\varphi _{mK}$ denotes the rational map from X to a projective space associated to the linear system |mK| then ${\kappa }(X)$ is the maximal dimension of the images $\varphi _{mK}(X)$ for $m\geqslant 1$.

It turns out that the Kodaira dimension can be defined for any complex compact analytic variety. For a surface X, ${\kappa }(X)$ can be $-\infty , 0,1$ or 2—see Definition D.4.8, Proposition D.4.9 and Remark D.4.10. In what follows, we will consider each possible Kodaira dimensions in turn.

Recall that a projective variety is said to be of general type if and only if its canonical bundle is big, or equivalently if ${\kappa }(X)=\dim X$. See Definitions 2.6.22 and 2.6.29 for more details.

Definition 4.1.4

A complex  projective surface X (resp. a projective $\mathbb {R}$-surface $(X,{\sigma })$) is said to be of general type if ${\kappa }(X)=2$ and of special type if ${\kappa }(X)<2$.

Remark 4.1.5

The Kodaira dimension of a scheme is invariant under base change so for any projective $\mathbb {R}$-scheme X we have that ${\kappa }(X)={\kappa }(X\times _{{\text {Spec}}\mathbb {R}} {\text {Spec}}\mathbb {C})$.

4.1.1 Intersection Form

The free $\mathbb {Z}$-module ${\text {Div}}(X)$ generated by curves on a non singular projective surface X has a symmetric bilinear form endowing $\mathrm{{Cl}}(X)$ with a quadratic module structure.

We start by generalising Definition 1.6.11 of the intersection multiplicity of two plane curves in $\mathbb {P}^2(\mathbb {C})$ to curves in an arbitrary non singular surface.

Definition 4.1.6

Let X be  a non singular complex quasi-projective variety, let $C_1$ and $C_2$ be two distinct irreducible curves in X and let P be a point in X. If $P\in C_1\cap C_2$ and $f_i$ is an equation for $C_i$ ($i=1,2$) in the local ring $\mathcal {O}_{X,P}$ of X at P then we set

$$ (C_1\cdot C_2)_P:=\dim _\mathbb {C}\mathcal {O}_{X,P}/(f_1,f_2)\;. $$

If $P\notin C_1\cap C_2$ then we set $(C_1\cdot C_2)_P:=0$ The number thus defined is called the intersection multiplicity of the curves $C_1$ and $C_2$ at the point P.

If $(C_1\cdot C_2)_P=1$ then we say that the curves $C_1$ and $C_2$ are transverse (or meet transversely) at P.

Exercise 4.1.7

• 1. Prove that if $P\in C_1\cap C_2$ then the ring $\mathcal {O}_{X,P}/(f_1,f_2)$ is a finite-dimensional complex vector space. (Use the Nullstellensatz.)

• 2. Prove that $(C_1\cdot C_2)_P=1$ if and only if $f_1$ and $f_2$ generate the maximal ideal ${\mathfrak m}_P$ (i.e. if and only if $f_1$ and $f_2$ form a local system of parameters of X in a neighbourhood of P—see Definition 1.5.47).

Definition 4.1.8

Let X be a non singular complex projective surface and let $C_1$, $C_2$ be distinct irreducible curves on X. We set

$$ (C_1\cdot C_2):=\sum _{P\in X}(C_1\cdot C_2)_P= \sum _{P\in C_1\cap C_2}(C_1\cdot C_2)_P \;. $$

This is called the intersection number of the curves $C_1$ and $C_2$.

Theorem 4.1.9

Let X be a non singular complex projective surface. There is a unique symmetric bilinear form

$$ {\text {Div}}(X)\times {\text {Div}}(X) \longrightarrow \mathbb {Z}\,,\quad (A,B)\longmapsto (A\cdot B) $$

with the following properties:

• If A and B are non singular curves who meet transversely then $(A\cdot B)=\#(A\cap ~B)$;

• if A and $A'$ are linearly equivalent then $(A\cdot B)=(A'\cdot B)$ for any divisor B on X.

Proof

See [Bea78, I.4].    $\square$

Definition 4.1.10

Let X  be a non singular complex projective surface. It follows from Theorem 4.1.9 that there is a symmetric bilinear form on the $\mathbb {Z}$-module $\mathrm{{Cl}}(X)$, the intersection form

$$ \mathrm{{Cl}}(X)\times \mathrm{{Cl}}(X) \longrightarrow \mathbb {Z}\,,\quad (A,B)\longmapsto (A\cdot B)\;. $$

If A and B are divisors on X then we call $(A\cdot B)$ the intersection number of A and B and we denote by $(A^2)=(A\cdot A)$ the self-intersection number of A.

When there is no risk of confusion we will sometimes abusively denote the intersection number $(A\cdot B)$ by $A\cdot B$.

Proposition 4.1.11

Let X be a non singular complex projective surface and let $\mathcal {L}_1$ and $\mathcal {L}_2$ be line bundles on X. We set

$$ (\mathcal {L}_1\cdot \mathcal {L}_2) = \chi (\mathcal {O}_X)-\chi (\mathcal {L}_1^{-1})-\chi (\mathcal {L}_2^{-1})+\chi (\mathcal {L}_1^{-1}\otimes \mathcal {L}_2^{-1})\;. $$

The map

$$ \mathrm{{Pic}}(X)\times \mathrm{{Pic}}(X) \longrightarrow \mathbb {Z}\,,\quad (\mathcal {L}_1,\mathcal {L}_2)\longmapsto (\mathcal {L}_1\cdot \mathcal {L}_2) $$

is then a symmetric bilinear form on the $\mathbb {Z}$-module $\mathrm{{Pic}}(X)$ and the isomorphism of $\mathbb {Z}$-modules $\mathrm{{Cl}}(X)\simeq \mathrm{{Pic}}(X)$ induced by $D\mapsto \mathcal {O}_X(D)$ is an isometry for the symmetric bilinear forms on $\mathrm{{Cl}}(X)$ and $\mathrm{{Pic}}(X)$. In other words, if A and B are two divisors on X then

$$ (\mathcal {O}_X(A)\cdot \mathcal {O}_X(B))=(A\cdot B)\;. $$

Proof

See [Bea78, Théorème I.4].    $\square$

The restriction of a line bundle to a projective curve has a well-defined degree.

Proposition 4.1.12

Let C be a non singular irreducible projective curve on X and let $\mathcal {L}$ be a line bundle on X. We then have that

$$ (\mathcal {O}_X(C)\cdot \mathcal {L})=\deg (\mathcal {L}|_C)\;. $$

Proof

See [Bea78, Lemme I.6].    $\square$

Example 4.1.13

• 1. If $X=\mathbb {P}^2(\mathbb {C})$ then $\mathrm{{Pic}}(X)=\mathbb {Z}$ is generated by the class of a line (see Exercise 2.6.5). Any curve of degree d on X is linearly equivalent to a divisor dH where H is a line. Let C and $C'$ be two curves of respective degrees d and $d'$ and let $L, L'$ be two distinct lines. Since $C\sim dL$ and $C'\sim d'L'$ we recover Bézout’s theorem

  $$ (C \cdot C')=(dL\cdot d'L')=dd'(L\cdot L')=dd'\;. $$

• 2. If $X=\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C})$ then $\mathrm{{Pic}}(X)=\mathbb {Z}\times \mathbb {Z}$ is generated by the classes $F_1=\{0\}\times \mathbb {P}^1(\mathbb {C})$ and $F_2=\mathbb {P}^1(\mathbb {C})\times \{0\}$. The multiplication table is given by $(F_1^2)=(F_2^2)=0$ and $(F_1\cdot F_2)=1$. A curve on X is determined by a bihomogeneous polynomial in four variables. Let $C, C'$ be two curves of bidegrees $(d_1,d_2)$ and $(d'_1,d'_2)$: we then have that

  $$ (C \cdot C')=(d_1F_1+d_2F_2)\cdot (d'_1F_1+d'_2F_2)=d_1d'_2+d'_1d_2\;. $$

Using the first Chern class map $c_1:\mathrm{{Pic}}(X)\rightarrow H^{2}(X;\mathbb {Z})$ (see Appendix D for more details) we can link the intersection form to the cup-product (see Section B.7):

Proposition 4.1.14

Let X be a non singular complex variety of dimension n and let Y be a non singular compact complex subvariety of codimension 1. The fundamental class of Y in $H_{2n-2}(X;\mathbb {Z})$ is then the Poincaré dual of $c_1(\mathcal {O}_X(Y))\in H^{2}_c(X;\mathbb {Z})$.

Proof

See [Hir66, Theorem 4.9.1].    $\square$

Proposition 4.1.15

Let X be a non singular complex projective surface and let D and $D'$ be divisors on X. We then have that $c_1(\mathcal {O}_X(D))\in H^2(X;\mathbb {Z})$, $c_1(\mathcal {O}_X(D'))\in H^2(X;\mathbb {Z})$ and

$$ (D\cdot D')=c_1(\mathcal {O}_X(D))\smile c_1(\mathcal {O}_X(D'))\;. $$

Proof

See [Ibid.].    $\square$

Proposition 4.1.16

The intersection form on a non singular projective $\mathbb {R}$-surface $(X,{\sigma })$ is compatible with the real structure. In other words

$$ \forall \mathcal {L},\mathcal {L}'\in \mathrm{{Pic}}(X), (\mathcal {L}\cdot \mathcal {L}')=({}^{\sigma }\mathcal {L}\cdot {}^{\sigma }\mathcal {L}') $$

and

$$ \forall A,B\in \mathrm{{Cl}}(X), (A\cdot B)=({\sigma }A\cdot {\sigma }B)\;. $$

Proof

In order to apply Proposition 4.1.11 recall that

$$ \chi (\mathcal {L})=\sum (-1)^k\dim _\mathbb {C}H^k(X,\mathcal {L})\;. $$

The first equation now follows from a simple application of Proposition 2.2.2. We then use Proposition 2.6.30 to obtain the second equation on linear divisor classes.

We note that by Section 3.7, this result also follows from Corollary 3.1.9 in singular cohomology. See [Sil89, II.1] for more details if necessary.    $\square$

Throughout the rest of this chapter we will freely identify $\mathrm{{Pic}}(X)$ and $\mathrm{{Cl}}(X)$ whenever X is a non singular projective surface.

Theorem 4.1.17

(Serre duality) Let X be  a non singular projective surface and let $\mathcal {L}$ be a line bundle on X. We then have that

$$ H^k(X,\mathcal {L}) \simeq H^{2-k}(X,\mathcal {K}_X\otimes \mathcal {L}^{-1}) $$

and in particular

$$ \chi (\mathcal {L})=\chi (\mathcal {K}_X\otimes \mathcal {L}^{-1})\;. $$

Proof

See [Bea78, Théorème I.11].    $\square$

Theorem 4.1.18

(Riemann–Roch formula for surfaces) Let X be a  non singular projective surface and let D be a divisor on X. We then have that

$$ \chi (\mathcal {O}_X(D)) =\frac{1}{2} D\cdot ( D-K_X) +\chi (\mathcal {O}_X)\;. $$

Proof

For any divisor A on X we have that $(\mathcal {O}_X(-A))^{-1}=\mathcal {O}_X(A)$. By Proposition 4.1.11 we therefore have that

$$\begin{aligned}&(-D)\cdot (D-K_X)=\\&\quad \chi (\mathcal {O}_X)-\chi (\mathcal {O}_X(D))-\chi (\mathcal {O}_X(K_X-D))+\chi (\mathcal {O}_X(D)\otimes \mathcal {O}_X(K_X-D))\;. \end{aligned}$$

Using Serre duality applied to $\mathcal {O}_X(K_X-D)$ we get that

$$ (-D)\cdot (D-K_X)=\chi (\mathcal {O}_X)-\chi (\mathcal {O}_X(D))-\chi (\mathcal {O}_X(D))+\chi (\mathcal {O}_X(K_X)) $$

and the required formula follows on applying Serre duality to the canonical bundle $\chi (\mathcal {O}_X(K_X))=\chi (\mathcal {O}_X)$.    $\square$

The holomorphic Euler characteristic of a complex surface X is linked to its topological Euler characteristic $\chi _{\text {top}}(X)=\sum _{k=0}^{4}(-1)^k\dim _\mathbb {Q}H_k(X;\mathbb {Q})$ by the following formula.

Theorem 4.1.19

(Noether’s formula) Let X be a  non singular complex projective surface. We then have that

$$ \chi (\mathcal {O}_X)=\frac{1}{12}(K_X^2+\chi _{\text {top}}(X))\;. $$

This formula is often written in terms of Chern numbers $c_1^2(X)=(K_X^2)$ and $c_2(X)=\chi _{\text {top}}(X)$, which yields

$$ \chi (\mathcal {O}_X)=\frac{1}{12}(c_1^2(X)+c_2(X))\;. $$

Proof

See [GH78, III.5].    $\square$

Definition 4.1.20

Let $(X,{\sigma })$ be  a non singular projective $\mathbb {R}$-surface. We recall (Definition 2.6.34, Theorem 2.6.35 and Definition 2.6.36) that ${\text {NS}}(X)=\mathrm{{Pic}}(X)/\mathrm{{Pic}}^0(X)$ is the Néron–Severi group of the complex surface X, that $\rho (X)={\text {rk}}(\mathrm{{Pic}}(X)/\mathrm{{Pic}}^0(X))$ is the Picard number of X and if $X(\mathbb {R})$ is non empty then $\rho _\mathbb {R}(X)= {\text {rk}}(\mathrm{{Pic}}(X)^G/{\mathrm{{Pic}}^0(X)}^G)$ is the real Picard number of the $\mathbb {R}$-surface $(X,{\sigma })$.

Remark 4.1.21

By definition we have that $\rho _\mathbb {R}(X)\leqslant \rho (X)$. By Proposition 2.6.37, if $q(X)=0$ then $\rho (X)={\text {rk}}\mathrm{{Pic}}(X)$ and moreover if $X(\mathbb {R})$ is non empty then $\rho _\mathbb {R}(X)={\text {rk}}\mathrm{{Pic}}(X)^G$ by Theorem 2.6.32.

Definition 4.1.22

Let X be a non singular complex projective surface and let A and B be divisors on X. We denote by $A\equiv B$ the numerical equivalence relation: $A\equiv B$ if and only if $(A\cdot C)=(B\cdot C)$ for any effective divisor C on X. We denote by

$$ {\text {Num}}(X):={\text {Div}}(X)/\equiv $$

the quotient group.

Proposition 4.1.23

For any non singular complex projective surface X we have that

$$ {\text {Num}}(X)\simeq {\text {NS}}(X)/{\text {Tor}}({\text {NS}}(X))\;. $$

Proof

See [GH78, Chapter V].    $\square$

Theorem 4.1.24

(Hodge index) Let X be a non  singular projective surface and let H be an ample divisor on X. If D is a divisor on X such that $D\cdot H=0$ then $(D^2)\leqslant 0$ with equality if and only if $D\equiv 0$.

Proof

We recall that for any divisor D on X we denote by $h^k(D)$ the dimension of the space $H^k(X,\mathcal {O}_X(D))$.

We claim that if D is a divisor on X such that $(D^2)>0$ then either $h^0(mD)\ne 0$ or $h^0(-mD)\ne 0$ for large enough m.

It follows that either mD or $-mD$ is equivalent to a non zero effective divisor for large enough m which implies that $H\cdot D > 0$ or $H\cdot D < 0$ and the first part of the theorem follows.

We now prove the claim. Let D be a divisor on X such that $(D^2)>0$. By Riemann–Roch $\chi (\mathcal {O}_X(mD))$ is then equivalent to $\frac{m^2}{2}(D^2)$ as m tends to infinity. As $h^0(mD)+h^2(mD)\geqslant \chi (\mathcal {O}_X(mD))$ either $h^0(mD)$ or $h^2(mD)$ tends to infinity as m tends to infinity. By Serre duality $h^2(mD)=h^0(K_X-mD)$. Using the same argument replacing D by $-D$, we conclude that either $h^0(-mD)$ or $h^0(K_X+mD)$ tends to infinity as m tends to infinity, but $h^0(K_X-mD)$ and $h^0(K_X+mD)$ cannot both tend to infinity. Indeed, if $s\in H^0(X,\mathcal {O}_X(K_X-mD))$ then multiplication by s defines an inclusion $H^0(X,\mathcal {O}_X(K_X+mD))\hookrightarrow H^0(X,\mathcal {O}_X(2K_X))$. It follows that either $h^0(mD)\ne 0$ or $h^0(-mD)\ne 0$ for large enough m.

To prove the second claim assume that $D\cdot H=0$ and $(D^2)=0$. Assume by contradiction that $D\cdot C>0$ for some effective divisor C. Let $\lambda =\frac{p}{q}\in \mathbb {Q}$ be defined by $(C-\lambda H)\cdot H=0$. The divisor $m D + q(C-\lambda H)$ then does not satisfy $(m D + q(C-\lambda H))^2\leqslant 0$ for large enough m despite the fact that $(m D + q(C-\lambda H))\cdot H=0$.    $\square$

Corollary 4.1.25

Let X be a non singular complex projective curve. The index of the intersection form (Definition 3.4.1) is then given by

$$ \tau (X)=2+2h^{0,2}(X)-h^{1,1}(X)=2+4p_g(X)-b_2(X)\;. $$

Proof

By the Hodge index theorem the restriction of the intersection form Q to $H^{1,1}(X)$ has signature $(1,h^{1,1}(X)-1)$. As the restriction of Q to $H^{2,0}(X)\oplus H^{0,2}(X)$ is definite positive the signature of Q is equal to $(h^{2,0}(X)+h^{0,2}(X)+1,h^{1,1}(X)-1)$. The result now follows from the identities $h^{2,0}(X)=h^{0,2}(X)=p_g(X)$ and $b_2(X)=h^{2,0}(X)+h^{1,1}(X)+h^{0,2}(X)$.    $\square$

4.1.2 Blow-Up

See Appendix F or [Bea78, II.1] for more details.

Let X be a complex projective surface and let $P\in X$ be a non singular point. There is then a surface $\widetilde{X}$ and a birational morphism $\pi :\widetilde{X} \rightarrow X$, unique up to isomorphism, such that

• 1. The restriction of $\pi$ to $\widetilde{X}\setminus \pi ^{-1}(P)\rightarrow X\setminus \{P\}$ is an isomorphism.

• 2. $E_P:=\pi ^{-1}(P)$ is isomorphic to $\mathbb {P}^1(\mathbb {C})$,

• 3. The variety $\widetilde{X}$ is non singular along the divisor $E_P$.

Definition 4.1.26

The morphism $\pi$ is called  the blow up of X at P (or centred at P, the surface $B_PX:=\widetilde{X}$ is called the blow up of X at P and the curve $E_P:=\pi ^{-1}(P)$ is called the exceptional curve of the blow up.

Fig. 4.1

Blow up: the exceptional curve is represented by the vertical line

Example 4.1.27

(Blow up of a point in the affine plane) Applying Definition F.2.1 and restricting ourselves to an affine neighbourhood of (0, 0), we see that the blow up $B_{(0,0)}\mathbb {A}^2$ of $\mathbb {A}^2$ at the point (0, 0) is the quadric hypersurface defined in $\mathbb {A}^2\times \mathbb {P}^1$ by

$$ B_{(0,0)}\mathbb {A}^2= \{((x,y),[u:v])\in \mathbb {A}^2_{x,y}\times \mathbb {P}^1_{u:v} \mathrel {}\mid \mathrel {}uy=vx\}\;. $$

See Figure 4.1.⁴

Example 4.1.28

(Blow up of a point in the projective plane) The blow up $B_{(0:0:1)}\mathbb {P}^2$ of $\mathbb {P}^2$ at $P=(0:0:1)$ is the algebraic surface $\widetilde{\mathbb {P}^2}$ defined locally over a neighbourhood $U=(z\ne 0)$ of P by

$$ B_PU:=\{((x,y),[u:v])\in U_{x,y}\times \mathbb {P}^1_{u:v} \mathrel {}\mid \mathrel {}uy=vx\}. $$

More generally, the blow up of the projective plane $\mathbb {P}^2_{x:y:z}$ at a point $P=(a:b:1)$ in the open affine set $(z\ne 0)$ is given by

$$\begin{aligned} B_{(a:b:1)}\mathbb {P}^2:=\{([x:y:z],[u:v])\in \mathbb {P}^2_{x:y:z}\times&\mathbb {P}^1_{u:v} \mathrel {}\mid \mathrel {}\\&\quad u(y-bz)-v(x-az)=0\}, \end{aligned}$$

and in particular

$$\begin{aligned} B_{(0:0:1)}\mathbb {P}^2:=\{([x:y:z],[u:v])\in \mathbb {P}^2_{x:y:z}\times \mathbb {P}^1_{u:v} \mathrel {}\mid \mathrel {}uy-vx=0\}. \end{aligned}$$

Remark 4.1.29

If X is a complex analytic space we can deduce a description of the blow up of X in a non singular point from the examples above. We simply carry out the blow up in a chart sending an open neighbourhood of P to an open set in $\mathbb {C}^2$. Note that when working with the Zariski topology we cannot generally use this “local” description of blow ups, since a surface containing a dense open subset isomorphic to a non empty Zariski open subset of $\mathbb {A}^2$ must be rational (Definition 4.4.1).

Proposition 4.1.30

Let X be a non singular complex projective surface, let $\pi :\widetilde{X} \rightarrow X$ be the blow up of X at a point P and let E be the exceptional curve of $\pi$.

• 1. The map $\mathrm{{Pic}}(X)\oplus \mathbb {Z}\rightarrow \mathrm{{Pic}}(\widetilde{X})$ defined by $(A,n)\mapsto \pi ^*A+nE$ is an isomorphism.

• 2. Let A and B be divisors on X. We then have that

  $$ (\pi ^*A\cdot \pi ^*B)=(A\cdot B), \qquad (E\cdot \pi ^*A)=0, \qquad (E)^2=-1\;. $$

• 3. We have that ${\text {NS}}(\widetilde{X})\simeq {\text {NS}}(X)\oplus \mathbb {Z}[E]$.

• 4. We have that $K_{\widetilde{X}}=\pi ^*K_X+E$.

Proof

See [Bea78, II.3].    $\square$

Remark 4.1.31

We can also blow up singular points. In Example 4.7.6 we calculate the blow up of a surface at an ordinary double point.

4.1.3 Adjunction Formula

Let $f :C \rightarrow X$ be the embedding of an effective divisor in a surface X and let D be a divisor on X. We set

$$ \mathcal {O}_C(D):=f^*(\mathcal {O}_X(D)) $$

and in particular $\mathcal {O}_C(C)=\mathcal {O}_X(C)|_C$. If C is non singular then $\mathcal {O}_C(C)$ is the normal bundle of C in X.

Theorem 4.1.32

(Non singular variety) Let X be  a non singular complex variety and let Y be a non singular complex subvariety of codimension 1. We then have that

$$ \mathcal {K}_Y=\mathcal {K}_X\otimes \mathcal {O}_X(Y)|_Y\;. $$

Proof

See [BHPVdV04, Theorem I.6.3].    $\square$

Remark 4.1.33

The canonical bundles $\mathcal {K}_X$ and $\mathcal {K}_Y$ (see Appendix D) are defined for any non singular varieties and subvarieties.

Corollary 4.1.34

(Non singular curves on a surface) Let X be  a complex surface (which is assumed non singular but not necessarily connected or compact) and let C be a non singular curve on X. The canonical sheaf on C is then given by

$$ \mathcal {K}_C=\mathcal {K}_X\otimes \mathcal {O}_C(C)\;. $$

Remark 4.1.35

When C is singular but X is non singular the right hand side of the previous formula is well defined and gives rise to a sheaf on C

$$ \omega _C :=\mathcal {K}_X\otimes \mathcal {O}_C(C)\;. $$

This definition appears to depend on the embedding of C in X but this turns out not in fact to be the case. The sheaf $\omega _C$ is known as the dualising sheaf of C. See [BHPVdV04, II.1] and [Har77, III.7] for more details.

4.1.4 Genus of an Embedded Curve

This subsection draws on [BHPVdV04, II.11]. Let C be a non singular connected complex curve: the geometric genus of C is the genus of the underlying topological surface (see Definition E.1.2). More generally, if C is a reduced and irreducible complex curve and $\nu :\widetilde{C} \rightarrow C$ is its normalisation (see Example 1.5.38) then the normalisation $\widetilde{C}$ is a connected non singular curve.

Definition 4.1.36

The geometric genus g(C) of  a reduced and irreducible complex algebraic curve C is defined to be the topological genus of its normalisation.

$$ g(C):=g(\widetilde{C})\;. $$

It is a birational invariant.

Definition 4.1.37

The arithmetic genus $p_a(C)$ of  a complex algebraic curve C (which is assumed neither reduced nor irreducible) is defined by:

$$ p_a(C):=1-\chi (\mathcal {O}_C)\;. $$

Remark 4.1.38

If C is non singular, irreducible and reduced then $p_a(C)=g(C)$.

Remark 4.1.39

Assume that C is irreducible and reduced and is embedded in a non singular surface X. The following then hold.

• 1. The arithmetic genus of C is equal to the geometric genus $g(C')$ of a non singular curve $C'$ obtained by perturbing C in the surface X whenever such a perturbation is possible. (The curve $C'\subset X$ is then linearly equivalent to C.)

• 2. By Remark 4.1.35 we have that

  $$ p_a(C)=1-\chi (\mathcal {O}_C)=1+\chi (\omega _C)\;. $$

Definition 4.1.40

Let C be a  curve on a non singular complex surface and let P be a point of multiplicity $r_P$ on C. The point P is said to be an ordinary multiple point of C if and only if it is locally analytically isomorphic to a singularity of the form $\prod _{k=1,\dots ,r_P} (x-\varepsilon ^k y)=0$ where $\varepsilon$ is a primitive $r_P$th root of unity.

Lemma 4.1.41

Let P be an ordinary multiple point of multiplicity $r_P$ of an irreducible curve C and let $\widetilde{C}$ be the strict transform of C on the blow up of X centred at P. We then have that

$$ \widetilde{C}^2=C^2-r_P^2\;. $$

Proof

By [Bea78, Lemme II.2] we have that $\pi ^*C=\widetilde{C}+rE_P$, so the formula follows from Proposition 4.1.30.    $\square$

Definition 4.1.42

Let X be  a surface, let $P\in X$ be a non singular point and let $X' \rightarrow X$ be the blow up of X centred at P with exceptional curve $E_P\subset X'$. Any point $Q\in E_P$ is said to be an infinitely close point of P. More generally, if $\pi :X''\rightarrow X$ is a sequence of blow ups then any point $Q\in X''$ such that $\pi (Q)=P$ is said to be an infinitely close point of P.

Let $C\subset X$ be a reduced curve on a non singular surface. We set $\delta _P(C)=\sum \frac{1}{2} r_Q(r_Q-1)$ where the sum is taken over all infinitely close points Q of P including P itself. In particular, if P is an ordinary multiple point of multiplicity r on C then $\delta _P(C)=\frac{1}{2} r_P(r_P-1)$: an ordinary double point counts for 1, a triple point counts for 3 and a quadruple point counts for 6 . See [Har77, Chapitre V, exercice 3.7] for more details.

Proposition 4.1.43

Let $C\subset X$ be an irreducible reduced curve on a non singular surface and let $\nu :\widetilde{C} \rightarrow C$ be the normalisation of C. We then have that

$$ p_a(C)= g(\widetilde{C})+\delta (C) $$

where $\delta (C)=\sum _{P\in C}\delta _P(C)$. If C is non singular then $\delta (C)=0$.

Proof

See [Har77, Chapitre V, exemple 3.9.2].    $\square$

Theorem 4.1.44

(Adjunction for singular curves) Let X be  a complex analytic surface which is assumed to be non singular but not necessarily connected or compact and let C be a compact curve on X which is assumed neither reduced nor irreducible. We then have that

$$ 2p_a(C)-2=\deg (\mathcal {K}_X\otimes \mathcal {O}_C(C))\;. $$

If moreover X is compact then the intersection form is well defined and the above equality can be written as

$$\begin{aligned} 2p_a(C)-2=C\cdot (K_X+C)\;. \end{aligned}$$

(4.1)

Exercise 4.1.45

Let $(C,{\sigma _\mathbb {P}}|_C)$ be a projective plane reduced and irreducible $\mathbb {R}$-curve of degree 4. Prove that if C is rational—i.e. $g(C)=0$—then at least one of its singular points is real, i.e. ${\text {Sing}}(C)\cap C(\mathbb {R})\ne \varnothing$.

Here is another application of adjunction to $\mathbb {R}$-curves, taken from [KM16, Proposition 23].

Proposition 4.1.46

Let $C\subset \mathbb {P}^1\times \mathbb {P}^1$ be a rational $\mathbb {R}$-curve whose real locus $C(\mathbb {R})$ is non singular, $C(\mathbb {R})\cap {\text {Sing}}(C)=\varnothing$. The fundamental class $[C(\mathbb {R})]\in H_1({\mathbb T}^2, \mathbb {Z}_2)$ is then non vanishing.

Proof

Let $\{E_1, E_2\}$ be a basis of $H_2(\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C});\mathbb {Z})$ such that $(E_k)^2=0$ and $E_1\cdot E_2=1$. The fundamental class of the complex curve C is therefore equal to $a_1E_1+a_2E_2$ where $a_1$ and $a_2$ are natural numbers. The fundamental class of the canonical divisor is given by $K_X=-2E_1-2E_2$. The adjunction formula then gives us

$$ 2p_a(C)-2=\bigl ( a_1E_1+a_2E_2\bigr )\cdot \bigl ( (a_1-2)E_1+(a_2-2)E_2\bigr ) =a_1(a_2-2)+a_2(a_1-2), $$

so that

$$\begin{aligned} p_a(C)=(a_1-1)(a_2-1)\;. \end{aligned}$$

(4.2)

As C is stable under ${\sigma }$ we have moreover that

$$ a_k=(C\cdot E_{3-k})\equiv \bigl (C(\mathbb {R})\cdot E_{3-k}(\mathbb {R})\bigr ) \mod 2 $$

for any $k\in \{1,2\}$. If the class $[C(\mathbb {R})]\in H_1({\mathbb T}^2, \mathbb {Z}_2)$ were zero then $a_1, a_2$ would both be even and $p_a(C)$ would be odd. Since C is rational $g(\widetilde{C})=0$ so C would then have an odd number of singular points one of which would be real.    $\square$

Using the  adjunction formula (4.1) we define the virtual genus of a divisor D on a compact surface by

$$\begin{aligned} p_v(D):=\frac{1}{2}\bigl (D\cdot (K_X+D)\bigr )+1\;. \end{aligned}$$

(4.3)

If $D=A+B$ where A and B are effective divisors then we have that

$$\begin{aligned} p_v(D):=p_a(A)+p_a(B)+A\cdot B -1 \end{aligned}$$

(4.4)

and

$$\begin{aligned} p_v(-D)=D^2-p_a(D)+2 \;. \end{aligned}$$

(4.5)

See [Har77, Chapitre V, exercice 1.3] for more details.

Proposition 4.1.47

([BHPVdV04, II.11.c]) Let C be a reduced connected curve on a surface X. We then have that $p_v(C)=p_a(C)\geqslant 0$.

Exercise 4.1.48

Let $C=C_1+C_2$ be the union of two non singular disjoint rational curves. We then have that $\chi _{top}(C)=4$ and $p_v(C)=-1$.

4.2 Examples of $\mathbb {R}$-Surfaces

We start by recalling the definitions of some special types of surfaces of negative Kodaira dimension. ${\kappa }=-\infty$.

Definition 4.2.1

(Hirzebruch surfaces [Hir51]) A complex surface  X is a Hirzebruch surface of index n, denoted $\mathbb {F}_n$, if it is the total space of a locally trivial $\mathbb {P}^1(\mathbb {C})$ bundle over $\mathbb {P}^1(\mathbb {C})$ and $\mathbb {F}_n = \mathbb {P}_{\mathbb {P}^1}(\mathcal {O}_{\mathbb {P}^1}\oplus \mathcal {O}_{\mathbb {P}^1}(n))$, by which we mean that $\mathbb {F}_n$ is the projectivisation of the 2-dimensional vector bundle $\mathcal {O}_{\mathbb {P}^1}\oplus \mathcal {O}_{\mathbb {P}^1}(n)$ over $\mathbb {P}^1$.

By convention, the real Hirzebruch surface of index n is obtained by equipping $\mathbb {F}_n$ with the canonical real structure induced by ${\sigma _\mathbb {P}}$.

Proposition 4.2.2

If $n>0$ then the curve $E_\infty =\mathbb {P}_{\mathbb {P}^1}( \mathcal {O}_{\mathbb {P}^1}(n))$ is an exceptional section of the line bundle $\mathbb {F}_n \rightarrow \mathbb {P}^1$ whose self-intersection is $(E_\infty ^2) = -n$.

Proof

See [BHPVdV04, Propositions 4.1 et 4.2, p. 141] and [Bea78, Chapitre III].    $\square$

Remark 4.2.3

The surface $\mathbb {F}_n$ is obtained by gluing the local charts $\mathbb {P}^1_{u:v}\times \mathbb {A}^1_{t}$ and $\mathbb {P}^1_{u_1:v_1}\times \mathbb {A}^1_{t_1}$ over the open sets $\{t\ne 0\}$ and $\{t_1\ne 0\}$ via the map

$$ \left( (u:v),t\right) \mapsto \left( (u_1:v_1),t_1\right) $$

where $t_1=\frac{1}{t}$ and $uv_1=t^nu_1v$.

Remark 4.2.4

Hirzebruch surfaces have negative ${\kappa }$ dimension because the general fibre of $\mathbb {F}_n\rightarrow \mathbb {P}^1$ has negative ${\kappa }$ dimension.

Exercise 4.2.5

• 1. Prove that the Hirzebruch surface $\mathbb {F}_1$ is isomorphic to the blow up of $\mathbb {P}^2(\mathbb {C})$ in a point.

• 2. Prove that if n is odd then $\mathbb {F}_n$ has only one equivalence class of real structures.

• 3. Prove that if $n=2k$ then $\mathbb {F}_{2k}$ has a second class of real structures whose real locus is empty.

Example 4.2.6

(Conic bundles over $\mathbb {P}^1$) Historically  a conic bundle over a field K was a surface given by an equation of the form

$$ x^2+axy+by^2=f(t) $$

with $a,b\in K$ and $f\in K[t]$. When $K=\mathbb {R}$, on reducing the quadratic form on the left, we can always reduce to the case of an equation of the form

$$ x^2-ay^2=f(t) $$

where $a=-1,0,1$. Completing the affine surface defined above gives us a variety $X_0$ whose equation is

$$ x^2-ay^2-f(t)z^2=0 $$

in $\mathbb {P}^2_{x:y:z}\times \mathbb {A}^1_{t}$.

Recall that we can define the round up $\left\lceil x\right\rceil$ of a real number x using the round down: $\left\lceil x\right\rceil =-\left\lfloor -x\right\rfloor$. We denote by $m:=\left\lceil \frac{\deg f}{2}\right\rceil$ so the  degree of f is equal to 2m or $2m-1$. Set $f_1:=t^{2m}f(\frac{1}{t})$ (classically $f_1$ is called the reciprocal polynomial of f) and glue the surface $X_1$ of equation $x_1^2-ay_1^2-f_1(t_1)z_1^2=0$ in $\mathbb {P}^2_{x_1:y_1:z_1}\times \mathbb {A}^1_{t_1}$ to the surface $X_0$ along the open sets $\{t\ne 0\}$ and $\{t_1\ne 0\}$ using the isomorphism

$$ ((x:y:z),t)\longmapsto ((x_1:y_1:z_1),t_1)=((x:y:zt^m),\frac{1}{t})\;. $$

If $a\ne 0$ and f has simple roots then X is a non singular projective surface and the map $\pi :X \rightarrow \mathbb {P}^1$ defined by $\pi :((x:y:z),t)\mapsto t$ on $X_0$ and $\pi :((x_1:y_1:z_1),t_1)\mapsto t_1$ on $X_1$ turns X into a conic bundle over $\mathbb {P}^1$.

If moreover the degree of f is even we can avoid having a root at infinity and we can choose the sign of the dominant coefficient in such a way that the real locus of the completed surface is diffeomorphic to that of the initial surface $X_0$.

Remark 4.2.7

If the degree of f is odd there is at least one fibre of the form $x^2-y^2=0$ consisting of two real lines meeting in a point.

Example 4.2.8

(Topology of conic bundles) Let X be the projective completion of the conic bundle of the equation

$$ x^2+y^2=f(t) $$

where $f\in \mathbb {R}[t]$ is a polynomial of even degree 2s which is negative at infinity and has exactly 2s distinct real simple zeros, for example $f(t)=-\prod _{i=1,\dots ,2s}(t-i)$ for $s\geqslant 2$. It follows immediately that $X(\mathbb {R})$ is compact and has s connected components. The variety $X(\mathbb {R})$ is a disjoint union of s spheres.

The examples above can be generalised to conic bundles over a curve of arbitrary genus.

Definition 4.2.9

(Conic bundles) A conic bundle  is a pair $(X,\pi )$ where X is a complex surface and $\pi :X \rightarrow B$ is a morphism to a non singular complex curve such that every fibre is isomorphic to a possibly singular or non reduced plane conic (see Exercise 1.2.68). A real conic bundle is a pair $((X,{\sigma }),\pi )$ where $(X,{\sigma })$ is an $\mathbb {R}$-surface and $\pi :X\rightarrow B$ is a morphism of $\mathbb {R}$-varieties to an $\mathbb {R}$-curve $(B,\sigma _B)$ such that every fibre is isomorphic as a complex curve to a plane conic.

Remark 4.2.10

A Hirzebruch surface is a conic bundle whose fibres are all non singular.

Exercise 4.2.11

(Conic bundle)

• 1. Prove that any surface with a conic bundle structure has negative ${\kappa }$ dimension.

• 2. Prove that the total space X of a conic bundle $\pi :X\rightarrow B$ with at least one irreducible fibre is non singular if and only if all the fibres of $\pi$ are reduced.

• 3. Prove that any conic bundle over $\mathbb {P}^1$ with reduced complex fibres is the blow up of a Hirzebruch surface in a finite number of points.

• 4. Give an example of a real conic bundle whose real locus is not connected in the Euclidean topology.

Definition 4.2.12

(Del Pezzo surfaces) A complex  surface X is said to be a del Pezzo surface if and only if its anti-canonical bundle $-K_X$ is ample. The degree of the del Pezzo surface X is then defined to be the integer $(K_X^2)$. A real del Pezzo surface is an $\mathbb {R}$-surface $(X,{\sigma })$ such that X is a del Pezzo surface.

We refer the interested reader to Demazure’s survey [DPT80, pp. 21–69] for a study of the multicanonical morphisms of del Pezzo surfaces and their generalisations, the weak del Pezzo surfaces, whose anti-canonical divisor $-K_X$ is only assumed nef and big.

Exercise 4.2.13

• 1. Prove that del Pezzo surfaces have negative ${\kappa }$ dimension.

• 2. Give an example of a del Pezzo surface with a conic bundle structure. (See [BM11] for a characterisation of such surfaces.)

• 3. Prove that $\mathbb {P}^1\times \mathbb {P}^1$ is a degree 8 del Pezzo surface.

• 4. Prove that a double cover of the projective plane branched along a non singular quartic curve is a del Pezzo surface of degree 2.

4.2.1 Topological Surfaces: Conventions and Notations

A topological surface is a topological manifold of dimension 2. Recall that any topological manifold of dimension 2 has a unique $\mathcal {C}^\infty$ differentiable manifold structure (see [Hir76, Chapter 9] for more details) and any homeomorphism between topological manifolds can be approximated by $\mathcal {C}^\infty$ diffeomorphisms. We will therefore always assume that any topological surface comes equipped with this differentiable structure and our topological surfaces will be differentiable manifolds of real dimension 2. It will therefore make sense to talk about diffeomorphisms between topological surfaces, for example.

Throughout this section our topological surfaces will be assumed compact:

Convention 4.2.14

A topological surface is a compact topological manifold without boundary of dimension 2.

Notation 4.2.15

If A and B are topological surfaces, we will write $A\approx B$ if A and B are $\mathcal {C}^\infty$-diffeomorphic. $A\sqcup B$ will be the disjoint union of A and B and $A \# B$ will be their connected sum as in Definition B.5.12 and Remark B.5.13. $\sqcup ^sA$ will denote the disjoint union of s copies of A and $\#^kA$ will denote the connected sum of k copies of A. By convention, $\sqcup ^0A=\varnothing$ and $\#^0A=\mathbb {S}^2$. We  denote by

• 1. $\mathbb {S}^2$ the sphere of dimension 2;

• 2. ${\mathbb T}^2\approx \mathbb {S}^1\times \mathbb {S}^1$ the torus of dimension 2;

• 3. ${\mathbb S}_g=\#^{g}{\mathbb T}^2$ the orientable topological surface of genus $g\geqslant 0$. In particular, ${\mathbb S}_0=\mathbb {S}^2$ and ${\mathbb S}_1={\mathbb T}^2$;

• 4. ${\mathbb {R}}{\mathbb {P}}^2\approx \mathbb {S}^2/\mathbb {Z}_2$ the real projective plane;

• 5. ${\mathbb K}^2$ the Klein bottle;

• 6. ${\mathbb V}_g=\#^{g}{\mathbb {R}}{\mathbb {P}}^2$ the non orientable surface of genus⁵ $g>0$. In particular ${\mathbb V}_1={\mathbb {R}}{\mathbb {P}}^2$ and ${\mathbb V}_2={\mathbb K}^2$.

Remark 4.2.16

For $g>0$, ${\mathbb V}_g$ is the non orientable surface of topological Euler characteristic $2-g$ since ${\mathbb V}_g$ is the connected sum of g copies of ${\mathbb {R}}{\mathbb {P}}^2={\mathbb V}_1$. For convenience we extend the notation ${\mathbb V}_g$ to the case $g=0$: ${\mathbb V}_0={\mathbb S}_0=\mathbb {S}^2$.

Exercise 4.2.17

Prove that the real locus of a Hirzebruch surface $\mathbb {F}_n$ equipped with its canonical real structure is diffeomorphic to the torus ${\mathbb T}^2$ if n is even and to the Klein bottle ${\mathbb K}^2$ if n is odd.

Example 4.2.18

See Appendix F for more details. If $(X,{\sigma })$ is an $\mathbb {R}$-surface and $P\in X(\mathbb {R})$ is real then by the universal property of blow ups (Corollary F.2.6) ${\sigma }$ lifts to a real structure on the blow up $B_PX$ and $E_P$ is an $\mathbb {R}$-curve for this structure. The real locus therefore satisfies $(B_PX)(\mathbb {R})=B_P(X(\mathbb {R}))$ and we can denote it by $B_PX(\mathbb {R})$ without risking confusion. Topologically, blow up corresponds to the following surgery of the real locus: we remove from $X(\mathbb {R})$ a disc centred at P (whose boundary is a circle) and we glue along this circle a Möbius band (whose boundary is also a circle) to get $B_PX(\mathbb {R})$. In other words:

$$ B_PX(\mathbb {R})\approx X(\mathbb {R})\#\mathbb {R}\mathbb {P}^2 \;. $$

Example 4.2.19

(Real algebraic models of compact surfaces) We now present real algebraic models (see Introduction) of all compact topological surfaces. In other words, for any finite family of integers $g_i\geqslant 0$ and $g_j'\geqslant 0$ we give an example of an $\mathbb {R}$-surface whose real locus is diffeomorphic to a disjoint union of the ${\mathbb S}_{g_i}$s and ${\mathbb V}_{g_i'}$s. We will explain the rationale behind the choice of these particular algebraic models in subsequent sections. Note that these algebraic models are not all of negative Kodaira dimension because Theorem 4.4.14 gives constraints on the topology of the real locus of such a variety. On the other hand, for each of these real algebraic models $(X,{\sigma })$ the complex surface X is simply connected in the Euclidean topology.

Fig. 4.2

Quadric sphere $\mathbb {S}^2$

Fig. 4.3

Hyperboloid in $\mathbb {R}^3$ whose projective completion is the quadric torus $Q_{2,2}(\mathbb {R})\subset \mathbb {P}^3(\mathbb {R})$

• 1. The real locus of $(X,{\sigma })$ is connected and non empty.

  • (a) The real projective plane $\mathbb {R}\mathbb {P}^2 \approx \mathbb {P}^2(\mathbb {R})$, $X=\mathbb {P}^2(\mathbb {C})$.

  • (b) The quadric sphere in $\mathbb {R}^3_{x,y,z}$

    $$ \mathbb {S}^2 \approx \mathcal {Z}(x^2+y^2+z^2-1) $$

    whose projective completion is the quadric sphere in $\mathbb {P}^3(\mathbb {R})$

    $$ \mathbb {S}^2 \approx Q_{3,1}(\mathbb {R}) $$

    where

    $$ X=Q_{3,1} :=\mathcal {Z}(x^2+y^2+z^2-w^2)\subset \mathbb {P}^3_{w:x:y:z}(\mathbb {C})\;. $$

  • (c) The quadric torus

    $$ {\mathbb T}^2\approx Q_{2,2}(\mathbb {R})\subset \mathbb {P}^3(\mathbb {R})\;, $$

    where $X=Q_{2,2} :=\mathcal {Z}(x^2+y^2-z^2-w^2)\subset \mathbb {P}^3(\mathbb {C})$. This is the projective completion of the hyperboloid of revolution $\mathcal {Z}(x^2+y^2-z^2-1)\subset \mathbb {R}^3$.

  • (d) The Klein bottle is a blow up of the projective plane ${\mathbb K}^2\approx B_P\mathbb {P}^2(\mathbb {R})$ at a point $P\in \mathbb {P}^2(\mathbb {R})$—see Example 4.2.18. The blow-up of the projective plane at a point is also a Hirzebruch surface of index 1 and ${\mathbb K}^2\approx \mathbb {F}_1(\mathbb {R})$. See Exercise 4.2.11.

  • (e) The non orientable surface of genus g can be obtained from the blow up of the projective plane in $g-1$ points

    $$ {\mathbb V}_g \approx B_{P_1,\dots ,P_{g-1}}\mathbb {P}^2(\mathbb {R}) $$

    where $P_1,\dots ,P_{g-1}\in \mathbb {P}^2(\mathbb {R})$ as in Example 4.2.18.

  • (f) The orientable surface ${\mathbb S}_g$ of genus $g\leqslant 10$ can be obtained as the real locus of a K3 surface; see Section 4.5 for more details.

  • (g) The orientable surface ${\mathbb S}_g$ of arbitrary genus g can be obtained as the real locus of a proper elliptic surface over $\mathbb {P}^1$: see Section 4.6 for more details.

• 2. The real locus of $(X,{\sigma })$ is empty or not connected.

  • (a) The empty set is the real locus of the quadric

    $$ \varnothing =Q_{4,0}(\mathbb {R}) \subset \mathbb {P}^3(\mathbb {R}) $$

    where

    $$ X=Q_{4,0}:=\mathcal {Z}(x^2+y^2+z^2+w^2)\subset \mathbb {P}^3(\mathbb {C})\;. $$

  • (b) For any $s\geqslant 2$ the disjoint union of s spheres can be obtained as the real locus of the projective completion of the conic bundle

    $$ \mathcal {Z}(x^2+y^2-f(t)) \subset \mathbb {R}^3 $$

    where $f(t)=-\prod _{i=1,\dots ,2s}(t-i)$. See Example 4.2.8 for more details.

  • (c) The disjoint union of a finite number $s\geqslant 2$ of spheres and non orientable surfaces can be obtained as the real locus of the surface described in Example (2b) by blowing up real points.

  • (d) The disjoint union of four spheres is the real locus of a certain del Pezzo surface $(X,{\sigma _\mathbb {P}}|_{X})$ of degree 2 (the exact values of the coefficients correspond to the diagram in Figure 4.4). Specifically, X is a projective completion in a weighted projective space $\mathbb {P}(1,1,1,2)$ (i.e. the quotient of $\mathbb {C}^4_{z_0,\dots ,z_3}$ by the $\mathbb {C}^*$ action given by $(z_0,\dots ,z_3)\mapsto (\lambda z_0,\lambda z_1,\lambda z_2,\lambda ^2 z_3)$) of the affine surface of equation

    $$\begin{aligned} z^2+8x^4+20x^2y^2-24x^2+8y^4-24y^2+16,25=0\;. \end{aligned}$$

    (4.6)

    Note that by Proposition 2.3.22 this surface is a geometrically rational non rational $\mathbb {R}$-surface as in Definition 2.3.18. It is also a minimal $\mathbb {R}$-surface, see Definition 4.3.10.

  • (e) The disjoint union of a finite number of orientable and non orientable surfaces can be obtained as the real locus of a surface obtained from an elliptic surface fibered over $\mathbb {P}^1$ as in Section 4.6 by blowing up real points.

Fig. 4.4

A del Pezzo surface of degree 2 with four connected components

Remark 4.2.20

All compact topological surfaces therefore have a real algebraic model $(X,{\sigma })$ whose complex surface X is simply connected in the Euclidean topology. We now present a selection of models for which X is not simply connected.

• 1. All topological types which do not contain an orientable connected component of genus strictly greater than 1 can be realised by a real conic bundle over a curve B of non zero genus g(B). See Theorem 4.4.14 for more details.

• 2. Only a finite number of topological types can be realised by real Enriques surfaces. See Theorem 4.5.16 for more details.

• 3. All topological types can be realised by real elliptic surfaces over a curve B of non zero genus g(B): see Section 4.6 for more details.

4.3 $\mathbb {R}$-Minimal Surfaces

We refer the interested reader to [Kol01a, Section 2]—containing most of the preprint [Kol97]—for a presentation of minimal surfaces based on Mori theory.

Definition 4.3.1

The inverse operation of a blow-up is called a contraction: see Appendix F for more details. A contraction $\pi :X \rightarrow Y$ is an $\mathbb {R}$-contraction if and only if the birational morphism $\pi$ is an $\mathbb {R}$-morphism.

Of course, not every curve can be contracted to a non singular point, despite the fact that it is possible to blow up any non singular point.

Definition 4.3.2

($(-n)$-curves)

• 1. A $(-1)$-curve L on  a non singular complex projective surface X is a curve isomorphic to $\mathbb {P}^1(\mathbb {C})$ whose self intersection $L\cdot L$ is $-1$. In particular, L is rational, irreducible and non singular.

• 2. A $(-1)$-real curve L on a non singular projective $\mathbb {R}$-surface $(X,{\sigma })$ is a complex $(-1)$-curve which is stable under ${\sigma }$. We equip any such curve with the restriction of ${\sigma }$.

• 3. More generally, for any natural number n, a $(-n)$-curve L on X is a curve isomorphic to $\mathbb {P}^1$ such that $L\cdot L=-n$.

Consider a point $P\in X$ and let $\pi _P:B_PX\rightarrow X$ be the blow up of X centred at P. It follows from Proposition 4.1.30 that the exceptional line $E_P:=\pi ^{-1}(P)$ is a $(-1)$-curve.

Exercise 4.3.3

Prove that any $(-1)$-curve C on a surface X satisfies $(K_X\cdot C)=-1$.

We have the following criterion for curve contractions on a complex surface:

Theorem 4.3.4

(Castelnuovo’s criterion) Suppose that Y is a non singular complex projective surface and that $E\subset Y$ is a $(-1)$-curve. There is then a projective surface X and a morphism $\pi :Y\rightarrow X$ such that $P=\pi (E)$ is a non singular point of X and $\pi$ is the blow up of X centred on P.

We refer to  [Bea78, II.17] for a proof. More generally, Grauert’s theorem enables us to contract curves to not necessarily non singular points.

Theorem 4.3.5

(Grauert) Let $E\subset Y$ be a connected reduced projective curve on a non singular complex projective surface Y and let $E=\sqcup E_i$ be its decomposition into irreducible components.

There is then a (not necessarily projective) normal algebraic surface X and a birational map $\pi :Y\rightarrow X$ such that $P=\pi (E)$ is a point of X and the restriction of $\pi$ to $Y\setminus E\rightarrow X\setminus P$ is an isomorphism if and only if the matrix $(E_i\cdot E_j)_{i,j}$ is negative definite.

See [BHPVdV04, Theorem III.2.1] for more details.

Corollary 4.3.6

For any non singular $\mathbb {R}$-surface $(Y,\tau )$ it follows from Castelnuovo’s criterion that any $(-1)$-real curve or any pair of disjoint conjugate $(-1)$-curves can be contracted to a non singular $\mathbb {R}$-surface $(X,{\sigma })$.

Proof

See [Sil89, II.6.2].    $\square$

Example 4.3.7

(See Example 4.2.18) In the first case of Corollary 4.3.6 we have that $Y(\mathbb {R})\approx X(\mathbb {R})\#\mathbb {R}\mathbb {P}^2$ and in the second case $Y(\mathbb {R})\approx X(\mathbb {R})$.

Proposition 4.3.8

(Strong factorisation) Any birational map between non singular complex projective algebraic surfaces factorises as a sequence of blow ups and contractions of $(-1)$-curves. More precisely, if $f :X \dashrightarrow Y$ is a birational map then there is a non singular complex algebraic surface Z and birational morphisms $\pi _1 :Z \rightarrow X$ and $\pi _2:Z \rightarrow Y$ such that the diagram below is commutative.

Proof

See [Bea78, II.12].    $\square$

Corollary 4.3.9

(Strong factorisation for $\mathbb {R}$-surfaces) Any birational real map between non singular projective $\mathbb {R}$-surfaces factorises as a sequence of blow ups of real points, blow ups of pairs of conjugate points, contractions of real $(-1)$-curves and contractions of disjoint conjugate pairs of $(-1)$-curves. More precisely, if $f :(X,{\sigma })\dashrightarrow (Y,\tau )$ is a real birational map then there is a non singular projective algebraic $\mathbb {R}$-surface $(Z,\sigma _Z)$ and $\mathbb {R}$-birational morphisms $\pi _1 :Z \rightarrow X$ and $\pi _2:Z \rightarrow Y$ such that the diagram below commutes

Proof

See [Sil89, II.6.4].    $\square$

Definition 4.3.10

(Minimal surfaces)

• 1. A non  singular complex surface X is said to be minimal if and only if it has no contraction to a non singular surface.

• 2. A non singular $\mathbb {R}$-surface $(X,{\sigma })$ is said to be minimal if and only if it has no $\mathbb {R}$-contraction to a non singular $\mathbb {R}$-surface.

Remark 4.3.11

Riemannian geometers also study minimal surfaces, by which they mean (compact) surfaces with a certain boundary whose area is minimal amongst (compact) surfaces with the same boundary in a given Riemannian manifold: the best known example of this phenomenon is soap bubbles. Obviously, there is no link between these two types of minimal surface.

Remark 4.3.12

By Theorem 4.3.4, a non singular complex surface X is minimal if and only if it contains no $(-1)$-curves. By Corollary 4.3.6, a non singular $\mathbb {R}$-surface is minimal if and only if it contains neither a real $(-1)$-curve nor a pair of disjoint conjugate $(-1)$-curves.

Remark 4.3.13

If the complex surface X is minimal then $(X,{\sigma })$ is $\mathbb {R}$-minimal, but the converse is false: this can be seen by considering an $\mathbb {R}$-surface with two conjugate $(-1)$-curves which meet in a real point. For example, the irreducible components of a singular fibre with equation of the form $x^2+y^2=0$ in a conic bundle are non real conjugate $(-1)$-curves meeting in a real point (0, 0). The complex surface is not minimal because we can contract one of the $(-1)$-curves, but there is no contraction to a non singular surface which respects the real structure.

Exercise 4.3.14

We use the same notations as in Example 4.2.6. If the polynomial f is of odd degree then Remark 4.2.7 implies that there is a fibre containing two real $(-1)$-curves. In particular, the $\mathbb {R}$-surface is not minimal.

Exercise 4.3.15

(Continuation of Exercise 4.2.11) Prove that if the total space X of a conic bundle over $\mathbb {P}^1$ is a non singular projective surface then it has $8-K_X^2$ singular fibres.

Definition 4.3.16

Let $(X,{\sigma })$ be  a non singular projective $\mathbb {R}$-surface, let $(B,\sigma _B)$ be a non singular $\mathbb {R}$-curve and let g be a natural number.

• 1. We say that a morphism of complex varieties $\pi :X\rightarrow B$ is a genus g bundle if its general fibre is a non singular projective curve of genus g or in other words if there is a non empty Zariski open set U in B such that $\forall x\in U$, $\pi ^{-1}(x)$ is isomorphic to a projective non singular curve of genus g.

• 2. An $\mathbb {R}$-morphism $\pi :(X,{\sigma })\rightarrow (B,\sigma _B)$ is said to be a real genus g bundle if the map of complex varieties $\pi :X\rightarrow B$ is a genus g bundle.

• 3. We say that the fibered complex surface $(X,\pi )$ (resp. the fibration $\pi$) is minimal if no fibre of $\pi$ contains a $(-1)$-curve. We sometimes say that $(X,\pi )$ is relatively minimal to underline the fact that this minimality is relative to the morphism.

• 4. We say that the fibered $\mathbb {R}$-surface $((X,{\sigma }),\pi )$ is minimal (or relatively minimal) if no fibre of $\pi$ contains either a real $(-1)$-curve or a pair of disjoint conjugate $(-1)$-curves.

Exercise 4.3.17

Let $\pi :X\rightarrow B$ be a complex surface which is a genus g bundle. Suppose that $(X,\pi )$ is relatively minimal and the surface X is not minimal. As no fibre of $\pi$ contains a $(-1)$-curve there is a horizontal $(-1)$-curve E, by which we mean that the image $\pi (E)$ is not a point. In this case B is a rational curve and $g=0$. In particular, the complex surface X is rational.

Exercise 4.3.18

Let $\pi :X\rightarrow B$ be a complex surface with a genus g bundle structure. Suppose that some fibre of $\pi$ contains a pair of non disjoint $(-1)$-curves. Prove that we then have that $g=0$.

Exercise 4.3.19

• 1. Prove that any conic bundle is a surface with a genus 0 bundle structure.

• 2. Prove that any projective non singular $\mathbb {R}$-surface with a genus 0 bundle structure is birationally equivalent to a real conic bundle. (See [Sil89, Corollary V.2.7].)

Proposition 4.3.20

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface with a real genus g bundle structure $\pi :X\rightarrow B$. We assume moreover that all the fibres of $\pi$ are geometrically connected.

• 1. If $g\geqslant 1$ then the $\mathbb {R}$-surface $(X,{\sigma })$ is relatively minimal if and only if the complex surface X is relatively minimal.

• 2. If $g=0$ and $(X,{\sigma })$ is relatively minimal then any fibre F of $\pi$ containing a $(-1)$-curve E is necessarily of the form $F=E+{\sigma }E$ with $E\cdot {\sigma }E =1$.

Proof

See [Man67, Man86] or [Sil89, V.1.6].    $\square$

Corollary 4.3.21

• 1. A complex conic  bundle $(X,\pi )$ is minimal if and only if $\pi$ has no singular fibres.

• 2. An real conic bundle $((X,{\sigma }),\pi )$ is minimal if and only if all its singular fibres are real (i.e. lie over $B(\mathbb {R})$) and no irreducible component of a singular fibre of $\pi$ is a real $(-1)$-curve.

Proof

All fibres are geometrically connected and a conic has at most two irreducible components.    $\square$

Recall that we denote by G the Galois group ${\text {Gal}}(\mathbb {C}|\mathbb {R})$ acting non trivially on X via the real structure. If X has an $\mathbb {R}$-bundle structure $\pi :X\rightarrow B$ over a projective $\mathbb {R}$-curve, then we denote by $\mathrm{{Pic}}(X/B)$ or $\mathrm{{Pic}}(X/\pi )$, the relative Picard group⁶

$$ \mathrm{{Pic}}(X/B)=\mathrm{{Pic}}(X)/\pi ^*(\mathrm{{Pic}}(B))\;. $$

Proposition 4.3.22

A real del Pezzo surface $(X,{\sigma })$ is minimal if and only if $\mathrm{{Pic}}(X)^G =\mathbb {Z}$. A real conic bundle $(X,{\sigma })\rightarrow (B,\sigma _B)$ is minimal if and only if $\mathrm{{Pic}}(X/B)^G =\mathbb {Z}$.

Proof

Exercise.    $\square$

Theorem 4.3.23

(Minimal $\mathbb {R}$-surfaces) Let $(X,{\sigma })$ be a non singular minimal projective $\mathbb {R}$-surface. The variety $(X,{\sigma })$ is then isomorphic to exactly one $\mathbb {R}$-surface from the following list.

$\bullet$ ${\kappa }(X)=-\infty$ (section 4.4)

• 1. $(\mathbb {P}^2(\mathbb {C}),{\sigma _\mathbb {P}})$;

• 2. $(Q_{3,1},{\sigma _\mathbb {P}}|_{Q_{3,1}})$ ;

• 3. $(\mathbb {F}_n,\sigma _{\mathbb {F}_n})$ where $\mathbb {F}_n$ is a real Hirzebruch surface such that $n\ne 1$;

  (in cases 1, 2 and 3, $(X,{\sigma })$ is rational. See Section 4.4 for more details)

• 4. $(X,{\sigma })$ such that X is a complex rational surface and $X(\mathbb {R})=\emptyset$, namely $Q_{4,0}$, $Q_{3,0}\times \mathbb {P}^1$, or a surface which is a real conic bundle over a conic with empty real locus $\pi :X\rightarrow (\mathbb {P}^1(\mathbb {C}),{\sigma _\mathbb {P}}')$ where ${\sigma _\mathbb {P}}'$ is the involution of $\mathbb {P}^1(\mathbb {C})$ defined by $(x_0:x_1) \mapsto (-\overline{x_1}:\overline{x_0})$ as in Remark 2.1.41;

• 5. a del Pezzo surface of degree 1 or 2 such that $\rho _\mathbb {R}(X)=1$;

• 6. an real conic bundle $\pi :X\rightarrow (\mathbb {P}^1,{\sigma _\mathbb {P}})$ with an even number of singular fibres $2r\geqslant 4$ such that $\rho _\mathbb {R}(X/\pi )=1$ or in other words $\rho _\mathbb {R}(X)=2$;

  (in cases 4, 5 and 6, $(X,{\sigma })$ is geometrically rational but not rational. See Section 4.4 for more details)

• 7. An real conic bundle $\pi :X\rightarrow B$ such that $g(B)>0$ and such that $\rho _\mathbb {R}(X/\pi )=1$ or in other words $\rho _\mathbb {R}(X)=2$;

  (in case 7, $(X,{\sigma })$ is a uniruled surface which is not geometrically rational. See Section 4.4 for more details)

$\bullet$ ${\kappa }(X)=0$ (See Section 4.5)

• 8. X is a K3 surface, see Definition 4.5.3;

• 9. X is an Enriques surface see Definition 4.5.13;

• 10. X is an abelian surface, see Definition 4.5.22;

• 11. X is a bi-elliptic surface, see Definition 4.5.28.

$\bullet$ ${\kappa }(X)=1$ (See Section 4.6)

• 12. X is a properly elliptic surface, see Definition 4.6.10.

$\bullet$ ${\kappa }(X)=2$ (section 4.7)

• 13. X is a surface of general type, see Definition 4.1.4.

Proof

See [Kol01a, Theorem 30].    $\square$

The above theorem is the basis for the classification of real and complex projective algebraic surfaces. See [BHPVdV04, Chapter VI] for the classification of compact complex analytic surfaces. The classification of projective surfaces in positive characteristic was carried out in a series of articles [Mum69, BM77, BM76, BH75]—see [Băd01] for a summary.

Exercise 4.3.24

($\mathbb {R}$-elementary transformations) Let $(X,{\sigma })$ be a Hirzebruch surface of index n and let $P\in X$ be a real point. The blow up of X centred at P transforms the fibre through P into a real $(-1)$-curve which can then be contracted to a new non singular $\mathbb {R}$-surface $X'$. Prove that if $n>0$ then $X'$ is a Hirzebruch surface of index $n+1$ (resp. $n-1$) if P lies on the exceptional section $E_\infty$ (resp. if P does not lie on this section). If $n=0$ there is no exceptional section and the surface obtained from this transformation is $\mathbb {F}_1$ for any P. The $\mathbb {R}$-surfaces X and $X'$ are birationally equivalent and minimal.

Similarly, let P and ${\sigma }(P)$ be two conjugate non real points on X and let $X''$ be the surface obtained by the elementary $\mathbb {R}$-transformation consisting of blowing up the two points and then contracting the conjugate non real $(-1)$-curves thus obtained. Calculate the index of the Hirzebruch surface obtained, distinguishing the cases where the two points do or do not lie on the exceptional section.

4.3.1 Deformation Families

In the following sections we study the topology of real algebraic surfaces and their deformation families. We also state some theorems on the group of algebraic cycles $H^1_{\mathrm {alg}}$, defined in Section 3.7, which enable us to compare the behaviour of various different families of surfaces. See [Man97, MvH98, Man00, Man03] for more details.

Definition 4.3.25

(Deformations)

• 1.

  • A complex analytic variety Y is a deformation of a complex variety X if and only if there is a complex analytic variety $\mathcal {M}$, a proper holomorphic submersion

    $$ \pi :\mathcal {M}\rightarrow D=\{z\in \mathbb {C}\mathrel {}\mid \mathrel {}| z | <1\} $$

    and a point $z_0\in D$ such that $X=\pi ^{-1}(0)$ and $Y=\pi ^{-1}(z_0)$.

  • An analytic $\mathbb {R}$-variety $(Y,\tau )$ is a deformation of an analytic $\mathbb {R}$-variety $(X,{\sigma })$ if and only if there is an analytic $\mathbb {R}$-variety $(\mathcal {M},\sigma _\mathcal {M})$, a proper holomorphic submersion $\pi :\mathcal {M}\rightarrow D$ and a point $z_0\in [-1,1]=D(\mathbb {R})$ such that $\sigma _D\circ \varphi = \varphi \circ \sigma _\mathcal {M}$, $X=\pi ^{-1}(0)$ and $Y=\pi ^{-1}(z_0)$. In particular we have that ${\sigma }=\sigma _\mathcal {M}|_X$ and $\tau =\sigma _\mathcal {M}|_Y$.

• 2. Two varieties X and Y are said to be deformation equivalent if and only if there is a finite family of varieties $Z_i$ $i=1\dots l$ such that $Z_1=X$, $Z_l=Y$ and for every i, $Z_{i+1}$ is either a deformation of $Z_i$ or isomorphic to $Z_i$.

Remark 4.3.26

The definition of deformation equivalence given above is justified by the fact that two varieties that are deformation equivalent do not necessarily belong to the the same non singular deformation family. For example, Horikawa proved in [Hor75] that the space of numerical quintics has two irreducible components of dimension 40 which meet along a subspace of dimension 39.

Definition 4.3.27

Two complex  surfaces X and Y are said to belong to the same complex family if and only if X and Y are fibres of a proper holomorphic submersion (sometimes called a large deformation)

$$ \pi :\mathcal {M}\rightarrow B $$

over an irreducible complex analytic variety B.

Two $\mathbb {R}$-surfaces $(X,{\sigma })$ and $(Y,\tau )$ belong to the same real family if and only if they are fibres of some equivariant large deformation whose base has connected real locus.

Theorem 4.3.28

(Ehresmann’s fibration theorem) Let $f:\mathcal {M}\rightarrow B$ be  a differentiable map between manifolds: f, $\mathcal {M}$ and B are supposed at least $\mathcal {C}^2$ and at most $\mathcal {C}^\infty$. If f is a surjective proper submersion then f is a locally trivial fibration (Definition C.3.5).

Proof

See [Ehr51, Ehr95].    $\square$

The Galois group $G={\text {Gal}}(\mathbb {C}| \mathbb {R})$ acts on X (resp. Y, resp. $\mathcal {M}$) by involution ${\sigma }$ (resp. $\tau$, resp. $\sigma _\mathcal {M}$). Adapting the proof of Ehresmann’s fibration theorem, we can prove that if two $\mathbb {R}$-varieties $(X,{\sigma })$ and $(Y,\tau )$ are deformation equivalent then X is diffeomorphic to Y via a G-equivariant diffeomorphism [Dim85, Lemma 4] and in particular $X(\mathbb {R})$ is diffeomorphic to $Y(\mathbb {R})$: the converse is false and there are many known examples where it fails.

In general, every complex deformation family corresponds to many real families. For example, there is a unique complex family of Enriques surfaces, but over 200 real families of real Enriques surfaces. See [DIK00] for more details.

Question 4.3.29

(Def=Diff) The Def$=$Diff problem is the following: if two complex surfaces X and Y are diffeomorphic, are they necessarily deformation equivalent?

See [Man01] for the proof that this is not always the case. See [KK02, Cat03, Cat08] for other examples. The precise real version of this question was given by Kharlamov.

Definition 4.3.30

(Quasi-simplicity of $\mathbb {R}$-surfaces) An $\mathbb {R}$-surface $(X,{\sigma })$ is said to be quasi-simple if and only if any $\mathbb {R}$-surface $(Y,\tau )$ such that there is a G-equivariant diffeomorphism $(X,{\sigma })\rightarrow (Y,\tau )$ is deformation equivalent to $(X,{\sigma })$ whenever the complex surface Y is deformation equivalent to X.

The following definition is useful for expressing classifications of topological types of real surfaces appearing in a given class of complex surfaces.

Definition 4.3.31

(Morse simplification) Given a  compact topological surface S without boundary, (which is neither assumed connected nor orientable) a topological Morse simplification of S is a Morse transformation that decreases the total Betti number by two. There are two types of Morse simplifications:

• removing a spherical component $\mathbb {S}^2 \rightarrow \varnothing$,

• contracting a handle ${\mathbb S}_{g+1} \rightarrow {\mathbb S}_g$ or ${\mathbb V}_{q+2} \rightarrow {\mathbb V}_q$.

Definition 4.3.32

(Topological type, extremal topological type) A topological type is a  class of $\mathbb {R}$-surfaces with diffeomorphic real loci. Given a class of complex surfaces (see Example 4.0.1) a topological type is said to be extremal if it cannot be obtained by topological Morse simplification from a topological type belonging to the same class of complex surfaces.

Example 4.3.33

In the diagrams shown in Figures 4.11 and 4.12, the extremal topological types are those corresponding to points with no ascending adjacent edge.

Remark 4.3.34

There is a stronger version of topological types in the literature which states that two $\mathbb {R}$-surfaces $(X,{\sigma })$ and $(Y,\tau )$ are of the same topological type if and only if there is an equivariant diffeomorphism $(X,{\sigma })\rightarrow (Y,\tau )$. It is then immediate that $X(\mathbb {R})$ is diffeomorphic to $Y(\mathbb {R})$, but the converse is false. See [DIK00] for more details.

Remark 4.3.35

When the surfaces being considered belong to the same complex deformation class the reader should be aware that Morse simplification is abstract in the sense that the existence of a continuous deformation realising the topological transformation is not guaranteed. It is simply a practical definition helping us list topological types. In certain special cases it is however possible to realise Morse transformations by explicit deformation: see Theorem 4.6.13 for more details.

4.4 Uniruled and Rational Surfaces (${\kappa }=-\infty$)

The aim of this section is to classify topological types of rational $\mathbb {R}$-surfaces and more generally classify $\mathbb {R}$-surfaces of negative Kodaira dimension using the topological type of their real locus. The complete classification of non singular projective surfaces of negative Kodaira dimension is Theorem 4.4.14. The main intermediate result is Theorem 4.4.15, sometimes described as a generalisation of Comessatti’s theorem 4.4.16, which bounds the genus of an orientable surface contained in the real locus of a rational surface. There are basically two different approaches to the proof of this classification. One is based on reduction to minimal surfaces followed by case by case analysis as in Theorem 4.3.23. The other is based on the action of the Galois group on the cohomology ring of X, and it is this second proof that will be presented in this section. Both methods have their advantages.

4.4.1 Rational $\mathbb {R}$-Surfaces

Let us mention two survey articles on rational $\mathbb {R}$-surfaces⁷: [Man17a] (continuing [Hui11]) dealing with topological classification and [BM14] dealing with birational geometry. We now specialise Definition 2.3.18 to surfaces.

Definition 4.4.1

(Rational and uniruled $\mathbb {R}$-surfaces) Let $(X,{\sigma })$ be  an algebraic $\mathbb {R}$-surface.

• 1. The $\mathbb {R}$-surface $(X,{\sigma })$ is said to be rational or $\mathbb {R}$-rational if and only if it is birationally equivalent to the $\mathbb {R}$-projective plane $(\mathbb {P}^2(\mathbb {C}),{\sigma _\mathbb {P}})$, by which we mean there is a birational map of $\mathbb {R}$-surfaces

  $$ (X,{\sigma })\dashrightarrow (\mathbb {P}^2(\mathbb {C}),{\sigma _\mathbb {P}}) \;. $$

  The real algebraic surface $X(\mathbb {R})$ is then rational (Definition 1.3.37).

• 2. The $\mathbb {R}$-surface $(X,{\sigma })$ is said to be geometrically rational or $\mathbb {C}$-rational if and only if it is $\mathbb {C}$-birationally equivalent to the projective plane $\mathbb {P}^2(\mathbb {C})$, or in other words if and only if there is a birational map of complex surfaces

  $$ X \dashrightarrow \mathbb {P}^2(\mathbb {C})\;. $$

  The real algebraic surface $X(\mathbb {R})$ is then geometrically rational if it is Zariski dense in X, since the complex algebraic surface X, which is a complexification of $X(\mathbb {R})$, is then rational (Definition 1.3.37).

• 3. The $\mathbb {R}$-surface $(X,{\sigma })$ is uniruled if and only if it is dominated by a cylinder of dimension 2, or in other words if and only if there exists an $\mathbb {R}$-curve $(Y,\tau )$ and a rational map of $\mathbb {R}$-varieties

  $$ (Y\times \mathbb {P}^1,\tau \times {\sigma _\mathbb {P}}) \dashrightarrow (X,{\sigma })$$

  whose image is dense in the Zariski topology.

Remark 4.4.2

Unlike rationality, uniruledness is invariant under change of base field: an $\mathbb {R}$-surface $(X,{\sigma })$ is uniruled if and only if the complex surface X is uniruled. See [Deb01, §4.1, Remark 4.2(5)] for more details.

Remark 4.4.3

If X is uniruled then ${\kappa }(X)=-\infty$ because X is dominated by a ruled variety. In dimension 2 the converse holds and in fact a stronger result turns out to be true: any surface X such that ${\kappa }(X)=-\infty$ is birationally ruled, i.e. birationally equivalent to a cylinder $Y\times \mathbb {P}^1$ of dimension 2. See [Bea78, Exemple VII.3 and Chapitre III] for more details. A complex surface is therefore uniruled if and only if it is birationally ruled and such surfaces are often said to be “ruled” in the literature. The notion of “ruled surface” becomes difficult to handle over the real numbers: a conic bundle can by $\mathbb {C}$-birationally equivalent to a ruled surface without being $\mathbb {R}$-birationally equivalent to it—we prove in Proposition 4.4.10 that this is the case in Example 4.2.8 whenever $s\geqslant 2$. This example is however uniruled over both $\mathbb {R}$ and $\mathbb {C}$.

Remark 4.4.4

It follows from Definition 1.3.37 and Proposition 4.3.8 that a complex surface is rational if and only if it is obtained by applying a sequence of blow ups and contractions of $(-1)$-curves to the complex projective plane. An $\mathbb {R}$-surface $(X,{\sigma })$ is therefore geometrically rational if and only if it can be obtained from the projective plane by a sequence of not necessarily real blow ups and contractions. The function field K(X) of the complex surface X is then isomorphic to the field of rational functions $\mathbb {C}(X_1,X_2)$. If we also require that these blow ups and contractions should be real⁸ then the $\mathbb {R}$-surface $(X,{\sigma })$ is rational. In this case the $\mathbb {R}$-algebra of restrictions to $X(\mathbb {R})$ of elements of K(X) is isomorphic as an $\mathbb {R}$-algebra to the field of rational fractions $\mathbb {R}(X_1,X_2)$.

Remark 4.4.5

In Definition 4.4.1 the complex surface X is not assumed to be complete, projective or non singular. We state a classification theorem for non singular projective X (Theorem 4.4.14) below. We will return to singular varieties at the end of this section and we will deal with affine varieties in Chapter 5 (Definition 5.5.2).

Remark 4.4.6

Let F be a real algebraic surface and let $(X,{\sigma })$ be a complexification of F. The surface F is then rational if and only if $(X,{\sigma })$ is $\mathbb {R}$-rational.

Remark 4.4.7

By definition of $\mathbb {R}$-morphisms, any rational $\mathbb {R}$-surface is geometrically rational. Similarly, as the product $\mathbb {R}$-surface $\mathbb {P}^1\times \mathbb {P}^1$ is birationally equivalent to the $\mathbb {R}$-surface $\mathbb {P}^2$, it is immediate that any geometrically rational $\mathbb {R}$-surface is uniruled.

Theorem 4.4.8

Let $(X,{\sigma })$ be  a non singular projective $\mathbb {R}$-surface such that ${\kappa }(X)=-\infty$. The following then hold.

• 1. X is uniruled and $(X,{\sigma })$ is birationally equivalent to a real conic bundle $\pi :X\rightarrow B$ with $g(B)=q(X)$;

• 2. $(X,{\sigma })$ is geometrically rational if and only if $q(X)=0$;

• 3. $(X,{\sigma })$ is rational if and only if $q(X)=0$ and $X(\mathbb {R})$ is connected and non empty.

Proof

• 1. By Remark 4.4.3, any complex surface such that ${\kappa }(X)=-\infty$ is uniruled (and indeed birationally ruled). Comessatti proved in [Com12] that any $\mathbb {R}$-surface $(X,{\sigma })$ such that X is birationally ruled is $\mathbb {R}$-birationally equivalent to an real conic bundle $\pi :X\rightarrow B$ such that $g(B)=q(X)$. See [Sil89, Chapter V] for more details.

• 2. This follows from the classification of complex surfaces. See [Bea78, Chapitre IV] for more details.

• 3. It remains to prove that if the complex surface X is rational then $(X,{\sigma })$ is rational if and only if $X(\mathbb {R})$ is connected and non empty. As the number of connected components of the real locus is invariant under birational maps defined over $\mathbb {R}$ this condition is necessary. It is sufficient by [Sil89, Corollary IV.6.5].

   $\square$

Corollary 4.4.9

Let $(X,{\sigma })$ be a uniruled non geometrically rational $\mathbb {R}$-surface. The surface $(X,{\sigma })$ is then birationally equivalent to a conic bundle $\pi :X\rightarrow B$ such that $g(B)=q(X)>0$.

We refer the interested reader to [Com12, Com14, Isk65, Isk67, Man67, Man86, Sil89, Kol97, Kol01a,DK02, Wel03, BM11] for classical and recent results on the classification of conic bundles.

Recall that ${\mathbb V}_g=\#^{g}\mathbb {R}\mathbb {P}^2$ denotes the non orientable surface of genus g whose Euler characteristic is $2-g$. For example, $g(\mathbb {R}\mathbb {P}^2)=1$ and $g({\mathbb K}^2)=2$. We now list the real algebraic models of Example 4.2.19 which are uniruled.

Proposition 4.4.10

(Examples of uniruled surfaces) We will now classify the real algebraic models $(X,{\sigma })$ described in Example 4.2.19 for each topological type of the real locus.

• 1. $(X,{\sigma })$ is an $\mathbb {R}$-rational surface.

  • (a) The real projective plane $X=\mathbb {P}^2(\mathbb {C})$, ${\sigma }={\sigma _\mathbb {P}}$, $X(\mathbb {R})=\mathbb {P}^2(\mathbb {R})$.

  • (b) The quadric sphere $X=Q_{3,1}\subset \mathbb {P}^3(\mathbb {C})$, ${\sigma }= {\sigma _\mathbb {P}}|_{Q_{3,1}}$, $X(\mathbb {R})= \mathbb {S}^2$.

  • (c) The quadric torus $X=Q_{2,2}$, ${\sigma }={\sigma _\mathbb {P}}|_{Q_{2,2}}$, ($(X,{\sigma })$ is isomorphic to the $\mathbb {R}$-surface $(\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C}),{\sigma _\mathbb {P}}\times {\sigma _\mathbb {P}})$ and $Q_{2,2}(\mathbb {R})= {\mathbb T}^2$.

  • (d) The torus considered as the real locus of even index Hirzebruch surfaces with their canonical real structure. $\mathbb {F}_{2k}(\mathbb {R})\approx {\mathbb T}^2$.

  • (e) The Klein bottle considered as the real locus of the blow up of $\mathbb {P}^2(\mathbb {R})$ at a point $B_P\mathbb {P}^2(\mathbb {R})= {\mathbb K}^2$.

  • (f) The Klein bottle considered as the real locus of the Hirzebruch surfaces of odd index $\mathbb {F}_{2k+1}(\mathbb {R})= {\mathbb K}^2$.

  • (g) The non orientable surface of genus $g>0$ obtained by blowing up $\mathbb {P}^2(\mathbb {R})$: $B_{P_1,\dots ,P_{g-1}}\mathbb {P}^2(\mathbb {R})= {\mathbb V}_g$ for any $P_1,\dots ,P_{g-1}\in \mathbb {P}^2(\mathbb {R})$.

  • (h) The non orientable surface $g>0$ obtained by blowing up the quadric sphere: $B_{P_1,\dots ,P_{g}}Q_{3,1}(\mathbb {R})= {\mathbb V}_g$ for any $P_1,\dots ,P_{g}\in Q_{3,1}(\mathbb {R})$.

• 2. $(X,{\sigma })$ is geometrically rational but not rational.

  • (a) The empty set considered as the real locus of the quadric $X=Q_{4,0}$, ${\sigma }={\sigma _\mathbb {P}}|_{Q_{4,0}}$, $X(\mathbb {R})=\varnothing$.

  • (b) The disjoint union of $s>1$ spheres considered as the real locus of the projective completion of the conic bundle

    $$ \mathcal {Z}\left( x^2+y^2+\prod _{i=1,\dots ,2s}(t-i)\right) \subset \mathbb {R}^3\;. $$

  • (c) The disjoint union of a finite union of $s>1$ spheres and non orientable surfaces considered as the real locus of the surface obtained by blowing up real points in the above example.

  • (d) The disjoint union of four spheres considered as the real locus of the degree 2 del Pezzo surface of equation (4.6), Sect. 4.2.1.

• 3. $(X,{\sigma })$ is a uniruled non geometrically rational variety.

  • (a) The disjoint union  of a finite number $s\geqslant 0$ of spheres, toruses and Klein bottles considered as the real locus of conic bundle over a curve of non zero geometric genus.

  • (b) The disjoint union of a finite number $s\geqslant 0$ of spheres, toruses and non orientable surface of arbitrary genus considered as the real locus of a surface produced by blowing up real points in the previous example.

Proof of Proposition 4.4.10

• 1. By Corollary 4.3.9 an $\mathbb {R}$-surface $(X,{\sigma })$ is $\mathbb {R}$-rational if and only if there is a sequence of blow ups of real points or conjugate pairs of points and contractions of real $(-1)$-curves or pairs of disjoint conjugate $(-1)$-curves producing this surface from the real projective plane.

  • (a) The $\mathbb {R}$-surface $(\mathbb {P}^2(\mathbb {C}),{\sigma _\mathbb {P}})$ is rational by definition.

  • (b) The quadric surface $Q_{3,1}$ in projective space $\mathbb {P}^3$ is rational. For any real point P in $Q_{3,1}$ let $T_PQ_{3,1}\subset \mathbb {P}^3(\mathbb {R})$ be the real projectivisation of the tangent plane to $Q_{3,1}$ at P. The stereographic projection $Q_{3,1}\setminus T_{P}Q_{3,1}\rightarrow \mathbb {A}^2$ is then an isomorphism of $\mathbb {R}$-surfaces. For example if P is the north pole $N=[1:0:0:1]$ let $\pi _N:Q_{3,1}\rightarrow \mathbb {P}^2_{U:V:W}$ be the rational map given by

    

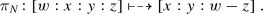
    The restriction of $\pi _N$ is then the stereographic projection of $Q_{3,1}\setminus T_{N}Q_{3,1}$ onto its image $\pi _N(Q_{3,1}\setminus T_{N}Q_{3,1})=\{w\ne 0\}\simeq \mathbb {A}^2$.

    (The inverse rational map $\pi _N^{-1}:\mathbb {P}^2\dashrightarrow Q_{3,1}$ is given by

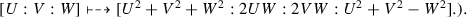
    The rational map $\pi _N$ can be decomposed as the blow up of $Q_{3,1}$ in N, followed by the contraction of the birational transform of the curve $z=w$ (or in other words the intersection of $Q_{3,1}$ with the tangent plane $T_NQ_{3,1}$), which is the union of two non real conjugate lines. The rational map $\pi _N^{-1}$ can be decomposed as the blow up of two non real conjugate points $[1:\pm i :0]$ followed by the contraction of the birational transform of the line $z=0$.

    The surface $Q_{3,1}$ is therefore birational to the surface Y obtained as follows. Let $P,\overline{P}$ be a pair of non real conjugate points in $\mathbb {P}^2(\mathbb {C})$ and let $L:=L_{P,\overline{P}}$ be the line passing through these two points. Note that $(L,{\sigma _\mathbb {P}}|_L)$ is an $\mathbb {R}$-line. The self-intersection number of the strict transform $\widetilde{L}$ of L in the blown up surface $\widetilde{X}=B_{P,\overline{P}}\mathbb {P}^2(\mathbb {C})$ is

    $$ (\widetilde{L}^2)=(L^2)-2=-1 $$

    and it follows that there is a contraction $c:\widetilde{X}\rightarrow Y$ to a non singular $\mathbb {R}$-surface whose real locus is a sphere. Indeed, by construction $\widetilde{X}(\mathbb {R})\approx X(\mathbb {R})=\mathbb {R}\mathbb {P}^2$ and the contraction c remplaces a Moebius band by a disc so $Y(\mathbb {R})\approx \mathbb {S}^2$.

  • (c) We carry out the same construction using two distinct real points P, Q in $\mathbb {P}^2(\mathbb {C})$. We obtain $B_{P,Q}\mathbb {P}^2(\mathbb {R})\approx {\mathbb V}_2$ and on contracting the $\mathbb {R}$-line $L_{P,Q}$ which is a real $(-1)$-curve we get a real locus $Y(\mathbb {R})$ diffeomorphic to a torus ${\mathbb T}^2$. Indeed, by construction $Y(\mathbb {R})$ is diffeomorphic to ${\mathbb T}^2$ or ${\mathbb K}^2$. Moreover, the complex surface thus obtained is isomorphic to $\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C})$ and we know (see Exercise 2.1.42) that the real locus of any real structure on $\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C})$ is $\varnothing , \mathbb {S}^2$ or ${\mathbb T}^2$.

  • (d) Simply note that the complex surface $\mathbb {F}_{2k}$ is obtained from $\mathbb {F}_{0}=\mathbb {P}^1(\mathbb {C})\times \mathbb {P}^1(\mathbb {C})$ by a succession of 2k elementary transformations. Choosing k elementary $\mathbb {R}$-transformations based at k pairs of non real conjugate points as in Exercise 4.3.24 we get that $\mathbb {F}_{2k}(\mathbb {R})\approx \mathbb {F}_{0}(\mathbb {R})\approx {\mathbb T}^2$.

  • (e) Let P be a real point in $\mathbb {P}^2(\mathbb {C})$. By Example 4.2.18 we know that $B_P\mathbb {P}^2(\mathbb {R}) \approx \mathbb {F}_{1}(\mathbb {R})\approx {\mathbb K}^2$.

  • (f) We use the same construction as in (1d) starting with $\mathbb {F}_{2k+1}(\mathbb {R})\approx \mathbb {F}_{1}(\mathbb {R})\approx ~{\mathbb K}^2$.

  • (g) Consider points $P_1,\dots ,P_{g-1}\in \mathbb {P}^2(\mathbb {R})$. By Example 4.2.18 we have that

    $$ B_{P_1,\dots ,P_{g-1}}\mathbb {P}^2(\mathbb {R})\approx {\mathbb V}_g\;. $$

  • (h) Consider points $P_1,\dots ,P_{g}\in Q_{3,1}(\mathbb {R})$. By Example 4.2.18 we have that

    $$ B_{P_1,\dots ,P_{g}}Q_{3,1}(\mathbb {R})=B_{P_1,\dots ,P_{g}}\mathbb {S}^2\approx {\mathbb V}_g\;. $$

• 2. Let $(X,{\sigma })$ be a geometrically rational $\mathbb {R}$-surface. By Proposition 2.3.22, if the $\mathbb {R}$-surface $(X,{\sigma })$ is $\mathbb {R}$-rational then $X(\mathbb {R})$ is connected and non empty.

  • (a) Any complex quadric surface is birational to $\mathbb {P}^2(\mathbb {C})$ so the $\mathbb {R}$-surface $(Q_{4,0},{\sigma _\mathbb {P}}|_{Q_{4,0}})$ is $\mathbb {C}$-rational but as its real locus is empty it is not rational.

  • (b) As X is a conic bundle over $\mathbb {P}^1$ it is a complex rational surface and $(X,{\sigma })$ is therefore geometrically rational. The number of connected components is at least half the number of simple singular fibres of the conic bundle, i.e. half the number of simple roots of f. By hypothesis this gives us $\#\pi _0(X(\mathbb {R}))>1$ so by Proposition 2.3.22 the $\mathbb {R}$-surface $(X,{\sigma })$ is not rational.

  • (c) Blowing up a real point does not change the number of connected components.

  • (d) As any complex del Pezzo surface is rational $(X,{\sigma })$ is geometrically rational. By construction $\#\pi _0(X(\mathbb {R}))>1$ so the $\mathbb {R}$-surface $(X,{\sigma })$ is not rational.

• 3.

  • (a) Let $X \rightarrow B$ be such a fibration. By [Deb01, Remarks 4.2(5), p. 87] the complex surface X is uniruled but not rational because $q(X)=g(B)>0$.

  • (b) Idem.

   $\square$

Theorem 4.4.11

(Real locus of a $\mathbb {C}$-rational surface) Let $(X,{\sigma })$ be a non singular projective geometrically rational $\mathbb {R}$-surface.

• 1. The $\mathbb {R}$-surface $(X,{\sigma })$ is rational if and only if $X(\mathbb {R})$ is connected and non empty. When moreover $(X,{\sigma })$ is also minimal $X(\mathbb {R})$ is diffeomorphic to one of the following surfaces: the real projective plane $\mathbb {R}\mathbb {P}^2$, a sphere $\mathbb {S}^2$, a torus ${\mathbb T}^2$ or a Klein bottle ${\mathbb K}^2$. In this last case, X is a Hirzebruch surface $\mathbb {F}_n$ of odd index $n=2k+1>1$.

• 2. When $(X,{\sigma })$ is a minimal real del Pezzo surface of degree 1, $X(\mathbb {R})$ is diffeomorphic to the disjoint union of a real projective planes and 4 spheres. If $(X,{\sigma })$ is a minimal real del Pezzo surface of degree  2, then $X(\mathbb {R})$ is diffeomorphic to the disjoint union of 4 spheres.

• 3. If $(X,{\sigma })$ is non rational and has a minimal real conic bundle structure with 2s singular fibres then $X(\mathbb {R})$ is diffeomorphic to a disjoint union of s spheres, $s \geqslant 2$.

Proof

As most of these statements have been proved earlier, we refer the reader to [Man14] or [Man17a] for the missing pieces. See also [Rus02] which includes a complete classification of minimal del Pezzo surfaces of degree 1 and 2 based on Silhol’s construction in [Sil89, § VI.4].    $\square$

Exercise 4.4.12

If $(X,{\sigma })$ has a minimal real conic bundle structure prove that $\#\pi _0(X(\mathbb {R}))=4-\frac{1}{2}K_X^2$ (see Exercise 4.3.15).

Remark 4.4.13

If $(X,{\sigma })$ is a geometrically rational minimal $\mathbb {R}$-surface such that $X(\mathbb {R})= \varnothing$ then X is a Hirzebruch surface of even index.

The main result of this section is the following theorem which summarises and completes previous results.

Theorem 4.4.14

(Topology of the real locus when ${\kappa }(X)=-\infty$) Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface of negative Kodaira dimension. We equip the real locus $X(\mathbb {R})$ with its Euclidean topology and consider topological surfaces up to homeomorphism. We denote by $s :=\#\pi _0(X(\mathbb {R}))$ the number of connected components of the real locus.

• 1. If $(X,{\sigma })$ is rational then $s=1$ and $X(\mathbb {R})$ is homeomorphic to one of the following compact connected surfaces:

  • (a) The torus ${\mathbb T}^2$;

  • (b) The sphere $\mathbb {S}^2$;

  • (c) A non orientable surface ${\mathbb V}_g$ for some $g\in \mathbb {N}$.

• 2. If $(X,{\sigma })$ is geometrically rational, or in other words if the complex surface X is rational, then $s\in \mathbb {N}$ can be arbitrary and $X(\mathbb {R})$ is homeomorphic to one of the following compact topological spaces (which are all surfaces except for $\varnothing )$:

  • (a) The empty set $\varnothing$;

  • (b) A torus ${\mathbb T}^2$;

  • (c) A disjoint union of spheres and non orientable surfaces

    $$ \sqcup ^l\mathbb {S}^2\sqcup {\mathbb V}_{g_1} \sqcup \dots \sqcup {\mathbb V}_{g_{s-l}} $$

    where $l,g_1,\dots ,g_{s-l}\in \mathbb {N}^*$.

• 3. If $(X,{\sigma })$ is uniruled (or in other words if the complex surface X is geometrically ruled) of irregularity $q:=q(X)$ then $s\in \mathbb {N}$ is arbitrary and $X(\mathbb {R})$ is homeomorphic to one of the following compact topological spaces (which are all surfaces apart from $\varnothing )$:

  • (a) The empty set $\varnothing$;

  • (b) A disjoint union of $q+1$ toruses

    $$ \sqcup ^{q+1}{\mathbb T}^2\;; $$

  • (c) A disjoint union of toruses, spheres and non orientable surfaces

    $$ \sqcup ^t{\mathbb T}^2\sqcup ^l\mathbb {S}^2 \sqcup {\mathbb V}_{g_1} \sqcup \dots \sqcup {\mathbb V}_{g_{s-t-l}} $$

    where $t< q+1$ and $l,g_1,\dots ,g_{s-t-l}\in \mathbb {N}$.

• 4. Conversely, any topological surface in the first list has a rational algebraic model, any topological surface in the second list has a geometrically rational algebraic model and any topological surface in the third list has a uniruled algebraic model.

Before attacking the proof of this theorem we give a series of intermediate results.

Some authors call the orientable topological surface of genus g a surface with g holes. The main result in the classification of uniruled $\mathbb {R}$-surfaces is that orientable components of such surfaces have at most one hole. The theorem below is actually more general because there are surfaces of general type whose geometric genus is zero. We refer the interested reader to the previously cited review article [BCP11] which studies surfaces of general type with geometric genus equal to 0.

Theorem 4.4.15

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface such that $p_g(X)=0$. Any orientable component of the real locus $X(\mathbb {R})$ is then diffeomorphic to the sphere $\mathbb {S}^2$ or the torus ${\mathbb T}^2$.

The following result is due to Comessatti [Com14].

Corollary 4.4.16

(Comessatti’s theorem) Let $(X,{\sigma })$ be  an non singular projective $\mathbb {R}$-surface which is rational over the real numbers. Its real locus is then non empty and connected and if $X(\mathbb {R})$ is orientable then it is diffeomorphic to a sphere $\mathbb {S}^2$ or a torus ${\mathbb T}^2$.

Proof

By Theorem 1.5.55 the number of connected components of the real locus is invariant under birational maps of $\mathbb {R}$-surfaces. By hypothesis the $\mathbb {R}$-surface $(X,{\sigma })$ is birational to the $\mathbb {R}$-surface $(\mathbb {P}^2(\mathbb {C}),{\sigma _\mathbb {P}})$ and it follows that

$$ \#\pi _0(X(\mathbb {R}))=\#\pi _0(\mathbb {P}^2(\mathbb {R}))=1\;. $$

As the geometric genus is a birational invariant and $p_g(\mathbb {P}^2(\mathbb {C}))=0$, Theorem 4.4.15 completes the proof.    $\square$

The proof of Theorem 4.4.15 given here is a “modern” proof. Comessatti’s original proof [Com14] of Corollary 4.4.16 starts by reducing to the case of minimal surfaces and then enumerating the possible topological types of real loci of minimal geometrically rational surfaces.

Lemma 4.4.17

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface and let $V\subset X(\mathbb {R})$ be an orientable connected component of its real locus. The fundamental class (Definition 3.7.1) $\alpha \in H^{2}(X;\mathbb {Z})$ of V is then ${\sigma }^*$-invariant and its square $(\alpha \cdot \alpha )$ is minus the topological Euler characteristic of V:

$$\begin{aligned} (\alpha \cdot \alpha ) = -\chi _{\text {top}}(V)\;. \end{aligned}$$

(4.7)

Proof

The fact that $\alpha$ is ${\sigma }^*$-invariant is immediate. We prove (4.7) as in [Sil89, p. 71].

See Propositions 2.2.27 and 2.2.28 for the differentiable manifold structures on X and $X(\mathbb {R})$. Since V is orientable the product $(\alpha \cdot \alpha )$ is the self intersection of the variety V in X which by [Hir76, p. 132] is the same thing as the self intersection of V in its normal bundle $N_{X | V}$. (See also [MS74, p. 119].) At any real point multiplication by i in the tangent space $T_X$ yields an orientation reversing isomorphism between $T_{X(\mathbb {R})}$ and the normal bundle $N_{X | X(\mathbb {R})}$. Indeed, consider a point $x\in X(\mathbb {R})$ and let $(u_1,u_2)$ be a basis for the vector space $T_{X(\mathbb {R}),x}$. Since x is a point in the real locus we have that $T_{X,x}=T_{X(\mathbb {R}),x}\otimes _\mathbb {R}\mathbb {C}$. The quadruplet $(u_1,iu_1,u_2,iu_2)$ is therefore a basis for the vector space $T_{X,x}$ and the pair $(iu_1,iu_2)$ is a basis for the normal vector space $N_{X | X(\mathbb {R}),x}$. Since the natural orientation of the differentiable manifold X of real dimension 4 is given by $(u_1,iu_1,u_2,iu_2)$ the induced orientation on $N_{X | X(\mathbb {R}),x}$ is given by $(iu_2,iu_1)$. As the Euler characteristic $\chi _{\text {top}}(V)$ is equal to the self intersection of V in its tangent bundle $T_{V}$ (see [Hir76, p. 13]) the result follows.    $\square$

Remark 4.4.18

Both the statement and the proof remain valid if we replace “projective” by “compact Kähler”. See Appendix D for more details.

Lemma 4.4.19

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface. The intersection form is then negative definite on the ${\sigma }^*$-invariant part of the real vector space $H^{1,1}(X)\cap H^{2}(X;\mathbb {R})$.

Proof

The Hodge index theorem 4.1.24 implies that the intersection form restricted to the subspace $H^{1,1}(X)\cap H^{2}(X;\mathbb {R})$ is Lorentzian, by which we mean that it has signature $(1,h^{1,1}(X)-1)$. As the surface is projective, Proposition 2.6.43 implies that it has a real embedding in a projective space $\varphi :X\hookrightarrow \mathbb {P}^N(\mathbb {C})$. As the surface is non singular, Bertini’s theorem D.9.1 implies is has a non singular hyperplane section $H'$: we denote by h the fundamental class of the $\mathbb {R}$-curve $(H,{\sigma }|_H)$ where $H=\varphi ^*(H')$. The class h is then ${\sigma }^*$-anti-invariant. Indeed, by Proposition 2.2.28, the anti-holomorphic involution ${\sigma }$ is orientation preserving on the differentiable manifold X of real dimension 4, but orientation reversing on the submanifold H of real dimension 2. The eigenspaces of the involution ${\sigma }^*$ are orthogonal and the eigenspace of eigenvalue 1 is therefore orthogonal to the line generated by the class of H.    $\square$

Corollary 4.4.20

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface: if the geometric genus $p_g(X)$ vanishes then the intersection form restricted to the ${\sigma }^*$-invariant part of the real vector space $H^{2}(X;\mathbb {R})$ is negative definite.

Proof

Simply recall the Hodge decomposition (see Appendix D) $H^{2}(X;\mathbb {C})=H^{2,0}(X)\oplus H^{1,1}(X) \oplus H^{0,2}(X)$ and $p_g(X) = h^{0,2}(X) = h^{2,0}(X)$ which gives us $H^{1,1}(X) = H^{2}(X;\mathbb {C})$.    $\square$

Remark 4.4.21

Once again, the same statement with almost the same proof (replacing “hyperplane section” by “Kähler class”) remains valid if we replace “projective” by “compact Kähler”. This is not however an actual generalisation because any compact Kähler manifold with $p_g=0$ is projective. See [BHPVdV04, Chapter VI] for more details.

Proof of Theorem 4.4.15

Let $V \subset X(\mathbb {R})$ be an orientable connected component of the real locus. Lemma 4.4.17 and Corollary 4.4.20 imply that $\chi _{\text {top}}(V)\geqslant 0$. It follows that V is diffeomorphic to the sphere or a torus.    $\square$

We will prove Theorem 4.4.14 using the following refinement of Theorem 4.4.15.

Proposition 4.4.22

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-surface such that $p_g(X)=0$. Let $q:=q(X)$ be its irregularity, let $s = \#\pi _0(X(\mathbb {R}))$ be the number of connected components of its real locus and let $t\leqslant s$ be the number of connected components of $X(\mathbb {R})$ which are diffeomorphic to a torus ${\mathbb T}^2$.

• 1. If $q=0$ and the homology of X has no 2-torsion then

  $$ t\leqslant 1 $$

  and if $t=1$, then $s=t$ and

  $$ X(\mathbb {R})\approx {\mathbb T}^2\;. $$

• 2. If ${\kappa }(X)=-\infty$ then

  $$ t\leqslant q+1 $$

  and if $t=q+1$ then $s=t$ and

  $$ X(\mathbb {R})\approx \sqcup ^{q+1}{\mathbb T}^2\;. $$

Remark 4.4.23

Note that the hypotheses of Proposition 4.4.22(1) cannot be weakened.

• 1. If X is a K3 surface (see Section 4.5) then $q(X)=\pi _1(X)=0$ and $p_g(X)=1$. Looking at Figure 4.11 of this section we see that if $g\leqslant 10$ then there is a real K3 surface whose real locus is diffeomorphic to a orientable surface of degree g. Similarly, there is a real K3 surface whose real locus is diffeomorphic to the disjoint union of a torus and several spheres and there is a real K3 surface whose real locus is diffeomorphic to the disjoint union of two toruses.

• 2. If X is  an Enriques surface (see Section 4.5) then $p_g(X)=q(X)=0$ and $\pi _1(X)=\mathbb {Z}_2$. Checking the list provided in Theorem 4.5.16 we see that there is a real Enriques surface whose real locus is diffeomorphic to the disjoint union of a torus and two Klein bottles and there is a real Enriques surface whose real locus is diffeomorphic to the disjoint union of two toruses.

On the other hand, we can weaken the hypothesis “${\kappa }(X)=-\infty$” in Proposition 4.4.22(2) by replacing it by “${\kappa }(X)\ne 1$ and the homology of X has no 2-torsion” as in Complement 4.4.24.

Proof of Proposition 4.4.22

This proof is based on an argument by Risler [Ris85, p. 161] quoted by Silhol [Sil89, p. 72]. As in Section 3.2, let $Y=X/G$ be the topological quotient of X by the involution and let $p:X \rightarrow Y$ be the canonical surjection. Note that the spaces Y and $Y\setminus X(\mathbb {R})$ are topological manifolds which have a $\mathcal {C}^\infty$ structure. It follows from Remark 1.5.28 that Y is a differentiable manifold of dimension 4 and from Proposition 2.2.27 that $X(\mathbb {R})$ is a differentiable manifold of real dimension 2. The subvariety $X(\mathbb {R})$ in Y is therefore of real codimension 2 in Y.

Recall that in the exact sequence (3.6) of Theorem 3.2.6,

$$\begin{aligned}&\cdots \rightarrow H_r(Y,X(\mathbb {R});\mathbb {Z}_2) \oplus H_r(X(\mathbb {R});\mathbb {Z}_2) \rightarrow H _r(X;\mathbb {Z}_2) \rightarrow \nonumber \\&\qquad H_r(Y,X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {\Delta _r} H_{r-1}(Y,X(\mathbb {R});\mathbb {Z}_2) \oplus H_{r-1}(X(\mathbb {R});\mathbb {Z}_2) \rightarrow \cdots \end{aligned}$$

(4.8)

the second component of $\Delta _r$ is the boundary map $\delta _r$ of the homology sequence associated to the pair $(Y,X(\mathbb {R}))$:

$$\begin{aligned} H_r(Y,X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {\delta _r} H_{r-1}(X(\mathbb {R});\mathbb {Z}_2) \rightarrow H_{r-1}(Y;\mathbb {Z}_2) \;. \end{aligned}$$

(4.9)

Since the homology has no 2-torsion we have that $b_1(X;\mathbb {Z}_2)=b_3(X;\mathbb {Z}_2)=b^1(X)=2q(X)$. Since $H_{4}(X(\mathbb {R});\mathbb {Z}_2)=H_{3}(X(\mathbb {R});\mathbb {Z}_2)=\{0\}$ the exact sequence (4.8) yields

$$\begin{aligned} 0 \rightarrow H_4(Y,X(\mathbb {R});\mathbb {Z}_2) \rightarrow H_4(X;\mathbb {Z}_2) \rightarrow H_4(Y,X(\mathbb {R});\mathbb {Z}_2)&\rightarrow \nonumber \\ \rightarrow H_3(Y,X(\mathbb {R});\mathbb {Z}_2) \rightarrow&H_3(X;\mathbb {Z}_2) \;. \end{aligned}$$

(4.10)

Since $H_4(X;\mathbb {Z}_2)\simeq \mathbb {Z}_2$, we can deduce from the first line that $H_4(Y,X(\mathbb {R});\mathbb {Z}_2)\simeq \mathbb {Z}_2$ and that $1 \leqslant \dim _{\mathbb {Z}_2}H_3(Y,X(\mathbb {R});\mathbb {Z}_2)\leqslant 2q+1$. The part of the exact sequence (4.9) that we need is:

$$ H_3(Y,X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {\delta _2} H_{2}(X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {i_2} H_{2}(Y;\mathbb {Z}_2) \;. $$

Using the above calculation it follows that

$$\begin{aligned} \dim _{\mathbb {Z}_2}\ker i_2\leqslant \dim _{\mathbb {Z}_2} H_3(Y,X(\mathbb {R});\mathbb {Z}_2)\leqslant 2q+1\;. \end{aligned}$$

(4.11)

Let $\{V_r\}_{r=1,\dots ,s}$ be the connected components of $X(\mathbb {R})$. The group morphism $H_{2}(X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {i_2} H_{2}(Y;\mathbb {Z}_2)$ sends the fundamental homology class of $V_r$ in $H_{2}(X(\mathbb {R});\mathbb {Z}_2)$ to its fundamental homology class in $H_{2}(Y;\mathbb {Z}_2)$.

We know by Lemma 4.4.17 that the fundamental homology class in $H_{2}(X;\mathbb {Z})$ of a connected component diffeomorphic to ${\mathbb T}^2$ is isotropic for the intersection form and it follows from Corollary 4.4.20 that it is zero. It follows that its fundamental class in $H_{2}(Y;\mathbb {Z})$ and hence in $H_{2}(Y;\mathbb {Z}_2)$ vanishes.

The fundamental classes in $H_{2}(X(\mathbb {R});\mathbb {Z}_2)$ of the connected components of $X(\mathbb {R})$ diffeomorphic to ${\mathbb T}^2$ are linearly independent and their images under $i_2$ all vanish. It follows from (4.11) that $t\leqslant 2q+1$.

We conclude by noting that as $p:X \rightarrow Y$ is a double covered ramified along $X(\mathbb {R})$ the fundamental class of $X(\mathbb {R})$ in $H_{2}(Y;\mathbb {Z}_2)$ vanishes. For example, if $X(\mathbb {R})$ is orientable then its fundamental class in $H_{2}(Y;\mathbb {Z})$ is 2-divisible (see Lemma 3.6.21 which applies because X is non singular).

Permuting terms if necessary we can assume that $V_1,\dots , V_t$ are the connected components of $X(\mathbb {R})$ diffeomorphic to ${\mathbb T}^2$. If $V_1\sqcup \dots \sqcup V_t \subsetneq X(\mathbb {R})$ then the fundamental classes of $V_1,\dots , V_t$ and $X(\mathbb {R})$ in $H_{2}(X(\mathbb {R});\mathbb {Z}_2)$ are linearly independent and by (4.11) we get that $t< 2q+1$ because the fundamental class of $X(\mathbb {R})$ belongs to $\ker i_2$. This result applied to $q=0$, proves the first part of the proposition.

To prove the second part of the proposition we recall that a non singular complex projective surface such that ${\kappa }(X)=-\infty$ is uniruled and its homology has no 2-torsion. Indeed, any such surface is birationally equivalent to a genus 0 fibration with non singular fibres which has a section. (See [Bea78, Exemple VII.3 and Chapitre III] for more details.) The existence of such a section implies the homology is torsion free and this property is invariant under birational maps. We can therefore apply the first part of the proposition to prove the result when $q=0$.

By Theorem 4.4.8 if X is uniruled and $q>0$ then X is a conic bundle $\pi :X \rightarrow C$ defined over $\mathbb {R}$ over a curve C of genus $g(C)=q(X)\geqslant 1$. Analysing the singular fibres of $\pi$ shows that they cannot meet a torus and we then apply Harnack’s inequality (3.3.7): $t\leqslant \#\pi _0(C(\mathbb {R}))\leqslant g(C)+1= q+1$.    $\square$

Proof of Theorem 4.4.14

Any surface X of negative Kodaira dimension has geometric genus $p_g=0$. Indeed, ${\kappa }(X)=-\infty$ means that all positive multiples of the canonical bundle have no global sections and in particular $p_g(X)=\dim H^2(X,\mathcal {O}_X)=\dim H^0(X,\Omega _X) =0$. Theorem 4.4.15 therefore applies and implies that the only orientable surfaces that can appear are $\mathbb {S}^2$ and ${\mathbb T}^2$. Point (1) follows from Comessatti’s Theorem 4.4.16. The upper bound on the number of toruses in (2) and (3) follows from Proposition 4.4.22 since $p_g$ and q are birational invariants of complex surfaces. If $(X,{\sigma })$ is geometrically rational then $p_g(X)=p_g(\mathbb {P}^2(\mathbb {C}))=0$ and $q(X)=q(\mathbb {P}^2(\mathbb {C}))=0$ (in general, uniruled surfaces have zero geometric genus but non zero irregularity). Finally (4) follows from Proposition 4.4.10.    $\square$

Complement 4.4.24

Let $(X,{\sigma })$ be a non singular projective $\mathbb {R}$-minimal $\mathbb {R}$-surface.

• 1. If $p_g(X)=0$, $q(X)>0$ and X is not uniruled then $q(X)=1$, $K_X^2=0$, $b_2(X)=2$ and ${\kappa }(X)\in \{0,1\}$.

• 2. If X is bi-elliptic and the homology of X has no 2-torsion then $t<3$, and if $t=2$ then $t=s$, see [CF03, Remark 7.3], [Suw69].

• 3. If the homology of X has no 2-torsion and $t\geqslant 3$ then ${\kappa }(X)=1$ (i.e. X is a properly elliptic surface).

Proof

1. Note that under these hypotheses, X must be of special type. Indeed if X is minimal and of general type $c_1^2(X)>0$ and it follows that $\chi (\mathcal {O}_X)\geqslant 1$ by the Noether formula 4.1.19 and hence $q(X)=0$. If X is not uniruled then $\chi _\text {top}(X)=c_2(X)\geqslant 0$ [Bea78, Theorem X.4] and then $\chi (\mathcal {O}_X)\geqslant 0$ by Noether: it follows that if $p_g(X)=0$ then $q(X)\leqslant 1$. By minimality $c_1^2(X)=0$ and by Noether’s formula $c_2(X)=0$. As $b_1(X)=b_3(X)=2q(X)$ it follows that $b_2(X)=2$. (See [Bea78, VI.1 et VI.2] for any alternative proof.)

2. There are bi-elliptic surfaces whose real locus is made up of three or four toruses—see Theorem 4.5.30—but in this case the homology of X contains 2-torsion [CF03, Remark 7.3], [Suw69].

3. The classification of complex compact surfaces [BHPVdV04, Chapter VI, Table 10] tells us that only bi-elliptic surfaces can satisfy ${\kappa }(X)=0$, $p_g(X)=0$ and $q(X)=1$. As such surfaces were dealt with in the previous question we have that ${\kappa }(X)=1$ or in other words X is a properly elliptic surface.

We have not had the time to construct explicit examples contradicting the conclusion of Proposition 4.4.22 when the hypotheses are weakened but we propose two sketch constructions.

• 1. By [BHPVdV04, Théorème III.18.2], if a fibration $\pi :X \rightarrow C$ has singular fibres they are all of the form mE where E is a non singular elliptic curve. If $t>\#\pi _0(C(\mathbb {R}))$ it follows from Silhol’s classification of singular real fibres [Sil84, Sil89, Chapitre VII] that $\pi$ has an even number of fibres with even multiplicity m.

• 2. We could also use [Bea78, Théorème VI.13, case II non bi-elliptic]: under our hypotheses, X is necessarily a quotient of the form $(B\times F)/H$ where F is a non singular elliptic curve, B is a non singular curve of genus at least 2, H is a finite group acting faithfully on both B and F, B/H is elliptic, F/H is rational and H acts freely on $B\times F$.

   $\square$

4.4.2 Singular Surfaces and Parabolas

In this subsection based on [Kol99b,CM08, CM09] we give a classification of possible topological types of singular geometrically rational Du Val $\mathbb {R}$-surfaces 4.4.30 (see Definition 1.3.37 for the definition of geometrically rational). We will do this using the orbifold structure with conic points (4.4.31) on the connected components of the topological normalisation (4.4.35). This will give us a generalisation of Comessatti’s theorem (4.4.36). Another consequence, which was initially our main motivation in this section, is the proof of three conjectures of Kollár’s on rationally connected varieties. See Theorem 6.2.11 in Chapter 6.

4.4.2.1 Du Val Surfaces

We start by recalling a definition of Artin’s, [Art66] (see also [Har77, p. 250]).

Definition 4.4.25

Let X be a normal complex surface defined over $\mathbb {C}$ and let P be a singular point of X. We say that P is a rational singularity if and only if there is a resolution $\pi :\widetilde{X} \rightarrow X$ of P such that $R^q\pi _*(\mathcal {O}_{\widetilde{X}})=0$ for all $q\geqslant 0$ where ($R^q\pi _*(\mathcal {O}_{\widetilde{X}}))$ denotes the q-th direct image of the sheaf $\mathcal {O}_{\widetilde{X}}$.

Theorem 4.4.26

Let X be a normal complex surface and let P be a singular point of X. The following properties are equivalent.

• 1. P is rational of embedding dimension 3.

• 2. P is rational of multiplicity 2: we say it is a rational double point.

• 3. P is of multiplicity 2 and can be resolved by a sequence of blow ups of points.

• 4. The minimal resolution of P has a configuration of exceptional curves of type $A_n$, $D_n$, $E_6$, $E_7$ or $E_8$. (See below for more details.)

Proof

See [Slo80, p. 71].    $\square$

Remark 4.4.27

There are double points on surfaces which are not rational—for example, $z^6+y^2+x^3=0$ is a elliptic double point—but any double point on a surface has embedding dimension 3, see [Lau71, p. 7].

Definition 4.4.28

If one of these four equivalent properties is satisfied then P is said to be a rational double point of type $A_n$, $n\geqslant 1$, $D_n$, $n\geqslant 4$ or $E_n$, $n=6,7,8$. Over $\mathbb {C}$ we have the following characteristic equations [BHPVdV04, p. 87]:

$$ \begin{aligned} A_n(n\geqslant 1)&: \\ D_n(n\geqslant 4)&: \\ E_6&: \\ E_7&: \\ E_8&: \\ \end{aligned}\qquad \begin{aligned} z^2+x^2+y^{n+1}&=0\\ z^2+y(x^2+y^{n-2})&=0\\ z^2+x^3+y^4&=0\\ z^2+x(x^2+y^3)&=0\\ z^2+x^3+y^5&=0\;. \end{aligned} $$

Remark 4.4.29

Rational double points on surfaces are the same thing as canonical singularities. These singularities are quotients of $\mathbb {C}^2$ by finite subgroups of ${\mathbf {SL}}_2(\mathbb {C})$. We also call them Du Val singularities.

Definition 4.4.30

A projective surface is said to be Du Val if and only if its only singularities are rational double points.

Over $\mathbb {C}$, Du Val singularities are classified in Definition 4.4.28 below: there are the cyclic singularities $A_n$, $n \geqslant 1$, the dihedral singularities $D_n$, $n \geqslant 4$, the tetrahedral singularity $E_6$, the octahedral singularity $E_7$ and the icosahedral singularity $E_8$. There are many other types of singularities over $\mathbb {R}$ and in this section we will only present two series of cyclic singularities. We refer to [CM08, section 1 and example 1.3] for more details.

A real surface X is said to have a singularity of type $A^\pm _n$ at a point $P\in X(\mathbb {R})$ if in some neighbourhoood of P X is $\mathbb {R}$-analytically isomorphic to

$$ x^2 \pm y^2 - z^{n + 1} = 0,\ n \geqslant 1\;. $$

Fig. 4.5

$A^+_n$, $x^2 + y^2 - z^{n + 1} = 0,\ n \geqslant 1$

Fig. 4.6

$A^-_n$, $x^2 - y^2 - z^{n + 1} = 0,\ n \geqslant 1$

Fig. 4.7

$A_1^+\simeq A_1^-$

The grey part of Figure 4.5 represents the zone in $\mathbb {R}^2_{z,x}$ where $z^{n + 1}-x^2$ is positive. The surface X which is locally a double cover of the plane branched over the curve $z^{n + 1}-x^2=0$ only has real points over this zone.

Note that all these singularities are non isomorphic except for $A_1^+$ and $A_1^-$.

4.4.3 Generalisation of Comessatti’s Theorem

4.4.3.1 Orbifolds of Dimension 2

The term orbifold derives from the expression n-manifold denoting a topological space M equipped with a family of charts $(\widetilde{U},\phi )$ where $\widetilde{U}$ is an open set and $\phi$ is a homeomorphism onto an open set $U\subset \mathbb {R}^n$.

An n-orbifold is a space equipped with an atlas whose charts $\phi :\widetilde{U} \rightarrow U\subset \mathbb {R}^n$ are finite branched covers: in the case where all the maps $\phi$ are of degree 1 the orbifold is simply a manifold. More precisely, every open chart of an orbifold is equipped with a G-action for some finite group G and $\phi$ factorises through a homeomorphism . See [BMP03, Chapter 2] for more details.

Definition 4.4.31

If G is cyclic and acts by rotation of angle $2\pi /m$ its unique fixed point is said to be a conic point of index m.

Orbifolds are not always homeomorphic to a manifolds, except in dimension 2 where any orbifold M is homeomorphic to a topological manifold denoted |M|. See [Sco83, §2], for example, for more details.

Definition 4.4.32

Let p and q be coprime integers, $(p,q)=1$. We denote by $\mathbb {S}(p,q)$ the orbifold whose underlying smooth surface is $| \mathbb {S}(p,q) |=\mathbb {S}^2$ with two conic points whose indices are respectively p and q.

Let M be a compact 2 dimensional orbifold with a global finite covering map of degree d from a smooth surface $\widetilde{M} \rightarrow M$. The orbifold Euler characteristic is then defined by

$$ \chi (M) :=\frac{1}{d} \chi (\widetilde{M}) \in \mathbb {Q}\;. $$

Let M be a 2-orbifold with k conic points of angles $2\pi /m_j$, $j = 1,\dots , k$ and let |M| be the smooth surface underlying M. We then have that

$$ \chi (M) = \chi (| M |) - \sum _{j=1}^k (1- \frac{1}{m_j})\;. $$

Definition 4.4.33

The orbifold M is said to be spherical (resp. Euclidean) if and only if $\chi (M)>0$ (resp. $\chi (M)=0$).

Proposition 4.4.34

The orbifold M is spherical or Euclidean if and only if |M| is spherical and $\sum _{j=1}^k (1- \frac{1}{m_j})\leqslant 2$ or |M| is Euclidean and $k=0$.

Fig. 4.8

M and $\overline{M}$ in a neighbourhood of a singular point of type $A^\pm _n$, n odd

4.4.3.2 Topological Normalisation

Kollár [Kol99a] introduced an operation imitating “branch separation” in algebraic geometry (Definition 1.5.37) in order to handle the situation where the real locus of an $\mathbb {R}$-variety is singular.

Definition 4.4.35

Let V be a simplicial complex whose singular locus ${\text {Sing}}(V)$ is finite, where here ${\text {Sing}}(V)$ is defined as being the set of points $x\in V$ whose star (the union of all the simplexes in V having x as a vertex) is not homeomorphic to a disc. The topological normalisation $\overline{\nu } :\overline{V} \rightarrow V$ is the unique continuous proper map such that

• 1. $\overline{\nu }$ is a homeomorphism over $V\setminus {\text {Sing}}(V)$,

• 2. If $P\in {\text {Sing}}(V)$ then the fibre $\overline{\nu }^{-1}(P)$ is in bijection with the set of local connected components of V in a neighbourhood of P.

Let X be a geometrically rational algebraic $\mathbb {R}$-surface and let $M \subset \overline{X(\mathbb {R})}$ be a connected component of the topological normalisation of its real locus. If X is non singular and the smooth surface M is orientable then Comessatti’s theorem 4.4.16 implies that M is a sphere or a torus. The generalisation below was proved in [CM09].

If X is Du Val then we equip M with an orbifold structure with conic points (Definition 4.4.38).

Theorem 4.4.36

Let X be a geometrically rational algebraic $\mathbb {R}$-surface and let $M \subset \overline{X(\mathbb {R})}$ be a connected component of the topological normalisation of its real locus. If X is Du Val and the orbifold M is orientable then M is spherical or Euclidean.

This result is a corollary of Theorem 4.4.39 below. Before stating this theorem we need one more technical definition When $X(\mathbb {R})$ is two dimensional the normalisation $\overline{X(\mathbb {R})}$ is a topological manifold and if $P \in X(\mathbb {R})$ is a singular point of type $A^\pm _n$ with n odd then $\overline{X(\mathbb {R})}$ has two locally connected components in a neighbourhood of P.

Definition 4.4.37

The point P is globally non separating if the two locally connected components in a neighbourhood of P are in the same connected component of $\overline{X(\mathbb {R})}$ and globally separating otherwise.

Let X be a Du Val $\mathbb {R}$-surface and let $\overline{\nu } :\overline{X(\mathbb {R})} \rightarrow X(\mathbb {R})$ be the topological normalisation of the real locus. We denote by $\Sigma _X$ the set of real singular points which are either of type $A^-_n$ with n even or globally separating and of type $A^-_n$ with n odd. We denote by $\mathcal {P}_X :={\text {Sing}}(X)\setminus \Sigma _X$ the set of all other singular points.

Definition 4.4.38

Let $M \subset \overline{X(\mathbb {R})}$ be a connected component of the topological normalisation of the real locus of a Du Val $\mathbb {R}$-surface. We equip M with an orbifold structure whose conic points of index m correspond to the singular points of type $A^\pm _m$ contained in $\mathcal {P}_X \cap \overline{\nu }(M)$.

We denote by k(M) the cardinality $\#\{\overline{\nu }^{-1}(\mathcal {P}_X) \cap M\}$ and for $i=1\dots k(M)$ we let $m_i(M)$ be the index of a point in $\mathcal {P}_X \cap \overline{\nu }(M)$.

Theorem 4.4.39

Let X be a Du Val $\mathbb {R}$-surface and let $M\subset \overline{X(\mathbb {R})}$ be a possibly non orientable connected component of the topological normalisation of its real locus. If X is geometrically rational then

• $k(M) \leqslant 4$,

• $\sum _{i=1}^k (1- \frac{1}{m_i+1}) \leqslant 2$,

• $| M | = \mathbb {S}^1\times \mathbb {S}^1 \implies k(M) = 0$.

Proof

See [CM08, Corollary 0.2, Theorem 0.3] and [CM09, Theorem 0.2] for a full proof: here we only discuss the inequality $k(M) \leqslant 4$. The heart of the proof is a reduction to the case of certain double covers of the quadratic cone branched along singular curves of degree 6. A clever counting argument then enables us to complete the proof.

The minimal model programme enables us to reduce to the case where X is a del Pezzo (Definition 4.2.12) Du Val surface of degree 1. See Lemma [CM08, Lemma 1.8] for more details.

The anticanonical model of X is a branched double cover $q :X \rightarrow Q$ of a quadric cone $Q \subset \mathbb {P}^3(\mathbb {C})$ whose branching locus is the union of the summit of the cone and a cubic section B not passing through the summit. See [DPT80, Exposé V] for more details. Note that the pull back under q of the summit of the cone is a non singular point. Let $X'$ be the singular elliptic surface obtained from X by blowing up this non singular point.⁹

We recall that $\overline{\nu } :\overline{X'(\mathbb {R})} \rightarrow X'(\mathbb {R})$ is the topological normalisation of the real locus. We therefore want to prove that for any connected component $M \subset \overline{X'(\mathbb {R})}$ we have that

$$ \#(\overline{\nu }^{-1}(\mathcal {P}_{X'}) \cap M) \leqslant 4 \;. $$

The surface $X'$ is a ramified double cover of a Hirzebruch surface $\mathbb {F}_2$ whose branching curve is the union of the unique section of negative self-intersection $\Sigma _\infty$ of the fibration $\mathbb {F}_2 \rightarrow \mathbb {P}^1(\mathbb {C})$ and a trisection B which does not meet $\Sigma _\infty$. The cone Q is isomorphic to the weighted projective space $\mathbb {P}(1,1,2)$ which we equip with coordinates $(x_0,x_1,y_2)$ and X is therefore the hypersurface in $\mathbb {P}(1,1,2,3)$ with coordinates $(x_0,x_1,y_2,z)$ defined by the equation

$$\begin{aligned} z^2 = y_2^3 + p_4(x_0,x_1)y_2 + q_6(x_0,x_1) \;. \end{aligned}$$

We now describe a plane model for Q in which the hyperplane sections of Q embedded in $\mathbb {P}^3$ via $H^0(Q,\mathcal {O}_Q(2))$ correspond to the parabolas tangent to the line at infinity $L_\infty = \{ w = 0\}$ at the point $O :=\{w = x = 0 \}$ in the projective plane equipped with coordinates (x, y, w). In other words, we blow up at O and then at the infinitely close point $O'$ in O corresponding to tangency to the line at infinity $L_\infty$, and denote by $\widetilde{Q}$ the surface thus obtained. Let E and $E'$ be the total transformations of O and $O'$ and note that $E = E' + E''$ where $E''$ is a $(-2)$-curve. The linear system $H^0(\widetilde{Q},\mathcal {O}_{\widetilde{Q}}(2H - E - E'))$ sends $\widetilde{Q}$ birationally to the quadric cone $Q \subset \mathbb {P}^3(\mathbb {C})$ contracting both the strict transform $\widetilde{L_\infty }$ of the line $L_\infty$ and the curve $E''$ to points. Since $\widetilde{L_\infty }$ and $E''$ are disjoint the contraction of $\widetilde{L_\infty }$ gives a Hirzebruch surface $\mathbb {F}_2$ whose $(-2)$-section $\Sigma _\infty$ is the image of $E''$. We write this using coordinates (x, y, w) on $\mathbb {P}^2$: $H^0(Q,\mathcal {O}_Q(1))$ then corresponds to $H^0(\widetilde{Q},\mathcal {O}_{\widetilde{Q}}(H - E))$ which is generated by w, x and $y_2 :=yw$ extends $w^2,wx,x^2$ to a basis of $H^0(\widetilde{Q},\mathcal {O}_{\widetilde{Q}}(2H - E - E')) \simeq H^0(Q,\mathcal {O}_Q(2))$. The morphism $\widetilde{Q}\rightarrow \mathbb {P}(1,1,2)$ is therefore given by $x_0 :=w$, $x_1 :=x$, $y_2 :=yw$.

The elliptic surface $X'$ is the double cover of $\mathbb {F}_2$ branched over $\Sigma _\infty$ and over the curve B corresponding to the curve in Q of equation $y^3 + p_4(x_0,x_1)y + q_6(x_0,x_1) = 0$. The curve B therefore corresponds to the plane curve of equation $w^3y^3 + p_4(w,x)yw + q_6(w,x) = 0$ whose affine part has equation

$$\begin{aligned} y^3 + p_4(1,x)y + q_6(1,x) = 0 \;. \end{aligned}$$

(4.12)

Note that a parabola of this form, by which we mean a curve of the form $C \in (2H - E - E')$ is disjoint from $E''$ (which contracts onto the summit of the cone) unless it degenerates as two lines passing through the point O. In particular, we can always modify the coordinates in the affine plane so that C is sent to the line $y = 0$.

In order to describe the geometry at infinity of parabolas of this form, recall that the surface $\mathbb {F}_2$ is covered by two open sets isomorphic to $\mathbb {C}\times \mathbb {P}^1(\mathbb {C})$. On one of these open charts we have affine coordinates $\frac{x}{w} \in \mathbb {C}$ and homogeneous coordinates $(w:y) \in \mathbb {P}^1(\mathbb {C})$, whereas on the other chart the coordinates are $\frac{w}{x} \in \mathbb {C}$ and $(\frac{x^2}{w} : y)\in \mathbb {P}^1(\mathbb {C})$ (or alternatively $\frac{x^2}{w} /w = (\frac{x}{w})^2$). The section at infinity $\Sigma _\infty$ corresponds to the curve $E'' \subset \widetilde{X}$ and is defined by $w = 0$ or $\frac{x^2}{w} = 0$ depending on the chart. A parabola $yw = a_0w^2 + a_1 xw + a_2 x^2$ is therefore given by an equation

$$ \frac{1}{\eta }= a_0 + a_1 \frac{x}{w} + a_2(\frac{x}{w})^2 $$

in the affine chart of coordinates $(\frac{x}{w}: \eta :=\frac{w}{y} )$. Using these coordinates at infinity it becomes easy to see when a domain “meets” $\mathbb {F}_2$ at infinity.

We now seek the normal form of equation (4.12). The singular points of $X'(\mathbb {R})$ are in one to one correspondence with singular points of $B(\mathbb {R})$. There are different cases to consider corresponding to different numbers of connected components of the trisection B.

Here we will restrict ourselves to the case where the trisection has three irreducible components and we refer to [CM08] for the other cases. We aim to prove that every connected component of the topological normalisation of each of the two double covers branched along B has at most 4 singular points. We start by noting that as B is real at least one of the irreducible components is real. Equation (4.12) becomes

$$ (y - \alpha (x))(y - \beta (x))(y - \gamma (x)) = 0 $$

and changing the real coordinates on $Q = \mathbb {P}(1,1,2)$ if necessary we can assume that $\gamma =0$. The case $\beta = \overline{\alpha }$ where there are two irreducible complex conjugate components only gives us 2 singular points: ${\text {Re}} \alpha (x) = 0, y = {\text {Im}} \alpha (x)$. We can therefore assume that all three irreducible components are real. Equation (4.12) then becomes $(y - \alpha )(y - \beta )y = 0$ where $\alpha (x) = \alpha _0 + \alpha _1 x + \alpha _2 x^2$ and $\beta (x) = \beta _0 + \beta _1 x + \beta _2 x^2$ are polynomials of degree 2.

4.4.3.3 Case Without Tangency

Suppose that none of the parabolas are tangent to each other. Since we can permute the three curves we can assume the smallest one is at infinity. (The smallest curve is the one that has the smallest value of $a_2$ when we write their equations in the form $y = a_0 + a_1 x + a_2 x^2$.) Changing coordinates we get a curve given by the equation $y = 0$ and two convex parabolas, i.e. parabolas for which $\alpha _2 >0$ and $\beta _2 >0$.

The 6 intersection points are distinct and are given by

$$ y = \alpha (x)\beta (x) = 0\;,\qquad \alpha (x) = \beta (x) = y \;. $$

The curve B is real so if one of these singular points is not real then the number of real singular points is bounded by 4. We suppose therefore that the 6 singular points are real and set

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha (x) = \alpha _2(x - a_1)(x - a_2),\ a_1 < a_2 \;;\\ \beta (x) = \beta _2(x - b_1)(x - b_2) \;. \end{array}\right. } \end{aligned}$$

(4.13)

Multiplying y by $\beta _2$ if necessary we can assume that $\beta _2 = 1$. Furthermore we can reduce to the case $0< \alpha _2 < 1$ by exchanging the roles of $\alpha$ and $\beta$ if necessary. Using a translation along the x axis we can assume that $b_1 = - b_2$. Equation (4.13) then becomes

$$ {\left\{ \begin{array}{ll} \alpha (x) = \alpha _2(x - a_1)(x - a_2),\ a_1< a_2,\ 0< \alpha _2< 1 \;;\\ \beta (x) = (x^2 - b^2),\ 0 < b\;. \end{array}\right. } $$

Up to symmetry $x \leftrightarrow -x$ this leaves us with 4 possibilities.

$$ b< a_1\;,\ -b< a_1< b< a_2\;,\ a_1< -b< b< a_2\;,\ -b< a_1< a_2 < b \;. $$

This configuration is shown in Figure 4.9. In order to help the reader visualise the situation we invite them to count the double points in each connected component of the complement of B. To do this, note that two connected components are connected at infinity if and only their boundary contains two non bounded curves belonging to the same pair of parabolas.

Fig. 4.9

6 $A_1$ points

4.4.3.4 Case with Tangency

A detailed study similar to the one carried out above enables us to reduce to the five cases shown in Figure 4.10.    $\square$

Fig. 4.10

4 $A_1$ points, 1 $A_2$ point

4.4.3.5 Non Orientable Components

All non orientable surfaces can be realised as components of real non singular rational surfaces by blowing up real points in the real projective plane. Similarly, it is easy to construct hyperbolic non orientable orbifolds.

When X is geometrically rational minimal and non singular Comessatti’s theorem implies that M is spherical or euclidean—in fact minimality implies that M is diffeomorphic to $\mathbb {S}^2$ or ${\mathbb {R}}{\mathbb {P}}^2$ (which are both spherical), $\mathbb {S}^1\times \mathbb {S}^1$ or ${\mathbb K}^2$ (which are both Euclidean). The singular case is rather different.

Theorem 4.4.40

There is a geometrically rational minimal Du Val $\mathbb {R}$-surface X which has a component $M \subset \overline{X(\mathbb {R})}$ which is a hyperbolic orbifold.

Proof

See [CM09, Theorem 0.4].    $\square$

4.5 K3, Enriques, Abelian and Bi-elliptic Surfaces (${\kappa }=0$)

The four classes of non singular minimal complex projective surfaces with Kodaira dimension ${\kappa }=0$ can be distinguished by their geometric genus $p_g$ and their irregularity q. We can show that if the Kodaira dimension of a surface X vanishes then there is a strictly positive integer m such that $mK_X\sim 0$.

Let $m_0$ be the smallest strictly positive integer such that $m_0K_X\sim 0$.

Theorem 4.5.1

Let X be a non singular minimal complex projective surface with ${\kappa }(X)=0$. There are then four possibilities for the pair $(p_g(X),q(X))$:

• 1. $p_g(X)=1$, $q(X)=0$: we then have that $m_0=1$ and X is a projective K3 surface (Definition 4.5.3).

• 2. $p_g(X)=0$, $q(X)=0$: we then have that $m_0=2$ and X is an Enriques surface (Definition 4.5.13).

• 3. $p_g(X)=1$, $q(X)=2$: we then have that $m_0=1$ and X is an abelian surface (Definition 4.5.22).

• 4. $p_g(X)=0$, $q(X)=1$: we then have that $m_0\in \{2,3,4,6\}$ and X is a bi-elliptic surface (Definition 4.5.28).

Proof

See [Bea78, Liste VI.20 and Théorème VIII.2].    $\square$

Corollary 4.5.2

Any non singular minimal complex projective surface X with ${\kappa }(X)=0$ satisfies $4K_X\sim 0$ or $6K_X\sim 0$.

4.5.1 K3 Surfaces

The book [X85] is a standard reference for complex K3 surfaces: we refer to [Sil89, Chapter VIII] for real K3 surfaces. The K3 surfaces in Theorem 4.5.1 are assumed to be projective. More generally, a K3 surface is a compact non singular complex analytic surface with trivial canonical divisor and vanishing first Betti number.

Definition 4.5.3

Let X be  a non singular compact complex analytic surface. X is said to be a K3 surface if and only if $K_X\sim 0$ and $b_1(X)=0$. A real K3 surface is an $\mathbb {R}$-surface $(X,{\sigma })$ such that X is a K3 surface.

Proposition 4.5.4

Let X be a K3 surface. X is then minimal: moreover ${\kappa }(X)=0$, $p_g(X)=1$, $q(X)=0$ and X is simply connected.

Proof

See [X85, BHPVdV04, Chapitre VIII].    $\square$

K3 surfaces are not all projective but by a fundamental theorem due to Siu they are all Kähler. See [X85, Exposé XII] for more details.

Theorem 4.5.5

(Kharlamov 1975) There are 66 topological types of real K3 surfaces. Each of them can be obtained by topological Morse simplification (Definition 4.3.31) from one of the 6 extremal types listed below. Conversely, any type obtained in this way can be realised as the real locus of a real K3 surface.

The 6 extremal types are:

• 1. M-surfaces, $b^*(X(\mathbb {R});\mathbb {Z}_2)=24$, $\chi (X(\mathbb {R}))=-16,0,16$,

  $$ {\mathbb S}_{10}\sqcup \mathbb {S}^2,\quad {\mathbb S}_6\sqcup 5\mathbb {S}^2,\quad {\mathbb S}_2\sqcup 9\mathbb {S}^2 \;; $$

• 2. $(M-2)$-surfaces, $b^*(X(\mathbb {R});\mathbb {Z}_2)=20$, $\chi (X(\mathbb {R}))=\pm 8$,

  $$ {\mathbb S}_7\sqcup 2\mathbb {S}^2,\quad {\mathbb S}_3\sqcup 6\mathbb {S}^2 \;; $$

• 3. Pair of toruses,

  $$ {\mathbb T}^2\sqcup {\mathbb T}^2\;. $$

Proof

See [Har76, Sil89, Chapter VIII].    $\square$

Figure 4.11 shows all pairs $(\chi (X(\mathbb {R})),b^*(X(\mathbb {R}));\mathbb {Z}_2)$ which can be realised by real K3 surfaces. We deduce from this figure the possible topological types of real K3 surfaces using the following proposition.

Proposition 4.5.6

Let $(X,{\sigma })$ be a real K3 surface. If $X(\mathbb {R})$ is non empty then it is an orientable topological surface. Moreover $X(\mathbb {R})$ has at most one connected component whose Euler characteristic is $\leqslant 0$ (the other components are therefore all diffeomorphic to the sphere) unless $X(\mathbb {R})$ is the disjoint union of two toruses.

Fig. 4.11

Topological types of real K3 surfaces with non empty real locus

Proof

Let $(X,{\sigma })$ be a real K3 surface whose real locus is non empty. Note first that $X(\mathbb {R})$ is orientable. Indeed, by definition $c_1(X)=b_1(X)=0$ so by Proposition 3.1.16 ${\text {w}}_2(X)=0$. Moreover we know by Proposition 4.5.4 that $\pi _1(X)=0$ which implies in particular that $b_1(X;\mathbb {Z}_2)=0$. Theorem 3.1.18 therefore applies.

As in the proof of Theorem 3.2.6 we set $Y=X/G$ and let $p:X \rightarrow Y$ be the associated branched double cover. Since the homology of X has no 2-torsion and $q(X)=0$ we have that $H_3(Y,X(\mathbb {R});\mathbb {Z}_2)\simeq \mathbb {Z}_2$ by Lemma 3.6.22 and as in the first part of the proof of Proposition 4.4.22 this yields an exact sequence arising from (4.9)

$$\begin{aligned} 0 \rightarrow \mathbb {Z}_2 \xrightarrow {\delta _2} H_{2}(X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {i_2} H_{2}(Y;\mathbb {Z}_2) \;. \end{aligned}$$

(4.14)

Let $\{V_r\}_{r=1,\dots ,s}$ be the connected components of $X(\mathbb {R})$ which are therefore compact orientable topological surfaces by previous results. For any $r=1,\dots ,s$, we denote by $\alpha _r$ the fundamental class of $V_r$ in $H_{2}(X;\mathbb {Z})$ and by $\beta _r$ the image of $\alpha _r$ in $H_{2}(Y;\mathbb {Z}_2)$ under the map $p_*$ induced by p. Obviously we have that $\alpha _r\cdot \alpha _{r'}=0$ if $r\ne r'$ and $\alpha _r$ is in the invariant part of $H_{2}(X;\mathbb {Z})$.

By construction the group morphism $H_{2}(X(\mathbb {R});\mathbb {Z}_2) \xrightarrow {i_2} H_{2}(Y;\mathbb {Z}_2)$ sends the fundamental homology class of $V_r$ in $H_{2}(X(\mathbb {R});\mathbb {Z}_2)$ to $\beta _r\in H_{2}(Y;\mathbb {Z}_2)$. Recall that as $p:X \rightarrow Y$ is a double cover ramified along $X(\mathbb {R})$ the fundamental class of $X(\mathbb {R})$ in $H_{2}(Y;\mathbb {Z}_2)$ vanishes by Lemma 3.6.21. This class is equal to the sum $\beta _1+\beta _2+\cdots +\beta _s$ which therefore vanishes. Moreover, the relationship $\beta _1+\beta _2+\cdots +\beta _s=0$ is the only relationship between the classes $\beta _r$ because of the exact sequence (4.14). There are therefore two possibilities for the classes $\alpha _r$:

• 1. the classes $\alpha _r$ are linearly independent;

• 2. there is exactly one relationship between the classes $\alpha _r$ which is of the form $\sum _{r=1}^s d_r\alpha _r$ with $\prod _{r=1}^s d_r\ne 0$.

Using Lemma 4.4.19 and the equalities $h^{2,0}=1$ and ${\sigma }^*H^{2,0}=H^{0,2}$, we can prove that the positive index of the intersection form restricted to the invariant part of $H_{2}(X;\mathbb {Z})$ is equal to 1. Moreover, $\alpha _r\cdot \alpha _{r}=-\chi _{\text {top}}(V_r)$ by Lemma 4.4.17.

In the first case it follows that there is at most one component which has negative or zero Euler characteristic.

In the second case it follows from the fact that $\sum _{r=1}^s d_r\alpha _r=0$ that $\alpha _r\cdot \alpha _{r}=0$ for all r because $\alpha _r\cdot \alpha _{r'}=0$ whenever $r\ne r'$. The fact that the positive index of the intersection form restricted to $H_{2}(X;\mathbb {Z})^G$ is 1 implies that $X(\mathbb {R})$ contains at most two connected components diffeomorphic to ${\mathbb T}^2$ and that if $\alpha _1$ and $\alpha _2$ are two such components then they are linearly dependent.    $\square$

Remark 4.5.7

There is a more sophisticated proof of the orientability of the real locus of a real K3 surface which proceeds as follows: we start by noting that by Proposition 3.1.10 the real locus of a real K3 surface of degree 4 in $\mathbb {P}^3(\mathbb {C})$ is orientable and then we apply the following theorem [Har76, Sil89, Chapter VIII]:

Theorem 4.5.8

Any real K3 surface is a deformation (Definition 4.3.25) of a quartic $\mathbb {R}$-surface in $\mathbb {P}^3$.

See [Sil89, Corollary VIII.4.2] for more details.

Let $(X,{\sigma })$ be a real K3 surface whose real locus is non empty. Let s be the number of connected components of $X(\mathbb {R})$ and let g be the sum of genuses of connected components of $X(\mathbb {R})$. If $g>0$ and $X(\mathbb {R})$ is not a union of two toruses then g is the genus of the unique component which is not diffeomorphic to a sphere. We then have that

$$ s= \frac{b^*(X(\mathbb {R});\mathbb {Z}_2)+\chi (X(\mathbb {R}))}{4},\qquad g=\frac{b^*(X(\mathbb {R});\mathbb {Z}_2)-\chi (X(\mathbb {R}))}{4} \;. $$

The topological type of $X(\mathbb {R})\ne \varnothing$ is therefore determined by the value of the pair $(\chi (X(\mathbb {R})),b^*(X(\mathbb {R}));\mathbb {Z}_2)$ except for the pair (0, 8) which corresponds to two topological types realised by real K3 surfaces:

$$ {\mathbb T}^2\sqcup {\mathbb T}^2\quad \text{ and }\quad {\mathbb S}_2\sqcup \mathbb {S}^2\;. $$

4.5.2 Algebraic Cycles on K3 Surfaces

In the moduli space of complex K3 surfaces, the isomorphism classes of complex surfaces of given Picard number $\rho$ form a countable union of subspaces of dimension $20 - \rho$. See [GH78, p. 594] for more details. We now prove a similar result for real K3 surfaces: it turns out that in the moduli space of real K3 surfaces satisfying certain conditions explained below, the isomorphism classes of real K3 surfaces such that $b^1_{\mathrm {alg}}\geqslant k$ form a countable union of subspaces of dimension $20-k$.

Example 4.5.9

(Quartic surface in $\mathbb {P}^3$ such that $b^1_{\mathrm {alg}}=0$) Consider the surface $\mathbb {S}^1\times \mathbb {S}^1$ realised as a quartic in $\mathbb {P}^3(\mathbb {R})$, for example as the real locus of the surface $X\subset \mathbb {P}^3(\mathbb {C})$ whose equation with real coefficients is $16(x_1^2+x_2^2)-(x_1^2+x_2^2+x_3^2+3x_0^2)^2=0$ as in Example 2.6.38. The surface in question has non real singularities: perturbing the equation slightly so that the real locus is still a torus we get a general non singular $\mathbb {R}$-surface $X'$. We then have that $\rho (X)=1$ by Noether’s theorem (see [Del73, 1.2.1]) and as $X'$ is a non singular quartic it is a K3 surface. The hyperplane section generates a non trivial algebraic cycle in $H^2(G,\mathrm{{Pic}}(X))$, but does not generate a real algebraic cycle—if the intersection of this plane with the torus is not empty then it contains two homologous circles or a circle homologous to 0. See [BKS82] for more details.

There is a unique complex family of complex K3 surfaces [X85], but there are 75 real families of real K3-surfaces [DIK00].

Let $(X,{\sigma })$ be an $\mathbb {R}$-surface. The number $b^1_\mathrm {alg}$ is not generally invariant under real deformation. If X is a K3 surface then

$$ b^1_{\mathrm {alg}}(X(\mathbb {R});\mathbb {Z}_2)\leqslant b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant h^{1,1}(X)=20\;. $$

Theorem 4.5.10

Let $(X,{\sigma })$ be a real K3 surface which is not an M-surface. For any subgroup K in $H^1(X(\mathbb {R});\mathbb {Z}_2)$ there is a real deformation Y of X and an isometry

$$ u:H^1(X(\mathbb {R});\mathbb {Z}_2)\rightarrow H^1(Y(\mathbb {R});\mathbb {Z}_2) $$

such that

$$ u(K)=H_\mathrm {alg}^1(Y(\mathbb {R});\mathbb {Z}_2)\;. $$

When X is a general K3 surface we have that

$$ b^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)\leqslant 1\;, $$

but Theorem 4.5.10 enables us to realise any value of $b^1_\mathrm {alg}$ authorised by topological constraints by specialisation.

Corollary 4.5.11

Let $(X,{\sigma })$ be a real K3 surface. The following then hold.

• 1. For any integer $1\leqslant k<b^1(X(\mathbb {R});\mathbb {Z}_2)$ there is a real deformation Y of X such that

  $$ b^1_\mathrm {alg}(Y(\mathbb {R});\mathbb {Z}_2)=k\;. $$

• 2. If X is not an M-surface there is also a real deformation Y of X such that

  $$ b^1_\mathrm {alg}(Y(\mathbb {R});\mathbb {Z}_2)=b^1(X(\mathbb {R});\mathbb {Z}_2)\;. $$

For completion’s sake, we note that for any maximal real K3 surface there cannot be a real deformation to a totally real algebraic surface because for any such surface the inequality $b^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)<b^1(X(\mathbb {R});\mathbb {Z}_2)$ holds by the following proposition.

Proposition 4.5.12

Let $(X,{\sigma })$ be a compact Kähler $\mathbb {R}$-surface such that $H_1(X;\mathbb {Z}_2)=0$. We have that

$$ b^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)\leqslant b^1(X(\mathbb {R});\mathbb {Z}_2) -(p_g(X)-a) $$

where $a=\frac{1}{2}(b^*(X;\mathbb {Z}_2)-b^*(X(\mathbb {R});\mathbb {Z}_2))$, so that $(X,{\sigma })$ is an $(M-a)$-surface (Definition 3.3.11).

Proof

See [Man97, Proposition 3.2].    $\square$

Proof of Theorem 4.5.10

We sketch the proof of Theorem 4.5.10: see [Man97] for the complete proof. Let X be a K3 surface. We know by [X85, Exposé IV] that $H^2(X;\mathbb {Z})$ equipped with the cup product is isomorphic to a certain free $\mathbb {Z}$-module L with an integral even non degenerate symmetric bilinear form Q of signature (3, 19). Let $f:H^2(X;\mathbb {Z})\rightarrow L$ be an isometry. We say that the pair (X, f) is a marked K3 surface. Consider the Hodge decomposition (see Appendix D)

$$ H^2(X ,\mathbb {C})= H^{2,0}(X){\oplus }H^{1,1}(X){\oplus }H^{0,2}(X)\;. $$

Here we have that $h^{2,0}=\dim H^{2,0}(X)=1$ and $h^{1,1}=\dim H^{1,1}(X) =20$. Let (X, f) be a marked K3 surface. We consider $P\subset L_{\mathbb {R}}=L\otimes \mathbb {R}$, the image under $f_{\mathbb {R}}$ of the subspace $H^2(X;\mathbb {R})\cap (H^{2,0}(X)\oplus H^{0,2}(X))$ in $H^2(X;\mathbb {R})$. Since $H^{2,0}(X)$ is of complex dimension 1, P is of real dimension 2 in $L_{\mathbb {R}}$. We choose an orientation of P such that for any holomorphic 2-form $\omega \in H^{2,0}(X)$ the basis $(\mathfrak {R}(\omega ),\mathfrak {I}(\omega ))$ is direct. This oriented plane P is called the period of the marked K3 surface (X, f).

Let $(X,{\sigma })$ be a real K3 surface. The real structure induces an involution $\sigma$ of (L, Q). For simplicity’s sake we consider the case where X is not an M-surface and set $K=H^1(X(\mathbb {R});\mathbb {Z})$. Following ideas due to Nikulin [Nik83] we show that in this case there is a primitive submodule $M\subset L^{-\sigma }$ whose quotient $M/((1-\sigma )L\cap M)$ has rank $b^1(X(\mathbb {R});\mathbb {Z}_2)$ and whose orthogonal $M_{\mathbb {R}}^\bot$ meets the cone of periods of real K3 surfaces deformation equivalent to X. For any real K3 surface (Y, g) whose period is orthogonal to M we have that $g^{-1}(M)\subset H^2_\mathrm {alg}(Y;\mathbb {Z})$ by the Lefschetz theorem on (1, 1)-cycles (Theorem D.9.3).

Consider an element $\alpha \in g^{-1}(M)$. By construction, $\alpha$ is anti-invariant for the real structure on Y and as Y is simply connected it is representable by a real divisor. The first Chern class induces an isomorphism $\mathrm{{Pic}}(X)^\sigma \longrightarrow H^2_\mathrm {alg}(X;\mathbb {Z})^{-\sigma }$. We complete the proof by establishing that $H^1(Y(\mathbb {R});\mathbb {Z}_2)$ is equal to $\varphi \circ c_1^{-1}\circ g^{-1}(M)$.    $\square$

4.5.3 Enriques Surfaces

Definition 4.5.13

Let X be  a non singular compact complex analytic surface. X is said to be an Enriques surface if and only if $q(X)=0$, $K_X\not \sim 0$ and $2K_X\sim 0$. A real Enriques surface is an $\mathbb {R}$-surface $(X,{\sigma })$ such that X is an Enriques surface.

Remark 4.5.14

Unlike K3 surfaces, all Enriques surfaces are projective.

Proposition 4.5.15

Let X be an Enriques surface. X is then a minimal projective surface such that ${\kappa }(X)=0$ and $p_g(X)=0$.

Proof

See [BHPVdV04, Chapitre VIII].    $\square$

There are 87 topological types of real Enriques surfaces [DK96b]. The theorem below completes the classification started by Nikulin in [Nik96].

In the list below $X(\mathbb {R})$ is the real locus of a real Enriques surface realising a given topological type. Recall that by definition of an $(M-a)$-surface, the modulo 2 Betti numbers satisfy the relationship $2a=\sum _{i=0}^{4} b_i(X;\mathbb {Z}_2)-\sum _{i=0}^2 b_i(X(\mathbb {R});\mathbb {Z}_2)$.

Theorem 4.5.16

(Degtyarev, Kharlamov 1996) There are 87 topological types of real Enriques surfaces. Each of them can be obtained by topological Morse simplification (Definition 4.3.31) from one of the 22 extremal types listed below. Conversely, except for $6\mathbb {S}^2$ and ${\mathbb T}^2\sqcup 5\mathbb {S}^2$ any type obtained in this way can be realised as a real Enriques surface.

The 22 extremal types are the following.

• 1. M-surfaces,

  • (a) $\chi (X(\mathbb {R}))=8$,

    $4{\mathbb {R}}{\mathbb {P}}^2\sqcup 2\mathbb {S}^2$,    ${\mathbb V}_3\sqcup {\mathbb {R}}{\mathbb {P}}^2\sqcup 4\mathbb {S}^2$,    ${\mathbb V}_4\sqcup 5\mathbb {S}^2$, ${\mathbb K}^2\sqcup 2{\mathbb {R}}{\mathbb {P}}^2\sqcup 3\mathbb {S}^2$,    $2{\mathbb K}^2\sqcup 4\mathbb {S}^2$,    ${\mathbb K}^2\sqcup {\mathbb T}^2\sqcup 4\mathbb {S}^2$,

  • (b) $\chi (X(\mathbb {R}))=-8$,

    $\{{\mathbb V}_{l} \sqcup {\mathbb V}_{12-l}\}_{l=1\dots 6}$,   ${\mathbb V}_{10}\sqcup {\mathbb T}^2$;

• 2. $(M-2)$-surfaces with $\chi (X(\mathbb {R}))=0$,

  ${\mathbb V}_4\sqcup 2{\mathbb {R}}{\mathbb {P}}^2$,    ${\mathbb V}_6\sqcup 2\mathbb {S}^2$,    ${\mathbb V}_3\sqcup {\mathbb K}^2\sqcup {\mathbb {R}}{\mathbb {P}}^2$,    ${\mathbb V}_4\sqcup {\mathbb T}^2\sqcup \mathbb {S}^2$, ${\mathbb V}_5\sqcup {\mathbb {R}}{\mathbb {P}}^2\sqcup \mathbb {S}^2$,    $2{\mathbb V}_3\sqcup \mathbb {S}^2$,    ${\mathbb V}_4\sqcup {\mathbb K}^2\sqcup \mathbb {S}^2$,   $2{\mathbb K}^2\sqcup {\mathbb T}^2$;

• 3. Pair of toruses ${\mathbb T}^2\sqcup {\mathbb T}^2$.

Proof

See [Nik96, DK96b,DK96a].    $\square$

4.5.4 Algebraic Cycles on Enriques Surfaces

There is a unique complex family of Enriques surfaces, but several hundred real families. See [DIK00] for more details. Let $(X,{\sigma })$ be a real Enriques surface. As $b^2(X)=10$ and $b^1(X;\mathbb {Z}_2)=1$ we have that $b^1_{\mathrm {alg}}(X(\mathbb {R});\mathbb {Z}_2)\leqslant b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant 12$ by Inequality (3.8) of Theorem 3.3.6.

Unlike K3 surfaces, the number $b^1_\mathrm {alg}$ is invariant under real deformation of Enriques surfaces. The theorem below characterises the group of algebraic cycles of a real Enriques surface topologically.

Theorem 4.5.17

Let $(X,{\sigma })$ be a real Enriques surface with $X(\mathbb {R})\ne \varnothing$. If all the connected components of the real part $X(\mathbb {R})$ are orientable we have that

$$ H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)= H^1(X(\mathbb {R});\mathbb {Z}_2)\;. $$

Otherwise

$$ \dim H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2) = \dim H^1(X(\mathbb {R});\mathbb {Z}_2) - 1\;. $$

Corollary 4.5.18

A real Enriques surface $(X,{\sigma })$ is totally algebraic if and only if $X(\mathbb {R})$ is empty or orientable.

Corollary 4.5.19

There are real families of Enriques surfaces such that $b^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)<b^1(X(\mathbb {R});\mathbb {Z}_2)$ for all members of the family. In particular, if X is a real Enriques surface with maximal first Betti number, $b^1(X(\mathbb {R});\mathbb {Z}_2)=12$, there is no real deformation of X which is totally algebraic.

Proof

We will give a proof of the first part of Theorem 4.5.17: we refer to  [MvH98] for a complete proof. For technical reasons we prove this theorem in homology. In other words, we will establish the following equivalence.

$$ H_1^\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)= H_1(X(\mathbb {R});\mathbb {Z}_2) \Longleftrightarrow X(\mathbb {R})\ \text {is orientable.} $$

As the canonical divisor of an Enriques theorem is 2-torsion, the condition is necessary by Theorem 4.5.21 below. The converse is tricky. If Y is a K3 surface then Y is simply connected and there is a surjective morphism

$$ H_2(Y;\mathbb {Z})^{-\sigma }\longrightarrow H_1(Y(\mathbb {R});\mathbb {Z}_2)\;. $$

This morphism is not well defined for an Enriques surface X because its fundamental group is $\pi _1(X)=\mathbb {Z}_2$. On the other hand, when X is an Enriques surface we can always define a morphism of equivariant cohomology [MvH98, Sec. 4]

$$ \alpha ^X:H_2(X;G,\mathbb {Z}(1))\longrightarrow H_1(X(\mathbb {R});\mathbb {Z}_2) $$

whose image is precisely the group $H_1^\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)$. Any Enriques surface is a quotient of a K3 surface by a holomorphic involution without fixed points [Bea78, Proposition VIII.17]. Let Y be a complex K3 surface such that X is the quotient of Y by a holomorphic involution $\eta$ without fixed points. The real structure on X naturally lifts to two real structures $\sigma _1$ and $\sigma _2=\eta \circ \sigma _1$ on Y which commute with each other [Sil89, Theorem $A_8$.6]. The real part $X(\mathbb {R})$ is covered by the union of the real parts $Y_1(\mathbb {R})=Y^{\sigma _1}$ and $Y_2(\mathbb {R})=Y^{\sigma _2}$. For any $j\in \{1,2\}$ let $X_j$ be the disjoint union of components of $X(\mathbb {R})$ covered by $Y_j(\mathbb {R})$. This gives us a natural decomposition of the real part of an Enriques surface in “halves”

$$ X(\mathbb {R})=X_1\sqcup X_2\;. $$

Recall that all the connected components of the real locus of a K3 surface are orientable. Let M be a connected component of one of the halves $X_j$. If M is orientable then it is covered by two components of $Y_j(\mathbb {R})$ which are exchanged by $\eta$. If M is non orientable then M is covered by a unique component of $Y_j(\mathbb {R})$ which is the orientation covering of M. This gives us a morphism

$$ H_1(Y_1(\mathbb {R});\mathbb {Z}_2)\oplus H_1(Y_2(\mathbb {R});\mathbb {Z}_2)\longrightarrow H_1(X(\mathbb {R});\mathbb {Z}_2) $$

which is surjective whenever $X(\mathbb {R})$ is orientable. This morphism gives us a commutative diagram.

(4.15)

The morphisms $\alpha ^{Y_1}$ and $\alpha ^{Y_2}$ are surjective because Y is simply connected and hence $\alpha ^X$ is surjective whenever $X(\mathbb {R})$ is orientable.    $\square$

The decomposition of the real locus in halves can also be used to characterise Galois-Maximality (Definition 3.6.5) of real Enriques surfaces

Theorem 4.5.20

Let $(X,{\sigma })$ be a real Enriques surface of non empty real locus $X(\mathbb {R})=X_1\sqcup X_2$.

• 1. Suppose that both the halves $X_1$ and $X_2$ are non empty. The surface X is then Galois-Maximal. Moreover, X is $\mathbb {Z}$-Galois-Maximal if and only if $X(\mathbb {R})$ is non orientable

• 2. Suppose one of the halves $X_1$ or $X_2$ is empty. The surface X is then Galois-Maximal if and only if $X(\mathbb {R})$ is non orientable. Moreover, X is $\mathbb {Z}$-Galois-Maximal if and only if $X(\mathbb {R})$ has at least one component which is of odd Euler characteristic.

Proof

See [MvH98].    $\square$

All cases of Galois-Maximality (see Example 3.6.14) are realised by Enriques surfaces: on inspecting the proof of Theorem 4.5.16 (see [DK96b, §5] or [DK96a]) we see that there exist examples of Enriques surfaces for each of the cases listed in the previous theorem.

Theorem 4.5.21

Let $d\geqslant 2$ be an integer. An algebraic $\mathbb {R}$-surface X whose canonical bundle $K_X$ is d-torsion can only be totally algebraic if its real part $X(\mathbb {R})$ is empty or orientable.

Proof

Let X be a totally algebraic $\mathbb {R}$-surface, by which we mean that

$$ H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)=H^1(X(\mathbb {R});\mathbb {Z}_2). $$

We use the properties (3.38) of $\varphi _X :\mathrm{{Pic}}(X)^\sigma \rightarrow H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)$ discussed in Proposition 3.7.16. Let D be a divisor whose class in the Néron–Severi group ${\text {NS}}(X)$ has a trivial multiple: we then have that $(D\cdot D')=0$ for any divisor $D'$. When D is real we have that $\varphi _X(D)=0$ in $H^1(X(\mathbb {R});\mathbb {Z}_2)$ since by hypothesis any cohomology class $u\in H^1(X(\mathbb {R});\mathbb {Z}_2)$ is the image under $\varphi _X$ of a real divisor $D'$ so $\varphi _X(D)\cdot u=0$. As the intersection form is non degenerate on $H^1(X(\mathbb {R});\mathbb {Z}_2)$ it follows that $\varphi _X(D)=0$. Now if $X(\mathbb {R})\ne \varnothing$ we can assume that $K_X$ is real by Theorem 2.6.32. As $K_X$ is torsion in ${\text {NS}}(X)$ we have that $\varphi _X(K_X)=0$ whence $\text {w}_1(X(\mathbb {R}))=0$ and therefore $X(\mathbb {R})$ is orientable.    $\square$

4.5.5 Abelian Surfaces

A detailed study of real abelian varieties is available in Comessatti’s articles [Com25, Com26]. Their moduli spaces and their compactifications are described in [Sil89, Chap IV] and [Sil92].

Definition 4.5.22

A complex torus of  dimension g is a quotient of $\mathbb {C}^g$ by a sub-$\mathbb {Z}$-module $\Lambda \subset \mathbb {C}^g$ of maximal rank 2g (also called a lattice). An abelian variety is a projective complex torus, or in other words a complex torus with an ample divisor. A real abelian surface is a complex torus of dimension 2 equipped with a real structure and an embedding into projective space. The embedding can be assumed equivariant by Theorem 2.6.44.

Remark 4.5.23

Complex toruses are Kähler because they inherit a Kähler metric from $\mathbb {C}^g$. On the other hand, like K3 surfaces, complex toruses of dimension 2 (or more) are not always projective.

Example 4.5.24

(Complex toruses associated to a variety) The Picard variety $\mathrm{{Pic}}^0(X)$ of a compact Kähler variety X of irregularity $q>0$ is a complex torus of dimension q. (See Definition D.6.6 for the definition of the Picard variety.) If X is projective it is a projective variety by Proposition D.6.7. If X is a complex torus then $\mathrm{{Pic}}^0(X)$ is isomorphic to X.

The Albanese variety ${\text {Alb}}(X)$ of a compact Kähler variety X of irregularity $q>0$ is a complex torus of dimension q. (See Definition D.6.10 for the definition of the Albanese variety.) It is an abelian variety if X is projective [Voi02, Corollaire 12.12]. If X is a complex torus, ${\text {Alb}}(X)$ is isomorphic to X.

The Jacobian ${\text {Jac}}(C)$ of a compact complex curve C of genus g is an abelian variety of dimension g. (See Definition E.4.1 for the definition of the Jacobian.) If C is a curve of genus 1 then ${\text {Jac}}(C)$ is a curve isomorphic to C.

Proposition 4.5.25

Let X be an abelian surface. X is then a minimal projective surface such that ${\kappa }(X)=0$, $p_g(X)=1$, $q(X)=2$ and $K_X\sim 0$.

Proof

See Theorem 4.5.1 and [Bea78, Liste VI.20 and Théorème VIII.2].    $\square$

Theorem 4.5.26

There are 4 topological types of real abelian surfaces.

$$ \varnothing ,\quad {\mathbb T}^2, \quad 2{\mathbb T}^2, \quad 4{\mathbb T}^2\;. $$

Proof

See [Sil89, Chapter IV].    $\square$

4.5.6 Algebraic Cycles on Abelian Surfaces

Like K3 surfaces, there is a unique complex family of complex abelian surfaces whereas real abelian surfaces are divided into several real families and $b^1_\mathrm {alg}$ is not invariant under real deformation.

Let $(X,{\sigma })$ be a real abelian surface. By Theorem 4.5.26 we have that $b^1(X(\mathbb {R}))\le 8$. Moreover, using [Kuc96, Theorem 2.1] we also have that $b^1_\mathrm {alg}(X(\mathbb {R}))\le 5$.

As for K3 surfaces we can identify certain topological constraints and prove that once these constraints are satisfied we can always deform an abelian surfaces so as to obtain a given $b^1_\mathrm {alg}(X(\mathbb {R}))$.

In particular, we can show that the real part of a totally algebraic real abelian surface is either connected or empty—see [Hui94]—and that a real abelian surface with connected real locus can always be deformed to a totally algebraic real abelian surface.

Proposition 4.5.27

Let X be a real abelian surface with a real point. We then have that

$$ H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)=H^1(X(\mathbb {R});\mathbb {Z}_2) \implies X(\mathbb {R})\approx {\mathbb T}^2\;. $$

4.5.7 Bi-elliptic Surfaces

Definition 4.5.28

Let X be  a non singular compact complex analytic surface. We say that X is a bi-elliptic surface¹⁰ if there are two elliptic curves E and F and a finite group H acting by translation on F and by automorphism on E such that $E/H=\mathbb {P}^1$ and X is the quotient of the product $E\times F$ by the product action of H. A real bi-elliptic surface is an $\mathbb {R}$-surface $(X,{\sigma })$ such that X is a bi-elliptic surface.

Proposition 4.5.29

Let X be a bi-elliptic surface. X is then a projective minimal surface such that ${\kappa }(X)=0$, $p_g(X)=0$, $q(X)=1$ and $m_0K_X\sim 0$ for some $m_0\in \{2,3,4,6\}$.

Proof

See Theorem 4.5.1 and [Bea78, Liste VI.20 and Théorème VIII.2].    $\square$

For any bi-elliptic surface X, the Albanese map (Definition D.6.13)

$$ \alpha :X=(E\times F)/H\rightarrow {\text {Alb}}(X) =F/H $$

is an elliptic fibration that is locally but not globally trivial. The fibres of $\alpha$ are all isomorphic to E over $\mathbb {C}$. When X is an $\mathbb {R}$-surface the Albanese fibration $\alpha$ is an $\mathbb {R}$-fibration and the curves F/H and E are real elliptic curves. The real locus of a non singular real elliptic curve is either empty or consists of one or two ovals, It is immediate that the number of connected components of the real locus of X satisfies $0\leqslant \#\pi _0X(\mathbb {R})\leqslant 4$ and every connected component is homeomorphic to a torus ${\mathbb T}^2$ or a Klein bottle ${\mathbb K}^2$. This gives us a list of 15 potential topological types of $X(\mathbb {R})$. Catanese and Frediani [CF03] determined the eleven topological types that are actually possible as a corollary of their description of the moduli space of real bi-elliptic surfaces. If $\alpha$ is further assumed to have a real section then only seven topological types can be realised.

Theorem 4.5.30

(Catanese, Frediani 2003) There are 11 topological types of real bi-elliptic surfaces.

• 1. $\varnothing$,    ${\mathbb T}^2$,    $2{\mathbb T}^2$,    $3{\mathbb T}^2$,    $4{\mathbb T}^2$,

• 2. ${\mathbb K}^2$,    $2{\mathbb K}^2$,    $3{\mathbb K}^2$,    $4{\mathbb K}^2$,

• 3. ${\mathbb T}^2\sqcup {\mathbb K}^2$,    ${\mathbb T}^2\sqcup 2{\mathbb K}^2$.

Proof

See [CF03].    $\square$

Theorem 4.5.31

There are 7 topological types of real bi-elliptic surfaces whose Albanese fibration has a real section.

• 1. ${\mathbb T}^2$,    $2{\mathbb T}^2$,    $3{\mathbb T}^2$,    $4{\mathbb T}^2$,

• 2. $2{\mathbb K}^2$,    $3{\mathbb K}^2$,    $4{\mathbb K}^2$.

Proof

See [Man03, Théorème 2.3].    $\square$

4.5.8 Algebraic Cycles on Bi-elliptic Surfaces

The canonical divisor $K_X$ of a bi-elliptic surface is torsion: we denote its order by $d_X\in \{2,3,4,6\}$.

There are exactly seven complex families of bi-elliptic surfaces and each of them corresponds to several real families. We refer to [CF03] for more details. Once again, the number $b^1_\mathrm {alg}$ is invariant under deformation and the article [Man03] contains a topological characterisation of totally algebraic real bi-elliptic surfaces.

Theorem 4.5.32

Let X be a real bi-elliptic surfaces with a real point.

• 1. If $H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)=H^1(X(\mathbb {R});\mathbb {Z}_2)$ then $X(\mathbb {R})$ is homeomorphic to a torus. If moreover $d_X$ is even then $\alpha$ has a real section.

• 2. Suppose that $X(\mathbb {R})$ is homeomorphic to a torus. If $d_X$ is odd or $\alpha$ has a real section then

  $$ H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)=H^1(X(\mathbb {R});\mathbb {Z}_2)\;. $$

Proof

We give a partial proof of this result and refer to [Man03] for the complete proof. Let $(X,{\sigma })$ be a real bi-elliptic surface. We denote by

$$ \pi :X\rightarrow E/H\simeq \mathbb {P}^1 $$

the second elliptic fibration whose only singular fibres are multiple fibres $m_t L_t$ where $L_t$ is a non singular elliptic curve. The Néron–Severi group ${\text {NS}}(X)$ is generated by a fibre $X_x$ of $\alpha$ and by the reductions $L_t$ of the multiple fibres of $\pi$. Let $m_tL_t$ and $m_{t'}L_{t'}$ be two multiple real fibres of $\pi$ and denote by d the gcd of $m_t$ and $m_{t'}$. Assume that $d\geqslant 2$: the divisor $D=(m_t/d)L_t-(m_{t'}/d)L_{t'}$ is then d-torsion in ${\text {NS}}(X)$. By the proof of Theorem 4.5.21 we then have that $\varphi _X(D)=0$. Permuting t and $t'$ if necessary we can assume that $m_t/d$ is odd and in this case

$$ \varphi _X((m_t/d)L_t)=\varphi _X(L_t)\;. $$

There are now two possibilities: either $\varphi _X(L_t)=\varphi _X(L_{t'})$ or $\varphi _X(L_t)=0$. Studying the seven possible configurations of multiples fibres, we deduce that the image under $\varphi _X$ of the subgroup of ${\text {NS}}(X)$ generated by the real curves $L_t$ is of dimension $\leqslant$1.

Suppose now that $(X,{\sigma })$ is totally algebraic. In this case we have that $\varphi _X(\mathrm{{Pic}}^0(X)^{\sigma })=\{0\}$ in $H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)$ by [Kuc96, Th. 2.1]. It follows that there is a well defined morphism

$$ {\text {NS}}(X)^{\sigma }\rightarrow H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2) $$

on ${\text {NS}}(X)^{\sigma }$ which is surjective onto $H^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)$. This gives an upper bound $\dim H^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)\leqslant 2$. By hypothesis, the dimension of the space $H^1(X(\mathbb {R});\mathbb {Z}_2)$ satisfies the same inequality so $X(\mathbb {R})$ is connected. Moreover, the canonical divisor $K_X$ of a bi-elliptic surface is $d_X$-torsion for some $d_X\in \{2,3,4,6\}$. By Theorem 4.5.21, if the real part of $X(\mathbb {R})$ is non empty then it is orientable and thus homeomorphic to a torus. We refer to the original article [Man03] for a proof of the converse.    $\square$

4.5.9 Summary: Algebraic Cycles on Surfaces with ${\kappa }\leqslant 0$

Gathering the results in this section on surfaces of Kodaira dimension ${\kappa }(X)=0$ and checking them directly (exercise for the reader) for surfaces of Kodaira dimension ${\kappa }(X)=-\infty$ (by [Kuc96, Theorem 2.1] we then have to choose an involution such that $\varphi _X(\mathrm{{Pic}}^0(X)^{\sigma })=\{0\}$ in $H_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)$) we note that when X is an algebraic surface of one of the following types: rational, uniruled, abelian, K3 or Enriques, we can always find an algebraic surface Y in the same complex family as X and a non empty real structure on Y which is totally algebraic. (This turns out to also hold for regular elliptic surfaces: see  Theorem 4.6.16 for more details.) On the other hand, there are two complex families of bi-elliptic surfaces containing $\mathbb {R}$-surfaces whose real part is diffeomorphic to a torus and which are never totally algebraic:

Theorem 4.5.33

Let E, F be elliptic curves and let H be the group $\mathbb {Z}_2\oplus \mathbb {Z}_2$ or $\mathbb {Z}_4\oplus \mathbb {Z}_2$. For any complex algebraic surface Y which is deformation equivalent to the bi-elliptic surface $X=(E\times F)/H$ and for any real structure on Y with real points we have that

$$ H_\mathrm {alg}^1(Y(\mathbb {R});\mathbb {Z}_2)\ne H^1(Y(\mathbb {R});\mathbb {Z}_2)\;. $$

Proof

See [Man03, Corollaire 3.3].    $\square$

In each of the five other complex families of bi-elliptic surfaces there is an $\mathbb {R}$-surface X such that $X(\mathbb {R})$ is homeomorphic to a torus and $H_\mathrm {alg}^1(Y(\mathbb {R});\mathbb {Z}_2)=H^1(Y(\mathbb {R});\mathbb {Z}_2)$.

Corollary 4.5.34

Except for the surfaces of Theorem 4.5.33, every complex family of surfaces with non positive Kodaira dimension contains an $\mathbb {R}$-surface Y with a real point such that $H_\mathrm {alg}^1(Y(\mathbb {R});\mathbb {Z}_2)= H^1(Y(\mathbb {R});\mathbb {Z}_2)$.

4.6 Elliptic Surfaces (${\kappa }\leqslant 1$)

Definition 4.6.1

A non  singular complex analytic surface X is said to be elliptic if and only if there is a non singular complex curve $\Delta$ and a proper surjective holomorphic map $\pi :X\longrightarrow \Delta$ such that the fibre $X_u= \pi ^{-1}(u)$ is a non singular curve of genus 1 for almost all points $u \in \Delta$.

Remark 4.6.2

As the complex variety X is non singular and of dimension 2 all the fibres of $\pi$ are of dimension 1. (This equidimensionality of fibres no longer holds in higher dimension: see [Uen73] for more details.) Moreover, since $\pi$ is proper its fibres are compact and X is compact if and only if $\Delta$ is compact.

Some elliptic surfaces are projective and hence algebraic by Chow’s theorem D.5.1. The algebraic definition is as follows.

Definition 4.6.3

A non  singular complex projective algebraic surface X is said to be elliptic if there is a non singular complex projective algebraic curve $\Delta$ and a regular surjective map $\pi :X\longrightarrow \Delta$ whose general fibre is a non singular complex projective algebraic curve of genus 1.

Remark 4.6.4

The image under $\pi$ of the set of its singular fibres is Zariski closed in $\Delta$ so the number of singular fibres of $\pi$ is finite.

Definition 4.6.5

An $\mathbb {R}$-surface $(X,{\sigma })$ is  said to be real elliptic if there is a real elliptic fibration $\pi :X\longrightarrow \Delta$, i.e. the curve $\Delta$ has a real structure $\sigma _\Delta$ and $\pi \circ {\sigma }=\sigma _\Delta \circ \pi$.

Remark 4.6.6

(Scheme theoretic definition) We give the corresponding scheme theoretic definition for the sake of completeness. An elliptic fibration of a geometrically integral non singular surface X is a faithfully flat morphism $\pi :X \longrightarrow C$ to a non singular curve whose generic fibre $X_{K(C)}$ is isomorphic to a non singular curve of genus 1 over the function field K(C) of rational functions on C. A closed general fibre $X_{\kappa (c)}=\pi ^{-1}(c)$ of $\pi$ is isomorphic to a non singular curve of genus 1 over the residue field $\kappa (c)$ of the point $c \in C$. A closed schematic fibre $\pi ^{-1}(c)$ which is not isomorphic to a non singular curve of genus 1 over $\kappa (c)$ is said to be degenerate.

Proposition 4.6.7

If X is an elliptic surface then ${\kappa }(X)\leqslant 1$.

Proof

See [BHPVdV04, Theorem V.12.5].    $\square$

Proposition 4.6.8

Let X be a non singular compact complex analytic surface such that ${\kappa }(X)=1$. The surface X is then canonically equipped with an elliptic fibration which is the only elliptic fibration on X.

Proof

See [BHPVdV04, § VI.3, case $a(X)=2$, ${\kappa }(X)=1$].    $\square$

Remark 4.6.9

If ${\kappa }(X)=1$ the variety X has an elliptic fibration given by the morphism $\varphi _{mK_X}$ associated to a multiple of the canonical divisor. In particular, if $(X,{\sigma })$ is an $\mathbb {R}$-surface then this fibration is a real elliptic fibration by Proposition 2.6.31.

Definition 4.6.10

A non  singular compact complex analytic surface X (resp. $\mathbb {R}$-surface $(X,{\sigma })$) is a properly elliptic surface (resp. a properly real elliptic surface) if ${\kappa }(X)=1$.

An algebraic surface is said to be regular or of zero irregularity if $H^1(X,\mathcal {O}_X)=\{0\}$. When X is an  elliptic surface this implies that the base curve has genus 0 and the fibration has at least one singular fibre. Conversely, let X be an elliptic fibration and suppose that $\pi :X\longrightarrow \mathbb {P}^1$ has at least one singular fibre. The surface X is then of zero irregularity. Recall (Definition 4.3.16) that the fibration $\pi$ is said to be minimal if and only if non of its fibres contains a $(-1)$-curve (by which we mean, generalising Definition 4.3.2 to non singular analytic surfaces, an irreducible non singular rational curve of self intersection $-1$). When a relatively minimal elliptic fibration $\pi :X\rightarrow \mathbb {P}^1$ has a section $s :\mathbb {P}^1 \rightarrow X$ we say that X is a Jacobian elliptic surface.¹¹  All of these definitions make sense over $\mathbb {R}$: a real elliptic surface is an elliptic surface whose fibration morphism commutes with the real structures on X and $\mathbb {P}^1$ and is said to be a real Jacobian elliptic surface if $\pi$ has a real section.

We recall two results on complex elliptic surfaces which will be useful in the rest of this section.

Lemma 4.6.11

Two relatively minimal complex elliptic surfaces of zero irregularity without multiple fibres are equivalent by deformation if and only if their holomorphic Euler characteristic are equal.

Proof

See [Kas77].    $\square$

Theorem 4.6.12

Two regular elliptic surfaces without multiple fibres X and Y are deformation equivalent if and only if

• 1. the minimal models $X'$ of X and $Y'$ of Y are deformation equivalent;

• 2. $\eta _X=\eta _Y$, where $\eta _Z$, $Z=X,Y$ is the minimal number of blow ups required to produce Z from $Z'$.

Proof

See [Kod64].    $\square$

The possible singular fibres of a real elliptic surface were classified by Silhol—see [Sil84] and [Sil89, Chapitre VII] for more details. The following theorem lists all possible topological types of real Jacobian elliptic surfaces in each complex family of complex Jacobian elliptic families.

Theorem 4.6.13

Let $k \geqslant 1$ be an integer. The possible extremal topological types of real Jacobian elliptic surfaces of zero irregularity and holomorphic Euler characteristic $\chi (\mathcal {O}_X)=k$ are:

• 1. M-surfaces, $a = k + 4\lambda - 1$, $l = 5k - 4\lambda$, $\lambda = 0,1,\dots , k$,

  • ${\mathbb S}_l \sqcup a\, \mathbb {S}^2$, k even

  • ${\mathbb V}_{2l} \sqcup a\mathbb {S}^2$, k odd.

• 2. $(M-2)$-surfaces, $a = k + 4\lambda$, $l = 5k - 4\lambda -3$, $\lambda = 0,1,\dots , k - 1$,

  • ${\mathbb S}_l \sqcup a\, \mathbb {S}^2$, k even or

  • ${\mathbb V}_{2l} \sqcup a\mathbb {S}^2$, k odd.

• 3. $\chi (X(\mathbb {R}))=0$,

  • pair of toruses ${\mathbb K}^2\sqcup {\mathbb K}^2$, k even or

  • pair of Klein bottles ${\mathbb T}^2\sqcup {\mathbb T}^2$, k odd.

Let X be a real Jacobian elliptic surface of Euler characteristic $\chi (\mathcal {O}_X)=k$. The topological type of $X(\mathbb {R})$ is then obtained by applying Morse simplification to one of the types listed above.

Conversely, any topological type obtained by Morse simplification applied to one of the above types which has total Betti number at least 2 can be realised as the real part of a real Jacobian elliptic surface X with Euler characteristic $\chi (\mathcal {O}_X)=k$.

Fig. 4.12

Topological types of real Jacobian regular elliptic surfaces of holomorphic Euler characteristic k

Proof

See [BM07].    $\square$

Note that in the definition of a Jacobian surface we have assumed the elliptic fibration is relatively minimal. The analogue of Theorem 4.6.13 without this hypothesis, i.e. the classification of topological types of real elliptic surfaces of zero irregularity with at least one real section contained in a given family of complex deformations, follows directly from Theorem 4.6.13. Indeed, by Theorem 4.6.12, two complex elliptic surfaces of zero irregularity without multiple fibres are deformation equivalent if and only if their holomorphic Euler characteristic are equal and their canonical fibres have the same degree.

To realise a given topological type in a certain complex family—with $k = \chi (\mathcal {O}_X)$ and $K_X^2 = -m < 0$, for example—consider a Jacobian elliptic surface Y of holomorphic Euler characteristic k. By definition we then have that $K_Y^2 = 0$. Let X be the surface obtained by blowing up a set of m points globally fixed by the real structure. We then have that $K^2_X = -m$. Each blow up at a real point produces a connected sum with an $\mathbb {R}\mathbb {P}^2$, as in Example 4.2.18. Conversely, the topological type of any real elliptic surface of zero irregularity with a real section can be obtained in this way.

4.6.1 Algebraic Cycles on Elliptic Surfaces such that $q=0$

Unlike surfaces of zero Kodaira dimension (K3, abelian, Enriques and bi-elliptic surfaces) there is an infinite number of complex families of regular elliptic surfaces and for each complex family there are several real families.

In general it is fairly difficult to find in a given family of complex surfaces real algebraic surfaces with “large” first Betti number $b^1(X(\mathbb {R});\mathbb {Z}_2)$. For example, we do not yet know whether there is a surface of degree 5 in $\mathbb {P}^3(\mathbb {R})$ with first Betti number equal to 47 (which is a known upper bound on the Betti number of such surfaces. See Section 4.7 for more details).

Proposition 4.6.14

(Kharlamov) Any regular real elliptic surface $(X,{\sigma })$ without multiple fibres satisfies the Ragsdale–Viro inequality

$$\begin{aligned} b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant h^{1,1}(X)\;. \end{aligned}$$

(4.16)

This result and an idea of its proof were communicated to us by V. Kharlamov in 1997. We do not know of any published proof other than [AM08], which we reproduce below.

Proof of Proposition 4.6.14

Set $b_*(X(\mathbb {R});\mathbb {Z}_2) = \sum _{k=0}^k b_k(X(\mathbb {R});\mathbb {Z}_2)$ and $b_*(X;\mathbb {Z}_2) = \sum _{k=0}^{2k} b_k(X;\mathbb {Z}_2)$. When $\pi :X\rightarrow \mathbb {P}^1$ has no multiple fibres it is easy to check (using the classification of possible singular fibres given in [Sil89, Chapitre VII]) that

$$ b_1(X(\mathbb {R});\mathbb {Z}_2) \leqslant b_1({\text {Jac}}(X)(\mathbb {R});\mathbb {Z}_2) $$

where ${\text {Jac}}(X)\rightarrow \mathbb {P}^1$ is the Jacobian bundle associated to $X\rightarrow \mathbb {P}^1$ as in [BHPVdV04, V.9]. By construction this fibration is a real elliptic surface with a real section such that

$$ h^{1,1}({\text {Jac}}(X)) = h^{1,1}(X)\;. $$

We may therefore assume without loss of generality that $\pi$ has a real section. The real structure ${\sigma }$ induces an involution, also denoted by ${\sigma }$, on $H_2(X , \mathbb {Z})$. Consider the following homological invariants:

The rank of the submodule invariant under ${\sigma }$,

$$ r_2 = {\text {rk}}H_2(X , \mathbb {Z})^{{\sigma }} = {\text {rk}}\ker (1-{\sigma }) $$

the Comessatti characteristic

$$ \lambda = {\text {rk}}\left( (1 + {\sigma }) H_2(X , \mathbb {Z}) \right) = {\text {rk}}{\text {Im}}(1+{\sigma })\;. $$

As the fibration $\pi :X \rightarrow \mathbb {P}^1$ has a section it does not have multiple fibres and the Betti numbers $b_1(X)$ and $b_3(X)$ vanish. By Theorem 3.6.11 the surface $(X,{\sigma })$ is therefore Galois-Maximal and for this reason (see also Corollary 3.6.12) the Comessatti characteristic corresponds to

$$ 2\lambda = b_*(X;\mathbb {Z}_2) - b_*(X(\mathbb {R});\mathbb {Z}_2) $$

and the first Betti number of $X(\mathbb {R})$ corresponds to

$$\begin{aligned} b_1(X(\mathbb {R});\mathbb {Z}_2) = b_2(X) - r_2 - \lambda \;. \end{aligned}$$

(4.17)

If there is no real non singular fibre of $\pi$ then $X(\mathbb {R})$ is the union of two toruses or two Klein bottles because $\pi$ has a real section. In this case inequality (4.16) holds. If $\pi$ has at least one singular real fibre then $X(\mathbb {R})$ has exactly one connected component which is not simply connected and a finite number of other components which are all homeomorphic to spheres. Let s be the number of spherical components: the sum of the Betti numbers of $X(\mathbb {R})$ is then $b_*(X(\mathbb {R});\mathbb {Z}_2) = 2 + 2 s + b_1(X(\mathbb {R});\mathbb {Z}_2)$ and the Comessatti characteristic is given by

$$\begin{aligned} \lambda = r_2 - 2 s \;. \end{aligned}$$

(4.18)

From Lemmas 4.4.17 and 4.4.19 it follows that s is a lower bound for the dimension of the invariant part of $H^{1,1}(X)$. As moreover ${\sigma }(H^{2,0}(X))=H^{0,2}(X)$ by Lemma D.3.17 and $h^{2,0}(X)=h^{0,2}(X)$ we deduce the following lower bound for $r_2$:

$$ h^{2,0}(X) + s \leqslant r_2 \;. $$

It follows from Equation (4.18) that $h^{2,0}(X) - s \leqslant \lambda$ and equality (4.17) implies that

$$ b_1(X(\mathbb {R});\mathbb {Z}_2) \leqslant b_2(X) - 2 h^{2,0}(X)\;. $$

   $\square$

For every complex family of regular elliptic surfaces without multiple fibres every $\mathbb {R}$-surface $(X,{\sigma })$ satisfies $b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant h^{1,1}(X)$ (Proposition 4.6.14). We prove below that in every complex family of regular elliptic surfaces without multiple fibres there is at least one subfamily of $\mathbb {R}$-surfaces such that $b^1= h^{1,1}$. Moreover, in each of these real families there is at least one $\mathbb {R}$-surface such that $b^1_\mathrm {alg}(X(\mathbb {R});\mathbb {Z}_2)=b^1(X(\mathbb {R});\mathbb {Z}_2)$. These two results are proved using the same construction. This establishes that the Ragsdale–Viro inequality $b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant h^{1,1}(X)$ is optimal for regular real elliptic surfaces without multiple fibres.

By the Hodge decomposition theorem, for any regular relatively minimal elliptic surface X we have that $h^{1,1}(X)=10\chi (\mathcal {O}_X)$ so when X is also without multiple fibres

$$\begin{aligned} b^1(X(\mathbb {R});\mathbb {Z}_2)\leqslant 10\chi (\mathcal {O}_X)\;. \end{aligned}$$

(4.19)

Theorem 4.6.15

For any $k > 0$ there is a regular relatively minimal real elliptic surface $(X,{\sigma })$ such that:

$$ \chi (\mathcal {O}_X)=k,\quad b^1(X(\mathbb {R});\mathbb {Z}_2) = 10k\;. $$

Proof

We give a sketch of the proof and refer to [Man00] for the full proof. The surfaces appearing in the above statement are said to be modular. A modular surface is constructed from a finite index subgroup $\Gamma$ of the modular group ${\mathbf {PSL}}_2(\mathbb {Z})={\mathbf {SL}}_2(\mathbb {Z})/\{\pm 1\}$. We adapt the classical construction [Shi71, Shi72b] to the real case and then use the real classification of possible singular fibres of an elliptic fibration given by Silhol [Sil84] to obtain the conditions that must hold on the group $\Gamma$ for the real surface to have maximal homology in rank 1.

Consider a finite index subgroup $\Gamma \subset {\mathbf {PSL}}_2(\mathbb {Z})$. As ${\mathbf {PSL}}_2(\mathbb {Z})$ is a subgroup of ${\mathbf {PSL}}_2(\mathbb {R})$, the group $\Gamma$ is a discrete subgroup of the group of isometries of the hyperbolic plane $\mathbb {H}$. It is therefore a Fuchsian group and the quotient $\Delta _\Gamma '=\mathbb {H}/\Gamma$ is a complex curve whose non compacity arises from parabolic classes or cusps. A natural compactification of this space can be obtained on noting that $\Gamma$ acts on $\mathbb {P}^1(\mathbb {Q})$ considered as a subspace of the boundary of $\mathbb {H}=\{z\in \mathbb {C}/\ \mathfrak {I}(z)>0\}$: we then consider the compact complex curve

$$ \Delta _\Gamma = (\mathbb {H}\cup \mathbb {P}^1(\mathbb {Q}))/\Gamma \;. $$

We then use the fact that $\Gamma$ is not only a group of isometries of $\mathbb {H}$ but also a group of automorphisms of elliptic curves, which allows us to construct a natural fibration in genus one curves over the open set $\Delta _\Gamma '$ in $\Delta _\Gamma$. There are then several different ways of extending this fibration over a cusp point P. To determine the complex type of the singular fibre over P it is enough to identify an element of the stabiliser of $P\in \Delta _\Gamma$. This gives us a monodromy representation

$$ \rho :\pi _1(\Delta _\Gamma ')\rightarrow {\mathbf {PSL}}_2(\mathbb {Z})\;. $$

For every lifting $\rho ':\pi _1(\Delta _\Gamma ') \rightarrow {\mathbf {SL}}_2(\mathbb {Z})$ of $\rho$ we obtain an elliptic surface with singular fibres whose complex types are in a prescribed list.

The action of the group ${\mathbf {PSL}}_2(\mathbb {R})$ on $\mathbb {H}$ is denoted $z\mapsto A.z$ where $A.z=\frac{az+b}{cz+d}$ if A is represented by $\left( \begin{matrix} a&{}b \\ c&{}d\\ \end{matrix}\right)$, $ad-bc=1$. The involution $\sigma _\mathbb {H}:z\mapsto -\bar{z}$ on $\mathbb {H}$ is anti-holomorphic. We set $S :{\mathbf {SL}}_2(\mathbb {R})\rightarrow {\mathbf {SL}}_2(\mathbb {R})$, $\left( \begin{matrix} a&{}b \\ c&{}d\\ \end{matrix}\right) \mapsto \left( \begin{matrix} a&{}-b \\ -c&{}d\\ \end{matrix}\right)$. The map S then induces an involution on ${\mathbf {PSL}}_2(\mathbb {R})$ which is also denoted by S. For any $z\in \mathbb {H}$ and $A\in {\mathbf {PSL}}_2(\mathbb {R})$ we have that $\sigma _\mathbb {H}\left( A.\sigma _\mathbb {H}(z)\right) =S(A).z$.

Let $\Gamma$ be a Fuchsian group (i.e. a discrete subgroup of ${\mathbf {PSL}}_2(\mathbb {R})$). The involution $\sigma _\mathbb {H}$ induces a real structure on the quotient $\mathbb {H}/\Gamma$ if and only if $\sigma _\mathbb {H}\Gamma =\Gamma \sigma _\mathbb {H}$, i.e. if and only if $\Gamma$ is stable under S.

In general we cannot entirely control the real types of the singular fibres arising in this construction. When this is possible, we obtain some necessary conditions on $\Gamma$ and then exhibit a sequence of groups which satisfy these necessary conditions.

For any $k\in \mathbb {N}^*$, let $\Gamma _k$ be the arithmetic group whose fundamental domain is shown in Figure 4.13. For every group $\Gamma _k$ there is a real modular elliptic surface $X_k\longrightarrow \Delta _{\Gamma _k}\simeq \mathbb {P}^1$ satisfying the conditions of Theorem 4.6.15. For every k, the real part $X_k(\mathbb {R})$ is connected. When k is even, $X_k(\mathbb {R})$ is diffeomorphic to the orientable real surface of genus $\frac{5k}{2}$: when k is odd, $X_k(\mathbb {R})$ is diffeomorphic to the non orientable surface of Euler characteristic $2-10k$.    $\square$

Fig. 4.13

Fundamental domain of the group $\Gamma _k$

Theorem 4.6.16

Every regular complex elliptic surface $Y\rightarrow \mathbb {P}^1$ without multiple fibres can be deformed over $\mathbb {C}$ to an elliptic surface X with a real structure such that

$$ b_\mathrm {alg}^1(X(\mathbb {R});\mathbb {Z}_2)=b^1(X(\mathbb {R});\mathbb {Z}_2)=h^{1,1}(X)\;. $$

Proof

Any regular elliptic surface with no multiple fibres $Y\longrightarrow \mathbb {P}^1$ has a relatively minimal model $Y'\longrightarrow \mathbb {P}^1$ which is an elliptic surface. By Lemma 4.6.11, relatively minimal regular elliptic surfaces without multiple fibres are classified by their holomorphic Euler characteristic. By Theorem  4.6.15, there is a relatively minimal regular elliptic surface $X'$ without multiple fibres such that $\chi (\mathcal {O}_{X'})=\chi (\mathcal {O}_{Y'})$ and $b_\mathrm {alg}^1(X'(\mathbb {R});\mathbb {Z}_2)=b^1(X'(\mathbb {R});\mathbb {Z}_2)=h^{1,1}(X')$. Now, if V is a real surface and $W\rightarrow V$ is a blow up at a point of $V(\mathbb {R})$, then W is a real surface and

$$ h^{1,1}(W)=h^{1,1}(V)+1,\quad b_\mathrm {alg}^1(W(\mathbb {R});\mathbb {Z}_2)=b_\mathrm {alg}^1(V(\mathbb {R});\mathbb {Z}_2)+1\;. $$

The surface Y is obtained from $Y'$ by a finite number of blow ups of points. The theorem follows by  Theorem 4.6.12.    $\square$

Remark 4.6.17

Unlike elliptic surfaces, a surface fibred in genus 2 curves can be of general type. The real theory of such surfaces is much less well developed than the real genus 1 theory but an initial step towards their classification has nevertheless been made, namely a classification of the possible singular fibres of a pencil of genus 2 curves established in [AM15].

4.7 Surfaces of General Type (${\kappa }=2$)

In this section we will construct some interesting examples of $\mathbb {R}$-surfaces of general type. In particular, we will study their algebraic cycles.

For any non singular complex projective algebraic surface X the image of the map $\mathrm{{Pic}}(X)\rightarrow H^2(X;\mathbb {C})= H^{2,0}(X){\oplus }H^{1,1}(X){\oplus }H^{0,2}(X)$ is contained in $H^{1,1}(X)$ (see Appendix D) so the Picard number $\rho (X)$ is bounded above by the Hodge number $h^{1,1}(X)$. Let $X_d$ be a non singular surface in $\mathbb {P}^3(\mathbb {C})$ of degree $d:=\deg (X_d)$. We then have that $\rho (X_d)\leqslant h^{1,1}(X_d)=\frac{d}{3}(2d^2-6d+7)$ (see Example D.4.4).

If $d\leqslant 3$, $X_d$ is a rational surface and $\rho (X_d)=h^{1,1}(X_d)$. If $d> 3$ and $X_d$ is very general amongst degree d surfaces then its Picard number satisfies $\rho (X_d) = 1$ by Noether’s theorem [Del73, 1.2.1] and it is fairly difficult to construct surfaces with Picard number close to $h^{1,1}(X_d)$.

If $d=4$, $X_d$ is a K3 surface, and we have a classification of such surfaces, see Theorem 4.5.10. If $d \geqslant 5$, X is a surface of general type (see [Bom73]) and only a few sporadic examples are understood.

Surfaces X which have “large” Picard number, or in other words for which $\rho$ is close to $h^{1,1}$, are exceptional. (See [Man94, KI96, Bih01a] for a study of surfaces in $\mathbb {P}^3$ of degree 5 and their deformations; see [Bih01b] and [Ren15] for more information on surfaces of degree 6.) On the other hand, $\mathbb {R}$-surfaces which have “lots” of algebraic cycles are even rarer. As we can see, it is extremely interesting to construct surfaces with such properties.

Algebraic cycles can be constructed by blowing up singular points on surfaces (namely the irreducible components of the exceptional divisor). Persson uses this method to construct examples of surfaces with maximal Picard number. We refer to [Per82] for more details.

In this section we show that in certain cases we can prove useful results in real algebraic geometry using this method, essentially thanks to Lemma 4.7.7 and an appropriate language for blow-ups, see Appendix F.

Definition 4.7.1

A compact  complex analytic surface X which has the same numerical invariants as a degree 5 surface in $\mathbb {P}^3$ is called a numerical quintic.

Remark 4.7.2

By [Hor75], for example, any surface X such that

$$ (c^2_1(X),h^{0,2}(X))=(5,4) $$

is a numerical quintic.

After studying real resolutions of singular points on a real surface we present two Examples 4.7.13 and 4.7.14, of numerical quintics. If X is a surface of degree 5 in $\mathbb {P}^3(\mathbb {C})$ then $h^{1,1}(X)=45$ as in Example D.4.4, and we have an upper bound

$$ {\text {rk}}\mathrm{{Pic}}(X) \leqslant 45\;. $$

In [Per82], Persson gives an example of a non singular numerical quintic for which $\rho = 43$ but this example is relatively uninteresting over the real numbers as we will see in Example 4.7.14. Specifically, the homology of its real locus contains only 31 classes generated by algebraic cycles. In Example 4.7.13, we revisit an example of Hirzebruch’s of a quintic with a non singular model with $\rho = 41$. We will see that the real locus of this model has homology of dimension 41 entirely generated by algebraic cycles.

Remark 4.7.3

In 2011, Mathias Schütt [Sch11] constructed a quintic such that $\rho = 45$ which is a quotient of a Fermat surface. (We refer the interested reader to [Shi81] or more generally [Bea14] for more information on Fermat surfaces.) Schütt’s surface has equation

$$ yzw^3 + xyz^3 + wxy^3 + zwx^3 = 0 $$

in $\mathbb {P}^3$ and is clearly defined over $\mathbb {R}$. It would be interesting to calculate $b^1$ and $b^1_\mathrm {alg}$ of the real locus of this surface. (See [Sch15] for the construction of complex quintic surfaces with Picard number between 1 and 45.)

4.7.1 Resolution of Singular Points and Double Covers

In this subsection we consider real resolutions of rational double points (Definition 4.4.28) and we prove Lemma 4.7.7 on which we will rely in the rest of the section.

The two examples of surfaces of general type studied in the last part of this chapter are obtained by resolution of singularities of special surfaces. Each exceptional curve obtained by blowing up a point generates a complex algebraic cycle whose real locus is not always easy to understand.

Example 4.7.4

A common phenomenon is illustrated by the surface $X_1\subset \mathbb {R}^3_{x,y,z}$ of equation $z^2 = x^4 -x^2-y^4-y^2$ constituted of two spheres meeting in an ordinary double point. (There are two other singular points in the complex locus which will be unimportant for our purposes.) Blowing up this point $\widetilde{X_1}\rightarrow X_1$ we get a smooth sphere $\widetilde{X_1}(\mathbb {R})$. There is therefore a complex algebraic cycle invariant under the real structure which does not give rise to any non trivial class in $H_1(\widetilde{X_1}(\mathbb {R});\mathbb {Z}_2)$.

Example 4.7.5

Our second example illustrates a slightly different phenomenon. The surface $X_2\subset \mathbb {R}^3_{x,y,z}$ of equation $z^2 = (x^2 + (y-1)^2-4) (x^2 + (y+1)^2-4)$ contains two spheres meeting in two ordinary double points. Blowing up these points $\widetilde{X_2}\rightarrow X_2$ we get a smooth torus $\widetilde{X_2}(\mathbb {R})$ and the two exceptional curves (which are $-2$-curves, see Definition 4.3.2) yield the same class in $H_1(\widetilde{X_2}(\mathbb {R});\mathbb {Z}_2)$ despite the fact that they generate distinct classes in the homology of the complex variety.

It is this second phenomenon that arises in Example 4.7.14. On the other hand, in Example 4.7.13, all the invariant algebraic cycles of the complex variety generate non trivial classes in $H_1(\widetilde{\mathcal {S}}(\mathbb {R});\mathbb {Z}_2)$ because the initial singular surface is homeomorphic to $\mathbb {P}^2(\mathbb {R})$.

Note that, unlike the complex case, a hyperplane section is not always homologically non trivial in the real locus.

Example 4.7.6

(Resolution of a double point on a surface) Consider a surface X and a double point P on this surface. As P is a double point its minimal embedding dimension is 3, see Remark 4.4.27. In other words, locally analytically we can assume that there is an open set V in $K^3$, $K=\mathbb {R}$ or $\mathbb {C}$, centred in (0, 0, 0) in which the equation of X is of the form $z^2=f(x,y)$ and $P = (0,0,0)$. The blow up $\widetilde{V}$ of V in 0 is the set of pairs $(a,\xi )$ in $V\times \mathbb {P}^2(K )$ satisfying the equations

$$ x\xi _2=y\xi _1 \quad \text {and}\quad x\xi _3=z\xi _1 $$

where (x, y, z) are coordinates on V and $[\xi _1,\xi _2,\xi _3]$ are the homogeneous coordinates on $\mathbb {P}^2(K)$.

We can cover the blow up $\widetilde{V}$ of V by charts,

$$ U_i=\{(a,\xi )\in \widetilde{V} : \xi _i\not =0\},\qquad i=1,2,3 \;; $$

with coordinates $(u_i,v_i,w_i)$ defined by:

$$ \begin{aligned}&u_1=x ,\quad v_1=\frac{\xi _2}{\xi _1} ,\quad w_1=\frac{\xi _3}{\xi _1} \quad \text {on } U_1 \;, \\&u_2=\frac{\xi _1}{\xi _2} ,\quad v_2=y ,\quad w_2=\frac{\xi _3}{\xi _2} \quad \text {on } U_2 \;,\\&u_3=\frac{\xi _1}{\xi _3},\quad v_3=\frac{\xi _2}{\xi _3} ,\quad w_3=z \quad \text {on } U_3\;. \end{aligned} $$

We can lift X via the blow up map $\pi :\widetilde{X} \rightarrow X$ to the charts $U_i$ defined above. In $U_1$ the equation of $\pi ^*(X)$ is of the form

$$ u_1^2 w_1^2=u_1^m f_1(u_1,v_1) $$

where m is the multiplicity of f in 0. The strict transform $\widetilde{X}$ of X therefore has equation $w_1^2=u_1^{m-2}f_1(u_1,v_1)$ in this chart In $U_2$ the equation is $w_2^2=v_2^{m-2}f_2(u_2,v_2)$ and in $U_3$ it is $1=w_3^{m-2}f_3(u_3,v_3,w_3)$.

In what follows we will be particularly interested in rational double points (Definition 4.4.28) since their resolution will generate algebraic cycles in the complex variety without changing the numerical invariants of the surface. (See [Art62] or [Slo80, p. 70] for more details.) Recall that singular surfaces all of whose singularities are rational double points are called Du Val surfaces (see Definition 4.4.30).

We want to determine the topology of the real locus of the non singular surface $\widetilde{X}$ obtained by blow up and calculate the rank of $H^{\mathrm {alg}}_1(\widetilde{X}(\mathbb {R});\mathbb {Z}_2)$.

Lemma 4.7.7

Let X be an $\mathbb {R}$-surface with non empty real locus on which we consider a singular point P belonging to $X(\mathbb {R})$. Let $\pi _P :\widetilde{X} \rightarrow X$ be an $\mathbb {R}$-resolution (by which we mean that $\pi _P$ commutes with the real structures on X and $\widetilde{X}$). If the real part $L(\mathbb {R})$ of the exceptional divisor is non empty then we have that

$$ \chi _{top}(\widetilde{X}(\mathbb {R}))=\chi _{top}(X(\mathbb {R}))+\chi _{top}(L(\mathbb {R}))-1 $$

where $\chi _{top}$ is the topological Euler characteristic.

Proof

To simplify notations we set $V:=X(\mathbb {R})$ and $W:=L(\mathbb {R})$. We then have that $\widetilde{V} = \widetilde{X}(\mathbb {R})$.

We consider the exact sequence of cohomology with compact support (B.5) from Proposition B.6.8 applied to the compact pair $(\widetilde{V}, W)$:

$$\begin{aligned} \cdots \rightarrow H^k_c(\widetilde{V} \smallsetminus W;\mathbb {Z}_2) \rightarrow H^k(\widetilde{V};\mathbb {Z}_2) \rightarrow H^k(W;\mathbb {Z}_2) \rightarrow H^{k+1}_c(\widetilde{V}\smallsetminus W;\mathbb {Z}_2) \rightarrow \cdots \end{aligned}$$

(4.20)

We have that

• 1. $\forall k\geqslant 0,\quad H^k_c(\widetilde{V} \smallsetminus W;\mathbb {Z}_2)= H^k_c( V \smallsetminus \{P\};\mathbb {Z}_2)$;

• 2. $\dim H^0_c( V \smallsetminus \{P\};\mathbb {Z}_2)=\dim H^0(V;\mathbb {Z}_2)-1$;

• 3. $\forall k > 0,\quad H^k_c( V \smallsetminus \{P\};\mathbb {Z}_2) = H^k(V;\mathbb {Z}_2)$;

• 4. $H^2(W;\mathbb {Z}_2)=0$.

By definition of $\pi$ there is a neighbourhood U of P in V and a neighbourhood $\widetilde{U}$ of W in $\widetilde{X}$ such that $\pi _P$ is biholomorphic to $\widetilde{U}\smallsetminus W$ over $U\smallsetminus \{P\}$. As $\widetilde{V}\smallsetminus W$ and $V \smallsetminus \{P\}$ are homeomorphic (1) follows. Statement (2) follows from the definition of cohomology with compact support. Indeed, if we denote by $V_1$ the connected component of V containing P we have that $H^0_c( V_1\smallsetminus \{P\};\mathbb {Z}_2)=0$. Statement (3) then follows from the exact sequence (4.20) applied to the pair $(V,\{P\})$, and finally (4) is simply a restatement of the fact that W has dimension 1.

We then simply write that the alternating sum of dimensions of $\mathbb {Z}_2$-vector spaces in the exact sequence is zero to obtain

$$ \chi _{top}(\widetilde{V})=\chi _{top}(V)+\chi _{top}(W)-1\;. $$

   $\square$

Corollary 4.7.8

If $L(\mathbb {R})$ is connected and the hypotheses of the previous lemma hold then we have that

$$ \chi _{top}(\widetilde{X}(\mathbb {R}))=\chi _{top}(X(\mathbb {R}))-\dim H^1(L(\mathbb {R});\mathbb {Z}_2)\;. $$

4.7.2 Resolutions of Real Double Covers

Let W  be a non singular $\mathbb {R}$-surface whose real locus is connected and non empty and let C be an $\mathbb {R}$-curve on W without multiple components. We assume there is a divisor B on W such that $C\in |2B|$: we will then say that C is an even curve. Let X be the double cover of W branched along C and let $\widetilde{X}$ be the canonical resolution of X (see below). We have the choice between two real structures on the surfaces X and $\widetilde{X}$. If W is a rational surface and locally P(x, y) is a polynomial defining C the choice of real structure corresponds to a choice of sign: $z^2 = \pm P(x,y)$. Having made this choice, we study the real locus $\widetilde{X}(\mathbb {R})$ of $\widetilde{X}$.

Remark 4.7.9

We check that

• 1. The surface X is singular if and only if the curve C is singular.

• 2. The surface X is projective if and only if W is projective, see [BHPVdV04, p. 182].

• 3. If the complex surface W is simply connected then the complex surface X is simply connected if and only if the complex curve C is connected.

There is a special method for resolving the singularities of a double cover, namely canonical resolution, which is sometimes more efficient than direct resolution by blow up. It has however the disadvantage of not always giving a minimal resolution, as we will see with the line passing through the quadruple points in Example 4.7.14. However, we will prove below that this method always yields a minimal resolution for rational double points.

Definition 4.7.10

Let W be a non singular complex projective algebraic surface and let $C\subset W$ be an even curve without multiple components. The canonical resolution of (W, C) is defined to be the pair $(\widetilde{W},\widetilde{C})$ defined recursively as follows:

• $(W_0,C_0)=(W,C)$;

• At step $(W_k,C_k)$:

If $C_k$ is non singular, we set $(\widetilde{W},\widetilde{C})=(W_k,C_k)$. If $C_k$ is singular we choose a singular point P on $C_k$. We denote by $\pi :W_{k+1}\rightarrow W_k$ the blow up of W centred at P and by L the corresponding exceptional divisor and we set $C_{k+1}=\pi ^*(C_k)-2\left\lfloor m/2\right\rfloor L$ where m is the multiplicity of $C_k$ at P. (We note that L is a component of $C_{k+1}$ if and only if m is odd.)

We can show that this definition makes sense, or in other words that the processus eventually stops and the order of the blow-ups does not affect the result. See [Per81, p. 10] for more details.

Consider the canonical resolution of a double cover X defined by a pair (W, C). The equation of C in an open affine subset of $K^2$ is $f(x,y)=0$: after blowing up (0, 0) in $K^2$ we obtain (with some obvious modifications of the notations introduced in Example 4.7.6) $u_1^mf_1(u_1,v_1)=0$ and $u_2^mf_2(u_2,v_2)=0$. We then take our new branching locus to be $C_1=2\left\lfloor m/2\right\rfloor L$ and consider the double cover. The equations of this double cover are:

$$ \begin{aligned}&z^2=u_if_i(u_i,v_i)\text { if }m \text { is odd,} \\&z^2=f_i(u_i,v_i) \text { if }m\text { is even.} \end{aligned} $$

Comparing with the calculations of Example 4.7.6 we see that this method is equivalent to resolving a singularity by blow up and resolution of the branching curve if $m=2,3$.

Lemma 4.7.11

If $(X,{\sigma })$ is a singular $\mathbb {R}$-surface the resolution $\widetilde{X} \rightarrow X$ of a rational double point P belonging to $X(\mathbb {R})$ does not change the number of connected components of $X(\mathbb {R})$. Moreover, if P is a point of type $A_n, n\text { odd}$ or $D_n, n\, \text {even}$ then we have that

$$ \chi _{top}(\widetilde{X}(\mathbb {R}))=\chi _{top}(X(\mathbb {R}))-n\;. $$

Proof

• 1. Let L be the exceptional divisor generated by resolution of P. We need to determine what happens to the real locus of L, or in other words what happens to P. Connectedness of $\widetilde{X}(\mathbb {R})$ depends on connectedness of $L(\mathbb {R})$.

• 2. When we blow up a singularity of type $D_n$, $E_6$, $E_7$ or $E_8$ the branching locus remains connected since the corresponding singularity of the branching locus is then triple. Moreover, when the singularity is of type $D_n$ with even n the real locus has exactly n double points of type $A_1$.

• 3. A singularity of type $A_n, n\geqslant 2$ becomes a singularity of type $A_{n-2}$ after blow up; the branching locus remains singular and connected until we reach $A_1$ and $A_2$ whose respective equations (over $\mathbb {C}$) are $z^2=x^2-y^2$ and $z^2=y^2-x^3$.

• 4. The blow up of $A_1$ gives us $w_1^2=1-v_1^2$ (in $U_1$ for example) and $L(\mathbb {R})$ is then the conic of equation $u_1=0,w_1^2+v_1^2=1$. This resolution therefore turns a point into a connected curve and the strict transform $\widetilde{X}(\mathbb {R})$ therefore has the same number of connected components as $X(\mathbb {R})$. Moreover, in this case $\chi _{\text {top}}(L(\mathbb {R}))=0$.

• 5. A point of type $A_2$ has two possible equations over $\mathbb {R}$: $z^2=y^2-x^3 \text { and } z^2=x^3-y^2$ which give rise after blow up to equations $w_1^2=v_1^2-u_1 \text { and } w_1^2=u_1-v_1^2$ respectively. The curve $L(\mathbb {R})$ (corresponding to $u_1=0$) consists of two lines, $w_1=v_1$ and $w_1=-v_1$, in the first case and the isolated point $w_1=v_1=0$ in the second case.

For $A_n$ with $n\text { odd}$ the locus $L(\mathbb {R})$ is connected and contains n double points of type $A_1$. We complete the proof by applying Lemma 4.7.7 to each blow up of a point of type$A_1$.    $\square$

Proposition 4.7.12

Let (W, C) be a pair where W is a non singular compact $\mathbb {R}$-surface and $C\subset W$ is a possibly reducible $\mathbb {R}$-curve. If the real part of C is connected and all its singularities are of type $A_n$, $D_n$, $E_6$, $E_7$ or $E_8$, then the double cover $\widetilde{X}(\mathbb {R})$ of the canonical resolution of (W, C) is connected for one of the two real structures lifting the real structure on W.

Proof

• 1. If $W(\mathbb {R})$ and $C(\mathbb {R})$ are connected it is clear that the double cover $X(\mathbb {R})$ defined by (W, C) is connected independently of the choice of real structure.

• 2. The resolution of a singularity that is not in $C(\mathbb {R})$ does not alter the connectedness of $W(\mathbb {R})$ or $C(\mathbb {R})$.

• 3. Since the singularities of the real part of C are of type $A_n$, $D_n$, $E_6$, $E_7$ or $E_8$ the corresponding singularities of X are rational double points of type $A_n$, $D_n$, $E_6$, $E_7$ or $E_8$.

By Theorem 4.4.26, we know that the canonical resolution of this type of singularity is equivalent to a sequence of blow ups of points on X, and moreover all the intermediate singularities are also rational double points. The proposition follows from Lemma 4.7.11.    $\square$

The first example we present is a non singular model of a certain degree 5 surface in $\mathbb {P}^3$.

Example 4.7.13

(A real quintic such that $b_1^{\mathrm {alg}}=b_1$) This example is based on a construction that Persson attributes to Hirzebruch in [Per82, Introduction]. A non singular complex surface X in $\mathbb {P}^3(\mathbb {C})$ is connected and simply connected and by the Lefschetz hyperplane theorem D.9.2:

$$ \begin{aligned} \pi _0(X)&\simeq \pi _ 0(\mathbb {P}^3(\mathbb {C})) \;,\\ \pi _1(\mathbb {P}^3(\mathbb {C}))&\rightarrow \pi _1(X)\rightarrow 0\;. \end{aligned} $$

It follows that the Picard group $\mathrm{{Pic}}(X)$ is a free, finitely generated $\mathbb {Z}$-module of rank $\rho$

Consider a curve C formed of five lines in general position in $\mathbb {P}^2(\mathbb {C})$. Let $f :\mathcal {S}\rightarrow \mathbb {P}^2(\mathbb {C})$ be the cyclic covering of order 5 of $\mathbb {P}^2(\mathbb {C})$ branched along C. The surface $\mathcal {S}$ is then a quintic in $\mathbb {P}^3(\mathbb {C})$ which has ten singularities, corresponding to the intersections of the lines. Let P be one of these singular points. In an affine neighbourhood of P we can write the equation of $\mathcal {S}$ in the form

$$ x^5=z^2-y^2 \;, $$

which implies that P is a rational double point of type $A_4$ (see Definition 4.4.28). We know that each rational double point can be resolved by successive blow ups and the non singular model thus obtained has the same numerical invariants as a quintic. In particular, the bound on the Picard number remains valid.

On the other hand, the resolution of a singular point of type $A_n$ increases the number of algebraic cycles by exactly n (i.e. the number of irreducible components of the exceptional divisor of the resolution). This yields a non singular surface $\widetilde{\mathcal {S}}$ such that $\rho (\widetilde{\mathcal {S}}) = 41$. The Picard group of $\widetilde{\mathcal {S}}$ is generated by the hyperplane section and 40 cycles arising from resolutions of singularities.

Choosing the lines in C to be real lines in general position in $\mathbb {P}^2(\mathbb {R})$ we obtain a real surface. We will use the topology of $\mathcal {S}(\mathbb {R})$ to calculate the topology of $\widetilde{\mathcal {S}}(\mathbb {R})$: in other words, we will study the behaviour of the real locus under resolution of singularities.

Restricting the covering map f to $\mathcal {S}(\mathbb {R})$ we get a homeomorphism from $\mathcal {S}(\mathbb {R})$ to $\mathbb {P}^2(\mathbb {R})$. As the equation of $\mathcal {S}$ is of the form $t^5 = Q(x,y,z)$ and as f is given by $f(x,y,z,t)= (x,y,z)$, it is easy to see that there is only one real point in each fibre of f. The surface $\mathcal {S}(\mathbb {R})$ is therefore connected and $\dim H_1(\mathcal {S}(\mathbb {R});\mathbb {Z}_2 ) = 1$. Moreover, its only homology class is algebraic, as it is simply the pull back via the map

$$ f^*:H_1(\mathbb {P}^2(\mathbb {R});\mathbb {Z}_2 ) \rightarrow H_1(\mathcal {S}(\mathbb {R});\mathbb {Z}_2) $$

of the hyperplane section of $\mathbb {P}^2(\mathbb {R})$.

We now consider the resolution of a point P of type $A_4$ on a surface X whose local equation is $z^2 = x^5 + y^2$. We use the notations of Example 4.7.6. Let $P\in V\subset X$ be a neighbourhood of P. After a first blow up $\widetilde{V}\rightarrow V$ we get equations

$$ w_1^2 = u_1^3 + v_1^2 \quad \text{ on } U_1\quad \text{ and }\quad w_2^2 = u_2^5 \, v_2^3 + 1 \quad \text{ on } U_2\;. $$

The real part of the exceptional curve is connected and consists of two lines (whose equations are $w_1 = v_1$ and $w_1 = -v_1$ in $U_1$ respectively) meeting in a singular point Q of $B_PX \supset \widetilde{V}=B_PV$.

We now blow up Q and we denote by $\widetilde{X}:=B_Q(B_P(X))$ the surface thus obtained. Changing notation slightly for this second blow up, the equation of $\widetilde{X}$ in $\widetilde{U}_1$ is of the form

$$ \widetilde{w_1}^2 = \widetilde{u_1} + \widetilde{v_1}^2 \;. $$

The real locus of the exceptional divisor L is again connected with two irreducible components. Moreover, the intersection point $\widetilde{Q}$ is not a singular point of the surface. To summarise,

• two blow ups are needed to resolve P;

• the real part of the exceptional divisor $\widetilde{L}$ is connected and has four irreducible components.

We now use Corollary 4.7.8 to show that these four irreducible components really give us four new homology classes in the real locus. In our case, $L(\mathbb {R})$ is topologically a chain of four circles, which gives us

$$ \chi _{\text {top}} (\widetilde{X}(\mathbb {R}))=\chi _{\text {top}} (X(\mathbb {R}))-4\;. $$

Moreover the new surface is connected, as we have simply replaced a point by a connected curve. As $\mathcal {S}$ has 10 such singularities, we get that

$$ \dim H_1(\widetilde{\mathcal {S}}(\mathbb {R});\mathbb {Z}_2) = 41\;. $$

Any finally as each new cohomology class was obtained as the real part of an exceptional curve we get that

$$ \dim H_1^{\mathrm {alg}}(\widetilde{\mathcal {S}}(\mathbb {R});\mathbb {Z}_2) = \dim H_1(\widetilde{\mathcal {S}}(\mathbb {R});\mathbb {Z}_2) = 41\;. $$

Fig. 4.14

Projection of $\mathcal {P}(\mathbb {R})$ onto $\mathbb {P}^2$

Example 4.7.14

(A real numerical quintic such that $b_1^{\mathrm {alg}}<b_1$) We now discuss an example of a numerical quintic constructed by Ulf Persson [Per82, p. 309] and calculate the invariants of its real part and a lower bound for the number $b^1_{\mathrm {alg}}$.

We start by constructing a real curve in $W=\mathbb {P}^2$. Consider a quadrilateral defined by two pairs of lines meeting in points p and q. Each side of $\Sigma$ meets two others in vertices of $\Sigma$. Each side of $\Sigma$ therefore has three canonical points, namely the intersections with the three other sides. The two diagonals of $\Sigma$ meet in a point r, the centre of $\Sigma$. Linking r to p and q respectively each side of $\Sigma$ is now cut in a fourth point. These four points on any given line form a harmonic set, by which we mean that if we normalise the coordinates such that the point p or q is $\infty$ and the vertices of $\Sigma$ are $\pm 1$ then the fourth point is 0.

This is in fact the classical construction of the fourth point in a harmonic set given three of them. There is now a unique conic which is tangent to all the sides of $\Sigma$ at the “0-points”. Let C be the reducible curve containing the six lines above, the conic and one of the diagonals (Figure 4.14), plus the curve E passing through p and q. This yields a curve of degree 10 with four ordinary quadruple points, five $A_1$ points, four $A_6$ points and three $D_4$ points.

Let $(\widetilde{W},\widetilde{C})$ be the canonical resolution of the pair (W, C) as in Definition 4.7.10. Let $\mathcal {P}$ be the double cover defined by the pair (W, C) and let $\widetilde{\mathcal {P}}$ be the double cover defined by the pair $(\widetilde{W},\widetilde{C})$.

The self intersection $E^2$ of E decreases by 1 each time we blow up one of its three singular points, so the line E in $\mathcal {P}$ satisfies $E^2=-2$. By [Per81, Proposition 1.3] the curve $\widetilde{E}$ obtained as a double cover of E is a $(-1)$-curve in $\widetilde{\mathcal {P}}$. Using [Per81, Proposition 1.3] once more we can check that $\widetilde{E}$ is the only $(-1)$-curve in $\widetilde{\mathcal {P}}$.

We contract $\widetilde{E}$ and we denote by $\mathcal {P}'$ the minimal surface thus obtained.

Proposition 4.7.15

Let $\widetilde{X}$ be the double cover obtained by canonical resolution of a pair $(\mathbb {P}^2(\mathbb {C}),D)$ where D is a curve in $\mathbb {P}^2(\mathbb {C})$ of degree 2d. If every singular point $P_k$ is of multiplicity $m_k=2d_k$ or $m_k=2d_k+1$ we have that

$$ \begin{aligned} c_1^2(\widetilde{X})&= 2(d-3)^2-2\sum _{P_k}(d_k-1)^2\;,\\ h^{0,2}(\widetilde{X})&= 1+\frac{1}{2}(d(d-3))-\sum _{P_k}\frac{1}{2}d_k(d_k-1)\;. \end{aligned} $$

Proof

See [BHPVdV04, p. 183].    $\square$

Corollary 4.7.16

The invariants of the surfaces $\widetilde{\mathcal {P}}$ and $\mathcal {P}'$ defined above are

$$ \begin{aligned} c^2_1(\widetilde{\mathcal {P}})&=4, \qquad c^2_1(\mathcal {P}')=5\;,\\ h^{0,2}(\widetilde{\mathcal {P}})&=4, \qquad h^{0,2}(\mathcal {P}')=4\;,\\ \rho (\widetilde{\mathcal {P}})&\geqslant 44, \qquad \rho (\mathcal {P}')\geqslant 43\;. \end{aligned} $$

Proof

For the first two equations we recall that as in Proposition 4.1.30 if $\pi :\widetilde{X} \rightarrow X'$ is the blow up of a point P of a non singular surface and $E_P$ is the exceptional line then $K_{\widetilde{X}}=\pi ^*K_{X'}+E_P$ and hence $c^2_1(X')= c^2_1(\widetilde{X})+1$. Moreover, as $h^{0,2}$ is a birational invariant we get two additional equations. To prove the last two equation, recall that as well as the cycles arising from resolution of singularities of type $A_n,D_n$ or $E_n$ which each generate n independent algebraic cycles, there is a cycle arising from the hyperplane section and two arising from the resolution of quadruple points.    $\square$

The non singular surface $\mathcal {P}'$ therefore has the same numerical invariants as a quintic in $\mathbb {P}^3(\mathbb {C})$ (see Remark 4.7.2) and its Picard number is bounded below by 43. We now calculate the real locus of $\mathcal {P}'$. Referring once more to Figure 4.14, we can calculate the Euler characteristic of the initial singular surface $\mathcal {P}(\mathbb {R})$ which is homeomorphic to a finite number of spheres glued together at singular points. In particular, $\mathcal {P}(\mathbb {R})$ is connected and

$$ \chi _{\text {top}}(\mathcal {P}(\mathbb {R}))=2({}^{\#}\{\text {spheres}\})-\sum _{P_k}(m_k-1) $$

where $m_k$ is the multiplicity of the point $P_k$. With its 13 spheres, 5 double points, 7 triple points and 2 quadruple points we therefore have that

$$ \chi _{\text {top}}(\mathcal {P}(\mathbb {R}))=1, \qquad b^1(\mathcal {P}(\mathbb {R});\mathbb {Z}_2)=13\;. $$

Proposition 4.7.17

The numerical quintic $\mathcal {P}'$ has a connected real locus.

After blowing up the two quadruple points the branching locus is connected (see Figure 4.15), and there are only simple singularities left in the real locus. By Lemma 4.7.11 the resolution of these singularities yields a connected surface and we complete the construction by contracting the curve E, which obviously preserves connectedness.

Fig. 4.15

The curve $\widetilde{C}$ on $\widetilde{W}$

Proposition 4.7.18

For the surfaces $\widetilde{\mathcal {P}}(\mathbb {R})$ and $\mathcal {P}'(\mathbb {R})$ defined above we have the following equations:

$$ \begin{aligned} \chi _{\text {top}}(\widetilde{\mathcal {P}}(\mathbb {R}))&=\chi _{\text {top}}(\mathcal {P}(\mathbb {R}))-\sum _{P_k}n_k, \qquad \chi _{\text {top}}(\mathcal {P}'(\mathbb {R}))= \chi _{\text {top}}(\widetilde{\mathcal {P}}(\mathbb {R}))+1 \\ b^1(\widetilde{\mathcal {P}}(\mathbb {R});\mathbb {Z}_2)&= \chi _{\text {top}}(\widetilde{\mathcal {P}}(\mathbb {R}))+2, \qquad b^1(\mathcal {P}'(\mathbb {R});\mathbb {Z}_2)= b^1(\widetilde{\mathcal {P}}(\mathbb {R});\mathbb {Z}_2) -1 \\ b^1_{\mathrm {alg}}(\mathcal {P}'(\mathbb {R});\mathbb {Z}_2)&= b^1_{\mathrm {alg}}(\mathcal {P}(\mathbb {R});\mathbb {Z}_2)+(b^1(\mathcal {P}'(\mathbb {R});\mathbb {Z}_2)-b^1(\mathcal {P}(\mathbb {R});\mathbb {Z}_2)) \end{aligned} $$

where $n_k=n$ if $P_k$ is a point of type $A_n, n\text { odd}$ or $D_n, n\text { even}$, and $n_k=1$ if $P_k$ is a quadruple ordinary point.

Proof

For simple singularities this follows from the second part of Lemma 4.7.11. Moreover, let P be a quadruple ordinary point of C: we can then find a neighbourhood of P such that $\mathcal {P}$ is locally defined by the equation:

$$ z^2=xy(x^2-y^2)\;. $$

The canonical resolution turns this equation into

$$ z^2=v-v^3\;, $$

so in the real world $E_P(\mathbb {R})$ is the union of two disjoint circles whence it follows that $\chi _{\text {top}}(E_P(\mathbb {R}))=0$. We now simply apply Lemma 4.7.7.    $\square$

Corollary 4.7.19

For the surfaces $\widetilde{\mathcal {P}}(\mathbb {R})$ and $\mathcal {P}'(\mathbb {R})$ defined above we have the equations:

$$ \chi _{\text {top}}(\mathcal {P}')=-41, \qquad b^1(\mathcal {P}'(\mathbb {R});\mathbb {Z}_2)=43, \qquad b^1_{\mathrm {alg}}(\mathcal {P}'(\mathbb {R});\mathbb {Z}_2)\geqslant 31\;. $$

Indeed, we have that $\sum _{P_k}n_k=43$ and $b^1_{\mathrm {alg}}(\mathcal {P}(\mathbb {R});\mathbb {Z}_2)\geqslant 1$ because of the hyperplane section class.

4.8 Solution to exercises of Chapter 4

4.1.45 If $C'$ is a non singular quartic then $g(C')=3$ by the genus formula, see Theorem 1.6.17. Since the genus of C is zero by hypothesis, we have that $\delta (C)=3$. The multiplicities of the singular points (including the infinitely close points) are therefore (2, 2, 2) or (3). Since the set of singular points is invariant under ${\sigma _\mathbb {P}}$, the only possibilities are: a unique triple point, three double ordinary points or a unique singular point whose sequence of multiplicities is (2, 2, 2) (which implies that it is either a ramphoid cusp or a double point whose first blow up contains two double ordinary points). Since the number of singular points is always odd, at least one of them must be real.

4.1.48 The Euler characteristic is additive so $\chi _{top}(C)=\chi _{top}(C_1)+\chi _{top}(C_2)=4$. Moreover $p_a(C_i)=g(C_i)=0$ for $i=1,2$ and the result follows from formula (4.4), Sect. 4.1.4.

4.2.11 2. Calculating the derivative at any point of a reduced fibre gives us the result.

4. Consider the conic bundle given by the equation

$$ x^2+y^2=(t-1)(t-2)(t-3)(t-4)\;. $$

4.3.3 By definition any $(-1)$-curve is rational and non singular so $p_a(C)=g(C)=0$ and $C^2=-1$. The result follows by the adjunction formula (4.1), Sect. 4.1.4.

4.3.14 Let $E_1$ and $E_2$ be the lines that are irreducible components of the fibre F in question. We then have that $0=F^2=E_1^2+E_2^2+2(E_1\cdot E_2)$ so $E_1^2=E_2^2=-1$.

4.3.15 Every singular fibre consist of two $(-1)$-curves meeting in a point. Let $X\rightarrow \mathbb {F}_n$ be the birational morphism obtained by contracting one $(-1)$-curve in each singular fibre. Let $E_1,\dots ,E_r$ be the contracted curves. We then have that

$$ \pi ^*(K_{\mathbb {F}_n})=K_X+E_1+\cdots +E_r\;, $$

whence $K_X^2=\pi ^*(K_{\mathbb {F}_n})^2-r$. We now simply calculate $K_{\mathbb {F}_n}^2$ given that $K_{\mathbb {F}_n}=-2\Sigma _0+(n-2)F$ for any fibre F and a general section $\Sigma _0$ as in [Bea78, III.18].

4.3.18 Recall that by the adjunction formula any $(-1)$-curve C satisfies $K_X\cdot C=-1$ as in Exercise 4.3.3. Let $C_1$ and $C_2$ be $(-1)$-curves such that $C_1\cdot C_2> 0$. We then have that $(C_1 + C_2)^2=-2+2C_1\cdot C_2\geqslant 0$ and $(C_1 + C_2)^2=0$ if and only if $C_1\cdot C_2=1$. By Zariski’s lemma, (see [BHPVdV04, Lemma III.8.2]) the fibre of $\pi$ containing $C_1$ and $C_2$ is therefore necessarily of the form $n(C_1 + C_2)$. Let F be a general (connected non singular) fibre. We then have that

$$ K_X\cdot F=n(K_X\cdot (C_1 + C_2))=-2n\;. $$

Moreover $F^2=0$ since it is a fibre and $p_a(F)=g(F)\geqslant 0$ because F is connected and non singular. The adjunction formula (4.1) (Sect. 4.1.4) then gives us $n=1$ and $g(F)=0$.

4.4.12 If the conic bundle is minimal the only singular fibres are of the form $x^2+y^2=0$ and their number is twice the number of connected components of $X(\mathbb {R})$. By Exercise 4.3.15, the number of singular fibres of the conic bundle is equal to $8-K_X^2$.