1 Introduction

A common approach to study the behavior of physical phenomena is to simulate them and then analyze the results—often visually. To overcome the problem of occlusions in 3D and the increasingly finer resolution of simulation models, the focus has shifted to identifying specific features, e.g. spatial regions that locally behave in a similar manner. It has been shown that certain topological structures yield suitable candidates of such features. Since some phenomena cannot be captured by criteria addressing spatiotemporal variation of just one physical quantity, feature detection needs to consider characteristic patterns in and relationships between multiple physical quantities. For a general overview of such multifield visualizations we refer the interested reader to the surveys by Fuchs and Hauser [13] and Heine et al. [16].

This paper introduces the idea, that the well-understood topological models for single real-valued functions can be trivially extended to multiple real-valued functions on a common domain, since each topological model for single functions gives rise to a subdivision of the domain and that these subdivisions can be combined to give a fine subdivision encompassing all information present in its constituents. Thus, unlike methods that extract features directly from multifields, our method possibly omits some information spread across multiple fields. But the combination of information extracted from single fields allows further applications: It can be applied to compare or combine different topological models for the same function.

2 Related Work

There have been multiple approaches to extend topological models of single real-valued fields to multifields. Edelsbrunner and Harer [9] defined Jacobi sets as the critical points of one function restricted to all preimages of the remaining functions. This extends the notion of critical points to multiple functions, but can be applied only when the number of functions does not exceed the dimension of the domain. Huettenberger et al. [17] use techniques from multicriteria optimization to define Pareto sets—an extension of critical points to multifields, but preserving the signedness of the single fields. While the number of input functions is not constrained as in the Jacobi set case, the more functions there are, the more likely a point becomes Pareto. Pareto sets get less informative and detailed the bigger they become. In contrast, our method always increases in detail the more functions the input comprises.

Edelsbrunner et al. [12] defined the Reeb space of a set of functions f i as the quotient space for the equivalence relation induced by the connected components of all of f is’ preimages, thereby extending the concept of Reeb graphs to multifields. However, while for single functions, the preimages’ components can be differentiated based on their topological properties, this does not happen for multiple functions. Without such built-in differentiation, preimage components need to be organized differently. Chattopadhyay et al. [6] proposed Jacobi structures, which map Jacobi sets into the Reeb space, integrating information of both models.

Carr and Duke [4] proposed joint contour nets (JCNs): a JCN is the quotient space induced by the connected components of all of \(\tilde {f}_i\)s’ preimages, where \(\tilde {f}_i\) denotes a range-quantized version of f i. Similarly, Singh et al. [22]’s Mapper algorithm defines a set of overlapping regions in the functions’ range space, covering it, and stores spatial relations among the regions’ preimages’ connected components. These methods work on the basis of preimages and their connected components, but make no direct use of topological features present in the single input functions to point out distinct or idiosyncratic subsets of the functions. Compared to this preimage-focused strategy, topological subdivision graphs focus on integrating information from topology-induced subdivisions of single fields. Still, they can be made to yield results similar to joint contour nets as will be shown in Sect. 6.

Another approach is presented by Schneider et al. [20]. It extracts so-called largest contours from the single functions, uses the spatial overlap between largest contours of different functions to quantify similarity, and then uses clustering techniques to identify groups of strongly overlapping largest contours. However, the result does not integrate the information from these single features to multifield features. If the input functions are sufficiently similar, one can use, e.g. Günther et al. [15], who presented a method to compute confidence regions for critical points and relate them by a nesting structure similar to merge trees. Wu and Zhang [25] proposed to compute the arithmetic mean of the input functions, use single-function topological methods on the result, and annotate it by measures of variation. Our method is not limited to input functions that are pairwise similar.

3 Background

This section contains the topological concepts used in the remainder of this paper. For brevity, we assume that the reader is familiar with certain topological concepts, notably topological spaces, simplicial complexes, as well as piecewise linear functions (see, e.g., Edelsbrunner and Harer [10]).

A critical point [1] p of a function \(f:\mathbb {M}\rightarrow {\mathbb {R}}\) defined on a d-manifold is a point where , i.e., where f’s gradient vanishes. We assume f to be a Morse function, meaning that critical points are isolated and have distinct function values.

A level set f −1(v) of a function f for a value v is simply the preimage of v with respect to f, i.e., the set of all points p where f(p) = v. Each level set may consist of multiple connected components. An equivalence relation can then be defined for points of the domain: p and q are equivalent, if they belong to the same component of some level set, called contour. We will refer to this equivalence relation as ∼C in the remainder of this paper. The Reeb graph [19] is defined as the quotient topology on \(\mathbb {M}\) with respect to ∼C. Informally, this process can be thought of as representing each contour as a point and contour adjacency as point adjacency. If the domain is simply connected, i.e. each closed curve can be smoothly contracted to a point, the Reeb graph contains no loops and is called the contour tree [2]. A superlevel set of f for the value v is defined as f’s preimage of the interval [v, ∞) and a sublevel set is defined analogously as f’s preimage of the interval (−∞, v]. Similar to level sets, superlevel and sublevel sets may consist of multiple connected components, and we may define an equivalence relation among points with function value v, based on whether they lie in the same superlevel or sublevel set for v, respectively. The quotient topology using this equivalence relation gives the merge tree.

An integral line of a smooth function f is a curve of maximal length along which the tangent is collinear to the function’s gradient. For each critical point, its descending cell comprises the integral lines that converge on it, and the ascending cell comprises the integral lines that originate from it. When ascending and descending cells intersect only transversally, the domain subdivision induced by this equivalence relation (two points are equivalent if each lies on an integral line that in the limit connects the same pair of critical points) is a CW complex called the Morse-Smale complex.

A subdivision of a set Ω is a collection of sets S such that (1) the union over all sets in S is Ω, and (2) the members of S are pairwise disjoint. We will only consider subdivisions where each set of S is connected. Subdivisions of a set arise naturally as the equivalence classes of equivalence relations. Given two subdivisions of Ω, S 1 and S 2, their joint subdivision S 1,2 is the subdivision of Ω where, whenever s 1 ∈ S 1 and s 2 ∈ S 2 are not disjoint, the connected components of their intersection are members of S 1,2. The definition extends naturally to the joint subdivision of more than two subdivisions.

4 Topology-Induced Spatial Subdivision

In this section, we use contour trees and Morse-Smale complexes to illustrate how topological models subdivide the domain and how to combine this information.

We were motivated by the question “What is the smallest structure from which the contour tree for each function of a collection can be reconstructed?” Its answer was inspired by joint contour nets, which can be viewed as solving the problem for augmented contour trees of range-quantized functions. We wished to remove these restrictions and in the process realized that joint contour nets combine the information from a preimage-based subdivision of each function. We first noted that the subdivision for each field can be constructed in other manners and later that the idea generalizes to when the subdivision for each field need not result from the same topological method for each field. Under this premise, the information from multiple topological models of the same function can be combined.

Recall that in the contour tree case, two points are called equivalent if they belong to the same connected component of a level set for their common function value, formally expressed by the equivalence relation ∼C. It may now be observed that each contour C partitions a simply-connected domain into at least two regions (\(\mathbb {M} \setminus C\) generally consists of multiple connected components) and that each critical point lies either on the contour itself or in exactly one of these regions. We can define an equivalence relation among contours in the following way: Two contours C 1, C 2 are equivalent, if any critical point p of f is either member of both C 1 and C 2 or it is member of some connected component X of \(\mathbb {M} \setminus C_1\) and member of some connected component Y  of \(\mathbb {M} \setminus C_2\) such that any critical point of f is member of X iff it is also member of Y . Informally, two contours are equivalent if they partition the set of critical points in the same way. Note that the definition implies that contours that have a critical point as member can only be equivalent to themselves. We will refer to this equivalence relation by ∼S, and we can combine it with ∼C to a new equivalence relation ∼CT that amounts to define two points as equivalent, if they lie on the same node or edge of the contour tree. We can use ∼CT to subdivide the domain; the result can be stored in a CW complex.

For the more general case of a Reeb graph in a non-simply-connected domain, ∼S is not discriminative enough. One anonymous reviewer suggested the following criterion, which is also simpler than ours for contour trees: Two contours c 1, c 2 of the preimage for f 1, f 2 are equivalent if they are identical or if they are both subset of one connected component X of the preimage of and X has no critical point as member. This definition is the basis for the algorithms presented by Doraiswamy and Natarajan [8] and Tierny and Carr [23].

For merge trees, we define two points p, q as equivalent, if the smallest superlevel/sublevel set component containing p is the same as the one for q. Just as with level sets we can construct a coarser equivalence relation: two superlevel/sublevel set components are equivalent, when they contain the same critical points and thus by extension, two points are equivalent, if they are mapped to the same edge of the merge tree. To ensure that the decomposition results in a proper CW complex, we furthermore need to distinguish superlevel/sublevel set components that contain a critical point on their boundary from those without.

Morse-Smale complexes are already CW complexes and their cells partition the domain. However, we would like to point out that the Morse-Smale complex results from combining two domain subdivisions: one that treats points as equivalent when they have the same critical point at the terminating end of their integral line and one similarly for the beginning of their integral line. Morse-Smale complexes already employ the principle we suggest to use for any topological model: combine the information from all single functions’ topologically-driven subdivision.

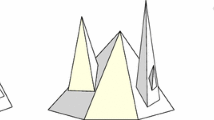
We were initially also considering whether, in straight analogy, the domain subdivision arising from a contour tree is just the combined domain subdivision induced by the superlevel and the sublevel merge tree. However, this is not the case, as can be seen from the counterexample in Fig. 1. The resulting combination would be too fine. However, one can define contour tree domain subdivisions via the equivalence of upward and downward monotone paths ending at critical points [7]. This emphasizes the difference between concepts of critical points that can be reached from a point p via monotone paths, i.e., domain paths along which the function’s values are changing monotonously, and the set of critical points that are contained in the smallest superlevel/sublevel set component containing the point p.

Fig. 1
figure 1

Counterexample to the hypothesis that the combined domain subdivision induced by the merge tree for super- and sublevel sets is the same as the domain subdivision induced by the contour tree. From left to right: input function, merge tree for superlevel sets, merge tree for sublevel sets, contour tree. The spurious red contours arise from the merge trees’ domain subdivision. The contour around 4 is part of the boundary of the sublevel set component for 3 and the contour around 1 is part of the superlevel set component for 2. The pattern in the contour tree seems to be the necessary and sufficient condition for the existence of spurious contours

Full size image

5 Topological Subdivision Complex and Graph

The topological subdivision complex is not a single mathematical concept. Rather it is any CW complex that is derived in a fashion similarly to the examples in the previous section from the topological models of single functions or a joint subdivision of multiple topological subdivision complexes. Given a set of domain subdivisions, regardless of whether they result from the topological models of the same kind for different functions, topological models of different kinds for the same function, or any combination thereof, we can trivially compute a joint subdivision, or, equivalently, combine the equivalence relations giving rise to the domain subdivisions.

The resulting subdivision can be displayed directly in two or three dimensions, but for three or more dimensions it will be easier to view its dual, which we call the topological subdivision graph. Its nodes are the set of d-cells of the joint subdivision, and we connect two nodes by an edge if they have a common d-1-face. Furthermore, we annotate each node with its cell volume (for visualization purposes) and annotate each edge with a list of subdivisions which do not separate the two cells, i.e., in which the union of the two cells are a subset of a common cell.

The latter annotation ensures that one can quickly compute a quotient graph that equals the topological subdivision graph for a subset of domain subdivisions. E.g., imagine two subdivisions (H and V) of a square, one splitting the square horizontally and one splitting the domain vertically. The topological subdivision graph of the joint subdivision contains four nodes corresponding to the four 2-cells: upper-left, upper-right, lower-left, and lower-right. There are now two H-edges connecting the lower with the upper nodes and two V-edges connecting the left with the right nodes. To get the topological subdivision graph for the H-subdivision one just collapses all nodes connected by V-edges. The process of computing a quotient topological subdivision graph thus becomes a simple graph algorithm in strict analogy to how joint contour nets for a subset of input functions can be computed from the joint contour net for all functions [4]. For merge trees and contour trees, edges can be additionally annotated with a direction, based on the ordering of function values in the connected nodes.

Our work was originally motivated by finding a small data structure that contains all information from the individual functions’ contour trees. Note that this annotation and the quotient graph operation on the topological subdivision graph will not give these contour trees, because the subdivision graph retains only information from the complex’s d-cells and their adjacencies, but critical points reside in 0-cells. Instead, a joint subdivision complex can be annotated as follows: for each cell of the joint subdivision we list all cells of the base subdivision complex’s cells that it is a subset of. Based on this information it is again simple to perform quotient complex operations. The contour tree can be reconstructed from the subdivision complex for one function as follows: Each cell of dimension less than d has a critical point, and two critical points are connected, when their cells are incident on a common d-cell.

6 Computation

A general algorithm for our method may only be sketched, because we do not limit ourselves to particular topological methods to drive construction of the base subdivisions. For illustration, we will give the details of our current proof-of-concept implementation that can combine information from multiple Morse-Smale complexes and contour trees. Our implementation is currently restricted to piecewise linear functions on a common simplicial complex in 2D. Before joining the information, we compute contour tree and Morse-Smale complex for each input function separately. To compute the contour trees, we use the algorithm by Carr et al. [5] and to compute Morse-Smale complexes we use the algorithm by Edelsbrunner et al. [11]. We choose this latter algorithm purely out of convenience. One may use instead the algorithm by Bremer et al. [3] that computes the geometry of the Morse-Smale complex’s cells more accurately, or a combinatorial Morse-Smale complex. Algorithms for this are present, e.g., in Shivashankar and Natarajan [21] or Tierny et al. [24].

When using the algorithm by Edelsbrunner or a combinatorial Morse-Smale complex, the 1-cells of the resulting Morse-Smale complex are a subset of the input domain’s edges. Therefore combining this information is trivial: two triangles of the domain belong to the same 2-cell in the joint subdivision complex if they share an edge that does not belong to any 1-cell of the Morse-Smale complexes. The triangles are further subdivided based on the functions’ contour trees.

Let S 0 be the domain subdivision given by the simplicial complex and f 1, …, f n be the input functions, our implementation conceptually first computes the topological subdivision complex for the subdivisions {S 0, …, S n} and then uses the quotient operation defined in the previous section to remove S 0. This is in strict analogy to the algorithm by Carr and Duke [4]. This approach allows us to work on a triangle-by-triangle basis, simplifying implementation: We never explicitly compute any S i, rather we compute the needed convex polygonal patches on the fly, and compute line intersections in local triangle coordinates, which is numerically preferable.

In particular, we iterate over all triangles. For each triangle we start with a set P of convex patches that is initially just the triangle’s geometry in local coordinates. Then we iterate over fields. The triangle’s endpoints, by construction of the contour tree, must lie along a monotone path in the tree. Thus, for each saddle that we pass along this path, the triangle contains a part of its contour which is a line segment. We extend this line segment to a line and split all patches it intersects, updating an incidence graph between points, line segments, and patches. Since all line segments from the same field are parallel withing the same triangle, we can perform the test and split efficiently by sweeping along the incidence graph. This sweeping also ensures consistency with the information in the contour trees. After computing all patches in this fashion, we sweep the incidence graphs of adjacent triangles and merge points and line segments along the shared edge. We use a simple connected components algorithm on the patches’ adjacency graph and compute the quotient graph to obtain the topological subdivision complex’s 2-cells and their adjacencies.

Since the patches are split iteratively with each field, one would like to manage the numerical error. However, since each point of each patch is at the intersection of two line segments which are parts of contours from different fields, their position in local coordinates numerically only depends on the saddles’ function values and the three triangle endpoints’ function values for two fields. We thus store geometry at the edges only, namely using the coefficients α i for the linear equation α 0 + α 1 β 1 + α 2 β 2 = 0 (β i refer to local coordinates), and compute points’ positions by intersecting adjacent faces of a patch. Since lines are only added, but their geometry is never changed, the numerical error is independent of the number of input fields.

The runtime of our algorithm is dominated by patch splitting and can be bounded from above by a function linear in the number of triangles N and linear in the number of saddles s i for each field: \(O(N\prod s_i)\). Since each saddle’s contour typically runs through few triangles and not all saddle contours of one field intersect all saddle contours of all other fields in all triangles, the runtime is much lower in practice. A stricter upper bound on the runtime is the number of patches. The computation of connected components and the quotient graph to remove the subdivision given by the triangulation are linear in the number of patches.

We use a simple straight-line graph drawing to show the topological subdivision graph: we center nodes on the cell they represent and use their sizes to indicate their cell’s volume. This enables comparison of topological models for different functions. If, say, the functions yield very similar contour-tree-based domain subdivisions, we can expect the topological subdivision graph to be mostly tree-like as well, with only minor additional loops, but whose node volumes are notably smaller. Note that the topological subdivision graph for each field does not contain loops, but the topological subdivision graph for the joint subdivision might. In our implementation, we currently use topological simplification for each field separately, but more appropriate would be a method to simplify the graph directly. We leave other visualizations of topological subdivision graphs and their simplification for future work.

7 Results

We used the cross-section of a fluid flow simulation inside a cylinder. The flow is steady and rotationally symmetric. We use a cross-section along the axis of rotation. The data set contains 29704 triangles on 15105 points. Of particular interest is the identification of vortical structures, which tend to occur in areas of low pressure and high vorticity. Furthermore, the quantities q-criterion and λ 2 [18] are typically associated with vortices. Figure 2 shows color maps overlayed by contour trees subdivision and Morse-Smale complexes for these four quantities. Note that asymmetries arise from simulation of simplicity that is used to compute the topological models. The computation of the single fields’ contour trees, Morse-Smale complexes, their subdivision, and the topological subdivision graph took less than 0.4 s. Our proof-of-concept implementation has not yet been optimized for speed.

Fig. 2
figure 2

Cross-section through a flow simulation inside a cylinder. Four quantities are shown. White lines show all contours that contain a critical point (as a set-theoretic member). Black lines indicate Morse cells (separatrices)

Full size image

Figure 3 illustrates and showcases the topological subdivision graph of a cross-section through a cylindrical flow. From the color maps alone, the fields look similarly complex, but the depiction of the Morse-Smale complex illustrate that pressure has fewer cells in its Morse-Smale complex. When we combine both Morse-Smale complexes, we can see that the resulting subdivision graph closely resembles the subdivision graph for vorticity, so vorticity already contained most information and pressure added little more. We can also see that the subdivision graph for q-criterion and λ 2 are highly similar, with the notable exception that the Morse-Smale complex for λ 2 contains many spurious cells at the boundary. We suppose this is because our λ 2 computation has less data near the boundary to compute smooth gradients. A next step would be to identify and remove such small features meaningfully (c.f. Sect. 8). We leave such considerations for future work. The joint subdivision graph also demonstrates that both subdivision are very similar, but we noticed the fan-like structures in the upper outer parts of the image. These result from the 1-cells of the two Morse-Smale complexes not being fully congruent. This could be an artifact of using the algorithm by Edelsbrunner et al. [11], where the gradient path can switch from one mesh edge to another for minute changes in function value at the mesh nodes. The problem could be alleviated by using a different algorithm. However, the graphs allow to study the systematic difference of these two models, most easily visible in the middle and lower middle part of the image. The joint subdivision graph integrates the information from both effectively. Figure 4 shows the topological subdivision graph for all four quantities. Apart from the mentioned spurious cells, the cells are roughly the same size and shape, indicating that the information from the different functions could be integrated quite well.

Fig. 3
figure 3

Combined topological subdivision graphs from the subdivision graphs induced by the Morse-Smale complex of different quantities in the cross-section of a cylindrical fluid flow. Black circles show cell centers, circle size is proportional to cell size, blue lines show cell adjacency

Full size image
Fig. 4
figure 4

Cross-section through a flow simulation inside a cylinder. Topological subdivision graph for four quantities are shown

Full size image

Figure 5 gives an example for the topological subdivision graph of the contour tree, the Morse-Smale complex, and their combination for the pressure field of the same dataset. Since gradient paths are always perpendicular to contours, the information of a contour tree and a Morse-Smale complex typically integrates well.

Fig. 5
figure 5

Topological subdivision graph for the MS complex, contour tree, and their combination, of the pressure field of a flow inside a cylinder

Full size image

8 Discussion

The presented method was largely inspired by joint contour nets [4]. One may view our method as a generalization: the domain subdivisions implicit in joint contour nets are based on a simple equivalence relation: connected components of the preimages \(f_i^{-1}([k\varDelta _i,(k+1)\varDelta _i))\) for all \(k\in \mathbb {Z}\). We basically replaced this by preimages of topological cells from a topological model for each field, removing the parameters Δ i in the process. Although not fully equivalent, topological subdivision models can be used to compute joint contour nets. For each input function’s range define the following intervals: [kΔ i], (kΔ i, (k + 1)Δ i), for all \(k \in \mathbb {Z}\), and define two points equivalent, if their functions’ values fall all inside the same interval. This slightly different construction is necessary to ensure the topological subdivision complex is indeed a complex. Similarly, the Mapper algorithm [22] uses a set of overlapping intervals (kΔ i − 𝜖, (k + 1)Δ i + 𝜖) for each function. When 𝜖 > 0 approaches 0, the above variation of our method can be considered equivalent. However, we would like to stress that such methods that only consider the functions’ range, fail to integrate important topological information present in the single functions.

The method currently can only be considered to be a building block. Although it uses all information present in the topological models of single functions, it only generates a set of possible feature candidates. Which of these correspond to features meaningful to a particular application depends both on the distribution of function values inside the regions, and ultimately also on the goal of the application. An open challenge here is to find typical patterns of value distributions.

The biggest challenge for the method is to find a suitable method of topological simplification. One option is to simplify the joint topological subdivision complex, but this can only consider the size of cells and may not always be consistent: it is not clear whether there are still subdivision complexes that will result in the joint complex when combined. Of course, one can always simplify the topological models for each field separately. But this will not help in a situation like in Fig. 3, where the 1-cells of two Morse-Smale complexes ran close but were not exactly identical. Also, when simplifying different topological models of the same field, it is not clear which simplification should take precedence when it comes to updating the underlying real-valued function, since the changes needed to make one topological model of a function simpler might conflict with the requirements of making a different topological model of the same function simpler. In particular if one wants the resulting function to be geometrically simple as well (c.f. Günther et al. [14]).

9 Conclusion

We presented a new method suitable for integrating the information from different topological models of the same scalar function, topological models of different scalar functions, and combinations thereof. The basic idea is to use domain subdivisions, which can serve as a “common language”, and integrate the information from all subdivisions in a finer subdivision. Our initial experiments on a real-world simulation dataset of a fluid flow inside a cylinder showed the feasibility of the approach. The proposed method needs an algorithm for removing small features that arise from noise or are insignificant. But it is challenging to find a method that is general enough to work with any kind and combination of topological model.

By construction, the topological subdivision complex for a set of contour trees contains information from them; the single contour trees can be extracted using a suitable quotient space operation. Can we prove that this is the smallest structure with this property? Finally, although we illustrated topological subdivision graphs only for Morse-Smale complexes and contour trees, the method can easily be adapted to other topological models—not necessarily models for single fields. For instance, Pareto sets [17] can also be interpreted as a domain subdivision. Under certain circumstances Jacobi sets [9] can also subdivide a domain. It would be interesting to apply our approach to these methods and extend it to vector and tensor field topology as well. We leave such considerations for the future.