Optimal Privatization in a Vertical Chain: A Delivered Pricing Model

Abstract

The chapter considers the introduction of a mixed ownership firm into a classic model in which downstream firms locate strategically so as to achieve accommodating upstream price reductions. These reductions happen endogenously but the strategic locations harm welfare. It shows that a mixed ownership firm downstream can limit such inefficiency but that its ability to do so depends on the extent to which its costs match those of a private firm. Thus, reconfirming in this spatial setting that the optimal share of privatization set by a government depends positively upon the cost disadvantage of the public firm.

In addition, Yes would like to add the following for his participation: “Financial support from the National Natural Science Foundation of China (No.71773129) and National Social Science Foundation of China (No. 19ZDA110) is gratefully acknowledged.”

1 Introduction

In an important earlier paper Gupta et al. (1994) examine the ability of downstream firms to strategically use location decisions to force an upstream monopoly to reduce its input price and transfer profit downstream. This transfer happens endogenously in equilibrium but generates large welfare loses. Additional research builds on this model to show that transport cost itself can also be set inefficiently high by downstream firms choosing a more costly transport mode. This forces the same accommodating behavior by the upstream monopoly (a lowering of the input price and a profit transfer downstream) and a similar loss of welfare (Gupta et al. 1995, 1997).

The fundamental insight of these showings is that downstream firms often face a spatial market that is largely irrelevant to an upstream firm. Thus, downstream firms make a product that has a high transport cost or for which horizontal differentiation is critical. Yet, the upstream firm produces a small critical input for which transportation costs are irrelevant. Indeed, it may provide intellectual property with no transport cost at all. Alternatively, while the downstream product faces consumers with horizontally differentiated preferences (proxied by distance in a spatial model), these simply need not apply to the input. Thus, consumers may care greatly about the characteristics of cell phones but these preferences may be largely irrelevant to the manufacturer of the basic chips. In such circumstances, the primary concern of the upstream firm is to avoid setting a price so high that it results in a dramatic loss of customers downstream. Given this concern, Gupta et al. (1994) show that the downstream firms can locate strategically to make such a dramatic loss of customers more likely for a given price increase. This, in turn, causes the upstream firm to lower its input price.

We return to these earlier models of vertical rivalry and incorporate the possibility that one of the downstream firms is a “mixed ownership firm.” The enormous literature on public firms and mixed oligopolies has largely grown up since these early location models and has much to offer. The basic view is that a public firm regulates by participating in a private oligopolistic market. While the private firms maximize profit, the public firm sets quantity or some other choice variable to maximize social welfare. In a quantity game the public firm can increase consumer surplus by increasing total production. Yet, the assumption in this literature is that the government-owned firm produces at elevated costs.¹

In a seminal article Matsumura (1998) recognizes that while a publically owned firm maximizing welfare can indeed improve welfare in an oligopoly, a mixed ownership firm can make an even larger improvement. The mixed ownership firm is presumed to maximize a combination of welfare, a public firm’s objective, and own profit, a private firm’s objective. As a consequence, it increases output to increase consumer surplus but not to the extent of the fully public firm saving on the total cost of production in the market and thereby increasing welfare.

Indeed, a large literature has followed this initial showing by determining the optimal private share in a mixed ownership firm in a wide variety of settings. Matsumura and Kanda (2005) imagine the optimal extent of privatization (the creation of a mixed ownership firm) in a free entry market. Fujiwara (2007) examines partial privatization in a differentiated product market. Heywood and Ye (2009b) examine optimal privatization in the context of an R&D rivalry while Heywood and Ye (2010) examine optimal privatization but assume a consistent conjecture equilibrium. Wang and Chen (2011) retain Cournot competition but include both foreign competition and multinational corporations. Heywood et al. (2017) imagine mixed ownership under asymmetric information in which only fully private firms directly know product demand. Tomaru and Wang (2017) and Lin and Matsumura (2018) each consider partial privatization in the face of state subsidy policies. Sato and Matsumura (2019) imagine a two-period model in which the government partially privatizes a state-owned public firm over multiple periods and includes the shadow cost of public funding. While far from an exhaustive review, this makes clear the strong ongoing interest in partial privatization policy.

For the first time in the literature, we imagine a mixed ownership firm that competes downstream with a private firm in a delivered pricing model and faces a monopoly upstream. We examine the ability of a public firm to locate in such a way so as to limit the private firm’s inefficient attempt to gain an upstream price accommodation. We recognize that this may come with the increased production costs associated with the public firm and, following the literature, assume these costs can be reduced by partial privatization. As the extent of partial privatization increases, production costs fall but so does the incentive of the mixed ownership firm to locate efficiently. Thus, we identify the optimal extent of partial privatization in the original context of the Gupta et al. (1994) vertical rivalry.

The assumption of an inefficient public firm is critical. This assumption fits well with the literature on mixed oligopolies (see among others Pal and White 1998; Wang and Mukherjee 2012 and Gelves and Heywood 2013). Moreover, Matsumura and Matsushima (2004) provide theoretical support for such a cost disadvantage while Megginson and Netter (2001) provide supporting empirical evidence. The related idea that partial privatization can serve to lower those costs is also well supported. Indeed, private ownership well short of majority control increases efficiency by bringing the improved incentives and information about managerial performance associated with a stock price. A theoretical treatment of the power of such minority ownership and “yard stick competition” is provided by Laffont and Tirole (1993) while Gupta (2005) and Bhaskar et al. (2006) provide confirming empirical evidence.

In the classic spatial price discrimination model that we expand upon, the firm delivers the product to the consumer, and the delivered price is the sum of the marginal production cost and the transport cost of the rival firm. Thisse and Vives (1988) demonstrate that such pricing will be endogenously adopted if available and Greenhut (1981) identifies spatial price discrimination as “nearly ubiquitous” among actual markets in which the products have substantial freight costs. More generally, Behrens et al. (2018) confirm the continuing importance of transportation cost as a determinant of plant location. Finally, as emphasized, in addition to cases where transport cost is important, the model describes circumstances with differences among consumers in a horizontal product dimension and where firms must locate along that dimension. These circumstances include, but are not limited to, political orientation of a newspaper, times of airline flights, and the sweetness of breakfast cereals.

2 Model Setup and Solution

An upstream private firm, with 0 production cost, sells an input to two downstream firms. Firm 1 is a mixed ownership firm, with a private share of λ, while Firm 2 is a fully private firm. The two firms engage in delivered price competition along the market of a unit line segment. Following Gupta et al. (1994), consumers are uniformly distributed along the market and each has a one unit demand for the product with reservation price r. The per-unit transportation cost is normalized to be 1. While this setting of inelastic demand is classic for delivered pricing, it eliminates a second dimension of price discrimination that has been examined. Thus, either with or without delivered pricing, there could be downward sloping demand at each location and the price set (or alternatively quantity) at each location can differ to reflect that demand (see, among others, Anderson et al. 1989; Colombo 2011 and Heywood et al. 2018).

Per-unit production cost of the private firm is 0. The per-unit production cost of the mixed firm is (1 − λ)c with c > 0. The presumption is that privatization decreases production cost and this is a simple way to capture that reality. Thus, when λ = 1, the mixed ownership firm becomes fully private and its per-unit cost is 0 matching the rival. Downstream production is characterized by fixed proportion such that each downstream product requires one unit of the upstream product. This can be particularly relevant when the upstream firm provides an essential input that cannot be substituted away from or when the downstream firms are viewed largely as retailers that add services and delivery for a wholesale product (Heywood et al. 2018).

The timing of the game begins with a welfare maximizing government adopting the optimal degree of privatization for the mixed ownership firm. Once this is known, the remainder of the time line follows Gupta et al. (1994) with the least reversible choice being first: the two downstream firms simultaneously choose locations {L ₁, L ₂} assuming for convenience that L ₁ ≤ L ₂ (for an example of sequential location see Heywood and Ye 2009a). In the third stage the upstream firm chooses an upstream price of w and in the final stage the two downstream firms determine the optimal delivered pricing schedule.

2.1 Equilibrium

We solve for the subgame perfect Nash equilibrium by backward induction.

In stage four the delivered pricing schedule emerges as the standard for spatial price discrimination and is the outer envelope of the rival’s marginal costs. The private firm has an incentive to raise price to the delivered cost of the private firm. The public firm or partially public firm generates no welfare loss from pricing this way as the profit gain is exactly offset by the consumer surplus loss for a given location. Thus, the public firm is indifferent to the classic delivered pricing equilibrium and charging its own transport cost and a firm with any private share strictly prefers the classic delivered pricing scheme. Thus, the delivered pricing is unchanged by the presence of a mixed firm (for more on this see Heywood and Ye 2009b).

The equilibrium downstream price for the public mixed firm is then

$$ {p}_1(x)=\left\{\begin{array}{l}r,0\le x\le -r+w+{L}_2\\ {}w+{L}_2-x,-r+w+{L}_2\le x\le \frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\end{array}\right. $$

The equilibrium price for the private firm is

$$ {\fontsize{9}{12}\begin{array}{l}{p}_2(x)=\left\{\begin{array}{l}w+x-{L}_1+\left(1-\lambda \right)c,\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\le x\le r+{L}_1-w-\left(1-\lambda \right)c\\ {}r,r+{L}_1-w-\left(1-\lambda \right)c\le x\le 1\end{array}\right. \end{array}}$$

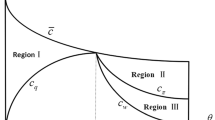
The equilibrium price schedule given the upstream price and downstream locations is depicted as the bold line in Fig. 9.1.

Fig. 9.1

(a) The delivered pricing equilibrium when the public firm is critical. (b) The delivered pricing equilibrium when the private firm is critical. Note: the solid thick line represents the equilibrium price schedule given the share of privatization, the costs, and locations

The solution to the third stage is built from Gupta et al. (1994). The upstream firm must decide given the locations of the two downstream firms whether to push the upstream price just to the point where one of the delivered cost schedules intersects in the corner of the willingness to pay (as for Firm 1 in Fig. 9.1a) or to push further and allow the market to be cut and customers go unserved. Obviously, the lowest upstream price will be that which just pushes the delivered cost to the corner as anything lower forgoes upstream profit. A higher price becomes justified only when the gain in increase profit from the higher price is larger than the loss in profit from cutting the market and losing customers.

This higher price is more likely when r is small relative to c and transport cost, set equal to 1 in our model. Indeed, it can be shown that the requirement for the upstream firm not to cut the market is $r\ge \frac{3}{2}+\left(1-\lambda \right)c$. We impose this condition so as to focus on the interesting case where the upstream firm accommodates strategic location and does not respond by cutting the market.²

The result of this logic is that the optimal wholesale price given downstream locations is $w=r-\max \left\{{L}_1+\left(1-\lambda \right)c,{L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2},\right. \left.1-{L}_2\right\}$. These represent respectively the cases in which the mixed firm or both firms or the private firm is “critical.” The full proof is in Appendix 1. Again, this is under the assumption that r is sufficiently large that it is not in the interest of the upstream firm to set a price that cuts the market.

In the second stage of the game the downstream firms locate so as to maximize their objective functions. The profit functions for the two firms are

${\pi}_1={\int}_0^{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}\left({p}_1(x)-\left|x-{L}_1\right|\right) dx$,${\pi}_2={\int}_{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}^1\left({p}_2(x)\right. \left.-\left|x-{L}_2\right|\right) dx$

The total cost is the sum of transportation cost T and production cost C, where $T={\int}_0^{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}\left|x-{L}_1\right| dx+{\int}_{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}^1\left|x-{L}_2\right| dx$,$C=\left(1-\lambda \right)c\left(\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\right)$

The social welfare function is W = r − (T + C).

While the private firm maximizes its own profit, π ₂, the mixed ownership firm follows Matsumura (1998) and maximizes G = λπ ₁ + (1 − λ)W. This generates two best response functions in the two locations that when solved simultaneously generate the locations.

We prove in Appendix 2 that the locations that make both firms critical cannot be an equilibrium and so the upstream price will take the form of w = r − (L ₁ + (1 − λ)c) or w = r − (1 − L ₂). When w = r − (L ₁ + (1 − λ)c), the public firm is critical (see Fig. 9.1a) but when w = r − (1 − L ₂), the private firm is critical (see Fig. 9.1b). As in Gupta et al. (1994), the critical firm is that which interacts directly with the input monopoly and can use location to generate accommodating pricing.

When the public firm is critical, the equilibrium downstream locations are

$$ { \begin{array}{l}{L}_1^{\ast }={L}_1^a=\dfrac{4c{\lambda}^2-2 c\lambda -2c+2\lambda +1}{2\left(2+\lambda \right)},{L}_2^{\ast }={L}_2^a=\dfrac{2c{\lambda}^2-2c+2\lambda +3}{2\left(2+\lambda \right)} \end{array}}$$

(9.1)

When the private firm is critical, the equilibrium downstream locations are

$$ {L}_1^{\ast }={L}_1^b=\frac{1}{6}-\frac{\left(1-\lambda \right)c}{3},{L}_2^{\ast }={L}_2^b=\frac{1}{2} $$

(9.2)

The details are in Appendix 2. Note that this represents a generalization of Gupta et al. (1994) and that when λ = 1 (and so c = 0), our model collapses to theirs. The optimal downstream locations mimic their work, $\left\{\frac{1}{2},\frac{5}{6}\right\}$ when the now privatized firm on the left is critical or $\left\{\frac{1}{6},\frac{1}{2}\right\}$ when the always assumed private firm on the right is critical. These two sets of locations deviate substantially from the transport cost minimizing first best of $\left\{\frac{1}{4},\frac{3}{4}\right\}$ and they result in an upstream price of w = r − ½.

Note that when the private firm is critical, it continues to behave strategically against the upstream firm. The public firm cannot change this behavior as its best response function merely has it locating in a socially optimal manner given that of the private firm. Thus, if one imagined a public firm without an elevated cost of production, it could do no better than a private firm and the locations would remain$\left\{\frac{1}{6},\frac{1}{2}\right\}$. This reflect the well-known result that the profit maximizing and transport cost minimizing best responses are identical with delivered pricing (Lederer and Hurter 1986).

With an elevated cost of production, the mixed or public firm moves left to minimize the sum of production and transport cost, ${L}_1^b\le \frac{1}{6}$. Indeed, as the public share λ increases the mixed firm moves increasingly into the corner (see eq. 9.2). This may seem somewhat counterintuitive but reflects that only the critical private firm is able to alter the behavior of the upstream firm and that the mixed firm takes the resulting location as given. For a given c, it can be easily shown ${L}_1=\frac{1}{6}$ yields the lowest total transportation cost T and L ₁ = 0 yields the lowest total production cost. This follows as ${L}_2^b=\frac{1}{2}$ and implies that the equilibrium location ${L}_1^b$ is between 0 and $\frac{1}{6}$ depending upon λ.

When the mixed firm is critical, it now directly interacts with the upstream firm. Its object in doing so dramatically differs from that of the private firm. This can again be illustrated by imagining a fully public firm without an elevated cost of production. If c = 0, the fully public firm locates at ¼ and the private firm maximizes profit at ¾. (see eq. 9.1). Here the public firm is able to completely eliminate the strategic behavior that Gupta et al. isolate and return to the first best. The public firm, in essence, allows the upstream price to increase to w = r − ¼ but improves welfare by doing so.

With an elevated cost of production, a fully public firm faces competing influences. The desire to reduce transport cost encourages it to retain a location close to ¼. Yet, the elevated production cost mutes this influence and encourages it to remain moving to the left of ¼. Specifically, the fully public firm would locate increasingly toward the left corner as c increases: ${L}_1^a\left(\lambda =0\right)=\frac{1}{4}-\frac{c}{2}$.

Given the elevated cost, the optimal location of the mixed firm depends both on the size of c and on the extent of privatization. Specifically, as the extent of privatization increases that location varies between ${L}_1^a\left(\lambda =0\right)=\frac{1}{4}-\frac{c}{2}$ and ${L}_1^a\left(\lambda =1\right)=\frac{1}{2}$. The latter again corresponds to Gupta et al. (1994) when the left-hand-side firm is fully private.³

Finally, the equilibrium locations in (9.1) and (9.2) are returned to the welfare function to allow the government to determine the optimal share of the privatization parameter λ ^∗.

Proposition 1

When the private firm is critical, the optimal privatization is λ ^∗= 1. There is nothing to be gained by a mixed ownership firm.

Proof: Substituting ${L}_1^b$ and ${L}_2^b$ into W yields the associated equilibrium social welfare of the whole industry as W ^b∗. It satisfies $\frac{\partial {W}^{b\ast }}{\partial \lambda }=\frac{c}{3}\left(1-2\left(1-\lambda \right)c\right)>0$; therefore, the optimal privatization is 1 when the private firm is critical.

Full privatization follows naturally as mixed ownership increases the cost of production and causes the mixed ownership firm to move further toward the left corner increasing transportation costs. Both of these reduce social welfare.

This changes when the mixed ownership firm is critical.

Proposition 2

When the mixed ownership firm is critical and $c<\frac{1}{6}$ the optimal privatization share is 0 <λ ^∗(c) <1. When c is large $\frac{1}{6}<c<\frac{1}{2}$, λ ^∗(c) = 1.

Proof: See proof in Appendix 3.

This broadly follows intuition as when the cost differential between the mixed and private firm is large enough, it dominates the privatization decision. The government recognizes that any cost savings in transportation are dominated by increases in production cost. At lower cost differentials, the trade-off becomes relevant and determines an interior optimal extent of privatization.

3 Implications of Proposition 2

In this section we draw out a series of implications of the equilibrium identified in the previous section and isolate the specific consequence of the cost differential. We limit our attention to when the mixed firm is critical and discuss locations, optimal privatization, and welfare.

When the public firm is critical, it can be directly verified from (9.1) that the $\frac{\partial {L}_1^a}{\partial \lambda }>0$ and $\frac{\partial {L}_2^a}{\partial \lambda }>0$, indicating that both firms move right with λ, the extent of privatization. Moreover, ${L}_2^a-{L}_1^a=\frac{1+ c\lambda -c{\lambda}^2}{2+\lambda }$ and this decreases with λ showing that privatization moves the firms closer together. This reflects the mixed firm placing greater emphasis on profit and so wishing to occupy a larger share of the market.

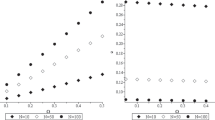
The object for the government in Proposition 2 is to use the public share to curtail this movement right without incurring an overly large increase in production cost. The optimal privatization share of λ ^∗ is less than 1 when the costs are small (c < 1/6) and we can calculate the specific value resulting using Cardano’s formula. The resulting relevant root from that formula isolates the relationship between the optimal private share and the production cost differential of the public firm, c. This is shown in Fig. 9.2.

Fig. 9.2

Optimal privatization when the public firm is critical

When c is small, the effect on production cost is modest for any given λ. Thus, higher levels of privatization generate equilibrium locations close to $\left\{{L}_1^a,{L}_2^a\right\}=\left\{\frac{1}{2},\frac{5}{6}\right\}$ that yield much higher transportation cost than the symmetric locations of $\left\{\frac{1}{4},\frac{3}{4}\right\}$. Thus, the government avoids privatization and starts with an almost completely public firm when the cost penalty is small so as to retain the more symmetric locations. As the cost differential increases, the government accepts great asymmetry in an effort to balance increasing production costs. As Fig. 9.2 shows, this relationship is continuous with the optimal privatization share starting at zero when c = 0 and increasing to one when c = 1/6.

We now illustrate various cost differentials that generate interior solutions and a mixed ownership firm. We use this to trace out the pattern of locations that result in equilibrium. These are shown in Table 9.1.

Table 9.1 Isolating equilibrium values as the cost differential increases

Starting with a very small differential of 0.02, the optimal extent of privatization is only around 6 percent. This largely public firm locates just to the right of the transport cost minimizing quartile. The location of the fully private firm and the resulting welfare are shown in the next two columns.⁴ Finally the gain in welfare relative to a two fully private firm is shown in the final column. As the sum of all transport and production cost is 0.1345, the welfare savings of 0.0321 is meaningfully large.

As the cost differential grows, the optimal extent of privatization grows and the mixed firm moves increasingly to the right. This pushes the private firm also increasingly to the right. The combination of increased production cost and more asymmetric locations means that welfare falls monotonically with the cost differential. The savings relative to two fully private firms shrinks and eventually vanishes as the optimal extent of privatization becomes 100 percent when the elevated cost of the public firm simply dominates the government’s decision.

4 An Extension: Examining When the Market Would Be Cut

In this section we recognize the point by Gupta et al. (1994) that when the reservation willingness to pay r is small enough relative to the transport cost, the upstream firm will not accommodate strategic downstream location. Instead, it becomes profitable for the upstream firm to retain a higher input price and simply allow a portion of the critical firm’s market not to be served. We previously ruled out such a circumstance by assuming that $r\ge \frac{3}{2}+\left(1-\lambda \right)c$. We note that this implies a new dimension, the possibility of simply fewer customers, to the welfare calculations associated with the mixed ownership firm. In this section, we explore when an optimally set private share less than one may forestall the welfare loss associated with the market being cut.

We consider three cases: (a) the private firm is critical and some portion of its market is cut; (b) the public firm is critical and some portion of its market will be cut and; and (c) the value of r is sufficiently low that the two firms have exclusive territories and both firms have their markets cut.

4.1 When the Private Firm Is Critical

When imagining that the upstream firm will optimally allow market to be cut, the price of the public firm in the SPD equilibrium above doesn’t change, while the price of the private firm becomes:

$$ {\fontsize{9}{12}\begin{array}{l}{p}_2(x)=\left\{\begin{array}{l}w+x-{L}_1+\left(1-\lambda \right)c,\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\le x\le r+{L}_1-w-\left(1-\lambda \right)c\\ {}r,r+{L}_1-w-\left(1-\lambda \right)c\le x\le {x}_1\end{array}\right. \end{array}}$$

where x ₁ = {x : r = x − L ₂ + w}. The demand in zone of [x ₁, 1] isn’t covered.

Similarly we can deduce the optimal location as

${L}_{1c}^{\ast }={L}_{1c}^b=\frac{r-5\left(1-\lambda \right)c}{7}$, ${L}_{2c}^{\ast }={L}_{2c}^b=\frac{3r-8\left(1-\lambda \right)c}{7}$

Notice that the market cut as a result of these locations is ${x}_c^b=1-{x}_1\left({L}_{1c}^b,{L}_{2c}^b\right)=1-\frac{5r}{7}+\frac{4c}{7}-\frac{4 c\lambda}{7}$. As ${x}_c^b>0$, we have $r<{r}_R^u$, where ${r}_R^u=\frac{7+4\left(1-\lambda \right)c}{5}$. As a consequence, it can be easily shown that the size of the cut market, ${x}_c^b$, decreases as privatization increases. Reversed, a larger public share causes the private firm to optimally move left resulting in a larger cut share of the market. This allows us to summarize.

Proposition 3

When the reservation price is sufficiently small that interaction between the upstream firm and the critical private firm results in a cut market, the optimal privatization is λ ^∗= 1. There is nothing to be gained by a mixed ownership firm.

Proof: Substituting ${L}_{1c}^b$ and ${L}_{2c}^b$ into W yields the associated equilibrium social welfare of the whole industry as ${W}_c^{b\ast }$. It satisfies $\frac{\partial {W}_c^{b\ast }}{\partial \lambda }=\frac{2c}{7}\left(3r-5\left(1-\lambda \right)c\right)>0$ given that ${L}_{1c}^b$ and ${L}_{2c}^b$ are interior solutions; therefore, the optimal privatization is 1 when the private firm is critical.

This carries over from the earlier presentation and argues that whenever the private firm is critical, the mixed firm should be completely privatized. The size of the reservation wage and whether the market is cut are irrelevant for this conclusion.

4.2 When the Mixed Ownership Firm Is Critical

Now the price of the private firm in the SPD equilibrium above doesn’t change from the earlier examination, while the price of the mixed firm becomes

$$ {p}_1(x)=\left\{\begin{array}{l}r,{x}_0\le x\le -r+w+{L}_2\\ {}w+{L}_2-x,-r+w+{L}_2\le x\le \frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\end{array}\right. $$

where x ₀ = {x : r = L ₁ − x + (1 − λ)c + w}. The portion of the market not covered or cut is [0, x ₀].

In this case, the profit of the upstream firm is π = (1 − x ₀)w, and the FOC of πwith respect to w yields the optimal wholesale price as ${w}_1=\frac{1}{2}\left(r+1-{L}_1-\left(1-\lambda \right)c\right)$.

The profit functions for the two downstream firms are

${\pi}_1={\int}_{x_0}^{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}\left({p}_1(x)-\left|x-{L}_1\right|\right) dx$,${\pi}_2={\int}_{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}^1\left({p}_2(x)\right. \left.-\left|x-{L}_2\right|\right) dx$

The total transportation cost is $T={\int}_{x_0}^{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}\left|x-{L}_1\right| dx+{\int}_{\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}}^1\left|x-{L}_2\right| dx$ and the total production cost is $C=\left(1-\lambda \right)c\left(\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}-{x}_0\right)$. The social welfare becomes W = (1 − x ₀)r − (C + T). Finally, the objective of the mixed ownership firm is G = λπ ₁ + (1 − λ)W.

Maximizing each firm’s objective function with respect to location generates two best response functions that when solved simultaneously yield the optimal equilibrium locations:

$$ {L}_{1c}^{\ast }={L}_{1c}^a=\frac{11c{\lambda}^2-12 c\lambda +3\lambda r+c+7\lambda -9r+7}{7\left(\lambda +1\right)}$$

$$ {L}_{2c}^{\ast }={L}_{2c}^b=\frac{6c{\lambda}^2-4 c\lambda +\lambda r-2c+7\lambda -3r+7}{7\left(\lambda +1\right)} $$

Note that the lost market, the market that is cut, becomes ${x}_c^a=\frac{2c{\lambda}^2-6 c\lambda -2\lambda r+4c+7\lambda -8r+7}{7\left(1+\lambda \right)}$, where ${x}_c^a>0$ requires that $r<{r}_L^u$, where ${r}_L^u=\frac{2c{\lambda}^2-6 c\lambda +4c+7\lambda +7}{2\left(4+\lambda \right)}$. Therefore, we have $\frac{\partial {x}_c^a}{\partial \lambda }=\frac{2\left(3r-\left(5-{\lambda}^2-2\lambda \right)c\right)}{7{\left(1+\lambda \right)}^2}$. This can be signed. Specifically, $\frac{\partial {x}_c^a}{\partial \lambda }>0$ when $\frac{c\left(5-{\lambda}^2-2\lambda \right)}{3}<r<{r}_L^u$, while $\frac{\partial {x}_c^a}{\partial \lambda }<0$ when $r<\frac{c\left(5-{\lambda}^2-2\lambda \right)}{3}$. Thus, when the reservation price is relatively large, the sale zone that is cut increases as privatization increases. This is the opposite of what we derived when the private firm was critical and allows us to summarize.

Proposition 4

When the reservation price is sufficiently small that interaction between the upstream firm and the critical mixed ownership firm results in a cut market, the optimal privatization can be less than one when r is relatively large.

Proof: Substituting ${L}_{1c}^a$ and ${L}_{2c}^a$ into W yields the associated equilibrium social welfare of the whole industry as ${W}_c^{a\ast }$. It satisfies ${\left.\frac{\partial {W}_c^{a\ast }}{\partial \lambda}\right|}_{\lambda =1}=\frac{3r}{14}\left(2c-r\right)$. Whenr > 2c, ${\left.\frac{\partial {W}_c^{a\ast }}{\partial \lambda}\right|}_{\lambda =1}<0$; therefore, the optimal privatization is less than 1 when r is large.

To illustrate Proposition 4 we imagine a specific value of c = 0.3 as shown in Fig. 9.3. While the exact range of r for the cut case is a little difficult to identify as lambda enters into the indifference condition of Gupta et al. (1994, p. 13). We have guaranteed an interior privatization ratio with a cut market as illustrated. We recognize that the range may be even larger and extend to an even smaller r.

Fig. 9.3

Optimal privatization with a cut market when c = 0.3

To be more specific take the illustrated case of c = 0.3 and imagine that r = 1.1, the optimal private share is then λ ^∗= 0.71. This generates a lost market share of ${x}_c^{a\ast }$=0.154 as a result of the upstream firm allowing the market to be cut. This can be compared with the fully private firm in which the lost market share will be ${\left.{x}_c^a\right|}_{\lambda =1}$=0.214. The welfare with the optimal degree of privatization is ${W}_c^{a\ast }$=0.8084 and this exceeds that with the fully private firm of ${\left.{W}_c^a\right|}_{\lambda =1}$=0.7779.

The critical point is that within the region where the market will be cut, a trade-off exists. A larger public share can decrease the market cut because of the mixed firm’s less strategic location. That less strategic location also plays a valuable role in reducing transport cost. On the other hand, the larger public share increases production cost.

This trade-off is evident in examining the locations. In our illustration with the mixed ownership firm (c = 0.3, r = 1.1, and so λ ^∗= 0.71), the market that is served starts at location 0.154 and goes to 1.0. The mixed ownership firm locates at 0.323 and the private rival at 0.746. This can be contrasted with a fully private where r remains 1.1 but where c=0 because of privatization. In this case the market runs from 0.214 to 1.0. The first private firm locates at 0.529 and the second at 0.843. The market for the mixed ownership firm is both larger and the two firms are more symmetrically located within it.

As the discussion above indicates, when r is relatively large, increasing privatization generates the more asymmetric locations we associate with private ownership for the earlier propositions and, in addition, the lost market increases $\left(\frac{\partial {x}_c^a}{\partial \lambda }>0\right)$. Both tend to decrease social welfare. Meanwhile, the increase of privatization is associated with the decrease of production cost, which tends to increase social welfare. Eventually, when r is relatively small, that is, c is relatively large, the benefit of lower production cost dominates, and being fully privatized is optimal. This happens directly because of the increased production cost of the mixed firm and indirectly because when that increased production cost is large enough, the cut market will actually be larger with a mixed firm.

4.3 When Both Firms Are Critical (Exclusive Territories)

Notice that when r is extremely small, exclusive territories may arise. In this case r intersects with two firms’ costs on both sides of L ₁ and L ₂, namely L ₁ − x + (1 − λ)c + w, x − L ₁ + (1 − λ)c + w,L ₂ − x + w, x − L ₂ + w. Let the four intersection points be x ₂, x ₃, x ₄, and x ₅. The upstream profit is π ^e = w(x ₃ − x ₂ + x ₅ − x ₄). The FOC yields the optimal wholesale price as ${w}^e=\frac{1}{2}r-\frac{1}{4}\left(1-\lambda \right)c$. When exclusive territories are about to emerge, we have thatx ₂(w ^e) = 0, x ₃(w ^e) = x ₄(w ^e), x ₅(w ^e) = 1, and this indicates that $r={r}^e=\frac{1+\left(1-\lambda \right)c}{2}$. This is the threshold value for r such that exclusive territories exist. Therefore when r becomes small, that is, when r < r ^e, exclusive territories can emerge. Notice that it can be easily proven that ${r}^e<{r}_L^u$, ${r}^e<{r}_R^u$.

The profit functions for the two firms under exclusive territories are ${\pi}_1^e={\int}_{x_1}^{x_2}\left(r-\left|x-{L}_1\right|\right) dx$, ${\pi}_2^e={\int}_{x_3}^{x_4}\left(r-\left|x-{L}_2\right|\right) dx$. As downstream price is r everywhere, the associated consumer surplus is 0. Thus the social welfare is ${W}^e={\pi}_1^e+{\pi}_2^e+{\pi}^e$, and the equilibrium social welfare is W ^e∗ = W ^e(w ^e), and it satisfies $\frac{\partial {W}^{e\ast }}{\partial \lambda }=\frac{c\left(6r-7\left(1-\lambda \right)c\right)}{4}$. Notice that there is a lower bound for r such that exclusive territories can exist, and this threshold value is reached when x ₂(w ^e) = x ₁(w ^e) or x ₄(w ^e) = x ₃(w ^e), then it must satisfy that $r\ge {\underline{r}}^e=\frac{3\left(1-\lambda \right)c}{2}$ to ensure the existence of exclusive territories for both firms. Then we have $\frac{\partial {W}^{e\ast }}{\partial \lambda }>0$, and full privatization is optimal, and then a proposition can be drawn as follows.

Proposition 5

When r is sufficiently small such that exclusive territories emerge, the optimal privatization is λ ^∗= 1. There is nothing to be gained by a mixed ownership firm.

Proposition 5 follows naturally as when exclusive territories arise, the downstream firms simply do not compete. One firm’s location does not influence that of the other. This insures that there is no room for mixed ownership to increase the level of social welfare as it simply increases production costs.

5 Conclusions

We have imagined a mixed ownership firm in a downstream spatial market. The issue is the extent to which the firm can regulate by participation. This regulation comes from its willingness to locate in such a way as to reduce wasteful strategic location downstream. We have assumed that the firm maximizes an objective function which is a convex combination of welfare (as weighted by the public ownership share) and profit (as weighted by the private ownership share). The greater the public ownership is, the greater is the production cost. As in the classic paper by Matsumura (1998), this increased cost can give rise to an optimal degree of privatization.

The first insight is that when the mixed ownership firm is not critical and so does not directly interact with the upstream firm, it cannot influence downstream locations and so simply produces at a higher cost. This means that there is no scope for a mixed ownership firm that is not critical. This applies both when the reservation price is large enough that the full market is served and when it is small enough that some of the market is left unserved and cut.

The interesting case in which a mixed ownership can regulate by participation is when it is the critical firm. Here it becomes less interested in strategic location as the share of public ownership increases. The result is more symmetric locations and lower transport costs. Yet, this advantage comes with increased production cost.

Specifically, when the reservation price is large, the entire market is served. Given this, the government optimizes by retaining a public share when the production cost differential, c, is below 1/6 (recalling this is all relative to the unit transport cost normalized to 1). The optimal private share can be completely zero if the mixed ownership firm has no cost disadvantage. The optimal private share increases monotonically as that cost disadvantage increases. At c ≥ 1/6, the production cost disadvantage completely outweighs the locational advantage and the fully private firm is optimal.

When the reservation price is small, the upstream engages in less accommodating pricing and the downstream market is cut with customers not being served. There remains a role for the mixed ownership firm when the reservation price is relatively larger within this case where the market will be cut. The critical comparison is now the size of the reservation price compared to the cost disadvantage. The logic now involves two advantages for having a public share. Within the market that is not cut, the mixed ownership firm locates more symmetrically saving transport cost. Moreover, the more symmetric location means that as the public share is larger, less market is cut increasing welfare. Yet, these advantages are completely outweighed by the increased production cost as the size of c grows relative to r.

Following the original work by Gupta et al. (1994) we assumed that either firm could be critical. Yet, the potential advantage of the mixed ownership firm arises only when it is the critical firm. Left undiscussed in that original work and in what we have presented is how the critical firm might be determined. The critical firm is that which interacts with the upstream monopoly by being located such that its most extreme delivered cost exceeds that of its rival.

Introducing timing might provide structure. Thus, if the government could locate first, it would choose to be critical. At the same time, if the private firm could locate first, it also would likely choose to be critical. This suggests that such timing would need to arise exogenously and could not be easily endogenized (Hamilton and Slutsky 1990).

Our interest has been in the role played by government ownership in regulating strategic behavior that hurts welfare. The government has a variety of policy tools and might undertake alternative actions short of simply dictating location. They might, for example, tax total transport cost. Designed appropriately such a tax might discourage the asymmetric locations that simultaneously waste resources but generate a lower input price. We leave such alternatives to future work.

Appendices

A.1 Appendix 1

The possible highest costs in the spatial market for firms are reached when x takes the values of 0, 1, or $\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}$, which is the sale bound between firms 1 and 2. See Fig. 9.1. When the two firms’ cost at any x exceeds r, there is no sale existing; therefore, the following conditions must hold:

$$ x=0:w+\left(1-\lambda \right)c+{L}_1\le r $$

$$ x=\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}:w+{L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\le r $$

$$ x=1:w+1-{L}_2\le r $$

Thus the wholesale price must satisfy

$$ w\le r-\max \left\{{L}_1+\left(1-\lambda \right)c,{L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2},1-{L}_2\right\} $$

As the upstream firm wants to maximize his profit, namely, the wholesale price, we have that

$$ w=r-\max \left\{{L}_1+\left(1-\lambda \right)c,{L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2},1-{L}_2\right\} $$

B.1 Appendix 2

As $w=r-\max \left\{{L}_1+\left(1-\lambda \right)c,{L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2},1-{L}_2\right\}$, the wholesale price in stage 2 can take three forms:w = r − (L ₁ + (1 − λ)c), or $w=r-\left({L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\right)$, orw = r − (1 − L ₂).

First we will prove that $w=r-\left({L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\right)$ is not equilibrium. When $w=r-\left({L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\right)$, we denote the public firm’s objective function as G ₁. FOC of G ₁ with respect to L ₁ yields public firm’s optimal location of L ₁(L ₂) as the function of L ₂. Then we obtain G ₁(L ₂) as the function of L ₂ and the associated wholesale price as ${w}_1=r-\left({L}_2-\frac{L_1\left({L}_2\right)+{L}_2-\left(1-\lambda \right)c}{2}\right)$.

If the public firm chooses a large location of ${L}_1^{\hbox{'}}$ that satisfies ${L}_1^{\hbox{'}}=\left\{{L}_1:{L}_1+\left(1-\lambda \right)c={L}_2-\frac{L_1\left({L}_2\right)+{L}_2-\left(1-\lambda \right)c}{2}\right\}$ and meanwhile keep the wholesale price remain at the same level as w ₁ (so that the upstream firm is indifferent), we can obtain the public firm’s associated objective as the function of L ₂, and we denote it as ${G}_2\left({L}_2\right)=G\left({L}_1^{\hbox{'}}\right)$.

We find that ${G}_2\left({L}_2\right)-{G}_1\left({L}_2\right)=\frac{\lambda^2{\left( c\lambda +{L}_2-c\right)}^2}{{\left(6+\lambda \right)}^2}\ge 0$, and the equality holds only when λ = 0. Therefore we have that the wholesale price of $w=r-\left({L}_2-\frac{L_1+{L}_2-\left(1-\lambda \right)c}{2}\right)$ is not equilibrium.

Now we derive downstream locations associated with the other two expressions.

Take w = r − (L ₁ + (1 − λ)c) as an example. The FOCs of $\left\{\frac{\partial G}{\partial {L}_1}=0,\frac{\partial {\pi}_2}{\partial {L}_2}=0\right\}$ yield the optimal downstream location as

${L}_1^a=\frac{4c{\lambda}^2-2 c\lambda -2c+2\lambda +1}{2\left(2+\lambda \right)}$,${L}_2^a=\frac{2c{\lambda}^2-2c+2\lambda +3}{2\left(2+\lambda \right)}$

Then the associated wholesale price is ${w}^a=r-\left({L}_1^a+\left(1-\lambda \right)c\right)$.

When the private firm is critical, FOCs yield the downstream locations of other forms as ${\overline{L}}_1^b=\frac{1}{6}-\frac{2\left(1-\lambda \right)c}{3}$, ${\overline{L}}_2^b=\frac{1}{2}-\left(1-\lambda \right)c\le \frac{1}{2}$, we will prove that this is not equilibrium.

When the private firm chooses ${\overline{L}}_2^b$ and the mixed firm chooses to jump to the right of the private competitor, then mixed firm is on the right side while the private firm is in the left side, and the equilibrium price of mixed firm becomes

$$ {p}_1(x)=\left\{\begin{array}{l}w+x-{L}_2^b,\frac{L_1+{\overline{L}}_2^b+\left(1-\lambda \right)c}{2}\le x\le r+{\overline{L}}_2^b-w\\ {}r,r+{\overline{L}}_2^b-w\le x\le 1\end{array}\right. $$

The equilibrium price of private firm becomes

$$ { \begin{array}{l}{p}_2(x)=\left\{\begin{array}{l}r,0\le x\le {L}_1+w+\left(1-\lambda \right)c-r\\ {}w+{L}_1-x+\left(1-\lambda \right)c,{L}_1+w+\left(1-\lambda \right)c-r\le x\le \frac{L_1+{\overline{L}}_2^b+\left(1-\lambda \right)c}{2}\end{array}\right.\end{array}} $$

Denote the new profit functions and social welfare as ${\pi}_1^{\hbox{'}}$, ${\pi}_2^{\hbox{'}}$, and W ^'. The objective of the mixed firm is ${G}^{\hbox{'}}={\lambda \pi}_1^{\hbox{'}}+\left(1-\lambda \right){W}^{\hbox{'}}$.

The wholesale price may take three forms: $w=r-{\overline{L}}_2^b$, or $w=r-\left(\frac{L_1+{\overline{L}}_2^b+\left(1-\lambda \right)c}{2}-{\overline{L}}_2^b\right)$, or w = r − (1 − L ₁ + (1 − λ)c).

Take $w=r-{\overline{L}}_2^b$ as an example. The FOC of ${\pi}_1^{\hbox{'}}$ with respect to L ₁ yields the optimal location of mixed firm as ${L}_1^{\hbox{'}}=\frac{5}{6}$. Denote the associated maximized objective of mixed firm as G ^'∗ and the one under the original location of $\left\{{\overline{L}}_1^b,{\overline{L}}_2^b\right\}$ asG ^∗. Then we have

$$ {G}^{\ast }-{G}^{\hbox{'}\ast }=\frac{2c}{3}\left(\lambda -1\right)\left(\left(3\lambda +2\right)\left(\lambda -1\right)c+1\right)\le 0 $$

“ = ” holds only when λ = 1. (Notice that in this case ${\overline{L}}_2^b$ is the largest among$\left\{{\overline{L}}_2^b,\frac{L_1+{\overline{L}}_2^b+\left(1-\lambda \right)c}{2}-{\overline{L}}_2^b,1-{L}_1+\left(1-\lambda \right)c\right\}$, which indicates that (1 − λ)c ≤ 1/6.)

The above condition indicates that the mixed firm can achieve higher value of its objective function if he jumps to the right side of the private firm who chooses ${\overline{L}}_2^b$.

The cases of $w=r-\left(\frac{L_1+{\overline{L}}_2^b+\left(1-\lambda \right)c}{2}-{\overline{L}}_2^b\right)$ and w = r − (1 − L ₁  + (1 − λ)c) are similar; therefore, the mixed firm would jump to the right side when the private firm chooses ${\overline{L}}_2^b$.

Therefore, the private firm cannot locate anywhere left of $\frac{1}{2}$. The optimal location for the private firm becomes ${L}_2^b=\frac{1}{2}$. In this case, FOC yields the mixed firm’s optimal location as ${L}_1^b=\frac{1}{6}-\frac{\left(1-\lambda \right)c}{3}$, which is right to ${\overline{L}}_1^b=\frac{1}{6}-\frac{2\left(1-\lambda \right)c}{3}$.

Notice that when λ = 1, $\left\{{L}_1^a,{L}_2^a\right\}=\left\{\frac{1}{2},\frac{5}{6}\right\}$ and $\left\{{L}_1^b,{L}_2^b\right\}=\left\{\frac{1}{6},\frac{1}{2}\right\}$. This is precisely as in Gupta et al. (1994).

C.1 Appendix 3

When the mixed firm is critical, the derivative of the associated social welfare W ^∗ with respect to λ is $\frac{\partial {W}^{\ast }}{\partial \lambda }=- AS$, where $A=\frac{1-2c+2\lambda c}{{\left(2+\lambda \right)}^2}>0$ and S = 2cλ ³ + 6cλ ² − 18cλ − 8c + 3λ.

When $0<c<\frac{1}{6}$, $\frac{\partial S}{\partial \lambda }=6c{\lambda}^2+12 c\lambda +3\left(1-6c\right)>0$; therefore, S increases as λincreases. As S(λ = 0) =  − 8c < 0, S(λ = 1) = 3(1 − 6c) > 0, there exists only a threshold value of $\overline{\lambda}$ so that $S\left(\overline{\lambda}\right)=0$ and $0<\overline{\lambda}<1$. Then we have that for $0\le \lambda <\overline{\lambda}$, S(λ) < 0, $\frac{\partial {W}^{\ast }}{\partial \lambda}\left(\lambda \right)=-A\cdotp S\left(\lambda \right)>0$, for $\overline{\lambda}<\lambda \le 1$, S(λ) > 0, $\frac{\partial {W}^{\ast }}{\partial \lambda}\left(\lambda \right)=-A\cdotp S\left(\lambda \right)<0$, and $\frac{\partial {W}^{\ast }}{\partial \lambda}\left(\lambda =\overline{\lambda}\right)=0$. Thus, it can be concluded that an interior solution of $\overline{\lambda}$ for optimal privatization is reached when $0<c<\frac{1}{6}$.

When $\frac{1}{6}<c<\frac{1}{2}$, let the two solutions of equation $\left\{\lambda :\frac{\partial S}{\partial \lambda }=0\right\}$ be λ ₁ and λ ₂. As ${\lambda}_1+{\lambda}_2=-\frac{12c}{2\cdotp 6c}=-1<0$ and ${\lambda}_1\cdotp {\lambda}_2=\frac{3\left(1-6c\right)}{6c}=\frac{1-6c}{2c}<0$, only one of λ ₁ and λ ₂ can be in λ ∈ [0, 1]. As ${\left.\frac{\partial S}{\partial \lambda}\right|}_{\lambda =0}=3\left(1-6c\right)<0$, ${\left.\frac{\partial S}{\partial \lambda}\right|}_{\lambda =1}=3>0$; there is one threshold value satisfying $\left\{\lambda :\frac{\partial S}{\partial \lambda }=0\right\}$, so S first decreases and then increases with λ ∈ [0, 1], and then S ≤  max {S(λ = 0), S(λ = 1)} =  max {−8c, 3(1 − 6c)} < 0; therefore, $\frac{\partial {W}^{\ast }}{\partial \lambda }=-A\cdotp S>0$, and it can be concluded that the optimal privatization is λ = 1 when $\frac{1}{6}<c<\frac{1}{2}$.