Algorithms for Radon Partitions with Tolerance

Abstract

Let P be a set n points in a d-dimensional space. Tverberg theorem says that, if n is at least $(k-1)(d+1)$, then P can be partitioned into k sets whose convex hulls intersect. Partitions with this property are called Tverberg partitions. A partition has tolerance t if the partition remains a Tverberg partition after removal of any set of t points from P. A tolerant Tverberg partition exists in any dimensions provided that n is sufficiently large. Let N(d, k, t) be the smallest value of n such that tolerant Tverberg partitions exist for any set of n points in $\mathbb {R}^d$. Only few exact values of N(d, k, t) are known.

In this paper, we study the problem of finding Radon partitions (Tverberg partitions for $k=2$) for a given set of points. We develop several algorithms and found new lower bounds for N(d, 2, t).

1 Introduction

Tverberg’s theorem and Tverberg partitions are of crucial importance in combinatorial convexity and stands on the intersection of combinatorics, topology and linear algebra. Tverberg partitions with tolerance showed importance in these fields, years after the main theorem.

Theorem 1

(Tverberg [32]). For any set $P \subset \mathbb {R}^d$ of at least $(k-1)(d+1)+1$ points, there exists a partition of $P \subset \mathbb {R}^d$ into k sets $P_1,P_2,\dots ,P_k$ such that their convex hulls intersect

$$\begin{aligned} \bigcap _{i=1}^k \mathsf {conv}(P_i) \ne \emptyset . \end{aligned}$$

(1)

This is a generalization of Radon’s theorem from 1921 [26] which provides a partition of at least $d+1$ points for $k=2$. We call a partition satisfying Equation (1) a Tverberg partition. If $k=2$, we call it a Radon partition.

The computational complexity of finding a Tverberg partition according to Theorem 1 is not known. Teng [31] showed that testing whether a given point is in the intersection of convex hulls of a partition is coNP-complete. On the other hand, such a point can be computed in $n^{d^2}$ time if d is fixed [2]. Mulzer and Werner [24] found an approximation algorithm for Tverberg partitions with linear running time.

A Tverberg partition has tolerance t if after removing t points from P it still remains Tverberg partition.

Definition 2

(t-tolerant Tverberg partition) Let P be set of point in $\mathbb {R}^d$. $\varPi = \{ P_1, P_2, \dots , P_k \}$ be a partition of size k of P. A partition $\varPi = \{ P_1, P_2, \dots , P_k \}$ of P is called t-tolerant if for every $C \subset P$ with $|C| \le t$

$$\bigcap _{i=1}^k \mathsf {conv}(P_i \setminus C) \ne \emptyset .$$

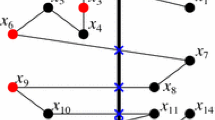
In 1972, Larman [21] proved that every set of size $2d+3$ admits a 1-tolerant Tverberg partition into two sets, i.e., a 1-tolerant Radon partition. García-Colín [13] proved the existence of a Radon partition for any tolerance t, see also [14]. Soberon et al. [30] proved if $|P| > (t + 1)(k - 1)(d + 1)$ then P has a t-tolerant Tverberg partition. Examples of a Tverberg partition (with tolerance 0) and tolerant Tverberg partitions are shown in Fig. 1.

Fig. 1.

(a) A Tverberg partition for $k=3$ (the intersection of 3 convex hulls is shaded). Points from the same set of the partition have the same shape (disk, circle or square). (b) A 1-tolerant Tverberg partition for $k=2$. (c) A 2-tolerant Tverberg partition for $k=2$.

The problem of finding Tverberg partitions with tolerance seems more difficult. For example, Tverberg’s theorem provides a tight bound for the number of points. On the other hand, only a few tight bounds are known for Tverberg partitions with tolerance. Let N(d, k, t) be minimum number such that every set of points $P \subset \mathbb {R}^d$ with $|P| \ge N(d, k, t)$ has a t-tolerant Tverberg partition. For fixed t and d, Garcia et al. showed [15], $N(d, k, t) = kt + o(t)$ using a generalization of the Erdos-Szekeres theorem for cyclic polytopes in $\mathbb {R}^d$. Soberon [29] improved the bound to $N(d, k, t) = kt + O(\sqrt{t})$. Mulzer and Stein [23] provided an algorithm for finding a t-tolerant Tverberg partition of size k for a set $P \subset \mathbb {R}^d$ in $O(2^{d-1}dkt + kt\log t)$ time. The algorithm by Mulzer and Stein [23] for finding a t-tolerant Tverberg partition uses large number of points. A natural question is to find algorithms when n is relatively small. In this paper, we consider the following problems.

Problem 1

(ComputingTolerantPartition)

• Given a finite set $P\subset \mathbb {R}^d$ and an integer t.

• Compute a t-tolerant Tverberg partition for P if it exists.

Our motivation for this problem is to construct sets of points in $\mathbb {R}^d$ with large tolerance t to find new lower bounds for N(d, t, k) for some small values of d and t. One approach to this problem is to check all possible partitions and solve the following problem for them. This is possible in practice only for relatively small n, k,  and d.

Problem 2

(ComputingMaxTolerance)

• Given a finite set $P\subset \mathbb {R}^d$, a Tverberg partition $\varPi = \{P_1, P_2, \dots , P_k\}$ of P.

• Compute the largest t such that $\varPi$ is t-tolerant Tverberg partition.

For a Tverberg partition $\varPi$, we say that the tolerance of $\varPi$ is t and write $\tau (\varPi )=t$ if partition $\varPi$ is t-tolerant but not $(t+1)$-tolerant. Thus, the problem ComputingMaxTolerance is to compute the tolerance of a Tverberg partition. The decision problem of ComputingMaxTolerance has been studied by Mulzer and Stein [23].

Problem 3

(TestingTolerantTverberg)

• Given a finite set $P\subset \mathbb {R}^d$, a partition $\varPi = \{P_1, P_2, \dots , P_k\}$ of P, and an integer $t\ge 0$.

• Decide whether $\varPi$ is a t-tolerant Tverberg partition of P.

Mulzer and Stein [23] proved that TestingTolerantTverberg is coNP-complete by a reduction from the problem of testing a centerpoint. In fact, their proof is for $k=2$. We call the problem TestingTolerantTverberg in this case TestingTolerantRadon.

In this paper we study algorithms for problems ComputingTolerantPartition, ComputingMaxTolerance and TestingTolerantTverberg aiming to compute point configurations in d dimensions with high tolerance. These problems are hard even for $k = 2$, i.e., for Radon Partitions. In this paper we focus on Radon Partitions only. We use $M(d, t) = N(d, 2, t)$ for simplicity. They would provide new lower bounds for M(d, t). We are not aware of any program supporting lower bounds for M(d, t). Our results can be summarized as follows.

• 1. We found that the problem ComputingMaxTolerance for $k=2$ (Radon partitions) is related to linear classifiers with outliers which is a well-known classification problem in machine learning and statistics. The literature on linear classifiers is vast, see for example [3, 9, 16, 18, 25, 27, 33]. This classification problem is also known as the weak separation problem [5, 10, 12, 19, 22] and linear programming with violations [7]. In fact, our Theorem 3 states that two optimization problems are equivalent (ComputingMaxTolerance and optimal weak separation problem).

• 2. The relation between ComputingTolerantPartition and the classification problem can be used to solve ComputingTolerantPartition more efficiently. We provide three algorithms for the problem ComputingTolerantPartition. The first algorithm is simple and easy to implement. The second algorithm improved testing separable partition (Step 3) in the first algorithm by using BFS and hamming distances. As a result, the second algorithm is faster. To provide a more memory efficient algorithm, we used gray code in the last algorithm.

• 3. Using the algorithms for ComputingRadonPartition, we established new lower bounds on M(d, t). For this purpose, we design algorithms for generating sets of points and improving them. The bounds computed by the program are shown in Table 1 (different algorithms for different pairs of d and t). Because of the efficiency of these algorithms, we could solve ComputingRadonPartition for set of points as large as 26.

Following [5, 19, 20], in this paper we assume that the points of set P are in general position. In Sect. 2 we show that Radon partitions and linear classifiers are related. In Sect. 3 we discuss algorithms for Radon partitions. In Section 4 we discuss experiments and lower bounds for M(d, t).

2 Radon Partitions and Linear Classifiers

In this section we show a relation between the problem ComputingMaxTolerance for two sets (i.e. the problem of computing the maximum tolerance of a Radon partition in d dimensions) and linear classifiers with outliers which is a well-known classification problem in machine learning and statistics, see for example [3, 25, 27, 33]. Outlier detection algorithms are often computationally intensive [27] (Fig. 2).

Fig. 2.

Example of a classification problem in the plane that can be solved with a linear classifier and few outliers.

This classification problem is also known as the weak separation problem [5, 10, 12, 19, 22] and can be defined as follows. Let P be a bicolored set of points in $\mathbb {R}^d$, i.e. $P=R\cup B$ where R be a set red points in $\mathbb {R}^d$ and B is a set blue points. Let h be a hyperplane $a_1x_1\dots +a_dx_d=a_0$. Let $h^+$ be the halfspace that contains the points satisfying $a_1x_1\dots +a_dx_d\le a_0$ and let $h^-$ be the halfspace that contains the points satisfying $a_1x_1\dots +a_dx_d\ge a_0$. If h were a separator (or classifier) of P, we would have $R\subset h^+$ and $B\subset h^-$. A red point x is an outlier, if $x\notin h^+$. A blue point x is an outlier, if $x\notin h^-$. The weak separation problem is to find a hyperplane h minimizing the number of misclassified points (outliers)

$$ mis(h)=|R\setminus h^+|+|B\setminus h^-|. $$

The weak separation problem in the plane is well studied. Gajentaam and Overmars [12] showed the weak separation problem is 3Sum-hard by reducing the point covering problem to it. An algorithm with $O(n^2)$ time complexity is provided for the weak separation problem by Houle [19]. Cole et al. [8] presented an $O(N_k(n)\log ^2 k+n\log n)$ time algorithm to compute the k-hull of n points in the plane where $N_k(n)$ is the maximum number of k-sets for a set of n points. This algorithm can be used to compute the space of all classifiers misclassifying up to k points in the plane in $O(nt\log ^2 t+n\log n)$ time [5]. Thus, a t-weak separator can be computed within the same time. A better algorithm with $O(nt\log t + n \log n)$ time have been found by Everett et al. [10]. In higher dimensions, Aronov et al. [5] proved that the weak separation problem can be solved using duality in $O(n^d)$ time.

The connection of tolerant Radon partitions and the weak separations is estableshed in the next theorem.

Theorem 3

Let $\varPi = \{ P_1, P_2\}$ be a Radon partition of a set $P \subset \mathbb {R}^d$ (i.e. $\mathsf {conv}(P_1) \cap \mathsf {conv}(P_2) \ne \emptyset$). The tolerance of partition $\varPi$ is t if and only if the number of outliers in an optimal solution for the weak separation problem for $P_1$ and $P_2$ is $t+1$.

Theorem 3 shows the equivalence between the weak separation problem and the problem ComputingMaxTolerance for $k = 2$, see Fig. 3 for an example.

Fig. 3.

A linear classifier with 2 outliers (and maximum margin) corresponding to the 1-tolerant Radon partition in Fig. 1(b).

Proof

Recall that $\varPi$ is a t-tolerant Radon partition if and only if for any set $C \subset P$ of at most t points

$$\mathsf {conv}(P_1 \setminus C) \cap \mathsf {conv}(P_2 \setminus C) \ne \emptyset .$$

Suppose that $\varPi$ is a t-tolerant Radon partition. We show that the number of outliers in an optimal solution for the weak separation problem for $P_1$ and $P_2$ is at least $t+1$. The proof is by contradiction. Suppose that there is a hyperplane h such that the number of misclassified points $mis(h)=|P_1\setminus h^+|+|P_2\setminus h^-|$ is at most t. Let $C_h$ be the set of points misclassified by h, i.e. $C_h=(P_1\setminus h^+) \cup (P_2\setminus h^-)$. Then $P_1 \setminus C_h\subset h^+$ and $P_2 \setminus C_h\subset h^-$. Therefore

$$\mathsf {conv}(P_1 \setminus C_h) \cap \mathsf {conv}(P_2 \setminus C_h) \subset h.$$

The hyperlane h contains at most d points of $P_1\cup P_2$ (due to general position). Then

$$\mathsf {conv}(P_1\cap h) \cap \mathsf {conv}(P_2 \cap h) =\emptyset .$$

Therefore

$$\mathsf {conv}(P_1 \setminus C_h) \cap \mathsf {conv}(P_2 \setminus C_h) = \mathsf {conv}(P_1\cap h) \cap \mathsf {conv}(P_2 \cap h) =\emptyset . $$

and $\varPi$ is not t-tolerant. Contradiction.

Now, suppose that $\varPi$ is not a $(t+1)$-tolerant Radon partition. We show that the number of outliers in an optimal solution for the weak separation problem for $P_1$ and $P_2$ is at most $t+1$. There is a set C of size at most $t+1$ such that

$$\mathsf {conv}(P_1 \setminus C) \cap \mathsf {conv}(P_2 \setminus C) = \emptyset .$$

By Minkowski hyperplane separation theorem [6, Section 2.5.1]¹ there is a separating hyperplane h for $\mathsf {conv}(P_1 \setminus C)$ and $\mathsf {conv}(P_2 \setminus C)$, i.e., $\mathsf {conv}(P_1 \setminus C)\subset h^+$ and $\mathsf {conv}(P_2 \setminus C)\subset h^-$. Then, the number of misclassified points $mis(h)=|P_1\setminus h^+|+|P_2\setminus h^-|$ is at most $|C|\le t+1$.

Therefore, if the tolerance of partition $\varPi$ is t, then the number of outliers in an optimal solution for the weak separation problem for $P_1$ and $P_2$ is $t+1$. The converse is true and the theorem follows.    $\square$

3 Algorithms for Tolerant Radon Partitions

In this section, we design several algorithms for the problem ComputingTolerantPartition in order to find new lower bounds for tolerant Radon partitions. In this section, we assume that given points are in general position. The first idea is based on the connection of the problem ComputingMaxTolerance for $k=2$ to linear classifiers with outliers that we discussed in the previous section. We can iterate through all possible partitions of given set into two sets and check if the partition is t-tolerant or not (Problem TestingTolerantRadon). The test can be done using an algorithm for weak separation with $O(nt\log t + n \log n)$ time for the plane [10] and $O(n^d)$ time for higher dimensions. This approach has $O(2^nT_d(n))$ running time complexity where $T_d(n)$ is the time complexity of the problem TestingTolerantRadon.

Since the problem is computationally difficult, all our algorithms have exponential running time and can be used only for bounded n, t and d. However, the algorithms have different running time and space bounds. This allows us to obtain lower bounds for n up to 27 in Sect. 4. We assume in this section that $t=O(1)$ is a constant.

The above approach uses TestingTolerantRadon with $O(n^d)$ running time which is not easy to implement. Our first algorithm is simpler. The algorithm uses separable partitions. A partition of P into k subsets is seprable [20] if their convex hulls are pair-wise disjoint. The number of separable partitions for $k = 2$ is well-known Harding number H(n, d) [17]. Harding proved

$$H(n,d) = \sum _{j=0}^d \left( {\begin{array}{c}n-1\\ j\end{array}}\right) = \varTheta (n^d).$$

Hwang and Rothblum [20] provided a method for enumerating separable 2-partitions in O(nH(n, d)) time. It is based on the following recursive formula

$$H(n,d) = H(n-1,d) + H(n-1,d-1).$$

Algorithm 1

• 1. Let $P=\{p_1,p_2,\dots ,p_n\}$. Construct $\mathcal{S}$, the set of all separable partitions using the enumeration from [20]. For any separable partition $P=P_1\cup P_2$, we assume that $p_1\in P_1$ and we encode the partition with a binary code $b_1\dots b_n$ where $b_i=j - 1$ if $p_i\in P_j$. Note hat $|\mathcal{S}|=H(n,d)$.

• 2. Construct $\mathcal{P}$, the set of all partitions of $P=P_1\cup P_2$ with $p_1\in P_1$. Encode the partitions as in Step 1.

• 3. For every binary code $b =(b_1, b_2, \dots , b_n) \in \mathcal{S}$ and every $C \subset [n]$ with $|C| \le t$, we make a $b'$ by flipping $b_i$ for all $i\in C$ and remove $b'$ from $\mathcal{P}$.

• 4. Return any remaining partition in $\mathcal{P}$ as tolerant partition of points P.

Running Time Analysis. The partitions of $\mathcal{S}$ and their correspondent binary codes can be computed in $O(n^{d+1})$. The number of all binary codes in $\mathcal{P}$ is $2^{n-1}$, and creating each of them takes O(n). Therefore, Step (2) takes $O(n2^n)$ time. Step (3) searches $|\mathcal{S}|n^t=O(n^{d+t})$ binary codes in $\mathcal{P}$. Thus, Step (3) takes $O(n^{d+t+1})$ time. Each binary code contains n bits. The total time for Algorithm 1 is $O(n2^n+n^{d+t+1})$.

Correctness. We prove the following for the correctness of the algorithm.

• (1) Every binary code deleted from $\mathcal{S}$ is not t-tolerant,

• (2) Every binary code remained in $\mathcal{S}$ is t-tolerant.

Clearly, every binary code b deleted from $\mathcal{P}$ can be transformed into a binary code in $\mathcal{S}$ by flipping at most t bits. Since a binary code in $\mathcal{S}$ corresponds to a separable partition, the partition of b is not t-tolerant.

For the second part, suppose that a binary code b in $\mathcal{P}$ corresponds to a partition that is not t-tolerant. Then, it can be transformed to a separable code by flipping at most t bits. Therefore, b must be deleted from $\mathcal{P}$.

Algorithm 1 can be improved using the fact that it tries to delete the same binary code a multiple numbers of times. The second algorithm avoids it.

Algorithm 2

• 1. Construct $\mathcal{S}$ and $\mathcal{P}$ as in Algorithm 1.

• 2. Let $S_0 = \mathcal{S}$ and remove $S_0$ element form $\mathcal{P}$. For each $i\in [t]$ compute $S_i$ as follows.

• 2a. For each $b \in S_{i - 1}$ and each position $j \in [n]$, we change j-th position of b and call it $b'$. Then, if $b'$ is in $\mathcal{P}$, we remove it from $\mathcal{P}$ and add it to $S_i$.

• 3. Return remaining elements in $\mathcal{P}$ as tolerant partition of points P.

We show that Algorithm 2 is correct. First if binary code $b'$ is removed from $\mathcal P$ in Step (2a) there is a binary code b in S such that hamming distance between $b'$ and b is at most t. So the partition corresponding to $b'$ is not t-tolerant.

It remains to show that every binary code $b \in \mathcal P$ corresponding to a partition $\varPi$ with $\tau (\varPi ) < t$ is removed from $\mathcal P$. Let $t_1 = \tau (\varPi )$. There exists $b'' \in \mathcal S$ such that hamming distance between b and $b''$ is $t_1$. Algorithm 2 will change $t_1$ bits in $b''$ in Step (2a), and create binary code b. Then binary code b will be removed from $\mathcal P$. Only codes correspondent to t-tolerant partition will be left in $\mathcal P$.

Since both $\mathcal{S}$ and $\mathcal{P}$ contain at most $2^{n-1}$ binary codes, Algorithm 2 takes only $O(n2^n + n^{d+1})$ time. Using Algorithm 2 we were able to obtain more bounds on M(d, t) (the bounds are shown in Sect. 4).

We also develop Algorithm 3, which is slower than Algorithm 2 but it is memory efficient. The idea is to apply gray code to enumerate all binary codes for $\mathcal{P}$. Let hd(u, v) be the hamming distance between binary codes u and v (the number of positions where u and v are different). For each binary code b, we compute a hamming vector $v_b = (v_1, v_2, \dots , v_{N})$ where

• $N=|\mathcal{S}| = H(n, d)$ is the size of $\mathcal S$,

• $v_i=hd(b,s_i)$, $i=1,2,\dots ,N$ and

• $s_i$ is the binary code of the i-th partition of $\mathcal S$.

Algorithm 3

• 1. Construct $\mathcal{S}$ as in Algorithm 1.

• 2. For each binary code $b\in \mathcal{P}$, generated by the gray code, compute the hamming vector $v_b$ as follows.

  • 2.1 For the first binary code b, compute $v_b$ directly by computing every $v_i=hd(b,s_i)$ in O(n) time.

  • 2.2 For every other binary code b following binary code $b'$, b and $b'$ are different in only one position. Then $hd(b,s_i)=hd(b',s_i)\pm 1$ and the hamming vector $v_b$ can be computed in O(N) time.

  • 2.3 If all entries of $v_b$ are greater than t, then the Radon partition corresponding to binary code b is t-tolerant and the algorithms stops.

• 3. If the algorithm does not stop in Step (2.3), then P does not admit a t-tolerant Radon partition.

For the correctness of Algorithm 3 it is sufficient to proof following lemma.

Lemma 1

Let $\varPi$ be a Radon partition, and b is binary representation of it. All entries of $v_b$ are greater than k if and only if $\varPi$ is t-tolerant.

Proof

It follows as a sequence of equivalences. All entries of $v_b$ are greater than k $\iff$ $hd(s_i, b) > k$ for every $i \in N$ $\iff$ for every separable partition $s_i \in \mathcal{S}$ there is at least $k + 1$ outliers $\iff$ $\varPi$ is a t-tolerant Radon partition.    $\square$

Running Time Analysis. Step (2.1) calculates $v_b$ in O(nN) time, and it only happens one time through the algorithm. Step (2.2) takes $O(2 ^ nN)$ time. So, the time complexity of above algorithm is $O(2^nn^d)$.

4 Experimental Results

There have been some known lower bound for M(d, t) which are listed as follows. Larman [21] proved for $M(d,1) \ge 2d+3$ for d = 2, 3. Forge et al. [11] proved $M(4,1) \ge 11$. Ramírez-Alfonsí [4] proved that, for any $d\ge 4$,

$$\begin{aligned} M(d,1) \ge \left\lceil \frac{5d}{3} \right\rceil + 3. \end{aligned}$$

(2)

García-Colín and Larman [14] proved

$$\begin{aligned} M(d,t) \ge 2d+t+1. \end{aligned}$$

(3)

Soberón [28] proved a lower bound for N

$$\begin{aligned} N(d,k,t) \ge k(t+\lfloor d/2\rfloor +1). \end{aligned}$$

(4)

As we concern about lower bound of M, $M(d,t) \ge 2t+ d$ for odd d, and $M(d,t) \ge 2t+ d + 1$ for even d.

Table 1. Lower bounds on M(d, t) using point configurations computed by algorithms from Sect. 2 for tolerance $t\le 10$ and dimension $d=2,3,4$. We omit bounds for $d = 1$ and $t = 1$ because the tight bounds are known [4, 21, 23].

To improve a lower bound on M(d, t) for a pair of d and t, it is sufficient to find a set of points in $\mathbb {R}^d$ which its size is larger than previous lower bound on M(d, t) such that every partition of it into two sets is not t-tolerant. One approach finding such a set of points is as follows. For a given number of points n, we start with initial points set P computed randomly. We can use one of the algorithms for problem ComputingTolerantPartition from the previous section. There are two possible outcomes. If a t-tolerant Radon partition for P does not exists, then $M(d, t) \ge n + 1$, which a lower bound for M. Otherwise, the algorithm output a t-tolerant Radon partition for P, say $\varPi = \{P_1, P_2\}$. Since P is t-tolerant Radon partition every classifier of $\varPi$ has at least $t + 1$ outliers. We compute all classifiers of $\varPi$, and choose a classifier c which has the minimum number of misclassification. We want to decrease the number of misclassifications of c by moving one of the points of P. Therefore, we compute the distance of c and all outliers of c and pick one of the outliers p which has the minimum distance to c. Finally, we move p to the other side of c randomly and continue this process with the new set of points.

Table 1 shows the lower bounds we obtained by using of mentioned algorithms in this paper. Using Algorithm 1, we have achieved new lower bounds for M(2, 5) and M(2, 6); however, it is slow for larger t in the plane. The results in the Table for $d = 3$ and $d = 4$ are computed by Algorithm 2. Algorithm 3 is more memory efficient than Algorithm 2 and it is used larger number of points in the plane, including $M(2,10) \ge 27$. In higher dimensions, Algorithm 2 performed better than others since it has less dependency on the dimension of points than other Algorithms.

We provide a website with the point sets corresponding to the lower bounds in Table 1 at [1]. A point set providing a lower bound for M(d, t) must have points in general position and there must be no t-tolerant Radon partition for it. The following basic tests can be used for verification.

• 1. Test whether $d+1$ points lie on the same hyperplane,

• 2. Given a point p and a hyperplane $\pi$ such that $p\notin \pi$, test whether $p\in \pi ^+$ or $p\in \pi ^-$.

Both tests can be done using the determinant of the following matrix defined by points $p_1,p_2,\dots ,p_{d+1}\in \mathbb {R}^d$

$$ \begin{bmatrix} p_{1,1} &{} p_{2,1} &{} p_{3,1} &{} \dots &{} p_{d+1,1} \\ p_{1,2} &{} p_{2,2} &{} p_{3,2} &{} \dots &{} p_{d+1,2} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ p_{1,d} &{} p_{2,d} &{} p_{3,d} &{} \dots &{} p_{d+1,d} \\ 1 &{} 1 &{} 1 &{} \dots &{} 1 \end{bmatrix} . $$

If the determinant is equal to 0, then the points lie on the same hyperplane. Otherwise, let $\pi$ be the hyperplane passing through the points $p_1,p_2,\dots ,p_{d}$. Then the sign of the determinant corresponds to one of the cases $p_{d+1}\in \pi ^+$ or $p_{d+1}\in \pi ^-$. The points in our sets have integer coordinates and the determinant can be computed without rounding errors.