Keywords

1 Introduction

Hydraulic jump constitutes at the transition from supercritical regime to subcritical regime and characterized by highly turbulent flow, macro-scale vortices, kinetic energy dissipation and bubbly two-phase flow due to air entrainment. In the literature, there are lots of studies concerned with the hydraulic jump flow patterns. However, the self-aeration aspect of hydraulic jumps took less attention (Kucukali and Cokgor 2007). The term self-aeration means transfer of oxygen from air into water and it has important environmental and ecological implications for polluted streams. Aeration efficiency is calculated with the equation suggested by Gameson (1957)

$$ E = \frac{{C_{d} - C_{u} }}{{C_{s} - C_{u} }} = 1 - \frac{1}{\exp (K.t)} $$
(1)

In Eq. (1), E denotes aeration efficiency, which has a range between 0 for no aeration, to 1 for total downstream saturation. Cu and Cd are dissolved oxygen concentrations up- and downstream of a hydraulic structure, respectively, Cs is the saturation concentration of dissolved oxygen for a given ambient condition, K is the reaeration rate (1/s), and t is the bubble residence time. At different temperatures, the physical and chemical properties of water change. This in turn will influence the air-water gas transfer rate. Self-aeration efficiency therefore converted to a standard temperature. In this study Gulliver et al. (1990) formula was used to adjust aeration efficiency to 20 °C and it is defined as E20. On the basis of a small-eddy model, Lamont and Scott (1970) correlated the reaeration rate with the energy dissipation rate and their result suggested that the gas transfer efficiency is controlled locally by the energy dissipation. One can calculate the average energy dissipation rate per unit mass εa along a reach as follows,

$$ \varepsilon_{a} = \frac{\Delta H.Q.\gamma }{V.\rho } $$
(2)

where ΔH (m) is head loss, Q (m3 s−1) is the discharge, V is the volume of the reach (m3), γ is the specific weight and ρ is the density of water. Melching and Flores (1999) collected data sets from 166 streams in USA in order to develop empirical equations to predict reaeration rates of streams. The data of Melching and Flores (1999) were re-analyzed in Fig. 1 and the reaeration rates were plotted as a function of the average energy dissipation rate. The relationship was best fitted by a linear function as

Fig. 1
figure 1

Data source Melching and Flores (1999)

Reaeration K20 versus average energy dissipation rate per unit mass εa for uniform flow conditions.

Full size image
$$ K_{20} = 1102 \times \varepsilon_{a} + 4.4 $$
(3)

Equation (3) has a sound physical basis, because air entrainment takes place when the turbulence kinetic energy overcomes the surface tension forces (Ervine and Falvey 1987). For non-uniform flow conditions, Moog and Jirka (1998) related the gas transfer efficiency of macro roughness elements with the energy dissipation rate on the basis of small-eddy model. Kucukali and Cokgor (2008) investigated the aeration performance of boulder structures at sudden expansions and plunging jets, where they found an interrelation between the aeration efficiency and the energy dissipation. Indeed, hydrodynamic processes which ensure the self-aeration mechanism such as: (1) hydraulic jump, (2) plunging jet or water fall, and (3) stepped channels have other common property: they are also used as energy dissipaters at hydraulic structures. From this point of view, one can expect to find a positive correlation between the aeration efficiency and the energy dissipation. It could be suggested that the macro-scale eddies, which are responsible for the mixing and energy dissipation, could also be responsible for the suction of air into water (Hoyt and Sellin 1989). In this reasoning, Vischer and Hager (1995) defined the energy dissipation as a mixing process, which is originated from the vortex flow and turbulence. For instance, in fish passage design standards, energy dissipation rate is used as an indicator for turbulence (Kucukali and Hassinger 2018). The objective of this experimental study is to investigate reaeration rate of hydraulic jumps in terms of energy dissipation and to reveal the important role of turbulence in the process.

2 Experimental Set-Up and Methods

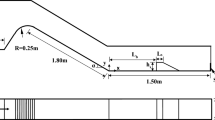
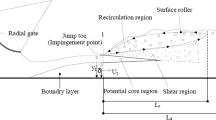
The hydraulic jump is a rapidly varied flow occurring at the transition from the supercritical to the subcritical flow regime. Figure 2 shows the main variables, U1 and U2, as the up- and downstream average flow velocities; d1 and d2 are the corresponding flow depths, x is the streamwise distance from the toe of the hydraulic jump and, Lj is the jump length. The upstream Froude number is the main parameter of a hydraulic jump, Fr1 = U1/(gd1)0.5, where g is the acceleration of gravity. The experiments were carried out in a horizontal rectangular flume, 0.50 m wide, 0.45 m deep and 13.15 m long, with glass sidewalls and a concrete bottom (Fig. 3). The discharge was measured with a V-notch weir to ±2%. The flow depths were measured by pointer gages with an accuracy of ±1 mm. The jump lengths were determined visually and, beyond the end of jump, the flow is practically not perturbed by the jump. The hydraulic jumps were generated with the aid of sluice and tail gates (Fig. 2). The longitudinal distance from the sluice gate to the jump toe varied in the range of 0.1–0.94 m, resulting in partially developed flow conditions. The jumps were grouped into seven different unit width discharges q in the range of 0.020–0.053 m2/s. The head loss \( \Delta H \) of the hydraulic jump was calculated from

Fig. 2
figure 2

Definition sketch for reaeration in a hydraulic jump

Full size image
Fig. 3
figure 3

Macro-scale vortices in a hydraulic jump for: Fr1 = 4.85; Re = 5.3 × 104. For oxygen transfer, the energy containing large scale eddies should overcome surface tension forces by creating surface disturbances

Full size image
$$ \Delta H = \left( {d_{1} + \frac{{U_{1}^{2} }}{2g}} \right) - \left( {d_{2} + \frac{{U_{2}^{2} }}{2g}} \right) $$
(4)

and the average energy dissipation rate per unit mass for the hydraulic jump equals to

$$ \varepsilon_{a} = \frac{\Delta H.Q.g}{{(d_{1} + d_{2} ).0.5.L_{j} }} $$
(5)

Dissolved Oxygen (DO) measurements were conducted simultaneously upstream and downstream of the hydraulic jump with manual oxygen meters (Model WTW Oxi 330i). The air calibration technique was used in the experiments with Cs values measured in the air. The uncertainties during the measurements were ±0.5% for the oxygen concentration and ±0.1% K for water temperature. To drop the DO concentration of the approaching flow, Sodium Sulfide and Cobalt Chlorite were added into the chamber (Fig. 4). The two minutes time-averaged values of Cu and Cd were measured 0.50 m up- and downstream of the hydraulic jump at the central flow depths, respectively. The measurement distance was sufficiently far from downstream for turbulent mixing to ensure the uniformity of flow conditions. The deficit ratios were calculated for each experiment from Eq. (1) and formula of Gulliver et al. (1990) was used to adjust the deficit ratio to a standard temperature.

Fig. 4
figure 4

Plan view of the experimental set-up

Full size image

The turbulence quantities were collected by a Nortek 10 MHz type Acoustic Doppler Velocimeter (ADV) at 25 Hz during a sampling time of 2 min, with velocities from about 1 mm/s to 2.5 m/s with an accuracy of ±1%. From the time-series of the velocity measurements, the root-mean-square of the turbulent fluctuation velocities in the longitudinal u′, lateral v′, and vertical w′ directions, respectively, were calculated at the each measurement point. Then, the turbulent kinetic energy per unit mass k is calculated from

$$ k = \frac{1}{2}(\overline{{u^{{{\prime }2}} }} + \overline{{v^{{{\prime }2}} }} + \overline{{w^{{{\prime }2}} }} ) $$
(6)

The distribution of the turbulent kinetic energy in the flow field is important, because the energy dissipation is resulted from the turbulence generation. Also, the presence of turbulence in the flow domain plays an important role in conversion of flow kinetic energy to turbulent kinetic energy. For the turbulent kinetic energy analysis, also the data of Liu et al. (2004) were used. The flow conditions of the turbulence measurements are given in Table 1, with Re = q/υ the Reynolds number and kmax the maximum turbulent kinetic energy per unit mass measured at any streamwise location in the hydraulic jump. Moreover, Reynolds shear stress is calculated by using Eq. (7)

Table 1 The flow conditions of the hydraulic jump turbulence measurements
Full size table
$$ \tau = - \rho \overline{{u^{\prime}v^{\prime}}} $$
(7)

The Reynolds shear stress is a transport effect resulting from turbulent motion induced by velocity fluctuations with its subsequent increase of momentum exchange and of mixing (Piquet 2010).

Both the DO and the turbulence quantities collection methods and related calculations are used by several researches in the literature. Making measurements by using manual oxygen meters and ADV is relatively cheaper and easier. Hence, we selected those reliable and proven test methods. Moreover, the ADV technique has a limitation in bubbly flow; therefore, the turbulence measurements were applied only to the low Froude numbers 1.9 < Fr1 < 2.3 (Table 1).

3 Experimental Results and Discussion

In this study, it is expected to find a positive correlation between the aeration efficiency and energy dissipation. For this purpose, E20 values were plotted against head loss ∆H including the oxygen transfer data at the V-notch weir of the experimental set-up. Figure 5 depicts the E20 dependence on ∆H but data were scattered around a linear line suggesting an influence of another parameter on the process. This parameter was thought to be a unit discharge.

Fig. 5
figure 5

Variation of aeration efficiency as a function of head loss at a hydraulic jump and weir

Full size image

Moreover, the analysis of the measured data indicated a direct proportion between the reaeration and the average energy dissipation rate of a hydraulic jump. As εa increases from 0.14 to 0.29 m2 s−3, the reaeration rate increased by a factor of two. Figure 6 shows the hydraulic jump reaeration rate K20 versus the average energy dissipation rate per unit mass εa with the best fit (R2 = 0.97)

Fig. 6
figure 6

Reaeration K20 versus average energy dissipation rate per unit mass εa for hydraulic jump

Full size image
$$ K_{20} = 56873.\varepsilon_{a}^{1.08} \quad for\;\;2.4 \le Fr_{1} \le 6.5 $$
(8)

Equation (8) suggests that the gas transfer efficiency of a hydraulic jump is controlled by the energy dissipation rate. The comparison of Eqs. (8) and (3) suggests that the re-aeration rate of a hydraulic jump has about 50 times higher value as compared to uniform flow condition at the same energy dissipation rate.

The turbulent kinetic energy has its maximum value at the jump toe and decays along the hydraulic jump (Fig. 7), because of the energy cascade process in which turbulent kinetic energy is transformed into micro-scale vortices. This resulting correlation was explained with the equation:

Fig. 7
figure 7

Distribution of dimensional maximum turbulence kinetic energy in a hydraulic jump

Full size image
$$ \begin{array}{*{20}c} {\frac{{k^{1/2} }}{{U_{1} }} = - 0.012x/d_{2} + 0.2} & {(R^{2} = 0.90)} \\ \end{array} $$
(9)

where x is the longitudinal distance from the jump toe.

Moreover, Fig. 8 shows the relationship between εa and the kmax, given that

Fig. 8
figure 8

Variation of the average energy dissipation rate per unit mass εa as a function of the maximum turbulent kinetic energy per unit mass kmax

Full size image
$$ \begin{array}{*{20}c} {\varepsilon_{a} = 19.52.k_{\text{max} }^{1.5} } & {(R{}^{2} = 0.90)} \\ \end{array} $$
(10)

Equation (10) suggests that the energy dissipation rate was under the control of the turbulent kinetic energy. It was attempted to adjust Eq. (10) to the Prandtl-Kolmogorov formula. Therefore, the average of the upstream flow depths (Table 1) davr = 49 mm was taken as the integral turbulent length scale, in agreement with Kucukali and Chanson (2008) who related the macro-scale turbulent length scale L with upstream flow depth. Substituting this value in Eq. (10) leads to the dimensionally homogenous equation

$$ \varepsilon_{a} = 0.97.\frac{{k_{\text{max} }^{1.5} }}{L} $$
(11)

Equation (11) has an exponent consistent with the formula of Prandtl-Kolmogorov, although this formula deals with local energy dissipation and turbulent kinetic energy. Moreover, in Fig. 9, Reynolds shear stress (τ) variation through the hydraulic jump is shown. Figure 9 depicts the intensive vertical mixing and momentum transfer near the free-surface of the hydraulic jump.

Fig. 9
figure 9

Reynolds shear stress contour for Fr1= 3.35; Re = 86,100

Full size image

4 Conclusions

The reaeration rate of hydraulic jumps was experimentally investigated in terms of the average energy dissipation rate per unit mass. 40 test series were conducted to relate the gas transfer efficiency to the energy dissipation rate, supporting the small-eddy model of Lamont and Scott (1970). The reaeration and the average energy dissipation rate of the hydraulic jump may be described with Eq. (8). The proposed equation predicts and captures the system dynamics. Equation (8) has the following features: (i) it is a single parameter equation, (ii) it may be tested for other rapidly varied flow conditions like plunging jets and sudden expansions. In the experiments, viscous scale effects might exist; hence, the validity of Eq. (8) should be tested at higher Reynolds numbers in a field study. It is discussed that a functional relationship between reaeration and energy dissipation rate exists both for uniform and nonuniform flow conditions. At site conditions, measuring energy dissipation is much easier than measuring turbulence quantities. The functional dependence between the reaeration and energy dissipation rate can provide engineers to estimate gas transfer coefficients in the field. The authors believe that the present results bring a fresh perspective towards better understanding of hydraulic jump reaeration process. The overall contribution of this study is thought to be that we showed the main role of macro turbulence in self-aeration and energy dissipation mechanisms. Consequently, experimental findings suggest that hydraulic jump can be used as a self-aerator device in waste water treatment plants to enhance the DO levels of an effluent.