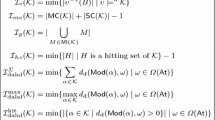Inconsistency Measurement

Abstract

The field of Inconsistency Measurement is concerned with the development of principles and approaches to quantitatively assess the severity of inconsistency in knowledge bases. In this survey, we give a broad overview on this field by outlining its basic motivation and discussing some of these core principles and approaches. We focus on the work that has been done for classical propositional logic but also give some pointers to applications on other logical formalisms.

1 Introduction

Inconsistency is a ubiquitous phenomenon whenever knowledge¹ is compiled in some formal language. The notion of inconsistency refers (usually) to multiple pieces of information and represents a conflict between those, i. e., they cannot hold at the same time. The two statements “It is sunny outside” and “It is not sunny outside” represent inconsistent information and in order to draw meaningful conclusions from a knowledge base containing these statements, this conflict has to be resolved somehow. In applications such as decision-support systems, a knowledge base is usually compiled by merging the formalised knowledge of many different experts. It is unavoidable that different experts contradict each other and that the merged knowledge base becomes inconsistent. The field of Knowledge Representation and Reasoning (KR) [7] is the subfield of Artificial Intelligence (AI) that deals with the issues of logical formalisations of information and the modelling of rational reasoning behaviour, in particular in light of inconsistent or uncertain information. One paradigm to deal with inconsistent information is to abandon classical inference and define new ways of reasoning. Some examples of such formalisms are, e. g., paraconsistent logics [6], default logic [34], answer set programming [15], and, more recently, computational models of argumentation [1]. Moreover, the fields of belief revision [21] and belief merging [10, 28] deal with the particular case of inconsistencies in dynamic settings.

The field of Inconsistency Measurement—see the seminal work [20] and the recent book [19]—provides an analytical perspective on the issue of inconsistency. Its aim is to quantitatively assess the severity of inconsistency in order to both guide automatic reasoning mechanisms and to help human modellers in identifying issues and compare different alternative formalisations. Consider the following two knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ formalised in classical propositional logic (see Sect. 2 for the formal background) modelling some information about the weather:

$$\begin{aligned} \mathcal {K}_{1}&= \{\text {sunny}, \lnot \text {sunny}, \text {hot}, \lnot \text {hot}\} \\ \mathcal {K}_{2}&= \{\lnot \text {hot}, \text {sunny}, \text {sunny} \rightarrow \text {hot}, \text {humid}\} \end{aligned}$$

Both $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ are classically inconsistent, i. e., there is no interpretation satisfying any of them. But looking closer into the structure of the knowledge bases one can identify differences in the severity of the inconsistency. In $\mathcal {K}_{1}$ there are two “obvious” contradictions, i. e., $\{\text {sunny},\lnot \text {sunny}\}$ and $\{\text {hot},\lnot \text {hot}\}$ are directly conflicting formulas. In $\mathcal {K}_{2}$, the conflict is a bit more hidden. Here, three formulas are necessary to produce a contradiction ($\{\lnot \text {hot}, \text {sunny}, \text {sunny} \rightarrow \text {hot}\}$). Moreover, there is one formula in $\mathcal {K}_{2}$ ($\text {humid}$), which is not participating in any conflict and one could still infer meaningful information from this by relying on e. g. paraconsistent reasoning techniques [6]. In conclusion, one should regard $\mathcal {K}_{1}$ as more inconsistent than $\mathcal {K}_{2}$. So a decision-maker should prefer using $\mathcal {K}_{2}$ instead of $\mathcal {K}_{1}$.

The analysis of the severity of inconsistency in the knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ above was informal. Formal accounts to the problem of assessing the severity of inconsistency are given by inconsistency measures and there have been a lot of proposals of those in recent years. Up to today, the concept of severity of inconsistency has not been axiomatised in a satisfactory manner and the series of different inconsistency measures approach this challenge from different points of view and focus on different aspects on what constitutes severity. Consider the next two knowledge bases (with abstract propositions a and b)

$$\begin{aligned} \mathcal {K}_{3}&= \{a,\lnot a, b\}&\mathcal {K}_{4}&= \{a \vee b, \lnot a \vee b, a \vee \lnot b, \lnot a \vee \lnot b\} \end{aligned}$$

Again both $\mathcal {K}_{3}$ and $\mathcal {K}_{4}$ are inconsistent, but which one is more inconsistent than the other? Our reasoning from above cannot be applied here in the same fashion. The knowledge base $\mathcal {K}_{3}$ contains an apparent contradiction ($\{a,\lnot a\}$) but also a formula not participating in the inconsistency ($\{b\}$). The knowledge base $\mathcal {K}_{4}$ contains a “hidden” conflict as four formulas are necessary to produce a contradiction, but all formulas of $\mathcal {K}_{4}$ are participating in this. In this case, it is not clear how to assess the inconsistency of these knowledge bases and different measures may order these knowledge bases differently. More generally speaking, it is not universally agreed upon which so-called rationality postulates should be satisfied by a reasonable account of inconsistency measurement, see [3, 5, 41] for a discussion. Besides concrete approaches to inconsistency measurement the community has also proposed a series of those rationality postulates in order to describe general desirable behaviour and the classification of inconsistency measures by the postulates they satisfy is still one the most important ways to evaluate the quality of a measure, even if the set of desirable postulates is not universally accepted. For example, one of the most popular rationality postulates is monotony which states that for any $\mathcal {K}\subseteq \mathcal {K}'$, the knowledge base $\mathcal {K}$ cannot be regarded as more inconsistent as $\mathcal {K}'$. The justification for this demand is that inconsistency cannot be resolved when adding new information but only increased². While this is usually regarded as a reasonable demand there are also situations where monotony may be seen as counterintuitive, even in monotonic logics. Consider the next two knowledge bases

$$\begin{aligned} \mathcal {K}_{5}&= \{a,\lnot a\}&\mathcal {K}_{6} = \{a, \lnot a, b_{1},\ldots , b_{998}\} \end{aligned}$$

We have $\mathcal {K}_{5}\subseteq \mathcal {K}_{6}$ and following monotony, $\mathcal {K}_{6}$ should be regarded as least as inconsistent as $\mathcal {K}_{5}$. However, when judging the content of the knowledge bases “relatively”, $\mathcal {K}_{5}$ may seem more inconsistent: $\mathcal {K}_{5}$ contains no useful information and all formulas of $\mathcal {K}_{5}$ are in conflict with another formula. In $\mathcal {K}_{6}$, however, only 2 out of 1000 formulas are participating in the contradiction. So it may also be a reasonable point of view to judge $\mathcal {K}_{5}$ more inconsistent than $\mathcal {K}_{6}$.

In this survey paper, we give a brief overview on formal accounts to inconsistency measurement. We focus on approaches building on classical propositional logic but also briefly discuss approaches for other formalisms. A more technical survey of inconsistency measures can be found in [41] and the book [19] captures the recent state-of-the-art as a whole. An older survey can also be found in [22].

The remainder of this paper is organised as follows. In Sect. 2 we give some necessary technical preliminaries. Section 3 introduces the concept of inconsistency measures formally and discusses rationality postulates. In Sect. 4 we discuss some of the most important concrete approaches to inconsistency measurement for classical propositional logic and in Sect. 5 we give an overview on approaches for other formalisms. Section 6 concludes.

2 Preliminaries

Let $\mathsf {At}$ be some fixed set of propositions and let $\mathcal {L}(\mathsf {At})$ be the corresponding propositional language constructed using the usual connectives $\wedge$ (conjunction), $\vee$ (disjunction), $\rightarrow$ (implication), and $\lnot$ (negation).

Definition 1

A knowledge base $\mathcal {K}$ is a finite set of formulas $\mathcal {K}\subseteq \mathcal {L}(\mathsf {At})$. Let $\mathbb {K}$ be the set of all knowledge bases.

If X is a formula or a set of formulas we write $\mathsf {At}(X)$ to denote the set of propositions appearing in X.

Semantics for a propositional language is given by interpretations where an interpretation $\omega$ on $\mathsf {At}$ is a function $\omega :\mathsf {At}\rightarrow \{\mathsf {true},\mathsf {false}\}$. Let $\varOmega (\mathsf {At})$ denote the set of all interpretations for $\mathsf {At}$. An interpretation $\omega$ satisfies (or is a model of) a proposition $a\in \mathsf {At}$, denoted by $\omega \models a$, if and only if $\omega (a)=\mathsf {true}$. The satisfaction relation $\models$ is extended to formulas in the usual way.

For $\varPhi \subseteq \mathcal {L}(\mathsf {At})$ we also define $\omega \models \varPhi$ if and only if $\omega \models \phi$ for every $\phi \in \varPhi$. A formula or set of formulas $X_{1}$ entails another formula or set of formulas $X_{2}$, denoted by $X_{1}\models X_{2}$, if and only if $\omega \models X_{1}$ implies $\omega \models X_{2}$. If there is no $\omega$ with $\omega \models X$ we also write $X\models \perp$ and say that X is inconsistent.

3 Measuring Inconsistency

Let $\mathbb {R}^{\infty }_{\ge 0}$ be the set of non-negative real values including infinity. The most general form of an inconsistency measure is as follows.

Definition 2

An inconsistency measure $\mathcal {I}$ is any function $\mathcal {I}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$.

The above definition is, of course, under-constrained for the purpose of providing a quantitative means to measure inconsistency. The intuition we intend to be behind any concrete approach to inconsistency measure $\mathcal {I}$ is that a larger value $\mathcal {I}(\mathcal {K})$ for a knowledge base $\mathcal {K}$ indicates more severe inconsistency in $\mathcal {K}$ than lower values. Moreover, we wish to reserve the minimal value (0) to indicate the complete absence of inconsistency. This is captured by the following postulate [23]:

• Consistency $\mathcal {I}(\mathcal {K})=0$ iff $\mathcal {K}$ is consistent.

Satisfaction of the consistency postulate is a basic demand for any reasonable inconsistency measure and is satisfied by all known concrete approaches [39, 41]. Beyond the consistency postulates a series of further postulates has been proposed in the literature [41]. We only recall the basic ones initially proposed in [23]. In order to state these postulates we need two further definitions.

Definition 3

A set $M\subseteq \mathcal {K}$ is a minimal inconsistent subset of $\mathcal {K}$ iff $M\models \perp$ and there is no $M'\subsetneq M$ with $M'\models \perp$. Let $\mathsf {MI}(\mathcal {K})$ be the set of all minimal inconsistent subsets of $\mathcal {K}$.

Definition 4

A formula $\alpha \in \mathcal {K}$ is called free formula if $\alpha \notin \bigcup \mathsf {MI}(\mathcal {K})$. Let $\mathsf {Free}(\mathcal {K})$ be the set of all free formulas of $\mathcal {K}$.

In other words, a minimal inconsistent subset characterises a minimal conflict in a knowledge base and a free formula is a formula that is not directly participating in any derivation of a contradiction. Let $\mathcal {I}$ be any function $\mathcal {I}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$, $\mathcal {K},\mathcal {K}'\in \mathbb {K}$, and $\alpha ,\beta \in \mathcal {L}(\mathsf {At})$. The remaining rationality postulates from [23] are:

• Normalisation $0\le \mathcal {I}(\mathcal {K})\le 1$.

• Monotony If $\mathcal {K}\subseteq \mathcal {K}'$ then $\mathcal {I}(\mathcal {K})\le \mathcal {I}(\mathcal {K}')$.

• Free-formula independence If $\alpha \in \mathsf {Free}(\mathcal {K})$ then

  $\mathcal {I}(\mathcal {K})=\mathcal {I}(\mathcal {K}\setminus \{\alpha \})$.

• Dominance If $\alpha \not \models \perp$ and $\alpha \models \beta$ then $\mathcal {I}(\mathcal {K}\cup \{\alpha \})\ge \mathcal {I}(\mathcal {K}\cup \{\beta \})$.

The postulate normalisation states that the inconsistency value is always in the unit interval, thus allowing inconsistency values to be comparable even if knowledge bases are of different sizes. Monotony requires that adding formulas to the knowledge base cannot decrease the inconsistency value. Free-formula independence states that removing free formulas from the knowledge base should not change the inconsistency value. The motivation here is that free formulas do not participate in inconsistencies and should not contribute to having a certain inconsistency value. Dominance says that substituting a consistent formula $\alpha$ by a weaker formula $\beta$ should not increase the inconsistency value. Here, as $\beta$ carries less information than $\alpha$ there should be less opportunities for inconsistencies to occur.

The five postulates from above are independent (no single postulates entails another one) and compatible (as e. g. the drastic measure $\mathcal {I}_{d}$, see below, satisfies all of them). However, they do not characterise a single concrete approach but leave ample room for various different approaches. Moreover, for all rationality postulates (except consistency) there is at least one inconsistency measure in the literature that does not satisfy it [41] and there is no general agreement on whether these postulates are indeed desirable at all [3, 5, 41]. We already gave an example why monotony may not be desirable in the introduction. Here is another example for free-formula independence taken from [3].

Example 1

Consider the knowledge base $\mathcal {K}_{7}$ defined via

$$\begin{aligned} \mathcal {K}_{7} = \{a \wedge c, b\wedge \lnot c, \lnot a \vee \lnot b\} \end{aligned}$$

Notice that $\mathcal {K}_{7}$ has a single minimal inconsistent subset $\{a \wedge c, b\wedge \lnot c\}$ and $\lnot a \vee \lnot b$ is a free formula. If $\mathcal {I}$ satisfies free-formula independence we have $\mathcal {I}(\mathcal {K}_{7})=\mathcal {I}(\mathcal {K}_{7}\setminus \{\lnot a \vee \lnot b\})$. However, $\lnot a \vee \lnot b$ adds another “conflict” about the truth of propositions a and b.

We will continue the discussion on rationality postulates later in Sect. 6. But first we will have a look at some concrete approaches.

4 Approaches

There is a wide variety of inconsistency measures in the literature, the work [41] alone lists 22 measures in 2018 and more have been proposed since then³. In this paper we consider only a few to illustrate the main concepts.

The measure $\mathcal {I}_{d}$ is usually referred to as a baseline for inconsistency measures as it only distinguishes between consistent and inconsistent knowledge bases.

Definition 5

([24]). The drastic inconsistency measure $\mathcal {I}_{d}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{d}(\mathcal {K})&= \left\{ \begin{array}{cc} 1 &{} \text {if } \mathcal {K}\models \perp \\ 0 &{} \text {otherwise} \end{array}\right. \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$.

While not being particularly useful for the purpose of actually differentiating between inconsistent knowledge bases, the measure $\mathcal {I}_{d}$ already satisfies the basic five postulates from above [24].

In [22] several dimensions for measuring inconsistency have been discussed. A particular observation from this discussion is that inconsistency measures can be roughly divided into two categories: syntactic and semantic approaches. While this distinction is not clearly defined⁴ it has been used in following works to classify many inconsistency measures. Using this categorisation, syntactic approaches refer to inconsistency measures that make use of syntactic objects such as minimal inconsistent sets (or maximal consistent sets). On the other hand, semantic approaches refer to measures employing non-classical semantics for that purpose. However, there are further measures which fall into neither (or both) categories. In the following, we will look at some measures from each of these categories.

4.1 Measures Based on Minimal Inconsistent Sets

A minimal inconsistent subset M of a knowledge base $\mathcal {K}$ represents the “essence” of a single conflict in $\mathcal {K}$. Naturally, a simple approach to measure inconsistency is to take the number of minimal inconsistent subsets as a measure.

Definition 6

([24]). The $\mathsf {MI}$-inconsistency measure $\mathcal {I}_{\mathsf {MI}}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as $\mathcal {I}_{\mathsf {MI}}(\mathcal {K}) =|\mathsf {MI}(\mathcal {K})|$ for $\mathcal {K}\in \mathbb {K}$.

The above measure complies with the postulates of consistency, monotony, and free-formula independence but fails to satisfy dominance and normalisation (although a normalised variant that suffers from other shortcomings can easily be defined). Table 2 below gives an overview on the compliance of the measures formally considered in this paper with the basic postulates from above, see [41] for proofs or references to proofs. The idea behind the $\mathsf {MI}$-inconsistency measure can be refined in several ways, taking e. g. the sizes of the individual minimal inconsistent sets and how they overlap into account [13, 25, 26]. One example being the following measure.

Definition 7

([24]). The $\mathsf {MI}^{c}$-inconsistency measure $\mathcal {I}_{\mathsf {MI^{C}}}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{\mathsf {MI^{C}}}(\mathcal {K})&= \sum _{M\in \mathsf {MI}(\mathcal {K})}\frac{1}{|M|} \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$.

The $\mathsf {MI}^{c}$-inconsistency measure takes also the sizes of the individual minimal inconsistent subsets into account. The intuition here is that larger minimal inconsistent subsets represent less inconsistency (as the conflict is more “hidden”) and small minimal inconsistent subsets represent more inconsistency (as it is more “apparent”).

Example 2

Consider again knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ from before defined via

$$\begin{aligned} \mathcal {K}_{1}&= \{\text {sunny}, \lnot \text {sunny}, \text {hot}, \lnot \text {hot}\} \\ \mathcal {K}_{2}&= \{\lnot \text {hot}, \text {sunny}, \text {sunny} \rightarrow \text {hot}, \text {humid}\} \end{aligned}$$

Here we have

$$\begin{aligned} \mathcal {I}_{\mathsf {MI}}(\mathcal {K}_{1})&= 2&\mathcal {I}_{\mathsf {MI}}(\mathcal {K}_{2})&=1\\ \mathcal {I}_{\mathsf {MI^{C}}}(\mathcal {K}_{1})&= 1&\mathcal {I}_{\mathsf {MI^{C}}}(\mathcal {K}_{2})&=1/3 \end{aligned}$$

Observe that, while $\mathcal {I}_{\mathsf {MI}}$ and $\mathcal {I}_{\mathsf {MI^{C}}}$ disagree on the exact values of the inconsistency in $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ they do agree on their order ($\mathcal {K}_{1}$ is more inconsistent than $\mathcal {K}_{2}$). This is not generally true, consider

$$\begin{aligned} \mathcal {K}_{8} =&\{a,\lnot a\} \\ \mathcal {K}_{9} =&\{a_{1}, \lnot a_{1} \vee b_{1}, \lnot b_{1} \vee c_{1}, \lnot \vee d_{1}, \lnot d_{1} \vee \lnot a_{1},\\&\,\,\, a_{2}, \lnot a_{2} \vee b_{2}, \lnot b_{2} \vee c_{2}, \lnot \vee d_{2}, \lnot d_{2} \vee \lnot a_{2}\} \end{aligned}$$

$$\begin{aligned} \mathcal {I}_{\mathsf {MI}}(\mathcal {K}_{8})&= 1&\mathcal {I}_{\mathsf {MI}}(\mathcal {K}_{9})&=2\\ \mathcal {I}_{\mathsf {MI^{C}}}(\mathcal {K}_{8})&= 1/2&\mathcal {I}_{\mathsf {MI^{C}}}(\mathcal {K}_{9})&=2/5 \end{aligned}$$

where $\mathcal {K}_{8}$ is less inconsistent than $\mathcal {K}_{9}$ according to $\mathcal {I}_{\mathsf {MI}}$ and the other way around for $\mathcal {I}_{\mathsf {MI^{C}}}$.

4.2 Measures Based on Non-classical Semantics

Measures based on minimal inconsistent subsets provide a formula-centric view on the matter of inconsistency [22]. If a formula (as a whole) is part of a conflict, it is taken into account for measuring inconsistency. Another possibility is to focus on propositions rather than formulas. Consider again the knowledge base $\mathcal {K}_{7}=\{a \wedge c, b\wedge \lnot c, \lnot a \vee \lnot b\}$ from Example 1 which possesses one minimal inconsistent subset $\{a \wedge c, b\wedge \lnot c\}$. However, it is clear that there is also a conflict involving the propositions a and b, which is not “detected” by measures based on minimal inconsistent subsets. Thus, another angle for measuring inconsistency consists in counting how many propositions participate in the inconsistency. A possible means for doing this is by relying on non-classical semantics. The contension measure [17] makes use of Priest’s logic of paradox, which has a paraconsistent semantics that we briefly recall now. A three-valued interpretation $\upsilon$ on $\mathsf {At}$ is a function $\upsilon :\mathsf {At}\rightarrow \{T, F, B\}$ where the values T and F correspond to the classical $\mathsf {true}$ and $\mathsf {false}$, respectively. The additional truth value B stands for both and is meant to represent a conflicting truth value for a proposition. The function $\upsilon$ is extended to arbitrary formulas as shown in Table 1. An interpretation $\upsilon$ satisfies a formula $\alpha$, denoted by $\upsilon \models ^{3}\alpha$ if either $\upsilon (\alpha )=T$ or $\upsilon (\alpha )=B$. Define $\upsilon \models ^{3}\mathcal {K}$ for a knowledge base $\mathcal {K}$ accordingly. Now inconsistency can be measured by seeking an interpretation $\upsilon$ that assigns B to a minimal number of propositions.

Definition 8

([17]). The contension inconsistency measure $\mathcal {I}_{c}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{c}(\mathcal {K})&= \min \{|\upsilon ^{-1}(B)\cap \mathsf {At}|\mid \upsilon \models ^{3} \mathcal {K}\} \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$.

Note that $\mathcal {I}_{c}$ is well-defined as for every knowledge $\mathcal {K}$ there is always at least one interpretation $\upsilon$ satisfying it, e. g., the interpretation that assigns B to all propositions.

Table 1. Truth tables for propositional three-valued logic.

A further approach—that is in contrast to $\mathcal {I}_{c}$ still formula-centric—is to make use of probability logic to define an inconsistency measure [27]. A probability function P on $\mathcal {L} (\mathsf {At})$ is a function $P:\varOmega (\mathsf {At})\rightarrow [0,1]$ with $\sum _{\omega \in \varOmega (\mathsf {At})}P(\omega )=1$. We extend P to assign a probability to any formula $\phi \in \mathcal {L} (\mathsf {At})$ by defining

$$\begin{aligned} P(\phi )&=\sum _{\omega \models \phi }P(\omega ) \end{aligned}$$

Let $\mathcal {P}(\mathsf {At})$ be the set of all those probability functions.

Definition 9

([27]). The $\eta$-inconsistency measure $\mathcal {I}_{\eta }:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{\eta }(\mathcal {K})&= 1-\max \{\xi \mid \exists P\in \mathcal {P}(\mathsf {At}):\forall \alpha \in \mathcal {K}:P(\alpha )\ge \xi \} \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$.

The measure $\mathcal {I}_{\eta }$ looks for a probability function P that maximises the minimum probability of all formulas in $\mathcal {K}$. The larger this probability the less inconsistent $\mathcal {K}$ is assessed (if there is a probability function assigning 1 to all formulas then $\mathcal {K}$ is obviously consistent).

Example 3

Consider again knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ from before defined via

$$\begin{aligned} \mathcal {K}_{1}&= \{\text {sunny}, \lnot \text {sunny}, \text {hot}, \lnot \text {hot}\} \\ \mathcal {K}_{2}&= \{\lnot \text {hot}, \text {sunny}, \text {sunny} \rightarrow \text {hot} , \text {humid}\} \end{aligned}$$

Here we have

$$\begin{aligned} \mathcal {I}_{c}(\mathcal {K}_{1})&= 2&\mathcal {I}_{c}(\mathcal {K}_{2})&=1\\ \mathcal {I}_{\eta }(\mathcal {K}_{1})&= 0.5&\mathcal {I}_{\eta }(\mathcal {K}_{2})&=1/3 \end{aligned}$$

where, in particular, $\mathcal {I}_{c}$ also agrees with $\mathcal {I}_{\mathsf {MI}}$ (see Example 2). Consider now

$$\begin{aligned} \mathcal {K}_{10}&= \{a,\lnot a\}&\mathcal {K}_{11}&= \{ a\wedge b \wedge c, \lnot a \wedge \lnot b\wedge \lnot c\} \end{aligned}$$

where

$$\begin{aligned} \mathcal {I}_{c}(\mathcal {K}_{1})&= 1&\mathcal {I}_{c}(\mathcal {K}_{2})&=3\\ \mathcal {I}_{\eta }(\mathcal {K}_{1})&= 0.5&\mathcal {I}_{\eta }(\mathcal {K}_{2})&=0.5\\ \mathcal {I}_{\mathsf {MI}}(\mathcal {K}_{1})&= 1&\mathcal {I}_{c}(\mathcal {K}_{2})&=1 \end{aligned}$$

So $\mathcal {I}_{c}$ looks inside formulas to determine the severity of inconsistency.

While $\mathcal {I}_{c}$ makes use of paraconsistent logic and $\mathcal {I}_{\eta }$ of probability logic other logics can be used for that purpose as well. In [38] a general framework is established that allows to plugin any many-valued logic (such as fuzzy logic) to define inconsistency measures.

4.3 Further Measures

There are further ways to define inconsistency measures that do not fall strictly in one of the two paradigms above. We have a look at some now.

A simple approach to obtain a more proposition-centric measure (as $\mathcal {I}_{c}$) while still relying on minimal inconsistent sets is the following measure.

Definition 10

([44]). The mv inconsistency measure $\mathcal {I}_{mv}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{mv}(\mathcal {K})&=\frac{|\bigcup _{M\in \mathsf {MI}(\mathcal {K})}\mathsf {At}(M)|}{|\mathsf {At}(\mathcal {K})|} \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$.

In other words, $\mathcal {I}_{mv}(\mathcal {K})$ is the ratio of the number of propositions that appear in at least one minimal inconsistent set and the number of all propositions.

Another approach that makes no use of either minimal inconsistent sets or non-classical semantics is the following one. A subset $H\subseteq \varOmega (\mathsf {At})$ is called a hitting set of $\mathcal {K}$ if for every $\phi \in \mathcal {K}$ there is $\omega \in H$ with $\omega \models \phi$.

Definition 11

([37]). The hitting-set inconsistency measure $\mathcal {I}_{hs}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ is defined as

$$\begin{aligned} \mathcal {I}_{hs}(\mathcal {K})&= \min \{|H| \mid H \text { is a hitting set of }\mathcal {K}\} - 1 \end{aligned}$$

for $\mathcal {K}\in \mathbb {K}$ with $\min \emptyset = \infty$.

So $\mathcal {I}_{hs}$ seeks a minimal number of (classical) interpretations such that for each formula there is at least one model in this set.

Example 4

Consider again knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ from before defined via

$$\begin{aligned} \mathcal {K}_{1}&= \{\text {sunny}, \lnot \text {sunny}, \text {hot}, \lnot \text {hot}\} \\ \mathcal {K}_{2}&= \{\lnot \text {hot}, \text {sunny}, \text {sunny} \rightarrow \text {hot}, \text {humid}\} \end{aligned}$$

Here we have

$$\begin{aligned} \mathcal {I}_{mv}(\mathcal {K}_{1})&= 1&\mathcal {I}_{mv}(\mathcal {K}_{2})&=2/3 \\ \mathcal {I}_{hs}(\mathcal {K}_{1})&= 1&\mathcal {I}_{hs}(\mathcal {K}_{2})&=1 \end{aligned}$$

Moreover, Grant and Hunter [18] define new families of inconsistency measures based on distances of classical interpretations to being models of a knowledge base. Besnard [4] counts how many propositions have to be forgotten—i. e. removed from the underlying signature of the knowledge base—to turn an inconsistent knowledge base into a consistent one.

Table 2. Compliance of inconsistency measures with rationality postulates consistency (CO), normalisation (NO), monotony (MO), free-formula independence (IN), and dominance (DO)

5 Beyond Propositional Logic

While most work in the field of inconsistency measurement is concerned with using propositional logic as the knowledge representation formalism, there are some few works, which consider measuring inconsistency in other logics. We will have a brief overview on some of these works now, see [19] for some others.

5.1 First-Order and Description Logic

In [16], first-order logic is considered as the base logic. Allowing for objects and quantification brings new challenges to measuring inconsistency as one should distinguish in a more fine-grained manner how much certain formulas contribute to inconsistency. For example, a formula $\forall X: bird(X)\rightarrow flies(X)$—which models that all birds fly—is probably the culprit of some inconsistency in any knowledge base. However, depending on how many objects actually satisfy/violate the implication, the severity of the inconsistency of the overall knowledge base may differ (compare having a knowledge base with 10 flying birds and 1 non-flying bird to a knowledge base with 1000 flying birds and 1 non-flying bird). [16] address this challenge by proposing some new inconsistency measures for first-order logic.

There are also several works—see e. g. [29, 45]—that deal with measuring inconsistency in ontologies formalised in certain description logics.

5.2 Probabilistic Logic

In probabilistic logic, classical propositional formulas are augmented by probabilities yielding statements such as $(\text {sunny}\wedge \text {humid}) [0.7]$ meaning “it will be sunny and humid with probability 0.7”. Semantics are given to such a logic by means of probability distributions over sets of propositions. Inconsistencies in modelling with such a logic can appear, in particular, when “the numbers do not add up”. In addition to the previous formula consider $(\text {humid}) [0.5]$ which states that “it will be humid with probability 0.5”. Both formulas together are inconsistent as it cannot be the case the probability of being humid is at least 0.7 (which is implied by the first formula) and 0.5 at the same time. Measures for probabilistic logic, see the recent survey [12], focus on measuring distances of the probabilities of the formulas to a consistent state or propose weaker notions of satisfying probability distributions and measure distances between those and classical probability distributions.

5.3 Non-monotonic Logics

In non-monotonic logics, inconsistency in a knowledge base may be resolved by adding formulas. Consider e. g. the following rules in answer set programming [8]: $\{b\leftarrow , \lnot b\leftarrow \textsf {not}~a\}$. Informally, these rules state that b is the case and that if a is not the case, $\lnot b$ is the case. The negation “not” is a negation-as-failure and the whole program is inconsistent as both b and $\lnot b$ can be derived. However, adding the rule $a\leftarrow$ stating that a is the case, makes the program consistent again as the second rule is not applicable any more. An implication of this observation is that consistent programs may have inconsistent subsets, which make the application of classical measures based on minimal inconsistent sets useless. In [9] a stronger notion for minimal inconsistent sets for non-monotonic logics is proposed that is used for inconsistency measurement in [43], and, in particular, for answer set programming in [42].

6 Summary and Discussion

In this paper we gave a brief overview on the field of inconsistency measurement. We motivated the field, discussed several rationality postulates for concrete measures, and surveyed some of its basic approaches. We also gave a short overview on approaches that use formalisms other than propositional logic as the base knowledge representation formalism.

Inconsistency measures can be used to compare different formalisations of knowledge, to help debug flawed knowledge bases, and guide automatic repair methods. For example, inconsistency measures have been used to estimate reliability of agents in multi-agent systems [11], to allow for inconsistency-tolerant reasoning in probabilistic logic [33], or to monitor and maintain quality in database settings [14].

Inconsistency measurement is a problem that is not easily defined in a formal manner. Many approaches have been proposed, in particular in recent years, each taking a different perspective on this issue. We discussed rationality postulates as a means to prescribe general desirable behaviour of an inconsistency measure and there have also been a lot of proposals in the recent past, [41] lists an additional 13 compared to the five postulates we discussed here. Many of them are mutually exclusive, describe orthogonal requirements, and are not generally accepted in the community. Besides rationality postulates, other dimensions for comparing inconsistency measures are their expressivity and their computational complexity. Expressivity [36, 41] refers to the capability of an inconsistency to differentiate between many inconsistent knowledge base. For example, the drastic inconsistency measure—which assigns 1 to every inconsistent knowledge base—has minimal expressivity as it can only differentiate between consistency and inconsistency. On the other hand, the contension measure $\mathcal {I}_{c}$ can differentiate up to $n+1$ different states of inconsistency, where n is the number of propositions appearing in the signature. As for computational complexity, it is clear that all problems related to inconsistency measurement are coNP-hard, as the identification of unsatisfiability is always part of the definition. In fact, the decision problem of deciding whether a certain value is a lower bound for the actual inconsistency value of a given inconsistency measure, is coNP-complete for many measures such as $\mathcal {I}_{c}$ [35, 41]. However, the problem is harder for other measures, e. g., the same problem for $\mathcal {I}_{mv}$ is already $\varSigma ^{p}_{2}$-complete [44].

This paper points to a series of open research questions that may be interesting to pursue. For example, the discussion on the “right” set of postulates is not over. What is needed is a characterising definition of an inconsistency measure using few postulates, as the entropy is characterised by few simple properties as an information measure. However, we are currently far away from a complete understanding of what an inconsistency measure constitutes. Moreover, the algorithmic study of inconsistency measurement has (almost) not been investigated at all. Although straightforward prototype implementations of most measures are available⁵, those implementations do not necessarily optimise runtime performance. Only a few papers [2, 30,31,32, 37] have addressed this challenge previously, mainly by developing approximation algorithms. Besides more work on approximation algorithms, another venue for future work is also to develop algorithms that work effectively on certain language fragments—such as certain description logics—and thus may work well in practical applications.