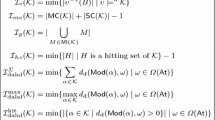An Experimental Study on the Behaviour of Inconsistency Measures

Abstract

We apply a selection of 19 inconsistency measures from the literature on artificially generated knowledge bases and study the distribution of their values and their pairwise correlation. This study augments previous analytical evaluations on the expressivity and the pairwise incompatibility of these measures and our findings show that (1) many measures assign only few distinct values to many different knowledge bases, and (2) many measures, although founded on different theoretical concepts, correlate significantly.

1 Introduction

An inconsistency measure $\mathcal {I}$ is a function that assigns to a knowledge base $\mathcal {K}$ (usually assumed to be formalised in propositional logic) a non-negative real value $\mathcal {I}(\mathcal {K})$ such that $\mathcal {I}(\mathcal {K})=0$ iff $\mathcal {K}$ is consistent and larger values of $\mathcal {I}(\mathcal {K})$ indicate “larger” inconsistency in $\mathcal {K}$ [3, 5, 12]. Thus, each inconsistency measure $\mathcal {I}$ formalises a notion of a degree of inconsistency and a lot of different concrete approaches have been proposed so far, see [11,12,13] for some surveys. The quest for the “right” way to measure inconsistency is still ongoing and many (usually controversial) rationality postulates to describe the desirable behaviour of an inconsistency measure have been proposed so far [2, 12].

Our study aims at providing a new perspective on the analysis of existing approaches to inconsistency measurement by experimentally analysing the behaviour of inconsistency measures. More precisely, our study provides a quantitative analysis of two aspects of inconsistency measures:

• A1 the distribution of inconsistency values on actual knowledge bases, and

• A2 the correlation of different inconsistency measures.

Regarding the first item, [11] investigated the theoretical expressivity of inconsistency measures, i. e., the number of different inconsistency values a measure attains when some dimension of the knowledge base is bounded (such as the number of formulas or the size of the signature). One result in [11] is that e. g. the measure $\mathcal {I}^{\varSigma }_{\text {dalal}}$ (see Sect. 3) has maximal expressivity and the number of different inconsistency values is not bounded if only one of these two dimensions is bounded. However, [11] does not investigate the distribution of inconsistency values. It may be the case that, although a measure can attain many different values, most inconsistent knowledge bases are clustered on very few inconsistency values. Regarding the second item, previous works have shown—see [12] for an overview—that all inconsistency measures developed so far are “essentially” different. More precisely, for each pair of measures one can find a property that is satisfied by one measure but not by the other. Moreover, for each pair of inconsistency measures one can find knowledge bases that are ordered different wrt. their inconsistency. However, until now it has not been investigated how “significant” the difference between measures actually is. It may be the case that two measures order all but just a very few knowledge bases differently (or the other way around). In order to analyse these two aspects we applied 19 different inconsistency measures from the literature on artificially generated knowledge bases and performed a statistical analysis on the results. After a brief review of necessary preliminaries in Sect. 2 and the considered inconsistency measures in Sect. 3, we provide some details on our experiments and our findings in Sect. 4 and conclude in Sect. 5.

2 Preliminaries

Let $\mathsf {At}$ be some fixed propositional signature, i. e., a (possibly infinite) set of propositions, and let $\mathcal {L}(\mathsf {At})$ be the corresponding propositional language constructed using the usual connectives $\wedge$ (and), $\vee$ (or), and $\lnot$ (negation).

Definition 1

A knowledge base $\mathcal {K}$ is a finite set of formulas $\mathcal {K}\subseteq \mathcal {L}(\mathsf {At})$. Let $\mathbb {K}$ be the set of all knowledge bases.

If X is a formula or a set of formulas we write $\mathsf {At}(X)$ to denote the set of propositions appearing in X. Semantics to a propositional language is given by interpretations and an interpretation $\omega$ on $\mathsf {At}$ is a function $\omega :\mathsf {At}\rightarrow \{\mathsf {true},\mathsf {false}\}$. Let $\varOmega (\mathsf {At})$ denote the set of all interpretations for $\mathsf {At}$. An interpretation $\omega$ satisfies (or is a model of) an atom $a\in \mathsf {At}$, denoted by $\omega \models a$, if and only if $\omega (a)=\mathsf {true}$. The satisfaction relation $\models$ is extended to formulas in the usual way.

For $\varPhi \subseteq \mathcal {L}(\mathsf {At})$ we also define $\omega \models \varPhi$ if and only if $\omega \models \phi$ for every $\phi \in \varPhi$. Define furthermore the set of models $\mathsf {Mod}(X)=\{\omega \in \varOmega (\mathsf {At})\mid \omega \models X\}$ for every formula or set of formulas X. By abusing notation, a formula or set of formulas $X_{1}$ entails another formula or set of formulas $X_{2}$, denoted by $X_{1}\models X_{2}$, if $\mathsf {Mod}(X_{1})\subseteq \mathsf {Mod}(X_{2})$. Two formulas or sets of formulas $X_{1}, X_{2}$ are equivalent, denoted by $X_{1}\equiv X_{2}$, if $\mathsf {Mod}(X_{1})=\mathsf {Mod}(X_{2})$. If $\mathsf {Mod}(X)=\emptyset$ we also write $X\models \perp$ and say that X is inconsistent.

3 Inconsistency Measures

Let $\mathbb {R}^{\infty }_{\ge 0}$ be the set of non-negative real values including $\infty$. Inconsistency measures are functions $\mathcal {I}:\mathbb {K}\rightarrow \mathbb {R}^{\infty }_{\ge 0}$ that aim at assessing the severity of the inconsistency in a knowledge base $\mathcal {K}$. The basic idea is that the larger the inconsistency in $\mathcal {K}$ the larger the value $\mathcal {I}(\mathcal {K})$. We refer to [11,12,13] for surveys.

The formal definitions of the considered inconsistency measures can be found in Fig. 1 while the necessary notation for understanding these measures follows below. Please see the above-mentioned surveys and the original papers referenced therein for explanations and examples.

Fig. 1.

Definitions of the considered measures

A set $M\subseteq \mathcal {K}$ is called minimal inconsistent subset (MI) of $\mathcal {K}$ if $M\models \perp$ and there is no $M'\subset M$ with $M'\models \perp$. Let $\mathsf {MI}(\mathcal {K})$ be the set of all MIs of $\mathcal {K}$. Let furthermore $\mathsf {MC}(\mathcal {K})$ be the set of maximal consistent subsets of $\mathcal {K}$, i. e., $\mathsf {MC}(\mathcal {K})=\{\mathcal {K}'\subseteq \mathcal {K}\mid \mathcal {K}'\not \models \perp \wedge \forall \mathcal {K}''\supsetneq \mathcal {K}':\mathcal {K}''\models \perp \}$, and let $\mathsf {SC}(\mathcal {K})$ be the set of self-contradictory formulas of $\mathcal {K}$, i. e., $\mathsf {SC}(\mathcal {K})=\{\phi \in \mathcal {K}\mid \phi \models \perp \}$.

A probability function P is of the form $P:\varOmega (\mathsf {At})\rightarrow [0,1]$ with $\sum _{\omega \in \varOmega (\mathsf {At})}P(\omega )=1$. Let $\mathcal {P}(\mathsf {At})$ be the set of all those probability functions and for a given probability function $P\in \mathcal {P}(\mathsf {At})$ define the probability of an arbitrary formula $\phi$ via $P(\phi )=\sum _{\omega \models \phi }P(\omega )$.

A three-valued interpretation $\upsilon$ on $\mathsf {At}$ is a function $\upsilon :\mathsf {At}\rightarrow \{T, F, B\}$ where the values T and F correspond to the classical $\mathsf {true}$ and $\mathsf {false}$, respectively. The additional truth value B stands for both and is meant to represent a conflicting truth value for a proposition. Taking into account the truth order $\prec$ defined via $T\prec B \prec F$, an interpretation $\upsilon$ is extended to arbitrary formulas via $\upsilon (\phi _{1}\wedge \phi _{2})=\min _{\prec }(\upsilon (\phi _{1}),\upsilon (\phi _{2}))$, $\upsilon (\phi _{1}\vee \phi _{2})=\max _{\prec }(\upsilon (\phi _{1}),\upsilon (\phi _{2}))$, and $\upsilon (\lnot T)=F$, $\upsilon (\lnot F)=T$, $\upsilon (\lnot B)=B$. An interpretation $\upsilon$ satisfies a formula $\alpha$, denoted by $\upsilon \models ^{3}\alpha$ if either $\upsilon (\alpha )=T$ or $\upsilon (\alpha )=B$.

The Dalal distance $d_{\text {d}}$ is a distance function for interpretations in $\varOmega (\mathsf {At})$ and is defined as $d(\omega ,\omega ')=|\{a \in \mathsf {At}\mid \omega (a)\ne \omega '(a)\}|$ for all $\omega ,\omega '\in \varOmega (\mathsf {At})$. If $X\subseteq \varOmega (\mathsf {At})$ is a set of interpretations we define $d_{\text {d}}(X,\omega )=\min _{\omega '\in X}d_{\text {d}}(\omega ',\omega )$ (if $X=\emptyset$ we define $d_{\text {d}}(X,\omega )=\infty$). We consider the inconsistency measures $\mathcal {I}^{\varSigma }_{\text {dalal}}$, $\mathcal {I}^{\max }_{\text {dalal}}$, and $\mathcal {I}^{\text {hit}}_{\text {dalal}}$ from [4] but only for the Dalal distance. Note that in [4] these measures were considered for arbitrary distances and that we use a slightly different but equivalent definition of these measures.

For every knowledge base $\mathcal {K}$, $i=1,\ldots ,|\mathcal {K}|$ define $\mathsf {MI}^{(i)}(\mathcal {K})=\{M\in \mathsf {MI}(\mathcal {K})\mid |M|=i\}$ and $\mathsf {CN}^{(i)}(\mathcal {K})=\{C\subseteq \mathcal {K}\mid |C|=i \wedge C\not \models \perp \}$. Furthermore define $R_i(\mathcal {K})=0$ if $|\mathsf {MI}^{(i)}(\mathcal {K})|+|\mathsf {CN}^{(i)}(\mathcal {K})|=0$ and otherwise $R_i(\mathcal {K})=|\mathsf {MI}^{(i)}(\mathcal {K})|/(|\mathsf {MI}^{(i)}(\mathcal {K})|+|\mathsf {CN}^{(i)}(\mathcal {K})|)$. Note that the definition of $\mathcal {I}_{D_{f}}$ in Table 1 is only one instance of the family studied in [9], other variants can be obtained by different ways of aggregating the values $R_i(\mathcal {K})$.

A set of maximal consistent subsets $\mathcal {C}\subseteq \mathsf {MC}(\mathcal {K})$ is called an $\mathsf {MC}$-cover [1] if $\bigcup _{C\in \mathcal {C}}C =K$. An $\mathsf {MC}$-cover $\mathcal {C}$ is normal if no proper subset of $\mathcal {C}$ is an $\mathsf {MC}$-cover. A normal $\mathsf {MC}$-cover is maximal if $\lambda (\mathcal {C}) = |\bigcap _{C\in \mathcal {C}}C|$ is maximal for all normal $\mathsf {MC}$-covers.

For a formula $\phi$ let $\phi [a_{1}, i_{1} \rightarrow \psi _{1}; \ldots , a_{k}, i_{k} \rightarrow \psi _{k}]$ denote the formula $\phi$ where the $i_{j}$th occurrence of the proposition $a_{j}$ is replaced by the formula $\psi _{j}$, for all $j=1,\ldots ,k$.

A set $\{K_{1},\ldots , K_{n}\}$ of pairwise disjoint subsets of $\mathcal {K}$ is called a conditional independent MUS (CI) partition of $\mathcal {K}$ [6], iff each $K_{i}$ is inconsistent and $\mathsf {MI}(K_{1}\cup \ldots \cup K_{n})$ is the disjoint union of all $\mathsf {MI}(K_{i})$.

An ordered set $\mathcal {P}=\{P_{1},\ldots , P_{n}\}$ with $P_{i}\subseteq \mathsf {MI}(\mathcal {K})$ for $i=1,\ldots , n$ is called an ordered CSP-partition [7] of $\mathsf {MI}(\mathcal {K})$ if 1.) $\mathsf {MI}(\mathcal {K})$ is the disjoint union of all $P_{i}$ for $i=1,\ldots , n$, 2.) each $P_{i}$ is a conditional independent MUS partition of $\mathcal {K}$ for $i=1,\ldots , n$, and 3.) $|P_{i}|\ge |P_{i+1}|$ for $i=1,\ldots , n-1$. For such $\mathcal {P}$ define furthermore $\mathcal {W}(\mathcal {P})=\sum _{i=1}^{n}|P_{i}|/i$.

4 Experiments

In the following, we give some details on our experiments, the evaluation methodology, and our findings.

4.1 Knowledge Base Generation

Due to the lack of a dataset of real-world knowledge bases with a significantly rich profile of inconsistencies, we used artificially generated knowledge bases. In order to avoid biasing our study on random instances of a specific probabilistic model for knowledge base generation, we developed an algorithm that enumerates all syntactically different knowledge bases with increasing size and considered the first 188900 bases generated this way. For example, the first five knowledge bases generated this way are $\emptyset , \{x_{1}\}, \{\lnot x_{1}\}, \{\lnot \lnot x_{1}\}, \{x_{1},x_{2}\}$ and, e. g., number 72793 is $\{x_{1}, x_{2}, \lnot x_{2}, \lnot (\lnot x_{2}\wedge \lnot \lnot x_{2})\}$. From the 188900 generated knowledge bases, 127814 are consistent and 61086 are inconsistent. For the remainder of this paper, let $\hat{K}$ denote the set of all 188900 knowledge bases and let $\hat{K}^{\perp }\subseteq \hat{K}$ be only the inconsistent ones.

The implementation¹ for this algorithm is available in the Tweety project² [10]. The generated knowledge bases and their inconsistency values wrt. each of considered inconsistency measures are available online³.

4.2 Evaluation Measures

In order to evaluate A1, we apply the entropy on the distribution of inconsistency values of each measure. For $K\subseteq \mathbb {K}$ let $\mathcal {I}(K)=\{\mathcal {I}(\mathcal {K})\mid \mathcal {K}\in K\}$ denote the image of K wrt. $\mathcal {I}$.

Definition 2

Let K be a set of knowledge bases and $\mathcal {I}$ be an inconsistency measure. The entropy $H_{K}(\mathcal {I})$ of $\mathcal {I}$ wrt. K is defined via

$$\begin{aligned} H_{K}(\mathcal {I})&= -\sum _{x\in \mathcal {I}(K)} \frac{|\mathcal {I}^{-1}(x)|}{|K|}\ln \frac{|\mathcal {I}^{-1}(x)|}{|K|} \end{aligned}$$

where $\ln x$ denotes the natural logarithm with $0\ln 0=0$.

For example, if a measure $\mathcal {I}^{*}$ assigns to a set $K^{*}$ of 10 knowledge bases 5 times the value X, 3 times the value Y, and 2 times the value Z, we have

$$\begin{aligned} H_{K^{*}}(\mathcal {I}^*)&= - \frac{5}{10}\ln \frac{5}{10}-\frac{3}{10}\ln \frac{3}{10}-\frac{2}{10}\ln \frac{2}{10}\approx 1.03 \end{aligned}$$

The interpretation behind the entropy here is that a larger value $H_{K}(\mathcal {I})$ indicates a more uniform distribution of the inconsistency values on elements of K, a value $H_{K}(\mathcal {I})=0$ indicates that all elements are assigned the same inconsistency value. Thus, the larger $H_{K}(\mathcal {I})$ the “more use” the measure makes of its available inconsistency values.

Table 1. Entropy values of the investigated measures wrt. $\hat{K}^{\perp }$ (rounded to two decimals and sorted by increasing entropy).

Table 2. Correlation coefficients $C_{\hat{K}^{\perp }}(\cdot ,\cdot )$ of the investigated measures wrt. $\hat{K}^{\perp }$ (rounded to two decimals).

In order to evaluate A2, we use a specific notion of a correlation coefficient. For two measures $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ and two knowledge bases $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$ we say that $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ are order-compatible wrt. $\mathcal {K}_{1}$ and $\mathcal {K}_{2}$, denoted by $\mathcal {I}_{1}\sim _{\mathcal {K}_{1},\mathcal {K}_{2}}\mathcal {I}_{2}$ iff

$$\begin{aligned}&\mathcal {I}_{1}(\mathcal {K}_{1})> \mathcal {I}_{1}(\mathcal {K}_{2}) \wedge \mathcal {I}_{2}(\mathcal {K}_{1})> \mathcal {I}_{2}(\mathcal {K}_{2})\\ \text {or}~~~&\mathcal {I}_{1}(\mathcal {K}_{1})< \mathcal {I}_{1}(\mathcal {K}_{2}) \wedge \mathcal {I}_{2}(\mathcal {K}_{1})< \mathcal {I}_{2}(\mathcal {K}_{2})\\ \text {or}~~~&\mathcal {I}_{1}(\mathcal {K}_{1})= \mathcal {I}_{1}(\mathcal {K}_{2}) \wedge \mathcal {I}_{2}(\mathcal {K}_{1})= \mathcal {I}_{2}(\mathcal {K}_{2}) \end{aligned}$$

Let $\Vert A\Vert$ be the indicator function, which is defined as $\Vert A\Vert =1$ iff A is true and $\Vert A\Vert =0$ otherwise.

Definition 3

Let K be a set of knowledge bases and $\mathcal {I}_{1},\mathcal {I}_{2}$ be two inconsistency measures. The correlation coefficient $C_{K}(\mathcal {I}_{1},\mathcal {I}_{2})$ of $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ wrt. K is defined via

$$\begin{aligned} C_{K}(\mathcal {I}_{1},\mathcal {I}_{2})&= \frac{\sum _{\mathcal {K},\mathcal {K}'\in K, \mathcal {K}\ne \mathcal {K}'}\Vert \mathcal {I}_{1}\sim _{\mathcal {K},\mathcal {K}'}\mathcal {I}_{2}\Vert }{|K|(|K|-1)} \end{aligned}$$

In other words, $C_{K}(\mathcal {I}_{1},\mathcal {I}_{2})$ gives the ratio of how much $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ agree on the inconsistency order of any pair of knowledge bases from K.⁴ Observe that $C_{K}(\mathcal {I}_{1},\mathcal {I}_{2})=C_{K}(\mathcal {I}_{2},\mathcal {I}_{1})$.

4.3 Results

Tables 1 and 2 show the results of analysing the considered measures on $\hat{K}^{\perp }$ wrt. the two evaluation measures from before⁵.

Regarding A1, it can be seen that $\mathcal {I}_{d}$ has minimal entropy (by definition). However, also measures $\mathcal {I}^{\text {hit}}_{\text {dalal}}$ and $\mathcal {I}_{\text {CC}}$ and to some extent most of the other measures are quite indifferent in assigning their values. For example, out of 61086 inconsistent knowledge bases, $\mathcal {I}_{\text {CC}}$ assigns to 58523 of them the same value 1. On the other hand, measure $\mathcal {I}_{D_{f}}$ has maximal entropy among the considered measures.

Regarding A2, we can observe some surprising correlations between measures, even those which are based on different concepts. For example, we have $C_{\hat{K}^{\perp }}(\mathcal {I}^{\max }_{\text {dalal}},\mathcal {I}_{hs})\approx 0.99$ indicating a high correlation between $\mathcal {I}^{\max }_{\text {dalal}}$ and $\mathcal {I}_{hs}$ although $\mathcal {I}^{\max }_{\text {dalal}}$ is defined using distances and $\mathcal {I}_{hs}$ is defined using hitting sets. Equally high correlations can be observed between the three measures $\mathcal {I}_{\mathsf {MI}}$, $\mathcal {I}_{\text {CSP}}$, and $\mathcal {I}_{\text {is}}$. Further high correlations (e. g. above 0.8) can be observed between many other measures. On the other hand, the measure $\mathcal {I}_{D_{f}}$ has (on average) the smallest correlation to all other measures, backing up the observation from before.

5 Conclusion

Our experimental analysis showed that many existing measures have low entropy on the distribution of inconsistency values and correlate significantly in their ranking of inconsistent knowledge bases. A web application for trying out all the discussed inconsistency measures can be found on the website of TweetyProject⁶, cf. [10]. Most of these measures have been implemented using naive algorithms and research on the algorithmic issues of inconsistency measure is still desirable future work, see also [13].