Abstract
We survey some recent results on traveling waves and pattern formation in spatially discrete bistable reaction-diffusion equations. We start by recalling several classic results concerning the existence, uniqueness and stability of travelling wave solutions to the discrete Nagumo equation with nearest-neighbour interactions, together with the Fredholm theory behind some of the proofs. We subsequently discuss extensions involving wave connections between periodic equilibria, long-range interactions and planar lattices. We show how some of the results can be extended to the two-component discrete FitzHugh–Nagumo equation, which can be analyzed using singular perturbation theory. We conclude by studying the behaviour of the Nagumo equation when discretization schemes are used that involve both space and time, or that are non-uniform but adaptive in space.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The purpose of this article is to survey recent results concerning the pattern forming properties of spatially discrete reaction diffusion equations. Our guiding example will be the Nagumo lattice differential equation (LDE)
posed on \(j\in \mathbb {Z}\), with the bistable cubic nonlinearity
However, we also consider variants of this LDE that involve planar lattices, inhomogeneous diffusion coefficients, long-range interactions and additional components. Furthermore, we discuss the consequences of replacing the time-derivative in (1) by appropriate discretizations, which leads to difference equations in both space and time.
The recurring theme throughout this paper is that the discrete nature of the model (1) allows it to exhibit a much richer class of behaviour than its continuous counterpart, the Nagumo PDE
Indeed, we will explore the profound effects that different discretization choices for the Laplacian can have on the dynamical behaviour of the underlying systems. In fact, important differences already appear at the level of the equilibrium solutions.
Bistable systems The pair of stable equilibria for the nonlinearity g can be used to represent material phases or biological species that compete for dominance in a spatial domain [5]. The high frequency oscillations caused by this bistability are damped by the diffusion term in (3), which leads to interesting pattern forming behaviour. In particular, solutions generally develop interface layers that separate the spatial domain into regions governed by the two stable phases [3, 112]. The evolution of these interfaces can be seen as a desingularized version of the mean curvature flow [2, 66].
The PDE (3) has served as a prototype system for the understanding of many basic concepts at the heart of dynamical systems theory. An important role is reserved for travelling wave solutions, which can be written as
and hence provide a mechanism by which one of the two stable phases can invade the spatial domain. Such pairs \((c,\varPhi )\) must satisfy the travelling wave ODE
which admits the explicit solutions
These special solutions play a key role in the dynamics of the full PDE (3). Indeed, the classical work by Fife and McLeod [72] shows that these waves are stable under a broad range of perturbations that need not be small.
These pairs \((c, \varPhi )\) can also be interpreted as solutions to the planar Nagumo PDE
by writing
This is a direct consequence of the isotropy of the Laplacian, which causes \(\zeta \) to drop out from the resulting wave equation.
These planar waves are also stable [17, 111], but the underlying analysis is much more subtle as deformations of the wave interface decay at an algebraic rate; see Sect. 4. The seminal work by Weinberger [6] uses these planar waves as building blocks to study the speed at which sufficiently large but compact sets of the favourable species spread throughout the domain.
Spatially discrete systems For many physical phenomena such as crystal growth in materials [25], the formation of fractures in elastic bodies [146] and the motion of dislocations [32] and domain walls [52] through crystals, the discreteness and the topology of the underlying spatial domain both have a major impact on the dynamical behaviour. For example, the spreading of auxin through plant leaves depends crucially on the active PIN-induced transport through the cell-membranes [129]. Peierls–Nabarro barriers typically prevent small defects from spreading through discrete media, but can be eliminated by carefully tuning system parameters [46]. Recent experiments show that even light waves can be trapped inside well-designed photonic lattices [131, 156].
Motivated by these considerations, LDEs have been used to describe a wide range of propagation phenomena in spatially discrete systems. Examples include the propagation of electrical signals through transmission lines [63] and myelinated nerve fibres [115], the formation of compression waves through Hertzian chains of elastic beads [144], the occurrence of denaturation bubbles in strands of DNA [47] and the self-trapping of wave packets in coupled optical waveguides [121].
Bistable discrete reaction-diffusion systems such as (1) have been used to describe action potentials in myelinated nerve fibers [115], phase transitions in Ising models [12] and predator-prey interactions in patchy environments [145]. They were even implemented on circuit boards in order to develop fast pattern recognition algorithms in image processing [41, 42].
The non-local diffusion in (1) introduces a natural length scale into applications and breaks the continuous translational symmetry of \(\mathbb {R}\). The coupling with the bistable nonlinearity leads to a wide range of interesting behaviour that we explore in this paper. On the other hand, (1) still admits a comparison principle, which in some cases allows global effects to be captured rigorously. For these reasons, (1) has served as a prototype system to explore the effects of non-locality and spatial discreteness.
Spatially discrete travelling waves Substituting the travelling wave ansatz
into the LDE (1), one arrives at the system
Our main interest here is in connections between the two stable equilibria of g, which leads to the boundary conditions
No explicit solutions are known to exist for this wave equation. However, this changes if the cubic g is replaced by suitable specially constructed nonlinearities [1] or if the nonlinear term in the LDE (1) is allowed to involve the values of u at multiple lattice sites [9, 53, 76, 116, 148]. For example, the LDE
admits the explicit solutions
A useful procedure that has been widely used to gain insight into the behaviour of system such as (10) is to replace the cubic g by the discontinuous piecewise linear ‘caricature’
This allows linear techniques such as the Fourier transform to be applied. The resulting expressions for \(\varPhi \) involve explicit Fourier sums that allow interesting conclusions to be extracted. These results have often helped to guide the exploration of systems with smooth nonlinearities. In Sect. 3.3 we discuss an analysis of this type for a version of (1) that includes next-to-nearest-neighbour couplings. Earlier results of this type can be found in [27, 56, 57, 62, 67, 91, 151,152,153].
Returning to (10), we refer the reader to Sect. 2.2 for an overview of the different types of techniques that can be used to obtain the existence of travelling waves. For now, we simply note that the comparison principle can be used [35, 126] to show that c is uniquely determined by the detuning parameter a. However, the character of (10) depends crucially on whether c vanishes or not. Indeed, the continuous translational symmetry of \(\mathbb {R}\) is broken by the transition \(\mathbb {R}\rightarrow \mathbb {Z}\), causing the wavespeed c to act in (10) as a singular parameter. It is therefore natural to discuss the two cases \(c =0\) and \(c \ne 0\) separately.
Pinned waves For \(c = 0\) one can restrict the spatial variable in (10) to the integers and look for solutions \(\varPhi : \mathbb {Z}\rightarrow \mathbb {R}\). In fact, the travelling wave system (10) reduces to the difference equation
upon writing \(\big (\varPhi _j, \varPhi _{j+1} \big ) = (r_j, s_j)\). The fixed points of this system are (0, 0), (a, a) and (1, 1). In particular, the boundary conditions (11) mean that for any \(j \in \mathbb {Z}\), the pair \((\varPhi _j, \varPhi _{j+1})\) lies in the intersection of the stable manifold \(\mathcal {W}^s(1,1)\) and the unstable manifold \(\mathcal {W}^u(0,0)\) associated to (15).
The symmetry of the cubic at \(a = \frac{1}{2}\) allows us to apply a result by Qin and Xiao [134, Theorem 2.7] and conclude that (10)–(11) admits (at least) two solutions
These solutions are referred to as site-centered and bond-centered, since they are point symmetric around \((0, \frac{1}{2})\) respectively \((\frac{1}{2}, \frac{1}{2})\). In particular, the intersection \(\mathcal {W}^s(1,1) \cap \mathcal {W}^u(0,0)\) is non-empty and contains (at least) the two families \((\varPhi ^{(s)}_j, \varPhi ^{(s)}_{j+1})\) and \((\varPhi ^{(u)}_j, \varPhi ^{(u)}_{j+1})\).
If these intersections are transverse, both solutions \(\varPhi ^{(s)}\) and \(\varPhi ^{(b)}\) will persist as pinned waves for \(a \approx \frac{1}{2}\). It is then natural to expect that these branches coalesce and terminate in a saddle–node bifurcation at \(a = a_{\pm }\); see panels (i) and (ii) in Fig. 1. In particular, this would mean that \(c(a) = 0\) for a in the nontrivial interval \([a_-, a_+]\).
This phenomenon is referred to as propagation failure and has been observed among a wide class of discrete systems. In fact, Hoffman and Mallet-Paret show [88] that it is ‘generic’ in a suitable sense by establishing a Melnikov condition on the nonlinearity in (1) that is sufficient to guarantee its occurrence. For the cubic nonlinearity that we consider here, early results by Keener [114] guarantee that (1) admits propagation failure when \(d >0\) is sufficiently small. For general \(d > 0\) the problem is still open, but the results in [18, 71] suggest that the width of the pinning interval \([a_-, a_+]\) decreases exponentially with \(d > 0\). Further results confirming this phenomenon can be found in [1, 27, 61, 65, 67, 127].
Let us emphasize that these issues depend very subtly on the nonlinearity. For example, the explicit solutions (13) clearly indicate that (12) does not suffer from propagation failure. In this case, the two solutions \(\varPhi ^{(s)}\) and \(\varPhi ^{(b)}\) are part of a continuous one-parameter family of standing waves; see panel (iii) in Fig. 1. In such settings the intuition developed above fails and more subtle bifurcation scenarios can arise [98]. Similar observations can already be found in early work by Elmer [54]. Indeed, after replacing g by a piecewise linear zigzag nonlinearity, propagation failure can be excluded for a countable set of diffusion coefficients d.
Returning to (1), we illustrate the consequences of this behaviour on the pairs \((c, \varPhi )\) in Fig. 2. These numerical results confirm that wave profiles lose their smoothness as the pinning region is approached, while the derivative \(\partial _a c\) blows up. This latter fact appears to be related to the discreteness of the LDE (1) rather than its non-locality. Indeed, pinning phenomena have also been investigated in nonlocal problems featuring smooth convolution kernels [4, 140]. In certain cases the behaviour of c near the pinning boundary can be described by power laws with various exponents.
The stable and unstable manifolds \(\mathcal {W}^s(1,1)\) and \(\mathcal {W}^u(0, 0)\) associated to the discrete system (10) with \(c = 0\) can intersect in several ways. Left: the generic situation expected at \(a = \frac{1}{2}\). Middle: the saddle-node bifurcation at \(a = a_\pm \). Right: the degenerate situation at \(a = \frac{1}{2}\) corresponding to the multi-site discretization (13)
Functional differential equations When \(c \ne 0\), the travelling wave equation (10) is referred to as a functional differential equation of mixed type (MFDE), since it involves delayed terms and advanced terms simultaneously. Such equations are generally not well-posed as initial value problems. This can be seen by looking at the linear equation [137]
which only has discontinuous solutions.
When studying such ill-posed infinite-dimensional problems, exponential dichotomies, Fredholm theory and dimension reduction techniques become the methods of choice. Initiated by the pioneering work of Rustichini [137, 138], research in this area features spectral flow results to compute the Fredholm index for operators with finite range shifts [125], infinite-range shifts [68] or neutral terms [119], various state-space decompositions based on exponential dichotomies [82, 93, 108, 128], techniques to construct local [70, 106, 107] and global [99] center manifolds and extensions of geometric singular perturbation theory [100].
Several of these results are discussed in Sects. 2.1 and 5.1. We emphasize that this theory is useful not only for establishing the existence of travelling wave solutions, but also for the analysis of their stability.
Planar travelling waves The two-dimensional analogue of (1) is given by the planar Nagumo LDE
where we take \((i,j) \in \mathbb {Z}^2\). Planar travelling wave solutions propagating at an angle \(\zeta \) relative to the horizontal can be written in the form
where we again impose the boundary condition (11). Substitution into the LDE (18) now yields the travelling wave MFDE
The broken rotational invariance in the \(\mathbb {R}^2 \rightarrow \mathbb {Z}^2\) transition is manifested by the explicit presence of the propagation direction in (20).
In particular, the speed \(c = c_{\zeta }\) of planar waves typically depends on the angle \(\zeta \). This dependence can be very intricate when \(a \approx \frac{1}{2}\); see panel (iii) in Fig. 2 and [27, 58, 105]. In fact, planar waves can fail to propagate in certain directions that resonate with the lattice, whilst travelling freely in other directions [27, 88, 127]. Several of the resulting peculiarities will be discussed in detail in Sect. 4.
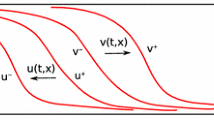
Numerical simulations for the Nagumo LDEs (1) and (18) with \(d = 0.1\). Left: the behaviour of the waveprofiles as a is increased towards \(a = 0.5\). The zero-speed profiles for \(a \in \{0.46, 0.5\}\) are discontinuous step functions. Center: the behaviour of c(a) near the critical value \(a_-\) where pinning sets in. Right: Polar plots of the speed \(c_{\zeta }\) as a function of the propagation angle \(\zeta \) for different values of a. The curves have been rescaled by a factor \(r_a\) for comparison purposes, so that every curve can be written as \(c_\zeta r_a \big (\cos (\zeta ),\sin (\zeta )\big )\) for \(0\le \zeta \le \pi /2\)
Equilibrium patterns Besides the pinned waves discussed above, we have so far only considered equilibrium solutions to (1) that are spatially homogeneous. However, the discrete nature of the problem allows this LDE to have a much richer set of equilibria than the corresponding PDE (3). For example, in Sect. 3.1 we discuss solutions to the difference equation (15) that admit the periodicity \((r_{j+n} , s_{j+n}) = (r_{j}, s_j)\). Such solutions exist for small \(d > 0\) and correspond with equilibria for (1) that are spatially n-periodic. In fact, one can show [114] that (15) admits a horseshoe for small \(d > 0\), which implies the presence of chaos in the set of equilibria for (1).
It is not hard to see that n-periodic equilibria for (1) can be seen as equilibria for the Nagumo equation posed on the cyclic graph \(C_n\). In [96] exact expressions are given for the number of equivalence classes of such equilibria, after factoring out the graph symmetries. It is natural to ask which other finite graphs can arise in this fashion by studying regular lattices. A brief discussion can be found in [130, Sect. 1], where various colouring schemes are described for hexagonal lattices that lead to the crown graph \(K_{3,3}\), the utility graph \(S_4^0\) and the complete graph \(K_4\). In general however, full classifications are still unavailable. Results that can be used to count the number of equilibria on several types of graphs can be found in [149].
For the planar LDE (18), equilibrium patterns that are 2-periodic in both horizontal and vertical directions again lead to the graphs \(C_2\) or \(C_4\), allowing us to reuse the one-dimensional results discussed in Sect. 3.1. However, one can also construct patterns that are \(3\times 2\)-periodic which lead to the ladder graph \(CL_3\), or use five colours to arrive at the complete graph \(K_5\). In general, the study of planar equilibrium patterns is still in its infancy. An illuminating discussion can be found in [40, 124], where the periodicity and chaos present in the set of such patterns is explored using simplified nonlinearities.
Outline This paper is organized as follows. In Sect. 2 we outline the basic machinery that has been developed for MFDEs and discuss a range of approaches that can be used to establish the existence, uniqueness and stability of the travelling waves (9). We move on in Sect. 3 to apply this theory to study the pattern forming properties of several extensions to (1) that are all posed on the one-dimensional lattice \(\mathbb {Z}\).
We subsequently consider the planar lattice \(\mathbb {Z}^2\) in Sect. 4. A large part of this section is concerned with the stability of the planar waves (19) under various types of perturbations, which includes the removal of lattice points. However, we also use these waves as building blocks to analyze more general types of solutions such as corners and expanding interfaces.
In Sect. 5 we return to the one-dimensional lattice \(\mathbb {Z}\), but now consider discrete FitzHugh–Nagumo equations. These are two-component LDEs that arise by coupling a second variable to (1). Various types of singular perturbations are considered that allow us to reduce the complexity of the underlying problem by invoking familiar results for the limiting subsystems.
We conclude in Sect. 6 by discussing discretization schemes for the Nagumo PDE (3) that are relevant in the context of numerical analysis. In particular, we construct fully-discrete travelling waves that solve (1) after discretizing the only remaining derivative with a family of schemes referred to as backward differentiation formula (BDF) methods. In addition, we explore the effects of using an adaptive spatial grid to solve (3), instead of the standard spatially uniform grid that leads to (1).
2 Background: Tools and Techniques
We here review the basics of some of the crucial techniques that have been developed to analyze travelling waves in spatially discrete settings. For simplicity and explicitness, we present all the main ideas in the context of the spatially homogeneous Nagumo LDE
with \(d > 0\) and the cubic nonlinearity \(g(u;a) = u ( 1- u) (u -a)\). However, as we will discuss in detail below, many of the tools can be extended to a diverse range of more complicated systems. In this case the travelling wave MFDE is given by
and we look for solutions that satisfy the limits
The linearization around any solution to this MFDE can be described by the linear operator
We start in Sect. 2.1 by discussing several key aspects of the theory that has been developed for operators such as \(\mathcal {L}_{\mathrm {tw}}\) that are associated to linear MFDEs. We proceed in Sect. 2.2 by exploring several different approaches that can be used to obtain the existence and uniqueness of solutions to (22) and to understand their parameter-dependence. In Sect. 2.3 we subsequently investigate the nonlinear stability of these waves under the dynamics of (21). Finally, in Sect. 2.4 we discuss numerical techniques that can be used to visualize the behaviour of (21) and compute approximations for the speed and shape of the waves.
2.1 Linear Theory
An important feature of the linear operator \(\mathcal {L}_{\mathrm {tw}}\) is that it reduces to a constant coefficient operator in the limits \(\xi \rightarrow \pm \infty \). In particular, looking for solutions of the form \(e^{z \xi }\) for these limiting systems, we readily see that the spatial eigenvalues z are given by the roots of the characteristic functions
For \(0< a < 1\), the inequalities \(g'(0 ; a) < 0 \) and \(g'(1 ; a) < 0\) imply that both
On account of this fact, the linear operator \(\mathcal {L}_{\mathrm {tw}}\) is said to be asymptotically hyperbolic. Several powerful results are available for such operators.
Fredholm properties For \(c \ne 0\), the results in [125, 137] show that \(\mathcal {L}_{\mathrm {tw}}\) is a Fredholm operator from \(W^{1, p}\) into \(L^p\) for all \(1 \le p \le \infty \). In particular, we have the inequalities
In addition, upon writing
we see that \(\varDelta _{\mu }(i \nu ) \ne 0\) for all \(\nu \in \mathbb {R}\) and \(\mu \in [0,1]\). In particular, one can construct a homotopy between the limiting systems at \(\pm \infty \) during which no spatial eigenvalues cross the imaginary axis. The spectral flow result [125, Theorem C] for the Fredholm index of \(\mathcal {L}_{\mathrm {tw}}\) then implies that
in which the adjoint linear operator \(\mathcal {L}^{\mathrm {adj}}_{\mathrm {tw}}: W^{1,p} \rightarrow L^p\) is given by
This terminology is motivated by the fact that
holds for any pair of smooth functions v and w that decay sufficiently fast.
In [68] this Fredholm theory was extended to nonlocal linear operators that involve infinite-range interactions and/or smooth convolution kernels. Such operators arise frequently when studying neural field models [22, 69, 70]; see also Sect. 5.3.
Kernel of \(\mathcal {L}_{\mathrm {tw}}\) In order to further exploit the identity (29), it is essential to gain a thorough understanding of the kernel of \(\mathcal {L}_{\mathrm {tw}}\). The translational invariance of (22) immediately implies that \(\mathcal {L}_{\mathrm {tw}} \varPhi ' = 0\), but the specific structure of this wave equation must be used to rule out the presence of additional linearly independent kernel elements.
Such an analysis is performed in [126], where one establishes
In addition, both \(\varPhi '\) and \(\varPsi \) are found to be strictly positive exponentially decaying functions, which means that we can impose the normalization
The key point in the analysis above is to obtain precise asymptotics for the behaviour of \(\varPhi '\) as \(\xi \rightarrow \pm \infty \). In particular, the spatial eigenvalue system \(\varDelta _+(z) = 0\) has a single real negative root \(z = - \beta _+\), which using contour integration [125, Proposition 7.2] allows one to show that
for some \(\epsilon > 0\).
Using the comparison principle it is easy to show that \(\varPhi ' \ge 0\) and hence \(C_+ \ge 0\), but the delicate task is to sharpen this to \(C_+ > 0\). Assuming to the contrary that \(C_+ = 0\), it is natural to expect the asymptotic behaviour of \(\varPhi \) to be governed by the roots of \(\varDelta _+(z) =0\) with \(\mathfrak {R}z < -\beta _+\). This possibility can easily be excluded by the comparison principle, since the non-zero imaginary parts of these roots all lead to forbidden oscillatory behaviour.
However, in this setting one also needs to exclude the case that \(\varPhi '\) decays at a rate that is faster than any exponential. This requires subtle estimates on (22) involving differential inequalities. In a sense, these computations can be seen as a non-autonomous counterpart to the completeness theory discussed in [51, 78]. This theory can be used to decide whether a given set of eigenfunctions for a delay differential operator can be used as a basis for the underlying statespace.
By developing a graph-theoretic framework to keep track of the interactions [103], it is possible to generalize this completeness result to multi-component versions of (21). In this way, the characterization (32) can also be obtained for multi-component systems such as those encountered in Sect. 3.
The resolvent of \(\mathcal {L}_{\mathrm {tw}}\) By applying the general Fredholm theory in [125] to the identifications (32), we can identify the range of \(\mathcal {L}_{\mathrm {tw}}\) as the set
The normalization condition (33) hence implies that \(\varPhi ' \notin \mathrm {Range}(\mathcal {L}_{\mathrm {tw}})\).
This fact can be reformulated as the statement that the algebraic multiplicity of the zero eigenvalue of \(\mathcal {L}_{\mathrm {tw}}\) is equal to one. Indeed, a Lyapunov–Schmidt decomposition can be used [143, Lemma 6.10] to obtain the meromorphic expansion
in which the map
is analytic in a neighbourhood of \(\lambda = 0\). As we will see in Sect. 2.3, such expansions are very powerful tools when analyzing the stability of travelling waves. In the continuous setting, Zumbrun and Howard [161] pioneered the use of such expansions to obtain pointwise bounds on the Green’s functions associated to a wide range of linear and nonlinear stability problems.
Exponential dichotomies While the theory above focussed on the properties of \(\mathcal {L}_{\mathrm {tw}}\) acting on functions that are defined on the full line, it is often very advantageous to consider half-lines and compact intervals. In particular, we consider the homogeneous equation
and look for solutions in the space of bounded continuous functions
defined on intervals \(\mathcal {I} \subset \mathbb {R}\).
In order to consider the half-lines \(\mathbb {R}_-\) and \(\mathbb {R}_+\), we now introduce the solution spaces
and look at their initial segments
Functions that are in both P and Q can be extended to solutions on the entire real line, which means that
In addition, the expansions in [125, Proposition 7.2] together with the hyperbolicity condition (26) imply that functions in \(\mathfrak {P}\) and \(\mathfrak {Q}\) decay exponentially as \(\xi \rightarrow - \infty \) respectively \(\xi \rightarrow + \infty \).
The results in [128] show that the sum \(S =P+Q\) forms a set of codimension one. More precisely, we have
in which the so-called Hale inner product is given by
Such a splitting of the space S is referred to as an exponential dichotomy on the full line. Related results in a Hilbert space setting were obtained independently by Härterich, Sandstede and Scheel [82].
It is also worthwhile to consider exponential dichotomies on half-lines, in which case one introduces for \(L \ge 0\) the solution spaces
together with their initial segments
In this case, the results in [108] show that the full space \(C([-1,1];\mathbb {R})\) can be decomposed as
for any \(L \ge 0\).
In [108] we show how the characterization (35) can be exploited to construct solutions to equations of the form \(\mathcal {L}_{\mathrm {tw}} v = f\) for functions f that are only defined on half-lines. These solutions are by no means unique. Indeed, the power of the exponential splittings above is that they correspond precisely to the freedom that we have to solve such problems. This allows a general technique referred to as Lin’s method [123] to be lifted from the finite dimensional world of ODEs to the infinite dimensional setting of MFDEs.
For example, one can vary the parameters c and a in (22) and construct so-called quasi-solutions, which are two-valued on \([-1,1]\) with a difference that can be explicitly quantified by the Hale inner product. By closing the gap one can obtain information on the c(a) relation. Alternatively, these quasi-solutions can be combined and used as building blocks to construct travelling waves to more complicated problems; see Sect. 5.1.
2.2 Existence of Waves
By now it is well-known that for each \(a \in [0,1]\) there is a unique \(c = c(a)\) for which the wave MFDE (22)–(23) admits a solution. When \(c(a) \ne 0\), the waveprofile \(\varPhi \) is unique up to translations and the pair \((c,\varPhi )\) depends smoothly on a.
In this subsection we discuss several different methods that can be used to establish these properties. Each of these methods has its own strengths and weaknesses, but together they form a powerful toolbox that can be applied in a wide range of different settings.
Qualitative features As a preparation, we first discuss three important properties of the c(a) relationship that can be deduced directly from (22) and the linear theory discussed in Sect. 2.1. We remark that all the arguments here can be found in [126].
First of all, we claim that in the boundary cases \(a \in \{0, 1 \}\) one must have \(c \ne 0\). Indeed, assuming to the contrary that \(c = 0\), one can integrate (22) and use the identity
to conclude that
Since we have the inequalities
for all \(u \in (0,1)\), this implies that \(\varPhi \) must be a constant function, contradicting (23).
The second claim is that a solution \((c, \varPhi )\) to (22)–(23) that has \(c \ne 0\) extends smoothly to a branch of solutions for nearby parameters (a, d). To see this, one can rephrase (22) in the form
and compute the derivative
This operator has full range on account of the characterization (35), which allows the implicit function theorem to be applied.Footnote 1
Under the assumption \(c \ne 0\), this smoothness allows us to differentiate (22) with respect to a, which yields
Applying (35) and recalling the normalization (33), we hence obtain the useful monotonicity condition
Global homotopy The main idea in [126] is to establish the existence of travelling waves by constructing a global homotopy between families of bistable MFDEs. In particular, the collection of MFDEs (22) formed by taking \(a \in [0,1]\) is connected to the family
with \(\gamma = \tanh 1\). For \(a = \frac{1}{2}\) and \(c = -1\), one can explicitly verify that this latter MFDE has the solution
The monotonicity property (54) also holds in this case, which allows us to conclude that (55) has solutions with \(c < 0\) for all \(a \in [\frac{1}{2},1]\).
By using a similar continuation argument as above, these solutions can be continued to the original family (22). The key issue is that the inequality \(c \ne 0\) must be maintained throughout this homotopy. This can be done uniformly for all \(a \in [1 - \epsilon , 1]\) by applying coercivity arguments similar to those described above.
By exploiting the comparison principle, one can subsequently show that there is a unique wavespeed \(c = c(a)\) for which (22)–(23) admits solutions. If \(c \ne 0\), then the waveprofile \(\varPhi \) is also unique up to translations. These arguments can be readily generalized to general scalar equations of bistable type, but the use of the specific reference system (55) prevents an easy generalization to the multi-component case.
Spectral convergence In [11] the authors develop a perturbative technique to construct solutions to (22)–(23) near the continuum regime. In particular, they pick \(d \,{=}\, h^{-2} {\gg }1\) and spatially rescale (22) to arrive at the MFDE
The main goal is to construct solutions that can be written as
for small perturbations \((\tilde{c}, v)\), in which the pair \((c_0, \varPhi _0)\) satisfies the travelling wave ODE
associated to the Nagumo PDE (3).
The crucial linear operator to understand in this respect is
which arises upon linearizing the MFDE (57) around the PDE wave \((c_0, \varPhi _0)\). This operator is a singularly perturbed version of its PDE counterpart
The main contribution in [11] is that Fredholm properties of \(\mathcal {L}_{0}\) are transferred to \(\mathcal {L}_{h}\). In particular, the authors fix a constant \(\delta >0\) and use the invertibility of \(\mathcal {L}_{0}-\delta \) to show that also \(\mathcal {L}_{h}-\delta \) is invertible for small \(h > 0\). To achieve this, they consider bounded weakly-converging sequences \(\{v_j\} \subset H^1\) and \(\{w_j\} \subset L^2\) with \((\mathcal {L}_{h}-\delta )v_j=w_j\) and set out to find a lower bound for \(w_j\) that is uniform in \(\delta \) and h.
The strategy is to show that such a lower bound can be found even if \(w_j\) is restricted to a large but compact interval K. Indeed, one can then extract a subsequence of \(\{v_j\}\) that converges strongly in \(L^2(K)\) and use properties of the limiting operator \(\mathcal {L}_{0}\) to obtain the desired bounds.
Special care must therefore be taken to rule out the limitless transfer of energy into oscillatory or tail modes, which are not visible in this strong limit. Spectral properties of the (discrete) Laplacian together with the bistable structure of the nonlinearity g provide the control on \(\{v_j\}\) that is necessary for this.
The power of this approach is that it does not use the comparison principle and is not limited to finite range interactions. In particular, the results in [11] also hold for general LDEs of the form
provided that the coefficients \(\{\alpha _k\}\) satisfy the second-moment constraints
together with the spectral bounds
Together, these properties ensure that several key properties of the Laplacian carry over to the discretization (62).
Recently, we generalized this approach to multi-component systems such as the FitzHugh–Nagumo LDE [142, 143]; see Sects. 5.2 and 5.3. In addition, we considered situations where the discrete Laplacian includes a (localized) spatial dependence or where the Nagumo PDE is fully discretized; see Sect. 6.1.
Monotonic iteration The approach taken by Chen, Guo and Wu in [35] is to recast (22) as an integral equation that can be interpreted as a fixed point problem. In particular, for any \(\nu > 0\) and \(c \ne 0\) the authors introduce the linear operator
Using \(\mathrm {exp}[- \nu \xi / c]\) as an integrating factor, the travelling wave MFDE (22) can be integrated to yield
It turns out to be worthwhile to attack (66) indirectly by first restricting the problem to finite intervals \([-m,m]\). To this end, let us introduce the truncation operator \(P_m\) that acts as
By choosing \(\nu \gg 1\) to be sufficiently large, one can ensure that the integrand in (65) increases monotonically with respect to the arguments \(\varPhi (\cdot )\) and \(\varPhi (\cdot \pm 1)\). In particular, if \(\varPhi _A \le \varPhi _B\) holds in a pointwise fashion, then also \(P_m T_c \varPhi _A \le P_m T_c \varPhi _B\).
In order to exploit this, the authors develop a monotonic iteration scheme by writing
and subsequently
Indeed, the ordering properties above imply that
which allows us to take the \(j \rightarrow \infty \) limit and obtain two limiting functions that we denote by \(\varPhi _{(m,c)}^-\) and \(\varPhi _{(m,c)}^+\).
Naturally, one now wishes to take the limit \(m \rightarrow \infty \) in order to obtain a solution to (22). The hard part in this procedure is to show that the limiting waveprofile is not constant and indeed satisfies the boundary conditions (23).
For finite m, the truncation \(P_m\) helps in this respect as one can readily see that
When \(c \ne 0\), one can actually show that \(\varPhi _{(m,c)}^- = \varPhi _{(m,c)}^+\). In addition, whenever \(c_1 < c_2\) we have
Suppose now that \(\liminf _{m \rightarrow \infty } \varPhi _{(m,0)}^+ \le \frac{1}{2} \). This allows us to define a sequence \(c_l > 0\), \(m_l > l\) for which
By taking the limit \(m \rightarrow \infty \) we obtain a non-trivial solution to the travelling wave problem (22)–(23). A similar procedure works when \(\limsup _{m \rightarrow \infty } \varPhi _{(m,0)}^- \ge \frac{1}{2} \), but more delicate arguments are needed if both these conditions fail.
This procedure can be readily generalized to multi-component versions of (21). In fact, the results in [35] are formulated for (21) with a diffusion coefficient \(d = d_j\) that depends periodically on j. Besides the existence of travelling wave solutions, the authors also establish the uniqueness and stability of these solutions by exploiting the comparison principle.
Topological methods The techniques developed in [7, 8] aim to exploit the variational structure present in the wave MFDE (22). Indeed, upon picking a primitive G that has \(G'(\cdot ;a ) = g(\cdot ; a)\), the authors introduce the energy functional
together with a boundary term
A short computation shows that any solution to (22) must also satisfy the identity
which means that \(\mathcal {H}_A + \mathcal {H}_B\) can be used as a spatial Lyapunov function.
Exploiting this observation, one can construct a global Conley-Floer homology that encodes information concerning the travelling wave connections between the three equilibria of g. Such connections satisfy (22) but not necessarily (23). This homology is invariant under a large class of perturbations of g. In particular, this allows the authors to reduce the problem to the much simpler case where \(g(u) = u^3\), which only admits a single equilibrium. The Conley-Floer homology can be explicitly computed in this case, which subsequently allows one to formulate a forcing theorem to conclude that the travelling wave MFDE admits a solution for each \(c \ne 0\). However, this theorem (at present) provides no information concerning the possible limiting values of the waveprofile \(\varPhi \).
This technique can be generalized to multi-component versions of (21) as long as the nonlinearity has the structure of a gradient. However, there is no need for the discretization of the Laplacian to have only positive off-diagonal coefficients. In addition, it is also possible to consider models that have infinite range interactions or that involve smooth non-local convolution kernels.
Spatial regularization The main feature of this indirect approach is that it replaces (21) by the spatially smoothened system
The first step is to show that this regularized system with \(\gamma > 0\) admits travelling wave solutions. By taking the limit \(\gamma \downarrow 0\) and considering an appropriate subsequence, one can subsequently recover a solution to the original wave problem (22)–(23).
The travelling waves for (77) can be obtained by studying the time-evolution of the initial condition
In particular, one can show that the corresponding solution u(x, t) converges to a travelling wave for \(t \rightarrow \infty \). To accomplish this, one first proves that \(u(\cdot , t)\) is strictly increasing for all \( t> 0\) and that is satisfies the limits \(u(-\infty ,t) = 0\) and \(u(+\infty ,t) = 1\). This allows us to define quantities \(\xi _-(t)\) and \(\xi _+(t)\) by demanding
The key technical step is to obtain time uniform bounds
which can be seen as an a-priori steepness result for the interface.
One can subsequently use the comparison principle to build a sequence of shifts \(\{\xi _j\}\) and times \(\{t_j\} \rightarrow \infty \) so that we have the convergence
in the space of bounded continuous functions. The uniform bounds (80) allow us to conclude that the limiting function satisfies \(\varPhi ' > 0\) and has the limits (23). After some manipulations this limiting function turns out to be the desired waveprofile. These arguments were first introduced by Chen [34] in the context of general nonlocal PDEs. In [103] we generalized this procedure to spatially regularized multi-component versions of (21).
In order to construct a converging subsequence for the singular limit \(\gamma \downarrow 0\), it suffices to obtain a uniform bound on the wavespeed c for small \(\gamma \). The key issue is to show that the limits (23) are maintained throughout this limiting procedure. This can be achieved by establishing that the difference \(\xi _+(t) - \xi _-(t)\) also remains bounded as \(\gamma \downarrow 0\). Arguments of this type can be found in [103, 105].
2.3 Stability of Waves
Here we discuss several different methods that can be used to establish the nonlinear stability of the travelling waves (22)–(23) in the case where \(c \ne 0\). In particular, one can show that there exists \(\delta > 0\) so that any solution to (21) with
must satisfy the limit
as \(t \rightarrow \infty \) for some asymptotic phaseshift \(\vartheta \). In addition, the rate of convergence is exponentially fast.
Wave squeezing This method builds upon the classic approach developed by Fife and McLeod for the Nagumo PDE (3). In particular, one sets out to exploit the comparison principle by constructing sub- and super-solutions of the form
with z decreasing from \(z_0\) to 0 and with Z increasing from 0 to \(Z_\infty \). These functions hence transform initial global additive perturbation of size \(z_0\) into phaseshifts of size \(Z_\infty \).
To better understand the crucial relationship between the asymptotic phaseshift \(Z_\infty \) and the additive perturbation z, we note that the super-solution residual
is given by
with \(\xi _j(t) = j + ct + Z(t)\). Close to the interface, the term \(g(\varPhi ) - g(\varPhi + z) \sim - g'(\varPhi )z\) is negative and must be dominated by the positive term \(\dot{Z}\varPhi '\). This requires that \(\dot{Z}\) dominates z and \(\dot{z}\). On the other hand, close to the spatial limits \(\varPhi \rightarrow 0\) and \(\varPhi \rightarrow 1\) we have \(g'(\varPhi ;a) < 0\), so this regime requires z to dominate \(\dot{z}\). These observations allow us to define z(t) as a slowly decaying exponential, which gives the relation
between the asymptotic phase shift and the size of the initial perturbation.
In [35, Sect. 5.4] the authors provide an elaborate argument to show how these explicit sub- and super-solutions can be used to trap a broad class of perturbations from \(\varPhi \) and steer them towards a phase-shifted version of this wave. The key ingredient is a careful mechanism to track the position of the perturbed wave by means of a phase condition. A variant of this method was used in [87] to establish the existence of an entire solution to (21) in the presence of obstacles; see Sect. 4.6.
Temporal Green’s function In the remainder of this subsection we refrain from using the comparison principle, which widens the class of LDEs that can be considered. In this case one can only expect to handle perturbations from \(\varPhi \) that are small, since the linear behaviour of (21) can then be used to control the nonlinear effects.
Looking for solutions to (21) of the form
we find that v must satisfy the time-dependent LDE
in which
This nonlinearity behaves as \(\left| \mathcal {N}_j(t, v)\right| = O( \left\| v(t)\right\| _\infty ^2)\) for \(v \rightarrow 0\), uniformly for \(t \in \mathbb {R}\).
This allows us to focus on the linear part
which for each pair \((j_0, t_0) \in \mathbb {Z} \times \mathbb {R}\) has a unique solution \(W^{t_0 j_0}\) that satisfies the initial condition
These special solutions can be used to define a Green’s function \(\mathcal {G}(t, t_0) \in \mathcal {L}(\ell ^{\infty })\) that acts as the convolution
Indeed, for any pair \(t > t_0\) solutions to (91) can be found by writing
In general, it is very hard to analyze non-autonomous evolution equations. In this case we are aided by the special structure of wave solutions. Indeed, the system (89) remains invariant under the replacements
In particular, upon introducing the right-shift operator \(\mathcal {S} \in \mathcal {L}(\ell ^{\infty })\) that acts as \( (\mathcal {S} U)_j = U_{j-1}\), we have the shift-periodicity
In a sense, this compactifies the set of time differences \(t - t_0\) that need to be considered.
Shift-periodic Floquet theory A first approach to exploit the identity (96) was developed by Chow, Mallet-Paret and Shen in [39]. In particular, they introduce the operator
which can be seen as a shift-periodic version of the monodromy map that is usually considered for periodic systems. By checking that \(v_j(t) = \varPhi '(j + ct)\) is a solution to (91), one readily sees that \(\mathcal {R} \varPhi ' = \varPhi '\). In particular, we have
If this unit eigenvalue is simple and the remainder of the spectrum satisfies the inclusion
the general results in [39] show that the travelling wave is nonlinearly stable. This was achieved by constructing a local \(\ell ^{\infty }\)-coordinate system around the travelling wave and analyzing the monodromy map in these new coordinates. The arguments used to construct this coordinate system are very technical and it is therefore not straightforward to generalize this approach to spectral scenarios that are more complicated than (99).
For general problems the spectrum of \(\mathcal {R}\) is hard to analyze in a direct fashion. However, for our specific system (21) one can use the comparison principle to show that (99) indeed holds.
Spatial Green’s functions A second approach towards analyzing the temporal Green’s function \(\mathcal {G}\) was pioneered by Benzoni-Gavage and her coworkers [14, 15]. The main idea is to sacrifice the discreteness of the spatial variable by passing to a reference frame that moves along with the wave. In particular, one replaces the non-autonomous linear system (91) by the autonomous non-local PDE
In order to solve this system by Laplace transform techniques, it is very useful to understand the pointwise behaviour of the resolvents of \(\mathcal {L}_{\mathrm {tw}}\). This is encoded in the spatial Green’s functions \(G_{\lambda }\), which solve the resolvent problem
in the sense of distributions.
The link between the temporal and spatial Green’s functions is provided by the representation formula
which was established in [15, Theorem 4.2]. A-priori one must take \(\gamma \gg 1\), but in order to obtain useful decay rates on \(\mathcal {G}\) one needs to shift the contour as far to the left as possible.
In order to achieve this in the context of (21), one can exploit the meromorphic splitting (36) to write
with a remainder term \(\widetilde{G}_{\lambda }(\xi , \xi _0)\) that is analytic for small \(\left| \lambda \right| \). This allows us to shift the contour in (102) to the left of the imaginary axis, picking up a simple pole in the process. For small \(\beta > 0\) this yields the pointwise bound
With this bound in hand, one can proceed to construct stable manifolds for the family of travelling wave solutions \(u_j(t) = \varPhi (j + ct + \vartheta )\) to (21) obtained by varying the phase \(\vartheta \in \mathbb {R}\). Together these manifolds span the entire \(\ell ^p\)-neighbourhood of the travelling wave solution, which leads to the nonlinear stability result.
This procedure is explained in detail in [101]. Generalizations to problems with infinite-range interactions can be found in [143]. On the other hand, problems with complicated spectral scenarios involving curves of essential spectrum that touch the origin were analyzed in [13].
2.4 Numerical Aspects
Since the travelling waves (22)–(23) are stable, they can in principle be observed numerically by simulating the dynamics of the LDE (21) with an initial condition that resembles the wave profile. In practice, the choice
often suffices for the Nagumo (21), but other systems can require a more subtle construction. Naturally, one must truncate the problem to a finite domain \(j \in \{-L, \ldots , L\}\) and enforce appropriate boundary conditions. The Dirichlet conditions \(u_{-L} = 0\) and \(u_L = 1\) give reliable results, but more refined choices also fit the leading order coefficients in the asymptotic expansions (34).
Naturally, simulations of (21) only allow travelling waves to be tracked for the limited amount of time that their ‘core’ is contained in the domain under consideration. In principle, this can be improved by using so-called freezing methods [20], which introduce an extra phase variable to keep track of the position of wave-like solutions. In a sense, this is the numerical equivalent of passing to a reference frame that moves along with the wave.
An alternative - more direct - approach is to look for numerical solutions of the travelling wave system (22)–(23). The early work by Chi, Bell and Hassard [38] already contains computations of this nature. This numerical work was continued by Elmer and Van Vleck, who have performed extensive calculations on MFDEs in [1, 55,56,57,58].
To our knowledge, the most recent and versatile tools in this area are collocation solvers that are able to solve MFDEs on finite intervals [1, 105]. In particular, these codes solve n-dimensional problems of the form
for given functions \(f: \mathbb {R}^{n(N+1)} \rightarrow \mathbb {R}^n\), \(\tau : \mathbb {R}\rightarrow \mathbb {R}^n\) and shifts \(\sigma _i: \mathbb {R}^{1+n} \rightarrow \mathbb {R}\). This is achieved by subdividing the interval under consideration into M subintervals \([t_i, t_{i+1}]\) and representing \(\phi (\xi )\) on each subinterval in terms of a standard Runge-Kutta monomial basis. The representation is required to be continuous at the boundary points between subintervals and in addition to satisfy (106) at the Md collocation points \(t_i + (t_{i+1} - t_i) c_j\), for \(i = 1 \ldots M\) and \(j = 1 \ldots d\), where \(0< c_1< \ldots< c_d < 1\) are the Gaussian collocation points of degree d for some \(d \ge 3\). Using Newton iterations such a piecewise polynomial \(\phi \) can be found, provided that a sufficiently close initial estimate is available.
Various types of boundary conditions can be used to close the system (106). Since the shifts \(\sigma _i\) may depend on the spatial variable \(\xi \) as well as on the function value \(\phi (\xi )\) itself, this allows us to compute periodic solutions to MFDEs even when the period is unknown [92].
The occurrence of propagation failure presents serious difficulties for this numerical scheme when solving (22)–(23), since solutions may lose their smoothness in the singular limit \(c \rightarrow 0\). This difficulty can be overcome by introducing a term \(-\gamma \varPhi ^{\prime \prime }\) to the left hand side of (22) and using numerical continuation techniques to take the positive constant \(\gamma \) as small as possible. In [103, 105] this approach is analyzed from a theoretical viewpoint. In particular, convergence results are provided to show that this approximation still allows us to uncover the behaviour that occurs at \(\gamma = 0\).
3 Periodic Patterns
The interplay between different interactions on different length scales in a spatially discrete system often leads to the formation of periodic patterns. Examples include twinning microstructures in shape memory alloys [21], domain-wall microstructures in dielectric crystals [150] and oscillations in neural networks [64]. The dynamics of these patterns is both interesting and relatively unexplored.
Early results in this area were obtained in the context of material science, where spatially discrete equations have long been considered. The model of Hillert [84] is a one-dimensional model to describe phase separation in binary solids that allows for periodic patterns with no restriction on the amplitude of oscillations. The three-dimensional counterpart in [43] allows for periodic patterns with small amplitude. Subsequent work of Cahn and Novick-Cohen [28] developed a quasi-continuum approach to the model by deriving formal limiting PDEs that are able to capture the oscillatory behaviour; see also [141].
In [26] several spatially periodic structures were investigated for spatially discrete Allen–Cahn and Cahn–Hilliard equations with ‘negative diffusion’ and with both first and second neighbor couplings. It was noted in [27] that two-periodic patterns could be smoothened out by rewriting the scalar LDE as a vector LDE in order to split the odd and even numbered lattice sites. In [152] a model for martensitic phase transformations was derived that resulted in a bistable system with repelling first neighbor interactions.
In this section we focus on four recent projects related to this theme. The first of these [95, 97] reconsiders the Nagumo LDE (21) but now looks at the existence of spatially periodic equilibria and the possibility of forming connections between such patterns by multi-component travelling waves. In Sect. 3.2 we consider repelling interactions by taking \(d < 0\) in (21). We show how the system can be reformulated as a vector equation and discuss results from [24] concerning the existence and stability of bistable and monostable traveling waves for a large range of parameter values. Co-existence of traveling solutions and propagation failure are investigated as well. Finally, in Sect. 3.3 we add next-to-nearest neighbour interactions to (21). Several results from [153, 155] are summarized to show how the competition between the two types of interactions affects the patterns that can be formed.
3.1 Multichromatic Waves
We are here again interested in the Nagumo LDE
with \(d > 0\). The discrete nature of this problem allows for a much richer class of equilibrium solutions than its spatially continuous counterpart. For example, one can search for n-periodic equilibria by writing
for some \(\mathrm {u}\in \mathbb {R}^n\).
Upon introducing the nonlinear mapping \(G(\cdot ; a, d): \mathbb {R}^n \rightarrow \mathbb {R}^n\) that acts asFootnote 2
such equilibria must satisfy \(G(\mathrm {u};a,d) = 0\). Since the system decouples at \(d = 0\), we have \(G( \mathrm {w}_a; a, 0) = 0\) for any \(\mathrm {w}_a \in \{0, a, 1 \}^n\). Using the implicit function theorem, these \(3^n\) simple roots can be locally continued for \(d >0\) until they collide with another branch.
The solid lines denote the upper boundary of the regions \(\Omega _{\mathrm {w}}\) where roots of type \(\mathrm {w}\in \{ \mathfrak {0001},\mathfrak {0011},\mathfrak {0111}\}\) are defined. The dashed lines denote the boundaries above which the indicated wave connections have non-zero speed. Notice that regions exist in which the \(\mathfrak {0} \rightarrow \mathfrak {0001}\), \(\mathfrak {0001} \rightarrow \mathfrak {1}\) and \(\mathfrak {0} \rightarrow \mathfrak {1}\) waves all travel
To formalize this procedure, we say that a solution to \(G( \mathrm {u}; a, d) = 0\) is an equilibrium of type \(\mathrm {w}\in \{\mathfrak {0}, \mathfrak {a} , \mathfrak {1} \}^n\) if there exists a path through \([0,1]^n \times (0,1) \times [0, \infty )\) of simple roots that connects \((\mathrm {u}; a, d)\) to \((\mathrm {w}_a ; a, 0)\). Here \(\mathrm {w}_a\) is obtained from \(\mathrm {w}\) by replacing \(\{\mathfrak {0}, \mathfrak {a}, \mathfrak {1}\}\) by \(\{0, a, 1\}\). We use this symbolic distinction to emphasize the fact that the type \(\mathrm {w}\) remains fixed, while the actual root \(\mathrm {u}\) varies as the parameters (a, d) are changed. Indeed, we can now define the parameter set
see Fig. 3 for several examples.
We will be specially interested in the cases \(\mathrm {w}\in \{\mathfrak {0}, \mathfrak {1} \}^n\), since equilibria of this type are stable solutions to (107). Indeed, the monotonic iteration theory in [35] that was described in Sect. 2.2 can then be used to establish the existence of wave solutions that connect ordered pairs of such stable equilibria.
For \(n = 2\), the upper boundary of \(\Omega _{\mathfrak {01}}\) can be written as a graph \(d = d_{\mathfrak {01}}(a)\). Writing \(\mathrm {u}= \mathrm {u}_{\mathfrak {01}}(a,d)\) for the corresponding equilibrium (108), the wave solution that connects the homogeneous equilibrium \(u_j \equiv 0\) to this two-periodic pattern can be written as
Here we write \(c = c_{\mathfrak {0} \rightarrow \mathfrak {01}}(a,d)\) and impose the limits
This sequence of snapshots from a simulation of the Nagumo LDE (21) with \(a = 0.63\) and \(d = 0.0625\) features a collision between a wave of type \(\mathfrak {0} \rightarrow \mathfrak {0111}\) and a counterpropagating wave of type \(\mathfrak {0111} \rightarrow \mathfrak {1}\). The right part of the intermediate buffer zone is first pulled towards one by the incoming wave on the right, but then gets pulled towards zero by the final travelling monochromatic wave
It is an interesting and delicate problem to decide whether these so-called bichromatic waves can travel or whether they are pinned. For small \(d > 0\) the latter is the case, which allows us to consider the bichromatic pinning boundary
The main result in [95] is that there exists \(a_- \in (0, \frac{1}{2})\) so that
holds for all \(a \in (a_-, 1)\), which forces waves to travel for intermediate values of d. This can be seen as a generalization of the coercivity results for the standard monochromatic waves discussed in Sect. 2.2.
The cases \(n = 3\) and \(n =4\) were analyzed numerically in [97]. In these cases there exist (small) intervals of a in which the upper boundaries of the sets \(\Omega _{\mathrm {w}}\) can no longer be written as graphs \(d = d_{\mathrm {w}}(a)\); see the inset of the cusp in Fig. 3. This is the reason that we must allow a to vary along the defining paths through the regions \(\Omega _{\mathrm {w}}\). As a consequence, for fixed a the number of n-periodic equilibria does not decrease monotononically as the diffusion d is increased.
Upon writing \(d_{\mathfrak {0} \rightarrow \mathfrak {1}}(a)\) for the pinning boundary corresponding to the standard monochromatic waves (22) and generalizing the notation (113), the numerical results indicate that the ordering
holds for all \(a \in (0.63, 1)\). In particular, while bichromatic waves can only exist for parameters (a, d) where monochromatic waves are pinned, travelling quadrichromatic waves can co-exist with travelling monochromatic waves; see Fig. 3. This allows several types of intricate collision processes to take place. For example, a travelling \(\mathfrak {0} \rightarrow \mathfrak {0111}\) wave can collide with a counter-propagating \(\mathfrak {0111} \rightarrow \mathfrak {1}\) connection to form a travelling monochromatic \(\mathfrak {0} \rightarrow \mathfrak {1}\) wave; see Fig. 4.
3.2 Negative Diffusion
In [24], the existence and stability of traveling waves solutions with ‘negative diffusion’ is investigated. In particular, let us consider the LDE
again with \(d > 0\). This system has been used in [152] to describe martensitic phase transitions in a chain of particles that features interactions between first and second neighbours. The latter interactions are modelled by standard springs, but the former are governed by a non-convex biquadratic potential representing two elastic phases. After a suitable rescaling, (116) can be seen as the overdamped limit of the resulting system.
Instead of flattening variations, the diffusion term in (116) now promotes oscillatory behaviour. Unlike its PDE counterpart, this system is still well-posed on account of the fact that the discrete Laplacian is simply a bounded linear operator. In particular, the cubic g can keep the oscillations under control.
Of course, the comparison principle no longer holds for (116). It can be recovered by introducing the new variables \(v_j = (-1)^j u_j\), which satisfy the spatially periodic system
with alternating nonlinearities
In principle, this equation fits into the general spatially periodic framework of [35]. The challenge is to identify and classify the equilibrium solutions to (117). To this end, we look for stationary solutions of the form
which must hence satisfy the coupled system
Eliminating \(v_o\) from these equations, we must find the roots \(G(v_e;a,d) = 0\) of the ninth-degree polynomial
which can be factored as
for some sixth-degree polynomial \(\tilde{G}(\cdot ; a, d)\). This polynomial can have between zero and six real roots. Taking into account the three equilibria (0, 0), \((a,-a)\) and \((1, -1)\) induced by the factor g, there are hence up to 81 potential connecting orbits between two-periodic stationary patterns.
In [24], we give a detailed description of the roots of G and their dependence on the parameters (a, d). This allows us us to study the existence, uniqueness and stability of traveling wavefront solutions to the antidiffusion Nagumo LDE (116). In particular, we uncover the different regions in the (a, d)-plane where bistable and monostable dynamics occur.
We analyze the propagation failure phenomenon in the bistable region and provided expressions for minimum wavespeeds in the monostable region. Our computations show that there are values for the parameters (a, d) where bistable and monostable connections co-exist.
3.3 Competing Interactions
In order to explore the effects of interactions with different length scales, we extend (21) by including a diffusion term that involves next-to-nearest neighbours. In particular, we introduce the discrete diffusions
and consider the system
on the one-dimensional lattice \(j \in \mathbb {Z}\). Motivated by our earlier work [152], we focus much of our attention on the case where at least one of the interactions is repulsive (\(d_1\) and/or \(d_2\) are negative). Note that this is certainly not a necessary condition for pattern formation, as we have seen in Sect. 3.1.
The results in [153, 155] consider spatially p-periodic equilibrium solutions to (124) and the potential for connecting them via travelling waves. The focus is on \(p \in \{1, 2, 4\}\), but larger periods, longer interaction lengths and higher dimensional lattices can also be considered using similar techniques.
In order to gain insight, we started in [153] by replacing the cubic g with its piecewise linear caricature \(g_{\mathrm {pl}}\) defined in (14). As in Sect. 3.2, the first step was to find the periodic equilibria and identify the range of parameters where these solutions and their homogeneous counterparts are stable. We then took advantage of the piecewise linear form of the nonlinearity \(g_{\mathrm {pl}}\) to apply Fourier transform techniques and constructed explicit traveling wave solutions along the lines of the approach in [27]. We conducted a detailed analysis of the solution in the \(p = 2\) case and considered some examples in the \(p = 3\) and \(p = 4\) cases. In particular, we investigated the dependence of the detuning parameter a on the wavespeed c and the parameters \(d_1\) and \(d_2\).
Summary of results on existence of traveling wave solutions with spatially periodic patterns in \((d_1,d_2)\) parameter space. The results by Chen et al. [36] are directly applicable to region \(\mathcal {A}\). When \(\left| (d_1, d_2)\right| \gg 1\), the techniques by Bates et al. [11] can be applied in regions \(\mathcal {A}\) and \(\mathcal {B}\). In region \(\mathcal {C}\) the computations in [155] can be used, which for \(d_2 < 0\) require either \(\left| d_1/d_2\right| \ll 1\) or \(\left| d_2/d_1\right| \ll 1\). The line \(\mathcal {D}\) was investigated in [24]
In [155] we returned to (124) with the cubic nonlinearity and used techniques similar to those in [11] to establish the existence of traveling wave solutions in the presence of competing interactions. When \(d_2 > 0\) and \(d_1 < 0\), the variable transformation \(v_j = (-1)^j u_j\) can again be used to recover the comparison principle and apply the framework of [35]. However, when \(d_2 < 0\) one must resort to perturbative techniques. Figure 5 summarizes the parameter regions where the various approaches can be applied.
4 Nagumo Equations on Planar Lattices
In this section we focus on bistable equations posed on two-dimensional lattices. To set the stage, let us consider the Nagumo LDE
with \((i,j)\in \mathbb {Z}^2\). As in the continuous setting [6], we will see that planar travelling waves (see Fig. 6) can be used as a skeleton to help uncover the global dynamics of (125). Such waves can be written in the form
in which \(\zeta \) denotes the angle of propagation. Substituting this expression into (125) leads to the \(\zeta \)-dependent MFDE
The global homotopy argument discussed in Sect. 2.2 can also be used to construct solutions to this system [126]. In particular, after fixing \(a \in (0,1)\), the wavespeed \(c_{\zeta }\) depends uniquely on \(\zeta \) and the waveprofiles \(\varPhi _{\zeta }\) are unique up to translation provided that \(c_{\zeta } \ne 0\).
Schematic representation of a planar wave (126) travelling in the horizontal direction \(\zeta = 0\)
It turns out to be a much more subtle question to decide upon the stability of these planar waves. Early work in this direction for four-dimensional nonlocal problems can be found in [10], but in two dimensions the relevant decay rates associated to a brute-force linearization of (125) are simply too slow. One encounters similar problems when analyzing the Nagumo PDE, but two main approaches have been developed in recent years to overcome them [17, 111]. Both these approaches build upon the realization that transverse deformations of the wave interface are governed by a heat equation that can be analyzed separately from the remainder of the perturbation.
In order to discuss these issues, it is convenient to introduce the new variables
which are parallel respectively tranverse to the direct of propagation of the wave. We will write \(\Lambda _{\zeta } \subset \mathbb {R}^2\) for the collection of all pairs (n, l) obtained by applying (128) to the original lattice \((i,j) \in \mathbb {Z}^2\). This set is dense when \(\tan \zeta \notin \mathbb {Q}\). On the other hand, when \(\tan \zeta \) is rational or infinite it is possible to find a \(\delta > 0\) so that we have the inclusion
In this case, it is often convenient to extend the problem (by repetition) onto the entire grid \((n,l) \in \delta \mathbb {Z}^2\).
For any \(\zeta \), the coordinates (128) transform the LDE (125) into
which now admits the planar wave solutions
The refined splitting alluded to above is now given by
In Sect. 4.1 we discuss the linearized equations for the pair \((\theta , v)\) and show how to extend the one-dimensional Green’s functions from Sect. 2.3. We use this in Sect. 4.2 to generalize [111] and establish the local nonlinear stability of the planar waves (131) using bootstrapping arguments. On the other hand, in Sect. 4.3 we obtain the global stability of these waves by building on the arguments in [17], which are based on the comparison principle.
Moving on to solutions that are more general than travelling waves, we discuss the expansion of compactly supported initial conditions in Sect. 4.4. The limiting shapes often resemble polygons that can be predicted from the structure of the \(\zeta \mapsto c_{\zeta }\) function. This leads naturally to the study of travelling corners in Sect. 4.5.
The last part of this section is focused on versions of (125) with spatially-varying diffusion coefficients, i.e.,
In Sect. 4.6 we allow the diffusion coefficient to be modified on a single lattice site, which can be interpreted as an obstacle. We discuss the results in [87] that show that planar waves can pass around such an obstacle and regain their shapes.
We conclude in Sect. 4.7 by allowing \(d_{ij}\) to vary periodically or become negative, analogous to the one-dimensional setup in Sect. 3. In particular, we describe results from [103] on the existence of travelling checkerboard patterns.
4.1 Linear Theory
A key ingredient towards analyzing the behaviour of (125) in the neighbourhood of the planar waves (126) is to linearize the LDE around these waves. The anistropy of the lattice plays an important role here, as the resulting structure of the linear equations depends heavily on the direction of propagation \(\zeta \).
Lattice directions Performing this linearization for the horizontal direction \(\zeta = 0\), we arrive at the system
which as in the one-dimensional case discussed in Sect. 2.3 is temporally non-autonomous. The j-direction however is unaffected by this issue, which allows us to take a discrete Fourier transform in this direction. This readily leads to the decoupled family of systems
for \(\omega \in [-\pi , \pi ]\).
Using the procedure outlined in Sect. 2.3, it is possible to construct Green’s functions for each of these spatially one-dimensional systems. The relevant linear operators can be found by searching for solutions of the form
which leads to the eigenvalue problem
for the linear operator
Upon writing \(\lambda _z = 2 (\cosh (z) - 1)\), we have
To find the evolution of perturbations of the form
under (134), it now suffices to solve the discrete heat equation
Indeed, taking the discrete Fourier transform of this system yields \(\frac{d}{dt} \hat{\theta }_{\omega } = \lambda _{i \omega } \hat{\theta }_{\omega }\). These perturbations are important because they correspond at the linear level with transverse deformations of the planar wave interface. We remark that the situation here closely resembles that encountered for the Nagumo PDE in [111].
General directions For general angles \(\zeta \), the relevant linear system can be written as
The corresponding operator is given by
In particular, the dependence on z is now non-trivial. This means that one can no longer hope to find an exact solution similar to (140).
On the other hand, for small values of \(\left| z\right| \) it is possible to find \(\zeta \)-dependent branches \(z \mapsto (\lambda (z), \phi _{z} )\) of the eigenvalue problem
Upon introducing the quantities
it is not hard to compute [94]
For \(\zeta \in \frac{1}{4} \pi \mathbb {Z}\) we have \(\lambda '(0) = 0\) and \(\lambda ''(0) > 0\). We have numerical evidence to show that the second inequality persists for all angles \(\zeta \), but the first identity is typically violated. In fact, making the dependence on \(\zeta \) explicit, we have
and this quantity is typically referred to as the group velocity. However, we do remark here that the function \(\zeta \mapsto c_{\zeta }\) can behave rather wildly in the critical regime where \(a \approx \frac{1}{2}\), allowing the group velocity to vanish at specific values for a even if \(\zeta \notin \frac{\pi }{4} \mathbb {Z}\).
Since the group velocity is a real number, we have
for \(\omega \approx 0\), which means that we can still expect linear decay estimates similar to those of the discrete heat equation.
Let us now assume that \(\tan \zeta \) is rational and recall the inclusion (129). Extending our solution to the entire grid \((n,l) \in \delta \mathbb {Z}^2\) and imposing the decomposition
we normalize w by demanding
for all \(t \ge 0\) and \(l \in \delta \mathbb {Z}\). Formally writing the coupled system for \((v, \theta )\) as
we can combine the Green’s function techniques from Sect. 2.3 with the Fourier decomposition above to obtain a full two-dimensional Green’s function \(\mathcal {G}_{\zeta }\) for (151); see [86, Sect. 4]. The decay rates for \(\theta \) correspond to those for the discrete heat equation, while v decays at rates that are \(t^{-1/2}\) faster. In the diagonal direction \(\zeta = \frac{\pi }{4}\) this factor increases to \(t^{-1}\), while in the horizontal direction \(\zeta = 0\) the v component even decays exponentially rather than algebraically.
4.2 Local Stability
Our first approach [86] to establish the stability of planar waves only considers small perturbations from the wave and hence avoids using the comparison principle. In particular, this technique can be applied to a wide range of problems, as long as several standard spectral conditions can be verified. It is based on a surprisingly recent result due to Kapitula [111], who used semigroup methods and fixed-point arguments to obtain the corresponding result for the Nagumo PDE.
In particular, we pick an angle \(\zeta \) for which \(c_{\zeta } \ne 0\) and for which \(\tan \zeta \) is rational. Based on the intuition obtained in Sect. 4.1, we consider the evolution under the LDE (125) of patterns of the form
with (n, l) given by (128). We assume that the initial perturbation from the travelling wave is small in the sense that
In order to fix the coordinate system in such a way that the variables \(\theta _l(t)\) represent genuine phaseshifts, we impose the normalization condition
After some algebra, the resulting system for \((\theta , v)\) can be written in the abstract form
in which the linear operator \(B_{\zeta }(t)\) was introduced in (151). Using the Green’s function for this latter system, one can use Duhamel’s principle to recast (155) into the mild form
Based on the linear theory in Sect. 4.1, the choice for \(\ell ^1\)-based norms in the transverse direction implies that \(\theta \) can be expected to decay as \(t^{-1/4}\) in \(\ell ^2\). However, the decay rate for v depends on the angle \(\zeta \).
We now explore the effect of the nonlinear terms \(\mathcal {N}_{\zeta }\), which also depend crucially on \(\zeta \). As a preparation, we introduce the first differences
together with the second differences
The linear theory predicts the decay rates
for these expressions.
Horizontal and diagonal directions For \(\zeta \in \frac{\pi }{4} \mathbb {Z}\) the nonlinear term for v satisfies the pointwise bounds
with similar behaviour for \(\mathcal {N}^{(\theta )}_\zeta \). In particular, the standard Cauchy–Schwarz bound \(\left\| ab\right\| _{\ell ^1} \le \left\| a\right\| _{\ell ^2} \left\| b\right\| _{\ell ^2}\) together with the linear behaviour
show that in the norm (153) we can expect \((\mathcal {N}^{(v)}, \mathcal {N}^{(\theta )})\) to decay as \(t^{-3/2}\). This is very similar to the corresponding bounds obtained in [111] for the PDE setting. In particular, setting up a variation-of-constants argument using the Green’s function \(\mathcal {G}_{\zeta }\) defined in Sect. 4.1 allows us to conclude that the expected linear decay bounds carry over to the nonlinear setting.
General directions For general rational directions \(\zeta \) the geometry of the lattice affects both the linear and nonlinear terms in our problem. Indeed, we have seen in Sect. 4.1 that the expected linear decay in v slows down to
In addition, the lack of symmetry weakens the pointwise bounds for \(\mathcal {N}^{(v)}_{\zeta }\) to
In particular, the terms of order \(\left| v\theta \right| \) and \(\left| \theta \theta ^\diamond \right| \) now cause complications, since they can only be expected to decay as \(t^{-1}\) in \(\ell ^1\). Indeed, the crude estimate
shows that the \(t^{-1/4}\) decay for \(\left\| \theta \right\| _{\ell ^2}\) cannot be recovered from a simple application of the Duhamel formula.
In order to refine this estimate, it is essential to consider the explicit structure of the problematic terms. Consider for example the simple, yet crucial, identity
The square of the first difference can be expected to behave as \(t^{-3/2}\), which does not pose a problem. The difference of the squares though only decays like \(t^{-1}\). However, using a summation by parts procedure the difference operator can be transferred to the Green’s function. The bad estimate (164) can now be replaced by the good estimate
A careful analysis of the troublesome nonlinear terms shows that they can all be treated by tricks of this kind, allowing us to close the nonlinear stability argument. We remark that the identity (165) can be regarded as a discrete form of \(uu_x = \big (\frac{1}{2}u^2\big )_x\), which plays a crucial role when studying the stability of travelling waves for PDEs with a conservation law structure [160].
4.3 Global Stability
The approach in [87] leverages the comparison principle to show that the planar waves (126) are stable under a much larger class of initial perturbations. This generalizes the techniques developed in the landmark paper [17], where the authors constructed explicit super- and sub-solutions to the Nagumo PDE (3) that trap perturbations that can be arbitrarily large (but localized).
These sub-solutions can be seen as two-dimensional refinements of (84). Indeed, they take the form
with global functions
for small \(\epsilon > 0\) and \(\eta > 0\) that turn small additive perturbations into a phaseshift. The function \(\theta \) is used to control transverse perturbations and is given by
Here \(\gamma = \gamma (\beta ) \gg \beta \) and \(\beta \gg 1\) can be chosen to be arbitrarily large, allowing localized perturbations of any size to be controlled. In particular, the function \(\theta \) can be seen as a modified heat-kernel where the diffusion is sped up by a factor \(\gamma \) and the decay rate at the center \(y = 0\) is slowed down to \((t + 1)^{-2 \gamma ^{-1}}\).
In [16] this idea was generalized to the LDE (125) for waves travelling in the horizontal direction \(\zeta = 0\). This was achieved by replacing the Gaussian in (169) by the corresponding kernel for the discrete heat equation (141). This kernel can be expressed in the form of modified Bessel functions of the first kind.
This procedure relies on a specific factorization similar to (140) that fails to hold for general directions \(\zeta \). In order to fully account for all the slowly decaying resonances spawned by the anisotropy of the lattice, the sub-solution (167) needs to be adjusted significantly. In particular, for suitably chosen functions
it is possible [87] to use
Here we interpret the first and second difference \(\theta ^\diamond _l\) and \(\theta ^{\diamond \diamond }_l\) defined in (157)–(158) as vectors in \(\mathbb {R}^{4\times 1}\) and \(\mathbb {R}^{16 \times 1}\) respectively. In addition, the decay of the function z needs to be slowed down to \(z(t) \sim t^{-3/2}\) for \(t \gg 1\) and the function \(\theta \) needs to be modified to
Notice that the group velocity (146) appears here as an extra convective term.
One can use normal form techniques to find the specific form of the functions (170). Indeed, their purpose is to neutralize any terms in the sub-solution residual that decay at rates that cannot be integrated uniformly in \(\gamma \). Since we are artificially slowing down the decay of \(\theta \), this means that we need to pay special consideration to terms of order \(\theta ^{\diamond \diamond }\) and \((\theta ^\diamond )^2\), which could be neglected in Sect. 4.2.
4.4 Spreading Phenomena
Let us here assume that \(c_{\zeta } > 0\) for all angles \(\zeta \) and consider the compactly supported initial condition
for some sufficiently large \(R > 0\). In the PDE setting, a classic result [6, Theorem 5.3] obtained by Weinberger states that such regions containing the energetically favourable state will spread throughout the space with a radial speed equal to the speed of the planar travelling waves. The proof of this result uses radially expanding sub- and super-solutions that can be constructed by glueing together planar travelling waves travelling in different directions.
In [87] a weak version of this expansion result was established for the LDE (125) with (173). However, the underlying sub- and super-solutions expand at the speeds \(\min _{0 \le \zeta \le 2\pi } c_{ \zeta }\) and \(\max _{0 \le \zeta \le 2\pi } c_{\zeta }\) respectively, which generally differ from each other. This still leaves a considerable hole in our knowledge of the expansion process.
The numerical results in [154] provide strong evidence that the limiting shape formed by the evolution of (173) can be found by applying the Wulff construction [136] to the polar plot of the \(\zeta \mapsto c_{\zeta }\) relation. In particular, for each \(\zeta \in [0, 2\pi ]\) one considers the line
which is tangent to the circle of radius \(c_{\zeta }\) at the angle \(\zeta \). The set that is enclosed by the collection of these lines is referred to as the Wulff shape; see Fig. 7. For a large subset of parameters a this limiting shape resembles a polygon.
Let us mention here that the Wulff shape plays an important role in the field of crystallography, where it is used to predict the limiting shape of growing crystals [158]. In such applications it is usually constructed from a polar plot of a free energy functional.
4.5 Travelling Corners
The main motivation behind [94] is to take a step towards understanding the polygonal expansion process described in Sect. 4.4 by looking at the evolution of a single corner. Indeed, when the expanding blob is sufficiently large, it would seem to be very reasonable to assume that the corners of the polygon behave in an almost independent fashion.
A natural starting point is to look at so-called travelling corner solutions, which arise from the regular planar travelling waves by ‘bending’ the level sets of the waves. More specifically, the level sets are transformed from straight lines | perpendicular to the direction of propagation into shapes resembling a > or < sign; see Fig. 8.
For technical reasons the results in [94] only apply to propagation directions for which the group velocity vanishes. Recalling (147), this means that
Although the group velocity can always be transformed away in the PDE setting by a simple change of variables, the discreteness prevents us from doing this for LDEs. In particular, (175) is a genuine restriction. On the other hand, an important role in the Wulff construction is reserved for the directions where the wavespeed is minimal and these are all obviously covered.
The admissable bending angles are determined by the directional dispersion
which measures the speed at which the level-sets of the planar wave travelling in the direction \(\zeta + \varphi \) move along the vector \((\cos \zeta , \sin \zeta )\). In view of (175) we have \(d_{\zeta }(0) = c_{\zeta }\) and \(d_{\zeta }'(0) = 0\).
Assuming that \(d''(0) > 0\), we hence see that for all \(\tilde{c} > c_{\zeta }\) sufficiently close to \(c_{\zeta }\), there exist two small angles \(\varphi _-< 0 < \varphi _+\) for which
holds. The main result in [94] now states that there exists a sequence of phaseshifts \(\{\theta _l\}_{l \in \delta \mathbb {Z}}\) that satisfies the limits
together with a sequence of perturbations \(\{v_l\}_{l \in \delta \mathbb {Z}} \subset H^1\) so that the function
is a solution to (125). In particular, the level sets are bent away from the vector \((\cos \zeta , \sin \zeta )\) to form a > shape. When \(d''(0) < 0\) this orientation is reversed and one must take \(\tilde{c} < c_{\zeta }\).
The main idea behind the proof of this result was inspired by the series of papers written by Scheel and Haragus [79,80,81] for the planar Nagumo PDE, where they used a two-dimensional global center manifold to capture the corner solutions. The key feature of this approach is that the phaseshifts \(\theta \) can be factored out from the analysis due to the translational symmetry of the problem. However, the loss of regularity in the discrete case causes severe complications and forces one to analyze the full coupled system for v and \(\theta \) along the lines of [99].
In any case, the delicate behaviour of the \(c_{\zeta }\) map for the Nagumo LDE (125) leads to a rich class of behaviour. For example, the second derivative \(d''(0)\) can have both signs, while in the spatially homogeneous case one always has \(d''(0) > 0\). In addition, it is possible to find so-called bichromatic corners, which connect spatially homogeneous equilibria to checkerboard patterns.
4.6 Obstacles
In many situations it is desirable to understand the impact that localized spatial impurities have on the dynamical behaviour of systems. In the context of (133), this can be modelled by choosing diffusion coefficients that are homogeneous everywhere except at (0, 0), i.e., \(d_{ij} = d + \beta \delta _{i 0} \delta _{ j 0}\) with \(d > 0\) and \(\beta > - d\). Alternatively, one can consider the system on the punctured grid \(\mathbb {Z}^2 \setminus \{(0, 0)\}\), replacing the nearest-neighbour discrete Laplacian by the graph Laplacian. In particular, the equation for \(u_{1,0}\) is modified to
with similar modifications for \(u_{0, \pm 1}\) and \(u_{-1,0}\).
In both cases, one can study the existence of entire solutions that resemble a planar travelling wave as \(t \rightarrow \pm \infty \) but have large transients in between caused by the impurity. In [87] we show how the subsolutions (171) can be adapted to control these large transients. In essence, we allow the global term z(t) to grow instead of decay during the time that the steep part of the waveprofile is in the vicinity of the obstacle. In particular, the results show that planar waves can pass around large compact obstacles and still eventually recover their shape.
Our techniques are a variant of those developed fairly recently in [17] for the Nagumo PDE. However, we do need to require that \(c_{\zeta } \ne 0\) for all \(\zeta \in [0, 2 \pi ]\) in order to utilize the spreading result discussed in Sect. 4.4. It is an interesting open problem to determine the behaviour of the large transients when certain directions are pinned.
4.7 Travelling Checkerboards
In [103], we focussed on (133) with coefficients that are allowed to vary periodically, e.g. \(d_{ij} = d_o > 0\) whenever \(i + j\) is odd and \(d_{ij} = d_e > 0\) whenever \(i + j\) is even. Following the approach in Sect. 3.1, we look for solutions that can be written in the form of travelling checkerboards
in which we impose the spatially homogeneous limiting values
These waves must satisfy the coupled system
In this multi-component case it is no longer clear how the global homotopy argument described in Sect. 2.2 can be extended. In addition, the potential irrationality of the shifts prevents a direct application of the results from [35]. In [103] we generalized the ideas in [34] to the present multi-component setting, which allowed us to develop a spatial regularization method to obtain the existence and uniqueness of travelling waves. We also extended the Fredholm theory for the linearized operator \(\mathcal {L}_{\mathrm {tw}}\), which for \(c \ne 0\) allows us to conclude that these checkerboards are nonlinearly stable and depend smoothly on the parameters \((a,\zeta , d_{o}, d_e)\).
These techniques can also be applied to (133) with homogeneous negative diffusion coefficients \(d_{ij} = d < 0\). As before, one can introduce new variables \(v_{ij} = (-1)^{i + j} u_{ij}\) to transform the problem into a two-component system that admits a comparison principle. Under certain restrictions on the nonlinearity, we were able to again obtain travelling checkerboards. However, in this case the limiting rest states are typically not spatially homogeneous.
5 Discrete FitzHugh–Nagumo Equations
In this section we focus on several versions of the discrete FitzHugh–Nagumo equation, which can be used to describe the propagation of signal through myelinated nerve fibres [113]. In its simplest form, this system can be written as
For each lattice point \(j \in \mathbb {Z}\), the variable \(v_j\) encodes the on-site action potential while \(w_j\) acts as a generic recovery component. The parameter \(\epsilon > 0\) is related to the speed of this recovery, which is relatively slow compared to the firing process. The cubic g models the local ionic interactions. Notice that (184) reduces to the Nagumo LDE for \(\epsilon = 0\) and \(w =0\).
The discrete nature of the problem is a direct consequence of the properties of the myelin coating. This coating is essential to ensure that electrical pulses travel at adequate speed, but leads to rapid signal degradation. In order to repair this, the coating admits regularly spaced gaps at the so-called nodes of Ranvier [135]. Through a process called saltatory conduction, the electrical spikes effectively jump from one node to the next [122].
By restricting the size of \(\epsilon > 0\) in (184) one effectively creates a two-timescale problem that fits into the general framework of singular perturbation theory. In Sect. 5.1 we discuss how several important techniques from this area can be generalized to the discrete setting. This allows the existence and stability of travelling pulse solutions for (184) to be established.
In Sect. 5.2 we setup a bifurcation argument that allows these pulses to be extended to versions of (184) where the diffusion coefficient alternates between small and large values. Finally, in Sect. 5.3 we replace the finite-range discrete Laplacian in (184) by a class of counterparts that feature infinite-range interactions.
5.1 Singular Perturbation Theory
The LDE (184) can be seen as the nearest-neighbour discretization of the FitzHugh–Nagumo PDE
which was originally proposed [73, 74] as a simplification of the Hodgkin-Huxley equations [85] to describe the propagation of signals through the nerve fibres of giant squids. Early numerical experiments by FitzHugh [75] provided clear evidence that (185) supports travelling pulse solutions, but a rigorous analysis of these solutions turned out to be quite delicate. By now, existence and nonlinear stability results for these pulses have been obtained in various settings using a wide range of techniques such as geometric singular perturbation theory [29, 83, 109, 110], Lin’s method [30, 31, 118], the variational principle [33] and the Maslov index [44, 45].
Returning to the LDE (184), substitution of the travelling wave ansatz
leads naturally to the two-component MFDE
For certain specially tailored nonlinearities g, several ad-hoc techniques involving asymptotic expansions and Fourier transforms have been used to construct pulse solutions [37, 62, 151]. However, in order to handle the cubic and other general bistable nonlinearities, it turned out to be worthwhile to adapt several key constructions from the field of geometric singular perturbation to the infinite-dimensional setting considered here [100, 101].
The left panel describes the manifolds \(\mathcal {M}_L\) and \(\mathcal {M}_R\) and contains the singular orbit \(\varGamma _0\). The right panel despicts a quasi-solution to (187), which has two jumps that can be captured in the one-dimensional spaces \(\varGamma _f\) and \(\varGamma _b\)
To set the stage, we note that in the limiting case \(\epsilon = 0\) all equilibria of (193) lie on the graph \(\mathcal {M} = \big ( \phi , g(\phi ; a) \big )\). Choosing manifolds \(\mathcal {M}_L\) and \(\mathcal {M}_R\) as in Fig. 9, one can use the travelling wave solutions of the Nagumo LDE discussed in Sect. 2.2 to construct front and back connections \((\phi _f, 0)\) and \((\phi _b, w_*)\) between \(\mathcal {M}_L\) and \(\mathcal {M}_R\) that both travel at the same wave speed \(c_*\) that we assume to be positive. These connections can be combined with segments of \(\mathcal {M}_L\) and \(\mathcal {M}_R\) to form the (fast) singular orbit \(\varGamma _0\) depicted on the left in Fig. 9.
The main goal is to show that that this singular orbit can be continued into a branch of regular orbits \(\varGamma (\epsilon )\) for small \(\epsilon > 0\). In the PDE case, a typical proof proceeds by showing that the unstable manifold of (0, 0) intersects the stable manifold of \(\mathcal {M}_L\) in a transverse fashion, using the Exchange Lemma [110] to study the passage of these manifolds near \(\mathcal {M}_R\). Such an analysis relies on the Hadamard graph transform and the Fenichel normal form to describe the dynamics near \(\mathcal {M}_L\) and \(\mathcal {M}_R\). Unfortunately, these tools are not readily available in infinite dimensional settings.
The main contribution in [100] is that analytical constructions are used to underpin the geometric intuition behind the ideas described above. Building on earlier work by Sakamoto [139], we used the exponential dichotomies discussed in Sect. 2.1 to construct a branch of global invariant manifolds for \(\mathcal {M}_L\) and \(\mathcal {M}_R\) that persist for small \(\epsilon > 0\). The analytic proof of the exchange lemma developed by Krupa, Sandstede and Szmolyan in [118] could subsequently be combined with the Lin’s method machinery discussed in Sect. 2.1 to construct quasi-solutions to (187). These solutions have two discontinuities that can both be captured in one-dimensional spaces and quantified by means of the Hale inner product (44); see the right panel in Fig. 9.
All that remains to construct the pulse solutions for (187) is to close these two gaps. This can be done by analyzing the associated two-component nonlinear bifurcation problem. Interestingly enough, the same setup can be used to reduce the spectral characterization of these pulses to a related two-dimensional problem involving the spectral parameter \(\lambda \); see [101].
The structure of these bifurcation equations is almost identical to their counterparts for the PDE (185). In particular, this allows the existence and nonlinear stability of travelling pulse solutions for the LDE (184) to be obtained.
5.2 Periodic Diffusion
Recent developments in optical nanoscopy clearly show [49, 50, 159] that certain proteins in the cytoskeleton of nerve fibres are organized periodically. This periodicity turns out to be a universal feature of all nerve systems, not just those which are insulated with a myelin coating. Since it also manifests itself at the nodes of Ranvier, it is natural to allow the parameters in (184) to vary in a periodic fashion.
In particular, let us consider the LDE
with 2-periodic diffusion coefficients
Note that we are now using \(\rho >0\) for the recovery speed variable in order to emphasize that the relevant scale separation is now contained in the diffusion coefficients.
Searching for solutions of the form
we obtain the travelling wave system
Multiplying the first line of (191) by \(\epsilon ^2\) and taking the limit \(\epsilon \downarrow 0\), we obtain the formal relation
between the singular waveprofiles \(\overline{\phi }_o\) and \(\overline{\phi }_e\). The limiting even subsystem hence decouples from the odd system and formally satisfies
This is simply a spatially rescaled version of the travelling wave equation for the FitzHugh–Nagumo LDE (184) with constant diffusion. In particular, the results in Sect. 5.1 guarantee that this even limiting system has pulse solutions that are spectrally stable for small \(\rho > 0\).
The main results in [142] state that any spectrally stable solution to the limiting system (193) can be extended to a branch of nonlinearly stable travelling wave solutions (190) to the full 2-periodic system (188) for small values of \(\epsilon > 0\). This is hence another singular perturbation result, but the underlying bifurcation at \(\epsilon =0\) is of a completely different nature than in Sect. 5.1.
The key ingredient behind the proof of this result is the realization that the spirit of the spectral convergence technique discussed in Sect. 2.2 can be used to study a wide range of singular limits for families of differential operators. The main technical complication that needs to be overcome in the current context is that the four components of (191) and their derivatives need to be rescaled with various powers of \(\epsilon \) before taking the appropriate limits.
5.3 Infinite-Range Interactions
Recently, an active interest has arisen in non-local equations that feature infinite-range interactions. Neural field models for example aim to describe the dynamics of large networks of neurons, which interact with each other by exchanging signals across long distances through their interconnecting nerve axons [22, 23, 133, 147]. One model that has been proposed [22, Eq. (3.31)] to describe these complex interactions features a FitzHugh–Nagumo type system with infinite-range interactions.
Motivated by the above, the results in [69, 143] consider a class of infinite-range FitzHugh–Nagumo LDEs that includes the prototype
in which \(h>0\) represents the grid-spacing. By replacing the phase-space approach in Sect. 5.1 with Fredholm-based functional-analytic considerations, Faye and Scheel were able [69] to obtain the existence of travelling pulses to (194) for arbitrary \(h > 0\), provided that \(\rho > 0\) is sufficiently small.
In [143] the nonlinear stability of these pulses was established in the continuum regime where \(h > 0\) is sufficiently small. On the other hand, the only requirement on \(\rho > 0\) is that a spectrally stable travelling pulse exists for the FitzHugh–Nagumo PDE that arises as the formal \(h \downarrow 0\) limit of (194). In particular, the two main insights obtained in [143] are that the spectral convergence method discussed in Sect. 2.2 can be generalized to multi-component systems and that it can also be used to study the spectral properties of the constructed solutions.
The latter point turns out to be rather subtle. To see this, let us write \(\mathcal {L}^{(h)}_{\mathrm {tw}}\) for the linearization of (194) around the pulse solution corresponding to the grid size \(h > 0\). For a fixed \(\lambda \ne 0\) with \(\mathfrak {R}\lambda \ge 0\), the spectral convergence method can be used to show that the operator \(\mathcal {L}^{(h)}_{\mathrm {tw}} - \lambda \) is invertible for small \(h > 0\). However, for a spectral stability argument one must consider all such \(\lambda \) simultaneously for a fixed small \(h>0\). This requires careful control on all the parameter dependencies appearing in the problem.
6 Applications to Numerical Analysis
The primary motivation behind the papers discussed in this section is to contribute to the on-going systematic approach to understand the impact of discretization schemes on the dynamics that they are designed to capture. Of course, there is a tremendous amount of literature concerning the accuracy of numerical schemes, but these studies typically focus on finite time error bounds [117, 120]. Our concern here is more related to the persistence of structures that exist for all time. Interesting pioneering work on this topic can be found in [19, 77], where the authors discuss the impact of discretization on attractors for ODEs and PDEs.
We take one step further here and study in what sense individual stable travelling structures such as waves survive common discretization techniques. Building on previous work in [59,60,61], we study full spatial-temporal discretizations of the Nagumo PDE in Sect. 6.1, restricting our attention to grids that are fixed in space and time. We loosen this restriction in Sect. 6.2, where we allow the spatial grid to adjust itself to the shape of the solution.
6.1 Spatial-Temporal Discretizations
In [104] we revisited the spatially-discrete Nagumo LDE (21) and set out to replace the remaining temporal derivative by an appropriate discretized operator. We considered the family of six Backward Differentiation Formula (BDF) methods, which are multistep methods that admit good numerical stability properties for parabolic equations. They are referred to as regular methods, which means that they don’t create or destroy equilibrium solutions. For our purposes here they are relatively easy to analyze, since they do not involve any of the intermediate stage values that are required by many popular one-step methods. Related results for the standard forward Euler scheme can be found in [39], but the smaller stability region severely limits the time-steps that can be used.
The first order BDF method coincides with the backward Euler scheme. Applying this to the LDE (21) with \(d =1\) and time-step \(\varDelta t\), we arrive at the fully discretized system
Systems of this type are often referred to as coupled map lattices (CMLs). They are of independent interest and have been used for a wide range of purposes, including the construction of hash functions [157] and the study of population dynamics [48].
The main contribution in [104] is the construction of fully discretized travelling wave solutions
to (195). Such fronts must satisfy the difference equation
By a peculiar coincidence, this equation fits into the global homotopy framework of [126] that we discussed in Sect. 2.2, after adding an artificial term \(\tilde{c} \varPhi '(\xi )\) to the left hand side. Indeed, solutions to (197) live inside the parameter region of this artificially enhanced system where \(\tilde{c} =0\). As we have seen, such pinning regions generically encompass an open set of detuning parameters a.
As a consequence, it is natural to conjecture that the a(c) relation for (197) can be multi-valued even for \(c \ne 0\). This is confirmed by the numerical results in Fig. 10, which shows the upper and lower bounds \(a^\pm (c)\) of the detuning parameter a for which (196)–(197) admits a solution \(\varPhi \). For comparison, the curve \(a_0(c)\) gives the corresponding a(c) relation for the semi-discrete problem (22) with \(d=1\). We note that monostable KPP systems [132] in the presence of inhomogeneities have been found to exhibit similar behaviour.
Range of a for which fully discrete traveling wave solutions exist for BDF methods of first and second order, compared to the corresponding curve \(a_0(c)\) for the spatially discrete problem. For these computations we used \(\varDelta t = 2\) and we replaced g by the nonlinearity \(\frac{121}{12} u ( 1- u)(u-a)\); see [104]
Let us write \((\overline{c}, \overline{\varPhi })\) for the solution to the semi-discrete travelling wave MFDE (22) with \(d = 1\). The key technical ingredient in our construction of solutions to (196)–(197) is the understanding of the fully discrete operator
for \(\xi \) in an appropriate subset of \(\mathbb {R}\). This operator is associated to the linearization of (195) around the pair \((\overline{c}, \overline{\varPhi })\). The main question is whether this operator inherits properties from its semi-discrete counterpart \(\mathcal {L}_{\mathrm {tw}}\) defined in (24). This highly singular transition can be analyzed by a variant of the spectral convergence technique described in Sect. 2.2. The main complication in this setting is that the natural domain for \(\xi \) varies from the whole line to a subset of the line, which required the use of a delicate interpolation procedure.
6.2 Adaptive Grids
Most efficient modern solvers concentrate their meshpoints in areas where the solution under consideration fluctuates the most. This often leads to a significant increase in performance compared to fixed-grid algorithms. In order to explore this, let us write \(\{ x_j(t) \}\) for the positions of the grid points and introduce the approximants
Instead of approximating the second derivative in (3) by the standard second difference
we can now apply the non-uniform discretization
In particular, by differentiating (199) and inspecting (3), we arrive at the LDE
In order to close this system, we need to specify a rule for computing the gridpoint velocity \(\dot{x}_j(t)\). This is usually achieved by formulating an elliptic or parabolic equation that incorporates the local behaviour of the solution U. The approach taken in many codes to solve two point boundary value problems is to distribute a suitable prediction for the numerical error equally along each mesh-interval. Indeed, for accuracy and efficiency a fine mesh is desired where the solution changes rapidly and a course mesh is sufficient where the solution is relatively constant.
In [102] we considered moving mesh equations that aim to equidistribute the arclength of the numerical solution. In particular, we use the MMPDE5 [90] grid update scheme, which can be written as
for some tunable coefficient \(\tau \ge 0\) that determines the speed of the gridpoints. We studied the limiting case \(\tau =0\), which means that the mesh instantaneously adjusts itself to equalize the arclength of the solution U between neighbouring gridpoints. This allows us to pick a constant \(h > 0\) for which
holds for all \(j \in \mathbb {Z}\) and \(t \ge 0\). The boundary condition \(x_j(t) \rightarrow jh \) as \(j \rightarrow - \infty \) subsequently fixes the mesh in a unique fashion. The quantity \(h > 0\) can hence be seen as the ‘background’ grid size that is observed in regions where U is flat.
The main results in [102] state that for each sufficiently small \(h > 0\), the resulting coupled system admits a travelling wave solution
that is unique up to translation. Upon introducing the wave variable \(\xi = x_j(t) + ct\), we note that the grid spacing can be recovered from such wave solutions by writing
for a pair of suitably chosen functions \(h_\pm \). The second difference (201) for this wave can now be written as
The full wave equation for the pair \((c, \phi )\) will hence become an MFDE with state-dependent advances and shifts, for which hardly any theory is available.
Fortunately, this issue can be avoided by using the computational coordinates \(\tau = jh + ct\) instead of the physical coordinates \(\xi \). However, it is a delicate and cumbersome task to switch between the two points of view. An interesting consequence is that the correct linear operator that needs to be understood for \(h =0\) is not the standard linearization (61), but rather a spatially stretched version that takes into account the arclength equidistribution of the PDE waveprofile.
We are specially interested to uncover if and why the size of the pinning interval is smaller here when compared to stationary grids. In particular, this will give additional insight into the theoretical benefits of adaptive grids compared to the practical benefits of increased performance. Preliminary results pertaining to this issue can be found in [89].
Notes
- 1.
Actually, in order to ensure that the boundary conditions (23) are satisfied one needs to consider perturbations \(v \in W^{1,p}\) for \(1 \le p < \infty \) while taking \(\varPhi \in W^{1, \infty }\).
- 2.
Here we use modulo arithmetic on i.
References
Abell, K.A., Elmer, C.E., Humphries, A.R., Van Vleck, E.S.: Computation of mixed type functional differential boundary value problems. SIAM J. Appl. Dyn. Syst. 4, 755–781 (2005)
Alfaro, M., Droniou, J., Matano, H.: Convergence rate of the Allen-Cahn equation to generalized motion by mean curvature. J. Evol. Equ. 12(2), 267–294 (2012)
Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27(6), 1085–1095 (1979)
Anderson, T., Faye, G., Scheel, A., Stauffer, D.: Pinning and unpinning in nonlocal systems. J. Dyn. Differ. Equ. 28(3–4), 897–923 (2016)
Aronson, D.G., Weinberger, H.F.: Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. Partial differential equations and related topics (Program, Tulane Univ., New Orleans, La., 1974). Lecture Notes in Mathematics, vol. 446, pp. 5–49. Springer, Berlin (1975)
Aronson, D.G., Weinberger, H.F.: Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 30(1), 33–76 (1978)
Bakker, B.: Nonlinear waves in local and nonlocal media: a topological approach. Ph.D. Thesis (2019)
Bakker, B., Scheel, A.: Spatial Hamiltonian identities for nonlocally coupled systems. Forum of Mathematics, Sigma, vol. 6. Cambridge University Press, Cambridge (2018)
Barashenkov, I., Oxtoby, O., Pelinovsky, D.: Translationally invariant discrete kinks from one-dimensional maps. Phys. Rev. E 72, 035602 (2005)
Bates, P.W., Chen, F.: Spectral analysis and multidimensional stability of traveling waves for nonlocal Allen-Cahn equation. J. Math. Anal. Appl. 273(1), 45–57 (2002)
Bates, P.W., Chen, X., Chmaj, A.J.J.: Traveling waves of bistable dynamics on a lattice. SIAM J. Math. Anal. 35(2), 520–546 (2003)
Bates, P.W., Chmaj, A.: A discrete convolution model for phase transitions. Arch. Ration. Mech. Anal. 150, 281–305 (1999)
Beck, M., Hupkes, H.J., Sandstede, B., Zumbrun, K.: Nonlinear stability of semidiscrete shocks for two-sided schemes. SIAM J. Math. Anal. 42, 857–903 (2010)
Benzoni-Gavage, S., Huot, P.: Existence of semi-discrete shocks. Discret. Contin. Dyn. Syst. 8, 163–190 (2002)
Benzoni-Gavage, S., Huot, P., Rousset, F.: Nonlinear stability of semidiscrete shock waves. SIAM J. Math. Anal. 35, 639–707 (2003)
Berendsen, J.: Horizontal travelling waves on the lattice. Ph.D. thesis, Masters thesis, Leiden University (2015)
Berestycki, H., Hamel, F., Matano, H.: Bistable traveling waves around an obstacle. Commun. Pure Appl. Math. 62(6), 729–788 (2009)
Beyn, W.J.: The numerical computation of connecting orbits in dynamical systems. IMA J. Numer. Anal. 9, 379–405 (1990)
Beyn, W.J., Pilyugin, S.Y.: Attractors of reaction diffusion systems on infinite lattices. J. Dyn. Diff. Equ. 15, 485–515 (2003)
Beyn, W.-J., Thümmler, V.: Freezing solutions of equivariant evolution equations. SIAM J. Appl. Dyn. Syst. 3(2), 85–116 (2004)
Bhattacharya, K.: Microstructure of Martensite: Why it Forms and How it Gives Rise to the Shape-Memory Effect, Vol. 2. Oxford University Press, Oxford (2003)
Bressloff, P.C.: Spatiotemporal dynamics of continuum neural fields. J. Phys. A: Math. Theor. 45, 3 (2011)
Bressloff, P.C.: Waves in Neural Media: From Single Neurons to Neural Fields. Lecture Notes on Mathematical Modeling in the Life Sciences. Springer, Berlin (2014)
Brucal-Hallare, M., Van Vleck, E.: Traveling wavefronts in an antidiffusion lattice Nagumo model. SIAM J. Appl. Dyn. Syst. 10(3), 921–959 (2011)
Cahn, J.W.: Theory of crystal growth and interface motion in crystalline materials. Acta Metall. 8, 554–562 (1960)
Cahn, J.W., Chow, S.-N., Van Vleck, E.S.: Spatially discrete nonlinear diffusion equations. Rocky Mountain J. Math. 25(1), 87–118 (1995). Second Geoffrey J. Butler Memorial Conference in Differential Equations and Mathematical Biology (Edmonton, AB, 1992)
Cahn, J.W., Mallet-Paret, J., Van Vleck, E.S.: Traveling wave solutions for systems of ODE’s on a two-dimensional spatial lattice. SIAM J. Appl. Math. 59, 455–493 (1999)
Cahn, J.W., Novick-Cohen, A.: Evolution equations for phase separation and ordering in binary alloys. J. Stat. Phys. 76, 877–909 (1994)
Carpenter, G.: A geometric approach to singular perturbation problems with applications to nerve impulse equations. J. Differ. Equ. 23, 335–367 (1977)
Carter, P., de Rijk, B., Sandstede, B.: Stability of traveling pulses with oscillatory tails in the FitzHugh-Nagumo system. J. Nonlinear Sci. 26(5), 1369–1444 (2016)
Carter, P., Sandstede, B.: Fast pulses with oscillatory tails in the FitzHugh-Nagumo system. SIAM J. Math. Anal. 47(5), 3393–3441 (2015)
Celli, V., Flytzanis, N.: Motion of a screw dislocation in a crystal. J. Appl. Phys. 41(11), 4443–4447 (1970)
Chen, C., Choi, Y.: Traveling pulse solutions to FitzHugh-Nagumo equations. Calc. Var. Partial Differ. Equ. 54(1), 1–45 (2015)
Chen, X.: Existence, uniqueness and asymptotic stability of traveling waves in nonlocal evolution equations. Adv. Differ. Equ. 2, 125–160 (1997)
Chen, X., Guo, J.-S., Wu, C.-C.: Traveling waves in discrete periodic media for bistable dynamics. Arch. Ration. Mech. Anal. 189(2), 189–236 (2008)
Chen, X., Guo, J.S., Wu, C.C.: Traveling waves in discrete periodic media for bistable dynamics. Arch. Ration. Mech. Anal. 189, 189–236 (2008)
Chen, X., Hastings, S.P.: Pulse waves for a semi-discrete Morris-Lecar type model. J. Math. Bio. 38, 1–20 (1999)
Chi, H., Bell, J., Hassard, B.: Numerical solution of a nonlinear advance-delay-differential equation from nerve conduction theory. J. Math. Bio. 24, 583–601 (1986)
Chow, S.-N., Mallet-Paret, J., Shen, W.: Traveling waves in lattice dynamical systems. J. Differ. Equ. 149(2), 248–291 (1998)
Chow, S.-N., Mallet-Paret, J., Van Vleck, E.S.: Pattern formation and spatial chaos in spatially discrete evolution equations. Random Comput. Dyn. 4(2–3), 109–178 (1996)
Chua, L.O., Yang, L.: Cellular neural networks: applications. IEEE Trans. Circuits Syst. 35, 1273–1290 (1988)
Chua, L.O., Yang, L.: Cellular neural networks: theory. IEEE Trans. Circuits Syst. 35, 1257–1272 (1988)
Cook, H., de Fontaine, D., Hilliard, J.: A model for diffusion on cubic lattices and its application to the early stages of ordering. Acta Metall. 17, 765–773 (1969)
Cornwell, P.: Opening the Maslov Box for Traveling Waves in Skew-Gradient Systems (2017). arXiv:1709.01908
Cornwell, P., Jones, C.K.R.T.: On the existence and stability of fast traveling waves in a doubly-diffusive FitzHugh-Nagumo system. SIAM J. Appl. Dyn. Syst. 17(1), 754–787 (2018)
Cuevas, J., English, L.Q., Kevrekidis, P., Anderson, M.: Discrete breathers in a forced-damped array of coupled pendula: modeling, computation, and experiment. Phys. Rev. Lett. 102(22), 224101 (2009)
Dauxois, T., Peyrard, M., Bishop, A.R.: Dynamics and thermodynamics of a nonlinear model for DNA denaturation. Phys. Rev. E 47, 684–695 (1993)
de Camino-Beck, T., Lewis, M.: Invasion with stage-structured coupled map lattices: application to the spread of scentless chamomile. Ecol. Modell. 220(23), 3394–3403 (2009)
D’Este, E., Kamin, D., Göttfert, F., El-Hady, A., Hell, S.E.: STED nanoscopy reveals the ubiquity of subcortical cytoskeleton periodicity in living neurons. Cell Rep. 10(8), 1246–1251 (2015)
D’Este, E., Kamin, D., Velte, C., Göttfert, F., Simons, M., Hell, S.E.: Subcortical cytoskeleton periodicity throughout the nervous system. Sci. Rep. 6(6), 22741 (2016)
Diekmann, O., van Gils, S.A., Verduyn-Lunel, S.M., Walther, H.O.: Delay Equations. Springer, New York (1995)
Dmitriev, S.V., Abe, K., Shigenari, T.: Domain wall solutions for EHM model of crystal: structures with period multiple of four. Phys. D: Nonlinear Phenom. 147(1–2), 122–134 (2000)
Dmitriev, S.V., Kevrekidis, P.G., Yoshikawa, N.: Discrete Klein-Gordon models with static kinks free of the Peierls-Nabarro potential. J. Phys. A. 38, 7617–7627 (2005)
Elmer, C.E.: Finding stationary fronts for a discrete Nagumo and wave equation; construction. Phys. D 218, 11–23 (2006)
Elmer, C.E., Van Vleck, E.S.: Computation of traveling waves for spatially discrete bistable reaction-diffusion equations. Appl. Numer. Math. 20, 157–169 (1996)
Elmer, C.E., Van Vleck, E.S.: Analysis and computation of traveling wave solutions of bistable differential-difference equations. Nonlinearity 12, 771–798 (1999)
Elmer, C.E., Van Vleck, E.S.: Traveling wave solutions for bistable differential difference equations with periodic diffusion. SIAM J. Appl. Math. 61, 1648–1679 (2001)
Elmer, C.E., Van Vleck, E.S.: A variant of Newton’s method for the computation of traveling waves of bistable differential-difference equations. J. Dyn. Differ. Equ. 14, 493–517 (2002)
Elmer, C.E., Van Vleck, E.S.: Anisotropy, propagation failure, and wave speedup in traveling waves of discretizations of a Nagumo PDE. J. Comput. Phys. 185(2), 562–582 (2003)
Elmer, C.E., Van Vleck, E.S.: Existence of monotone traveling fronts for BDF discretizations of bistable reaction-diffusion equations. Dyn. Contin. Discret. Impuls. Syst. Ser. A Math. Anal. 10(1–3), 389–402 (2003). Second International Conference on Dynamics of Continuous, Discrete and Impulsive Systems (London, ON, 2001)
Elmer, C.E., Van Vleck, E.S.: Dynamics of monotone travelling fronts for discretizations of Nagumo PDEs. Nonlinearity 18, 1605–1628 (2005)
Elmer, C.E., Van Vleck, E.S.: Spatially Discrete FitzHugh-Nagumo Equations. SIAM J. Appl. Math. 65, 1153–1174 (2005)
English, L.Q., Thakur, R.B., Stearrett, R.: Patterns of traveling intrinsic localized modes in a driven electrical lattice. Phys. Rev. E 77, 066601 (2008)
Ermentrout, B.: Neural networks as spatio-temporal pattern-forming systems. Rep. Prog. Phys. 61(4), 353 (1998)
Erneux, T., Nicolis, G.: Propagating waves in discrete bistable reaction-diffusion systems. Phys. D 67, 237–244 (1993)
Evans, L.C., Soner, H.M., Souganidis, P.E.: Phase transitions and generalized motion by mean curvature. Commun. Pure Appl. Math. 45(9), 1097–1123 (1992)
Fath, G.: Propagation failure of traveling waves in a discrete bistable medium. Phys. D 116, 176–190 (1998)
Faye, G., Scheel, A.: Fredholm properties of nonlocal differential operators via spectral flow. Indiana Univ. Math. J. 63, 1311–1348 (2014)
Faye, G., Scheel, A.: Existence of pulses in excitable media with nonlocal coupling. Adv. Math. 270, 400–456 (2015)
Faye, G., Scheel, A.: Center manifolds without a phase space. Trans. Am. Math. Soc. 370(8), 5843–5885 (2018)
Fiedler, B., Scheurle, J.: Discretization of homoclinic orbits, rapid forcing and “invisible” chaos. Mem. Am. Math. Soc. 119(570) (1996)
Fife, P.C., McLeod, J.B.: The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal. 65(4), 335–361 (1977)
FitzHugh, R.: Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1, 445–466 (1966)
FitzHugh, R.: Mathematical Models of Excitation and Propagation in Nerve. Publisher Unknown (1966)
Fitzhugh, R.: Motion picture of nerve impulse propagation using computer animation. J. Appl. Physiol. 25(5), 628–630 (1968)
Flach, S., Zolotaryuk, Y., Kladko, K.: Moving lattice kinks and pulses: an inverse method. Phys. Rev. E 59, 6105–6115 (1999)
Grüne, L.: Attraction rates, robustness, and discretization of attractors. SIAM J. Numer. Anal. 41(6), 2096–2113 (2003)
Hale, J.K., Verduyn-Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (1993)
Haragus, M., Scheel, A.: Almost planar waves in anisotropic media. Commun. Partial Differ. Equ. 31(5), 791–815 (2006)
Haragus, M., Scheel, A.: Corner defects in almost planar interface propagation. Annales de l’Institut Henri Poincare (C) Non Linear Analysis, vol. 23, pp. 283–329. Elsevier, New York (2006)
Haragus, M., Scheel, A.: A bifurcation approach to non-planar traveling waves in reaction-diffusion systems. GAMM-Mitteilungen 30(1), 75–95 (2007)
Härterich, J., Sandstede, B., Scheel, A.: Exponential dichotomies for linear non-autonomous functional differential equations of mixed type. Indiana Univ. Math. J. 51(5), 1081–1109 (2002)
Hastings, S.: On travelling wave solutions of the Hodgkin-Huxley equations. Arch. Ration. Mech. Anal. 60, 229–257 (1976)
Hillert, M.: A solid-solution model for inhomogeneous systems. Acta Metall. 9, 525–535 (1961)
Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117 (1952)
Hoffman, A., Hupkes, H.J., Van Vleck, E.S.: Multi-dimensional stability of waves travelling through rectangular lattices in rational directions. Trans. Am. Math. Soc. 367(12), 8757–8808 (2015)
Hoffman, A., Hupkes, H.J., Van Vleck, E.S.: Entire solutions for bistable lattice differential equations with obstacles. Mem. Am. Math. Soc. 250(1188), 1–119 (2017)
Hoffman, A., Mallet-Paret, J.: Universality of crystallographic pinning. J. Dyn. Differ. Equ. 22, 79–119 (2010)
Huang, W., Hupkes, H.J., Lozada-Cruz, G., Van Vleck, E.S.: Propagation failure for traveling waves of reaction-diffusion equations under moving mesh discretization. In preparation
Huang, W., Russell, R.D.: Adaptive mesh movement in 1D. Adaptive Moving Mesh Methods, pp. 27–135. Springer, Berlin (2011)
Humphries, A.R., Moore, B.E., Van Vleck, E.S.: Front solutions for bistable differential-difference equations with inhomogeneous diffusion. SIAM J. Appl. Math. 71(4), 1374–1400 (2011)
Hupkes, H.J.: Invariant Manifolds and Applications for Functional Differential Equations of Mixed Type. Ph.D. Thesis(2008)
Hupkes, H.J., Augeraud-Véron, E.: Well-Posedness of Initial Value Problems for Vector-Valued Functional Differential Equations of Mixed Type. Preprint
Hupkes, H.J., Morelli, L.: Travelling Corners for Spatially Discrete Reaction-Diffusion System. Pure Appl. Anal. (2019). arXiv:1901.02319
Hupkes, H.J., Morelli, L., Stehlík, P.: Bichromatic travelling waves for lattice Nagumo equations. SIAM J. Appl. Dyn. Syst. 18.2(2019), 973–1014 (2018). arXiv:1805.10977
Hupkes, H.J., Morelli, L., Stehlík, P., Švígler, V.: Counting and ordering periodic stationary solutions of lattice Nagumo equations. Appl. Math. Lett. (2019). arXiv:1905.06107v1
Hupkes, H.J., Morelli, L., Stehlík, P., Švígler, V.: Multichromatic travelling waves for lattice Nagumo equations. Appl. Math. Comput. 361(2019), 430–452 (2019). arXiv:1901.07227
Hupkes, H.J., Pelinovsky, D., Sandstede, B.: Propagation failure in the discrete Nagumo equation. Proc. Am. Math. Soc. 139(10), 3537–3551 (2011)
Hupkes, H.J., Sandstede, B.: Modulated Wave Trains for Lattice Differential Systems. J. Dyn. Differ. Equ. 21, 417–485 (2009)
Hupkes, H.J., Sandstede, B.: Travelling pulse solutions for the discrete FitzHugh-Nagumo system. SIAM J. Appl. Dyn. Syst. 9, 827–882 (2010)
Hupkes, H.J., Sandstede, B.: Stability of Pulse Solutions for the Discrete FitzHugh-Nagumo System. Trans. AMS 365, 251–301 (2013)
Hupkes, H.J., Van Vleck, E.S.: Travelling Waves for Adaptive Grid Discretizations of Reaction-Diffusion Systems. Preprint
Hupkes, H.J., Van Vleck, E.S.: Negative diffusion and traveling waves in high dimensional lattice systems. SIAM J. Math. Anal. 45(3), 1068–1135 (2013)
Hupkes, H.J., Van Vleck, E.S.: Travelling waves for complete discretizations of reaction diffusion systems. J. Dyn. Differ. Equ. 28(3–4), 955–1006 (2016)
Hupkes, H.J., Verduyn-Lunel, S.M.: Analysis of Newton’s method to compute travelling waves in discrete media. J. Dyn. Differ. Equ. 17, 523–572 (2005)
Hupkes, H.J., Verduyn-Lunel, S.M.: Center manifold theory for functional differential equations of mixed type. J. Dyn. Differ. Equ. 19, 497–560 (2007)
Hupkes, H.J., Verduyn-Lunel, S.M.: Center manifolds for periodic functional differential equations of mixed type. J. Differ. Equ. 245, 1526–1565 (2008)
Hupkes, H.J., Verduyn-Lunel, S.M.: Lin’s method and homoclinic bifurcations for functional differential equations of mixed type. Indiana Univ. Math. J. 58, 2433–2487 (2009)
Jones, C.K.R.T.: Stability of the travelling wave solutions of the FitzHugh-Nagumo system. Trans. AMS 286, 431–469 (1984)
Jones, C.K.R.T., Kopell, N., Langer, R.: Construction of the FitzHugh-Nagumo pulse using differential forms. In: Swinney, H., Aris, G., Aronson, D.G. (eds.) Patterns and Dynamics in Reactive Media. IMA Volumes in Mathematics and its Applications, vol. 37, pp. 101–116. Springer, New York (1991)
Kapitula, T.: Multidimensional stability of planar travelling waves. Trans. Am. Math. Soc. 349(1), 257–269 (1997)
Kawasaki, K., Ohta, T.: Kinetic drumhead model of interface I. Prog. Theor. Phys. 67(1), 147–163 (1982)
Keener, J., Sneed, J.: Mathematical Physiology. Springer, New York (1998)
Keener, J.P.: Propagation and its failure in coupled systems of discrete excitable cells. SIAM J. Appl. Math. 47, 556–572 (1987)
Keener, J.P.: Propagation of waves in an excitable medium with discrete release sites. SIAM J. Appl. Math. 61(1), 317–334 (2000)
Kevrekidis, P., Frantzeskakis, D., Theocharis, G., Kevrekidis, I.: Guidance of matter waves through Y-junctions. Phys. Lett. A 317(5), 513–522 (2003)
Kleefeld, B., Khaliq, A., Wade, B.: An ETD Crank-Nicolson method for reaction-diffusion systems. Numer. Methods PDEs 28(4), 1309–1335 (2012)
Krupa, M., Sandstede, B., Szmolyan, P.: Fast and slow waves in the FitzHugh-Nagumo equation. J. Differ. Equ. 133, 49–97 (1997)
Lamb, C., Van Vleck, E.S.: Neutral mixed type functional differential equations. J. Dyn. Differ. Equ. 28(3–4), 763–804 (2016)
Lax, P.D., Richtmyer, R.D.: Survey of the stability of linear finite difference equations. Commun. Pure Appl. Math. 9(2), 267–293 (1956)
Lederer, F., Stegeman, G.I., Christodoulides, D.N., Assanto, G., Segev, M., Silberberg, Y.: Discrete solitons in optics. Phys. Rep. 463(1–3), 1–126 (2008)
Lillie, R.S.: Factors affecting transmission and recovery in the passive iron nerve model. J. General Physiol. 7, 473–507 (1925)
Lin, X.B.: Using Melnikov’s method to Solve Shilnikov’s problems. Proc. Roy. Soc. Edinb. 116, 295–325 (1990)
Mallet-Paret, J.: Spatial patterns, spatial chaos and traveling waves in lattice differential equations. In: Stochastic and Spatial Structures of Dynamical Systems, Royal Netherlands Academy of Sciences. Proceedings, Physics Section. Series 1, Vol. 45. Amsterdam, pp. 105–129 (1996)
Mallet-Paret, J.: The Fredholm alternative for functional-differential equations of mixed type. J. Dyn. Differ. Equ. 11(1), 1–47 (1999)
Mallet-Paret, J.: The global structure of traveling waves in spatially discrete dynamical systems. J. Dynam. Differ. Equ. 11(1), 49–127 (1999)
Mallet-Paret, J.: Crystallographic Pinning: Direction Dependent Pinning in Lattice Differential Equations. Citeseer (2001)
Mallet-Paret, J., Verduyn-Lunel, S.M.: Exponential dichotomies and Wiener-Hopf factorizations for mixed-type functional differential equations. J. Differ. Equ. (to appear)
Merks, R.M., Van de Peer, Y., Inzé, D., Beemster, G.T.: Canalization without flux sensors: a traveling-wave hypothesis. Trends Plant Sci. 12(9), 384–390 (2007)
Morelli, L.: Travelling Patterns on Discrete Media. Ph.D. Thesis (2019) http://pub.math.leidenuniv.nl/~morellil/Thesis.pdf
Mukherjee, S., Spracklen, A., Choudhury, D., Goldman, N., Öhberg, P., Andersson, E., Thomson, R.R.: Observation of a localized flat-band state in a photonic lieb lattice. Phys. Rev. Lett. 114, 245504 (2015)
Nolen, J., Roquejoffre, J.-M., Ryzhik, L., Zlatoš, A.: Existence and non-existence of fisher-KPP transition fronts. Arch. Ration. Mech. Anal. 203(1), 217–246 (2012)
Pinto, D.J., Ermentrout, G.B.: Spatially structured activity in synaptically coupled neuronal networks: 1. Traveling fronts and pulses. SIAM J. Appl. Math. 62, 206–225 (2001)
Qin, W.-X., Xiao, X.: Homoclinic orbits and localized solutions in nonlinear Schrödinger lattices. Nonlinearity 20, 2305–2317 (2007)
Ranvier, L.A.: Lećons sur l’Histologie du Système Nerveux, par M. L. Ranvier, recueillies par M. Ed. Weber. F. Savy, Paris (1878)
Roosen, A.R., McCormack, R.P., Carter, W.C.: Wulffman: a tool for the calculation and display of crystal shapes. Comput. Mater. Sci. 11(1), 16–26 (1998)
Rustichini, A.: Functional-differential equations of mixed type: the linear autonomous case. J. Dyn. Differ. Equ. 1(2), 121–143 (1989)
Rustichini, A.: Hopf bifurcation for functional-differential equations of mixed type. J. Dyn. Differ. Equ. 1(2), 145–177 (1989)
Sakamoto, K.: Invariant manifolds in singular perturbation Problems. Proc. Roy. Soc. Edinb. A 116, 45–78 (1990)
Scheel, A., Tikhomirov, S.: Depinning asymptotics in ergodic media. In: International Conference on Patterns of Dynamics, pp. 88–108. Springer (2016)
Scheel, A., Van Vleck, E.S.: Lattice differential equations embedded into reaction-diffusion systems. Proc. Roy. Soc. Edinb. Sect. A 139(1), 193–207 (2009)
Schouten-Straatman, W.M., Hupkes, H.J.: Travelling waves for spatially discrete systems of FitzHugh-Nagumo type with periodic coefficients. SIAM J. Math. Anal. 51(4), 3492–3532 (2018). arXiv:1808.00761
Schouten-Straatman, W.M., Hupkes, H.J.: Nonlinear stability of pulse solutions for the discrete FitzHugh-Nagumo equation with infinite-range interactions. Discret. Contin. Dyn. Syst. A 39(9) (2019)
Sen, S., Hong, J., Bang, J., Avalos, E., Doney, R.: Solitary waves in the granular chain. Phys. Rep. 462(2), 21–66 (2008)
Slavík, A.: Invariant regions for systems of lattice reaction-diffusion equations. J. Differ. Equ. 263(11), 7601–7626 (2017)
Slepyan, L.I.: Models and Phenomena in Fracture Mechanics (2012). Springer Science & Business Media
Sneyd, J.: Mathematical modeling of calcium dynamics and signal transduction. Tutorials in Mathematical Biosciences II. Lecture Notes in Mathematics, vol. 187. Springer, New York (2005)
Speight, J.M.: Topological discrete kinks. Nonlinearity 12, 1373–1387 (1999)
Stehlík, P.: Exponential number of stationary solutions for Nagumo equations on graphs. J. Math. Anal. Appl. 455(2), 1749–1764 (2017)
Tagantsev, A.K., Cross, L.E., Fousek, J.: Domains in Ferroic Crystals and Thin Films. Springer, Berlin (2010)
Tonnelier, A.: McKean Caricature of the FitzHugh-Nagumo model: traveling pulses in a discrete diffusive medium. Phys. Rev. E 67, 036105 (2003)
Vainchtein, A., Van Vleck, E.S.: Nucleation and propagation of phase mixtures in a bistable chain. Phys. Rev. B 79, 144123 (2009)
Vainchtein, A., Van Vleck, E.S., Zhang, A.: Propagation of periodic patterns in a discrete system with competing interactions. SIAM J. Appl. Dyn. Syst. 14(2), 523–555 (2015)
van Hal, B.: Travelling Waves in Discrete Spatial Domains. Bachelor Thesis (2017)
Van Vleck, E.S., Zhang, A.: Competing interactions and traveling wave solutions in lattice differential equations. Commun. Pure Appl. Anal. 15(2), 457–475 (2016)
Vicencio, R.A., Cantillano, C., Morales-Inostroza, L., Real, B., Mejía-Cortés, C., Weimann, S., Szameit, A., Molina, M.I.: Observation of localized states in Lieb photonic lattices. Phys. Rev. Lett. 114, 245503 (2015)
Wang, Y., Liao, X., Xiao, D., Wong, K.-W.: One-way hash function construction based on 2D coupled map lattices. Inf. Sci. 178(5), 1391–1406 (2008)
Wolf, P.E., Balibar, S., Gallet, F.: Experimental observation of a third roughening transition on hcp He 4 crystals. Phys. Rev. Lett. 51(15), 1366 (1983)
Xu, K., Zhong, G., Zhuang, X.: Actin, spectrin, and associated proteins form a periodic cytoskeletal structure in axons. Science 339(6118), 452–456 (2013)
Zumbrun, K.: Instantaneous shock location and one-dimensional nonlinear stability of viscous shock waves. Q. Appl. Math. 69(1), 177–202 (2011)
Zumbrun, K., Howard, P.: Pointwise semigroup methods and stability of viscous shock waves. Indiana Univ. Math. J. 47(3), 741–871 (1998)
Acknowledgements
HJH, LM and WSS acknowledge support from the Netherlands Organization for Scientific Research (NWO) (grants 639.032.612 and 613.001.304). EVV was supported in part by NSF grant # DMS-1714195.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Hupkes, H.J., Morelli, L., Schouten-Straatman, W.M., Van Vleck, E.S. (2020). Traveling Waves and Pattern Formation for Spatially Discrete Bistable Reaction-Diffusion Equations. In: Bohner, M., Siegmund, S., Šimon Hilscher, R., Stehlík, P. (eds) Difference Equations and Discrete Dynamical Systems with Applications. ICDEA 2018. Springer Proceedings in Mathematics & Statistics, vol 312. Springer, Cham. https://doi.org/10.1007/978-3-030-35502-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-35502-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35501-2
Online ISBN: 978-3-030-35502-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)