Parametric Vibrations of Functionally Graded Sandwich Plates with Complex Forms

Abstract

Buckling behavior and parametric vibrations of sandwich plates with arbitrary forms and made of isotropic and functionally graded materials (FGM) are studied. Different types of lamination schemes were considered: a sandwich plate with FGM face sheets and isotropic (metal or ceramic) core and a plate with a FGM core and ceramics or metal on top and bottom face sheets. Effective material properties are computed according to Voigt’s rule in thickness direction. To calculate mechanical characteristics for different types of lamination schemes, the analytical expressions were obtained. The formulation of the problem was carried out using the first-order shear deformation theory (FSDT) of the plate. A subcritical state of the plate was taken into account.

1 Introduction

Nowadays, functionally graded materials (FGM) are widely used in many fields of industry as heat-resistant thin-constructed elements. There are many published papers devoted to studying the dynamic and static behavior of FGM plates and shells as designed objects [1, 2] and others. The application of FGM can help reduce mechanically and thermally induced stresses caused by the material properties mismatch as well as improves the bonding strength in the case of coatings and laminated facings. This explains the growing interest in studying laminated composite and sandwich plates often used in modern engineering applications. Many theories and methods for the mathematic modeling and analysis of such elements have been proposed [3,4,5]. Among these methods, one of an important method is Ritz’s method. It is known that one of the main difficulties related with the use of Ritz’s method in case of the complex plate geometry is a choice of a basic system of functions that satisfy the boundary conditions. In this work, the R-functions theory [6] is used for solving this problem. Earlier, Ritz’s variational method and the R-functions theory (RFM) have been effectively applied for investigation of vibration of layered plates and shallow shells [7, 8].

In this study, we first develop RFM to research of linear and parametric vibrations of FG sandwich plates using the first-order shear deformation theory (FSDT). The plate is composed of three layers, one or two of which are functionally graded in the thickness direction. Material properties of the FGM are calculated by power law. Pre-buckling state is taken into account. Proposed algorithm is applied to square plate with two cut outs. Initial nonlinear system with partial derivatives is reduced to Mathieu equation by method proposed authors earlier in [8].

2 Mathematical Problem

Let us consider a sandwich plate with a metal core and FGM facing (Type A) and a sandwich plate with a FGM core and the lower layer made of ceramic and upper layer made of metal (Type B). It is considered that the FGM layers are made of a mixture of ceramics and metals. The thickness of the layers from the bottom to the top h ⁽¹⁾, h ⁽²⁾, h ⁽³⁾ can be varied. The general thickness h is a constant defined as a sum h = h ⁽¹⁾ + h ⁽²⁾ + h ⁽³⁾. Let us assume that the plate is subjected to periodic in-plane load p _N = p _st + p _dyn cos θt, where p _st is a static component, p _dyn is the amplitude of the periodic part, and θ is the frequency of the load. Note that all external forces are varied proportionally to the parameter λ. The material properties of the plate vary continuously and smoothly in the thickness direction. Effective material properties P _eff, like Young’s modulus E, Poisson’s ratio ν, and mass density ρ for FGM can be estimated by the following Voigt’s law:

$$ {P}_{\mathrm{eff}}^{(r)}=\left({P}_{\mathrm{u}}-{P}_{\mathrm{l}}\right){V}_{\mathrm{c}}^{(r)}(z)+{P}_{\mathrm{l}}, $$

(1)

where P _u and P _l are corresponding properties of the upper and lower surfaces of the r-layer, respectively; $\kern0.5em {V}_c^{(r)}(z)$ is the volume fraction of ceramics.

Parametric excitation of the plate subjected to periodic loads is investigated by the first-order shear deformation theory (FSDT) [9] taking into account a shear deformation. In this case, the governing differential equations of equilibrium for free vibration of a plate subjected to external in-plane loading can be expressed as

$$ {N}_{11}{,}_x+{N}_{12}{,}_y={I}_0u{,}_{tt}+{I}_1{\psi}_x{,}_{tt},\kern1em {N}_{12}{,}_x+{N}_{22}{,}_y={I}_0v{,}_{tt}+{I}_1{\psi}_y{,}_{tt}, $$

(2)

$$ {M}_{11}{,}_x{+}{M}_{12}{,}_y-{Q}_x{=}{I}_2{\psi}_x{,}_{tt}+{I}_1u{,}_{tt},\kern1em {M}_{12}{,}_x+{M}_{22}{,}_y-{Q}_y{=}{I}_2{\psi}_y{,}_{tt}{+}{I}_1v{,}_{tt}, $$

(3)

$$ {Q}_x{,}_x+{Q}_y{,}_y+\left({N}_{11}^0w{,}_{xx}+2{N}_{12}^0w{,}_{xy}+{N}_{22}^0w{,}_{yy}\right)={I}_ow{,}_{tt}, $$

(4)

where I ₀, I ₁, I ₂ are defined as follows

$$ \left({I}_0,{I}_1,{I}_2\right)=\sum \limits_{r=1}^3\underset{z_r}{\overset{z_{r+1}}{\int }}\left({\rho}^{(r)}\right)\left(1,z,{z}^2\right) dz, $$

where ρ ^(r) is the mass density of r-th layer, and the values $\left\{N\right\}={\left\{{N}_{11}^0,{N}_{22}^0,{N}_{12}^0\right\}}^{\mathrm{T}}$ denote the force resultant in the pre-buckling state.

The in-plane force resultant vector {N} = {N ₁₁, N ₂₂, N ₁₂}^T, bending and twisting moments resultant vector{M} = {M ₁₁, M ₂₂, M ₁₂}^T, and transverse shear force resultant {Q} = {Q _x, Q _y}^T are calculated by integration along Oz-axes and can be recast to the following form:

$$ \left\{N\right\}=\left[A\right]\left\{\varepsilon \right\}+\left[B\right]\left\{\chi \right\},\kern1em \left\{M\right\}=\left[B\right]\left\{\varepsilon \right\}+\left[D\right]\left\{\chi \right\}, $$

(5)

where [A], [B], [D] are square matrices of the third order with elements A _ij, B _ij, D _ij, (i, j = 1, 2, 6) defined in the following way:

$$ {A}_{ij}=\sum \limits_{r=1}^3\underset{z_r}{\overset{z_{r+1}}{\int }}{Q}_{ij}^{(r)} dz,\kern1em {B}_{ij}=\sum \limits_{r=1}^3\underset{z_r}{\overset{z_{r+1}}{\int }}{Q}_{ij}^{(r)} zdz,\kern1em {D}_{ij}=\sum \limits_{r=1}^3\underset{z_r}{\overset{z_{r+1}}{\int }}{Q}_{ij}^{(r)}{z}^2 dz, $$

where z ₁ =  − h/2, z ₂ = h ₁, z ₃ = h ₂, z ₄ = h/2. Values h ₁, h ₂  are corresponding lower and upper borders of the middle layer. Expressions of integrand functions ${Q}_{ij}^{(r)}\;\left(i,j=1,2,6\right)$ have the following form

$$ {Q}_{11}^{(r)}={Q}_{22}^{(r)}=\frac{E^{(r)}}{1-{\left({\nu}^{(r)}\right)}^2},\kern2em {Q}_{12}^{(r)}=\frac{\nu^{(r)}{E}^{(r)}}{1-{\left({\nu}^{(r)}\right)}^2},\kern2em {Q}_{66}^{(r)}=\frac{E^{(r)}}{2\left(1+{\nu}^{(r)}\right)}, $$

where E ^(r), ν ^(r) are defined by formulas (1).

Strain components {ε} = {ε ₁₁, ε ₁₂, ε ₂₂}^T, {χ} = {χ ₁₁, χ ₁₂, χ ₂₂}^T at an arbitrary point of the plate are as follows:

$$ {\varepsilon}_{11}=u{,}_x+\frac{1}{2}w{,}_x^2,\kern1em {\varepsilon}_{22}=v{,}_y+\frac{1}{2}w{,}_y^2,\kern1em {\varepsilon}_{12}=u{,}_y+v{,}_x+w{,}_xw{,}_y $$

(6)

$$ {\varepsilon}_{13}{=}w{,}_x{+}{\psi}_x,\kern0.5em {\varepsilon}_{23}{=}w{,}_y+{\psi}_y,\kern0.5em {\chi}_{11}{=}{\psi}_x{,}_x,\kern0.5em {\chi}_{22}{=}{\psi}_y{,}_y,\kern0.5em {\chi}_{12}{=}{\psi}_x{,}_y+{\psi}_y{,}_x. $$

The transverse shear force resultants Q _x, Q _y are as follows:

$$ {Q}_x={K}_{\mathrm{s}}^2{A}_{33}{\varepsilon}_{13},\kern1em {Q}_y={K}_{\mathrm{s}}^2{A}_{33}{\varepsilon}_{23}, $$

(7)

where ${K}_{\mathrm{s}}^2$ denotes the shear correction factor. In this chapter, we take ${K}_{\mathrm{s}}^2=5/6$. Coefficients A _ij, B _ij, D _ij were obtained in an analytical form [8].

3 Method of Solution

Since the pre-buckling state can be inhomogeneous, first, we should determine the parameters $\left\{N\right\}={\left\{{N}_{11}^0,{N}_{22}^0,{N}_{12}^0\right\}}^{\mathrm{T}}.$ It is possible to prove that this problem can be reduced to a variational problem related to finding the minimum of the following functional:

$$ {\displaystyle \begin{array}{c}I\left(u,v,w,{\psi}_x,{\psi}_y\right)=\frac{1}{2}\underset{\varOmega }{\iint}\left({N}_{11}^{(L)}{\varepsilon}_{11}^{(L)}+{N}_{22}^{(L)}{\varepsilon}_{22}^{(L)}+{N}_{12}^{(L)}{\varepsilon}_{12}^{(L)}+\right.\\ {}\left.+{M}_{11}^{(L)}{\chi}_{11}+{M}_{22}^{(L)}{\chi}_{22}+{M}_{12}^{(L)}{\chi}_{12}{+}{Q}_x{\varepsilon}_{13}{+}{Q}_y{\varepsilon}_{23}\right) d\varOmega {+}\underset{\partial {\varOmega}_1}{\int }{N}_n^{(L)}\left( ul{+} vm\right)d{\varOmega}_1,\end{array}} $$

(8)

where the terms with superscripts L correspond to the linear terms in formulas (5).

To find the buckling load the dynamical approach is applied. Then the problem is reduced to an equivalent variational problem of the minimization of the following functional

$$ {\displaystyle \begin{array}{c}I\left(u,v,w,{\psi}_x,{\psi}_y\right)=\frac{1}{2}\underset{\varOmega }{\iint}\Big[{N}_{11}^{(L)}{\varepsilon}_{11}^{(L)}+{N}_{22}^{(L)}{\varepsilon}_{22}^{(L)}+{N}_{12}^{(L)}{\varepsilon}_{12}^{(L)}+\\ {}+{M}_{11}^{(L)}{\chi}_{11}+{M}_{22}^{(L)}{\chi}_{22}+{M}_{12}^{(L)}{\chi}_{12}+{Q}_x{\varepsilon}_{13}+{Q}_y{\varepsilon}_{23}+\\ {}+{p}_{\mathrm{st}}\left({N}_{11}^0{\left({w}_{,x}\right)}^2+{N}_{22}^0{\left({w}_{,y}\right)}^2+{N}_{12}^0{w}_{,x}{w}_{,y}\right)\Big]\; d\varOmega -\\ {}-\frac{1}{2}{\omega}_L^2\underset{\varOmega }{\iint}\left({I}_0\left({u}^2+{v}^2+{w}^2\right)+{I}_1\left({\psi}_x^2+{\psi}_y^2\right)\right)\; d\varOmega .\end{array}} $$

(9)

The value of the parameter p _st increases when the natural frequency ω _L is a real number. The value of the buckling load N _cr is defined by the value of the parameter p _st corresponding to the smallest nonnegative value of the frequency. Minimization of the functionals (8 and 9) is performed using Ritz’s method. The sequence of coordinate functions is constructed by the R-functions theory [6].

In order to solve the nonlinear vibration problem we develop the approach proposed in [7, 8]. As a result, we get ordinary differential equation, investigation of which is performed by Bolotin’s approach. The equation has the following form:

$$ \ddot{y}(t)+2\varepsilon y(t)+{\varOmega}_{\mathrm{L}}^2\left(1-2k\cos \theta t\right)y(t)+{y}^2(t)\beta +{y}^3(t)\gamma =0, $$

(10)

where $2k=\frac{\alpha {p}_{\mathrm{dyn}}}{\varOmega_{\mathrm{L}}^2}$ _, ${\varOmega}_{\mathrm{L}}^2={\omega}_{\mathrm{L}}^2-{p}_{\mathrm{st}}\alpha$ is the frequency of the plate compressed by the static load p _st, ω _L stands for the natural frequency of free vibration, ε is the damping ratio of the plate, and the expressions for the coefficients α, β, and γ are obtained in an analytical form, similarly as it has been done in the paper [8].

4 Numerical Results

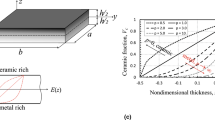
In order to show the possibilities of the proposed method we investigate vibration and buckling analysis of a plate shown in Fig. 1. Consider the plate with fixed geometrical parameters: b/a = 1; с/2a = 0.3; d/2a = 0.25; h/2a = 0.1. The material properties of the FGM mixture Al/Al₂O₃ used in the study are as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{Al}:\kern1em {E}_{\mathrm{m}}=70\;\mathrm{GPA},\kern1em {\nu}_{\mathrm{m}}=0.3,\kern1em {\rho}_{\mathrm{m}}=2707\;\mathrm{kg}/\mathrm{m};\\ {}{\mathrm{Al}}_2{\mathrm{O}}_3:\kern1em {E}_{\mathrm{c}}=380\;\mathrm{GPA},\kern1em {\nu}_{\mathrm{c}}=0.3,\kern1em {\rho}_{\mathrm{c}}=3800\;\mathrm{kg}/\mathrm{m}.\end{array}} $$

Fig. 1

Form of the plate (a) and its planform (b)

Suppose that the plate is simply supported and uniformly compressed on the border of the region. Boundary conditions take the following form:

$$ {\displaystyle \begin{array}{l}w=0,\kern1em \forall \left(x,y\right)\in \partial \varOmega, \kern1em u=0,\kern1em \forall \left(x,y\right)\in \partial {\varOmega}^{(u)},\kern1em \\ {}\partial {\varOmega}^{(u)}:\kern0.5em \left(y=-b,\kern0.5em \left|x\right|\le a\right)\cup \kern0.5em \left(y=d,\kern0.5em c\le x\le a\kern0.5em \cup \kern0.5em -a\le x\le -c\right)\\ {\hspace*{116pt}}\cup \kern0.5em \left(y=b,\kern0.5em \left|x\right|\le c\right),\vspace*{-12pt}\end{array}} $$

$$ v{=}0,\kern0.5em \forall \left(x,y\right)\,{\in}\,\partial {\varOmega}^{(v)},\kern0.5em \partial {\varOmega}^{(v)}:\kern0.3em \left(x{=}\pm a,\kern0.3em -b{\le} y{\le}d\right)\cup \kern0.3em \left(x{=}\pm c,\kern0.3em d\le y\le b\kern0.3em \right), $$

$$ {\displaystyle \begin{array}{l}{\psi}_x=0,\kern1em \forall \left(x,y\right)\in \partial {\varOmega}^{\left({\psi}_x\right)},\\ {}\partial {\varOmega}^{\left({\psi}_x\right)}:\kern0.5em \left(y=-b,\kern0.5em \left|x\right|\le a\right)\cup \kern0.5em \left(y=d,\kern0.5em c\le x\le a\kern0.5em \cup \kern0.5em -a\le x\le -c\right)\\ \hspace*{120pt}{}\cup \kern0.3em \left(y=b,\kern0.5em \left|x\right|\le c\right),\end{array}} $$

$$ {\psi}_y=0,\kern1em \forall \left(x,y\right)\in \partial {\varOmega}^{\left({\psi}_y\right)},\kern1em \partial {\varOmega}^{\left({\psi}_y\right)}:\kern0.5em \left(x=\pm a,\kern0.5em -b\le y\le d\right)\\ {}\cup \kern0.5em \left(x=\pm c,\kern0.5em d\le y\le b\kern0.5em \right). $$

In order to construct the admissible functions by the RFM [6], we should build the solution structure satisfying at least main boundary conditions. It can be chosen in the following way:

$$ w={\omega}^{(w)}{\varPhi}_1,\kern1em u={\omega}^{(u)}{\varPhi}_2,\kern1em v=\omega {{}^{(v)}\varPhi}_3,\kern1em {\psi}_x={\omega}^{\left({\psi}_x\right)}{\varPhi}_4,\kern1em {\psi}_y={\omega}^{\psi_y}{\varPhi}_5, $$

(11)

where functions ${\omega}^{(u)},\kern0.5em {\omega}^{(v)},\kern0.5em {\omega}^{(w)},\kern0.5em {\omega}^{\left({\psi}_x\right)},\kern0.5em {\omega}^{\left({\psi}_y\right)}$ are constructed by the RFM. They have to vanish on those parts of the boundary, where the corresponding functions $u,\kern0.5em v,\kern0.5em w,\kern0.5em {\psi}_x,\kern0.5em {\psi}_y$ are equal to zero. Indefinite components Φ _i ∈ C ²(Ω ∪ ∂Ω), i = 1, 2, …, 5 of the structure are presented as an expansion in a series of a complete system (power polynomials). In order to check the reliability of the obtained results in case of a complex geometry, let us change the size of the domain in such a way that the domain will be close to a square. For example, let us put с/2a = 0.48, d/2a = 0.48, h/2a = 0.1. A comparison of the obtained values of buckling ${\overset{\frown }{N}}_{\mathrm{cr}}=\frac{N_{\mathrm{cr}}}{100{E}_0{h}^3}$ for the plate of the Type A and p = 0.5 with available results [10,11,12] for the square plate is shown in Table 1.

Table 1 Buckling load ${\overset{\frown }{N}}_{\mathrm{cr}}$ (Al/Al₂O₃, E ₀ = 1 GPa, ρ ₀ = 1 kg/m³, Type A)

The values of results are almost the same. As can be seen from Table 1, the buckling load is slightly higher for the complex plate than for the square one, what is in agreement with the physical meaning.

The values of the buckling load and the natural frequency $\varLambda {=}{\omega}_{\mathrm{L}}{(2a)}^2\sqrt{\rho_0/{E}_0}/h$ for a plate with geometrical parameters c/2a = 0.3, d/2a = 0.25 for Type A and B are presented in Table 2. The power law exponent p is varied.

Table 2 Effect of the power law exponent p on the buckling load and the natural frequency FG plate (1-2-1; c/2a = 0.3, d/2a = 0.25, h/2a = 0.1, E ₀ = 1 GPa, ρ ₀ = 1 kg/m³)

Figure 2 shows zones of dynamic instability of the plate (Type A) for different values of the static load. The ratio of layers thickness is taken as h ⁽¹⁾ − h ⁽²⁾ − h ⁽³⁾ = 1 − 2 − 1, power low exponent p = 1.

Fig. 2

Zones of dynamic instability (Type A)

From Fig. 2 one can observe that static constituent of the load p _st influences essentially on placement and size of the instability regions. Increase of this parameter causes to a shift of the instability domains toward the smaller values of exciting frequency.

Figure 3 shows backbone curves for the plate (Type B) with the same ratio of layers thickness, power law exponent p = 1. The effect of the static component of the load on the behavior of backbone curves is investigated. It can be concluded that all curves have the monotonically increasing character. The bigger values of the static component of the compression load causes the bigger increasing the value of ratio of nonlinear frequency to linear one.

Fig. 3

Backbone curves of the plate (Type B)

5 Conclusions

The first time the R-functions theory and variational Ritz’s method are used and developed to study buckling and parametric vibrations of three-layered FGM plates with an arbitrary geometry. Considered specific examples of sandwich plates with complex planform and different arrangement of layers compressed by load in the middle surface demonstrate the possibility of application of the R-functions theory to such class of problems. Effect of the layers thickness and arrangement of the material and gradient index in power law on the buckling critical load and frequencies of the plates are investigated. Instability regions and backbone curves are presented for different value of compressing load.