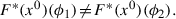Abstract
In this paper, nonsmooth vector fields are considered, where the discontinuity is located in a codimension-2 subset of the phase space (called extended Filippov systems). Although there are continuously many directions which are orthogonal to the discontinuity set, the trajectories of the system typically tend to the discontinuity along a few specific directions (called limit directions). During the current research, we present two types of bifurcations related to these limit directions: the tangency bifurcation and the fold of two limit directions. The analysis of this type of discontinuity is motivated by three-dimensional contact of rigid bodies in the presence of Coulomb friction.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
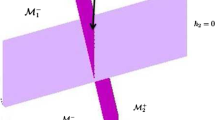
Filippov systems are nonsmooth dynamical systems which possess codimension-1 discontinuities in the phase space (see [1] or [2] for an overview). One of the physical sources of these systems is dry friction with the assumption of the Coulomb friction model. But when spatial (three-dimensional) contact of rigid bodies is modelled by dry friction, the resulting dynamical system contains more complicated discontinuities in their phase space.
In the limit case where the contacting bodies are completely rigid and the contact area is infinitesimally small, the simple three-dimensional Coulomb friction leads to codimension-2 discontinuities (see [3]). This type of vector field can be called an extended Filippov system, whose basic definitions and properties have been published recently (see [4]). Note that the assumption of finite contact area with drilling friction and rolling resistance (see [5, 6]) would lead to higher codimensional discontinuities, which systems are not covered by the present analysis.
In the present work, we focus on the bifurcations of the so-called limit directions of extended Filippov systems. These objects are the possible directions where the trajectories of the system are connected to the discontinuity set.
2 Extended Filippov Systems
2.1 Definition of Extended Filippov Systems
Consider the vector field F(x) where x = (x 1, x 2, …, x n) and n ≥ 3. Assume that F(x) is defined everywhere in \(\mathbb {R}^n\) except for the set
As the vector field F(x) is not defined in Σ, the n − 2 dimensional space Σ is called a codimension-2 discontinuity set of F.
There are continuously many unit vectors orthogonal to Σ, denoted by
where ϕ ∈ [0, 2π) shows the angle around the discontinuity set. Let us formally calculate the directional limit depending on the angle ϕ at a point x 0 ∈ Σ:
At a chosen x 0, we denote the limit vector field shorty by F ∗(ϕ).
Definition 1 (Extended Filippov System)
A system
is called an extended Filippov system, if the following three properties are satisfied:
-
(a)
The vector field F(x) is smooth on \(\mathbb {R}^n\setminus \varSigma \).
-
(b)
The limit (3) exists for all x 0 ∈ Σ and ϕ ∈ [0, 2π).
-
(c)
For all
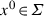 , there exist ϕ
1, ϕ
2 ∈ [0, 2π) such that
, there exist ϕ
1, ϕ
2 ∈ [0, 2π) such that 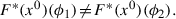
In other words: the discontinuity is restricted to Σ (see (a)), there is indeed a discontinuity in all points of Σ (see (c)), and the discontinuity is regular in some sense (see (b)).
In the definition of extended Filippov systems, the state space could be an open set in \(\mathbb {R}^n\) and Σ could be a smooth n − 2 dimensional manifold (see [4]), but the restricted definitions above can be used without loss of generality. Note that F(x) is not defined on Σ. By using a convex combination (see [4]), the vector field can be extended to some parts of Σ, but this is not covered by the current paper.
2.2 Limit Directions
Consider a point x 0 ∈ Σ of the discontinuity set. The orthogonal complement of Σ at x 0 is a plane defined by
which is referred simply as orthogonal space. Let us write the limit vector field F ∗(ϕ) into the form
where \(F^*_O(\phi )\) lays in the orthogonal space and \(F^*_T(\phi )\) is tangent to Σ. The scalar-valued, 2π-periodic functions R(ϕ) and V (ϕ) are defined by
where \(F^*_1\) and \(F^*_2\) are the first two components of F ∗. The component R(ϕ) describes the radial part of the limit vector around the discontinuity set Σ. The component V (ϕ) describes the circumferential dynamics around Σ. This structure gives the idea to transform the system into polar coordinates (see the next section).
To describe the structure of the dynamics in the vicinity of the discontinuity set Σ, we look for the trajectories which are connected to Σ. Although the vector field F(x) is not defined in Σ, the trajectories of F(x) can tend to Σ in forward or in backward time. Assume that a trajectory of F tends to a point x 0 ∈ Σ and the trajectory has a well-defined asymptote at x 0 with a direction of ϕ 0 measured around the discontinuity set. Along the line of the asymptote, the orthogonal part \(F^*_O(\phi )\) must be parallel to n(ϕ). Then, we can see from (6) that the circumferential dynamics V (ϕ 0) vanishes. This motivates the following definition:
Definition 2 (Limit Direction)
Consider a point x 0 ∈ Σ with the functions defined in (7). If V (ϕ 0) = 0 for ϕ 0 ∈ [0, 2π), then the angle ϕ 0 is called a limit direction of x 0.
The limit directions have important role in organizing the dynamics in the vicinity of Σ (see Fig. 1). If x 0 possesses limit directions then all trajectories of F(x) connected to x 0 must tend to x 0 along one of these limit directions. In some sense, the limit directions are similar to the eigenvectors of nodes and saddles of smooth systems, but there are some fundamental differences: The limit directions are uni-directional, and it can be shown that the trajectories reach the discontinuity in finite time along a limit direction. It is possible that x 0 does not have any limit directions, that is, V (ϕ) ≠ 0 for all ϕ ∈ [0, 2π).
Example of different types of limit directions. Left panel: the phase portrait of the system \(F(x)=(-x_1/(x_1^2+x_2^2)^{1/2}+2x_1^2/(x_1^2+x_2^2)-1/2,\,\,-x_2/(x_1^2+x_2^2)^{1/2},\,\,-x_3)\) projected into the orthogonal plane of x 0 = 0. Right panel: the radial R(ϕ) and the circumferential V (ϕ) components of the dynamics and the phase portrait of the associated system (11). Attracting directions: ϕ 2, ϕ 3, ϕ 4, ϕ 5, ϕ 6, repelling direction: ϕ 1. Dominant directions: ϕ 3, ϕ 5, isolated directions: ϕ 1, ϕ 2, ϕ 4, ϕ 6
2.3 Types of Limit Directions
Let us categorize the limit directions according to the structure of the surrounding trajectories. According to the radial component, the trajectories either tend towards the discontinuity set Σ (attracting) or they move outwards from Σ (repelling). These two cases can be separated according to the sign of the radial component R(ϕ) of the dynamics:
Definition 3 (Attracting and Repelling Limit Directions)
Consider a point x 0 ∈ Σ and a corresponding limit direction ϕ 0 satisfying V (ϕ 0) = 0. The limit direction is called attracting if R(ϕ 0) < 0 and it is called repelling if R(ϕ 0) > 0.
The sign of the derivative V ′ := dV∕dϕ(ϕ 0) decides whether the nearby trajectories are getting closer or further to each other in the circumferential direction as the time is evolving. If the sign of R(ϕ 0) is considered, as well, we can decide whether the trajectories are contracting in the direction towards the discontinuity set:
Definition 4 (Dominant and Isolated Limit Directions)
Consider a point x 0 ∈ Σ and a corresponding limit direction ϕ 0 satisfying V (ϕ 0) = 0. The limit direction is called dominant if R(ϕ 0) ⋅ V ′(ϕ 0) > 0 and it is called isolated if R(ϕ 0) ⋅ V ′(ϕ 0) < 0.
The change of the type of a limit direction causes structural change in the dynamics in the vicinity of the discontinuity set. In the next section, we create a 2D system by projecting F(x) into the orthogonal space O Σ(x 0). The analysis of that system helps to explore the bifurcations of limit directions.
3 Analysis of the Associated Smooth System
3.1 The Associated Smooth System in Polar Coordinates
For each point x 0 of the discontinuity set Σ, we create an associated smooth system, whose equilibrium point corresponds to the limit direction of the original system. Let us express the variables x 1 and x 2 in polar coordinates in the form
where r > 0 is the distance from the discontinuity set Σ and ϕ ∈ [0, 2π) is the angle around Σ which we have already used. The dynamics of these variables is given by
where F 1 and F 2 are the first two components of F.
Let us restrict (9) to the orthogonal space O Σ(x 0) (see (5)) and take the projection of F(x) into this orthogonal space. Then (9) leads to a planar dynamical system of the variables r and ϕ in the form
where F r and F ϕ are smooth functions on (r, ϕ) ∈ [0, ∞) × [0, 2π).
Note that (10) is singular at r = 0, which corresponds to x = x 0 ∈ Σ. Let us introduce a new time variable τ defined by \(\mathrm {d}r/\mathrm {d}\tau =\dot r\cdot r\), where the dash denotes the differentiation with respect to the new time variable. Then, it can be shown that (10) becomes
where R(ϕ) and V (ϕ) are the same functions we defined in (7), S(ϕ) and W(ϕ) are 2π-periodic functions, and \(\mathcal {O}\) denotes the higher order terms in r. Note that the terms R(ϕ) and V (ϕ) originate from the discontinuous part of F(x), while the terms S(ϕ) and W(ϕ) originate from the linear part of F(x).
The equilibrium points of the system (11) are strongly related to those of the limit directions of the original system. As (11) is a smooth 2D system, a usual bifurcation analysis can be applied to its equilibrium points.
3.2 Equilibrium Points and Bifurcations
The trivial equilibrium points of (11) are (r, ϕ) = (0, ϕ 0) where V (ϕ 0) = 0. The Taylor expansion around an equilibrium (0, ϕ 0) is given by
It can be seen from the Jacobian matrix that the eigenvalues of the equilibrium are λ 1 = R(ϕ 0) and λ 2 = V ′(ϕ 0).
Bifurcations of the equilibrium points can occur when one of these eigenvalues becomes zero. These are expressed in the following two theorems. The theorems can be proved by careful but straightforward application of the general conditions of the basic bifurcations (see, e.g., [7, p. 338]).
Theorem 1 (Transcritical Bifurcation)
Consider a family of the systems in the form (11) depending smoothly on a scalar parameter p. At p = 0, consider an equilibrium point (r, ϕ) = (0, ϕ 0) satisfying V (ϕ 0) = 0, and assume that the following statements are true:
Moreover, assume that by considering the dependence of the parameter p, the derivative ∂R∕∂p is non-zero. Then, a transcritical bifurcation occurs at (r, ϕ) = (0, ϕ 0) and p = 0.
In the case of this transcritical bifurcation, the examined trivial equilibrium passes over a non-trivial equilibrium with r ≠ 0 for p ≠ 0. The coordinate r of this non-trivial equilibrium would change sign at the critical parameter value p = 0. However, the region r < 0 is not part of the phase space of the system, that is, the non-trivial equilibrium exists either below or above of the critical parameter value p = 0.
Theorem 2 (Saddle-Node Bifurcation)
Consider a family of the systems in the form (11) depending smoothly on a scalar parameter p. At p = 0, consider an equilibrium point (r, ϕ) = (0, ϕ 0) satisfying V (ϕ 0) = 0, and assume that the following statements are true:
Moreover, assume that by considering the dependence of the parameter p, the derivative ∂V∕∂p is non-zero. Then, a saddle-node bifurcation occurs at (r, ϕ) = (0, ϕ 0) and p = 0.
In this saddle-node bifurcation, two trivial equilibria are involved on the line r = 0. Due to this bifurcation, the number of the trivial equilibria changes by two, which is simply the number of roots of the function V (ϕ) on [0, 2π).
4 Bifurcations of the Limit Directions
4.1 Relation Between the Associated System and the Original System
Based on the results of the associated smooth planar system presented above, we can analyse the bifurcations of the limit directions in extended Filippov systems.
The line r = 0 in the system (11) corresponds to the selected point x 0 of the discontinuity set in the original system (4). Moreover, the location of the trivial equilibria of (11) is determined by V (ϕ 0) = 0, which coincides with the condition of Definition 2. That leads to the following statement:
Proposition 1
Each limit direction ϕ 0 of x 0 ∈ Σ, corresponds to an equilibrium point of the associated system (11) at (r, ϕ) = (0, ϕ 0).
When we want to transfer the results about the bifurcations to the original system (4), we should not forget about the effect of the projection performed at the creation of the associated system (11). It is possible to repeat the calculations of the previous section in the whole space \(\mathbb {R}^n\), where the polar coordinates r and ϕ are complemented by coordinates x 3, …, x n of x 0 ∈ Σ (see (1)). Then, it can be showed that the bifurcations presented in the previous section do not suffer a qualitative change by the projection.
Consequently, we can transfer the bifurcations declared in Theorems 1–2 to the limit directions of the extended Filippov system (4). Note that the parametric dependence of the system (4) is not considered. However, the choice of x 0 modifies the associate system (11) as a dependence of n − 2 parameters. Therefore, the simple codimension-1 bifurcations of (11) become n − 3 dimensional bifurcation surfaces in the discontinuity set Σ. These surfaces divide Σ into parts according to the structurally different kinds of behaviour of the trajectories in the vicinity of the discontinuity.
In case of both bifurcations, we first define the new type of bifurcation and then state a theorem about the structural properties of the bifurcation. The proof of these theorems are the direct consequences of Theorems 1–2 and Definitions 2–4.
4.2 Tangency Bifurcation
Definition 5 (Tangency Bifurcation)
Consider a point x 0 ∈ Σ with the functions defined in (7). Assume that there exists ϕ 0 ∈ [0, 2π) such that V (ϕ 0) = 0, R(ϕ 0) = 0, V ′(ϕ 0) ≠ 0 and (S ⋅ V ′− W ⋅ R′)(ϕ 0) ≠ 0. Then, we say that a tangency bifurcation occurs at x 0.
Theorem 3 (Structural Changes at the Tangency Bifurcation)
In the tangency bifurcation, one limit direction of x 0 is changing from attracting to repelling or vice versa. In the meantime, the limit direction is changing from dominant to isolated or vice versa. The corresponding limit vector F ∗(ϕ 0) is tangent to the discontinuity set Σ.
Note that the non-trivial equilibrium involved to the transcritical bifurcation of (11) corresponds to the intersection of the nullclines of F 1(x) and F 2(x), which causes the tangency of F ∗(ϕ 0) field to Σ at x 0. The phrase tangency bifurcation is based on the strong analogy to the tangency bifurcation of classical Filippov systems (see [1]). Note that for the evaluation of the conditions of Definition (5), the linear part of the vector field F(x) is required (contained in S(ϕ) and W(ϕ)).
4.3 Fold of Limit Directions
Definition 6 (Fold of Limit Directions)
Consider a point x 0 ∈ Σ with the functions defined in (7). Assume that there exists ϕ 0 ∈ [0, 2π) such that V (ϕ 0) = V ′(ϕ 0) = 0, R(ϕ 0) = 0 and V ″(ϕ 0) ≠ 0. Then, we say that a fold of limit directions occurs at x 0.
Theorem 4 (Structural Changes at the Fold of Limit Directions)
In the fold of limit directions, two limit directions are joined and destroyed. Both limit directions are either attracting or repelling. One of the involved limit directions is dominant and the other one is isolated.
The term fold (or saddle-node) bifurcation is a natural choice based on the corresponding bifurcation in Theorem 2. Independently on the linear and higher order terms of F(x), this type of bifurcation depends on the limit vector field F ∗(ϕ) only.
5 Conclusion
Limit directions have an important role in understanding the structure of trajectories tending to the codimension-2 discontinuities in extended Filippov systems. At each point of the discontinuity set, an associated planar smooth system was created in polar coordinates. The results of the bifurcation analysis of this smooth system were transferred to the original nonsmooth system. A bifurcation of the limit directions can occur either when the limit direction turns around (tangency bifurcation) or when two limit directions merge (fold bifurcation). Both types of these bifurcations have been identified in mechanical systems containing dry friction between rigid bodies (see [3]). Further research will explore the detailed mechanical consequences of these bifurcations.
References
di Bernardo, M., et al.: Piecewise-smooth Dynamical Systems. Springer, London (2008)
Leine, R., Nijmeijer, H.: Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Springer, Berlin (2004)
Antali, M., Stepan, G.: Nonsmooth analysis of three-dimensional slipping and rolling in the presence of dry friction. Nonlinear Dyn. 97(3), 1799–1817 (2019)
Antali, M., Stepan, G.: Sliding and crossing dynamics in extended Filippov systems. J. Appl. Dyn. Syst. 17(1), 823–858 (2019)
Kudra, G., Awrejcewicz, J.: Tangens hyperbolicus approximations of the spatial model of friction coupled with rolling resistance. Int. J. Bifurcation and Chaos 21(10), 2905–2917 (2011)
Kudra, G., Awrejcewicz, J.: Approximate modelling of resulting dry friction forces and rolling resistance for elliptic contact shape. Eur. J. Mech. A Solids 42, 358–375 (2013)
Perko, L.: Differential Equations and Dynamical Systems. Springer, Berlin (2001)
Acknowledgements
The research work of the first author is supported by the Hungarian Academy of Sciences in the Premium Postdoctoral Fellowship Programme under the grant number PPD2018-014/2018.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Antali, M., Stepan, G. (2020). Bifurcations of Limit Directions at Codimension-2 Discontinuities of Vector Fields. In: Lacarbonara, W., Balachandran, B., Ma, J., Tenreiro Machado, J., Stepan, G. (eds) Nonlinear Dynamics of Structures, Systems and Devices. Springer, Cham. https://doi.org/10.1007/978-3-030-34713-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-34713-0_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34712-3
Online ISBN: 978-3-030-34713-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)



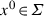 , there exist ϕ
1, ϕ
2 ∈ [0, 2π) such that
, there exist ϕ
1, ϕ
2 ∈ [0, 2π) such that