Abstract
\(\lambda \)-calculi come with no fixed evaluation strategy. Different strategies may then be considered, and it is important that they satisfy some abstract rewriting property, such as factorization or normalization theorems. In this paper we provide simple proof techniques for these theorems. Our starting point is a revisitation of Takahashi’s technique to prove factorization for head reduction. Our technique is both simpler and more powerful, as it works in cases where Takahashi’s does not. We then pair factorization with two other abstract properties, defining essential systems, and show that normalization follows. Concretely, we apply the technique to four case studies, two classic ones, head and the leftmost-outermost reductions, and two less classic ones, non-deterministic weak call-by-value and least-level reductions.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The \(\lambda \)-calculus is the model underlying functional programming languages and proof assistants. The gap between the model and its incarnations is huge. In particular, the \(\lambda \)-calculus does not come with a fixed reduction strategy, while concrete frameworks need one. A desirable property is that the reduction which is implemented terminates on all terms on which \(\beta \) reduction has a reduction sequence to normal form. This is guaranteed by a normalization theorem. Two classic examples are the leftmost-outermost and head normalization theorems (theorems 13.2.2 and 11.4.8 in Barendregt [4]). The former states that if the term has a \(\beta \)-normal form, leftmost-outermost reduction is guaranteed to find it; the latter has a similar but subtler statement, roughly head reduction computes a head normal form, if the term has any.
Another classic theorem for head reduction states that head reduction approximates the \(\beta \)-normal form by computing an essential part of every evaluation sequence. The precise formulation is a factorization theorem: a sequence of \(\beta \) steps \(t\rightarrow _{\beta }^*s\) can always be re-arranged as a sequence of head steps (\(\rightarrow _{h}\)) followed by a sequence of non-head steps (\(\rightarrow _{\lnot h}\)), that is, \(t\rightarrow _{h}^* u\rightarrow _{\lnot h}^* s\). Both head and leftmost-outermost reductions play a key role in the theory of the \(\lambda \)-calculus as presented in Barendregt [4] or Krivine [16].
Variants of the \(\lambda \)-calculus abound and are continuously introduced: weak, call-by-value, call-by-need, classical, with pattern matching, sharing, non-determinism, probabilistic choice, quantum features, differentiation, etc. So, normalization and factorization theorems need to be studied in many variations. Concepts and techniques to prove these theorems do exist, but they do not have the essential, intuitive structure of other fundamental properties, such as confluence.
This Paper. Here we provide a presentation of factorization and normalization revisiting a simple technique due to Takahashi [28], making it even simpler and more widely applicable. We separate the abstract reasoning from the concrete details of head reduction, and apply the revisited proof method to several case studies. The presentation is novel and hopefully accessible to anyone familiar with the \(\lambda \)-calculus, without a background in advanced notions of rewriting theory.
We provide four case studies, all following the same method. Two are revisitations of the classic cases of head and leftmost-outermost (shortened to \(\ell o\)) reductions. Two are folklore cases. The first is weak (i.e. out of \(\lambda \)-abstractions) call-by-value (shortened to CbV) reduction in its non-deterministic presentation. The second is least-level (shortened to \({\ell \ell } \)) reduction, a reduction coming from the linear logic literature—sometimes called by levels—and which is usually presented using proof nets (see de Carvalho, Pagani and Tortora de Falco [6] or Pagani and Tranquilli [24]) or calculi related to proof nets (see Terui [30] or Accattoli [1]), rather than in the ordinary \(\lambda \)-calculus. The \(\ell o\) and \({\ell \ell } \) cases are full reductions for \(\beta \), i.e. they have the same normal forms as \(\beta \). The head and weak CbV cases are not full, as they may not compute \(\beta \) normal forms.
Takahashi. In [28], Takahashi uses the natural inductive notion of parallelFootnote 1 \(\beta \) reduction (which reduces simultaneously a number of \(\beta \)-redexes; it is also the key concept in Tait and Martin-Löf’s classic proof of confluence of the \(\lambda \)-calculus) to introduce a simple proof technique for head factorization, from which head normalization follows. By iterating head factorization, she also obtains leftmost-outermost normalization, via a simple argument on the structure of terms due to Mitschke [19].
Her technique has been employed for various \(\lambda \)-calculi because of its simplicity. Namely, for the \(\lambda \)-calculus with \(\eta \) by Ishii [13], the call-by-value \(\lambda \)-calculus by Ronchi Della Rocca and Paolini [25, 27], the resource \(\lambda \)-calculus by Pagani and Tranquilli [23], pattern calculi by Kesner, Lombardi and Ríos [14], the shuffling calculus by Guerrieri, Paolini and Ronchi Della Rocca [8,9,10], and it has been formalized with proof assistants by McKinna and Pollack [17] and Crary [7].
Takahashi Revisited. Despite its simplicity, Takahashi’s proof [28] of factorization relies on substitutivity properties not satisfied by full reductions such as \(\ell o\) and \({\ell \ell } \). Our first contribution is a proof that is independent of the substitutivity properties of the factorizing reductions. It relies on a simpler fact, namely the substitutivity of an indexed variant \(\overset{n}{\Rightarrow }_{\beta }\) of parallel \(\beta \) reduction \(\Rightarrow _{\beta }\). The definition of \(\overset{n}{\Rightarrow }_{\beta }\) simply decorates the definition of \(\Rightarrow _{\beta }\) with a natural number n that intuitively corresponds to the number of redexes reduced in parallel by a \(\Rightarrow _{\beta }\) step.
We prove factorization theorems for all our four case studies following this simpler scheme. We also highlight an interesting point: factorization for the two full reductions cannot be obtained directly following Takahashi’s methodFootnote 2.
From Factorization to Essential Normalization. The second main contribution of our paper is the isolation of abstract properties that together with factorization imply normalization. First of all we abstract head reduction into a generic reduction \(\rightarrow _{{\mathtt e}}\), called essential, and non-head reduction \(\rightarrow _{\lnot h}\) into a non-essential reduction \(\rightarrow _{{\lnot {\mathtt e}}}\). The first additional property for normalization is persistence: steps of the factoring reduction \(\rightarrow _{{\mathtt e}}\) cannot be erased by the factored out \(\rightarrow _{{\lnot {\mathtt e}}}\). The second one is a relaxed form of determinism for \(\rightarrow _{{\mathtt e}}\). We show that in such essential rewriting systems \(\rightarrow _{{\mathtt e}}\) has a normalization theorem. The argument is abstract, that is, independent of the specific nature of terms. This is in contrast to how Takahashi [28] obtains normalization from factorization: her proof is based on an induction over the structure of terms, and cannot then be disentangled by the concrete nature of the rewriting system under study.
Normalizing Reductions for \(\beta \). We apply both our techniques to our case studies of full reduction: \(\ell o\) and \({\ell \ell } \), obtaining simple proofs that they are normalizing reductions for \(\beta \). Let us point out that \(\ell o\) is also—at present—the only known deterministic reduction to \(\beta \) normal form whose number of steps is a reasonable cost model, as shown by Accattoli and Dal Lago [2]. Understanding its normalization is one of the motivations at the inception of this work.
Normalization with Respect to Different Notions of Results. As a further feature, our approach provides for free normalization theorems for reductions that are not full for the rewrite system in which they live. Typical examples are head and weak CbV reductions, which do not compute \(\beta \) and CbV normal forms, respectively. These normalization theorems arise naturally in the theory of the \(\lambda \)-calculus. For instance, functional programming languages implement only weak notions of reduction, and head reduction (rather than \(\ell o\)) is the key notion for the \(\lambda \)-definability of computable functions.
We obtain normalization theorems for head and weak CbV reductions. Catching normalization for non-full reductions sets our work apart from the recent studies on normalization by Hirokawa, Middeldorp, and Moser [12] and Van Oostrom and Toyama [22], discussed below among related works.
Factorization, Normalization, Standardization. In the literature of the \(\lambda \)-calculus, normalization for \(\ell o\) reduction is often obtained as a corollary of the standardization theorem, which roughly states that every reduction sequence can be re-organized as to reduce redexes according to the left-to-right order (Terese [29] following Klop [15] and Barendregt [4], for instance). Standardization is a complex and technical result. Takahashi [28], using Mitschke’s argument [19] that iterates head factorization, obtains a simpler proof technique for \(\ell o\) normalization—and for standardization as well. Our work refines that approach, abstracts from it and shows that factorization is a general technique for normalization.
Related Work. Factorization is studied in the abstract in [1, 18]. Melliès axiomatic approach [18] builds on standardization, and encompasses a wide class of rewriting systems; in particular, like us, he can deal with non-full reductions. Accattoli [1] relies crucially on terminating hypotheses, absent instead here.
Hirokawa, Middeldorp, and Moser [12] and Van Oostrom and Toyama [22] study normalizing strategies via a clean separation between abstract and term rewriting results. Our approach to normalization is similar to the one used in [12] to study \(\ell o\) evaluation for first-order term rewriting systems. Our essential systems strictly generalize their conditions: uniform termination replaces determinism (two of the strategies we present here are not deterministic) and—crucially—persistence strictly generalizes the property in their Lemma 7. Conversely, they focus on hyper-normalization and on extending the method to systems in which left-normality is relaxed. We do not deal with these aspects. Van Oostrom and Toyama’s study [22] of (hyper-)normalization is based on an elegant and powerful method based on the random descent property and an ordered notion of commutative diagrams. Their method and ours are incomparable: we do not rely on (and do not assume) the random descent property (for its definition and uses see van Oostrom [21])—even if most strategies naturally have that property—and we do focus on factorization (which they explicitly avoid), since we see it as the crucial tool from which normalization can be obtained.
As already pointed out, a fundamental difference with respect to both works is that we consider a more general notion of normalization for reductions that are not full, that is not captured by either of those approaches.
In the literature, normalization is also proved from iterated head factorization (Takahashi [28] for \(\ell o\), and Terui [30] or Accattoli [1] for \({\ell \ell } \) on proof nets-like calculi, or Pagani and Tranquilli [24] for \({\ell \ell } \) on differential proof nets), or as a corollary of standardization (Terese [29] following Klop [15] and Barendregt [4] for \(\ell o\)), or using semantic principles such as intersection types (Krivine [16] for \(\ell o\) and de Carvalho, Pagani and Tortora de Falco [6] for \({\ell \ell } \) on proof nets). Last, Bonelli et al. develop a sophisticated proof of normalization for a \(\lambda \)-calculus with powerful pattern matching in [5]. Our technique differs from them all.
Proofs. Omitted proofs are available online in [3], the long version of this paper.
2 Factorization and Normalization, Abstractly
In this section, we study factorization and normalization abstractly, that is, independently of the specific structure of the objects to be rewritten.
A rewriting system (aka abstract reduction system, see Terese [29, Ch. 1]) \(\mathcal S\) is a pair \((S, \rightarrow _{})\) consisting of a set \(S\) and a binary relation \(\rightarrow _{}\, \subseteq S\times S\) called reduction, whose pairs are written \(t \rightarrow _{}s\) and called \(\rightarrow _{}\)-steps. A \(\rightarrow _{}\)-sequence from \(t\) is a sequence \(t\rightarrow _{}s\rightarrow _{}\dots \) of \(\rightarrow _{}\)-steps; \(t\rightarrow _{}^k s\) denotes a sequence of k \(\rightarrow _{}\)-steps from \(t\) to \(s\). As usual, \(\rightarrow _{}^*\) (resp. \(\rightarrow _{}^=\)) denotes the transitive-reflexive (resp. reflexive) closure of \(\rightarrow _{}\). Given two reductions \(\rightarrow _{1}\) and \(\rightarrow _{2}\) we use \(\rightarrow _{1}\!\cdot \!\rightarrow _{2}\) for their composition, defined as \(t\rightarrow _{1}\!\cdot \! \rightarrow _{2}s\) if \(t\rightarrow _{1}u\rightarrow _{2}s\) for some \(u\).
In this section we focus on a given sub-reduction \(\rightarrow _{{\mathtt e}}\) of \(\rightarrow _{}\), called essential, for which we study factorization and normalization with respect to \(\rightarrow _{}\). It comes with a second sub-reduction \(\rightarrow _{{\lnot {\mathtt e}}}\), called inessential, such that \(\rightarrow _{{\mathtt e}}\cup \rightarrow _{{\lnot {\mathtt e}}}\,=\,\rightarrow _{}\). Despite the notation, \(\rightarrow _{{\mathtt e}}\) and \(\rightarrow _{{\lnot {\mathtt e}}}\) are not required to be disjoint. In general, we write \((S,\{\rightarrow _{a},\rightarrow _{b}\})\) for the rewriting system \((S,\rightarrow _{})\) where \(\rightarrow _{}\,=\,\rightarrow _{a} \cup \rightarrow _{b}\).
2.1 Factorization
A rewriting system \((S,\{\rightarrow _{{\mathtt e}},\rightarrow _{{\lnot {\mathtt e}}}\})\) satisfies \(\rightarrow _{{\mathtt e}}\)-factorization (also called postponement of \(\rightarrow _{{\lnot {\mathtt e}}}\) after \(\rightarrow _{{\mathtt e}}\)) if \(t\rightarrow _{}^* s\) implies that there exists \(u\) such that \(t\rightarrow _{{\mathtt e}}^* u\rightarrow _{{\lnot {\mathtt e}}}^* s\). Compactly, we write \(\rightarrow _{}^* \, \subseteq \, \rightarrow _{{\mathtt e}}^*\!\cdot \!\rightarrow _{{\lnot {\mathtt e}}}^*\). In diagrams, see Fig. 1a.
Proving Factorization. Factorization is a non-trivial rewriting property, because it is global, that is, quantified over all reduction sequences from a term. To be able to prove factorization, we would like to reduce it to local properties, i.e. properties quantified only over one-step reductions from a term. At first sight it may seem that a local diagram such as the one in Fig. 1b would give factorization by a simple induction. Such a diagram however does not allow to infer factorization without further hypotheses—counterexamples can be found in Barendregt [4].
The following abstract property is a special case for which a local condition implies factorization. It was first observed by Hindley [11].
Lemma 1
(Hindley, local postponement). Let \((S,\{\rightarrow _{{\mathtt e}},\rightarrow _{{\lnot {\mathtt e}}}\})\) be a rewriting system. If \(\rightarrow _{{\lnot {\mathtt e}}}\!\cdot \! \rightarrow _{{\mathtt e}}\,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^=\) then \(\rightarrow _{}^* \,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\).
Proof
The assumption \(\rightarrow _{{\lnot {\mathtt e}}}\!\cdot \! \rightarrow _{{\mathtt e}}\,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^=\) implies (#) \(\rightarrow _{{\lnot {\mathtt e}}}\!\cdot \! \rightarrow _{{\mathtt e}}^* \,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^=\) (indeed, it is immediate to prove that \(\rightarrow _{{\lnot {\mathtt e}}}\!\cdot \! \rightarrow _{{\mathtt e}}^k \,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^=\) by induction on k).
We then prove that \(\rightarrow _{}^k \,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\), by induction on k. The case \(k=0\) is trivial. Assume \( \rightarrow _{}\!\cdot \! \rightarrow _{}^{k-1}\). By i.h., \( \rightarrow _{}\!\cdot \! \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\). If the first step is \(\rightarrow _{{\mathtt e}}\), the claim is proved. Otherwise, by \((\#)\), from \((\rightarrow _{{\lnot {\mathtt e}}}\!\cdot \! \rightarrow _{{\mathtt e}}^*) \cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\) we obtain \((\rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^=) \cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\). \(\square \)
Hindley’s local condition is a strong hypothesis for factorization that in general does not hold in \(\lambda \)-calculi—not even in the simple case of head reduction. However, the property can be applied in combination with another standard technique: switching to macro steps that compress \(\rightarrow _{{\mathtt e}}^* \) or \(\rightarrow _{{\lnot {\mathtt e}}}^*\) into just one step, at the price of some light overhead. This idea is the essence of both Tait–Martin-Löf’s and Takahashi’s techniques, based on parallel steps. The role of parallel steps in Takahashi [28] is here captured abstractly by the notion of macro-step system.
Definition 2
(Macro-step system). A rewriting system \(\mathcal S=(S, \{\rightarrow _{{\mathtt e}}, \rightarrow _{{\lnot {\mathtt e}}}\})\) is a macro-step system if there are two reductions \(\Rightarrow _{}\) and \(\Rightarrow _{\lnot {\mathtt e}}\) (called macro-steps and inessential macro-steps, respectively) such that
-
Macro: \(\rightarrow _{{\lnot {\mathtt e}}}~\subseteq ~\Rightarrow _{\lnot {\mathtt e}}~\subseteq ~\rightarrow _{{\lnot {\mathtt e}}}^*\).
-
Merge: if \(t\Rightarrow _{\lnot {\mathtt e}}\!\cdot \! \rightarrow _{{\mathtt e}}u\) then \(t\Rightarrow _{}u\). That is, the diagram in Fig. 1c holds.
-
Split: if \(t\Rightarrow _{}u\) then \(t\rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}u\). That is, the diagram in Fig. 1d holds.
Note that \(\Rightarrow _{}\) just plays the role of a “bridge” between the hypothesis of the merge condition and the conclusion of the split condition—it shall play a crucial role in the concrete proofs in the next sections. In this paper, concrete instances of \(\Rightarrow _{}\) and \(\Rightarrow _{\lnot {\mathtt e}}\) shall be parallel \(\beta \) reduction and some of its variants.
Proposition 3
(Factorization). Every macro-step system \((S, \{\rightarrow _{{\mathtt e}}, \rightarrow _{{\lnot {\mathtt e}}}\})\) satisfies \(\rightarrow _{{\mathtt e}}\)-factorization.
Proof
By Merge and Split, \(\Rightarrow _{\lnot {\mathtt e}}\!\cdot \! \rightarrow _{{\mathtt e}}\,\subseteq \, \Rightarrow _{}\,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}\,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}^=\). By Hindley’s lemma (Lemma 1) applied to \(\rightarrow _{{\mathtt e}}\) and \(\Rightarrow _{\lnot {\mathtt e}}\) (rather than \(\rightarrow _{{\mathtt e}}\) and \(\rightarrow _{{\lnot {\mathtt e}}}\)), we obtain \((\rightarrow _{{\mathtt e}}\cup \Rightarrow _{\lnot {\mathtt e}})^* \,\subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}^*\). Since \(\rightarrow _{{\lnot {\mathtt e}}}\,\subseteq \, \Rightarrow _{\lnot {\mathtt e}}\), we have \( (\rightarrow _{{\mathtt e}}\cup \rightarrow _{{\lnot {\mathtt e}}})^* \subseteq \, (\rightarrow _{{\mathtt e}}\cup \Rightarrow _{\lnot {\mathtt e}})^* \subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}^* \). As \(\Rightarrow _{\lnot {\mathtt e}}\,\subseteq \, \rightarrow _{{\lnot {\mathtt e}}}^*\), we have \(\rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}^* \, \subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\). Therefore, \(\rightarrow _{}^* = (\rightarrow _{{\mathtt e}}\cup \rightarrow _{{\lnot {\mathtt e}}})^* \subseteq \, \rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*\). \(\square \)
2.2 Normalization for full reductions
The interest of factorization comes from the fact that the essential reduction \(\rightarrow _{{\mathtt e}}\) on which factorization pivots has some good properties. Here we pinpoint the abstract properties which make factorization a privileged method to prove normalization; we collect them into the definition of essential system (Definition 5).
Normal Forms and Normalization. Let us recall what normalization is about. In general, a term may or may not reduce to a normal form. And if it does, not all reduction sequences necessarily lead to normal form. A term is weakly or strongly normalizing, depending on if it may or must reduce to normal form. If a term \(t\) is strongly normalizing, any choice of steps will eventually lead to a normal form. However, if \(t\) is weakly normalizing, how do we compute a normal form? This is the problem tackled by normalization: by repeatedly performing only specific steps, a normal form will be computed, provided that \(t\) can reduce to any.
Recall the statement of the \(\ell o\) normalization theorem: if \(t\rightarrow _{\beta }^* u\) with \(u\) \(\beta \)-normal, then \(t\) \(\ell o\)-reduces to \(u\). Observe a subtlety: such a formulation relies on the determinism of \(\ell o\) reduction. We give a more general formulation of normalizing reduction, valid also for non-deterministic reductions.
Formally, given a rewriting system \((S, \rightarrow _{})\), a term \(t\in S\) is:
-
\(\rightarrow _{}\)-normal (or in \(\rightarrow _{}\)-normal form) if \(t\not \rightarrow _{}\), i.e. there are no \(s\) such that \(t\rightarrow _{}s\);
-
weakly \(\rightarrow _{}\)-normalizing if there exists a sequence \(t\rightarrow _{}^*s\) with \(s\) \(\rightarrow _{}\)-normal;
-
strongly \(\rightarrow _{}\)-normalizing if there are no infinite \(\rightarrow _{}\)-sequence s from \(t\), or equivalently, if all maximal \(\rightarrow _{}\)-sequence s from \(t\) are finite.
We call \(reduction \) for \(\rightarrow _{}\) any \(\rightarrow _{{\mathtt e}}\,\subseteq \, \rightarrow _{}\). It is full if \( \rightarrow _{{\mathtt e}}\) and \(\rightarrow _{}\) have the same normal forms.Footnote 3
Definition 4
(Normalizing reduction). A full reduction \(\rightarrow _{{\mathtt e}}\) for \(\rightarrow _{}\) is normalizing (for \(\rightarrow _{}\)) if, for every term \(t\), \(t\) is strongly \(\rightarrow _{{\mathtt e}}\)-normalizing whenever it is weakly \(\rightarrow _{}\)-normalizing.
Note that, since the normalizing reduction \(\rightarrow _{{\mathtt e}}\) is full, if \(t\) is strongly \(\rightarrow _{{\mathtt e}}\)-normalizing then every maximal \(\rightarrow _{{\mathtt e}}\)-sequence from \(t\) ends in a \(\rightarrow _{}\)-normal form.
Definition 5
(Essential system). A rewriting system \((S,\{\rightarrow _{{\mathtt e}},\rightarrow _{{\lnot {\mathtt e}}}\})\) is essential if the following conditions hold:
-
1.
Persistence: if \(t\rightarrow _{{\mathtt e}}s\) and \(t\rightarrow _{{\lnot {\mathtt e}}}u\), then \(u\rightarrow _{{\mathtt e}}r\) for some \(r\).
-
2.
Uniform termination: if \(t\) is weakly \(\rightarrow _{{\mathtt e}}\)-normalizing, then it is strongly \(\rightarrow _{{\mathtt e}}\)-normalizing.
-
3.
Terminal factorization: if \(t\rightarrow _{}^* u\) and \(u\) is \(\rightarrow _{{\mathtt e}}\)-normal, then \( t\rightarrow _{{\mathtt e}}^* \!\cdot \! \rightarrow _{{\lnot {\mathtt e}}}^*u\).
It is moreover full if \(\rightarrow _{{\mathtt e}}\) is a full reduction for \(\rightarrow _{}\).
Comments on the definition:
-
Persistence: it means that essential steps are out of reach for inessential steps, that cannot erase them. The only way of getting rid of essential steps is by reducing them, and so in that sense they are essential to normalization.
-
From determinism to uniform termination: as we already said, in general \(\rightarrow _{{\mathtt e}}\) is not deterministic. For normalization, then, it is not enough that there is a sequence \(t\rightarrow _{{\mathtt e}}^*u\) with \(u\) \(\rightarrow _{}\)-normal (as in the statement of \(\ell o\)-normalization). We need to be sure that there are no infinite \(\rightarrow _{{\mathtt e}}\)-sequence s from \(t\). This is exactly what is ensured by the uniform termination property. Note that if \(\rightarrow _{{\mathtt e}}\) is deterministic (or has the diamond or random descent properties) then it is uniformly terminating.
-
Terminal factorization: there are two subtleties. First, we need only a weak form of factorization, namely factorization is only required for \(\rightarrow _{}\)-sequence s ending in a \(\rightarrow _{{\mathtt e}}\)-normal formFootnote 4. Second, the reader may expect terminal factorization to be required with respect to \(\rightarrow _{}\)-normal rather than \(\rightarrow _{{\mathtt e}}\)-normal forms. The two notions coincide if \(\rightarrow _{{\mathtt e}}\) is full, and for the time being we only discuss full essential systems. We discuss the more general case in Sect. 2.3.
Example 6
In the \(\lambda \)-calculus with \(\beta \) reduction, head reduction \(\rightarrow _{h}\) and its associated \(\rightarrow _{\lnot h}\) reduction (defined in Sect. 4) form an essential system. Similarly, leftmost-outermost \(\rightarrow _{\ell o}\) reduction and its associated \(\rightarrow _{\lnot \ell o}\) reduction (Sect. 7) form a full essential system. Two more examples are in Sects. 6 and 8.
Theorem 7
(Essential full normalization). Let \((S,\{\rightarrow _{{\mathtt e}},\rightarrow _{{\lnot {\mathtt e}}}\})\) be a full essential system. Then \(\rightarrow _{{\mathtt e}}\) is a normalizing reduction for \(\rightarrow _{}\).
Proof
Let \(t\) be a weakly \(\rightarrow _{}\)-normalizing term, i.e. \(t\rightarrow _{}^* u\) for some term \(u\) in \(\rightarrow _{}\)-normal form (and so in \(\rightarrow _{{\mathtt e}}\)-normal form, since \(\rightarrow _{{\mathtt e}}\,\subseteq \, \rightarrow _{}\)).
-
1.
Terminal factorization implies \(t\rightarrow _{{\mathtt e}}^*s\rightarrow _{{\lnot {\mathtt e}}}^* u\) for some \(s\), since \(u\) is \(\rightarrow _{{\mathtt e}}\)-normal.
-
2.
Let us show that \(s\) is \(\rightarrow _{{\mathtt e}}\)-normal: if not, then \(s\rightarrow _{{\mathtt e}}r\) for some \(r\), and a straightforward induction on the length of \(s\rightarrow _{{\lnot {\mathtt e}}}^*u\) iterating persistence gives that \(u\rightarrow _{{\mathtt e}}p\) for some \(p\), against the hypothesis that \(u\) is \(\rightarrow _{{\mathtt e}}\)-normal. Absurd.
-
3.
By the previous point, \(t\) is weakly \(\rightarrow _{{\mathtt e}}\)-normalizing. By uniform termination, \(t\) is strongly \(\rightarrow _{{\mathtt e}}\)-normalizing. \(\square \)
2.3 A More General Notion of Normalizing reduction.
Essential systems actually encompass also important notions of normalization for reductions that are not full, such as head normalization. These cases arise naturally in the \(\lambda \)-calculus literature, where partial notions of result such as head normal forms or values are of common use. Normalization for non-full reductions is instead not so common in the rewriting literature outside the \(\lambda \)-calculus. This is why, to guide the reader, we presented first the natural case of full reductions.
Let us first discuss head reduction: \(\rightarrow _{h}\) is deterministic and not full with respect to \(\rightarrow _{\beta }\), as its normal forms may not be \(\rightarrow _{\beta }\)-normal forms. The well-known property of interest is head normalization (Cor. 11.4.8 in Barendregt’s book [4]):
The statement has two subtletiesFootnote 5 . First, \(t\) may \(\rightarrow _{\beta }\)-reduce to a term in \(\rightarrow _{h}\)-normal form in many different ways, possibly without using \(\rightarrow _{h}\), so that the hypotheses may not imply that \(\rightarrow _{h}\) terminates. Second, the conclusion is “\(\rightarrow _{h}\) terminates on \(t\)” and not \(t\rightarrow _{h}^*s\), because in general the maximal \(\rightarrow _{h}\)-sequence from \(t\) may end in a term \(u\ne s\). For instance, let \(I=\lambda y.y\): then \(I(x(II))\rightarrow _{\beta }I(xI)\rightarrow _{\beta }xI\) is a \(\rightarrow _{\beta }\)-sequence to head normal form, and yet the maximal \(\rightarrow _{h}\)-sequence \(I(x(II))\rightarrow _{h}x(II)\) ends in a different term.
Now, let us abstract from head normalization, taking into account that in general the essential reduction \(\rightarrow _{{\mathtt e}}\)—unlike head reduction—may not be deterministic, and so we ask for strong \(\rightarrow _{{\mathtt e}}\)-normalization rather than for \(\rightarrow _{{\mathtt e}}\)-termination.
Theorem 8
(Essential normalization). Let \((S,\{\rightarrow _{{\mathtt e}},\rightarrow _{{\lnot {\mathtt e}}}\})\) be an essential system. If \(t\rightarrow _{}^* u\) and \(u\) is \(\rightarrow _{{\mathtt e}}\)-normal, then \(t\) is strongly \(\rightarrow _{{\mathtt e}}\)-normalizing.
Proof
Exactly as for Theorem 7, fullness is not used in that proof. \(\square \)
In the next section we shall apply Theorem 8 to head reduction and obtain the head normalization theorem we started with. Another example of a normalization theorem for a non-full reduction is in Sect. 6. Note that the full variant of the theorem (Theorem 7) is in fact an instance of the general one (Theorem 8).
3 The \(\lambda \)-Calculus
This short section recalls basic definitions and properties of the \(\lambda \)-calculus and introduces the indexed variant of parallel \(\beta \).
The set \(\varLambda \) of terms of the \(\lambda \)-calculus is given by the following grammar:
We use the usual notions of free and bound variables,  for the meta-level capture-avoiding substitution of \(s\) for the free occurrences of \(x\) in \(t\), and \(|t|_{x}\) for the number of free occurrences of \(x\) in \(t\). The definition of \(\beta \) reduction \(\rightarrow _{\beta }\) is:
for the meta-level capture-avoiding substitution of \(s\) for the free occurrences of \(x\) in \(t\), and \(|t|_{x}\) for the number of free occurrences of \(x\) in \(t\). The definition of \(\beta \) reduction \(\rightarrow _{\beta }\) is:

Let us recall two basic substitutivity properties of \(\beta \) reduction.
-
1.
Left substitutivity of \(\rightarrow _{\beta }\): if \(t\rightarrow _{\beta }t'\) then
 .
. -
2.
Right substitutivity of \(\rightarrow _{\beta }\): if \(s\rightarrow _{\beta }s'\) then
 . It is possible to spell out the number of \(\rightarrow _{\beta }\)-steps, which is exactly the number of free occurrences of \(x\) in \(t\), that is,
. It is possible to spell out the number of \(\rightarrow _{\beta }\)-steps, which is exactly the number of free occurrences of \(x\) in \(t\), that is,  .
.
Parallel \(\beta \) reduction. Parallel \(\beta \)-reduction \(\Rightarrow _{\beta }\) is defined by:

Tait–Martin-Löf’s proof of the confluence of \(\rightarrow _{\beta }\) relies on the diamond property of \(\Rightarrow _{\beta }\)Footnote 6, in turn based on the following property (see Takahashi [28, p. 1])

While the diamond property of \(\Rightarrow _{\beta }\) does not play a role for factorization, one of the contributions of this work is a new proof technique for factorization relying on the substitutivity property of an indexed refinement of \(\Rightarrow _{\beta }\).
Indexed parallel \(\beta \) reduction. The new indexed version \(\overset{n}{\Rightarrow }_{\beta }\) of parallel \(\beta \) reduction \(\Rightarrow _{\beta }\) is equipped with a natural number n which is, roughly, the number of redexes reduced in parallel by a \(\Rightarrow _{\beta }\); more precisely, n is the length of a particular way of sequentializing the redexes reduced by \(\Rightarrow _{\beta }\). The definition of \(\overset{n}{\Rightarrow }_{\beta }\) is as follows (note that erasing the index one obtains exactly \(\Rightarrow _{\beta }\), so that \(\Rightarrow _{\beta }\,=\, \bigcup _{n \in \mathbb {N}} \overset{n}{\Rightarrow }_{\beta }\)):

The intuition behind the last clause is: \((\lambda x.t)s\) reduces to  by
by
-
1.
first reducing \((\lambda x.t)s\) to
 (1 step);
(1 step); -
2.
then reducing in
 the n steps corresponding to the sequence \(t\overset{n}{\Rightarrow }_{\beta } t'\), obtaining
the n steps corresponding to the sequence \(t\overset{n}{\Rightarrow }_{\beta } t'\), obtaining  ;
; -
3.
then reducing \(s\) to \(s'\) for every occurrence of \(x\) in \(t'\) replaced by \(s\), that is, m steps \(|t'|_{x}\) times, obtaining
 .
.
Points 2 and 3 hold because of the substitutivity properties of \(\beta \) reduction.
It is easily seen that \(\overset{0}{\Rightarrow }_{\beta }\) is the identity relation on terms. Moreover, \(\rightarrow _{\beta }\ =\ \overset{1}{\Rightarrow }_{\beta }\), and \(\overset{n}{\Rightarrow }_{\beta } \ \subseteq \ \rightarrow _{\beta }^n\), as expected. The substitutivity of \(\overset{n}{\Rightarrow }_{\beta }\) is proved by simply indexing the proof of substitutivity of \(\Rightarrow _{\beta }\).
Lemma 9
(Substitutivity of \(\overset{n}{\Rightarrow }_{\beta }\) ). If \(t\overset{n}{\Rightarrow }_{\beta } t'\) and \(s\overset{m}{\Rightarrow }_{\beta } s'\), then  where \(k = n + |t'|_{x}\cdot m\).
where \(k = n + |t'|_{x}\cdot m\).
Proof
By induction on the derivation of \(t\overset{n}{\Rightarrow }_{\beta } t'\). Consider its last rule. Cases:
-
Variable: two sub-cases
-
\(t= x\): then \(t= x\overset{0}{\Rightarrow }_{\beta } x= t'\) then
 that satisfies the statement because \(n + |t'|_{x}\cdot m = 0+1\cdot m = m\).
that satisfies the statement because \(n + |t'|_{x}\cdot m = 0+1\cdot m = m\). -
\(t= y\): then \(t= y\overset{0}{\Rightarrow }_{\beta } y= t'\) and
 that satisfies the statement because \(n + |t'|_{x}\cdot m = 0 +0\cdot m=0\).
that satisfies the statement because \(n + |t'|_{x}\cdot m = 0 +0\cdot m=0\).
-
-
Abstraction, i.e. \(t= \lambda y.{u} \overset{n}{\Rightarrow }_{\beta } \lambda y.{u'} = t'\) because \(u\overset{n}{\Rightarrow }_{\beta } u'\); we can suppose without loss of generality that \(y\ne x\) and \(y\) is not free in \(s\) (and hence in \(s'\)), so \(|u'|_{x} = |t'|_{x}\) and
 and
and  . By i.h.,
. By i.h.,  , thus
, thus 
-
Application, i.e. \(t= ur\overset{n}{\Rightarrow }_{\beta } u' r'= t'\) with \(u\overset{n_u}{\Rightarrow }_{\beta } u'\), \(r\overset{n_r}{\Rightarrow }_{\beta } r'\) and \(n = n_u+ n_r\). By i.h.,
 and
and  . Then
. Then 
where \(k = n_u+ |u'|_{x}\!\cdot m + n_r+ |r'|_{x}\!\cdot m = n + (|u'|_{x}+ |r'|_{x})\cdot m = n + |t'|_{x}\!\cdot m\).
-
\(\beta \)-step, i.e.
 with \(u\overset{n_u}{\Rightarrow }_{\beta } u'\), \(r\overset{n_r}{\Rightarrow }_{\beta } r'\) and \(n = n_u+ |u'|_{y}\cdot n_r+1\). We can assume without loss of generality that \(y\ne x\) and \(y\) is not free in \(s\) (and so in \(s'\)), hence
with \(u\overset{n_u}{\Rightarrow }_{\beta } u'\), \(r\overset{n_r}{\Rightarrow }_{\beta } r'\) and \(n = n_u+ |u'|_{y}\cdot n_r+1\). We can assume without loss of generality that \(y\ne x\) and \(y\) is not free in \(s\) (and so in \(s'\)), hence  and
and 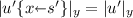 and
and  and
and  . By i.h.,
. By i.h.,  and
and  . Then
. Then 
where \(k = n_u+|u'|_{x}\cdot m +|u'|_{y}\cdot (n_r+|r'|_{x}\cdot m)+1 = n_u+ |u'|_{y}\cdot n_r+ 1 + |u'|_{x}\cdot m + |u'|_{y}\cdot |r'|_{x}\cdot m = n + |t'|_{x}\cdot m.\) \(\square \)
4 Head Reduction, Essentially
We here revisit Takahashi’s study [28] of head reduction. We apply the abstract schema for essential reductions developed in Sect. 2, which is the same schema used by Takahashi, but we provide a simpler proof technique for one of the required properties (split). First of all, head reduction \(\rightarrow _{h}\) (our essential reduction here) and its associated inessential reduction \(\rightarrow _{\lnot h}\) are defined by:

Note that \(\rightarrow _{\beta }\, = \, \rightarrow _{h}\cup \rightarrow _{\lnot h}\) but \(\rightarrow _{h}\) and \(\rightarrow _{\lnot h}\) are not disjoint: \(I (II) \rightarrow _{h}II\) and \(I(II) \rightarrow _{\lnot h}II\) with \(I = \lambda z.{z}\). Indeed, I(II) contains two distinct redexes, one is I(II) and is fired by \(\rightarrow _{h}\), the other one is II and is fired by \(\rightarrow _{\lnot h}\); coincidentally, the two reductions lead to the same term.
As for Takahashi, a parallel \(\lnot \)head step \(t\Rightarrow _{\lnot h}s\) is a parallel step \(t\Rightarrow _{\beta }s\) such that \(t\rightarrow _{\lnot h}^* s\). We give explicitly the inference rules for \(\Rightarrow _{\lnot h}\):

Easy inductions show that \(\rightarrow _{\lnot h}\,\subseteq \, \Rightarrow _{\lnot h}\,\subseteq \, \rightarrow _{\lnot h}^*\). It is immediate that \(\rightarrow _{h}\)-normal terms are head normal forms in the sense of Barendregt [4, Def. 2.2.11]. We do not describe the shape of head normal forms. Our proofs never use it, unlike Takahashi’s ones. This fact stresses the abstract nature of our proof method.
Head Factorization. We show that \(\rightarrow _{h}\) induces a macro-step system, with respect to \(\rightarrow _{\lnot h}\), \(\Rightarrow _{\beta }\), and \(\Rightarrow _{\lnot h}\), to obtain \(\rightarrow _{h}\)-factorization by Proposition 3.
Therefore, we need to prove merge and split. Merge is easily verified by induction on \(t\Rightarrow _{\lnot h}s\). The interesting part is the proof of the split property, that in the concrete case of head reduction becomes: if \(t\Rightarrow _{\beta }s\) then \(t\rightarrow _{h}^* \!\cdot \! \Rightarrow _{\lnot h}s\). This is obtained as a consequence of the following easy indexed split property based on the indexed variant of parallel \(\beta \). The original argument of Takahashi [28] is more involved, we discuss it after the new proof.
Proposition 10
(Head macro-step system)
-
1.
Merge: if \(t\Rightarrow _{\lnot h}\!\cdot \! \rightarrow _{h}u\) then \(t\Rightarrow _{\beta }u\).
-
2.
Indexed split: if \(t\overset{n}{\Rightarrow }_{\beta } s\) then \(t\Rightarrow _{\lnot h}s\), or \(n>0\) and \(t\rightarrow _{h}\!\cdot \! \overset{n-1}{\Rightarrow }_{\beta } s\).
-
3.
Split: if \(t\Rightarrow _{\beta }s\) then \(t\rightarrow _{h}^* \!\cdot \! \Rightarrow _{\lnot h}s\).
That is, \((\varLambda , \{ \rightarrow _{h}, \rightarrow _{\lnot h}\})\) is a macro-step system with respect to \(\Rightarrow _{\beta }\) and \(\Rightarrow _{\lnot h}\).
Proof
-
1.
Easy induction on \(t\Rightarrow _{\lnot h}s\). Details are in [3].
-
2.
By induction on \(t\overset{n}{\Rightarrow }_{\beta } s\). We freely use the fact that if \(t\overset{n}{\Rightarrow }_{\beta } s\) then \(t\Rightarrow _{\beta }s\). Cases:
-
Variable: \(t= x\overset{0}{\Rightarrow }_{\beta } x= s\). Then \(t= x\Rightarrow _{\lnot h}x= s\).
-
Abstraction: \(t= \lambda x.t' \overset{n}{\Rightarrow }_{\beta } \lambda x.s' = s\) with \(t' \overset{n}{\Rightarrow }_{\beta } s'\). It follows from the i.h.
-
Application: \(t= rp\overset{n}{\Rightarrow }_{\beta } r' p' = s\) with \(r\overset{n_1}{\Rightarrow }_{\beta } r'\), \(p\overset{n_2}{\Rightarrow }_{\beta } p'\) and \(n = n_1 + n_2\). There are only two subcases:
-
either \(rp\Rightarrow _{\lnot h}r' p'\), and then the claim holds;
-
or \(rp\not \Rightarrow _{\lnot h}r' p'\), and then neither \(r\Rightarrow _{\lnot h}r'\) nor \(r\) is an abstraction (otherwise \(rp\Rightarrow _{\lnot h}r' p'\)). By i.h. applied to \(r\overset{n_1}{\Rightarrow }_{\beta } r'\), \(n_1>0\) and there exists \(r''\) such that \(r\rightarrow _{h}r'' \overset{n_1-1}{\Rightarrow }_{\beta } r'\). Thus, \(t= rp\rightarrow _{h}r'' p\) and

-
-
\(\beta \)-step:
 with \(u\overset{n_1}{\Rightarrow }_{\beta } u'\), \(r\overset{n_2}{\Rightarrow }_{\beta } r''\) and \(n = n_1 + |u'|_{x}\cdot n_2 +1 > 0\). We have
with \(u\overset{n_1}{\Rightarrow }_{\beta } u'\), \(r\overset{n_2}{\Rightarrow }_{\beta } r''\) and \(n = n_1 + |u'|_{x}\cdot n_2 +1 > 0\). We have  and by substitutivity of \(\overset{n}{\Rightarrow }_{\beta }\) (Lemma 9)
and by substitutivity of \(\overset{n}{\Rightarrow }_{\beta }\) (Lemma 9)  .
.
-
-
3.
If \(t\Rightarrow _{\beta }s\) then \(t\overset{n}{\Rightarrow }_{\beta } s\) for some n. We prove the statement by induction n. By indexed split (Point 2), there are only two cases:
-
\(t\Rightarrow _{\lnot h}s\). This is an instance of the statement (since \(\rightarrow _{h}^*\) is reflexive).
-
\(n>0\) and there exists \(r\) such that \(t\rightarrow _{h}r\overset{n-1}{\Rightarrow }_{\beta } s\). By i.h. applied to \(r\overset{n-1}{\Rightarrow }_{\beta } s\), there is \(u\) such that \(r\rightarrow _{h}^* u\Rightarrow _{\lnot h}s\), and so \(t\rightarrow _{h}^* u\Rightarrow _{\lnot h}s\). \(\square \)
-
Theorem 11
(Head factorization). If \(t\rightarrow _{\beta }^* u\) then \(t\rightarrow _{h}^* \!\cdot \! \rightarrow _{\lnot h}^* u\).
Head Normalization. We show that \((\varLambda , \{ \rightarrow _{h}, \rightarrow _{\lnot h}\})\) is an essential system (Definition 5); thus the essential normalization theorem (Theorem 8) provides normalization. We already proved factorization (Theorem 11, hence terminal factorization). We verify persistence and determinism (which implies uniform termination) of \(\rightarrow _{h}\).
Proposition 12
(Head essential system)
-
1.
Persistence: if \(t\rightarrow _{h}s\) and \(t\rightarrow _{\lnot h}u\) then \(u\rightarrow _{h}r\) for some \(r\).
-
2.
Determinism: if \(t\rightarrow _{h}s_1\) and \(t\rightarrow _{h}s_2\) then \(s_1 = s_2\).
Then, \((\varLambda , \{ \rightarrow _{h}, \rightarrow _{\lnot h}\})\) is an essential system.
Theorem 13
(Head normalization). If \(t\rightarrow _{\beta }^* s\) and \(s\) is a \(\rightarrow _{h}\)-normal form, then \(\rightarrow _{h}\) terminates on \(t\).
4.1 Comparison with Takahashi’s Proof of the Split Property
Our technique differs from Takahashi’s in that it is built on simpler properties: it exploits directly the substitutivity of \(\Rightarrow _{\beta }\), which is instead not used by Takahashi. Takahashi’s original argument [28] for the split property (if \(t\Rightarrow _{\beta }s\) then \(t\rightarrow _{h}^* \cdot \Rightarrow _{\lnot h}\), what she calls the main lemma) is by induction on the (concrete) definition of \(\Rightarrow _{\beta }\) and relies on two substitutivity properties of \(\rightarrow _{h}\) and \(\Rightarrow _{\lnot h}\). Looking at them as the reductions \(\rightarrow _{{\mathtt e}}\) and \(\rightarrow _{{\lnot {\mathtt e}}}\) of an essential system, these properties are:
-
Left substitutivity of \(\rightarrow _{{\mathtt e}}\): if \(u\rightarrow _{{\mathtt e}}q\) then
 ;
; -
Left substitutivity of \(\Rightarrow _{\lnot {\mathtt e}}\): if \(u\Rightarrow _{\lnot {\mathtt e}}q\) then
 .
.
From them, left substitutivity of the composed reduction \(\rightarrow _{{\mathtt e}}^* \!\cdot \! \Rightarrow _{\lnot {\mathtt e}}\) easily follows. That is, Takahashi’s proof of the split property is by induction on \(t\Rightarrow _{}s\) using left substitutivity of \(\rightarrow _{{\mathtt e}}^*\cdot \Rightarrow _{\lnot {\mathtt e}}\) for the inductive case.
We exploit the substitutivity of \(\overset{n}{\Rightarrow }\) instead of left substitutivity of \(\rightarrow _{{\mathtt e}}\) and \(\Rightarrow _{\lnot {\mathtt e}}\). It holds for a larger number of essential systems because \(\overset{n}{\Rightarrow }\) is simply a decoration of \(\Rightarrow _{}\), which is substitutive by design. There are important systems where Takahashi’s hypotheses do not hold. One such case is \(\ell o\) reduction (Sect. 7)—the normalizing reduction of the \(\lambda \)-calculus—we discuss the failure of left substitutivity for \(\ell o\) at the end of Sect. 7; another notable case is \({\ell \ell } \) reduction (Sect. 8); both are full reductions for \(\beta \).
Let us point out where the idea behind our approach stems from. In a sense, Takahashi’s proof works by chance: the split hypothesis is about a parallel step \(\Rightarrow _{\beta }\) but then the key fact used in the proof, left substitutivity of \(\rightarrow _{h}^* \!\cdot \! \Rightarrow _{\lnot h}\), does no longer stay in the borders of the parallel step, since the prefix \(\rightarrow _{h}^*\) is an arbitrary long sequence that may reduce created steps. Our proof scheme instead only focuses on the (expected) substitutivity of \(\overset{n}{\Rightarrow }\), independently of creations.
5 The Call-by-Value \(\lambda \)-Calculus
In this short section, we introduce Plotkin’s call-by-value \(\lambda \)-calculus [26], where \(\beta \) reduction fires only when the argument is a value. In the next section we define weak reduction and prove factorization and normalization theorems using the essential technique, exactly as done in the previous section for head reduction.
The set \(\varLambda \) of terms is the same as in Sect. 3. Values, call-by-value (CbV) \(\beta \)-reduction \(\rightarrow _{\beta _v}\), and CbV indexed parallel reduction \(\overset{n}{\Rightarrow }_{\beta _v}\) are defined as follows:


The only difference with the usual parallel \(\beta \) (defined in Sect. 3) is the requirement that the argument is a value in the last rule. As before, the non-indexed parallel reduction \(\Rightarrow _{\beta _v}\) is simply obtained by erasing the index, so that \(\Rightarrow _{\beta _v}\,=\, \bigcup _{n \in \mathbb {N}} \overset{n}{\Rightarrow }_{\beta _v}\). Similarly, it is easily seen that \(\overset{0}{\Rightarrow }_{\beta _v}\) is the identity relation on terms, \(\rightarrow _{\beta _v}\,=\, \overset{1}{\Rightarrow }_{\beta _v}\) and \(\overset{n}{\Rightarrow }_{\beta _v} \,\subseteq \, \rightarrow _{\beta _v}^n\). Substitutivity of \(\overset{n}{\Rightarrow }_{\beta _v}\) is proved exactly as for \(\overset{n}{\Rightarrow }_{\beta }\) (Lemma 9).
Lemma 14
(Substitutivity of \(\overset{n}{\Rightarrow }_{\beta _v}\)). If \(t\overset{n}{\Rightarrow }_{\beta _v} t'\) and \(v\overset{m}{\Rightarrow }_{\beta _v} v'\), then  where \(k = n + |t'|_{x}\cdot m\).
where \(k = n + |t'|_{x}\cdot m\).
6 Weak Call-by-Value Reduction, Essentially
The essential step we study for the CbV \(\lambda \)-calculus is weak CbV reduction \(\rightarrow _{w}\), which does not evaluate function bodies (the scope of \(\lambda \)-abstractions). Weak CbV reduction has practical importance, because it is the base of the ML/CAML family of functional programming languages. We choose it also because it admits the natural and more general non-deterministic presentation that follows, even if most of the literature rather presents it in a deterministic way.

Note that in the case of an application there is no fixed order in the \(\rightarrow _{w}\)-reduction of the left and right subterms. Such a non-determinism is harmless as \(\rightarrow _{w}\) satisfies a diamond-like property implying confluence, see Proposition 17.2 below. It is well-known that the diamond property implies uniform termination, because it implies that all maximal sequence s from a term have the same length. Such a further property is known as random descent, a special form of uniform termination already considered by Newman [20] in 1942, see also van Oostrom [21].
The inessential reduction \(\rightarrow _{\lnot w}\) and its parallel version \(\Rightarrow _{\lnot w}\) are defined by:


It is immediate to check that \(\rightarrow _{\beta _v}\, = \, \rightarrow _{w}\cup \rightarrow _{\lnot w}\) and \(\rightarrow _{\lnot w}\,\subseteq \, \Rightarrow _{\lnot w}\,\subseteq \, \rightarrow _{\lnot w}^*\).
Weak CbV Factorization. We show that \((\varLambda , \{ \rightarrow _{w}, \rightarrow _{\lnot w}\})\) is a macro-step system, with \(\Rightarrow _{\beta _v},\Rightarrow _{\lnot w}\) as macro-steps. Merge and split are proved exactly as in Sect. 4.
Proposition 15
(Weak CbV macro-step system)
-
1.
Merge: if \(t\Rightarrow _{\lnot w}\cdot \rightarrow _{w}u\) then \(t\Rightarrow _{\beta _v}u\).
-
2.
Indexed split: if \(t\overset{n}{\Rightarrow }_{\beta _v} s\) then \(t\Rightarrow _{\lnot w}s\), or \(n>0\) and \(t\rightarrow _{w}\!\cdot \! \overset{n-1}{\Rightarrow }_{\beta _v} s\).
-
3.
Split: if \(t\Rightarrow _{\beta _v}s\) then \(t\rightarrow _{w}^* \!\cdot \! \Rightarrow _{\lnot w}s\).
That is, \((\varLambda , \{\rightarrow _{w}, \rightarrow _{\lnot w}\})\) is a macro-step system with respect to \(\Rightarrow _{\beta _v}\) and \(\Rightarrow _{\lnot w}\).
Theorem 16
(Weak CbV factorization). If \(t\rightarrow _{\beta _v}^* s\) then \(t\rightarrow _{w}^* \!\cdot \! \rightarrow _{\lnot w}^* s\).
Plotkin’s Left Reduction. The same argument at work in this section adapts easily to factorization with respect to leftmost weak reduction (used by Plotkin [26]), or to rightmost weak reduction, the two natural deterministic variants of \(\rightarrow _{w}\).
Weak CbV Normalization. To obtain a normalization theorem for \(\rightarrow _{w}\) via the essential normalization theorem (Theorem 8), we need persistence and uniform termination. The latter follows from the well-known diamond property of \(\rightarrow _{w}\).
Proposition 17
(Weak CbV essential system)
-
1.
Persistence: if \(t\rightarrow _{w}s\) and \(t\rightarrow _{\lnot w}u\) then \(u\rightarrow _{w}r\) for some \(r\).
-
2.
Diamond: if \(s\; _{w}{\leftarrow }\ \!\cdot \! \rightarrow _{w}u\) with \(s\ne u\) then \(s\rightarrow _{w}\!\cdot \! \; _{w}{\leftarrow }\ u\).
Then, \((\varLambda , \{ \rightarrow _{w}, \rightarrow _{\lnot w}\})\) is an essential system.
Theorem 18
(Weak CbV normalization). If \(t\rightarrow _{\beta _v}^* s\) and \(s\) is a \(\rightarrow _{w}\)-normal form, then \(t\) is strongly \(\rightarrow _{w}\)-normalizing.
CbV is often considered with respect to closed terms only. In such a case the \(\rightarrow _{w}\)-normal forms are exactly the (closed) values. Then weak CbV normalization (Theorem 18) implies the following, analogous to Corollary 1 in Plotkin [26] (the result is there obtained from standardization).
Corollary 19
Let \(t\) be a closed term. If \(t\rightarrow _{\beta _v}^* v\) for some value \(v\), then every maximal \(\rightarrow _{w}\)-sequence from \(t\) is finite and ends in a value.
7 Leftmost-Outermost Reduction, Essentially
Here we apply our technique to leftmost-outermost (shortened to \(\ell o\)) reduction \(\rightarrow _{\ell o}\), the first example of full reduction for \(\rightarrow _{\beta }\). The technical development is slightly different from the ones in the previous sections, as factorization relies on persistence. The same shall happen for the full \({\ell \ell } \) reduction of the next section. It seems to be a feature of full reductions for \(\rightarrow _{\beta }\).
\(\ell o\) and \(\lnot \) \(\ell o\) reductions.The definition of \(\ell o\) reduction relies on two mutually recursive predicates defining normal and neutral terms (neutral = normal and not an abstraction):

Dually, a term is not neutral if it is an abstraction or it is not normal. It is standard that these predicates correctly capture \(\beta \) normal forms and neutrality.
The reductions of the \(\ell o\) macro-step system are:



As usual, easy inductions show that \(\rightarrow _{\beta }\,=\, \rightarrow _{\ell o}\cup \rightarrow _{\lnot \ell o}\) and \(\rightarrow _{\lnot \ell o}\subseteq \Rightarrow _{\lnot \ell o}\subseteq \rightarrow _{\lnot \ell o}^*\).
Factorization depends on persistence, which is why for \(\ell o\) reduction most essential properties are proved before factorization. The proofs are easy inductions.
Proposition 20
(\(\ell o\) essential properties)
-
1.
Fullness: if \(t\rightarrow _{\beta }s\) then there exists \(u\) such that \(t\rightarrow _{\ell o}u\).
-
2.
Determinism: if \(t\rightarrow _{\ell o}s_1\) and \(t\rightarrow _{\ell o}s_2\) then \(s_1 = s_2\).
-
3.
Persistence: if \(t\rightarrow _{\ell o}s_1\) and \(t\rightarrow _{\lnot \ell o}s_2\) then \(s_2 \rightarrow _{\ell o}u\) for some \(u\).
Proposition 21
(\(\ell o\) macro-step system)
-
1.
Merge: if \(t\Rightarrow _{\lnot \ell o}\cdot \rightarrow _{\ell o}u\) then \(t\Rightarrow _{\beta }u\).
-
2.
Indexed split: if \(t\overset{n}{\Rightarrow }_{\beta } s\) then \(t\Rightarrow _{\lnot \ell o}s\), or \(n>0\) and \(t\rightarrow _{\ell o}\!\cdot \! \overset{n-1}{\Rightarrow }_{\beta } s\).
-
3.
Split: if \(t\Rightarrow _{\beta }s\) then \(t\rightarrow _{\ell o}^* \!\cdot \! \Rightarrow _{\lnot \ell o}s\).
That is, \((\varLambda , \{\rightarrow _{\ell o}, \rightarrow _{\lnot \ell o}\})\) is a macro-step system with respect to \(\Rightarrow _{\beta }\) and \(\Rightarrow _{\lnot \ell o}\).
Proof
We only show the merge property, and only the case that requires persistence—the rest of the proof is in the Appendix of [3]. The proof of the merge property is by induction on \(t\Rightarrow _{\lnot \ell o}s\). Consider the rule

Since \(r\) is not neutral, it is an abstraction or it is not normal. If \(r\) is an abstraction this case continues as the easy case of \(\Rightarrow _{\lnot \ell o}\) for \(\beta \)-redexes (see the Appendix of [3]). Otherwise, \(r\) is not normal, i.e. \(r\rightarrow _{\beta }q\). By fullness \(r\rightarrow _{\ell o}q'\) for some \(q'\), and by persistence (Prop. 20.3) \(r'\rightarrow _{\ell o}r''\) for some \(r''\). The hypothesis becomes \(t= rp\Rightarrow _{\lnot \ell o}r' p' \rightarrow _{\ell o}r'' p' = u\) with \(r\Rightarrow _{\lnot \ell o}r' \rightarrow _{\ell o}r''\). By i.h., \(r\Rightarrow _{\beta }r''\). Then,

\(\square \)
\(\ell o\) split. As pointed out in Sect. 4.1, Takahashi’s proof [28] of the split property relies on left substitutivity of head reduction, that is, if \(t\rightarrow _{h}s\) then  for all terms \(u\). Such a property does not hold for \(\ell o\) reduction. For instance, \(t= x(I y) \rightarrow _{\ell o}xy= t'\) but
for all terms \(u\). Such a property does not hold for \(\ell o\) reduction. For instance, \(t= x(I y) \rightarrow _{\ell o}xy= t'\) but  . Therefore her proof technique for factorization cannot prove the factorization theorem for \(\ell o\) reduction (see also footnote 2).
. Therefore her proof technique for factorization cannot prove the factorization theorem for \(\ell o\) reduction (see also footnote 2).
From Proposition 21 it follows the factorization theorem for \(\ell o\) reduction, that together with Proposition 20 proves that \((\varLambda , \{\rightarrow _{\ell o}, \rightarrow _{\lnot \ell o}\})\) is an essential system, giving normalization of \(\rightarrow _{\ell o}\) for \(\rightarrow _{\beta }\).
Theorem 22
-
1.
\(\ell o\) factorization: if \(t\rightarrow _{\beta }^* u\) then \(t\rightarrow _{\ell o}^* \!\cdot \!~ \rightarrow _{\lnot \ell o}^* u\).
-
2.
\(\ell o\) normalization: \(\rightarrow _{\ell o}\) is a normalizing reduction for \(\rightarrow _{\beta }\).
8 Least-Level Reduction, Essentially
In this section we study another normalizing full reduction for \(\rightarrow _{\beta }\), namely least-level (shortened to \({\ell \ell } \)) reduction \(\rightarrow _{{\ell \ell }}\), which is non-deterministic. The intuition is that \({\ell \ell } \) reduction fires a \(\beta \)-redex of minimal level, where the level of a \(\beta \)-redex is the number of arguments containing it.
The definition of \(\rightarrow _{{\ell \ell }}\) relies on an indexed variant \(\rightarrow _{\beta :{k}}\) of \(\rightarrow _{\beta }\), where \(k \in \mathbb {N}\) is the level of the fired \(\beta \)-redex (do not mix it up with the index of \(\overset{n}{\Rightarrow }_{\beta }\)). We also define a parallel version \(\Rightarrow _{\beta :{n}}\) (with \(n \in \mathbb {N}\cup \{\infty \}\)) of \(\rightarrow _{\beta :{k}}\), obtained as a decoration of \(\Rightarrow _{\beta }\), where n is the minimal level of the \(\beta \)-redexes fired by a \(\Rightarrow _{\beta }\) step (\(\Rightarrow _{\beta :{\infty }}\) does not reduce any \(\beta \)-redex). From now on, \(\mathbb {N}\cup \{\infty \}\) is considered with its usual order and arithmetic, that is, \(\infty + 1 = \infty \).


Note that \(t\rightarrow _{\beta }s\) if and only if \(t\rightarrow _{\beta :{k}} s\) for some \(k \in \mathbb {N}\).
The least (reduction) level \({\ell \ell } (t)\in \mathbb {N}\cup \{\infty \}\) of a term \(t\) is defined as follows:
The definitions of \({\ell \ell } \), \(\lnot \) \({\ell \ell } \), and parallel \(\lnot \) \({\ell \ell } \) reductions are:

As usual, easy inductions show that \(\rightarrow _{\beta }= \rightarrow _{{\ell \ell }}\cup \rightarrow _{\lnot {\ell \ell }}\) and \(\rightarrow _{\lnot {\ell \ell }}\subseteq \Rightarrow _{\lnot {\ell \ell }}\subseteq \rightarrow _{\lnot {\ell \ell }}^*\).
Proposition 23
(Least level properties). Let \(t\) be a term.
-
1.
Computational meaning of \({\ell \ell } \): \({\ell \ell } (t) = \inf \{ k \in \mathbb {N}\mid t\rightarrow _{\beta :{k}} u\text { for some term } u\}\).
-
2.
Monotonicity: if \(t\rightarrow _{\beta }s\) then \({\ell \ell } (s) \ge {\ell \ell } (t)\).
-
3.
Invariance by \(\rightarrow _{\lnot {\ell \ell }}\): if \(t\rightarrow _{\lnot {\ell \ell }}s\) then \({\ell \ell } (s) = {\ell \ell } (t)\).
Point 1 captures the meaning of the least level, and gives fullness of \(\rightarrow _{{\ell \ell }}\). In particular, \({\ell \ell } (t) = \infty \) if and only if \(t\) is \(\rightarrow _{\beta }\)-normal, since \(\inf \, \emptyset = \infty \). Monotonicity states that \(\beta \) steps cannot decrease the least level. Invariance by \(\rightarrow _{\lnot {\ell \ell }}\) says that \(\rightarrow _{\lnot {\ell \ell }}\) cannot change the least level. Essentially, this is persistence.
Proposition 24
(\({\ell \ell } \) essential properties)
-
1.
Fullness: if \(t\rightarrow _{\beta }s\) then \(t\rightarrow _{{\ell \ell }}u\) for some \(u\).
-
2.
Persistence: if \(t\rightarrow _{{\ell \ell }}s_1\) and \(t\rightarrow _{\lnot {\ell \ell }}s_2\) then \(s_2 \rightarrow _{{\ell \ell }}u\) for some \(u\).
-
3.
Diamond: if \(s\; _{{\ell \ell }}{\leftarrow }\ \cdot \rightarrow _{{\ell \ell }}u\) with \(s\ne u\) then \(s\rightarrow _{{\ell \ell }}\cdot \; _{{\ell \ell }}{\leftarrow }\ u\).
As for \(\ell o\), merge needs persistence, or, more precisely, invariance by \(\rightarrow _{\lnot {\ell \ell }}\).
Proposition 25
(\({\ell \ell } \) macro-step system)
-
1.
Merge: if \(t\Rightarrow _{\lnot {\ell \ell }}s\rightarrow _{{\ell \ell }}u\), then \(t\Rightarrow _{\beta }u\).
-
2.
Indexed split: if \(t\overset{n}{\Rightarrow }_{\beta } s\) then \(t\Rightarrow _{\lnot {\ell \ell }}s\), or \(n>0\) and \(t\rightarrow _{{\ell \ell }}\cdot \overset{n-1}{\Rightarrow _{\beta }} s\).
-
3.
Split: if \(t\Rightarrow _{\beta }s\) then \(t\rightarrow _{{\ell \ell }}^* \cdot \Rightarrow _{\lnot {\ell \ell }}s\).
That is, \((\varLambda , \{\rightarrow _{{\ell \ell }}, \rightarrow _{\lnot {\ell \ell }}\})\) is a macro-step system with respect to \(\Rightarrow _{\beta }\) and \(\Rightarrow _{\lnot {\ell \ell }}\).
Theorem 26
-
1.
\({\ell \ell } \) factorization: if \(t\rightarrow _{\beta }^* u\) then \(t\rightarrow _{{\ell \ell }}^* \cdot \rightarrow _{\lnot {\ell \ell }}^* u\).
-
2.
\({\ell \ell } \) normalization: \(\rightarrow _{{\ell \ell }}\) is a normalizing reduction for \(\rightarrow _{\beta }\).
\({\ell \ell } \) split and \(\ell o\) vs. \({\ell \ell } \). As for \(\ell o\) reduction, left substitutivity does not hold for \(\rightarrow _{{\ell \ell }}\). Consider \(t= x(I y) \rightarrow _{{\ell \ell }}xy= t'\) where the step has level 1, and  since now there also is a step \((\lambda z.zz)(Iy)\rightarrow _{{\ell \ell }}(I y)(I y)\) at level 0.
since now there also is a step \((\lambda z.zz)(Iy)\rightarrow _{{\ell \ell }}(I y)(I y)\) at level 0.
Moreover, \({\ell \ell } \) and \(\ell o\) reductions are incomparable. First, note that \(\rightarrow _{{\ell \ell }}\) but \(\not \rightarrow _{\ell o}\): \(t= (\lambda x.{II})y\rightarrow _{{\ell \ell }}(\lambda x.{I})y= s\), because \(t\rightarrow _{\beta :{0}} (\lambda x.{I})y\) and \({\ell \ell } (t) = 0\), but \(t\not \rightarrow _{\ell o}s\), indeed \(t\rightarrow _{\ell o}II\). This fact also shows that \(\rightarrow _{{\ell \ell }}\) is not left–outer in the sense of van Oostrom and Toyama [22]. Second, \(\rightarrow _{\ell o}\) but \(\not \rightarrow _{{\ell \ell }}\): \(t= x(x(II)) (II) \rightarrow _{\ell o}x(xI)(II) = s\) but \(t\not \rightarrow _{{\ell \ell }}s\), indeed \(t\rightarrow _{\lnot {\ell \ell }}s\) because \(t\rightarrow _{\beta :{2}} s\) and \({\ell \ell } (t) = 1\), and \(t\rightarrow _{{\ell \ell }}x(x(II)) I \ne s\).
9 Conclusions
We provide simple proof techniques for factorization and normalization theorems in the \(\lambda \)-calculus, simplifying Takahashi’s parallel method [28], extending its scope and making it more abstract at the same time.
About the use of parallel reduction, Takahashi claims: “once the idea is stated properly, the essential part of the proof is almost over, because the inductive verification of the statement is easy, even mechanical” [28, p. 122]. Our work reinforces this point of view, as our case studies smoothly follow the abstract schema.
Range of Application. We apply our method for factorization and normalization to two notions of reductions that compute full normal forms:
-
the classic example of \(\ell o\) reduction, covered also by the recent techniques by Hirokawa, Middeldorp and Moser [12] and van Oostrom and Toyama [22];
-
\({\ell \ell } \) reduction, which is out of the scope of [12, 22] because it is neither deterministic (as required by [12]), nor left–outer in the sense of [22] (as pointed out here in Sect. 8).
Our approach naturally covers also reductions that do not compute full normal forms, such as head and weak CbV reductions. These results are out of reach for van Oostrom and Toyama’s technique [22], as they clarify in their conclusions.
Because of the minimality of our assumptions, we believe that our method applies to a large variety of other cases and variants of the \(\lambda \)-calculus.
Notes
- 1.
The terminology at work in the literature on \(\lambda \)-calculus and the rewriting terminology often clash: the former calls parallel \(\beta \) reduction what the latter calls multi-step \(\beta \) reduction—parallel reduction in rewriting is something else.
- 2.
It can be obtained indirectly, as a corollary of standardization, proved by Takahashi [28] using the concrete structure of terms. Thus the proof is not of an abstract nature.
- 3.
In rewriting theory, a full reduction for \(\rightarrow _{}\) is called a reduction strategy for \(\rightarrow _{}\). We prefer not to use the term strategy because it has different meaning in the \(\lambda \)-calculus, where it is a deterministic, not necessarily full, reduction for \(\rightarrow _{}\).
- 4.
The difference between factorization and its terminal case is relevant for normalization: van Oostrom and Toyama [22, footnote 8] give an example of normalizing full reduction for a rewriting system in which factorization fails but terminal factorization holds.
- 5.
“\(t\) has a head normal form” is the usual formulation for “\(t\rightarrow _{\beta }^* s\) for some \(s\) that is head normal”. We prefer the latter to avoid the ambiguity of the former about the reduction leading from \(t\) to one of its head normal forms (\(\rightarrow _{\beta }^*\) or \(\rightarrow _{h}^*\)?).
- 6.
Namely, if \(s_1 \; _{\beta }{\Leftarrow }\ t\Rightarrow _{\beta }s_2\) then there exists \(u\) such that \(s_1 \Rightarrow _{\beta }u\; _{\beta }{\Leftarrow }\ s_2\).
References
Accattoli, B.: An abstract factorization theorem for explicit substitutions. In: 23rd International Conference on Rewriting Techniques and Applications, RTA 2012. LIPIcs, vol. 15, pp. 6–21 (2012). https://doi.org/10.4230/LIPIcs.RTA.2012.6
Accattoli, B., Dal Lago, U.: (Leftmost-Outermost) Beta-reduction is invariant, indeed. Logical Methods Comput. Sci. 12(1) (2016). https://doi.org/10.2168/LMCS-12(1:4)2016
Accattoli, B., Faggian, C., Guerrieri, G.: Factorization and normalization, essentially (extended version). CoRR abs/1902.05945 (2019). http://arxiv.org/abs/1908.11289
Barendregt, H.P.: The Lambda Calculus - Its Syntax and Semantics. Studies in Logic and the Foundations of Mathematics, vol. 103. North-Holland, Amsterdam (1984)
Bonelli, E., Kesner, D., Lombardi, C., Ríos, A.: On abstract normalisation beyond neededness. Theor. Comput. Sci. 672, 36–63 (2017). https://doi.org/10.1016/j.tcs.2017.01.025
de Carvalho, D., Pagani, M., de Falco, L.T.: A semantic measure of the execution time in linear logic. Theor. Comput. Sci. 412(20), 1884–1902 (2011). https://doi.org/10.1016/j.tcs.2010.12.017
Crary, K.: A simple proof of call-by-value standardization. Technical report, CMU-CS-09-137, Carnegie Mellon University (2009)
Guerrieri, G.: Head reduction and normalization in a call-by-value lambda-calculus. In: 2nd International Workshop on Rewriting Techniques for Program Transformations and Evaluation, WPTE 2015. OASICS, vol. 46, pp. 3–17 (2015). https://doi.org/10.4230/OASIcs.WPTE.2015.3
Guerrieri, G., Paolini, L., Ronchi Della Rocca, S.: Standardization of a Call-By-Value Lambda-Calculus. In: 13th International Conference on Typed Lambda Calculi and Applications, TLCA 2015. LIPIcs, vol. 38, pp. 211–225 (2015). https://doi.org/10.4230/LIPIcs.TLCA.2015.211
Guerrieri, G., Paolini, L., Ronchi Della Rocca, S.: Standardization and conservativity of a refined call-by-value lambda-calculus. Logical Methods Comput. Sci. 13(4) (2017). https://doi.org/10.23638/LMCS-13(4:29)2017
Hindley, J.: The Church-Rosser property and a result in combinatory logic. Ph.D. thesis, University of Newcastle-upon-Tyne (1964)
Hirokawa, N., Middeldorp, A., Moser, G.: Leftmost outermost revisited. In: 26th International Conference on Rewriting Techniques and Applications, RTA 2015. LIPIcs, vol. 36, pp. 209–222 (2015). https://doi.org/10.4230/LIPIcs.RTA.2015.209
Ishii, K.: A proof of the leftmost reduction theorem for \(\lambda \)\(\beta \)\(\eta \)-calculus. Theor. Comput. Sci. 747, 26–32 (2018). https://doi.org/10.1016/j.tcs.2018.06.003
Kesner, D., Lombardi, C., Ríos, A.: A standardisation proof for algebraic pattern calculi. In: 5th International Workshop on Higher-Order Rewriting, HOR 2010. EPTCS, vol. 49, pp. 58–72 (2010). https://doi.org/10.4204/EPTCS.49.5
Klop, J.W.: Combinatory reduction systems. Ph.D. thesis, Utrecht University (1980)
Krivine, J.: Lambda-Calculus. Ellis Horwood Series in Computers and Their Applications. Masson, Types and Models. Ellis Horwood (1993)
McKinna, J., Pollack, R.: Some lambda calculus and type theory formalized. J. Autom. Reasoning 23(3–4), 373–409 (1999). https://doi.org/10.1007/BFb0026981
Melliès, P.-A.: A factorisation theorem in rewriting theory. In: Moggi, E., Rosolini, G. (eds.) CTCS 1997. LNCS, vol. 1290, pp. 49–68. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0026981
Mitschke, G.: The standardization theorem for \(\lambda \)-calculus. Math. Logic Q. 25(1–2), 29–31 (1979). https://doi.org/10.1002/malq.19790250104
Newman, M.: On theories with a combinatorial definition of “Equivalence”. Ann. Math. 43(2), 223–243 (1942)
Oostrom, V.: Random descent. In: Baader, F. (ed.) RTA 2007. LNCS, vol. 4533, pp. 314–328. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73449-9_24
van Oostrom, V., Toyama, Y.: Normalisation by random descent. In: 1st International Conference on Formal Structures for Computation and Deduction, FSCD 2016. LIPIcs, vol. 52, pp. 32:1–32:18 (2016). https://doi.org/10.4230/LIPIcs.FSCD.2016.32
Pagani, M., Tranquilli, P.: Parallel reduction in resource lambda-calculus. In: Hu, Z. (ed.) APLAS 2009. LNCS, vol. 5904, pp. 226–242. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10672-9_17
Pagani, M., Tranquilli, P.: The conservation theorem for differential nets. Math. Struct. Comput. Sci. 27(6), 939–992 (2017). https://doi.org/10.1017/S0960129515000456
Paolini, L., Ronchi Della Rocca, S.: Parametric parameter passing lambda-calculus. Inf. Comput. 189(1), 87–106 (2004). https://doi.org/10.1016/j.ic.2003.08.003
Plotkin, G.D.: Call-by-name, call-by-value and the lambda-calculus. Theor. Comput. Sci. 1(2), 125–159 (1975). https://doi.org/10.1016/0304-3975(75)90017-1
Ronchi Della Rocca, S., Paolini, L.: The Parametric Lambda Calculus - A Metamodel for Computation. TTCS. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-10394-4
Takahashi, M.: Parallel reductions in \(\lambda \)-calculus. Inf. Comput. 118(1), 120–127 (1995). https://doi.org/10.1006/inco.1995.1057
Terese: Term Rewriting Systems. Cambridge Tracts in Theoretical Computer Science, vol. 55. Cambridge University Press, Cambridge (2003)
Terui, K.: Light affine lambda calculus and polynomial time strong normalization. Arch. Math. Log. 46(3–4), 253–280 (2007). https://doi.org/10.1007/s00153-007-0042-6
Acknowledgments
This work has been partially funded by the ANR JCJC grant COCA HOLA (ANR-16-CE40-004-01) and by the EPSRC grant EP/R029121/1 “Typed Lambda-Calculi with Sharing and Unsharing”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Accattoli, B., Faggian, C., Guerrieri, G. (2019). Factorization and Normalization, Essentially. In: Lin, A. (eds) Programming Languages and Systems. APLAS 2019. Lecture Notes in Computer Science(), vol 11893. Springer, Cham. https://doi.org/10.1007/978-3-030-34175-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-34175-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34174-9
Online ISBN: 978-3-030-34175-6
eBook Packages: Computer ScienceComputer Science (R0)






 .
. . It is possible to spell out the number of
. It is possible to spell out the number of  .
. (1 step);
(1 step); the n steps corresponding to the sequence
the n steps corresponding to the sequence  ;
; .
. that satisfies the statement because
that satisfies the statement because  that satisfies the statement because
that satisfies the statement because  and
and  . By i.h.,
. By i.h.,  , thus
, thus 
 and
and  . Then
. Then 
 with
with  and
and 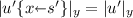 and
and  and
and  . By i.h.,
. By i.h.,  and
and  . Then
. Then 

 with
with  and by substitutivity of
and by substitutivity of  .
. ;
; .
.