Abstract
The central result of this chapter is the Alaoglu–Bourbaki theorem: Polars of neighbourhoods of zero in a locally convex space E are σ(E′, E)-compact subsets of E′. As a consequence in a dual pair 〈E, F〉 one concludes that, for a locally convex topology τ on E with (E, τ)′ = F, one always has σ(E, F) ⊆ τ ⊆ μ(E, F), where μ(E, F) is the Mackey topology on E, corresponding to the collection of absolutely convex σ(F, E)-compact subsets of F. As a prerequisite we show Tikhonov’s theorem, and as a prerequisite to the proof of Tikhonov’s theorem we introduce filters describing convergence and continuity of mappings in topological spaces.
Access provided by Autonomous University of Puebla. Download chapter PDF
The central result of this chapter is the Alaoglu–Bourbaki theorem: Polars of neighbourhoods of zero in a locally convex space E are σ(E′, E)-compact subsets of E′. As a consequence in a dual pair 〈E, F〉 one concludes that, for a locally convex topology τ on E with (E, τ)′ = F, one always has σ(E, F) ⊆ τ ⊆ μ(E, F), where μ(E, F) is the Mackey topology on E, corresponding to the collection of absolutely convex σ(F, E)-compact subsets of F. As a prerequisite we show Tikhonov’s theorem, and as a prerequisite to the proof of Tikhonov’s theorem we introduce filters describing convergence and continuity of mappings in topological spaces.
Let
 be a family of compact topological spaces. Then the product
be a family of compact topological spaces. Then the product
 is compact.
is compact.
We will prove this theorem here, even if it is rather part of general topology. However, the proof gives us the opportunity to introduce the notion of filters, which we will need anyway in the further treatment.
We recall that a topological space (X, τ) is called compact if every open covering of X (i.e., every collection \(\mathcal S\subseteq \tau \) satisfying \(\bigcup \mathcal S=X\)) contains a finite subcovering (i.e., a finite collection \(\mathcal F\subseteq \mathcal S\) such that \(\bigcup \mathcal F=X\)). Equivalently, X is compact if every collection \(\mathcal C\) of closed subsets of X with the finite intersection property (i.e., \(\bigcap \mathcal F\neq \varnothing \) for all finite \(\mathcal F\subseteq \mathcal C\)) satisfies \(\bigcap \mathcal C\neq \varnothing \). Note that we use the notion of compactness in the sense that a compact space need not be Hausdorff.
A subset C of a topological space (X, τ) is called compact if (C, τ ∩ C) is compact. (The topology  denotes the initial topology on C with respect to the injection C↪X, also called the induced topology
.) If X is a Hausdorff topological space, and C is a compact subset, then it is easy to see that the complement of C is open, i.e., that C is closed.
denotes the initial topology on C with respect to the injection C↪X, also called the induced topology
.) If X is a Hausdorff topological space, and C is a compact subset, then it is easy to see that the complement of C is open, i.e., that C is closed.
Let X be a set. A filter \(\mathcal F\) in X is a non-empty collection \(\mathcal F\subseteq \mathcal P(X)\) satisfying the following properties:
-
\(\varnothing \notin \mathcal F\);
-
if
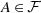 , A ⊆ B ⊆ X, then
, A ⊆ B ⊆ X, then 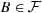 ;
; -
if
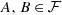 , then
, then 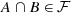 .
.
A filter base \(\mathcal F_0\) in X is a non-empty collection \(\mathcal F_0\subseteq \mathcal P(X)\) with:
-
\(\varnothing \notin \mathcal F_0\);
-
if
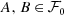 , then there exists
, then there exists 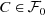 such that C ⊆ A ∩ B.
such that C ⊆ A ∩ B.
If \(\mathcal F_0\) is a filter base, then

is a filter, called the filter generated by \(\mathcal F_0\). A filter \(\mathcal F\) is called an ultrafilter if there is no filter properly containing \(\mathcal F\).
Let now X be a topological space, \(\mathcal F\) a filter in X,  . Then \(\mathcal F\)converges tox (or xis a limit of
\(\mathcal F\)), \(\mathcal F\to x\), if
. Then \(\mathcal F\)converges tox (or xis a limit of
\(\mathcal F\)), \(\mathcal F\to x\), if  . If \(\mathcal F_0\) is a filter base, then one also writes \(\mathcal F_0\to x\) if the generated filter
. If \(\mathcal F_0\) is a filter base, then one also writes \(\mathcal F_0\to x\) if the generated filter  converges to x, i.e., if for all
converges to x, i.e., if for all  there exists
there exists  with A ⊆ U. The point x is called a cluster point
(also ‘accumulation point’) of a filter \(\mathcal F\), if for all
with A ⊆ U. The point x is called a cluster point
(also ‘accumulation point’) of a filter \(\mathcal F\), if for all  ,
,  one has \(U\cap A\neq \varnothing \), or equivalently, if
one has \(U\cap A\neq \varnothing \), or equivalently, if  .
.
Let X be a set.
(a) If  , then \(\mathcal F_0:=\bigl \{\{x\}\bigr \}\) is a filter base. The generated filter is called the filter fixed at
x.
, then \(\mathcal F_0:=\bigl \{\{x\}\bigr \}\) is a filter base. The generated filter is called the filter fixed at
x.
(b) If (x
n) is a sequence in X, then  is a filter base. The generated filter is called an elementary filter
.
is a filter base. The generated filter is called an elementary filter
.
If additionally X is a topological space and  , then \(\mathcal F_0\to x\) if and only if x
n → x as n →∞.
, then \(\mathcal F_0\to x\) if and only if x
n → x as n →∞.
(c) Let X be a topological space,  . Then
. Then  is a filter (the neighbourhood filter of x). △
is a filter (the neighbourhood filter of x). △
Let X be a set.
(a) If \(\mathcal F\) is a filter in X, A ⊆ X such that \(A\cap B\neq \varnothing \) for all  , then obviously
, then obviously  is a filter base, and the generated filter is finer
than \(\mathcal F\) (i.e., it contains \(\mathcal F\)).
is a filter base, and the generated filter is finer
than \(\mathcal F\) (i.e., it contains \(\mathcal F\)).
(b) Let \(\mathcal F\) be a filter. Then \(\mathcal F\) is an ultrafilter if and only if for all A ⊆ X one has  or
or  . (Necessity: If \(A\cap B\neq \varnothing \) for all
. (Necessity: If \(A\cap B\neq \varnothing \) for all  , then (a) implies that there is a finer filter containing A, and this filter is equal to \(\mathcal F\) because \(\mathcal F\) is an ultrafilter; thus
, then (a) implies that there is a finer filter containing A, and this filter is equal to \(\mathcal F\) because \(\mathcal F\) is an ultrafilter; thus  . Otherwise there exists
. Otherwise there exists  such that \(A\cap B=\varnothing \), and then
such that \(A\cap B=\varnothing \), and then  . Sufficiency: The condition implies that there is no finer filter.)
. Sufficiency: The condition implies that there is no finer filter.)
(c) For every filter \(\mathcal F\) in X there exists a finer ultrafilter. This is an immediate consequence of Zorn’s lemma. (In the proof that a maximal element is an ultrafilter one uses (a) and (b).)
(d) If X is a topological space, \(\mathcal F\) is an ultrafilter in X, and  is a cluster point of \(\mathcal F\), then \(\mathcal F\to x\). (If
is a cluster point of \(\mathcal F\), then \(\mathcal F\to x\). (If  , then \(U\cap A\neq \varnothing \) for all
, then \(U\cap A\neq \varnothing \) for all  , therefore
, therefore  , because \(\mathcal F\) is an ultrafilter.)△
, because \(\mathcal F\) is an ultrafilter.)△
In our treatment we will use filters to discuss convergence and continuity in topological spaces. Filters generalise sequences – see Example 4.2(b) – which are sufficient for this purpose in metric spaces. (Another generalisation of sequences are ‘nets’, a notion that we will not need.) The proof of Theorem 4.1 becomes particularly nice with filters, but also for the discussion of completeness (Chapter 9) filters will be convenient. △
FormalPara Proposition 4.5Let X be a topological space. Then the following properties are equivalent:
-
(i)
X is compact;
-
(ii)
every filter in X possesses a cluster point;
-
(iii)
every ultrafilter in X is convergent.
(i) ⇒ (ii). Let \(\mathcal F\) be a filter in X. Then the collection  has the finite intersection property, and therefore
has the finite intersection property, and therefore  , i.e., \(\mathcal F\) has a cluster point.
, i.e., \(\mathcal F\) has a cluster point.
(ii) ⇒ (i). Let \(\mathcal C\subseteq \mathcal P(X)\) be a collection of closed sets with the finite intersection property. Then  is a filter base. The generated filter \(\mathcal F\) has a cluster point, i.e.,
is a filter base. The generated filter \(\mathcal F\) has a cluster point, i.e.,  .
.
‘(ii) ⇒ (iii)’ is obvious, in view of Remark 4.3(d).
(iii) ⇒ (ii). If \(\mathcal F\) is a filter in X, then there exists a finer ultrafilter; see Remark 4.3(c). Every limit of this filter is a cluster point of \(\mathcal F\). □
Let X, Y be sets, f : X → Y , \(\mathcal F\) a filter in X. Then  is a filter base in Y , and the generated filter
is a filter base in Y , and the generated filter  is called the image filter
.
is called the image filter
.
If \(\mathcal F\) is an ultrafilter, then \(f(\mathcal F)\) is an ultrafilter base. Indeed, for B ⊆ Y one has  or
or  . In the first case one concludes that
. In the first case one concludes that  , in the second case that
, in the second case that  .
.
-
(a)
Let X, Y be topological spaces,
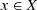 ,
\(\mathcal F\)a filter in X,
\(\mathcal F\to x\), f : X → Y continuous at x. Then
\(f(\mathcal F)\to f(x)\).
,
\(\mathcal F\)a filter in X,
\(\mathcal F\to x\), f : X → Y continuous at x. Then
\(f(\mathcal F)\to f(x)\). -
(b)
Let X, X ι
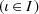 be topological spaces, f
ι: X → X
ι
be topological spaces, f
ι: X → X
ι
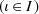 , and let the topology on X be the initial topology with respect to
, and let the topology on X be the initial topology with respect to
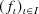 . Let
. Let
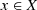 ,
\(\mathcal F\)a filter in X. Then
\(\mathcal F\to x\)if and only if
\(f_\iota (\mathcal F)\to f_\iota (x)\)for all
,
\(\mathcal F\)a filter in X. Then
\(\mathcal F\to x\)if and only if
\(f_\iota (\mathcal F)\to f_\iota (x)\)for all
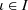 .
.
(a) Let V be a neighbourhood of f(x). Then f
−1(V ) is a neighbourhood of x, and therefore  . From f(f
−1(V )) ⊆ V one then obtains
. From f(f
−1(V )) ⊆ V one then obtains  .
.
(b) The necessity is clear from (a). For the sufficiency let  . Then there exist a finite set F ⊆ I and neighbourhoods U
ι of f
ι(x)
. Then there exist a finite set F ⊆ I and neighbourhoods U
ι of f
ι(x)  such that
such that  . There exists
. There exists  such that f
ι(A) ⊆ U
ι
such that f
ι(A) ⊆ U
ι
 . Therefore
. Therefore

□
FormalPara Proof of Theorem 4.1Without restriction all \(X_\iota \neq \varnothing \). Let \(\mathcal F\) be an ultrafilter in  . Then \( \mathop {\mathrm {pr}} \nolimits _\iota (\mathcal F)\) is an ultrafilter base in X
ι, therefore convergent by Proposition 4.5,
. Then \( \mathop {\mathrm {pr}} \nolimits _\iota (\mathcal F)\) is an ultrafilter base in X
ι, therefore convergent by Proposition 4.5, 
 . Then Proposition 4.6(b) implies that
. Then Proposition 4.6(b) implies that  . □
. □
As in the case of Banach spaces Tikhonov’s theorem implies the Banach–Alaoglu theorem, i.e., the closed dual ball is weak∗-compact, we now derive the corresponding result for locally convex spaces.
Let E be a locally convex space, U ⊆ E a neighbourhood of zero. Then U ∘⊆ E′ is σ(E′, E)-compact.
FormalPara Lemma 4.8
Let E be a vector space. Then E
∗
is closed in
 with respect to the product topology.
with respect to the product topology.
For  ,
,  the mapping
the mapping

is continuous. (Note that, for  , the mapping
, the mapping  is one of the projections defining the product topology.) Therefore
is one of the projections defining the product topology.) Therefore  is closed. □
is closed. □
Without loss of generality we may assume that U is absolutely convex. We note that  if and only if
if and only if  and \(|\langle x,x'\rangle |\leqslant p_U(x)\) (
and \(|\langle x,x'\rangle |\leqslant p_U(x)\) ( ). The condition is clearly sufficient. On the other hand, if
). The condition is clearly sufficient. On the other hand, if  ,
,  , λ > p
U(x), then
, λ > p
U(x), then  , \(|\langle \frac 1\lambda x,x'\rangle |\leqslant 1\), \(|\langle x,x'\rangle |\leqslant \lambda \); therefore, \(|\langle x,x'\rangle |\leqslant p_U(x)\). This implies that
, \(|\langle \frac 1\lambda x,x'\rangle |\leqslant 1\), \(|\langle x,x'\rangle |\leqslant \lambda \); therefore, \(|\langle x,x'\rangle |\leqslant p_U(x)\). This implies that

Theorem 1.2 implies that the weak topology on E′ and the product topology on  are the restrictions of the product topology on
are the restrictions of the product topology on  to these sets. Because of Lemma 4.8 it therefore follows that U
∘ is a closed subset of the compact set
to these sets. Because of Lemma 4.8 it therefore follows that U
∘ is a closed subset of the compact set  . □
. □
Let 〈E, F〉 be a dual pair. Let

Obviously one has \(\mathcal M_\mu \subseteq \mathcal B_\sigma (F,E)\). Then the polar topology
on E is called the Mackey topology . The Mackey topology μ(F, E) on F is defined correspondingly.
In the following Chapter 5 we will show that (E, μ(E, F))′ = b 2(F), and that μ(E, F) is the strongest topology with dual b 2(F), in the following sense: If 〈E, F〉 is a separating dual pair, then a locally convex topology τ on E is compatible with 〈E, F〉 if and only if σ(E, F) ⊆ τ ⊆ μ(E, F).
In the last statement, the necessity of the condition is easily obtained from our treatment presented so far. If τ is compatible, the property σ(E, F) ⊆ τ follows from the definition of the topology σ(E, F) (and Theorem 1.2), whereas the property τ ⊆ μ(E, F) is a consequence of Theorem 4.7, as follows. The space (E, τ) possesses a neighbourhood base of zero  consisting of closed absolutely convex sets; hence
consisting of closed absolutely convex sets; hence

by Theorem 4.7, and therefore \(\tau =\tau _{\mathcal M}\subseteq \tau _{\mathcal M_\mu }=\mu (E,F)\).
The definition of \(\mathcal M_\mu \) suggests the question whether in a locally convex space the closed absolutely convex hull of a compact set is again compact. Example 4.10 given below shows that this is not always the case. We will show in Chapter 11 that it is true if E is quasi-complete (Corollary 11.5). In particular it is true if E is a Banach space (‘Mazur’s theorem’). In Chapter 14 we will show that it is also true for the weak topology in a Banach space (‘Krein’s theorem’). However, it is always true that the closed absolutely convex hull of a compact convex set is compact; this is the content of the following lemma. As a consequence one obtains \(\mu (E,F)=\tau _{\mathcal {M}_{\mu }^{\prime }}\) also for

Let E be a topological vector space, and let A ⊆ E be a compact convex subset. Then \( \mathop {\overline {\mathrm {aco}}} A\)is compact.
FormalPara Proof(i) If B ⊆ E is a balanced subset, then \( \mathop {\mathrm {aco}} B= \mathop {\mathrm {co}} B\). This holds because

is easily seen to be balanced.
(ii) If  , then \( \mathop {\mathrm {bal}} A=[-1,1]\cdot A\subseteq \mathop {\mathrm {co}}(A\cup (-A))\), and the latter set is compact (as the image of the compact set
, then \( \mathop {\mathrm {bal}} A=[-1,1]\cdot A\subseteq \mathop {\mathrm {co}}(A\cup (-A))\), and the latter set is compact (as the image of the compact set  under the continuous mapping (λ
1, λ
2, x
1, x
2)↦λ
1x
1 + λ
2x
2). Hence \( \mathop {\overline {\mathrm {aco}}} A=\overline { \mathop {\mathrm {co}}( \mathop {\mathrm {bal}} A)}\subseteq \mathop {\mathrm {co}}(A\cup (-A))\) is compact.
under the continuous mapping (λ
1, λ
2, x
1, x
2)↦λ
1x
1 + λ
2x
2). Hence \( \mathop {\overline {\mathrm {aco}}} A=\overline { \mathop {\mathrm {co}}( \mathop {\mathrm {bal}} A)}\subseteq \mathop {\mathrm {co}}(A\cup (-A))\) is compact.
(iii) If  , then
, then

where again the latter set is compact. The remaining argument is as in (ii). □
FormalPara Example 4.10 (cf. [ Kha82, Chap. II, Example 10])Consider the dual pair 〈c
c, ℓ
1〉, where  , with the ‘unit vectors’ e
n in c
0 (or ℓ
1). The sequence (2ne
n)n in ℓ
1 is σ(ℓ
1, c
c)-convergent to 0; therefore
, with the ‘unit vectors’ e
n in c
0 (or ℓ
1). The sequence (2ne
n)n in ℓ
1 is σ(ℓ
1, c
c)-convergent to 0; therefore  is σ(ℓ
1, c
c)-compact. For
is σ(ℓ
1, c
c)-compact. For  , the element \(y^n:=\sum _{j=1}^ne_j=\sum _{j=1}^n2^{-j}(2^je_j)\) belongs to \( \mathop {\mathrm {co}} B\). For a σ(ℓ
1, c
c)-cluster point y = (y
j) of the sequence (y
n), the coordinate y
j would have to be a cluster point of the sequence \((y^n_j)_n\), i.e., y
j = 1
, the element \(y^n:=\sum _{j=1}^ne_j=\sum _{j=1}^n2^{-j}(2^je_j)\) belongs to \( \mathop {\mathrm {co}} B\). For a σ(ℓ
1, c
c)-cluster point y = (y
j) of the sequence (y
n), the coordinate y
j would have to be a cluster point of the sequence \((y^n_j)_n\), i.e., y
j = 1  . However, the element (1, 1, 1.… ) does not belong to ℓ
1. This shows that the sequence (y
n)n does not have a cluster point, and therefore the set \( \mathop {\mathrm {co}} B\) is not relatively compact with respect to σ(ℓ
1, c
c).
. However, the element (1, 1, 1.… ) does not belong to ℓ
1. This shows that the sequence (y
n)n does not have a cluster point, and therefore the set \( \mathop {\mathrm {co}} B\) is not relatively compact with respect to σ(ℓ
1, c
c).
We include an additional information on metrisability in the context of the Alaoglu–Bourbaki theorem.
Let E be a separable locally convex space, U ⊆ E a neighbourhood of zero. Then the topology σ(E′, E) is metrisable on U ∘⊆ E′.
FormalPara ProofLet A ⊆ E be a countable dense set, and denote by ρ the initial topology on E′ with respect to the family  . Then ρ is coarser than σ(E′, E), and ρ is metrisable, by Proposition 2.17 (where the denseness of A in E implies that ρ is Hausdorff). As (U
∘, σ(E′, E) ∩ U
∘) is compact by the Alaoglu–Bourbaki theorem, one concludes from Lemma 4.12, proved below, that ρ ∩ U
∘ = σ(E′, E) ∩ U
∘. □
. Then ρ is coarser than σ(E′, E), and ρ is metrisable, by Proposition 2.17 (where the denseness of A in E implies that ρ is Hausdorff). As (U
∘, σ(E′, E) ∩ U
∘) is compact by the Alaoglu–Bourbaki theorem, one concludes from Lemma 4.12, proved below, that ρ ∩ U
∘ = σ(E′, E) ∩ U
∘. □
For completeness we recall (from general topology) the following important basic observation concerning compactness.
Let X, Y be topological spaces, X compact, Y Hausdorff, f : X → Y continuous and bijective. Then f is a homeomorphism.
FormalPara ProofWe only have to show that f is an open mapping. Let U ⊆ X be an open set. Then X ∖ U is closed, hence compact. This implies that Y ∖ f(U) = f(X ∖ U) is compact, hence closed, i.e., f(U) is open. □
FormalPara NotesTikhonov’s theorem is one of the basic theorems of topology, in some sense the first result in the development of set theoretic topology which does not come along with a straightforward ‘evident’ proof. Tikhonov (in early German transcription “Tychonoff”) proved the theorem for compact intervals in [Tyc30] and mentioned later that the proof carries over to the general case. The main result of this chapter, the Alaoglu–Bourbaki theorem (Theorem 4.7), uses Tikhonov’s theorem. For the case of normed spaces it usually is called the Banach–Alaoglu theorem, proved for the separable case by Banach [Ban32, VIII, § 5, Théorème 3] and for the general case by Bourbaki [Bou38, Corollaire de Théorème 1] (and shortly after by Alaoglu [Ala40, Theorem 1:3]). The first appearance of the general case may be in a paper of Arens [Are47, proof of Theorem 2]. (It is also contained in Bourbaki [Bou64b, Chap. IV, § 2.2, Proposition 2].) The Mackey topology was first defined and used by Arens [Are47]; we use the notation μ(E, F), for a dual pair 〈E, F〉, thereby following Floret [Flo80]. (A more traditional notation, used by many authors, would be τ(E, F), and the author has been told the reason for this notation: σ(E, F) is the ‘beginning’ of the scale of compatible locally convex topologies, and τ(E, F) is the ‘end’; like one often uses [a, b] for intervals in \(\mathbb R\), the idea is to use the neighbouring letters σ and τ in the Greek alphabet as the ends of the ‘interval’. As we use ‘τ’ quite generally for topologies, we prefer Floret’s notation. Anyway, ‘σ’ in weak topologies probably comes from the ‘s’ in the German “schwach”. The earliest place where the author could localise the use of ‘σ(E, E′)’ for the weak topology, is the note [Die40].)
Summarising the previous discussion, if the names given to theorems should indicate their authors, then the Banach–Alaoglu theorem should be called ‘Banach–Bourbaki theorem’, the Alaoglu–Bourbaki theorem should be called ‘Bourbaki–Arens theorem’, and the Mackey topology should be called ‘Arens topology’ (although in the latter case ‘Arens–Mackey topology’ would be equally justified).
Concerning Lemma 4.9, we refer to [Edw65, Remark 8.13.4(3)].
References
L. Alaoglu: Weak topologies of normed linear spaces. Ann. of Math. (2)41, 252–267 (1940).
R. Arens: Duality in linear spaces. Duke Math. J. 14, 787–794 (1947).
S. Banach: Théorie des Opérations Linéaires. Chelsea, New York, 1932.
N. Bourbaki: Sur les espaces de Banach. C. R. Acad. Sci. Paris206, 1701–1704 (1938).
N. Bourbaki: Espaces Vectoriels Topologiques, Chap. III à V. Hermann, Paris, 1964.
J. Dieudonné: Topologies faibles dans les espaces vectoriels. C. R. Acad. Sci. Paris211, 94–97 (1940).
R. E. Edwards: Functional Analysis, Theory and Applications. Holt, Rinehart and Winston, New York, 1965.
K. Floret: Weakly Compact Sets. Springer-Verlag, Berlin, 1980.
S. M. Khaleelulla: Counterexamples in Topological Vector Spaces. Springer, Berlin, 1982.
A. Tychonoff: Über die topologische Erweiterung von Räumen. Math. Ann. 102, 544–561 (1930).
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Voigt, J. (2020). The Tikhonov and Alaoglu–Bourbaki Theorems. In: A Course on Topological Vector Spaces. Compact Textbooks in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-32945-7_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-32945-7_4
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-32944-0
Online ISBN: 978-3-030-32945-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


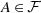 , A ⊆ B ⊆ X, then
, A ⊆ B ⊆ X, then 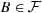 ;
;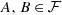 , then
, then 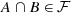 .
.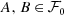 , then there exists
, then there exists 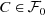 such that C ⊆ A ∩ B.
such that C ⊆ A ∩ B.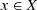 ,
,
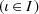 be topological spaces, f
ι: X → X
ι
be topological spaces, f
ι: X → X
ι
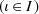 , and let the topology on X be the initial topology with respect to
, and let the topology on X be the initial topology with respect to
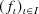 . Let
. Let
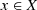 ,
,
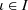 .
.