A New Linear-Time Algorithm for Centroid Decomposition

Abstract

The centroid of a tree is a node that, when removed, breaks the tree in connected components of size at most half of that of the original tree. By recursing this procedure on the components, one obtains the centroid decomposition of the tree, also known as centroid tree. The centroid tree has logarithmic height and its construction is a powerful pre-processing step in several tree-processing algorithms. The folklore recursive algorithm for computing the centroid tree runs in $O(n\log n)$ time. To the best of our knowledge, the only result claiming O(n) time is unpublished and relies on (dynamic) heavy path decomposition of the original tree. In this short paper, we describe a new simple and practical linear-time algorithm for the problem based on the idea of applying the folklore algorithm to a suitable decomposition of the original tree.

Partially supported by the project MIUR-SIR CMACBioSeq (“Combinatorial methods for analysis and compression of biological sequences”) grant n. RBSI146R5L and by the project MIUR-PRIN 2017 “Algorithms, Data Structures and Combinatorics for Machine Learning”.

1 Introduction

The centroid decomposition of a tree $\mathcal T$ (also known as separator decomposition) is a popular and powerful technique to obtain a tree $\mathcal T_C$ of logarithmic height. The centroid tree in employed in several applications: cache-oblivious string B-trees [2, 5, 6], dynamic farthest point queries [1], balanced decomposition of simple polygons [9], jumbled pattern matching on trees [7], counting of square substrings in a tree [11], just to cite a few.

The decomposition is based on a theorem proved by Jordan in 1869 [10]: Any tree $\mathcal T$ of n nodes has at least a node, called centroid, whose removal leaves connected components of size at most n/2.

The centroid decomposition is defined recursively. Given $\mathcal T$, we identify a centroid node u, which is chosen to be the root of the new tree $\mathcal T_C$. Then, we remove u from $\mathcal T$ and recurse on each connected component to get u’s subtrees in $\mathcal T_C$. The resulting decomposition is a new tree $\mathcal T_C$ on the same nodes whose height is $O(\log n)$. Tree $\mathcal T_C$ preserves some information about the topology of the original tree $\mathcal T$. For example, for any pair of nodes u and v, the path from u to v in $\mathcal T$ can be decomposed in two subpaths of $\mathcal T_C$: the path from u to w and the path from w to v, where w is the lowest common ancestor of u and v in $\mathcal T_C$.

A folklore algorithm computes the centroid decomposition in $\varTheta (n\log n)$ time as follows. We first observe that a centroid node of $\mathcal T$ can be easily identified in linear time. Indeed, we can arbitrary choose a root in $\mathcal T$ and visit the tree to compute the size of each subtree. Then, we start from the root and move to the largest subtree until we reach a node whose subtrees have size at most n/2. This node is a centroid of the tree. Thus, it easily follows that the decomposition of the tree can be computed in $\varTheta (n\log n)$ time.

The first linear time algorithm to compute the centroid decomposition of a tree is due to Giubas et al. [9] but it assumes that $\mathcal T$ is a binary tree. The first linear time algorithm for arbitrary trees is by Brodal et al. [3]. Actually paper [3] claims the result which is described in its unpublished extension [4]. This algorithm is based on the heavy path decomposition [12] of $\mathcal T$ which is kept updated after subtrees removal. Let us say a node u is heavy if u is the children of its parent with the largest subtree (ties are broken arbitrarily). The heavy path decomposition is the set of paths, called heavy paths, that connect heavy nodes. Brodal et al. [3] show that the use of this decomposition leads to an alternative description of the folklore algorithm. First the algorithm computes the heavy path decomposition of $\mathcal T$, and then searches for the centroid node which must be a node in the heavy path that contains the root. The algorithm can now recur on each connected component. The main inefficiency of this algorithm is that it recomputes the sizes of all subtrees and the heavy paths for each recursive call. Brodal et al. [3] improves the algorithm by showing how to update the already computed heavy paths in $O(\log ^2 k)$ time, where k is the number of nodes of the component processed by the current recursive call. This requires to keep a binary search tree for each heavy path supporting split, join and successor operations, and a priority queue for each node of $\mathcal T$.

In this short paper, we describe a new simple and practical linear-time algorithm for the problem based on the idea of applying the folklore algorithm to a suitable (static) decomposition of the original tree.

2 The Algorithm

The overall idea of our algorithm is to break the input tree in $\varTheta (n/\log n)$ subtrees of size $O(\log n)$ and replace each group with a node to form a new meta-tree. The core property that we exploit is that a centroid can be identified by navigating this meta-tree of size $\varTheta (n/\log n)$, plus $O(\log n)$ nodes of the original tree. The strategy is then applied recursively on the connected components obtained by removing the centroid. After some level of recursion, we obtain components that are small enough so that their centroid decomposition can be pre-computed in a small table and thus retrieved in linear time.

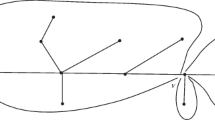
Tree Cover. Let $\mathcal T$ be a rooted tree of size n. The notation $\pi (x)$, where x is a node of $\mathcal T$, denotes the parent of x (or NULL for the root). When two nodes u and v are connected, we assume that both the edges (u, v) and (v, u) are present (this simplifies the description). We use the tree covering procedure described in [8, Sec. 2.1] to decompose $\mathcal T$ in $\varTheta (n/\log n)$ sub-trees containing $\varTheta (\log n)$ nodes each (except, possibly, the root). Two subtrees are either disjoint or intersect only at their common root. We make all subtrees disjoint as follows, with a procedure that also colors nodes in red or black. At the beginning, all nodes of $\mathcal T$ are colored black. When $k>1$ subtrees share a common root x, we (i) delete x, (ii) create k new red nodes $x_1, \dots , x_k$ and make each of them be the root of each of the k subtrees, and (iii) create a new black node $x'$ with parent $\pi (x') = \pi (x)$ and let $x_1, \dots , x_k$ be its children. The new node $x'$ belongs to a new subtree containing only $x'$. We denote as $\mathcal T'$ the tree obtained from $\mathcal T$ by performing these splitting and coloring operations, and keep a map $\beta$ mapping black nodes of $\mathcal T'$ to the corresponding nodes of $\mathcal T$ (note that there is a bijection between black nodes of $\mathcal T'$ and nodes of $\mathcal T$). Let $\pi '(x)$ denote the parent of node x in $\mathcal T'$. We extend $\beta$ to red nodes x as $\beta (x) = \beta (\pi '(x))$ (i.e., we take the black parent of x and apply $\beta$). Figures 1 and 2 illustrate our tree covering procedure. In the example, we have $\beta (\bar{0}) = 0,\ \dots ,\ \beta (\bar{7}) = 7,\ \beta (\bar{8}') = \beta (\bar{8}_1) = \beta (\bar{8}_2) = 8,\ \beta (\bar{9}) = 9, \dots , \beta (\overline{19}) = 19$.

From now on, when we say subtree of $\mathcal T'$ we always refer to the subtrees obtained by our modified tree covering procedure. Note that $\mathcal T'$ is divided in $\varTheta (n/\log n)$ subtrees, each containing $O(\log n)$ nodes (some of these subtrees may contain just one node, read above). We denote as $\mathcal T''$ the tree whose nodes are the subtrees (now disjoint) of $\mathcal T'$. Note that $\mathcal T''$ has $\varTheta (n/\log n)$ nodes as well. We store explicitly $\mathcal T''$ and keep a map $\alpha$ mapping nodes of $\mathcal T''$ to the roots of the corresponding subtrees in $\mathcal T'$. Figure 3 illustrates the tree $\mathcal T''$ obtained from the previous example (in the next paragraph we describe the meaning of the weights associated with nodes and edges). In the example, we have $\alpha (A) = \bar{0},\ \alpha (B) = \bar{3},\ \alpha (C) = \bar{8}',\ \alpha (D) = \bar{8}_1,\ \alpha (E) = \overline{13}$, and $\alpha (F) = \bar{8}_2$.

Fig. 1.

Input tree $\mathcal T$, covered using the procedure described in [8, Sec. 2.1] with parameter $M=4$.

Fig. 2.

Modified tree $\mathcal T'$. We overline node names to distinguish them from those in $\mathcal T$. Note that sub-trees are disjoint.

Fig. 3.

Tree $\mathcal T''$, obtained by collapsing each sub-tree of $\mathcal T'$ into a node. Between square brackets, we show each node’s weight (For example, $\delta (B)=5$). We also show weights on the edges: for example, $\delta (C,F)=3$ and $\delta (F,C)=17$.

For each node $u''$ of $\mathcal T''$, we compute and store the number $\delta (u'')$ of black nodes contained in the subtree of $\mathcal T'$ rooted in $\alpha (u'')$. We call $\delta (u'')$ the weight of $u''$. After that, with a visit of $\mathcal T''$ we cumulate those weights and extend them to edges as follows. Let $(u'',v'')$ be an edge of $\mathcal T''$. With $\delta (u'',v'')$ we denote the sum of all weights $\delta (w'')$ in the connected component rooted in $v''$ obtained after removing $u''$ from $\mathcal T''$. Said otherwise, $\delta (u'',v'')$ is the sum of the weights $\delta (w'')$ for all nodes $w''$ reached traversing $(u'',v'')$ only once (and without counting $\delta (u'')$). We store $\delta (u'',v'')$ for each edge $(u'',v'')$ of $\mathcal T''$ (remember also that, for each edge $(u'',v'')$, also the reversed edge $(v'',u'')$ exists therefore $\delta (v'',u'')$ is also defined). Intuitively, $\delta (u'',v'')$ corresponds to the number of black nodes in one of the connected components (the one containing node $\alpha (v'')$) obtained after removing the subtree rooted in $\alpha (u'')$ from $\mathcal T'$. In turn, this is exactly the number of nodes in the corresponding connected component of $\mathcal T$, and will be used to quickly compute a centroid. Figure 3 illustrates our construction.

Finding a Centroid. We now show that a centroid of $\mathcal T$ can be found in $O(n/\log n)$ time by visiting $\mathcal T''$ and a small (logarithmic) number of nodes of $\mathcal T'$. We prove the following lemma:

Lemma 1

The following two properties hold:

• 1. If c is a centroid of $\mathcal T$, then there exist a subtree $\mathcal R = (V_{\mathcal R}, E_{\mathcal R})$ of $\mathcal T'$ and a node $x'\in V_{\mathcal R}$ such that $\beta (x') = c$ and $\delta (x'',y'') \le n/2$ for all $(x'',y'')$ in $\mathcal T''$ such that $\alpha (x'')$ is the root of $\mathcal R$.

• 2. If $u''$ is a node of $\mathcal T''$ such that $\delta (u'',v'') \le n/2$ for all $(u'',v'')$ in $\mathcal T''$, then the subtree $\mathcal R$ rooted in $\alpha (u'')$ contains a node $x'$ such that $\beta (x')$ is a centroid of $\mathcal T$.

Proof

Consider the function $\delta$ extended to edges of $\mathcal T'$ (we call it $\delta '$ to distinguish it from $\delta$): $\delta '(u',v')$ is the number of black nodes in the tree containing $v'$ obtained after removing node $u'$. Similarly, we will talk about the weights of edges of $\mathcal T$ (which are defined analogously). We start by proving claim (1), and consider two main cases.

(1.a) The centroid c is mapped to a black node $c'$ of $\mathcal T'$ (i.e., $\beta (c') = c$) having only black children. Since c is a centroid and c is mapped to a node $c'$ with black children, also its edges are preserved and thus we have that $\delta '(c',v') \le n/2$ for all edges leaving $c'$ (see, in contrast, case 1.b: in that case, edges leaving c are distributed among red children of $c'$ and this property no longer holds). Let $(c',v')$ be such an edge. Clearly, also $\delta '(v',w') \le n/2$ holds for all edges leaving $v'$ such that $w'\ne c'$: this follows from the fact that $\delta '(c',v') \le n/2$ implies that the tree containing $v'$ obtained after removing $c'$ contains at most n/2 black nodes. Let $\mathcal R = (V_{\mathcal R}, E_{\mathcal R})$ be the subtree of $\mathcal T'$ containing $c'$. Iterating the above reasoning, we obtain that all edges $(u',v')$ leaving $\mathcal R$ (i.e., such that $u'\in V_{\mathcal R}$ and $v' \notin V_{\mathcal R}$) satisfy $\delta '(u',v') \le n/2$. Let $z'$ be the root of $\mathcal R$, and let $x''$ be the node of $\mathcal T''$ such that $\alpha (x'') = z'$. Then, by definition of $\delta$ we have that $\delta (x'',y'') \le n/2$ for all $(x'',y'')$ in $\mathcal T''$, since $\delta '$ and $\delta$ coincide on edges leaving $\mathcal R$ and $x''$, respectively, and our claim holds for $x'=c'$.

(1.b) The centroid c is mapped to a black node $c'$ of $\mathcal T'$ (i.e., $c'$ is the only black node with $\beta (c') = c$) with only red children. Let $c'_1, \dots , c'_k$ be the red children of $c'$. By construction of our tree decomposition, the edges leaving c have been partitioned. Each class of the partition contains either just the original edge connecting c with its parent in $\mathcal T$, or at least one edge connecting c with its children. The former class corresponds to the edge in $\mathcal T'$ connecting $c'$ with its parent. Classes of the latter kind correspond to edges in $\mathcal T'$ connecting $c'$ with red children. For example, in Figs. 1 and 2 the edges leaving node 8 have been partitioned in $\{(8,0)\},\ \{(8,9), (8,11)\}$, and $\{(8,17)\}$. The first class $\{(8,0)\}$ contains just the edge connecting 8 with its parent, and becomes edge $(\bar{8}', \bar{0})$ in $\mathcal T'$. The latter two classes become edges $(\bar{8}', \bar{8}_1)$ and $(\bar{8}', \bar{8}_2)$ in $\mathcal T'$. Now, the fact that we collapse edges means that $\delta '(c',v') \le n/2$ does not necessarily hold when $v'$ is a red node (it surely holds only if $v'$ is the black parent of $c'$), since $\delta '(c',v')$ corresponds to a sum of the weights of multiple edges. For example, in Fig. 2, $\delta '(\bar{8}',\bar{8}_1) = 8$ corresponds to the sum of the weights $\delta '(\bar{8}_1, \bar{9}) = 2$ and $\delta '(\bar{8}_1, \bar{11}) = 6$. While the weights of the latter two are surely at most n/2 (by definition of centroid), their sum could exceed n/2 (this is not the case of Fig. 2, where $n/2 = 10$). We consider two further sub-cases. (1.b.1) $\delta '(c',c'_{k}) \le n/2$ for all edges leaving $c'$ (this is the case of Fig. 2). Then, the same argument used in case (1.a) applies (it is actually simpler, since the subtree containing $c'$ is a singleton subtree), and our claim holds with $x' = c' = \alpha (x'')$ and $\mathcal R$ being the singleton subtree containing $c'$. (1.b.2) $\delta '(c',c'_{k}) > n/2$ for at least one edge $(c',c'_{k})$ leaving $c'$. Then, our claim holds for $x' = c'_{k} = \alpha (x'')$ and $\mathcal R$ being the subtree containing $c'_{k}$: since $\delta '(c',c'_{k}) > n/2$, then $\delta '(c'_{k},c') \le n/2$. Moreover, the other edges $(c'_{k},w')$ leaving $c'_{k}$ correspond to edges of the original tree $\mathcal T$ (i.e., not to group of edges), therefore $\delta '(c'_{k},w') \le n/2$. We can apply the argument used in case (1.a) and conclude that $\delta (x'',y'') \le n/2$ for all edges leaving $x''$.

We now prove claim (2). Let $u''$ be a node of $\mathcal T''$ such that $\delta (u'',v'') \le n/2$ for all $(u'',v'')$ in $\mathcal T''$. Let moreover $\mathcal R$ be the subtree rooted in $\alpha (u'') = y'$. Then, $\delta '(y',w') \le n/2$, where $w'$ is the parent of $y'$ in $\mathcal T'$. We have two cases. (2.a) $\delta '(y',w') \le n/2$ for all children $w'$ of $y'$ in $\mathcal T'$. Then, clearly $\beta (y')$ is a centroid of $\mathcal T$: if $y'$ is a red node, then the weights of edges leaving $\beta (y')$ are at most n/2. If $y'$ is a black node then the weights of edges leaving $\beta (y')$ correspond precisely to those leaving $y'$. (2.b) $\delta '(y',w') > n/2$ for some child $w'$ of $y'$. Then, $\delta '(w',y') \le n/2$ (i.e., the edge leading to the parent of $w'$ weights at most n/2) and we can recurse the above reasoning to the children of $w'$. Clearly, sooner or later we will find a node $q'$ in $\mathcal R$ such that $\delta '(q',w') \le n/2$ for all edges leaving $q'$ (including the edge leading to its parent, for which the property always holds true if we have moved to $q'$). Otherwise, it is easy to see that we obtain a contradiction. Suppose we reach a node $q'$ of $\mathcal R$ such that some of its children lie outside $\mathcal R$. Denote $q'_1, \dots , q'_k$ the children of $q'$ leaving $\mathcal R$. Then, clearly $\delta '(q',q'_i) \le n/2$ for all $i=1, \dots , k$ must hold since we are assuming that $\delta (u'',v'') \le n/2$ for all edges $(u'',v'')$ leaving $u''$ in $\mathcal T''$. This shows that we can recurse only on children internal to $\mathcal R$. However, at some point we will reach a node $x'$ whose children (all of them) lie outside $\mathcal R$. Then, clearly all edges leaving $x'$ must weight at most n/2.    $\square$

By Lemma 1, this algorithm finds a centroid of $\mathcal T$ in $O(n/\log n + \log n)$ time: (i) visit $\mathcal T''$ and find a node $u''$ such that $\delta (u'',v'') \le n/2$ for all edges $(u'',v'')$ leaving $u''$. Let $\mathcal R$ be the subtree of $\mathcal T'$ associated with $u''$, i.e., the subtree rooted in $\alpha (u'')$. (ii) Visit $\mathcal R$ and find a node $u'$ such that, if removed, it splits $\mathcal T'$ into connected components having at most n/2 black nodes each. (iii) Return $\beta (u')$.

Step (i) takes $O(n/\log n)$ time. Step (ii) can be implemented with a visit of $\mathcal R$. Note that the weights we store on $\mathcal T''$’s edges are precisely the sizes of the connected components of $\mathcal T$ obtained after removing nodes $u'$ in $\mathcal R$ whenever $(u',v')$ is an edge that leaves $\mathcal R$. Since we can afford visiting the whole $\mathcal R$, those weights can be easily used to compute the sizes of the subtrees of $\mathcal T$ obtained after removing any node $u'$ in $\mathcal R$. Steps (i), (ii) run in $O(n/\log n+ \log n)$ time.

In the above example, we have $n=20$. The node of $\mathcal T''$ whose outgoing edges weight at most $n/2 = 10$ is C (its outgoing edges weight 8, 8, and 3). In this particular case, C corresponds to a unary subtree therefore step (ii) finds node $\bar{8}'$, and step (iii) returns $\beta (\bar{8}')=8$.

Recursion. Note that Lemma 1 does not make any assumption on the subtree-decomposition of $\mathcal T'$. It follows that the above algorithm for finding a centroid can be iterated as follows. After finding a node $u'$ of $\mathcal T'$ such that $\beta (u')$ is a centroid of $\mathcal T$, we remove from $\mathcal T'$ all nodes $v'$ such that $\beta (v') = \beta (u')$ (i.e., all nodes that map to the centroid). We break every subtree $\mathcal R$ of $\mathcal T'$ containing one of the removed nodes into one singleton subtree (i.e., a subtree consisting of just one node) per remaining node of $\mathcal R$ (i.e., one subtree for each node that was not removed). The process of removing nodes breaks the original tree $\mathcal T'$ into q trees $\mathcal T'_1, \dots , \mathcal T'_q$, for some $q\ge 2$, each of which contains at most n/2 black nodes. Crucially, note that each $\mathcal T'_i$ with $n_i$ nodes is partitioned into at most $O(n_i/\log n) + O(\log n)$ subtrees: those of the original tree $\mathcal T'$ that have not been split into singleton subtrees, and at most $O(\log n)$ singleton subtrees. Similarly, we break $\mathcal T''$ into a forest. Some of the trees belonging to this forest will contain new nodes corresponding to newly-created singleton subtrees in $\mathcal T'$. Each such new node $u''$ gets a weight $\delta (u'')=1$. The weight of the other nodes does not change, since they correspond to subtrees of $\mathcal T'$ that have not been modified. At this point, we can re-compute the weights $\delta (u'',v'')$ on the edges of the forest in overall $O(n/\log n + \log n)$ time by using the stored weights $\delta (u'')$ for each node $u''$ of the forest. Figure 4 shows how the trees of Figs. 2 and 3 change after removing all the nodes $u'$ such that $\beta (u')=8$.

Fig. 4.

The figure shows how $\mathcal T'$ changes after returning the centroid $\beta (\bar{8}') = 8$ and removing nodes $\bar{8}'$, $\bar{8}_1$, and $\bar{8}_2$. Each subtree of $\mathcal T'$ that contains a removed node (in particular, the subtrees D,F) has been split in singleton subtrees: D has been split in $D_1, \dots , D_4$, and F has been split in $F_1, \dots , F_3$. Note that node C disappears since it corresponds to a subtree of $\mathcal T'$ containing only a removed node ($\bar{8}'$). Tree $\mathcal T''$ changes similarly: it is broken into four trees whose nodes are the subtrees shown in the figure.

Lemma 1 can then be applied again recursively on $\mathcal T'_1, \dots , \mathcal T'_q$. It is easy to see that each connected component at recursion depth j has at most $n/2^j$ black nodes and is divided into at most $n/(\log n\cdot 2^j) + O(j\cdot \log n)$ subtrees (note that each recursive iteration adds at most $O(\log n)$ singleton subtrees to each component). The complexity of finding a centroid in such a tree using Lemma 1 is $O(n/(\log n\cdot 2^j) + j\cdot \log n + \log n)$ (i.e., number of subtrees plus size of a subtree). We stop recursion as soon as we obtain components of size at most $\log ^3 n$, i.e., at recursive depth $j = \log (n/\log ^3n)$. In this way, each component is a tree having at most $\log ^3 n$ black nodes and divided into at most $n/(\log n\cdot 2^j) + O(j\cdot \log n) = O(\log ^2 n)$ subtrees. Note that the base case of $\log ^3 n$ for the tree size is the minimum (asymptotically) guaranteeing that the two components contributing to the number of subtrees (i.e., $n/(\log n\cdot 2^j)$ and $j\cdot \log n$) sum up to $O(n'/\log n)$, $n'$ being the subtree’s size. The total number of nodes contained in the trees at each recursion depth j is O(n) and, by the above observation, applying Lemma 1 to one tree of size $n'$ at any recursion depth takes time $O(n'/\log n)$. Overall, this adds up to $O(n/\log n)$ time per recursion level. Since the recursion depth is $O(\log n)$, the overall procedure terminates in O(n) time. We obtain the following lemma.

Lemma 2

In O(n) time we can reduce the centroid decomposition problem to the same problem on a certain number of trees with at most $\log ^3 n$ nodes each, whose union contains at most n nodes.

We note that, in a practical implementation of the above algorithm, it is sufficient to apply the folklore algorithm to the trees of Lemma 2 (which are small enough to fit in cache). From the theoretical perspective, however, this solution runs in $O(n\log \log n)$ time. We now show how to reach linear time (though with a less practical solution).

Intuitively, we perform one more round of our recursive strategy on the trees of Lemma 2, obtaining trees of size $z = O(\log ^3 \log n)$. Finally, we use tabulation: there are $o(n/\log n)$ possible trees with z nodes, so we can pre-compute their centroid decomposition in O(n) time with the folklore algorithm. The following theorem states our final result.

Theorem 1

The centroid decomposition of a tree with n nodes can be computed in O(n) time and O(n) space.

Proof

By Lemma 2, we obtain trees of size at most $\log ^3 n$. Our idea is to apply one more round of our recursive strategy to those trees. As a result, in O(n) additional time we reduce the problem to that of computing the centroid decomposition of a certain number of trees of size at most $(\log \log ^3 n)^3 = 27\log ^3 \log n$ whose union contains at most n nodes. The trees are now small enough to use tabulation. The number of distinct (rooted) trees with at most $z = 27\log ^3 \log n$ nodes is upper-bounded by $N = 2^{2z} = 2^{54\log ^3 \log n}$. We compute the centroid decomposition of each of them in total $O(N\cdot z\log z) = o(n)$ time using the folklore algorithm. We store the centroid tree of each of these trees in a table U[k][p] indexed by the number k of nodes of the tree and a unique identifier p representing the rank of the tree among all trees with k nodes. This identifier can be, for example, the 2k-bits integer corresponding to the balanced parentheses representation of the tree, which can be computed in linear time with a DFS visit. Table U takes $O(N \cdot z^2)$ words of space, which is again o(n).

We use the table as follows. Given an unrooted tree $\mathcal T^*$ with $k' \le 27\log ^3 \log n$ nodes, we root it arbitrarily¹ (storing the permutation associating nodes of the rooted and unrooted versions of $\mathcal T^*$), we compute its DFS-identifier $p'$, and access $U[k'][p']$. This entry contains the centroid tree decomposition of the (rooted version) of $\mathcal T^*$. The process takes $O(k')$ (linear) time, therefore by applying the procedure to all those small trees we complete the centroid decomposition of our input tree $\mathcal T$ in additional O(n) time.    $\square$