Abstract
A prototyping high-level language is used to describe multi-agent systems using timeouts for migration between explicit locations and local communication in a distributed system. We translate such a high-level specification into the real-time Maude rewriting language. We prove that this translation is correct, and provide an operational correspondence between the evolutions of the mobile agents with timeouts and their rewriting translations. These results allow to analyze the multi-agent systems with timeouts for migration and communication by using the real-time Maude tools. A running example is used to illustrate the whole approach.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Multi-agent systems are composed of a large number of agents that behave according to their timed actions. The mobility of agents and the communication between agents may lead to unexpected behaviours. Components can be highly heterogeneous, having individual objectives and using different temporal scales to achieve them. As multi-agent systems are getting more complex, automated verification of such systems is needed. Actually, the specification and analysis of multi-agent systems represent an active research direction in the last years. It is important to have modelling techniques able to describe easily such systems, as well as tools to simulate and verify some complex (qualitative and quantitative) properties of their behaviours. We take a step in this direction by developing a high-level specification language for specifying the mobile agents with timeouts, and providing a way to perform automated verification of some complex systems involving explicit locations and timeouts for migration and local communication in distributed networks.
There exist already some approaches to formalize timed systems, for instance timed automata [1]. Software platforms as Uppaal [3] represent model checking tools used for the simulation and verification of real-time systems modelled as timed automata [10]. Logic-based models complement the timed automata models as they are able to capture other aspects of real-time systems: e.g., mobility of agents and the communication between agents. Rewriting logic is appropriate for providing a general semantic framework for various languages and models of concurrency [11]. Maude is a system that supports computations based on rewriting and equational logic, while real-time Maude [14] provides a specification formalism with several decidability results for many system properties. Also, in real-time Maude different types of communication used in process calculi can be modelled. The real-time Maude tool is developed using an extension of rewriting logic, and seem to be an appropriate tool for specification, validation and verification of real-time systems using features as migration of agents and communication between agents. This tool is useful in applications that use features not yet implemented in several existing model checkers for real-time systems [13].
For the specification of the multi-agent systems with timeouts for migration and local communication we use a real-time version of an existing high-level framework called TiMo , a framework able to describe easily interacting mobile agents in distributed systems. Then we translate this high-level specification into real-time Maude. There are some problems to overcome in order to obtain a fully executable specification in real-time Maude. Firstly, the transitions of a system need sometimes to use fresh names (to overcome binding problems); this is due to the fact that the communication of values takes place eventually after alpha-converting (to avoid clashes) in the high-level specification. Secondly, since infinite computations are not supported by real-time Maude, implementing an unbounded recursion operator is not possible; a solution to this problem is to consider a bounded recursion in which a process can be unfolded only a finite number of times during an execution. This restriction does not influence the results because we model real systems in which the recursive processes need to be unfolded only for a finite number of times.
2 Syntax and Semantics of the High-Level Specification
In the high-level specification language, the processes are allowed to migrate between explicit distributed locations and to communicate locally with other processes. The coordination of the processes in time and space is done by using timed migration and timed communication. The timeouts added to a migration action enforce the process to migrate to the target location after a period of time equal to the timeout constraint. Two processes are allowed to communicate only if they are both available into the same location at the same unit of time, and if the timeout restrictions of the active communication actions are non-negative. If a communication action cannot be executed before its timeout restriction expires, then the action is removed and the actions of an alternative process are executed as a continuation. The transitions involving either processes migration between locations, processes communication or unfolding of recursive processes are executed in a maximal parallel manner. This means that if a process can migrate, communicate or unfold, it has to do it. The transitions with timeouts are alternated with transitions involving the passage of time over all the processes; a global clock is used to model the passage of time. The operational semantics of the high-level specification is provided by using these two types of transitions: a transition relation for timed migration and communication actions executed in the maximal parallel manner, and a transition relation used to model the passage of time.
A timeout restriction assigned to a migration action is given as a natural number t, while a timeout restriction assigned to a communication action is given as \(\varDelta t\), where \(t\in \mathbb {N}\). The t notation means that migration action can be consumed exactly after t units of time, while the \(\varDelta t\) notation means that the communication can be consumed at any moment in the next t units of time.
The syntax of the high-level language is given in Table 1, where the following notations are used:
-
we use the set Loc of locations, set Chan of communication channels, and set Id of process identifiers;
-
for each process identifier \(id \in Id\) there exists a unique process definition \(id(u_1,\ldots ,u_{m_{id}}) {\mathop {=}\limits ^{def}}P_{id}\) in which the \(m_{id}\) parameters are identified by the distinct variables \(u_i\);
-
a, l, t denote a communication channel, a location or a location variable, and an action timeout, respectively; u and v denote a tuple of variables and a tuple of expressions built from values (e.g., strings, integers, bools), variables and allowed operations.
An output communication process \( a^{\varDelta t}!\langle z \rangle \) then P else Q describes the fact that for t time units the process is available for sending on channel a the value z. Whenever the process succeeds in sending the value before the deadline, it continues its evolution according to process P; otherwise, it continues its evolution by the alternative process Q. The input communication process \(a^{\varDelta t}?(x)\) then P else Q describes the fact that for t time units the process is available to receive on channel a a value to instantiate the variable x. In a similar manner as for the output communication process, the continuation of an input communication process depends on the success of the communication.
A migration process \({ go^{t}l~\mathsf{then}~P}\) indicates a location change after t time units, namely after t units of time the process continues its execution as P at location l (and not at the current location). Since variables are instantiated through communication, this means that the location variables can be instantiated; this feature allows a flexible behaviour as processes can adapt their migration based on received information. The process 0 models an inactive process, while the process \(P\mid Q\) models the parallel composition of the process P and Q that might also interact through communication. A process P currently located in location l is denoted by l[[P]], while a system is composed of located processes composed by using the parallel operator.
There is only one binding operator in our calculus: in the input process \({ a^{\varDelta t}?(u)~\mathsf{then}~P~\mathsf{else}~Q}\), the variable u is bound in process P. However, as process Q is an alternative process executed when the input action is not consumed, this means that variable u is not bound in process Q. Given a process P, we denote by fv(P) its set of free variables. In case \(u_i\) are the \(m_{id}\) parameters of the process \(P_id\), then the assumption \(fv(P_{id}) \subseteq \{u_1,\ldots ,u_{m_{id}}\}\) holds. As usually assumed in process calculi, we consider that processes are defined up to an alpha-conversion. Also, \(P\{v/u,\ldots \}\) denotes a process P in which v replaces all the free occurrences of the variable u, possible after using alpha-conversion inside P to remove possible clashes. A system N is said to be well-formed if \(fv(N)=\emptyset \).
Operational Semantics. The structural equivalence relation \(\equiv \) represents an ingredient of the operational semantics; it is defined as the smallest congruence relation satisfying the equations of Table 2. The purpose of this relation \(\equiv \) is to provide a way of rearranging the processes in a system such that they can evolve by using the operational semantics rules from Table 3.
The equalities of Table 2 are useful for transforming a system N into the system \(l_1[[P_1]]\mid \mid \ldots \mid \mid l_n[[P_n]]\) composed of located process \(l[[P_i]]\) such that there do not exist \(Q_i\) and \(R_i\) such that \(P_i \equiv Q_i \mid R_i\). A located process that cannot be split into parallel located processes by using the rule (LSplit) is called a component of N, while the component decomposition of a system N is the system \(l_1[[P_1]]\mid \mid \ldots \mid \mid l_n[[P_n]]\), where all \(l_i[[P_i]]\) are components.
Table 3 presents the operational semantics rules. The transitions of the form \(N \xrightarrow {} N'\) indicate either processes migrating between locations, processes communicating locally or unfolding of processes, all these executed in parallel in one step. The passing of t time units is given by transitions of the form  .
.
In rule (Com), two process \({ a^{\varDelta t} ! \langle v \rangle ~\mathsf{then}~P~\mathsf{else}~Q}\) and \({ a^{\varDelta t} ?(u)~\mathsf{then}~P'~\mathsf{else}~Q'}\), both located at location l, are using channel a to communicate a tuple of values v to be used for the instantiation of the variable u. Applying the rule (Com) does not lead to a location change for any of the involved processes, but to a consumption of the output and input action. Upon a successful communication, the processes \({a^{\varDelta t} ! \langle v \rangle ~\mathsf{then}~P~\mathsf{else}~Q}\) and \({a^{\varDelta t} ?(u)~\mathsf{then}~P'~\mathsf{else}~Q'}\) continue their executions as processes P and \(P'\{v/u\}\), respectively. If the process \({ a^{\varDelta 0} ! \langle v \rangle ~\mathsf{then}~P~\mathsf{else}~Q}\) exists in the system, then the communication action is discarded by using the rule (Put0), and the execution continues as the alternative process Q. In a similar manner, by using the rule (Get0), the process \({ a^{\varDelta 0} ?(u)~\mathsf{then}~P'~\mathsf{else}~Q'}\) continues its execution as the alternative process Q. In rule (Move0), a process \(go^{0}l'~\mathsf{then}~P\) is able to change its location by migrating from the current location l to the given location \(l'\) where it continues its execution as process P. The unfolding of recursive processes is performed by using the rule (Call). In order to use the structural equivalence relation \(\equiv \) to rearrange a system such that its components can interact for communication or migration, the rule (Equiv) its used. Composing larger systems from smaller systems is done by using the rule (Par) for the parallel composition operator.
The passage of time is described by the rules having their names starting with the capital letter D. The hypothesis  from the rule (DPar) indicates the fact that placing the two systems \(N_1\) and \(N_2\) in parallel does not trigger the application of a rule (Com) that would modify these systems. The negative premises are essential to separate the steps based on the execution of actions by those based on time passing (i.e., time cannot pass when an action is executed).
from the rule (DPar) indicates the fact that placing the two systems \(N_1\) and \(N_2\) in parallel does not trigger the application of a rule (Com) that would modify these systems. The negative premises are essential to separate the steps based on the execution of actions by those based on time passing (i.e., time cannot pass when an action is executed).
A transition of the form \(N \xrightarrow {} N_1\) followed by a time passing transition of the form  describe a complete step that can be written as:
describe a complete step that can be written as:

Thus, a complete step indicates that a parallel execution of processes migrating between locations, processes communicating or unfolding is necessarily followed by a time step. We say that the system \(N'\) is directly reachable from N if a complete computational step  exists. If
exists. If  , then only a time step
, then only a time step  can be performed in the system N.
can be performed in the system N.
Theorem 1
For all the systems N, \(N_1\) and \(N_2\),

Theorem 1 claims that nondeterminism cannot be introduced upon executing a time transition in a system, namely the obtained system is unique up to structural congruence.
Theorem 2
For all the systems N, \(N_1\), \(N_2\) and \(0<t'<t\), we have  if and only if there is a \(N_1\) such that
if and only if there is a \(N_1\) such that  and
and  .
.
Theorem 2 claims that whenever a time transition of length t can be performed in a system N leading to a system \(N_2\), then always a time transition of length \(t'\) with \(0<t'<t\) can be performed in the same system N leading to a system \(N_1\) followed by another time transition of length \(t-t'\) in the systems \(N_1\) leading to \(N_2\), and vice versa. This result ensures that the passage of time in a system is continuous (no jumps).
Example 1
Let us consider an example in which a client wants to buy, at a good price, a flight ticket to a given location. The scenario is depicted in Fig. 1, where the names and values have the meanings given below (we explain the names and values in the order they appear, from left to right).
-
The process client initially resides at location home . It has access to 130 cash units to be used for purchasing a flight ticket. Once the client reaches the travelshop location, an agent communicates to it the location of a standard offer. The client process goes to this location to receive the standard offer details. Here it also receives the location for a special offer. After receiving the information about the special offer, it goes to the bank for paying the cheaper offer between the standard and the special offers, and returns home (its initial location).
-
The process update is able to migrate to the special location by starting from its initial location travelshop in order to communicate locally a reduction for the price special from 90 to 60 cash units.
-
The process agent resides at the travelshop location, and has access to 100 cash units available in the cash register. Once a client reaches the travelshop location and the agent is available for communication, the client receives the location where the details of the standard offer are available. The agent has also the possibility to go to the bank to withdraw the available money from the till . Regardless of the amount of money taken from the bank , the agent always returns to travelshop , its initial location.
-
The process flightinfo process residing at the standard location is able to do only local communications in order to provide to any interested client the details about the standard offer: the price of 110 cash units, and the location where the special offer resides.
-
The process saleinfo process residing at the special location is able to do only local communications in order to provide (to any interested client) the details about the standard offer: the price of 90 cash units, and the location of the bank for the payment. The saleinfo process can also interact locally with the update process in order to modify the price of the special offer.
-
The process till process owning 10 cash units and residing at the bank location is able to do only local communications: it can interact with a client to receive the payment for a flight ticket, and can interact with the agent in order to transfer the accumulated cash to it.
After all the interactions described in Fig. 1, the system looks like in Fig. 2.
In the above example we have: (i) agents migrating in a distributed network with explicit locations; (ii) local communication of these agents (to get specific results); (iii) both migration and communication require certain time indicated by timeouts.
We show how this example can be easily described in our high-level language. First of all, in order to simplify the syntax, we consider that:
\(a^{\varDelta \infty }!\langle v \rangle \; ~\mathsf{then}~ P~ \mathsf{else}~Q\) can be written as \(a!\langle v \rangle \rightarrow P\),
\(a^{\varDelta \infty }?(u) ~\mathsf{then}~ P~ \mathsf{else}~Q\) can be written as \(a?(u) \rightarrow P\), and
\(\mathsf{go}^{ t}l ~\mathsf{then}~ P\) can be written as \(\mathsf{go}^{ t}l \rightarrow P\).
This is because branch Q is ignored as it can never be executed.
The system presented in Fig. 1 is described in the high-level language as:
where:

3 Translating the High-Level Specification into Maude
In what follows we define a rewriting theory corresponding to the semantics of our high-level language defined in Table 3. The syntax used to give the rewriting theory is that of real-time Maude. A rewrite theory \(\mathcal {R}\) is defined as a triple \((\varSigma ,E,R)\), where \(\varSigma \) stands for signature of function symbols, E and R are sets of \(\varSigma \)-equations and \(\varSigma \)-rewrite rules, respectively. The \(\varSigma \)-equations and \(\varSigma \)-rewrite rules can contain side conditions; for example, the conditions appearing in a rewrite rule can contain equations or other rewrite rules. Just like in [9], we use a typed setting given as an order-sorted equational logic \((\varSigma , E)\) including sorts and an inclusion relation subsort between sorts. Given a rewrite theory \(\mathcal {R}\), we write \(\mathcal {R}\vdash t \Rightarrow t'\) if \(t \Rightarrow t'\) is provable in \(\mathcal {R}\) by using the rewrite rules of R. Rewriting logic is basically a computational logic that combines term rewriting with equational logic.
Let us discuss first the high-level recursion operator that is not directly encodable into real-time Maude (because infinite computations are not supported into this tool). Our solution is to use the construction id(v, n) that is an extension of the constructions id(v) of our language with a number n that limits the number of recursive calls to be executed during the evolution of the system.
In order to translate the high-level language (whose syntax is given in Table 1), we consider sorts corresponding to sets from our language: e.g., for the set \({ Chan}\,\) of channels, the sort
 is created. Certain new aspects are provided by the sorts
is created. Certain new aspects are provided by the sorts
 and
and
 . The sort
. The sort
 contains the action parts \(a^{\varDelta t}!\langle v \rangle \) and \(a^{\varDelta t}?(u)\) of the communication processes \(a^{\varDelta t}!\langle v \rangle \) then P else Q and \(a^{\varDelta t}?(u)\) then P else Q, while the sort
contains the action parts \(a^{\varDelta t}!\langle v \rangle \) and \(a^{\varDelta t}?(u)\) of the communication processes \(a^{\varDelta t}!\langle v \rangle \) then P else Q and \(a^{\varDelta t}?(u)\) then P else Q, while the sort
 contains the action part \(\mathsf{go^t}l\) of the migration processes of the form \(go^{t}l~\mathsf{then}~P\). The elements of the sorts
contains the action part \(\mathsf{go^t}l\) of the migration processes of the form \(go^{t}l~\mathsf{then}~P\). The elements of the sorts
 and
and
 are essential in constructing the sequential processes of our language. Among the subsorting relations between the given sorts, we explain
are essential in constructing the sequential processes of our language. Among the subsorting relations between the given sorts, we explain

 that illustrates the fact that location names, channel names or values can be used to instantiate variables. To work with multisets of values, we use the sort
that illustrates the fact that location names, channel names or values can be used to instantiate variables. To work with multisets of values, we use the sort
 .
.

To each operator used in the syntax of Table 1 we attach the attribute
 marking the fact that this operator is used to construct the system, and attribute
marking the fact that this operator is used to construct the system, and attribute
 followed by a number marking its applicability precedence with respect to other operators. Moreover, in order to encode properly into real-time Maude the parallel operators \(\mid \) and \(\mid \mid \) from Table 1, we add to them the attributes
followed by a number marking its applicability precedence with respect to other operators. Moreover, in order to encode properly into real-time Maude the parallel operators \(\mid \) and \(\mid \mid \) from Table 1, we add to them the attributes
 and
and
 to illustrate that they are commutative and associative constructors that respect the rules of Table 2.
to illustrate that they are commutative and associative constructors that respect the rules of Table 2.

As already stated, most of the rules of the structural congruence (Table 2) are encoded by using the attributes
 and
and
 when defining the previous operators. For the rest of the rules we provide the following equations:
when defining the previous operators. For the rest of the rules we provide the following equations:

As communication between two processes by using rule (Com)) leads to a substitution of variables by the communicated values, we need to define this operation explicitly in real-time Maude. Such an operator acts only upon the free occurrences of a name, while leaving bound names as they are.

However, the above operator does not take into account the need for alpha-conversion in order to avoid name clashes once substitution takes place. To illustrate this issue, let us consider the process \(P = a^t(b)\) then \((go^{t'}l~\mathsf{then}~X)\) else stop) in which the name b is bound inside the input prefix. If the substitution \(\{b/X\}\) needs to be performed over this process, the obtained process would be \(P\{b/X\} = a^t(b)\) then \((go^{t'}l~\mathsf{then}~b)\) else stop). This means that once variable X is replaced by the name b, name b would become bound not only in the input action. To avoid this, we define an operator able to perform alpha-conversion by using terms of the form [X] that contain fresh names:

The terms of the form [X] containing fresh names are composed with the system by using the parallel operator ||. Using the given fresh names, the renaming is done (when necessary) before substitution. This is provided by the operator:

This operator has a definition similar with the substitution operator, except the case when we deal with bound names.

It is worth noting that this is different from the substitution operator that does not allow the change of the bound name:

As most of the rules in Table 3 contain hypotheses, translating these rules in real-time Maude requires the use of conditional rewrite rules in which the conditions are the hypotheses of rules of Table 3. Notice that in what follows we do not directly implement the rules (PAR), (DEquiv) and (Equiv) as rewrite rules into real-time Maude, due to the fact that the commutativity, associativity and the congruence rewriting of the parallel operators \(\mid \) and \(\mid \mid \) are already encoded into the matching mechanism of Maude. In order to identify for each of the below rewrite rule which rule from Table 3 it models, we consider simple intuitive names for these rewrite rules. More complicated names could be considered by using rewriting rules similar with the ones given for the executable specification of the \(\pi \)-calculus in Maude [15].

It is also worth noting that there are two instances for the rule
 . This is a consequence of the fact that after communication, before a substitution takes place, one may need to perform alpha-conversion to avoid name clashes. Rule
. This is a consequence of the fact that after communication, before a substitution takes place, one may need to perform alpha-conversion to avoid name clashes. Rule
 is applicable if the variable V is not bound inside process P (modelled by the condition
is applicable if the variable V is not bound inside process P (modelled by the condition
 ), and so only a simple substitution is enough to complete the replacement of the variable X by name V. On the other hand, rule
), and so only a simple substitution is enough to complete the replacement of the variable X by name V. On the other hand, rule
 is applicable if the variable V is bound inside process P (modelled by the condition
is applicable if the variable V is bound inside process P (modelled by the condition
 ); in this case an alpha-conversion is needed to avoid the clash of name V. To be able to perform the alpha-conversion we also check before applying the rule
); in this case an alpha-conversion is needed to avoid the clash of name V. To be able to perform the alpha-conversion we also check before applying the rule
 if a fresh name [Z] exists in the system, name not present in process \(P'\) (modelled by the condition
if a fresh name [Z] exists in the system, name not present in process \(P'\) (modelled by the condition
 ). The conditions of the rules
). The conditions of the rules
 and
and
 make use of the functions
make use of the functions
 ,
,
 and
and
 for checking the membership of a name to the set of bound names for a given process.
for checking the membership of a name to the set of bound names for a given process.
A tick rewriting rule is used to model the passing of time in the encoded system by a positive amount of time that is at most equal with the maximal times that can elapse in the system. Such a tick rule has the form:

The
 rule uses the function
rule uses the function
 to decrease all time constraints in a system by the same positive value. In order to correctly model the steps needed to obtain complete computational steps, namely the time cannot elapse if rewrite rules are applicable, we use the
to decrease all time constraints in a system by the same positive value. In order to correctly model the steps needed to obtain complete computational steps, namely the time cannot elapse if rewrite rules are applicable, we use the
 attribute for the function
attribute for the function
 . The attribute
. The attribute
 marks the argument to be frozen (first one in this case).
marks the argument to be frozen (first one in this case).

The function mte from the condition of rule
 is used to compute the maximal time that can be elapsed in a system, a time that is equal with the minimum time constraint of the applicable actions in the system.
is used to compute the maximal time that can be elapsed in a system, a time that is equal with the minimum time constraint of the applicable actions in the system.

The full description of the translation into real-time Maude is available at https://profs.info.uaic.ro/~bogdan.aman/RTMaude/TiMoSpec.rtmaude .
In order to study the correspondence between the operational semantics of our high-level specification language and that of the real-time Maude, we inductively define a mapping \(\psi :\) TiMo \(\rightarrow \mathsf{System}\) as


By \(\mathcal {R}_D\) we denote the rewrite theory defined previously in this section by the rewrite rules
 ,
,
 ,
,
 ,
,
 ,
,
 and
and
 , and also by the additional operators and equations appearing in these rewrite rules.
, and also by the additional operators and equations appearing in these rewrite rules.
The next result relates the structural congruence of the high-level specification language with the equational equality of the rewrite theory.
Lemma 1
\(M \equiv N\) if and only if \(\mathcal{{R}}_D \vdash \psi (M) = \psi (N)\).
Proof
\(\Rightarrow \): By induction on the congruence rules of our high-level language.
\(\Leftarrow \): By induction on the equations of the rewrite theory \(\mathcal {R}_D\).
The next result emphasizes the operational correspondence between the high-level systems M, N and their translations into a rewriting theory. We denote by \(M \xrightarrow {} N\) any rule of Table 3.
Theorem 3
\(M \xrightarrow {} N\) if and only if \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow \psi (N)\).
Proof
\(\Rightarrow \): By induction on the derivation \(M \xrightarrow {} N\).
-
(Com): We have \(M = l[[a^{\varDelta t}!\langle v \rangle ~\mathsf{then}~ P~\mathsf{else}~Q ]] \mid \mid l[[a^{\varDelta t'}?(u)~\mathsf{then}~ P'~\mathsf{else}~Q']]\) and \(N=l[[P]]\mid \mid l[[P'\{v/u\}]]\). By definition of \(\psi \), we obtain \(\psi (M) = l[[a^{\varDelta t}!\langle v \rangle \) \(~\mathsf{then}~ \varphi (P)~\mathsf{else}~\varphi (Q) ]] \mid \mid l[[a^{\varDelta t'}?(u)~\mathsf{then}~ \varphi (P')~\mathsf{else}~\varphi (Q')]]\). Depending on the fact that v appears or not as a bound name in \(P'\), we have two cases:
-
if \(v \notin bn(P')\): By applying
 , we have \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow l[[\varphi (P)]]\mid \mid l[[\varphi (P')\{v/u\}]]=N'\), and by the definition of \(\psi \), we have \(\psi (N)=N'\).
, we have \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow l[[\varphi (P)]]\mid \mid l[[\varphi (P')\{v/u\}]]=N'\), and by the definition of \(\psi \), we have \(\psi (N)=N'\). -
if \(v\in bn(P')\): We should apply first an alpha-conversion before the value is communicated. This is done by using a fresh name [Z] such that by applying the rule
 we get \(\mathcal{{R}}_D \vdash [Z] || \psi (M) \Rightarrow [[v]] || l[[\varphi (P)]]\mid \mid \) \(l[[\varphi (P')(Z/v)\{v/u\}]]\) = \(N'\). By the definition of \(\psi \), we have \(\psi (N)=N'\).
we get \(\mathcal{{R}}_D \vdash [Z] || \psi (M) \Rightarrow [[v]] || l[[\varphi (P)]]\mid \mid \) \(l[[\varphi (P')(Z/v)\{v/u\}]]\) = \(N'\). By the definition of \(\psi \), we have \(\psi (N)=N'\).
-
-
(Move0), (Put0) and (Get0): These cases are similar to the previous one, by using the rules
 ,
,
 and
and
 , respectively.
, respectively. -
(DMove): We have that \(M=l[[go^{t}l'~\mathsf{then}~P]]\) and \(N=l[[go^{t-t'}l'~\mathsf{then}~P]]\). By definition of \(\psi \), we obtain \(\psi (M)=l[[(go^t~l') ~. ~\varphi (P) ]]\). By applying the rule
 we get \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow l[[(go^{t-t'}~l') ~. ~\varphi (P) ]]=N'\). By definition of \(\psi \), we have \(\psi (N)=N'\).
we get \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow l[[(go^{t-t'}~l') ~. ~\varphi (P) ]]=N'\). By definition of \(\psi \), we have \(\psi (N)=N'\). -
(DStop), (DPut) and (DGet): These cases are similar to the previous one, by using also the rule
 .
. -
The rest of the rules are simulated using the implicit constructors of Maude.
\(\Leftarrow \): By induction on the derivation \(\mathcal{{R}}_D \vdash \psi (M) \Rightarrow \psi (N)\).
-
 : We have \(\psi (M)\! =\! l[[a^{\varDelta t}!\langle v \rangle ~\mathsf{then}~\! P~\mathsf{else}~Q ]]\! \mid \mid \! l[[a^{\varDelta t'}?(u)~\mathsf{then}~\! P'~\mathsf{else}~Q']]\) and \(\psi (N)=l[[P]]\mid \mid l[[P'\{v/u\}]]\). According to the definition of \(\psi \), we get \(M = l[[a^{\varDelta t}!\langle v \rangle ~\mathsf{then}~ P_1~\mathsf{else}~Q_1 ]] \mid \mid l[[a^{\varDelta t'}?(u)~\mathsf{then}~ P_1'~\mathsf{else}~Q_1']]\), where \(P=\varphi (P_1)\) and \(Q=\varphi (Q_1)\). By applying (Com), we get \(M\xrightarrow {} l[[P_1]]\mid \mid l[[Q_1\{v/u\}]] =N'\). By definition of \(\psi \), we have \(N=N'\).
: We have \(\psi (M)\! =\! l[[a^{\varDelta t}!\langle v \rangle ~\mathsf{then}~\! P~\mathsf{else}~Q ]]\! \mid \mid \! l[[a^{\varDelta t'}?(u)~\mathsf{then}~\! P'~\mathsf{else}~Q']]\) and \(\psi (N)=l[[P]]\mid \mid l[[P'\{v/u\}]]\). According to the definition of \(\psi \), we get \(M = l[[a^{\varDelta t}!\langle v \rangle ~\mathsf{then}~ P_1~\mathsf{else}~Q_1 ]] \mid \mid l[[a^{\varDelta t'}?(u)~\mathsf{then}~ P_1'~\mathsf{else}~Q_1']]\), where \(P=\varphi (P_1)\) and \(Q=\varphi (Q_1)\). By applying (Com), we get \(M\xrightarrow {} l[[P_1]]\mid \mid l[[Q_1\{v/u\}]] =N'\). By definition of \(\psi \), we have \(N=N'\). -
The other rules are treated in a similar manner.
4 Analyzing Timed Mobile Agents by Using Maude Tools
We have the translation of the high-level specification of the multi-agent systems into real-time Maude rewriting system, and have also the operational correspondence between their semantics. The \({ TravelShop}\,\) system presented in Example 1 can now be described in real-time Maude. The entire system looks like this:

where, e.g., the client syntax in real-time Maude is:

Since the recursion operator cannot be directly encoded into real-time Maude, we include for each recursion process appearing in TravelShop system a second parameter saying how many times the process can be unfolded. For our example this is 1 (but it could be any finite value).
Before doing any verification, we have the possibility in real-time Maude to define the length of the time units performed by the whole system. For our example we choose a time unit of length 1 by using the following command:

When using the rewrite command
 , the Maude platform executes
, the Maude platform executes
 by using the equations and rewrite rules of \(\mathcal {R}_D\) as given in the previous section, and outputs the following result:
by using the equations and rewrite rules of \(\mathcal {R}_D\) as given in the previous section, and outputs the following result:

We use the real-time Maude platform to perform timed reachability tests, namely if starting from the initial configuration of a system one can reach a given configurations of the system before a time threshold. The real-time Maude is able to provide answers to such inquires by searching into the state space obtained into the given time framework for the given configuration. As we are interested in searching the appearance of the given configuration within a time-framework, the fact that multiple computational steps can be performed is marked by the use of the
 . Also, the annotation
. Also, the annotation
 bounds the number of performed computational steps to n, thus reducing the possible state space.
bounds the number of performed computational steps to n, thus reducing the possible state space.

The result of performing the above inquiry is:

Instead of searching for the entire reachable system, we can also search only for certain parts of it: for instance, to check when the client remains with 70 cash units in a given interval of time. This can be done by using the command:

The answer returns that there exists such a situation at time 22.

The real-time Maude tool allows also the following command to find the shortest time to reach a desired configuration:

It returns the same solution as the previous one, and tells that it was reached
 .
.
If time is not relevant for such a search, we can use the untimed search command:

5 Conclusion and Related Work
In the current paper we translated our high-level specifications of the multi-agent systems with timeouts for migration and communication into an existing rewriting engine able to execute and analyze timed systems. This translation satisfies an operational correspondence result. Thus, such a translation is suitable for analyzing complex multi-agent systems with timeouts in order to be sure that they have the expected behaviours and properties. We analyze the multi-agent systems with timeouts by using the real-time Maude software platform. The approach is illustrated by an example.
The used high-level specification is given in a language forthcoming realistic programming systems for multi-agent systems, a language with explicit locations and timeouts for migration and communication. It is essentially a simplified version of the timed distributed \(\pi \)-calculus [7]. It can be viewed as a prototyping language of the TiMo family for multi-agent systems in which the agents can migrate between explicit locations in order to perform local communications with other agents. The initial version of TiMo presented in [5] lead to some extensions; e.g., with access permissions in perTiMo [6], with real-time in rTiMo [2]. In [4] it was presented a Java-based software in which the agents are able to perform timed migration just like in TiMo . Using the model checker Process Analysis Toolkit (PAT), the tool TiMo@PAT [8] was created to verify timed systems. In [16], the authors consider an UTP semantics for rTiMo in order to provide a different understanding of this formalism. Maude is used in [17] to define a rewrite theory for the BigTiMo calculus, a calculus for structure-aware mobile systems combining TiMo and the bigraphs [12]. However, the authors of [17] do not tackle the fresh names and recursion problems presented in our current approach.
References
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126, 183–235 (1994)
Aman, B., Ciobanu, G.: Real-time migration properties of rTiMo verified in Uppaal. In: Hierons, R.M., Merayo, M.G., Bravetti, M. (eds.) SEFM 2013. LNCS, vol. 8137, pp. 31–45. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40561-7_3
Behrmann, G., David, A., Larsen, K.G.: A tutorial on Uppaal. In: Bernardo, M., Corradini, F. (eds.) SFM-RT 2004. LNCS, vol. 3185, pp. 200–236. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30080-9_7
Ciobanu, G., Juravle, C.: Flexible software architecture and language for mobile agents. Concurrency Comput. Pract. Experience 24, 559–571 (2012)
Ciobanu, G., Koutny, M.: Timed mobility in process algebra and Petri nets. J. Logic Algebraic Program. 80, 377–391 (2011)
Ciobanu, G., Koutny, M.: Timed migration and interaction with access permissions. In: Butler, M., Schulte, W. (eds.) FM 2011. LNCS, vol. 6664, pp. 293–307. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21437-0_23
Ciobanu, G., Prisacariu, C.: Timers for distributed systems. Electron. Not. Theor. Comput. Sci. 164, 81–99 (2006)
Ciobanu, G., Zheng, M.: Automatic analysis of TiMo systems in PAT. In: IEEE Computer Society Proceedings 18th Engineering of Complex Computer Systems (ICECCS), pp. 121–124 (2013)
Goguen, J.A., Meseguer, J.: Order-sorted algebra I: equational deduction for multiple inheritance, overloading, exceptions and partial operations. Theoret. Comput. Sci. 105, 217–273 (1992)
Hessel, A., Larsen, K.G., Mikucionis, M., Nielsen, B., Pettersson, P., Skou, A.: testing real-time systems using UPPAAL. In: Hierons, R.M., Bowen, J.P., Harman, M. (eds.) Formal Methods and Testing. LNCS, vol. 4949, pp. 77–117. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78917-8_3
Meseguer, J.: Twenty years of rewriting logic. In: Ölveczky, P.C. (ed.) WRLA 2010. LNCS, vol. 6381, pp. 15–17. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16310-4_2
Milner, R.: The Space and Motion of Communicating Agents. Cambridge University Press, Cambridge (2009)
Ölveczky, P.C.: Real-time Maude and its applications. In: Escobar, S. (ed.) WRLA 2014. LNCS, vol. 8663, pp. 42–79. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12904-4_3
Ölveczky, P.C., Meseguer, J.: Semantics and pragmatics of real-time Maude. Higher-Order Symbolic Comput. 20, 161–196 (2007)
Thati, P., Sen, K., Martí-Oliet, N.: An executable specification of asynchronous \(\pi \)-calculus semantics and may testing in Maude 2.0. Electron. Not. Theor. Comput. Sci. 71, 261–281 (2004)
Xie, W., Xiang, S.: UTP semantics for rTiMo. In: Bowen, J.P., Zhu, H. (eds.) UTP 2016. LNCS, vol. 10134, pp. 176–196. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52228-9_9
Xie, W., Zhu, H., Zhang, M., Lu, G., Fang, Y.: Formalization and verification of mobile systems calculus using the rewriting engine Maude. In: IEEE 42nd Annual Computer Software and Applications Conference, pp. 213–218 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Aman, B., Ciobanu, G. (2019). Verification of Multi-agent Systems with Timeouts for Migration and Communication. In: Hierons, R., Mosbah, M. (eds) Theoretical Aspects of Computing – ICTAC 2019. ICTAC 2019. Lecture Notes in Computer Science(), vol 11884. Springer, Cham. https://doi.org/10.1007/978-3-030-32505-3_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-32505-3_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32504-6
Online ISBN: 978-3-030-32505-3
eBook Packages: Computer ScienceComputer Science (R0)



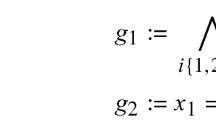



 , we have
, we have 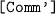 we get
we get  ,
,
 and
and
 , respectively.
, respectively. we get
we get  .
. : We have
: We have