Abstract
Formal methods are vast and varied. This paper reports the essentials of what I have observed and learned by teaching the Inductive Method for security protocol analysis for nearly twenty years. My general finding is something I realised after just a couple of years, that my target audience of post-graduate students with generally little appreciation of theory would need something different from digging deep down in the wonders of proof ever since class two. The core finding is a decalogue of steps forming the teaching methodology that I have been developing ever since the general finding became clear. For example, due to the nature of the Inductive Method, an important step is to convey the power and simplicity of mathematical induction, and this does not turn out too hard upon the sole basis that students are familiar with the informal analysis of security protocols. But the first and foremost step is to convince the learners that they already somewhat used formal methods, although for other applications, for example in the domains of Physics and Mathematics. The argument will convey as few technicalities as possible, in an attempt to promote the general message that formal methods are not extraterrestrial even for students who are not theorists. This paper introduces all steps individually and justifies them towards the general success of the teaching experience.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Formal methods form a very big chapter in the book of, at least, Informatics. It is widely recognised that they include a variety of approaches, for example, logic, algebraic or ad hoc approaches. With a “universal view” of formal methods, I contend that hey have been applied to virtually every real-world problem areas, ranging from Astrophysics to Economics to Engineering.
It is clear that my view of a formal method is broad, in fact I like to include in the pool any mathematically grounded, rigorous method. The distinctive feature implied here is that formal methods do not necessarily require the target phenomenon or system under study to be practically available or built at all. As opposed to empirical methods, formal methods can be profitably used on paper, ideally with some computer support, namely at the abstract, design level.
My main “local” preconditions are that students are not very inclined to theory in general. Broadly speaking, I find course modules more geared to practical competences such as (imperative) programming and system administration. In the cybersecurity area in particular, the most job-oriented competences lie in the area of Vulnerability Assessment and Penetration Testing (which I also introduce at Master’s level), hence formal methods again suffer this particular though well motivated trend of the present time. However, also formal methods continue to contribute to the goodness of cybersecurity [1], for example as it can be read from recent publications such as a NIST survey [2] or an NSF workshop report [3]. Hence, the motivation for this paper.
The teaching experience within such a large area as formal methods is bound to be diverse and multifaceted, and here I only engage into outlining my own, limited experience on teaching the Inductive Method [4, 5], which is embedded in the theorem prover Isabelle [6], for the analysis of security protocols. This would be the first encounter of my students with theorem proving and formal methods in general. A fundamental disclaimer stemming from my local preconditions is that none of my observations should be taken as general; by contrast, they are limited to the specific lecturing experience in my Institution, though over nearly two decades, at Master’s level in Informatics covering a module of at least 12 h intertwining theory and laboratory experiments tightly.
My general finding is that the entanglements of proof theory must be left to an advanced module, which I have never had the opportunity to teach. My core finding is that teaching an introductory module requires at least a decalogue of steps before any proof can be attempted profitably. Lecturing will resemble the tailor’s activity of sewing together patches of different fabrics, though dealing with somewhat heterogeneous notions from Informatics in our case.
To try and speed up readability, the style I take in this paper will be mixed, sometimes describing the steps of the decalogue and summarising parts of the lectures, sometimes as if I were speaking straight to the students. Hopefully, the context will resolve the inherent ambiguity. As we shall see, the main obstacle to overcome for students will be the perception of formal methods as something so theoretical and abstract to be unattractive and unsurmountable, hence the title of this paper. But the decalogue discussed below has yielded a very effective teaching experience with me.
2 My Experience with Teaching the IM
There is no room for introducing the Inductive Method [4] and the theorem prover Isabelle [6], so I must assume a basic familiarity of the readers’.
2.1 You Already Used Formal Methods
One of the first issues I encountered since the beginning and that I keep touching every year is some sort mental resistance that (my) students show to almost anything prefixed with “formal”. In consequence, there seems to be some psychological wall between themselves and formal methods in general.
At first, I set out to try and demolish that wall upfront. I started providing vast reference material, also appealing to books that can be found freely on the Internet [7], and presenting example applications to various scenarios in the areas of both hardware and software. However, this did not work, as the class felt kind of lost through the various methods, with each student looping through a contrastive analysis of the methods.
I decided that this approach was too vast. So, I selected First-Order Logics and tried to illustrate and variously demonstrate why it could be somewhat easy to use in practice, and also nice and ultimately rewarding; but all this did not seem to yield the results I was expecting. It was clear that students were almost memorizing notions and formulas rather than adopting and actively using them.
It was still in the early years of teaching when I started to feel that psychological wall as unsurmountable for them. So, I thought that the only way to have students on the other side would have been to make this true by assumption. I was then left with the problem of finding an appropriate, realistic interpretation that would make that assumption hold, which would have made students feel already beyond the wall. At some point, I thought I found that interpretation, and presented them with something as simple as this formula:
This was the first encouraging result because everyone could recognise the uniform linear motion formula with s indicating space, v for speed and t for time.
I decided to navigate this way and this is when I decided to take a somewhat loose definition of formal methods. So, I claimed that formula to be an application of a formal method, precisely a specification, namely some sort of abstract representation of a real-world phenomenon. The formula clearly shows independence from the actual phenomenon, it lives and computes in a world of its own, that of symbols with a clear, non-ambiguous interpretation. Yet, the formula models and describes the phenomenon closely, providing a realistic, written representation of it. I did not need to describe the language of the formula more in detail because I realised that students had already started to stair at the board pensively, so they were finally engaged.
I then unfolded the same argument with accelerated linear motion and projectile motion. Then, I switched application area, and discussed definite integrals as a very useful tool (not just to pass A levels but also to) calculate the area under a curve, something that we could effectively use to help a farmer determine the extension of his land. Formal methods everywhere! Yes, such formulas are formal because they leave (almost) no room for ambiguity but they are also very applied due to what they allow us to do and resolve in everyday life. This argument worked with the class, definitely, and keeps working every year.
I normally conclude this journey through heterogeneous applications of formal methods with an extra reference to Propositional Logics and First-Order Logics, whose basics the students regularly know from some foundational course. This time around, they look at whatever I try to formalise with these languages with renowned interest and, as far as I can tell, more familiarity and conscious understanding. For example, here I normally debate that there is no “wrong” specification of a phenomenon but, rather, there may be an unrealistic specification of it, for example like describing a river that flows from sea to peaks.
“Dear student, it is clear that you already used formal methods but did not know it!”.
2.2 The Need for Formal Methods and in Particular for the IM
The next step in the decalogue is to demonstrate that formal methods are needed in general. Here, it is useful to go back to the formula borrowed from Physics and Calculus, as well as to hint at Ancient Greece mathematician Eratosthenes, with his incredibly precise measurement of Earth’s circumference, and other Ancient Greece prodigies.
To approach our days, I normally linger around the Pentium processor bug (which luckily has a Wikipedia entry). With whatever microchip in hand to test, it is intuitive for students to see in their minds the act of feeding it with various inputs to inspect whether the output is correct. And here are the fundamentals of modern (industrial strength) testing. However, the Pentium bug shouted out to the world that testing may not be enough. This may be due, in general, to the ever increasing complexity of modern circuits, whose complexity roughly doubles every 18 months, as Moore started to predict ever since 1965. It may also be due to the tight time-to-market constraints of products, and this is likely to have been the case with the Pentium bug. While it is natural for everyone that testing requires time due to the number of tests to physically execute, the learners also understand that business success often correlates with early deployment. (An underlying, usefully embodied, assumption is that even if something is appropriately designed, it is not obvious that it will work as expected at design level when it is actually built, such as with houses or with any devices).
And here comes a clear need for an alternative that scientists may use, on paper or arguably with some computer assistance, to get confidence that the real-world phenomenon that is an actual industrial product works as intended by its designers. That alternative is the use of formal methods, whose application may not be constrained by execution times as testing is. This argument invites at least two useful considerations. One is that formal methods support some sort of reasoning on the target phenomenon, formal reasoning in fact, which can be tailored to assess specific properties of interest, (functional ones) such as correctness of computation, then (non-functional ones such as) secrecy and authentication. Another useful argument is the predictive use of formal methods. We can effectively study a phenomenon before it actually takes place, or a product before it is built, and this is an exclusive advantage.
This is the point when it becomes effective and useful to plunge into security protocols, thus nearing my actual target. Students are normally familiar with traditional attacks on toy security protocols, which are so popular in the literature of the area. For example, I use to entertain my undergraduates with an informal analysis of the original public-key Needham-Schröder protocol [8], and I always succeed in convincing everyone that nonces remain secret and that mutual authentication works; after that, I surprise them with Lowe’s attack, then help them overcome their frustration by observing that the attack was only published some 17 years after the protocol. Therefore, I easily emphasise the limitations of informal protocol analysis, calling for more rigour, hence for formal protocol analysis, which has the strength and rigour of mathematics. Examples are due here, but they still need to wait one more logical assertion.
That assertion is that a security protocol may be a strange, huge beast. There is potentially no bound for the length of protocol messages, for the number of protocol steps, of protocol participants, of nonces or keys they may invent and for the number of protocol sessions they may interleave. It becomes apparent that security protocols are potentially unbounded in size, hence it becomes intuitive that the empirical approach of testing (all) its potential executions falters. Consequently, the idea that some sort of mathematical wisdom could help starts to materialise at the mental horizons of the students.
Additionally, familiarity with the Needham-Schröder protocol implies acquaintance with the notion of threat model, and in particular with the standard Dolev-Yao attacker. Because that attacker may intercept messages and build new ones at will with the sole limitations imposed by encryption, students realise that the attacker is yet another source of potential unboundedness, and know by intuition that modelling it may not be straightforward.
Even if we took the approach of bounding all parameters and we magically knew that the resulting protocol reached its security goals, then we still would have no guarantee that those goals hold also when those parameters are exceeded during a practical use. It would seem that unboundedness cannot be neglected.
“So, dear all, you will be amazed at how the Inductive Method can cope with unboundedness!”.
2.3 A Parallel: How to Write a Biography
At this point, some students change the way the look at the lecturer, as if they start to wonder independently how to possibly use the Inductive Method to model security protocols. Here, I surprise them turning to talk about biographies, actual people’s biographies. The biographer faces a huge challenge: to condense a continuous (we could build a bijection with the reals) sequence of events in a finite manuscript. The biographer has no option except picking up a few significant events and describe those, perhaps connecting them logically, and sometimes drawing a general message about the chief character, either explicitly or implicitly. From a data structure standpoint, a biography is a list of events.
The same approach can be taken to model security protocols, somewhat surprisingly for students. So, our effort could be similar to the biographer’s. Running a protocol of course entails a number of tasks for each of its peers. But, as the biographer does, we need to abstract away from many of those and distill out the main ones. With security protocols, it is easy to convince everyone that the main ones are to send and to receive a cryptographic message.
Does this imply that a protocol can be compared to a human life? It would seem so in terms of modelling effort and approach. More precisely, a specific protocol execution can be compared to the biography of a life, and both can be modelled as a list of events. While a biography features events linking the chief character to other people in the character’s life, or sometimes other people among themselves, a protocol execution features events linking peers to each other via the events of sending or receiving the protocol messages (a specific peer could be isolated and interpreted as a chief character in the execution but this is irrelevant). A list representing a protocol execution is normally termed a trace, hence it is a list of events of sending or receiving the protocol messages. We could then address a biography as the trace of someone’s life. If we blur the focus on the chief character, then a biography is a representation of one possible development of society, simply because it may involve many characters.
This argument invites thinking about other possible executions of protocols in parallel to other possible developments of society, the very society of people on this planet. And here students find themselves curious to understand if and how all of the protocol executions and, equally of the society developments, could be represented compactly. They get all the more hungry as they start to perceive that such possible executions or developments are potentially unbounded. They will have to resist their hunger a bit longer.
“We now know that a list is a useful structure to model an abstract version of one possible protocol execution, but how can we ever model all possible executions?”.
2.4 The Use of Computational Logics for Reasoning
At this point in the development of the discourse, the learners’ eyes begin to glitter. It is hence the right time to instill the power of logics. I already mentioned that, in my experience, students normally come with some notions of Propositional Logics and First-Order Logics, and discussed how to make them feel familiar with such logics (Sect. 2.1). However, it would seem that logics is merely seen as a language for specifying (or formalising) some phenomenon. It is then not very clear to them what to do with a specification or how to use it profitably. Here come handy again the arguments unfolded above, suggesting that a specification is a somewhat compact representation of something real (Sect. 2.3) and that it may be used to understand that thing predictively (Sect. 2.2).
The only way to overcome the dogmatic flavour that such justifications may bring is to finally introduce elementary forms of classical reasoning to be conducted on top of specifications, with the aim of proving something about the specification. My favourite one is modus ponens, so I normally draw something like this on the board:

Stating that “if you have \(p \rightarrow q\) and you also have p, then you may also derive q” is simply not enough to convey the meaning of this essential rule. Students have often taken \(p \rightarrow q\) alone to magically derive q. This betrays their misunderstanding, whereas \(p \rightarrow q\) and p are both preconditions at the same logical level, and it is precisely their combination what allows us to derive q; here, it may help to denote p as the ammo that the weapon \(p \rightarrow q\) needs to shoot out q.
This is an essential yet powerful form of (formal) reasoning, and it may also be the students’ first close encounter with such a wonderful engine that, once they have certain formulas that hold, allows them to derive yet another formula that holds too. Should the learners show concern that they are touching something extraterrestrial again, I easily demolish that concern asserting that we all follow an essential rule: if I am hungry, then I eat something. At every moment in time, each of us is left wondering: am I hungry? It is clear that, only when this is affirmative, do both preconditions of the modus ponens rule hold, hence it is time to eat something. We all use modus ponens in all sorts of ways.
“Guys, you have only scratched the surface of formal reasoning, still you shall see that you’ll be able to do a lot with what you just found out!”.
2.5 The Basics of Functional Programming
Functional programming is, for some reasons beyond the aims of this paper, not very well received by my students, who tend to see it again as something overly formal and not as actual programming. Convincing them fully of the power of functional programming normally remains out of reach despite the fact that they took a short crash course (which, however, lacks the details of Turing completeness). The main issue that I take pains to convey is that it is just a different programming paradigm from their dearest imperative approach, the latter learned since school. They find it bewildering that a functional program has no variables to assign values to.
So, how on earth can we carry out any sort of computation? The notion of term rewriting must be introduced. Each rewriting derives from the application of a sound rewriting rule. For example, linking the argument back to the use of logics for reasoning (Sect. 2.4), modus ponens may be seen as a rewriting rule for the pair of facts forming its preconditions. Similarly, \(p \rightarrow q\) can be rewritten as \(\lnot p \vee q\) by applying the logical equivalence of the two formulas as a rule.
But rewriting may also be conditional. For example, evaluating the guard of:
allows us to rewrite the entire expression as \(X=Y\). And this was computation.
“Rewriting is the essence of computation with functional programming, stop thinking imperatively here, forget variables and assignments!”.
2.6 The Wonders of Mathematical Induction
Students are somewhat familiar with mathematical induction, in particular for what concerns the definition of the natural numbers:
Because they understand rule Ind, it is the right time to introduce its more formal version:

This lets me motivate the meta-level implication as the implication at the level of reasoning, as opposed to the object level of the encoded logics. And I can then introduce an equally formalised version of modus ponens:

I believe that with this and a few similar examples, the level of reasoning, as expressed by fat square braces, semicolon and the fat arrow, is uploaded.
And here is how beautiful it is to capture a clearly unbounded set by means of just two, formal, rules. Observe also the magic behind induction, at least due to the fact that nobody has ever tried to practically verify if, say, 4893 can be effectively built by an application of rule Base and a finite number of applications of rule Ind. Still, we know by intuition that all natural numbers are represented.
Observing that all natural numbers are caught this way brings back memories of an open problem, how to capture all possible society developments or protocol executions. The answer clearly is by induction but we need to cope with traces. Traces are lists, so can we build lists by induction? Yes, we can build them by structural induction on their length. Therefore, we expect to be able to specify all possible lists, even if unbounded, for our application, be is society or protocols, with just a few inductive rules. And, of course, yes, we may have more than one inductive rule in an inductive definition.
Before giving an example (Sect. 2.7), it is useful to go back to the reasoning part and observe that it may also follow predefined strategies aimed at proving a goal, thus proof strategies. Induction may also be viewed as a proof strategy, based on application of the mathematical induction proof principle. As it is a principle, there is no proof for itself. I often realise that students are able to prove facts such as an expression for the sum of the first n natural numbers \(S_n\):
They mechanically prove it for the Base case and then for the Ind case; in the latter, they know how to assume the property, say, for n and then attempt to prove it on that assumption for \(n+1\). They may, however, not be fully aware that they are inherently applying the induction proof principle. It is then important to spell it out formally on a property P:

I have memories of their surprise in front of this formal statement. This version is also useful to teach that the latest occurrence of n is scoped by the universal quantifier, hence not to be confused with the occurrences in the preconditions.
“You see now, induction is great for specifying and then for reasoning, namely for formalising something and then proving facts about it!”.
2.7 The Formal Protocol Definition
All pieces of the puzzle are now available to compose a formal protocol model. As noted above, students are familiar with toy security protocols at least, hence there will be little to discuss in front of an example like this:

Initiator A sends her identity along with a fresh nonce of hers to responder B, who sends it back, bundled with his identity, encrypted under his private key. The formal model for this example protocol is finally unveiled as shown in Fig. 1. I normally spend above an hour explaining it. It must be first looked at “from the outside-in”, namely you must first realise the general structure of what you have in front. It is five rules. They very often mention
 . This is a constant (not a variable!) termed as an acronym for
. This is a constant (not a variable!) termed as an acronym for
 formal
formal
 xample
xample
 rotocol, which is the formal model for our example protocol. I purposely defer the discussion of its type till now. Because we wanted to formalise all possible protocol executions, and each execution was a trace, namely a list of events (of sending or receiving the protocol messages), then
rotocol, which is the formal model for our example protocol. I purposely defer the discussion of its type till now. Because we wanted to formalise all possible protocol executions, and each execution was a trace, namely a list of events (of sending or receiving the protocol messages), then
 must be a set of lists of events.
must be a set of lists of events.
Going back to the rules defining
 , it can be seen that the first rule is very special because it has no preconditions. It is in fact the base case of the inductive definition. While the central rules,
, it can be seen that the first rule is very special because it has no preconditions. It is in fact the base case of the inductive definition. While the central rules,
 and
and
 , seem to be “similar” to the protocol steps, the final rule,
, seem to be “similar” to the protocol steps, the final rule,
 , seems to be a matter of receiving messages, but must be explained in depth. The remaining rule,
, seems to be a matter of receiving messages, but must be explained in depth. The remaining rule,
 , is incomprehensible without close inspection.
, is incomprehensible without close inspection.
It must be noted that all rules following
 mention a trace of
mention a trace of
 in the preconditions, respectively
in the preconditions, respectively
 ,
,
 ,
,
 ,
,
 and
and
 . Recalling that
. Recalling that
 is the list cons operator, it may also be seen that all those rules conclude that the respective trace, somehow extended on the left, is a trace of
is the list cons operator, it may also be seen that all those rules conclude that the respective trace, somehow extended on the left, is a trace of
 . These features signify that they are all inductive rules. So, we are facing a definition with a total of four inductive rules.
. These features signify that they are all inductive rules. So, we are facing a definition with a total of four inductive rules.
Rule
 models the first step of the protocol. Standing on a trace
models the first step of the protocol. Standing on a trace
 of the model, it also assumes a nonce that is not used on the trace, hence the nonce is fresh. Of course,
of the model, it also assumes a nonce that is not used on the trace, hence the nonce is fresh. Of course,
 is a function that is defined somewhere, but its definition can wait till later (Sect. 2.8). The nonce freshness is a requirement set by the protocol designers, hence we as analysers are merely adding it to our specification. Event
is a function that is defined somewhere, but its definition can wait till later (Sect. 2.8). The nonce freshness is a requirement set by the protocol designers, hence we as analysers are merely adding it to our specification. Event
 is a self explaining formalisation of the first event of the protocol, and also its justification through the datatype of events can wait (Sect. 2.8). The postcondition of the rule states that the given trace
is a self explaining formalisation of the first event of the protocol, and also its justification through the datatype of events can wait (Sect. 2.8). The postcondition of the rule states that the given trace
 , appropriately extended with the event that models the first protocol step, is a trace in the model. Thus, the rule’s structure resembles that of Ind (Sect. 2.6).
, appropriately extended with the event that models the first protocol step, is a trace in the model. Thus, the rule’s structure resembles that of Ind (Sect. 2.6).
Rule
 models the second step of the protocol. It rests on a trace
models the second step of the protocol. It rests on a trace
 with the special requirement that it features an event formalising B’s reception of the first protocol message,
with the special requirement that it features an event formalising B’s reception of the first protocol message,
 , and
, and
 casts a list to a set. The rule concludes that the suitably extended trace is in the model.
casts a list to a set. The rule concludes that the suitably extended trace is in the model.
The difference between these two rules is that
 puts no requirement on the trace in terms of traffic occurred on it, so the rule may fire at any time, modelling the real-world circumstance of any agent who may initiate the protocol at any time and with any peer. By contrast,
puts no requirement on the trace in terms of traffic occurred on it, so the rule may fire at any time, modelling the real-world circumstance of any agent who may initiate the protocol at any time and with any peer. By contrast,
 may only fire upon a trace that has already recorded the reception of the first message of the protocol.
may only fire upon a trace that has already recorded the reception of the first message of the protocol.
If the first message is sent through
 , what makes sure that it is received? The first message, and in fact any message that is sent, is received through rule
, what makes sure that it is received? The first message, and in fact any message that is sent, is received through rule
 . It insists on a trace on which a generic agent
. It insists on a trace on which a generic agent
 sends a generic message
sends a generic message
 to a generic agent
to a generic agent
 , and extends it with the event whereby
, and extends it with the event whereby
 receives
receives
 .
.
We are left with the
 rule, which models the attacker, arguably represented as
rule, which models the attacker, arguably represented as
 . The trace extension mechanism is clear, so it can be seen that this rule extends a given trace with an event whereby the attacker sends a fake message
. The trace extension mechanism is clear, so it can be seen that this rule extends a given trace with an event whereby the attacker sends a fake message
 to a generic agent
to a generic agent
 . The fake message is derived from a set modelled as a nesting of three functions, from the inside-out,
. The fake message is derived from a set modelled as a nesting of three functions, from the inside-out,
 , then
, then
 , finally
, finally
 , which are to be explained separately (Sect. 2.8). Intuitively, such a nesting simulates all possible malicious activity that a Dolev-Yao attacker can perform, yet without any cryptanalysis.
, which are to be explained separately (Sect. 2.8). Intuitively, such a nesting simulates all possible malicious activity that a Dolev-Yao attacker can perform, yet without any cryptanalysis.
Thus, the formal protocol model features a number of rules that equals the number of steps in the protocol, augmented with three extra rules, one for the base of the induction, one for the attacker and another one to enable message reception. Thanks to the wonders of induction, set
 will have all possible traces that can be built under the given protocol, thus modelling effectively all possible protocol executions. For example, it contains a trace on which ten agents begin the protocol with other agents but none of those messages is received, a trace that sees an agent sending off a message to another one and that message being received many times. We are guaranteed that all possible traces that can be built by any interleaving of the given rules appear in
will have all possible traces that can be built under the given protocol, thus modelling effectively all possible protocol executions. For example, it contains a trace on which ten agents begin the protocol with other agents but none of those messages is received, a trace that sees an agent sending off a message to another one and that message being received many times. We are guaranteed that all possible traces that can be built by any interleaving of the given rules appear in
 . It is now time to declare that the specific font indicates that the formal protocol model can be fed, as is, to Isabelle, which will parse it and ensure at least type coherency.
. It is now time to declare that the specific font indicates that the formal protocol model can be fed, as is, to Isabelle, which will parse it and ensure at least type coherency.
“And here is how we ultimately define the formal protocol model in Isabelle, including all possible protocol executions under the Dolev-Yao attacker!”.
2.8 The Main Functions
Intuitively, the innermost set,
 contains all messages that are ever sent on
contains all messages that are ever sent on
 by anyone. Then, function
by anyone. Then, function
 breaks down all messages of the set into components, for example by detaching concatenated messages and by decrypting cypher-texts built under available keys (no cryptanalysis at all). Finally,
breaks down all messages of the set into components, for example by detaching concatenated messages and by decrypting cypher-texts built under available keys (no cryptanalysis at all). Finally,
 uses available components to build messages by means of concatenation or encryption, still under available keys.
uses available components to build messages by means of concatenation or encryption, still under available keys.
Suppose that each event in the trace
 carried not a cryptographic message but some... bread, a ciabatta. Then,
carried not a cryptographic message but some... bread, a ciabatta. Then,
 would be a set of ciabattas. Suppose that ciabattas are one week old, hence too hard to be eaten. We could then decide to grind them off finely into powder, and this is captured by set
would be a set of ciabattas. Suppose that ciabattas are one week old, hence too hard to be eaten. We could then decide to grind them off finely into powder, and this is captured by set
 . If we want to mix this strange kind of flour again to try and build bread again (ignoring other ingredients), then the resulting fresh ciabattas would all be in the set
. If we want to mix this strange kind of flour again to try and build bread again (ignoring other ingredients), then the resulting fresh ciabattas would all be in the set
 .
.
The definitions of such functions, of
 and of the relevant types have been published in many other places [4, 5], but I want to stress the didactic value of the definition of
and of the relevant types have been published in many other places [4, 5], but I want to stress the didactic value of the definition of
 hence report it in Fig. 2. After justifying the declaration, the focus turns to the primitive recursive style, with two rules. Rule
hence report it in Fig. 2. After justifying the declaration, the focus turns to the primitive recursive style, with two rules. Rule
 describes the knowledge that a generic agent
describes the knowledge that a generic agent
 can form on observing an empty trace. It reduces to the agent’s initial knowledge, formalised as
can form on observing an empty trace. It reduces to the agent’s initial knowledge, formalised as
 , but it must be remarked that “state” is used loosely here and, in particular, it bears no relation to the states underlying model checking.
, but it must be remarked that “state” is used loosely here and, in particular, it bears no relation to the states underlying model checking.
The other rule pertains to a generic trace, and separates the case in which agent
 , whose knowledge is being defined, is the attacker from the case in which she is not. For each of these, the definition emphasises the latest event
, whose knowledge is being defined, is the attacker from the case in which she is not. For each of these, the definition emphasises the latest event
 in the trace, which is then split up as trace
in the trace, which is then split up as trace
 . It can be seen that knowledge is evaluated accordingly to the specific event, which can be the sending of a message, the reception of a message or a third type. This third type was introduced by Paulson with the work on TLS of 1999 [9]. He needed to enable agents to somewhat record the Master Secret of that protocol, and decided that defining an additional event for agents’ notes was a convenient way.
. It can be seen that knowledge is evaluated accordingly to the specific event, which can be the sending of a message, the reception of a message or a third type. This third type was introduced by Paulson with the work on TLS of 1999 [9]. He needed to enable agents to somewhat record the Master Secret of that protocol, and decided that defining an additional event for agents’ notes was a convenient way.
I then take a good amount of time to describe why and how the definition makes sure that the attacker knows everything that is sent by anyone or noted by compromised agents, those in the set
 . This is the students’ first encounter with such a set, and I will surprise them later showing that the set is only declared but never ever defined: all reasoning that follows will be typically parameterised over such a set. It means that the attacker has a full view of the network traffic. Incidentally, the attacker does not need to learn the messages that are received because these must have been sent in the first place, a theorem that can be proved thanks to the definition of rule
. This is the students’ first encounter with such a set, and I will surprise them later showing that the set is only declared but never ever defined: all reasoning that follows will be typically parameterised over such a set. It means that the attacker has a full view of the network traffic. Incidentally, the attacker does not need to learn the messages that are received because these must have been sent in the first place, a theorem that can be proved thanks to the definition of rule
 , already discussed. I need also time to explain that any agent who is not the attacker only learns from messages that she sends, receives or notes down herself, because, by being honest, she only has a limited view of the network traffic.
, already discussed. I need also time to explain that any agent who is not the attacker only learns from messages that she sends, receives or notes down herself, because, by being honest, she only has a limited view of the network traffic.
However, no matter how long I spend to signify this definition, students will be left thirsty for some form of computation. Tight in the mental shackles of imperative programming, they may still strive to see this definition as a rewriting rule that will, by its application, drive and determine computation. A few examples are due. Expression
 will get rewritten, by application of rule
will get rewritten, by application of rule
 , as
, as
 . I sometimes need to stress that the resulting expression is simpler because
. I sometimes need to stress that the resulting expression is simpler because
 is applied to a shorter trace; and, once more, that this rewriting is computation.
is applied to a shorter trace; and, once more, that this rewriting is computation.
“You see, this is the core of the Inductive Method in Isabelle, one rule to capture Dolev-Yao, a bunch of rules for the entire formal protocol model!”.
2.9 The Basic Interaction with the Theorem Prover
With all instruments on the workbench, it is time to discuss how they can be used practically in Isabelle. It must be noted that those instruments only form the essentials of the Inductive Method, and that the full suite can be found by downloading Isabelle, then inside the \src\HOL\Auth folder. Precisely, all constituents of the Inductive Method are neatly divided into three theory files:
 ,
,
 and
and
 . While the first two theory names are intuitive, the last perhaps is not fully so. In fact, it originally only contained an axiomatisation of asymmetric, or public-key cryptography, while symmetric, shared-key cryptography was in a separate file
. While the first two theory names are intuitive, the last perhaps is not fully so. In fact, it originally only contained an axiomatisation of asymmetric, or public-key cryptography, while symmetric, shared-key cryptography was in a separate file
 . However,
. However,
 now contains both versions, and the other file has been disposed with.
now contains both versions, and the other file has been disposed with.
Students are now ready to download Isabelle, find these theory files and familiarise with their contents. Depending on the available time, I may parse the specification part of all three theories. Before continuing to the proof part, I must introduce the fundamental proof methods, which can be applied by means of Isabelle command
 , and outline what they do:
, and outline what they do:
-
 calls the simplifier, namely the tool that applies term rewriting meaningfully; for example, to operate the rewriting just discussed (Sect. 2.8), the analyst needs to call
calls the simplifier, namely the tool that applies term rewriting meaningfully; for example, to operate the rewriting just discussed (Sect. 2.8), the analyst needs to call

-
 performs the obvious steps of a proof, such as applying the theorem that deduces both p and q from \(p \wedge q\);
performs the obvious steps of a proof, such as applying the theorem that deduces both p and q from \(p \wedge q\); -
 launches the classical reasoner, and the analyst may easily state extra available lemmas for the reasoner to invoke;
launches the classical reasoner, and the analyst may easily state extra available lemmas for the reasoner to invoke; -
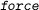 combines the simplifier with the classical reasoner;
combines the simplifier with the classical reasoner; -
 is similar to
is similar to
 but, contrarily to all other methods, applies to the entire proof state, namely to all subgoals to prove.
but, contrarily to all other methods, applies to the entire proof state, namely to all subgoals to prove.
I purposely keep the discussion on the proof methods brief because I aim at providing the students with something they can fire and see the outcome of. This will favour their empirical assessment of the proof as it unfolds. Of course, each method is very worth of a much deeper presentation, but this can be deferred depending on the aim of the course module and the available time.
“And now you have commands to try and see marvellous forms of computation unfolding through a proof!”.
2.10 Proof Attempts
And finally comes the time to show students how the instruments just learned can be used in practice over an example security protocol chosen from those that have been treated in the Inductive Method. A good choice could be to pick the theory for the original public-key Needham-Schröder protocol, theory
 , which also shows how to capture Lowe’s attack.
, which also shows how to capture Lowe’s attack.
I open the file and review the formal protocol model for the protocol. I continue arguing that one of the main protocol goals is confidentiality and debate how to capture it in the Inductive Method. If we aim at confidentiality of a nonce
 , we would like the attacker to be unable to deduce it from her malicious analysis of the observation of the traffic. It means that we leverage a generic trace, then apply
, we would like the attacker to be unable to deduce it from her malicious analysis of the observation of the traffic. It means that we leverage a generic trace, then apply
 and finally
and finally
 , and we would aim at
, and we would aim at
 . After skipping on various lemmas in the file, I reach the confidentiality theorem for the initiator’s nonce
. After skipping on various lemmas in the file, I reach the confidentiality theorem for the initiator’s nonce
 , quoted in Fig. 3, and there is a lot to discuss: the preconditions of a trace of the protocol model
, quoted in Fig. 3, and there is a lot to discuss: the preconditions of a trace of the protocol model
 that features the first protocol message, so as to pinpoint the nonce whose confidentiality is to be proved,
that features the first protocol message, so as to pinpoint the nonce whose confidentiality is to be proved,
 ; the two involved peers assumed not to be compromised;
; the two involved peers assumed not to be compromised;
 to be interpreted as a translation for
to be interpreted as a translation for
 (due to backward compatibility: Paulson originally defined
(due to backward compatibility: Paulson originally defined
 [4], then I generalised it as
[4], then I generalised it as
 [5]).
[5]).
The main effort must be devoted to playing with and understanding the proof script. The first proof method that is applied resolves the goal with
 , hence I introduce it as an implementation of modus ponens with swapped preconditions, then sketch the basics of resolution on the fly. Of course, I mostly leverage the intuition behind. Suppose you want to get rich and you are so lucky as to find a secret recipe that guarantees you that whatever you want to reach, you just need to do a couple of things to reach it. What would you then do? You would engage to accomplish that very couple of things. The same reasoning is implemented here through the first command, which leaves us with the preconditions of
, hence I introduce it as an implementation of modus ponens with swapped preconditions, then sketch the basics of resolution on the fly. Of course, I mostly leverage the intuition behind. Suppose you want to get rich and you are so lucky as to find a secret recipe that guarantees you that whatever you want to reach, you just need to do a couple of things to reach it. What would you then do? You would engage to accomplish that very couple of things. The same reasoning is implemented here through the first command, which leaves us with the preconditions of
 left to prove.
left to prove.
I then dissect the second command as a condensed syntax to apply three proof methods. The first resolves the only subgoal currently in the proof state with the inductive proof principle that Isabelle instantiates on the inductive protocol definition. Isabelle builds it automatically and makes it available as a lemma on top of any inductive definition; it is
 in this case.
in this case.
Here comes the general meta strategy that, after induction, we normally apply simplification, namely term rewriting, and then classical reasoning. This justifies
 , which solves the Base subgoal. And we are left facing the Fake case, which Paulson designed a special method to solve,
, which solves the Base subgoal. And we are left facing the Fake case, which Paulson designed a special method to solve,
 . It may be safely applied as a black box for the time being, but it can be dissected, if time, by following another article of mine [10].
. It may be safely applied as a black box for the time being, but it can be dissected, if time, by following another article of mine [10].
The next part of the lecture explains the two lemmas that are applied by
 , discussing the general differences between a destruction rule and an introduction rule, and understanding that the
, discussing the general differences between a destruction rule and an introduction rule, and understanding that the
 symbol reiterates the same command on all subgoals. It is didactic to assess which subgoal really requires application of which lemma, so that students also familiarise with forward-style reasoning.
symbol reiterates the same command on all subgoals. It is didactic to assess which subgoal really requires application of which lemma, so that students also familiarise with forward-style reasoning.
Finally, the same argument is repeated on the confidentiality conjecture on the responder’s nonce
 . The proof attempt for this conjecture, omitted here for brevity, cannot be closed, and we are left with a subgoal that describes Lowe’s attack whereby the attacker learns
. The proof attempt for this conjecture, omitted here for brevity, cannot be closed, and we are left with a subgoal that describes Lowe’s attack whereby the attacker learns
 . It is normally illuminating to note how the prover suggests, actually teaches us, scenarios that are so peculiar that we may not have known them by intuition. Every time such a subgoal remains, and we decode that the reasoning cannot be taken forward, then either we need to change line of reasoning entirely or we understand that the scenario indicates an attack (the very attack that contradicts the conjecture).
. It is normally illuminating to note how the prover suggests, actually teaches us, scenarios that are so peculiar that we may not have known them by intuition. Every time such a subgoal remains, and we decode that the reasoning cannot be taken forward, then either we need to change line of reasoning entirely or we understand that the scenario indicates an attack (the very attack that contradicts the conjecture).
3 General Lessons Learned and Conclusions
Formal methods are great help over innumerable application scenarios, and the Inductive Method remains a very effective tool that may at least serve exploratory reasoning on new systems or security goals, possibly to inspire the subsequent implementation of ad hoc tools.
In particular, Paulson also formalised the notion of an
 event ever since the inception of the Inductive Method to allow and agent to arbitrarily lose a secret to the attacker, without any particular precondition. The socio-technical understanding of cybersecurity and privacy is a very hot area today, grounding non-functional properties not only on technical systems such as security protocols but also on the use that humans may make of them. I believe that the
event ever since the inception of the Inductive Method to allow and agent to arbitrarily lose a secret to the attacker, without any particular precondition. The socio-technical understanding of cybersecurity and privacy is a very hot area today, grounding non-functional properties not only on technical systems such as security protocols but also on the use that humans may make of them. I believe that the
 event is the unique ancestor of all recent works in this area.
event is the unique ancestor of all recent works in this area.
The problem treated in this paper was how to transmit the above messages to post-graduate students with an embodied preconception that they do not like theory. While it may be obvious that the contents must be taught gently and incrementally, what I find less obvious is to convince them that they already somewhat used formal methods although they did not use to call them so.
Another far from obvious finding I distilled over the years towards teaching this discipline is the critical review, brought through the creases of my decalogue, of some useful notions they may already have. For example, induction, or just its basics, must be understood profoundly. And the essence of functional programming must be leveraged for the students’ proof experience to near their embodied imperative programming experience. I myself insisted on teaching them.
References
Parnas, D.L.: Really rethinking ‘formal methods’. Computer 43, 28–34 (2010)
Schaffer, K.B., Voas, J.M.: Whatever happened to formal methods for security? Computer 49, 70 (2016)
Chong, S., et al.: Report on the NSF workshop on formal methods for security (2016)
Paulson, L.C.: The inductive approach to verifying cryptographic protocols. IOS J. Comput. Secur. 6, 85–128 (1998)
Bella, G.: Formal Correctness of Security Protocols. Information Security and Cryptography. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-68136-6
Wenzel, M.: The Isabelle/Isar reference manual (2011). http://isabelle.in.tum.de/doc/isar-ref.pdf
MISC: Formal Methods (2019). https://www.freetechbooks.com/formal-methods-f28.html
Boyd, C., Mathuria, A.: Protocols for Authentication and Key Establishment. Information Security and Cryptography. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-662-09527-0
Paulson, L.C.: Inductive analysis of the internet protocol TLS. ACM Trans. Comput. Syst. Secur. 2, 332–351 (1999)
Bella, G.: Inductive study of confidentiality, for everyone. Form. Asp. Comput. 26, 3–36 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Bella, G. (2019). You Already Used Formal Methods but Did Not Know It. In: Dongol, B., Petre, L., Smith, G. (eds) Formal Methods Teaching. FMTea 2019. Lecture Notes in Computer Science(), vol 11758. Springer, Cham. https://doi.org/10.1007/978-3-030-32441-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-32441-4_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32440-7
Online ISBN: 978-3-030-32441-4
eBook Packages: Computer ScienceComputer Science (R0)






 , the formal model for our example protocol
, the formal model for our example protocol

 calls the simplifier, namely the tool that applies term rewriting meaningfully; for example, to operate the rewriting just discussed (Sect.
calls the simplifier, namely the tool that applies term rewriting meaningfully; for example, to operate the rewriting just discussed (Sect. 
 performs the obvious steps of a proof, such as applying the theorem that deduces both p and q from
performs the obvious steps of a proof, such as applying the theorem that deduces both p and q from  launches the classical reasoner, and the analyst may easily state extra available lemmas for the reasoner to invoke;
launches the classical reasoner, and the analyst may easily state extra available lemmas for the reasoner to invoke;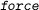 combines the simplifier with the classical reasoner;
combines the simplifier with the classical reasoner; is similar to
is similar to
 but, contrarily to all other methods, applies to the entire proof state, namely to all subgoals to prove.
but, contrarily to all other methods, applies to the entire proof state, namely to all subgoals to prove.
