Abstract
Many tasks often regarded as requiring some form of intelligence to perform can be seen as instances of query answering over a semantically rich knowledge base. In this context, two of the main problems that arise are: (i) uncertainty, including both inherent uncertainty (such as events involving the weather) and uncertainty arising from lack of sufficient knowledge; and (ii) inconsistency, which involves dealing with conflicting knowledge. These unavoidable characteristics of real world knowledge often yield complex models of reasoning; assuming these models are mostly used by humans as decision-support systems, meaningful explainability of their results is a critical feature. These lecture notes are divided into two parts, one for each of these basic issues. In Part 1, we present basic probabilistic graphical models and discuss how they can be incorporated into powerful ontological languages; in Part 2, we discuss both classical inconsistency-tolerant semantics for ontological query answering based on the concept of repair and other semantics that aim towards more flexible yet principled ways to handle inconsistency. Finally, in both parts we ponder the issue of deriving different kinds of explanations that can be attached to query results.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
In this article, we address query answering under two different, though related, approaches to uncertainty: probabilistic reasoning, and inconsistency-tolerant reasoning—as we will see, incompleteness is another dimension to uncertainty that can be addressed by leveraging the power of ontology languages, which are at the core of the material that we aim to cover. We focus on Datalog+/– [17], a family of ontological languages that was born from the database theory community extending the well-known formalism of Datalog. This family is closely related to Description Logics (DLs); cf. Fig. 1 for a mapping of some of the basic constructs in description logics to Datalog+/– formulas—note that this is meant only to illustrate the general relationship between the two formalisms, and that there are constructs on either side that cannot be expressed in the other, such as number restrictions and disjunctions in Datalog+/– and predicates of arity greater than two in DLs.
We first put these notes into context by briefly presenting some historical details and basic aspects of explanations in AI. Then, in Sect. 2 we provide a brief introduction to Datalog+/–, the family of ontology languages that we use in the rest of the text. Sections 3 and 4 then describe the two main parts: probabilistic and inconsistency-tolerant reasoning, respectively; in each case, we conclude the section by exploring current capabilities and next steps that can be taken towards making these formalisms explainable. Finally, in Sect. 5 we provide a summary and discuss a roadmap for future work in these directions.
Context: A Brief Discussion about Explanations in AI
In order to put this material into context, we would like to briefly discuss the history surrounding one of the main topics of these notes. The meaning of explanation, and the related notions of explainability and interpretability, has been studied for quite some time in philosophy and related disciplines in the social sciences (cf. the recent work of [40] for a survey of these aspects). Essentially, this topic is of interest to these disciplines because explanations are usually meant to be consumed by humans—for instance, a (human) user would like to know why a certain weather forecast is likely to be true or, more importantly, why they are being denied a loan at the bank. In computer science, explanations were a core aspect of the expert systems that were developed over four decades ago [46, 53]; ever since those foundational works, logic-based formalisms have often highlighted explainability as one of the strong points of developing AI in such a manner, contrasting with the fact that machine learning (ML) methods may in some cases perform very well but are incapable of offering users a satisfactory explanation. Structured argumentation is a good example,Footnote 1 in which dialectical trees are produced as part of the reasoning mechanism and can be examined by a user in order to gain insights into how conclusions are reached [25, 26]; the work of [24] also explores how belief revision operators can be designed using argumentation-based comparisons of alternatives, which can also be offered as explanations. As a response to this—and the success of many ML-based approaches on concrete problems—in recent years, there has been a strong resurgence of research into how AI (mostly ML) tools can be made to be explainable; the term “XAI” (for explainable artificial intelligence) was thus born. This recent explosion in popularity has already led to interesting developments; in the context of reasoning under uncertainty (of particular interest here), the notion of balanced explanation—giving reasons both why and why not a given answer may be correct—is especially useful [30]. We refer the interested reader to [1, 40, 44] for some recent surveys developed from different points of view.
From this brief analysis we can conclude that there are many aspects that need to be further studied in order to arrive at adequate solutions to the problem of deriving explanations. On the one hand, logic-based models have a strong foundation that allows them to be better poised to offer explanations, but not much research has gone in to designing explanations that can be of use to actual users. On the other hand, ML-based solutions typically can be made to perform quite well on certain tasks, but there inner workings are more obscure. In these notes, we will thus focus on taking some first steps towards explaining the results given by two approaches to reasoning under uncertainty—we cannot hope to solve such a formidable family of problems completely just yet.
2 The Datalog+/– Family of Ontology Languages
We now present the basics of Datalog+/– [17]—relational databases, (Boolean) conjunctive queries, tuple- and equality-generating dependencies and negative constraints, the chase, and ontologies. The material presented in this section is mainly based on [47], which in turn contains some material originally appearing in [48].
2.1 Preliminary Concepts and Notations
Let us consider (i) an infinite universe of (data) constants \(\varDelta \), which constitute the “normal” domain of a database), (ii) an infinite set of (labelled) nulls \(\varDelta _N\) (used as “fresh” Skolem terms, which are placeholders for unknown values, and can thus be seen as a special kind of variable), and (iii) an infinite set of variables \(\mathcal {V}\) (used in queries, dependencies, and constraints). Different constants represent different values (this is generally known as the unique name assumption), while different nulls may represent the same value. We assume a lexicographic order on \(\varDelta \cup \varDelta _N\), with every symbol in \(\varDelta _N\) following all symbols in \(\varDelta \). We denote with \(\mathbf {X}\) sequences of variables \(X_1,\ldots ,X_{k}\) with \(k\,{\geqslant }\,0\).
We will assume a relational schema \(\mathcal{R}\), which is a finite set of predicate symbols (or simply predicates), each with an associated arity. As usual, a term t is a constant, null, or variable. An atomic formula (or atom) \(a\) has the form \(p(t_1,\ldots ,t_n)\), where p is an n-ary predicate, and \(t_1,\ldots ,t_n\) are terms. A term or atom is ground if it contains no nulls and no variables. An instance I for a relational schema \(\mathcal {R}\) is a (possibly infinite) set of atoms with predicates from \(\mathcal {R}\) and arguments from \(\varDelta \cup \varDelta _N\). A database is a finite instance that contains only constants (i.e., its arguments are from \(\varDelta \)).
Homomorphisms. Central to the semantics of Datalog+/– is the notion of homomorphism between relational structures. Let \(A = \langle X, \sigma ^A \rangle \) and \(B = \langle Y, \sigma ^B \rangle \) be two relational structures, where \(\textit{dom}(A) = X\) and \(\textit{dom}(B) = Y\) are the domains of A and B, and \(\sigma ^A\) and \(\sigma ^B\) are their signatures (which are composed of relations and functions), respectively. A homomorphism from A to B is a function \(h: \textit{dom}(A) \rightarrow \textit{dom}(B)\) that “preserves structure” in the following sense:
-
For each n-ary function \(f^A \in \sigma ^A\) and elements \(x_1, ..., x_n \in \textit{dom}(A)\), we have:
$$ h\big (f^A(x_1,...,x_n)\big ) = f^B\big (h(x_1),...,h(x_n)\big ), $$and
-
for each n-ary relation \(R^A \in \sigma ^A\) and elements \(x_1, ..., x_n \in \textit{dom}(A)\), we have:
$$ \text {if } (x_1,...,x_n) \in R^A \text {, then } \big (h(x_1),...,h(x_n)\big ) \in R^B. $$
In the above statements, the superscripts used in function and relation symbols is simply a clarification of the structure in which they are being applied. Since we do not have function symbols, the first condition will not be necessary here (it is satisfied vacuously).Footnote 2
For the purposes of Datalog+/–, we need to extend the concept of homomorphism to contemplate nulls. We then define homomorphisms from a set of atoms \(A_1\) to a set of atoms \(A_2\) as mappings \(h:\varDelta \cup \varDelta _N\cup \mathcal {V}\rightarrow \varDelta \cup \varDelta _N\cup \mathcal {V}\) such that:
-
1.
\(c \in \varDelta \) implies \(h(c)=c\),
-
2.
\(c \in \varDelta _N\) implies \(h(c) \in \varDelta \cup \varDelta _N\),
-
2.
\(r(t_1,\ldots ,t_{n})\in A_1\) implies \(h(r(t_1,\ldots ,t_{n}))=r(h(t_1), \ldots , h(t_n)))\in A_2\).
Similarly, one can extend h to a conjunction of atoms. Conjunctions of atoms are often identified with the sets of their atoms.
2.2 Syntax and Semantics of Datalog+/–
Given a relational schema \(\mathcal {R}\), a Datalog+/– program consists of a finite set of tuple-generating dependencies (TGDs), negative constraints (NCs), and equality-generating dependencies (EGDs).
TGDs. A tuple-generating dependency (TGD) \(\sigma \) is a first-order (FO) rule that allows existentially quantified conjunctions of atoms in rule heads:
where \(\varPhi (\mathbf {X},\mathbf {Y})\) and \(\varPsi (\mathbf {X},\mathbf {Z})\) are conjunctions of atoms. Formulas \(\varPhi \) and \(\varPsi \) are often referred to as the body and head of \(\sigma \), respectively. By analyzing the general form of TGDs, one can see that variables in \(\mathbf {X}\) and \(\mathbf {Y}\) refer to objects that are already known, while those in \(\mathbf {Z}\) correspond to the result of so-called value invention. For instance, in the TGD \(\textit{person}(X) \rightarrow \exists Y \ \textit{person}(Y) \wedge \textit{father}(Y,X)\), variable Y refers to a new object that is a person who is the father of X.
Since TGDs with multiple atoms in the head can be converted into sets of TGDs with only single atom in the head [14], from now on we assume that all sets of TGDs have only a single atom in their head. An instance I for \(\mathcal {R}\) satisfies \(\sigma \), denoted  , if whenever there exists a homomorphism h that maps the atoms of \(\varPhi (\mathbf {X},\mathbf {Y})\) to atoms of I, there exists an extension \(h'\) of h that maps \(\varPsi (\mathbf {X},\mathbf {Z})\) to atoms of I.
, if whenever there exists a homomorphism h that maps the atoms of \(\varPhi (\mathbf {X},\mathbf {Y})\) to atoms of I, there exists an extension \(h'\) of h that maps \(\varPsi (\mathbf {X},\mathbf {Z})\) to atoms of I.
NCs. A negative constraint (NC) \(\nu \) is a first-order rule that allows to express negation:
where \(\varPhi (\mathbf {X})\) a conjunction of atoms; formula \(\varPhi \) is usually referred to as the body of \(\nu \). An instance I for \(\mathcal {R}\) satisfies \(\nu \), denoted  , if for each homomorphism h, \(h(\varPhi (\mathbf {X},\mathbf {Y}))\not \subseteq I\) holds.
, if for each homomorphism h, \(h(\varPhi (\mathbf {X},\mathbf {Y}))\not \subseteq I\) holds.
EGDs. An equality-generating dependency (EGD) \(\mu \) is a first-order rule of the form:
where \(\varPhi (\mathbf {X})\) is conjunction of atoms; as above, formula \(\varPhi \) is usually referred to as the body of \(\mu \). An instance I for \(\mathcal {R}\) satisfies \(\mu \), denoted  , if whenever there is a homomorphism h such that \(h(\varPhi (\mathbf {X},\mathbf {Y}))\,{\subseteq }\,I\), it holds that \(h(X_i){\,{=}\,}h(X_j)\).
, if whenever there is a homomorphism h such that \(h(\varPhi (\mathbf {X},\mathbf {Y}))\,{\subseteq }\,I\), it holds that \(h(X_i){\,{=}\,}h(X_j)\).
In the following, we will sometimes omit the universal quantification in front of TGDs, NCs, and EGDs, and assume that all variables appearing in their bodies are universally quantified. We will sometimes use the words constraints and dependencies to refer to NCs and EGDs.
Programs and Ontologies. A Datalog+/– program \(\varSigma \) is a finite set \(\varSigma _T\, \cup \, \varSigma _{\textit{NC}}\,\cup \, \varSigma _{\textit{E}}\) of TGDs, NCs, and EGDs. The schema of \(\varSigma \), denoted \(\mathcal {R}(\varSigma )\), is the set of predicates occurring in \(\varSigma \). A Datalog+/– ontology \( K\!B {\,{=}\,}(D,\) \(\varSigma )\) consists of a finite database D and a Datalog+/– program \(\varSigma \). The following example illustrates a simple Datalog+/– ontology, used in the sequel as a running example.
Example 1
Consider the ontology \( K\!B = (D, \varSigma )\), where D and \(\varSigma = \varSigma _T \cup \varSigma _E\) are defined as follows:

This ontology models a very simple knowledge base for restaurants—it could be used, for instance, as the underlying model in an online recommendation and reviewing system (e.g., in the style of TripAdvisor or Yelp). \(\blacksquare \)
Models. The conjunction of the first-order sentences associated with the rules of a Datalog+/– program \(\varSigma \) is denoted \(\varSigma _P\). A model of \(\varSigma \) is an instance for \(\mathcal {R}(\varSigma )\) that satisfies \(\varSigma _p\). For a database D for \(\mathcal {R}\), and a set of TGDs \(\varSigma \) on \(\mathcal {R}\), the set of models of D and \(\varSigma \), denoted \( mods (D,\varSigma )\), is the set of all (possibly infinite) instances I such that:
-
1.
\(D\subseteq I\), and
-
2.
every \(\sigma \,{\in }\,\varSigma \) is satisfied in I (i.e.,
 ).
).
The ontology is consistent if the set \( mods (D,\varSigma )\) is not empty.
The semantics of \(\varSigma \) on an input database D, denoted \(\varSigma (D)\), is a model I of D and \(\varSigma \) such that for every model \(I'\) of D and \(\varSigma \) there exists a homomorphism h such that \(h(I) \subseteq I'\); such an instance is called universal model of \(\varSigma \) w.r.t. D. Intuitively, a universal model contains no more and no less information than what the given program requires.
In general, there exists more than one universal model of \(\varSigma \) w.r.t. D, but the universal models are (by definition) the same up to homomorphic equivalence, i.e., for each pair of universal models \(M_1\) and \(M_2\), there exist homomorphisms \(h_1\) and \(h_2\) such that \(h_1(M_1)\subseteq M_2\) and \(h_2(M_2) \subseteq M_1\). Thus, \(\varSigma (D)\) is unique up to homomorphic equivalence.
2.3 Conjunctive Query Answering
We now introduce conjunctive query answering for Datalog+/–. A conjunctive query (CQ) over \(\mathcal {R}\) has the form:
where \(\varPhi (\mathbf {X},\mathbf {Y})\) is a conjunction of atoms (consisting also possibly of equalities, but not inequalities) involving variables in \(\mathbf {X}\) and \(\mathbf {Y}\), and possibly constants, but without nulls, and q is a predicate not occurring in \(\mathcal {R}\). A Boolean CQ (BCQ) over \(\mathcal {R}\) is a CQ of the form q(), often written as the set of all its atoms, without quantifiers. As mentioned above for the basic components of the language, formulas q and \(\varPhi \) are sometimes referred to as the head and body of the query, respectively.
The set of answers to a CQ \(q(\mathbf {X})\,{=}\,\exists \mathbf {Y}\,\varPhi (\mathbf {X},\mathbf {Y})\) over an instance I, denoted q(I), is the set of all tuples \(t\) over \(\varDelta \), for which there exists a homomorphism \(h:\mathbf {X}\,{\cup }\,\mathbf {Y}\,{\rightarrow }\,\varDelta \cup \varDelta _N\) such that \(h(\varPhi (\mathbf {X},\mathbf {Y}))\,{\subseteq }\,I\) and \(h(\mathbf {X}){\,{=}\,}t\). The answer to a BCQ q() over a database instance I is Yes, denoted  , if \(q(I)\,{\ne }\,\emptyset \).
, if \(q(I)\,{\ne }\,\emptyset \).
Formally, query answering under TGDs, i.e., the evaluation of CQs and BCQs on databases under a set of TGDs is defined as follows. The set of answers to a CQ q over a database D and a set of TGDs \(\varSigma \), denoted \( ans (q,D,\varSigma )\), is the set of all tuples \(t\) such that \(t \in q(I)\) for all \(I \,{\in }\, mods (D,\varSigma )\). The answer to a BCQ q over D and \(\varSigma \) is Yes, denoted  , if \( ans (q,D,\varSigma )\,{\ne }\,\emptyset \). Note that for query answering, homomorphically equivalent instances are indistinguishable, i.e., given two instances I and \(I'\) that are the same up to homomorphic equivalence, q(I) and \(q(I'\)) coincide. Therefore, queries can be evaluated on any universal model.
, if \( ans (q,D,\varSigma )\,{\ne }\,\emptyset \). Note that for query answering, homomorphically equivalent instances are indistinguishable, i.e., given two instances I and \(I'\) that are the same up to homomorphic equivalence, q(I) and \(q(I'\)) coincide. Therefore, queries can be evaluated on any universal model.
The decision problem of CQ answering is defined as follows: given a database D, a set \(\varSigma \) of TGDs, a CQ q, and a tuple of constants \(t\), decide whether \(t \in ans (q,D,\varSigma )\).
For query answering of BCQs in Datalog+/– with TGDs, adding negative constraints is computationally easy, as for each constraint \(\forall \mathbf {X} \varPhi (\mathbf {X}) \,{\rightarrow }\, \bot \) one only has to check that the BCQ \(\exists \mathbf {X}\,\varPhi (\mathbf {X})\) evaluates to false in D under \(\varSigma \); if one of these checks fails, then the answer to the original BCQ q is true, otherwise the constraints can simply be ignored when answering the BCQ q.
Adding EGDs over databases with TGDs along with negative constraints does not increase the complexity of BCQ query answering as long as they are non-conflicting [17]. Intuitively, this ensures that, if the chase (described next) fails (due to strong violations of EGDs), then it already fails on the database, and if it does not fail, then whenever “new” atoms are created in the chase by the application of the EGD chase rule, atoms that are logically equivalent to the new ones are guaranteed to be generated also in the absence of the EGDs, guaranteeing that EGDs do not influence the chase with respect to query answering. Therefore, from now on, we assume that all the fragments of Datalog+/– have non-conflicting rules.
There are two main ways of processing rules to answer queries: forward chaining (the chase) and backward chaining, which uses the rules to rewrite the query in different ways with the aim of producing a query that directly maps to the facts. The key operation is the unification between part of a current goal (a conjunctive query or a fact) and part of a rule. Here, we will only cover the chase procedure, which is described next.
The TGD Chase. Query answering under general TGDs is undecidable [9] and the chase is used as a procedure to do query answering for Datalog+/–. Given a program \(\varSigma \) with only TGDs (see [17] for further details and for an extended chase with also EGDs), \(\varSigma (D)\) can be defined as the least fixpoint of a monotonic operator (modulo homomorphic equivalence). This can be achieved by exploiting the chase procedure, originally introduced for checking implication of dependencies, and for checking query containment [28]. Roughly speaking, it executes the rules of \(\varSigma \) starting from D in a forward chaining manner by inferring new atoms, and inventing new null values whenever an existential quantifier needs to be satisfied. By “chase”, we refer both to the procedure and to its output.
Let D be a database and \(\sigma \) a TGD of the form \(\varPhi (\mathbf {X},\mathbf {Y}) \rightarrow \exists {\mathbf {Z}}\, \varPsi (\mathbf {X},\) \(\mathbf {Z})\). Then, \(\sigma \) is applicable to D if there exists a homomorphism h that maps the atoms of \(\varPhi (\mathbf {X},\mathbf {Y})\) to atoms of D. Let \(\sigma \) be applicable to D, and \(h_1\) be a homomorphism that extends h as follows: for each \(Z_j\in \mathbf {Z}\), \(h_1(Z_j)=z_j\), where \(z_j\) is a “fresh” null, i.e., \(z_j\in \varDelta _N\), \(z_j\) does not occur in D, and \(z_j\) lexicographically follows all other nulls already introduced. The application of \(\sigma \) on D adds to D the atom \(h_1(\varPsi (\mathbf {X},\mathbf {Z}))\) if not already in D. The chase rule described above is also called oblivious.
The chase algorithm for a database D and a set of TGDs \(\varSigma \) consists of an exhaustive application of the TGD chase rule in a breadth-first (level-saturating) fashion, which outputs a (possibly infinite) chase for D and \(\varSigma \).
Formally, the chase of level up to 0 of D relative to \(\varSigma \), denoted \(\textit{chase}^0(D,\varSigma )\), is defined as D, assigning to every atom in D the (derivation) level 0. For every \(k\,{\geqslant }\,1\), the chase of level up to k of D relative to \(\varSigma \), denoted \(\textit{chase}^k(D,\varSigma )\), is constructed as follows: let \(I_1,\ldots ,I_{n}\) be all possible images of bodies of TGDs in \(\varSigma \) relative to some homomorphism such that (i) \(I_1,\ldots ,I_{n}\,{\subseteq }\,\textit{chase}^{k-1}(D,\varSigma )\) and (ii) the highest level of an atom in every \(I_i\) is \(k-1\); then, perform every corresponding TGD application on \(\textit{chase}^{k-1}(D,\varSigma )\), choosing the applied TGDs and homomorphisms in a (fixed) linear and lexicographic order, respectively, and assigning to every new atom the (derivation) level k. The chase of D relative to \(\varSigma \), denoted \( chase (D,\varSigma )\), is defined as the limit of \(\textit{chase}^k(D,\varSigma )\) for \(k\,{\rightarrow }\,\infty \). This, possibly infinite chase, is a universal model of D and \(\varSigma \), i.e., there is a homomorphism from \( chase (D,\varSigma )\) onto every \(B \,{\in }\, mods (D,\varSigma )\) [17]—Fig. 2 provides an illustration. Thus, BCQs q over D and \(\varSigma \) can be evaluated on the chase for D and \(\varSigma \), i.e.,  is equivalent to
is equivalent to  . We will assume that the nulls introduced in the chase are named via Skolemization—this has the advantage of making the chase unique; \(\varDelta _N\) is therefore the set of all possible nulls that may be introduced in the chase.
. We will assume that the nulls introduced in the chase are named via Skolemization—this has the advantage of making the chase unique; \(\varDelta _N\) is therefore the set of all possible nulls that may be introduced in the chase.
The chase for the ontology in Example 1. The atoms in boxes with thicker border are part of the database, while those with dotted lines correspond to atoms with null values (denoted with \(z_i\)). The arrows point to the mapping of \(z_5\) to the constant “buenosAires” during the chase procedure.
Example 2
Figure 3 shows the application of the chase procedure over the Datalog+/– ontology from Example 1. As an example, the TGD \(r_1\) is applicable in D, since there is a mapping from atoms \(\textit{restaurant}(\textit{laCabrera})\) and \(\textit{restaurant}(\textit{laTartine})\) to the body of the rule. The application of \(r_1\) generates atoms \(\textit{business}(\textit{laCabrera})\) and \(\textit{business}(\textit{laTartine})\).
Consider the following BCQ:
asking if there exists a location for restaurant \(\textit{laTartine}\). The answer is Yes; in the chase, we can see that after applying TGDs \(r_1\) and \(r_4\), we obtain the atom \(\textit{locatedIn}(\textit{laTartine},z_6)\), where \(z_6\) is a null—we would also obtain the same answer, if we ask for restaurant \(\textit{laCabrera}\), because atom \(\textit{locatedIn}(\textit{laCabrera},z_5)\) is also produced.
Now, consider the CQ:
in this case, we only obtain one answer, namely \((\textit{laCabrera}, \textit{buenosAires})\), since null \(z_5\) eventually maps to \(\textit{buenosAires}\). In the case of \(\textit{laTartine}\), we do not obtain an answer corresponding to the city where it is located: we know there exists a city, but we cannot say which one it is; in every model of \( K\!B \), \(z_6\) may take a different value from the domain. This can be seen in the chase (a universal model of \( K\!B \)), since \(z_6\) does not unify with a constant after “chasing” D with \(\varSigma \). \(\blacksquare \)
Computational Complexity. The following complexity measures, partially proposed by Vardi [49], are commonly adopted in the literature:
-
The combined complexity of CQ answering is calculated by considering all the components—the database, the set of dependencies, and the query—as part of the input.
-
The bounded-arity combined complexity (or ba-combined complexity) is calculated by assuming that the arity of the underlying schema is bounded by an integer constant. In the context of DLs, the combined complexity is equivalent to the \( ba \)-combined complexity, since the arity of the underlying schema is at most two. In practical applications, the schema is usually small, and it can safely be assumed to be fixed—therefore, in this case the arity is also fixed.
-
The fixed-program combined complexity (or fp-combined complexity) is calculated by considering the set of constraints to be fixed.
-
The data complexity is calculated by taking only the database as input.
Some key facts about complexity and decidability of query answering with TGDs: (i) under general TGDs, the problem is undecidable [9], even when the query and set of dependencies are fixed [14]; (ii) the two problems of CQ and BCQ evaluation under TGDs are logspace-equivalent [13]; and (iii) the query output tuple (QOT) problem (as a decision version of CQ evaluation that asks if a tuple belongs to the output) and BCQ evaluation are AC\(_0\)-reducible to each other. Given the last two points, we focus only on BCQ evaluation, and any complexity results carry over to the other problems.
2.4 Datalog+/– Fragments: In Search of Decidability and Tractability
We now briefly discuss different restrictions that are designed to ensure decidability and tractability of conjunctive query answering with TGDs. While the addition of existential quantifiers in the heads of rules accounts for the “+” in Datalog+/–, these restrictions account for the “–”.
Generally, restrictions can be classified into either abstract (semantic) or concrete (syntactic) properties. Three abstract properties are considered in [6]: (i) the chase is finite, yielding finite expansion sets (\(\textsf {fes}\)); (ii) the chase may not halt but the facts generated have a tree-like structure, yielding bounded tree-width sets (\(\textsf {bts}\)); and (iii) a backward chaining mechanism halts in finite time, yielding finite unification sets (\(\textsf {fus}\)). Other abstract fragments are: (iv) parsimonious sets (\(\textsf {ps}\)) [33], where the main property for this class is that the chase can be precociously terminated, and (v) weakly-chase-sticky TGDs [39] that considers information about the finiteness of predicate positions (positions are infinite if there is an instance D for which an unlimited number of different values appear in that position during the chase).
The main conditions on TGDs that guarantee the decidability of CQ answering are: (i) guardedness [13, 15], (ii) stickiness [16], and (iii) acyclicity—each of these classes has a “weak” counterpart: weak guardedness [14], weak stickiness [16], and weak acyclicity [22, 23]. Finally, other classes that fall outside this main classification are Full TGDs (those that do not have existentially quantified variables), Tame TGDs [27] (a combination of the guardedness and sticky-join properties), and Shy TGDs [33] (the shyness property holds if during the chase procedure nulls do not meet each other to join but only to propagate—nulls thus propagate from a single atom).
We refer the reader to [48] and [47] for a more complete discussion of known classes, a summary of the currently known containment relations between classes, and summaries of known complexity results.
3 Query Answering over Probabilistic Knowledge Bases
We begin by addressing query answering under probabilistic uncertainty. In Sect. 3.1 we provide a very brief overview of some well-known probabilistic graphical models; Sect. 3.2 is devoted to presenting the basics of the probabilistic Datalog+/– model, and finally Sect. 3.3 outlines paths towards deriving explanations to query answers over this framework.
3.1 Brief Overview of Basic Probabilistic Graphical Models
In the spirit of making this document relatively self-contained, we now provide a quick introduction to a few basic probabilistic graphical models. Such models are essentially ways to specify joint probability distributions over a set of random variables, based on graph structures—they will come into play when defining the semantics of Probabilistic Datalog+/– (cf. Sect. 3.2).
For each of the models, we assume we have a (finite) set of random variables \(X = \{X_1, \dots , X_n\}\). Each random variable \(X_i\) may take on values from a finite domain \(\textit{Dom}(X_i)\). A value for \(X=\{X_1,\ldots {},X_n\}\) is a mapping \(x:X\rightarrow \bigcup _{i=1}^n \textit{Dom}(X_i)\) such that \(x(X_i)\in Dom (X_i)\); the domain of X, denoted \(\textit{Dom}(X)\), is the set of all values for X. We are generally interested in modeling the joint probability distribution over all values in \(x \in \textit{Dom}(X)\), which we denote \(\Pr (x)\). We thus have that \(0 \leqslant \Pr (x) \leqslant 1\) for all \(x \in \textit{Dom}(X)\), and \(\sum _{x\in X} \Pr _{x} = 1\).
Bayesian Networks. A Bayesian Network (BN, for short) is comprised of: (i) A directed acyclic graph in which each node corresponds to a single random variable in X (and vice versa). If there is an edge from \(X_i\) to \(X_j\), we say that \(X_i\) is a parent of \(X_j\)—this represents a direct dependence between the two variables. (ii) A conditional probability distribution \(\Pr (X_i | \textit{Parents}(X_i))\) for each node \(X_i\), also sometimes called a node probability table.
One of the advantages of the BN model is that the graph structure encodes the probabilistic dependence between variables. For instance, each variable is independent of its non-descendents if we are given values for its parents. Therefore, the probability for any value \(x = (x_1, ..., x_n) \in \textit{Dom}(X)\) can be computed as follows:
where \(\textit{par-val}(X_i)\) denotes the values of the variables in \(\textit{Parents}(X_i)\). Moreover, the absence of an edge between nodes represents conditional independence between the corresponding variables—the details of how such independence is characterized are non-trivial, and we refer the interested reader to the vast amount of material on BNs (cf. [41] for one of the earliest sources). Knowing the details behind variable (in)dependence is of great value if one is interested in tractable algorithms for computing probabilities, since the probability of the conjunction of independent variables is simply the product of their probabilities.
The most common problems (or probabilistic queries) associated with BNs are the following:
-
PE (Probability of evidence, also known as inference): Compute the probability of a group of variables having a specific value. This problem is \(\#\)P-complete.
-
MAP (Maximum A posteriori Probability): Given evidence e over variables \(E \subset X\), and variables \(Y \subseteq X - E\), compute the value of y of Y that maximizes \(\Pr (Y = y | E)\). This problem is NP\(^\text {PP}\)-complete in its decision version.
-
MPE (Most Probable Explanation): Given evidence, find the assignment of values to the rest of the variables that has the highest probability. This problem is NP-complete in its decision version.
Even though all of these problems are computationally intractable in general, there exist special cases for which they can be solved in polynomial time, either exactly or approximately.
Markov Random Fields. A Markov Random Field (MRF) [41] (sometimes also referred to as Markov Network) is a probabilistic model that is similar to a Bayesian network (BN) in that it includes a graph \(G = (V, E)\) in which each node corresponds to a variable, but, differently from a BN, the graph is undirected; in an MRF, two variables are connected by an edge in G iff they are conditionally dependent. Furthermore, the model contains a potential function \(\phi _i\) for each (maximal) clique in the graph; potential functions are non-negative real-valued functions of the values of the variables in each clique (called the state of the clique). Here, we assume the log-linear representation of MRFs, which involves defining a set of features of such states; a feature is a real-valued function of the state of a clique (we only consider binary features in this work). Given a value \(x \in \textit{Dom}(X)\) and a feature \(f_j\) for clique j, the probability distribution represented by an MRF can be computed as follows:
where j ranges over the set of cliques in the graph G, and \(w_j = \log \phi _j(x_{\{j\}})\) (here, \(x_{\{j\}}\) is the state of the j-th clique in x). The term Z is a normalization constant to ensure that the values given by the equation above are in [0, 1] and sum to 1; it is given by:
Probabilistic inference in MRFs is intractable (#P-complete); however, approximate inference mechanisms, such as Markov Chain Monte Carlo (discussed briefly below), have been developed and successfully applied to problems in practice.
Markov Logic. Markov Logic Networks (MLNs) [45], also sometimes referred to as Markov Logic, combine first-order logic with Markov Random Fields. The main idea behind MLNs is to provide a way to soften the constraints imposed by a set of classical logic formulas. Instead of considering possible worlds that violate some formulas to be impossible, we wish to make them less probable. An MLN is a finite set L of pairs \((F_i, w_i)\), where \(F_i\) is a formula in first-order logic, and \(w_i\) is a real number. Such a set L, along with a finite set of constants \(C = \{c_1, \dots , c_m\}\), defines a Markov network \(M_{L,C}\) that contains: (i) one binary node corresponding to each element of the Herbrand base of the formulas in L (i.e., all possible ground instances of the atoms), where the node’s value is 1 iff the atom is true; and (ii) one feature for every possible ground instance of a formula in L. The value of the feature is 1 iff the ground formula is true, and the weight of the feature is the weight corresponding to the formula in L. From this characterization and the description above of the graph corresponding to an MN, it follows that \(M_{L,C}\) has an edge between any two nodes corresponding to ground atoms that appear together in at least one formula in L. Furthermore, the probability of \(x \in Dom (X)\) in \(M_{L,C}\) and thus in the MLN is defined by \(P(X = x) = \frac{1}{Z} \exp (\sum _j w_j \cdot n_j(x))\), where \(n_j(x)\) is the number of ground instances of \(F_j\) made true by x, and Z is defined analogously as above. This formula can be used in a generalized manner to compute the probability of any setting of a subset of random variables \(X'\subseteq X\), as we show below.
Example 3
Consider the following simple MLN:
\(\psi _1\): \((p(X) \Rightarrow q(X), 0.5)\),
\(\psi _2\): \((p(X) \Rightarrow r(X), 2)\),
\(\psi _3\): \((s(X) \Rightarrow r(X), 4)\).
Suppose we have s single constant a; grounding the formulas above relative to set of constants \(\{a\}\), we obtain the set of ground atoms
Similarly, if we had two constants, a and b, we would get:
The graphical representation of the MRFs corresponding to these groundings are shown in Fig. 4.
Consider the former (with respect to a single constant). This MRF represents a probability distribution over the possible Boolean values for each node. Given that there are four ground atoms, there are \(2^4 = 16\) possible settings of the variables in the MRF; Fig. 5 shows all such possible settings, along with other information used to compute probabilities. The normalizing factor Z is the sum of the probabilities of all worlds, which is computed as shown above by summing the exponentiated sum of weights times the number of ground formulas satisfied (equivalent to summing e to the power of each number in the “potential” column in Fig. 5), yielding \(Z \approx 5593.0623\). Similarly, the probability that a formula, such as \(p(a) \wedge q(a) \wedge \lnot s(a)\), holds is the sum of the probabilities that all the satisfying worlds hold, which in this case corresponds to the worlds 13 and 15 (cf. Fig. 5); the resulting probability is \(\frac{e^{4.5} + e^{0.5}}{5593.0623} \approx 0.0265\). \(\blacksquare \)
The graphical representation of the MRF for the MLN from Example 3 (instantiated with set of constants \(\{a,b\}\)). There is one Boolean random variable for each ground atom in the grounding of the formulas \(\psi _1\), \(\psi _2\), and \(\psi _3\) with respect to the set of constants. The dotted lines show the different cliques in the graph.
Details of how to compute potentials for each possible setting of the random variables (worlds) of the MRF for the MLN from Example 3 (grounded with a single constant).
Markov Chains. Lastly, we wish to briefly mention a somewhat different model that is geared towards dynamically evolving systems. A Markov Chain (MC, for short), is a stochastic process \(\{X_n\}\), with \(n \in \mathbb {N} \cup \{0\}\)—essentially, an MC is a sequence of states, or values of variables. The Markov property holds if it is always the case that given \(n \in \mathbb {N} \cup \{0\}\) and states \(x_0, x_1, ..., x_n, x_{n+1}\), we have:
That is, the distribution of conditional probability of future states only depends on the current state; this property is also sometimes referred to as memoryless.
MCs can be represented as sequences of graphs where the edges of graph n are labeled with the probability of going from one state at moment n to other states at moment \(n+1\):
The same information can be represented via a transition matrix M where
Taking the power of this matrix with itself iteratively, we can answer queries regarding the probability that the system will be in a certain state after several time steps. One of the most important classes of MCs are the ones for which a stationary distribution exists—one that is invariant over time—since they represent stable stochastic processes.
One of the most important applications of MCs is as the basis of the Markov Chain Monte Carlo (MCMC) family of algorithms, which are random walk-based traversals of the state space that can be used to sample from an unknown probability distribution, thus arriving at approximations of the distribution itself or of queries of interest.
Brief Comparison Among Models. As a quick comparison of the strengths and weaknesses of the four models that we introduced above, we can point out a few salient aspects:
-
Bayesian Networks are useful when identified dependencies are acyclic, and information is available regarding conditional dependencies (i.e., the structure of the graph, plus the probability tables).
-
Markov Random Fields are more flexible in that they allow cycles and probabilities are derived from weights. The disadvantage associated with the latter is that the relationship between weights and probabilities is not always clear.
-
Markov Logic Networks are essentially first order templates for MRFs; their main strength with respect to them is that a model can be derived given a set of constants, which can change depending on the situation in which it is intended for.
-
One of the main applications of Markov Chains is as the basis of Markov Chain Monte Carlo (MCMC) methods that can be used to approximate unknown distributions, or distributions that are specified by other models like Bayesian Networks or Markov Random Fields that are intractable to compute exactly, or dynamical systems for which a closed form solution may not be possible.
As we will see in the next section, these and other probabilistic models can be leveraged as part of extended logic-based languages in order to deal with uncertainty in a principled manner.
Learning Models from Data. There are many, many different approaches and algorithms available for automatically or semi-automatically deriving these and other probabilistic models from available data—even a cursory treatment is outside the scope of this work. We refer the reader to the vast literature on these topics that has been developing for many years; good starting points can be found at [8] and [50].
3.2 Probabilistic Datalog+/–
In this section, considering the basic setup from Sects. 2 and 3.1, we introduce the syntax and the semantics of probabilistic Datalog+/–.
Syntax
As in Sect. 2, we assume an infinite universe of (data) constants \(\varDelta \), an infinite set of labeled nulls \(\varDelta _N\), and an infinite set of variables \(\mathcal {V}\). Furthermore, as in Sect. 3.1, we assume a finite set of random variables X. Informally, a probabilistic Datalog+/– ontology consists of a finite set of probabilistic atoms, probabilistic TGDs, probabilistic negative constraints, and probabilistic separable EGDs, along with a probabilistic model that yields a full joint distribution over the values in \(\times _{i=1}^{|X|} \textit{dom}(X_i)\).
We first define probabilistic annotations and more specifically worlds. Intuitively, a probabilistic annotation \(\lambda \) is an assignment of values \(x_i\) to random variables \(X_i\), representing the event in the probabilistic model where the \(X_i\)’s have the value \(x_i\). In particular, a world assigns a value to each random variable. In general, we use true and false to refer to the values 1 and 0 of Boolean random variables, respectively; furthermore, to simplify notation, we use X and \(\lnot X\) to denote \(X = true \) and \(X = false \), respectively.
Definition 1
A (probabilistic) annotation \(\lambda \) is a (finite) set of expressions \(X_i {\,{=}\,}x_i \), where \(X_i\in X\), \(x_i \,{\in }\, Dom (X_i)\), and the \(X_i\)’s are pairwise distinct. If \(|\lambda | \,{=}\, |X|\), then \(\lambda \) is a world. We denote by \( worlds (M)\) the set of all worlds of a probabilistic model M.
We next attach probabilistic annotations \(\lambda \) to classical Datalog+/– formulas F to produce annotated formulas \(F:\lambda \). Intuitively, F holds whenever the event associated with \(\lambda \) occurs. Note that whenever a random variable’s value is left unspecified in a probabilistic annotation, the variable is unconstrained; in particular, a formula annotated with an empty probabilistic annotation means that the formula holds in every world. As we discuss in detail in Sect. 3.2, this kind of annotation works much in the same way as in many other probabilistic formalisms where possible worlds are induced via probabilistic distributions coming from outside the model; typical examples are the independent choice logic [42], P-LOG [7], and background variables in Bayesian networks (where probabilities come from exogenous events) [41].
Definition 2
If a is an atom, \(\sigma _T\) is a TGD, \(\sigma _{N\!C}\) is a negative constraint, \(\sigma _E\) is an EGD, and \(\lambda \) is a probabilistic annotation, then: (i) \(a:\lambda \) is a probabilistic atom; (ii) \(\sigma _T:\lambda \) is a probabilistic TGD; (iii) \(\sigma _{N\!C}:\lambda \) is a probabilistic (negative) constraint; and (iv) \(\sigma _E:\lambda \) is a probabilistic EGD. We also refer to probabilistic atoms, TGDs, (negative) constraints, and EGDs as annotated formulas. Annotated formulas of the form \(F:\{\}\) are abbreviated as F.
We are now ready to define the notion of a probabilistic Datalog+/– ontology.
Definition 3
A probabilistic Datalog+/– ontology is a pair \(\varPhi = (O, M)\), where O is a finite set of probabilistic atoms, TGDs, (negative) constraints, and EGDs, and M is a probabilistic model.
Loosely vs. Tightly Coupled Ontologies. There are two ways in which probabilistic annotations can be combined with formulas: in loosely coupled ontologies, annotations cannot refer to elements in the ontology (the scope of variables reaches only the ontology or the annotation). As can be seen in the results in [29], this is an advantage from the complexity point of view, since the cost of computing probabilities in the probabilistic model does not grow with the database; however, it also represents a limitation in expressive power of the formalism. On the other hand, in tightly coupled probabilistic Datalog+/– variables in annotations can be shared with those in Datalog+/– formulas; an early version of this idea can be found in [34], which develops the same concept for \(\mathcal {EL}^{++}\) ontologies.
The annotation of Datalog+/– formulas offers a clear modeling advantage by separating the two tasks of ontological modeling and of modeling the uncertainty around the axioms in the ontology. More precisely, in our formalism, it is possible to express the fact that the probabilistic nature of an ontological axiom is determined by elements that are outside of the domain modeled by the ontology. The probabilistic distribution of events (and existence of certain objects, for instance as part of a heuristic process) is a separate concern relative to the knowledge encoded in the “classical part” of the ontology.
In the rest of this section, we will resort to the following as a running example.
Example 4
Let the Datalog+/– ontology  be given by the database D, set of TGDs \(\varSigma _T\), set of EGDs \(\varSigma _E\), and set of (negative) constraints
be given by the database D, set of TGDs \(\varSigma _T\), set of EGDs \(\varSigma _E\), and set of (negative) constraints  :
:

Furthermore, consider the MLN M from Example 3. The annotated formulas in Fig. 6 are the result of annotating the formulas in the Datalog+/– ontology with expressions assigning true or false to a subset of the random variables that arise from the atoms described above: \(\{p(a), q(a), r(a), s(a)\}\). Recall that annotated formulas \(F:\{\}\) are abbreviated as F; they hold irrespective of the setting of the random variables. \(\blacksquare \)
As described next, worlds induce certain subontologies of a probabilistic Datalog+/– ontology, according to whether or not they satisfy the annotation of each formula.
Definition 4
Let \(\varPhi = (O, M)\) be a probabilistic \(Datalog{+}/{--}\ \) ontology and \(\lambda \) be a world. Then, the (non-probabilistic) \(Datalog{+}/{--}\ \) ontology induced from \(\varPhi \) by \(\lambda \), denoted \(O_\lambda \), is the set of all \(F_i\) such that \(\lambda _i \subseteq \lambda \) for some \(F_i:\lambda _i \in O\); any such \(F_i\) is relevant in \(\lambda \).
In the sequel, we consider only probabilistic Datalog+/– ontologies \(\varPhi = (O, M)\) in which the EGDs in every induced ontology \(O_\lambda \) are separable from the TGDs in \(O_\lambda \).
The probabilistic Datalog+/– ontology from Example 4.
The notion of decomposition of a probabilistic ontology provides a convenient way of referring to its constituent subontologies with respect to the worlds.
Definition 5
Let \(\varPhi = (O, M)\) be a probabilistic \(Datalog{+}/{--}\) ontology. Then, the decomposition (or decomposed form) of \(\varPhi \), denoted \( decomp (\varPhi )\), is defined as follows:
where \( worlds (M)=\{\lambda _1,\dots , \lambda _n\}\). To simplify notation, we assume that the worlds are ordered according to a lexicographical order of the values of the variables, and therefore the i-th ontology in a decomposition corresponds to the i-th world in this ordering.
Example 5
Consider the probabilistic Datalog+/– ontology \(\varPhi = (O, M)\), with \(O=(D,\varSigma )\), from Example 4. There are 16 worlds, so the decomposition of \(\varPhi \) has the form
For example, the world \(\lambda _{16}\) is determined by \(\{p(a),\) \(q(a), r(a), s(a)\}\), while \(\lambda _{14}\) is determined by \(\{p(a),q(a), \lnot \,r(a), s(a)\}\). It is then easy to see that \(O_{\lambda _{16}}\,{=}\,(\{\alpha _1\},\varSigma )\) and \(O_{\lambda _{14}}\,{=}\,(\{\alpha _1,\alpha _2\},\varSigma -\{\sigma _1\})\). \(\blacksquare \)
We now define the canonical composition, the inverse of the decomposition.
Definition 6
Let \(\varPsi = ( [ O_{\lambda _1}, \dots , O_{\lambda _n} ], M ) \) be a probabilistic \(Datalog{+}/{--}\) ontology in decomposed form. Then, the canonical composition of \(\varPsi \), denoted \( decomp ^{-1}(\varPsi )\), is the probabilistic \(Datalog{+}/{--}\) ontology \(\varPhi = (\bigcup _{i=1}^n \{F:\lambda _i\mid F \in O_{\lambda _i}\}, M)\).
Example 6
Let \(\varPhi _{ decomp } = ( [O_{\lambda _1}, \dots , O_{\lambda _{16}}], M )\) be the probabilistic ontology in decomposed form from Example 5. Although it is easy to verify that \( decomp ^{-1}(\varPhi _{ decomp })\) yields an ontology that is equivalent to \(\varPhi \) (from Example 4), this ontology actually contains several instances of the same formula, each with different annotations. For example, the atom \(\alpha _1\) appears four times, with the annotations \(\{p(a), q(a), \lnot r(a), \lnot s(a)\}\), \(\{p(a), q(a),\) \(\lnot r(a), s(a)\}\), \(\{p(a), q(a), r(a), \lnot s(a)\}\), and \(\{p(a), q(a), r(a), s(a)\}\), respectively. \(\blacksquare \)
Semantics
Towards the semantics of probabilistic Datalog+/– ontologies, we first define classical interpretations and the satisfaction of annotated formulas in such interpretations. The former consist of a database and a world in the probabilistic model, while the latter is done by interpreting \(F:\lambda \) as \(F\Leftarrow \hat{\lambda }\) (or equivalently \(F\vee \lnot \hat{\lambda }\)), where \(\hat{\lambda }=\bigwedge _{ X_i = x_i \in \lambda } X_i {\,{=}\,}x_i\).
Definition 7
A classical interpretation \(\mathcal {I}{\,{=}\,}( D, v )\) consists of a database D and a value \(v {\,{\in }\,}D(X)\). We say that \(\mathcal {I}\) satisfies an annotated formula \(F:\lambda \), denoted  , iff
, iff  whenever \(v(X_i) {\,{=}\,}x_i\) for all \( X_i {\,{=}\,}x_i \in \lambda \).
whenever \(v(X_i) {\,{=}\,}x_i\) for all \( X_i {\,{=}\,}x_i \in \lambda \).
We next define probabilistic interpretations \( Pr \) as finite probability distributions over classical interpretations, and the probability of formulas and their satisfaction in such \( Pr \), as usual. Here, formulas are either annotated formulas (including classical Datalog+/– formulas as a special case) or events in the probabilistic model (i.e., Boolean combinations of expressions \(X_i{\,{=}\,}x_i\), where \(X_i{\,{\in }\,}X\) and \(x_i{\,{\in }\,} Dom (X_i)\)). Furthermore, we define the satisfaction of probabilistic Datalog+/– ontologies in \( Pr \), where (i) all annotated formulas in the ontology are satisfied by \( Pr \), and (ii) the probabilities that \( Pr \) assigns to worlds coincide with those of the probabilistic model.
Definition 8
A probabilistic interpretation \( Pr \) is a probability distribution \( Pr \) over the set of all classical interpretations such that only a finite number of classical interpretations are mapped to a non-zero value. The probability of a formula \(\phi \), denoted \( Pr (\phi )\), is the sum of all \( Pr (\mathcal {I})\) such that  . We say that \( Pr \) satisfies (or is a model of) \(\phi \) iff \( Pr (\phi ) {\,{=}\,}1\). Furthermore, \( Pr \) is a model of a probabilistic Datalog+/– ontology \(\varPhi {\,{=}\,}(O, M)\) iff: (i)
. We say that \( Pr \) satisfies (or is a model of) \(\phi \) iff \( Pr (\phi ) {\,{=}\,}1\). Furthermore, \( Pr \) is a model of a probabilistic Datalog+/– ontology \(\varPhi {\,{=}\,}(O, M)\) iff: (i)  for all \(\phi {\,{\in }\,}O\), and (ii) \( Pr (\hat{\lambda }){\,{=}\,} Pr _M(\hat{\lambda })\) for all \(\lambda {\,{\in }\,} worlds (M)\), where \(\hat{\lambda }\) is defined as above, and \( Pr _M\) is the probability in the model M.
for all \(\phi {\,{\in }\,}O\), and (ii) \( Pr (\hat{\lambda }){\,{=}\,} Pr _M(\hat{\lambda })\) for all \(\lambda {\,{\in }\,} worlds (M)\), where \(\hat{\lambda }\) is defined as above, and \( Pr _M\) is the probability in the model M.
Here, we are especially interested in computing the probabilities associated with ground atoms in a probabilistic Datalog+/– ontology, as defined next. Intuitively, the probability of a ground atom is defined as the infimum of the probabilities of that ground atom under all probabilistic interpretations that satisfy the probabilistic ontology.
Definition 9
Let \(\varPhi \) be a probabilistic Datalog+/– ontology, and a be a ground atom constructed from predicates and constants in \(\varPhi \). The probability of a in \(\varPhi \), denoted \( Pr ^\varPhi (a)\), is the infimum of \( Pr (a)\) subject to all probabilistic interpretations \( Pr \) such that  .
.
Based on this notion, we can define several different kinds of probabilistic queries, as discussed next.
Queries to Probablistic Datalog+/– Ontologies
There are three kinds of queries that have been proposed in this model [29, 35]. We now present a brief introduction to each of them, assuming we are given a probabilistic Datalog+/– ontology \(\varPhi {\,{=}\,}(O, M)\).
-
Threshold queries ask for the set of all ground atoms that have a probability of at least p, where p is specified as an input of the query. So, the answers to threshold query \(Q = ( \varPhi , p )\) (with \(p {\,{\in }\,}[0,1]\)) is the set of all ground atoms a with \( Pr ^\varPhi (a) \geqslant p\).
-
Ranking queries request the ranking of atomic consequences based on their probability values. So, the answer to a ranking query \(Q = \textit{rank}( K\!B )\) is a tuple \( ans (Q) = \big \langle a_1, \ldots , a_n \big \rangle \) such that \(\{a_1, \ldots , a_n\}\) are all of the atomic consequences of \(O_\lambda \) for any \(\lambda \in Worlds (M)\), and \(i < j \Rightarrow Pr ^ K\!B (a_i) \geqslant Pr ^ K\!B (a_j)\).
-
Finally, probabilistic conjunctive queries are exactly as defined in Sect. 2, except that its answers are accompanied by the probability value with which it is entailed by \(\varPhi \).
The following example illustrates each of these queries using the running example.
Example 7
Consider the probabilistic Datalog+/– ontology \(\varPhi = (O, M)\) from Example 4, and the threshold query \(Q = ( \varPhi , 0.15 )\). As seen in Example 5, and referring back to Fig. 5 for the computation of the probabilities, we have that \( Pr ^\varPhi (a(x_1)) = \approx 0.191\) and \( Pr ^\varPhi (d(x_3)) = 0.135\). Therefore, the former belongs to the output, while the latter does not.
The answer to query \(\textit{rank}( K\!B )\) is: \(\langle a(x_1), c(x_1), d(x_3), b(x_2), d(x_2)\rangle \). Finally, the answer to probabilistic conjunctive query \(Q(X) = a(X) \wedge c(X)\) is \((x_1,0.191)\).
\(\blacksquare \)
3.3 Towards Explainable Probabilistic Ontological Reasoning
As we discussed above, probabilistic Datalog+/– is an extension of “classical” Datalog+/– with labels that refer to a probabilistic model—essentially, there are two sub-models that are in charge of representing knowledge about the domain, and these models can be either loosely or tightly coupled, depending on whether or not they share objects. So, the question we would like to pose now is “What constitutes an explanation for a query to a probabilistic Datalog+/– knowledge base?”. As discussed in Sect. 1, the answer to this question will depend heavily on whom the explanation is intended for, the application domain, the specific formalism being used, and the kind of query. Note that there is some initial work [18] on some variants of this problem as a generalization of MAP/MPE queries (which were developed as kinds of explanations for probabilistic models) for the special case of tuple-independent probabilistic databases.
Therefore, here we will focus on foundational aspects of designing explanations for probabilistic Datalog+/–; the discussion will generally apply to all queries presented on Page 20, unless stated otherwise. The basic building blocks of reasoning with probabilities in our formalism are the following:
-
The annotated chase structure: The extension of the chase, the main algorithm used to answer queries in classical Datalog+/–, in order to take into account probabilistic annotations is the annotated chase, a structure that essentially keeps track of the probabilistic annotations required for each step to be possible [29]. There two basic ways in which this can be done:
-
Annotate each node with a Boolean array of size \(| Worlds (M)|\); during the execution of the chase procedure, annotations are propagated as inferences are made. This is best for cases in which: (i) the number of worlds is not excessively large, since the space used by the chase structure will grow by a factor of \(| Worlds (M)|\); or (ii) when a sampling-based approach to approximate the probabilities associated with query answers is used, since in this case the size of each array can be reduced to (a function of) the number of samples. Another advantage of this approach is that for models under which querying the probability of a specific world is tractable (often referred to as tractable probabilistic models), the Boolean array representation can be used to clearly obtain either the exact or approximate probability mass associated with each node of interest.
-
Annotate each node with a logical formula expressing the conditions that must hold for the node to be inferrable. This approach is more compact than the array-based method, since the size of the formulas are bounded by the length of the derivation (at most the depth of the deepest spanning tree associated with the chase graph) and the length of the original annotations in the probabilistic ontology. On the other hand, extracting the specific worlds that make up the probabilistic mass associated with a given atom (or set of atoms for a query) is essentially equivalent to solving a #SAT problem; for tractable probabilistic models there is a greater chance of performing feasible computations, though the structure of the resulting logical formula depends greatly on how rules interact—this is the topic of ongoing work.
By analyzing the resulting data structure, one can extract a clear map of how the probability of an atom is derived; this is discussed next.
-
-
Probabilities of atomic formulas: The annotated chase yields several tools that facilitate the provision of an explanation for the probability of an atom:
-
Different derivation paths leading to the same result (or summaries).
-
Examples of branches, perhaps highlighting well-separated ones to show variety.
-
Common aspects of worlds that make up most of the probability mass (such as atoms in the probabilistic model that appear in most derivations).
In all cases, if we wish to provide a balanced explanation (as discussed above) we can also focus on the dual situation, i.e., showing the cases in which the atom in question is not derived. Note that all of these elements are available independently of the specific probabilistic model used in the KB—depending on the characteristics of the chosen model, other data might be available as well.
-
-
Probabilities of more complex queries: The previous point covered the most basic probabilistic query (probability of atomic formulas); clearly, the same approach is useful for threshold queries, which can be answered simply by computing the probabilities of all atomic consequences and checking if their associated probabilities exceed the threshold. As discussed in the previous section, we have two other kinds of queries:
-
Probabilistic conjunctive queries: The basic building blocks described for atomic queries can be leveraged for the more complex case of conjunctive queries. Depending on the kind of annotated chase graph used (as discussed above), the probability of a set of atoms that must be true at once can be derived from that of each individual member. Opportunities for explanations of why a query is derived or not derived may also include, for instance, selecting one or more elements of the conjunction that are responsible for lowering the resulting probability of the query.
-
Ranking queries: The fundamental component of the result of a ranking query is the relationship between the probabilities of atoms—the most important question to answer regarding explanations of such results is: for a given pair of atoms (a, b) such that a is ranked above b, why is it \(a>b\) and not \(b>a\)? The basic elements discussed above can be used to shed light on this aspect.
Finally, sampling-based methods (for instance, taking into account a subset of the worlds chosen at random) yield probability intervals instead of point probabilities—the width of the resulting interval will be a function of the number and probability mass of the worlds taken into account vs. those left out [35]. So, explanations can involve examples or summaries of how the probability mass gets to a minimum (lower bound) and, conversely, why the maximum (upper bound) is not higher.
-
There is much work to be done in developing effective algorithms to leverage these and other building blocks for deriving explanations for probabilistic queries. Furthermore, developing adequate user interfaces so that the resulting explanations are useful is also a highly non-trivial task.
4 Inconsistency-Tolerant Query Answering with Datalog+/–
In this section we discuss a general approach to inconsistency-tolerant query answering in Datalog+/–; the material in this section is based mainly on [36].
We now discuss semantics for inconsistency-tolerant query answering that are based on the ideas of [2] but from the perspective of the area of belief change, which is an area of AI that is closely related to the management of inconsistent information, aiming to adequately model the dynamics of the knowledge that constitutes the set of beliefs of an agent when new information comes up. In [31], kernel consolidations are defined based on the notion of an incision function. Given a knowledge base \( K\!B \) that needs to be consolidated (i.e., \( K\!B \) is inconsistent), the set of kernels is defined as the set of all minimal inconsistent subsets of \( K\!B \). For each kernel, a set of sentences is removed (i.e., an “incision” is made) such that the remaining formulas in the kernel are consistent; note that it is enough to remove any single formula from the kernel because they are minimal inconsistent sets. The result of consolidating \( K\!B \) is then the set of all formulas in \( K\!B \) that are not removed by the incision function. In this work, we present a framework based on a similar kind of functions to provide alternative query answering semantics in inconsistent Datalog+/– ontologies. The main difference in our proposal is that incisions are performed over inconsistent subsets of the ontology that are not necessarily minimal.
We analyze three types of incision functions that correspond to three different semantics for query answering in inconsistent Datalog+/– ontologies: (i) consistent answers or AR semantics [2, 32], widely adopted in relational databases and DLs, (ii) intersection semantics or IAR, which is a sound approximation of AR [32], and (iii) a semantics first proposed in [36] that relaxes the requirements of AR semantics, allowing it to be computed in polynomial time for some fragments of Datalog+/–, without compromising the quality of the answers as much as the IAR semantics does, by allowing a certain budget within which the answers can be computed.
We first define the notion of a culprit relative to a set of constraints, which is informally a minimal (under set inclusion) inconsistent subset of the database relative to the constraints. Note that we define culprits relative to both negative constraints and EGDs, as \(\varSigma _{\textit{NC}}\) contains all EGDs written as NCs, as we mentioned above.
Definition 10
(Culprit). Given a Datalog+/– ontology \( K\!B =( D, \varSigma _T\cup \varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}})\), a culprit in \( K\!B \) relative to \(\varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}}\) is a set \(c \subseteq D\) such that \( mods (c,\varSigma _{T} \cup \textit{IC}) = \emptyset \) for some \(\textit{IC} \subseteq \varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}}\), and there is no \(c' \,{\subset }\,c\) such that \( mods (c',\varSigma _{T} \cup \textit{IC}) = \emptyset \). We denote by \(\textit{culprits}( K\!B )\) the set of culprits in \( K\!B \) relative to \(\varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}}\).
Note that we may also refer to \(\textit{culprits}( K\!B , \textit{IC})\) whenever we want to make the point that \(\textit{IC}\) is an arbitrary set of constraints or to identify a specific subset of \(\varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}}\). The following example shows a Datalog+/– ontology that we will use as a running example through out the chapter.
The following example shows a simple Datalog+/– ontology; the language and standard semantics for query answering in Datalog+/– ontologies is recalled in the next section.
Example 8
A (guarded) Datalog+/– ontology \( K\!B {\,{=}\,}( D, \varSigma _T \cup \varSigma _E \cup \varSigma _{\textit{NC}} )\) is given below. Here, the formulas in \(\varSigma _T\) are tuple-generating dependencies (TGDs), which say that each person working for a department is an employee (\(\sigma _1\)), each person that directs a department is an employee (\(\sigma _2\)), and that each person that directs a department and works in that department is a manager (\(\sigma _3\)). The formulas in \(\varSigma _{\textit{NC}}\) are negative constraints, which say that if X supervises Y, then Y cannot be a manager (\(\upsilon _1\)), and that if Y is supervised by someone in a department, then Y cannot direct that department (\(\upsilon _2\)). The formula \(\upsilon _3{\,{\in }\,}\varSigma _E\) is an equality-generating dependency (EGD), saying that the same person cannot direct two different departments.

We can easily see that this ontology is inconsistent. For instance, the atoms \(\textit{directs}(john, d_1)\) and \(\textit{works}\_\textit{in}(john, d_1)\) trigger the application of \(\sigma _3\), producing \(\textit{manager}(john)\), but that together with \(\textit{supervises}(tom, john)\) (which belongs to D) violates \(\upsilon _1\). The set of culprits relative to \(\varSigma _{\textit{E}} \cup \varSigma _{\textit{NC}}\) are:

. \(\blacksquare \)
We construct clusters by grouping together all culprits that share elements. Intuitively, clusters contain only information involved in some inconsistency relative to \(\varSigma \), i.e., an atom is in a cluster relative to \(\varSigma \) iff it is in contradiction with some other set of atoms in D.
Definition 11
(Cluster [38]). Given a Datalog+/– ontology \( K\!B {\,{=}\,}( D, \varSigma _T\cup \varSigma _{\textit{NC}})\) and \(IC \subseteq \varSigma _{\textit{NC}}\), two culprits \(c,c' \in \textit{culprits}( K\!B , IC)\) overlap, denoted \(c \; \varTheta \; c'\), iff \(c \cap c' \ne \emptyset \). Denote by \(\varTheta ^*\) the equivalence relation given by the reflexive and transitive closure of \(\varTheta \). A cluster is a set \(cl = \bigcup _{c \in e} c\), where e is an equivalence class of \(\varTheta ^*\). We denote by \(\textit{clusters}( K\!B , IC)\) (resp., \(\textit{clusters}( K\!B )\)) the set of all clusters in \( K\!B \) relative to IC (resp., \(IC = \varSigma _{ NC}\)).
Example 9
The clusters for \( K\!B \) in the running example are \(cl_1 = c_3\) and \(cl_2 = c_1 \cup c_2\) (cf. Example 8 for culprits \(c_1\), \(c_2\), and \(c_3\)). \(\blacksquare \)
We now recall the definition of incision function from [31], adapted for Datalog+/– ontologies. Intuitively, an incision function selects from each cluster a set of atoms to be discarded such that the remaining atoms are consistent relative to \(\varSigma \).
Definition 12
(Incision Function). Given a Datalog+/– ontology \( K\!B {\,{=}\,}( D,\varSigma )\), an incision function is a function \(\chi \) that satisfies the following properties:
-
(1)
\(\chi (\textit{clusters}( K\!B )) \subseteq \bigcup _{cl \in \textit{clusters}( K\!B )} cl\), and
-
(2)
\( mods (D-\chi (\textit{clusters}( K\!B )),\varSigma )\) \(\ne \) \(\emptyset \).
Note that incision functions in [31] do not explicitly require condition (2) from Definition 12; instead, they require the removal of at least one sentence from each \(\alpha \)-kernel. The notion of \(\alpha \)-kernel [31] translates in our framework to a minimal set of sentences in D such that, together with \(\varSigma \), entails the sentence \(\alpha \), where \( K\!B {\,{=}\,}(D,\varSigma )\). Culprits are then, no more than minimal subsets of D that, together with \(\varSigma \), entail \(\bot \). Here, \(\chi \) produces incisions over clusters instead, therefore, condition (2) is necessary to ensure that by making the incision, the inconsistency is resolved.
4.1 Relationship with (Classical) Consistent Answers
In the area of relational databases, the notion of repair was used in order to identify the consistent part of a possibly inconsistent database. A repair is a model of the set of integrity constraints that is maximally close, i.e., “as close as possible” to the original database. Repairs may not be unique, and in the general case, there can be a very large number of them. The most widely accepted semantics for querying a possibly inconsistent database is that of consistent answers [2].
We now adapt one notion of repair from [32] to Datalog+/– ontologies \( K\!B {\,{=}\,}( D, \varSigma )\). Intuitively, repairs are maximal consistent subsets of D. We also show that BCQ answering under the consistent answer semantics is co-NP-complete for guarded and linear Datalog+/– in the data complexity.
Definition 13
(Repair). A repair for \( K\!B {\,{=}\,}( D, \varSigma )\) is a set \(D'\) such that (i) \(D' \,{\subseteq }\,D\), (ii) \( mods (D',\varSigma ) \,{\ne }\,\emptyset \), and (iii) there is no \(D'' \,{\subseteq }\,D\) such that \(D' \,{\subset }\,D''\) and \( mods (D'',\varSigma ) \,{\ne }\,\emptyset \). We denote by \(\textit{DRep}( K\!B )\) the set of all repairs for \( K\!B \).
Example 10
The Datalog+/– ontology \( K\!B \) in Example 8 has six repairs:

Repairs play a central role in the notion of consistent answer for a query to an ontology, which are intuitively the answers relative to each ontology built from a repair. The following definition adapts the notion of consistent answers, defined in [32] for Description Logics, for Datalog+/– ontologies.
Definition 14
(Consistent Answers – AR Semantics). Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and Q be a BCQ. Then, Yes is a consistent answer for Q to \( K\!B \), denoted  , iff it is an answer for Q to each \( K\!B '{\,{=}\,}(D', \varSigma )\) with \(D' {\,{\in }\,}\textit{DRep}( K\!B )\).
, iff it is an answer for Q to each \( K\!B '{\,{=}\,}(D', \varSigma )\) with \(D' {\,{\in }\,}\textit{DRep}( K\!B )\).
Example 11
Consider the ontology \( K\!B \) from our running example. The atom \(\textit{emp}(john)\) can be derived from every repair, as each contains either the atom \(\textit{works}\_\textit{in}(john,d_1)\) or the atom \(\textit{directs}(john, d_1)\). Thus, BCQ \(Q{\,{=}\,}\textit{emp}(john)\) is true under the consistent answer semantics. \(\blacksquare \)
In accordance with the principle of minimal change, incision functions that make as few changes as possible when applied the set of clusters are called optimal incision functions.
Definition 15
(Optimal Incision Function). Given a Datalog+/– ontology \( K\!B {\,{=}\,}( D, \varSigma )\), an incision function \(\chi \) is optimal iff for every \(B \subset \chi (\textit{clusters}( K\!B ))\), it holds that \( mods (D -B,\varSigma ) = \emptyset \).
The following theorem shows the relationship between an optimal incision function and repairs for a Datalog+/– ontology \( K\!B {\,{=}\,}( D, \varSigma )\). More concretely, every repair corresponds to the result of removing from D all ground atoms according to some optimal incision \(\chi (\textit{clusters}( K\!B ))\) and vice versa.
Theorem 1
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology. Then, \(D'\) is a repair, i.e., \(D' {\,{\in }\,}\textit{DRep}( K\!B )\), iff there exists an optimal incision function \(\chi _{\textit{opt}}\) such that \(D' = D -\chi _{\textit{opt}}(\textit{clusters}( K\!B ))\).
4.2 Relationship with IAR Semantics
An alternative semantics that considers only the atoms that are in the intersection of all repairs was presented in [32] for DL-Lite ontologies. This semantics yields a unique way of repairing inconsistency; the consistent answers are intuitively the answers that can be obtained from that unique set. Here, we define IAR for Datalog+/– ontologies.
Definition 16
(Intersection Semantics – IAR). Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and Q be a BCQ. Then, Yes is a consistent answer for Q to \( K\!B \) under IAR, denoted  , iff it is an answer for Q to \( K\!B _I{\,{=}\,}( D_I, \varSigma )\), where \(D_I = \bigcap \,\{D'\,{\mid }\,D'\in \textit{DRep}( K\!B )\}\).
, iff it is an answer for Q to \( K\!B _I{\,{=}\,}( D_I, \varSigma )\), where \(D_I = \bigcap \,\{D'\,{\mid }\,D'\in \textit{DRep}( K\!B )\}\).
Example 12
Consider the ontology \( K\!B {\,{=}\,}( D, \varSigma )\) from the running example. Analyzing the set of all its repairs, it is easy to verify that \(D_I {\,{=}\,} \{\textit{manager}(\textit{tom},d_1)\}\). \(\blacksquare \)
The following theorem shows the relationship between the incision function \(\chi _{all}\), which is defined by \(\chi _{all}(\textit{clusters}( K\!B )) = \bigcup _{cl \in \textit{clusters}(KB)} cl\), and consistent answers under the IAR semantics. Intuitively, answers relative to IAR can be obtained by removing from D all atoms participating in some cluster, and answering the query using the resulting database.
Theorem 2
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and Q be a BCQ. Then,  iff
iff  .
.
4.3 Lazy Answers
In the following, we present a different semantics for consistent query answering in Datalog+/– ontologies. The motivation to seek for a different semantics comes from different reasons: first is the fact that computing the AR semantics is too expensive for any reasonable-sized Datalog+/– ontology, and second, the IAR semantics is unnecessarily restrictive in the set of answers that can be obtained from a query. The k-lazy semantics is an alternative to classical consistent query answering in Datalog+/– ontologies; the intuition behind lazy answers is that, given a budget (the k parameter), a maximal set of consistent answers (maximal relative to the k) can be computed, which are at least as complete as those that can be obtained under IAR.
We first define the notion of k-cut of clusters. Let \(\chi _{k\textit{-cut}}\) be a function defined as follows for \(cl \in \textit{cluster}( K\!B )\):
Intuitively, given a cluster cl, its k-cut \(\chi _{k\textit{-cut}}(cl)\) is the set of minimal subsets of cl of cardinality at most k, such that if they are removed from cl, what is left is consistent with respect to \(\varSigma \).
We next use the k-cut of clusters to define a new type of incision functions, called k-lazy functions, as follows.
Definition 17
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and \(k \,{\geqslant }\,0\). A k-lazy function for \( K\!B \) is defined as \(\chi _{\textit{lazy}}(k, \textit{clusters}( K\!B )) = \bigcup _{cl \in \textit{clusters}( K\!B )} c_{cl}\), where \(c_{cl} \in \chi _{k\textit{-cut}}(cl)\).
The above k-lazy functions are indeed incision functions.
Proposition 1
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and \(k \,{\geqslant }\,0\). All k-lazy functions for \( K\!B \) are incision functions.
The function \(\chi _{\textit{lazy}}\) is the basis of lazy repairs, as defined next. Intuitively, k-lazy repairs are built by analyzing ways in which to remove at most k atoms in every cluster.
Definition 18
(k-Lazy Repair). Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and \(k \,{\geqslant }\,0\). A k-lazy repair for \( K\!B \) is any set \(D' {\,{=}\,}D -\chi _{\textit{lazy}}(k, \textit{clusters}( K\!B ))\), where \(\chi _{\textit{lazy}}(k, \textit{clusters}( K\!B ))\) is a k-lazy function for \( K\!B \). \(\textit{LRep}(k, K\!B )\) denotes the set of all such repairs.
Example 13
Consider again our running example and the clusters in \( K\!B \) from Example 9. Let \(k {\,{=}\,}1\), then we have that
and that
There are four possible incisions: \(\textit{ins}_1 = d_1\cup e_1\), \(\textit{ins}_2 = d_1\cup e_2\), \(\textit{ins}_3 = d_2\cup e_1\), and \(\textit{ins}_4 = d_2\cup e_2\). Thus, there are four 1-lazy repairs, with \(\textit{lrep}_i = D -\textit{ins}_i\); for example,
\(\blacksquare \)
We can now define k-lazy answers for a query Q as the set of atoms that are derived from every k-lazy repair.
Definition 19
(k-Lazy Answers). Let \( K\!B = (D, \varSigma )\) be a Datalog+/– ontology, Q be a BCQ, and \(k \geqslant 0\). Then, Yes is a k-lazy answer for Q to \( K\!B \), denoted  , iff it is an answer for Q to each \( K\!B '{\,{=}\,}( D', \varSigma )\) with \(D' {\,{\in }\,}\textit{LRep}(k, K\!B )\).
, iff it is an answer for Q to each \( K\!B '{\,{=}\,}( D', \varSigma )\) with \(D' {\,{\in }\,}\textit{LRep}(k, K\!B )\).
Note that \(\textit{k-LCons}\) is used to identify the consistency-tolerant query answering semantics corresponding to k-lazy repairs. The following proposition states some properties of k-lazy repairs and lazy answers: each lazy repair is consistent relative to \(\varSigma \), and only atoms that contribute to an inconsistency are removed by a k-lazy function for \( K\!B \).
Proposition 2
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and \(k \,{\geqslant }\,0\). Then, for every \(D' {\,{\in }\,}\textit{LRep}(k, K\!B )\), (a) \( mods (D',\varSigma ) \,{\ne }\,\emptyset \), and (b) if \(\beta {\,{\in }\,}D\) and \(\beta \,{\not \in }\, D'\), then there exists some \(B\,{\subseteq }\,D\) such that \( mods (B,\varSigma ) \,{\ne }\,\emptyset \) and \( mods (B\cup \{\beta \},\varSigma ) {\,{=}\,}\emptyset \).
Proposition 2 shows that lazy repairs satisfy properties that are desirable for any belief change operator to have [31]. However, the incisions performed by function \(\chi _{\textit{lazy}}(k, \textit{clusters}( K\!B ))\) are not always minimal relative to set inclusion; i.e., if there is no subset of a cluster of size at most k that satisfies the conditions in Definition 1, then the whole cluster is removed, and therefore not every lazy repair is a repair.
The AR semantics from Definition 14 is a cautious semantics to query answering, since only answers that can be entailed from every repair are deemed consistent. Traditionally, the alternative to this semantics is a brave approach, which in our framework would consider an answer as consistent if it can be entailed from some repair. In the case of Example 13 with \(k {\,{=}\,}1\), \(\textit{works}\_\textit{in}(john,d_1)\) and \(\textit{works}\_\textit{in}(tom,d_1)\) are lazy consequences of \( K\!B \), which are clearly not consistent consequences of \( K\!B \). However, a brave approach for query answering would allow both \(\textit{supervise}(\textit{tom},\textit{john})\) and \(\textit{directs}(\textit{john},d_1)\) as answers. In this respect, lazy answers are a compromise between brave and cautious approaches: although it is “braver” than the cautious approach, it does not allow to derive mutually inconsistent answers.
Proposition 3
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, Q be a CQ, and \( ans _{ LCons }(k,Q,D,\varSigma )\) be the set of lazy answers for Q given k. Then, for any \(k \,{\geqslant }\,0\), \( mods ( ans _{ LCons }(k,Q,D,\varSigma ),\varSigma ) \ne \emptyset \).
The next proposition shows that the same property holds if we consider the union of k-lazy answers for different values of k.
Theorem 3
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology and Q be a CQ. Then, for any \(k \,{\geqslant }\,0\), \( mods (\bigcup _{0 \leqslant i \leqslant k} ans _{ LCons }(i,Q,D,\varSigma ),\varSigma ) \ne \emptyset \).
Theorem 3 shows that lazy answers can be used to obtain answers that are not consistent answers but are nevertheless consistent as a whole. We refer to this as the union-k-lazy semantics.
The next proposition shows the relationships between AR, IAR, and the lazy semantics.
Proposition 4
Let \( K\!B {\,{=}\,}( D, \varSigma )\) be a Datalog+/– ontology, and Q be a BCQ. Then, (a) if  , then
, then  , for any \(k \geqslant 0\), and (b)
, for any \(k \geqslant 0\), and (b)  iff
iff  . Furthermore, there is \(k \geqslant 0\) such that
. Furthermore, there is \(k \geqslant 0\) such that  iff
iff  .
.
Clearly, Proposition 4 entails that if we take the union of the lazy answers up to the k from the proposition, then the resulting set of lazy answers is complete with respect to AR. Example 14 shows that, in our running example, the 2-lazy answers correspond exactly to the consistent answers.
Example 14
In Example 13, if \(k {\,{=}\,}2\), then we have that \(\chi _{2\textit{-cut}}(cl_1) {\,{=}\,}\chi _{1\textit{-cut}}(cl_1)\) and
 . We can easily see that \(\textit{LRep}(2, K\!B ) = \textit{DRep}( K\!B )\). \(\blacksquare \)
. We can easily see that \(\textit{LRep}(2, K\!B ) = \textit{DRep}( K\!B )\). \(\blacksquare \)
The following (simpler) example shows the effects of changing the value of k as well as the results from Theorem 3.
Example 15
Consider the CQ \(Q(X,Y) = p(X) \,\wedge \, q(Y)\) and the following Datalog+/– ontology \( K\!B {\,{=}\,}( D, \varSigma )\):

The set of clusters in \( K\!B \) is \(\textit{clusters}( K\!B , \varSigma ) = \{ cl_1:\{p(a), p(b), p(d), p(e), p(f)\}\), \(cl_2:\{q(g), q(h), q(i)\}\). For \(k = 0\), the only 0-lazy repair is \(\textit{lrep}_0 = \{p(c), q(j)\}\), which coincides with \(D_I\); the set of 0-lazy answers (and the answers under IAR) to Q(X, Y) is \(\{p(c), q(j)\}\).
For \(k = 1\), note that there is no way of removing one element from \(cl_1\) making the rest consistent; therefore, the only possible cut removes the whole cluster. On the other hand, there is one 1-cut for \(cl_2\), namely \(\{q(h)\}\). Therefore, we have only one 1-lazy repair \(\textit{lrep}_1 = \{p(c), q(j), q(i), q(g)\}\). The set of 1-lazy answers to Q(X, Y) is \(\{p(c), q(j), q(i), q(g)\}\).
With \(k = 2\), we have two possible 2-cuts for \(cl_1\) and two for \(cl_2\), this is, \(\chi _{2\textit{-cut}}(cl_1) = \{\{p(a), p(d)\}, \{p(b), p(d)\}\}\) and \(\chi _{2\textit{-cut}}(cl_2) = \{\{q(h)\},\{q(g), q(i)\}\}\). In this case there are four 2-lazy repairs and the set of 2-lazy answers to Q(X, Y) is \(\{p(c), p(e), p(f), q(j)\}\).
For \(k = 3\), we have \(\chi _{3\textit{-cut}}(cl_1) = \{\{p(a), p(d)\}, \{p(b), p(d)\}, \{p(b), p(e), p(f)\}\}\) and \(\chi _{3\textit{-cut}}(cl_2) = \chi _{2\textit{-cut}}(cl_2) = \{\{q(h)\},\{q(g), q(i)\}\}\). The set of 3-lazy repairs coincide with the set of repairs and therefore the set of 3-lazy answers to Q(X, Y) is the set of consistent answers, namely \(\{p(c), q(j)\}\).
Finally, \(\bigcup _{0 \leqslant i \leqslant 3} ans _{ LCons }(i,Q,D,\varSigma ) = \{p(c), q(j), q(i), q(g), p(e), p(f) \}\), which is clearly consistent relative to \(\varSigma _{\textit{NC}}\). \(\blacksquare \)
After the formal presentation of lazy answers, based on the concept of incision functions, we can now provide an algorithm that computes lazy answers to conjunctive queries to Datalog+/– ontologies. In [36], an algorithm to compute lazy answers to conjunctive queries is provided; the algorithm uses the concept of finite chase graph [17] for a given ontology \( K\!B {\,{=}\,}( D, \varSigma )\), which is a graph consisting of the necessary finite part of \( chase (D,\varSigma )\) relative to query Q, i.e., the finite part of the chase graph for D and \(\varSigma \) such that  . The idea of the algorithm is pretty straight forward, it first computes the set of clusters in \( K\!B \), and next, for each cluster, function \(\chi _{k\textit{-cut}}\) is constructed by removing each possible subset (of size at most k) of the cluster in turn and checking if the remaining tuples are consistent (and that the subset in question is not a superset of an incision already found). A lazy repair then arises from each such possible combination by removing the incisions from D. The answer is finally computed using these repairs. Thought [36] proposes also an algorithm to compute clusters and kernels, there exists several algorithms in the literature to efficiently compute kernels in propositional logic that can be leveraged for Datalog+/– ontologies [43, 51, 52].
. The idea of the algorithm is pretty straight forward, it first computes the set of clusters in \( K\!B \), and next, for each cluster, function \(\chi _{k\textit{-cut}}\) is constructed by removing each possible subset (of size at most k) of the cluster in turn and checking if the remaining tuples are consistent (and that the subset in question is not a superset of an incision already found). A lazy repair then arises from each such possible combination by removing the incisions from D. The answer is finally computed using these repairs. Thought [36] proposes also an algorithm to compute clusters and kernels, there exists several algorithms in the literature to efficiently compute kernels in propositional logic that can be leveraged for Datalog+/– ontologies [43, 51, 52].
Lazy answers are based on a budget that restricts the size of removals that need to be made in a set of facts in order to make it consistent—if the budget is large enough, then we go to the trouble of considering all possible ways of solving the conflicts within the budget, but if it is not enough then we get rid of all the sentences that are involved in that particular conflict. If we think of the problem of querying inconsistent KBs as a reasoning task for an intelligent agent, then the value of the budget would be a bound on its reasoning capabilities (more complex reasoning can thus be afforded with higher budgets). On the other hand, considering clusters instead of culprits (or kernels) allows to identify a class of incision functions that solve conflicts from a global perspective; for more details on the relation of cluster incision functions and kernel incision functions cf. [20].
The key points that differentiates the k-lazy semantics from the Ar and its approximations is reflected in the fact that the set of repairs and the set of k-lazy repairs do not coincide in general, unless k is such that it forces to consider all the possible ways to solve the conflicts. This allows to consider answers that are not consistent answers in the sense of AR semantics but that are consistent with respect to the way conflicts are solved given the provided budget.
4.4 Towards Explainable Inconsistency-Tolerant Query Answering
Inconsistency-tolerant semantics for query answering provide a way to reason in logical knowledge bases in the presence of inconsistency. This is an important advantage over classical query answering processes, where answers may become meaningless. In this sense, the presence of inconsistency in the knowledge base remains transparent to the user that is issuing the query, which is, arguably, a good property as it does not disrupt the process. However, as these tools are often used to aid in the process of making decisions for different application domains (it may be an automated system itself the one that makes decisions based on the answers obtained from the knowledge base), it seems reasonable to try to provide information that complements the set of answers and helps the user understand why they obtained that set of answers and, particularly, if there was some piece of information, related to their query, that is subject to logical conflicts and how that affected the computed answers, especially if the answer was negative or did not include an individual that was expected.
For instance, suppose the user asks if the query \(q() = \exists X p(X)\) is true and they get the answer No. It is only natural to pose the following question:
“Was it the case that there is no possible way to derive p(X) from the knowledge base, so the answer is No in every possible repair, or was it the case that q is true in some repairs but false in others, such that the semantics cannot assure its truth value”.
This distinction may be significant depending on the implications of the answer and how it is used. With this example in mind, given a Datalog+/– ontology \((D, \varSigma )\) and a query Q, a natural question that one may be interested in asking for explanatory purposes is:
“What makes Q true under some semantics S?”, or alternatively
“What makes Q false under some semantics S?”.
The work of [11] proposes the notion of explanation for positive and negative query answers under the brave, AR, and IAR semantics, for Description Logics. An explanation for a query Q in this case is based on causes for Q, which are sets of facts from the original knowledge base that yield Q; this means that, in terms of Datalog+/–, causes are subsets of the D that together with \(\varSigma \) yield Q. Positive explanations for the brave semantics (the answer is true in some repair) is any cause for Q, that is, any consistent subset of D that entails the query by means of \(\varSigma \). For the IAR semantics, an explanation is any cause of Q that does not participate in any contradiction. In the case of AR it is not enough to provide just one set of facts that are a cause of the query, as different repairs may use different causes. Therefore, they provide explanations in the form of (minimal) disjunctions of causes that cover all repairs (every cause belongs to at least one repair and for each repair there is one cause in the set).
Explanations for negative answers for Q under AR are minimal subsets of D such that together with any cause for Q yield an inconsistency. On the other hand, explanations for negative answers under IAR it is only necessary to ensure that every cause is contradicted by some consistent subset of D, which is enough to show that no cause belongs to all repairs. The proposal is accompanied by a computational complexity study of the difficulty of the decision problems related to checking and computing the different types of explanations. Most of these problems are polynomial for the case of explanations for positive and negative answers under brave and IAR. Not surprisingly, explanations in both cases under the AR semantics are intractable.
The notion of explanation, both for positive and negative answers, are directly translatable for k-Lazy answers. In particular, incisions correspond to explanations for negative answers. If we look at Example 14 and take query \(Q()= p(e)\) for \(k = 1\), we have that  and the reason for that is that the only possible 1-cut for \(cl_1\) includes p(e) (in the general case we can actually see that the incision contradicts every possible cause of p(e)).
and the reason for that is that the only possible 1-cut for \(cl_1\) includes p(e) (in the general case we can actually see that the incision contradicts every possible cause of p(e)).
In addition, this proposal can provide other types of answers in relation to explaining the behavior of the semantics. Other interesting questions may include:
-
1.
What is the smallest k needed to make Q true under both k-lazy and union-k-lazy semantics?
-
2.
What are the causes that make Q change its truth value from k to \(k + 1\) under the k-lazy semantics (either from true to false or the other way around)?
-
3.
If Q is true under (union-) k-lazy semantics for some \(k \geqslant 0\) but it is not a consistent answer, what are the causes for this behavior? This question actually elaborates on the previous one, as we can try to find for which \(k' \geqslant k\) the truth value of Q changes, and find the reason by comparing \(k'\)-cuts against \(k'+1\)-cuts.
If we try to answer question (1) for Example 14 and \(Q()= p(e)\), we find that the smallest k is 2, which means that p(e) is involved in some inconsistency (it belongs or can be derived from a cluster) and that the conflict is such that it is necessary to remove two atoms at the same time from the cluster, so that p(e) appears or survives. Note that this number is actually related to the fact that there is a chain of conflicts: \(p(a) \wedge p(b) \rightarrow \bot \), \(p(b) \wedge p(d) \rightarrow \bot \), and \(p(d) \wedge p(e) \rightarrow \bot \). In this way we can use causes, together with NCs and incisions, to complement the required explanations and can show explanations that are local to specific k’s.
Finally, we will show examples of how argumentation theory can help in the construction of meaningful explanations for inconsistency-tolerant query answering. As mentioned in the introduction, argumentation provides a natural dialogic structure and mechanism as part of the reasoning process and that can, in principle, be examined by a user in order to understand both why and how conclusions (answers) are reached.
The work in [4], proposes explanations as a set of logical arguments supporting the query. Without going into the fine details, an argument can be seen as a set of premises (facts) that derives a conclusion by means of a logical theory, or in the case of Datalog+/– a set of TGDs. In this context, we can think of causes of a query, defined by [11], as arguments that entail or support the entailment of the query. Conversely, we can build arguments that contradict some sentence, and these can be used as reasons against a query or, more generally, explanations for negative answers. For more details on argumentation we refer the reader to [21, 25]. All the examples of explanation proposals mentioned so far can be considered as argument-based explanations, depending on the richness of the language and the framework, different notions of argument and counterarguments can be constructed as a means for explanations.
The proposals mentioned above provide arguments for and against conclusions but in a static way, after the user inquiry for explanations the system retrieves and shows the set of explanations. Alternative, it is possible to exploit the dynamical characteristics of argumentation frameworks in order to create an interactive explanation mechanism. In [3], the notion of dialectical explanations is developed where it is assumed that the explanation is an interactive process with the system where a dialogue is established. The idea is that the explainer (e.g., the system) aims to make an explainee (e.g., the user) understand why a query Q is or is not entailed by the query answering semantics. It is shown that the query answering process can be represented as such a dialogue, in which arguments for and against the entailment of the query are identified, analyzed, and weighed among each other. A query is entailed under a specific semantics if and only if the dialectical process ends with a winning argument in favor of the query. That work develops this dialectical process for the ICR semantics [10], which is a sound approximation of AR and generalizes IAR. In [3], the proposal is extended for the brave and IAR semantics.
In this same spirit, [37] introduces an inconsistency-tolerant semantics for Datalog+/– ontologies query asnwering based on defeasible argumentative reasoning, which allows consequences to represent statements whose truth can be challenged. The proposal incorporates argumentation theory within the Datalog+/– query answering process itself. This process has the ability of considering reasons for and against potential conclusions and deciding which are the ones that can be obtained (warranted) from the knowledge base. This provides the possibility of implementing different inconsistency-tolerant semantics depending on the comparison criterion selected, all within the same framework, and as part of the query answering process. Indeed, the paper shows that most inconsistency-tolerant semantics that are based on the notion of repair (AR and the family of semantics that approximates it), as well as other such as the k-support and k-defeater semantics [12], can be obtained within this framework. This proposal has two advantages; first, it is not necessary to use and compute elements that are outside of the logic, such as repairs, kernels, clusters, incisions, etc., as the query answering engine is inconsistency-tolerant in itself. Second, the argumentative process underlying the query answering task allows to compute the answers and the required explanations at the same time. This means that there is, in principle, not extra cost for computing explanations, as happens also in [3]. Of course, there is the potential of creating a more complex explanatory mechanism exploiting other elements that are explicitly built within the argumentative process.
5 Discussion and Future Research Directions
Querying and managing incomplete and inconsistent information in an automatic and systematic way is becoming more and more necessary in order to cope with the amount of information that feeds the systems that are used to make decisions in a wide variety of domains, from product or service recommendation systems to medical or political applications. In order to build automated systems that aid humans in the process of making decisions in such a way that they improve their performance and understanding, proper explanations and interpretability of results are of the utmost importance. As we mentioned before, what is considered a good or reasonable explanation—or explanation process—strongly depends on the application domain and the particular problem the user is trying to solve based on the system’s results.
Being able to produce adequate and meaningful explanations from automated systems is about being able to trust their results. This kind of trust is important from the system’s functional point of view, but also important from a regulatory perspective. As it has already being discussed in different forums, such as the European General Data Protection Regulation,Footnote 3 users (or subjects) of automated data processing have the right “to obtain human intervention, to express his or her point of view, to obtain an explanation of the decision reached after such assessment and to challenge the decision”. Such legal (and social) requirements clearly set the stage for discussions and further research efforts regarding adequate explanation models, mechanisms, and tools.
In this work we drafted some ideas on how to exploit the potential of knowledge based AI systems in order to produce meaningful explanations for query answering in the presence of uncertain information, where the uncertainty may arise from a probabilistic model or from the presence of inconsistency. After these first steps, it becomes clear that the road to designing and implementing explainable tools based on these and other formalisms is long; the roadmap includes the following activities, among others:
-
Research different kinds of explanations for each type of query that can be posed to the system, making full use of the knowledge encoded in the models.
-
Related to the previous point, take into account the actual users of the system, for whom the explanations are generated. This includes many different human-centered aspects, such as effective interfaces that don’t overwhelm the user, and conveying full transparency in order to gain the user’s trust.
-
Design explanation techniques that allow a level of detail to be set, so as to support the wide range between novice and expert users, as well as different levels of privacy and clearance (in terms of security).
-
Study the relationship between explainability and human-in-the-loop systems—for instance, it is possible for users to only require explanations for certain parts of a result, or only an explanation of why the result wasn’t one that they were expecting.
-
Explore how explainability relates to the vast body of work in software auditing—clearly, explanations might not only be required at query time, but at a later stage when other interested parties are reviewing the system’s outputs.
-
Ensure computational tractability: producing explanations should not be an excessive computational burden.
Each of these tasks can be considered a research and development program in its own right; we envision progress to continue being made slowly but steadily from ad hoc approaches to well-founded developments in the future.
Notes
- 1.
Note, however, that the human aspect is not necessarily present, since the argumentation process could be carried out between software agents.
- 2.
As an aside, and using concepts that will be defined shortly, the fundamental result linking homomorphisms to conjunctive query answering over relational databases can be informally stated as follows: let Q be a BCQ, and J be a database instance; then,
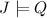 if and only if there exists a homomorphism from the canonical database instance \(I^Q\) (essentially, an instance built using the predicates and variables from Q) to J [5, 19].
if and only if there exists a homomorphism from the canonical database instance \(I^Q\) (essentially, an instance built using the predicates and variables from Q) to J [5, 19]. - 3.
References
Alonso, J.M., Castiello, C., Mencar, C.: A bibliometric analysis of the explainable artificial intelligence research field. In: Medina, J., et al. (eds.) IPMU 2018. CCIS, vol. 853, pp. 3–15. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-91473-2_1
Arenas, M., Bertossi, L.E., Chomicki, J.: Consistent query answers in inconsistent databases. In: Proceedings of PODS, pp. 68–79 (1999)
Arioua, A., Croitoru, M.: Dialectical characterization of consistent query explanation with existential rules. In: FLAIRS: Florida Artificial Intelligence Research Society (2016)
Arioua, A., Tamani, N., Croitoru, M.: Query answering explanation in inconsistent datalog\(+/-\) knowledge bases. In: Chen, Q., Hameurlain, A., Toumani, F., Wagner, R., Decker, H. (eds.) DEXA 2015. LNCS, vol. 9261, pp. 203–219. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22849-5_15
Atserias, A., Dawar, A., Kolaitis, P.G.: On preservation under homomorphisms and unions of conjunctive queries. J. ACM (JACM) 53(2), 208–237 (2006)
Baget, J., Mugnier, M., Rudolph, S., Thomazo, M.: Walking the complexity lines for generalized guarded existential rules. In: Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), pp. 712–717 (2011)
Baral, C., Gelfond, M., Rushton, N.: Probabilistic reasoning with answer sets. In: Lifschitz, V., Niemelä, I. (eds.) LPNMR 2004. LNCS (LNAI), vol. 2923, pp. 21–33. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24609-1_5
Barber, D.: Bayesian Reasoning and Machine Learning. Cambridge University Press, Cambridge (2012)
Beeri, C., Vardi, M.Y.: The implication problem for data dependencies. In: Even, S., Kariv, O. (eds.) ICALP 1981. LNCS, vol. 115, pp. 73–85. Springer, Heidelberg (1981). https://doi.org/10.1007/3-540-10843-2_7
Bienvenu, M.: Inconsistency-tolerant conjunctive query answering for simple ontologies. In: Kazakov, Y., Lembo, D., Wolter, F. (eds.) Proceedings of DL, vol. 846. CEUR-WS.org (2012)
Bienvenu, M., Bourgaux, C., Goasdoue, F.: Explaining inconsistency-tolerant query answering over description logic knowledge bases. In: Proceedings of AAAI 2016, pp. 900–906. AAAI Press (2016)
Bienvenu, M., Rosati, R.: Tractable approximations of consistent query answering for robust ontology-based data access. In: Proceedings of IJCAI, pp. 775–781 (2013)
Calì, A., Gottlob, G., Kifer, M.: Taming the infinite chase: query answering under expressive relational constraints. In: Proceedings of the International Conference on Principles of Knowledge Representation and Reasoning (KR), pp. 70–80 (2008)
Calì, A., Gottlob, G., Kifer, M.: Taming the infinite chase: query answering under expressive relational constraints. J. Artif. Intell. Res. (JAIR) 48, 115–174 (2013)
Calì, A., Gottlob, G., Lukasiewicz, T.: A general Datalog-based framework for tractable query answering over ontologies. In: Proceedings of the ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems (PODS), pp. 77–86 (2009)
Calì, A., Gottlob, G., Pieris, A.: Towards more expressive ontology languages: the query answering problem. Artif. Intell. J. (AIJ) 193, 87–128 (2012)
Calì, A., Gottlob, G., Lukasiewicz, T.: A general Datalog-based framework for tractable query answering over ontologies. J. Web Sem. 14, 57–83 (2012)
Ceylan, İ.İ., Borgwardt, S., Lukasiewicz, T.: Most probable explanations for probabilistic database queries. In: Proceedings of IJCAI, pp. 950–956 (2017)
Chandra, A.K., Merlin, P.M.: Optimal implementation of conjunctive queries in relational data bases. In: Proceedings of the ACM Symposium on Theory of Computing (STOC), pp. 77–90 (1977)
Deagustini, C.A.D., Martínez, M.V., Falappa, M.A., Simari, G.R.: Improving inconsistency resolution by considering global conflicts. In: Straccia, U., Calì, A. (eds.) SUM 2014. LNCS (LNAI), vol. 8720, pp. 120–133. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11508-5_11
Dung, P.M.: On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and \(n\)-person games. Artif. Intell. 77, 321–357 (1995)
Fagin, R., Kolaitis, P.G., Miller, R.J., Popa, L.: Data exchange: semantics and query answering. In: Calvanese, D., Lenzerini, M., Motwani, R. (eds.) ICDT 2003. LNCS, vol. 2572, pp. 207–224. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36285-1_14
Fagin, R., Kolaitis, P.G., Miller, R.J., Popa, L.: Data exchange: semantics and query answering. Theoret. Comput. Sci. 336(1), 89–124 (2005)
Falappa, M.A., Kern-Isberner, G., Simari, G.R.: Explanations, belief revision and defeasible reasoning. Artif. Intell. 141(1–2), 1–28 (2002)
García, A.J., Simari, G.R.: Defeasible logic programming: delp-servers, contextual queries, and explanations for answers. Argument Comput. 5(1), 63–88 (2014)
García, A.J., Simari, G.R.: Defeasible logic programming: an argumentative approach. TPLP 4(1–2), 95–138 (2004)
Gottlob, G., Manna, M., Pieris, A.: Combining decidability paradigms for existential rules. Theory Practice Logic Program. (TPLP) 13(4–5), 877–892 (2013)
Gottlob, G., Orsi, G., Pieris, A., Šimkus, M.: Datalog and its extensions for semantic web databases. In: Eiter, T., Krennwallner, T. (eds.) Reasoning Web 2012. LNCS, vol. 7487, pp. 54–77. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33158-9_2
Gottlob, G., Lukasiewicz, T., Martinez, M.V., Simari, G.I.: Query answering under probabilistic uncertainty in datalog+/- ontologies. Ann. Math. Artif. Intell. 69(1), 37–72 (2013)
Grover, S., Pulice, C., Simari, G.I., Subrahmanian, V.S.: BEEF: balanced English explanations of forecasts. IEEE Trans. Comput. Soc. Syst. 6(2), 350–364 (2019)
Hansson, S.O.: Semi-revision. J. Appl. Non-Classical Logic 7, 151–175 (1997)
Lembo, D., Lenzerini, M., Rosati, R., Ruzzi, M., Savo, D.F.: Inconsistency-tolerant semantics for description logics. In: Hitzler, P., Lukasiewicz, T. (eds.) RR 2010. LNCS, vol. 6333, pp. 103–117. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15918-3_9
Leone, N., Manna, M., Terracina, G., Veltri, P.: Efficiently computable Datalog programs. In: Proceedings of the International Conference on Principles of Knowledge Representation and Reasoning (KR), pp. 13–23 (2012)
Lukasiewicz, T., Martinez, M.V., Orsi, G., Simari, G.I.: Heuristic ranking in tightly coupled probabilistic description logics. In: Proceedings of UAI 2012, pp. 554–563 (2012)
Lukasiewicz, T., Martinez, M.V., Orsi, G., Simari, G.I.: Exact and approximate query answering in tightly coupled probabilistic datalog+/-. Forthcoming (2019)
Lukasiewicz, T., Martinez, M.V., Simari, G.I.: Inconsistency handling in Datalog+/- ontologies. In: Proceedings of ECAI, pp. 558–563 (2012)
Martinez, M.V., Deagustini, C.A.D., Falappa, M.A., Simari, G.R.: Inconsistency-tolerant reasoning in datalog\(^{\pm }\) ontologies via an argumentative semantics. In: Bazzan, A.L.C., Pichara, K. (eds.) IBERAMIA 2014. LNCS (LNAI), vol. 8864, pp. 15–27. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12027-0_2
Martinez, M.V., Pugliese, A., Simari, G.I., Subrahmanian, V.S., Prade, H.: How dirty is your relational database? An axiomatic approach. In: Proceedings of ECSQARU, pp. 103–114 (2007)
Milani, M., Bertossi, L.: Tractable query answering and optimization for extensions of weakly-sticky Datalog+/-. arXiv:1504.03386 (2015)
Miller, T.: Explanation in artificial intelligence: insights from the social sciences. Artif. Intell. 267, 1–38 (2019)
Pearl, J.: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (1988)
Poole, D.: The independent choice logic for modelling multiple agents under uncertainty. Artif. Intell. 94(1–2), 7–56 (1997)
Ribeiro, M.M., Wassermann, R.: Minimal change in AGM revision for non-classical logics. In: Principles of Knowledge Representation and Reasoning: Proceedings of the Fourteenth International Conference, KR 2014, 20–24 July 2014, Vienna, Austria (2014)
Richardson, A., Rosenfeld, A.: A survey of interpretability and explainability in human-agent systems. In: XAI Workshop on Explainable Artificial Intelligence, pp. 137–143 (2018)
Richardson, M., Domingos, P.: Markov logic networks. Mach. Learn. 62, 107–136 (2006)
Shortliffe, E.H., Davis, R., Axline, S.G., Buchanan, B.G., Green, C.C., Cohen, S.N.: Computer-based consultations in clinical therapeutics: explanation and rule acquisition capabilities of the mycin system. Comput. Biomed. Res. 8(4), 303–320 (1975)
Simari, G.I., Molinaro, C., Martinez, M.V., Lukasiewicz, T., Predoiu, L.: Ontology-Based Data Access Leveraging Subjective Reports. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-319-65229-0
Tifrea-Marciuska, O.: Personalised search for the social semantic web. Ph.D. thesis, Department of Computer Science, University of Oxford (2016)
Vardi, M.Y.: The complexity of relational query languages (extended abstract). In: Proceedings of the ACM Symposium on Theory of Computing (STOC), pp. 137–146 (1982)
Wainwright, M.J., Jordan, M.I., et al.: Graphical models, exponential families, and variational inference. Found. Trends® Mach. Learn. 1(1–2), 1–305 (2008)
Wang, S., Pan, J.Z., Zhao, Y., Li, W., Han, S., Han, D.: Belief base revision for datalog+/- ontologies. In: Kim, W., Ding, Y., Kim, H.-G. (eds.) JIST 2013. LNCS, vol. 8388, pp. 175–186. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06826-8_14
Wassermann, R.: An algorithm for belief revision. In: Proceedings of the Seventh International Conference Principles of Knowledge Representation and Reasoning, KR 2000, 11–15 April 2000, Breckenridge, Colorado, USA, pp. 345–352 (2000)
White, C.C.: A survey on the integration of decision analysis and expert systems for decision support. IEEE Trans. Syst. Man Cybern. 20(2), 358–364 (1990)
Acknowledgments
This work was partially supported by funds provided by CONICET, Agencia Nacional de Promoción Científica y Tecnológica, Universidad Nacional del Sur (UNS), Argentina, and by the EU H2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement 690974 for the project “MIREL: MIning and REasoning with Legal texts”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Martinez, M.V., Simari, G.I. (2019). Explanation-Friendly Query Answering Under Uncertainty. In: Krötzsch, M., Stepanova, D. (eds) Reasoning Web. Explainable Artificial Intelligence. Lecture Notes in Computer Science(), vol 11810. Springer, Cham. https://doi.org/10.1007/978-3-030-31423-1_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-31423-1_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-31422-4
Online ISBN: 978-3-030-31423-1
eBook Packages: Computer ScienceComputer Science (R0)






 ).
).




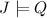 if and only if there exists a homomorphism from the canonical database instance
if and only if there exists a homomorphism from the canonical database instance