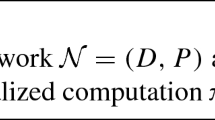Liveness in Broadcast Networks

Abstract

We study two liveness verification problems for broadcast networks, a system model of identical clients communicating via message passing. The first problem is liveness verification. It asks whether there is a computation such that one of the clients visits a final state infinitely often. The complexity of the problem has been open since 2010 when it was shown to be $\mathsf{P}$-hard and solvable in $\mathsf{EXPSPACE}$. We close the gap by a polynomial-time algorithm. The algorithm relies on a characterization of live computations in terms of paths in a suitable graph, combined with a fixed-point iteration to efficiently check the existence of such paths. The second problem is fair liveness verification. It asks for a computation where all participating clients visit a final state infinitely often. We adjust the algorithm to also solve fair liveness in polynomial time.

1 Introduction

Parameterized systems consist of an arbitrary number of identical clients that communicate via some mechanism like a shared memory or message passing [3]. Parameterized systems appear in various applications. In distributed algorithms, a group of clients has to form a consensus [29]. In cache-coherence protocols, coherence has to be guaranteed for data shared among threads [10]. Developing parameterized systems is difficult. The desired functionality has to be achieved not only for a single system instance but for an arbitrary number of clients that is not known a priori. The proposed solutions are generally tricky and sometimes buggy [2], which has lead to substantial interest in parameterized verification [7], verification algorithms for parameterized systems.

Broadcast networks are a particularly successful model for parameterized verification [4, 6, 8, 9, 11, 12, 17, 20, 21, 24, 36]. A broadcast network consists of an arbitrary number of identical finite-state automata communicating via passing messages. We call these automata clients, because they reflect the interaction of a single client in the parameterized system with its environment. When a client sends a message (by taking a send transition), at the same time a number of clients receive the message (by taking a corresponding receive transition). A client ready to receive a message may decide to ignore it, and it may be the case that nobody receives the message.

What makes broadcast networks interesting is the surprisingly low complexity of their verification problems. Earlier works have concentrated on safety verification. In the coverability problem, the question is whether at least one participating client can reach an unsafe state. The problem has been shown to be solvable in polynomial time [11]. In the synchronization problem, all clients need to visit a final state at the same time. Although seemingly harder than coverability, it turned out to be solvable in polynomial time as well [23]. Both problems remain in $\mathsf{P}$ if the communication topology is slightly restricted [4], a strengthening that usually leads to undecidability results [4, 12].

The focus of our work is on liveness verification. Liveness properties formulate good events that should happen during a computation. To give an example, one would state that every request has to be followed by a response. In the setting of broadcast networks, liveness verification was studied in [12]. The problem generalizes coverability in that at least one client needs to visit a final state infinitely many times. The problem was shown to be solvable in $\mathsf{EXPSPACE}$ by a reduction to repeated coverability in Petri Nets [18, 22]. The only known lower bound, however, is $\mathsf{P}$-hardness [11].

Our contribution is an algorithm that solves the liveness verification problem in polynomial time. It closes the aforementioned gap. We also address a fair variant of liveness verification where all clients participating infinitely often in a computation have to see a final state infinitely often, a requirement known as compassion [33]. We give an instrumentation that compiles away compassion and reduces the problem to finding cycles. By our results, safety and liveness verification have the same complexity, a phenomenon that has been observed in other models as well [17, 19, 24, 25].

Our results yield efficient algorithms for (fair) model checking broadcast networks against linear-time specifications [32]. If the specification is given as an automaton [37], we compute a product with the clients and run our algorithms.

At the heart of our liveness verification algorithm is a fixed-point iteration that terminates in polynomial time. It relies on an efficient representation of computations. We first characterize live computations in terms of paths in a suitable graph. Since the graph is of exponential size, we cannot immediately apply a path finding algorithm. Instead, we show that a path exists if and only if there is a path in some normal form. Paths in normal form can then be found efficiently by the fixed-point iteration. The normal form result is inspired by ideas presented in [23].

Related Work. We already discussed the related work on safety and liveness verification of broadcast networks. Broadcast networks [12, 20, 36] were introduced to verify ad hoc networks [28, 35]. Ad hoc networks are reconfigurable in that the number of clients as well as their communication topology may change during the computation. If the transition relation is compatible with the topology, safety verification has been shown to be decidable [27]. Related studies do not assume compatibility but restrict the topology [26]. If the dependencies among clients are bounded [30], safety verification is decidable independent of the transition relation [38, 39]. Verification tools turn these decision procedures into practice [15, 31]. D’Osualdo and Ong suggested a typing discipline for the communication topology [16]. In [4], decidability and undecidability results for reachability problems were proven for a locally changing topology. The case when communication is fixed along a given graph was studied in [1]. Topologies with bounded diameter were considered in [13]. Perfect communication where a sent message is received by all clients was studied in [20]. Networks with communication failures were considered in [14]. Probabilistic broadcast networks were studied in [5]. In [6], a variant of broadcast networks was considered where the clients follow a local strategy.

Broadcast networks are related to the leader-contributor model. It has a fixed leader and an arbitrary number of identical contributors that communicate via a shared memory. The model was introduced in [24]. The case when the leader and all contributors are finite-state automata was considered in [21] and the corresponding reachability problem was proven to be $\mathsf{NP}$-complete. In [9], the authors took a parameterized complexity look at the reachability problem and proved it fixed-parameter tractable. Liveness verification for this model was studied in [17]. The authors show that repeated reachability is $\mathsf{NP}$-complete. Networks with shared memory and randomized scheduler were studied in [8].

For a survey of parameterized verification we refer to [7].

2 Broadcast Networks

We introduce the model of broadcast networks of interest in this paper. Our presentation avoids an explicit characterization of the communication topology in terms of graphs. A broadcast network is a concurrent system consisting of an arbitrary but finite number of identical clients that communicate by passing messages to each other. Formally, it is a pair $\mathcal {N}= (D,P)$. The domain $D$ is a finite set of messages that can be used for communication. A message $a \in D$ can either be sent, $! a$, or received, $? a$. The set $Ops (D) = \lbrace ! a, ? a \mid a \in D \rbrace$ captures the communication operations a client can perform. For modeling the identical clients, we abstract away the internal behavior and focus on the communication with others via $Ops (D)$. With this, the clients are given in the form of a finite state automaton $P= (Q, I, \delta )$, where Q is a finite set of states, $I \subseteq Q$ is a set of initial states, and $\delta \subseteq Q \times Ops (D) \times Q$ is the transition relation. We extend $\delta$ to words in $Ops (D)^*$ and write $q \xrightarrow {w} q'$ instead of $(q,w,q') \in \delta$.

During a communication phase in $\mathcal {N}$, one client sends a message that is received by a number of other clients. This induces a change of the current state in each client participating in the communication. We use configurations to display the current states of the clients. A configuration is a tuple $c~=~(q_1, \dots , q_k) \in Q^k$, $k \in \mathbb {N}$. We use to denote the set of client states occurring in c. To access the components of c, we use $c[i] = q_i$. As the number of clients in the system is arbitrary but fixed, we define the set of all configurations to be $CF = \bigcup _{k \in \mathbb {N}} Q^k$. The set of initial configurations is given by $CF _0=\bigcup _{k \in \mathbb {N}} I^k$. The communication is modeled by a transition relation among configurations. Let $c' = (q'_1, \dots , q'_k)$ be another configuration with k clients and $a \in D$ a message. We have a transition $c \xrightarrow {a}_\mathcal {N}c'$ if the following conditions hold: (1) there is a sender, an $i \in [1..k]$ such that $q_i \xrightarrow {! a} q'_i$, (2) there is a number of receivers, a set $R \subseteq [1..k] \setminus \lbrace i \rbrace$ such that $q_j \xrightarrow {? a} q'_j$ for each $j \in R$, and (3) all other clients stay idle, for all $j \notin R \cup \lbrace i \rbrace$ we have $q_j = q'_j$. We use to denote the indices of clients that contributed to the transition. We extend the transition relation to words $w \in D^*$ and write $c \xrightarrow {w}_\mathcal {N}c'$. Such a sequence of consecutive transitions is called a computation of $\mathcal {N}$. Note that all configurations appearing in a computation have the same number of clients. We write $c \rightarrow ^*_\mathcal {N}c'$ if there is a word $w \in D^*$ with $c \xrightarrow {w}_\mathcal {N}c'$. If $|w| \ge 1$, we also use $c \rightarrow ^+_\mathcal {N}c'$. Where appropriate, we skip $\mathcal {N}$ in the index. We are interested in infinite computations, infinite sequences $\pi =c_0\rightarrow c_1\rightarrow \ldots$ of consecutive transitions. Such a computation is initialized, if $c_0\in CF _0$. We use to denote the set of clients that participate in the computation infinitely often. We let represent the set of clients that visit final states infinitely often.

3 Liveness

We consider the liveness verification problem for broadcast networks. Given a broadcast network $\mathcal {N}= (D,P)$ with $P= (Q, I, \delta )$ and a set of final states $F \subseteq Q$, the problem asks whether there is an infinite initialized computation $\pi$ in which at least one client visits a final state from F infinitely often, .

The liveness verification problem was introduced as repeated coverability in [12]. We show the following:

Theorem 1

The liveness verification problem is $\mathsf{P}$-complete.

$\mathsf{P}$-hardness is due to [11]. Our contribution is a matching polynomial-time decision procedure. Key to our algorithm is the following lemma which relates the existence of an infinite computation to the existence of a finite one.

Lemma 2

There is an infinite computation $c_0 \rightarrow c_1\rightarrow \ldots$ that visits states in F infinitely often if and only if there is a finite computation of the form $c_0 \rightarrow ^* c \rightarrow ^+ c$ with .

If there is a computation of the form $c_0 \rightarrow ^* c \rightarrow ^+ c$ with , then $c \rightarrow ^+ c$ can be iterated infinitely often to obtain an infinite computation visiting F infinitely often. In turn, in any infinite sequence from $Q^k$ one can find a repeating configuration (pigeon hole principle). This in particular holds for the infinite sequence of configurations containing final states.

Our polynomial-time algorithm for the liveness verification problem looks for an appropriate reachable configuration c that can be iterated. The difficulty is that we have a parameterized system, and therefore the number of configurations is not finite. Our approach is to devise a finite graph in which we search for a cycle that mimics the cycle on c. While the graph yields a decision procedure, it will be of exponential size and a naive search for a cycle will require exponential time. We show in a second step how to find a cycle in polynomial time.

The graph underlying our algorithm is inspired by the powerset construction for the determinization of finite state automata [34]. The vertices keep track of sets of states S that a client may be in. Different from finite-state automata, however, there is not only one client in a state $s\in S$ but arbitrarily (but finitely) many. As a consequence, a transition from s to $s'$ may have two effects. Some of the clients in s change their state to $s'$ while others stay in s. In that case, the set of states is updated to $S'=S\cup \lbrace s' \rbrace$. Alternatively, all clients may change their state to $s'$, in which case we get $S'=(S\setminus \lbrace s \rbrace )\cup \lbrace s' \rbrace$.

Formally, the graph of interest is $G = (V, \rightarrow _G)$. The vertices are tuples of sets of states, $V = \bigcup _{k\le |Q|}\mathcal {P}(Q)^{k}$. The parameter k will become clear in a moment. To define the edges, we need some more notation. For $S \subseteq Q$ and $a \in D$, let

$$\begin{aligned} post _{? a}(S)= \lbrace r' \in Q \mid \exists r \in S: r \xrightarrow {? a} r' \rbrace \end{aligned}$$

denote the set of successors of S under transitions receiving a. The set of states in S where receives of a are enabled is denoted by

$$\begin{aligned} enabled _{? a}(S) = \lbrace r \in S \mid post _{? a}( \lbrace r \rbrace ) \ne \emptyset \rbrace . \end{aligned}$$

There is a directed edge $V_1\rightarrow _{G} V_2$ from vertex $V_1=(S_1,\ldots ,S_k)$ to vertex $V_2 = (S'_1,\ldots ,S'_k)$ if the following three conditions are satisfied: (1) there is an index $j \in [1..k]$, states $s \in S_j$ and $s' \in S'_j$, and an element a from the domain $D$ such that $s \xrightarrow {!a} s'$ is a send transition. (2) For each $i \in [1..k]$ there are sets of states $Gen _i \subseteq post _{?a}(S_i)$ and $Kill _i \subseteq enabled _{? a}(S_i)$ such that

$$\begin{aligned} S'_i = \left\{ \begin{aligned}&(S_i \setminus Kill _i) \cup Gen _i,&\text { for } i \ne j, \\&(U_j \setminus Kill _j) \cup Gen _j \cup \lbrace s' \rbrace ,&\text { for } i = j \end{aligned} \right. \end{aligned}$$

where $U_j$ is either $S_j$ or $S_j \setminus \lbrace s \rbrace$. (3) For each index $i \in [1..k]$ and state $q \in Kill _i$, the intersection $post _{? a}(q) \cap Gen _i$ is non-empty.

Intuitively, an edge in the graph mimics a transition in the broadcast network without making explicit the configurations. Condition (1) requires a sender, a component j capable of sending a message a. Clients receiving this message are represented by (2). The set $Gen _i$ consists of those states that are reached by clients performing a corresponding receive transition. These states are added to $S_i$. As mentioned above, states can get killed. If, during a receive transition, all clients decide to move to the target state, the original state will not be present anymore. We capture those states in the set $Kill _i$ and remove them from $S_i$. Condition (3) is needed to guarantee that each killed state is replaced by a target state. Note that for component j we add $s'$ due to the send transition. Moreover, we need to distinguish whether state s gets killed or not.

The following lemma relates a cycle in the constructed graph with a cyclic computation of the form $c \rightarrow ^+ c$. It is crucial for our result.

Lemma 3

There is a cycle $( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ in G if and only if there is a configuration c with and $c \rightarrow ^+ c$.

The lemma explains the restriction of the nodes in the graph to k-tuples of sets of states, with $k\le |Q|$. We explore the transitions for every possible state in c, and there are at most $|Q|$ different states that have to be considered. We have to keep the sets of states separately to make sure that, for every starting state, the corresponding clients perform a cyclic computation.

Proof

We first fix some notations that we use throughout the proof. Let $c \in Q^n$ be any configuration and . By we denote the positions of c storing state s. Given a second configuration $d \in Q^n$, we use the set to represent those states that occur in d at the positions . Intuitively, if there is a sequence of transitions from c to d, these are the target states of those positions of c that store s.

Consider a computation $\pi = c \rightarrow ^+ c$ with . We show that there is a cycle $( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ in G. To this end, assume $\pi$ is of the form $\pi = c \rightarrow c_1 \rightarrow \dots \rightarrow c_\ell \rightarrow c$. Since $c \rightarrow c_1$ is a transition in the broadcast network, there is an edge

in G where each state $s_i$ gets replaced by the set of target states in $c_1$. Applying this argument inductively, we get a path in the graph:

Since ,we found the desired cycle.

For the other direction, let a cycle $\sigma = ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ be given. We construct from $\sigma$ a computation $\pi = c \rightarrow ^+ c$ in the broadcast network such that . The difficulty in constructing $\pi$ is to ensure that at any point in time there are enough clients in appropriate states. For instance, if a transition $s \xrightarrow {! a} s'$ occurs, we need to decide on how many clients to move to $s'$. Having too few clients in $s'$ may stall the computation at a later point: there may be a number of sends required that can only be obtained by transitions from $s'$. If there are too few clients in $s'$, we cannot guarantee the sends. The solution is to start with enough clients in any state. With invariants we guarantee that at any point in time, the number of clients in the needed states suffices.

Let cycle $\sigma$ be $V_0 \rightarrow _G V_1 \rightarrow _G \dots \rightarrow _G V_\ell$ with $V_0 = V_\ell = ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$. Further, let $V_j = (S^1_j, \dots , S^m_j)$. We will construct the computation $\pi$ over configurations in $Q^n$ where $n = m \cdot |Q|^\ell$. The idea is to have $|Q|^\ell$ clients for each of the m components of the vertices $V_i$ occurring in $\sigma$. To access the clients belonging to a particular component, we split up configurations in $Q^n$ into blocks, intervals $I(i) = [(i-1) \cdot |Q|^\ell + 1 \; .. \; i \cdot |Q|^\ell ]$ for each $i \in [1..m]$. Let $d \in Q^n$ be arbitrary. For $i \in [1..m]$, let $B_d(i) = \lbrace d[t] \mid t \in I(i) \rbrace$ be the set of states occurring in the i-th block of d. Moreover, we blockwise collect clients that are currently in a particular state $s \in Q$. Let the set be those positions of d in the i-th block that store state s.

We fix the configuration $c \in Q^n$. For each component $i \in [1..m]$, in the i-th block it contains $|Q|^\ell$ copies of the state $s_i$. Formally, $B_c(i) = \lbrace s_i \rbrace$. Our goal is to construct the computation $\pi = c_0 \rightarrow ^+ c_1 \rightarrow ^+ \dots \rightarrow ^+ c_\ell$ with $c_0 = c_\ell = c$ such that the following two invariants are satisfied. (1) For each $j \in [0..\ell ]$ and $i \in [1..m]$ we have $B_{c_j}(i) \subseteq S^i_j$. (2) For any state s in a set $S^i_j$ we have . Intuitively, (1) means that during the computation $\pi$ we visit at most those states that occur in the cycle $\sigma$. Invariant (2) guarantees that at each configuration $c_j$ there are enough clients available in these states.

We construct $\pi$ inductively. The base case is given by configuration $c_0 = c$ which satisfies invariants (1) and (2) by definition. For the induction step, assume $c_j$ is already constructed such that (1) and (2) hold for the configuration. Our first goal is to construct a configuration d such that $c_j \rightarrow ^+ d$ and d satisfies invariant (2). In a second step we show to construct a computation $d \rightarrow ^* c_{j+1}$.

In the cycle $\sigma$ there is an edge $V_j \rightarrow _G V_{j+1}$. From the definition of $\rightarrow _G$ we get a component $t \in [1..m]$, states $s \in S^t_j$ and $s' \in S^t_{j+1}$, and an $a \in D$ such that there is a send transition $s \xrightarrow {! a} s'$. Moreover, there are sets $Gen _t \subseteq post _{? a}(S^t_j)$ and $Kill _t \subseteq enabled _{? a}(S^t_j)$ such that the following equality holds:

$$\begin{aligned} S^t_{j+1} = (U_t \setminus Kill _t) \cup Gen _t \cup \lbrace s' \rbrace . \end{aligned}$$

Here, $U_t$ is either $S^t_j$ or $S^t_j \setminus \lbrace s \rbrace$. We focus on t and take care of other components later. We apply a case distinction for the states in $S_{j+1}^t$.

Let q be a state in $S_{j+1}^t \setminus \lbrace s' \rbrace$. If $q \in Gen _t$, there exists a $p \in S^t_j$ such that $p \xrightarrow {? a} q$. We apply this transition to $|Q|^{\ell - (j+1)}$ many clients in the t-th block of configuration $c_j$. If $q \in U_t \setminus Kill _t$ and q not in $Gen _t$, then certainly $q \in U_t \subseteq S^t_j$. In this case, we let $|Q|^{\ell -(j+1)}$ many clients of block t stay idle in state q. For state $s'$, we apply a sequence of sends. More precise, we apply the transition $s \xrightarrow {! a} s'$ to $|Q|^{\ell - (j+1)}$ many clients in block t of $c_j$. The first of these sends synchronizes with the previously described receive transitions. The other sends do not have any receivers. For components different from t, we apply the same procedure. Since there are only receive transitions, we also let them synchronize with the first send of a. This leads to a computation $\tau$

We argue that the computation $\tau$ is valid: there are enough clients in $c_j$ such that $\tau$ can be carried out. We again focus on component t, the reasoning for the other components is similar. Let . Note that the equality is due to invariants (1) and (2). We count the clients of $c_j$ in state p (in block t) that are needed to perform $\tau$. We need

of these clients. The set $post _{? a}(p) \cup \lbrace p,s' \rbrace$ appears as a consequence of the case distinction above: there may be transitions mapping p to a state in $post _{? a}(p)$, it may happen that clients stay idle in p, and in the case $p = s$, we need to add $s'$ for the send transition. Since by invariant (2), we get that $\tau$ is a valid computation. Moreover, note that configuration d satisfies invariant (2) for $j+1$: for each state $q \in S_{j+1}^t$, the computation $\tau$ was constructed such that .

To satisfy invariant (1), we need to erase states that are present in d but not in $S_{j+1}^t$. To this end, we reconsider the set $Kill _t \subseteq enabled _{? a}(S_j^t)$. For each state $p \in Kill _t$, we know by the definition of $\rightarrow _G$ that $post _{? a}(p) \cap Gen _t \ne \emptyset$. Hence, there is a $q \in S_{j+1}^t$ such that $p \xrightarrow {? a} q$. We apply this transition to all clients in d currently in state p that were not active in the computation $\tau$. In case $U_t = S_j^t \setminus \lbrace s \rbrace$, we apply the send $s \xrightarrow {! a} s'$ to all clients that are still in s and were not active in $\tau$. Altogether, this leads to a computation $\eta = d \rightarrow ^* c_{j+1}$.

There is a subtlety in the definition of $\eta$. There may be no send transition for the receivers to synchronize with since s may not need to be erased. In this case, we synchronize the receive transitions of $\eta$ with the last send of $\tau$. This does not change the result.

Computation $\eta$ substitutes the states in $Kill _t$ and state s, depending on $U_t$, by states in $S_{j+1}^t$. But this means that in the t-th block of $c_{j+1}$, there are only states of $S_{j+1}^t$ left. Hence, $B_{c_{j+1}}(t) \subseteq S_{j+1}^t$, and invariant (1) holds.

After the construction of $\pi = c \rightarrow ^+ c_\ell$, it is left to argue that $c_\ell = c$. But this is due to the fact that invariant (1) holds for $c_\ell$ and $S_{\ell }^t = ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$.   $\square$

The graph G is of exponential size. To obtain a polynomial-time procedure, we cannot just search it for a cycle as required by Lemma 3. Instead, we now show that if such a cycle exists, then there is a cycle in a certain normal form. Hence, it suffices to look for a normal-form cycle. As we will show, this can be done in polynomial time. We define the normal form more generally for paths.

A path is in normal form, if it takes the shape $V_1\rightarrow _G^* V_m\rightarrow _G^* V_n$ such that the following conditions hold. In the prefix $V_1\rightarrow _G^* V_m$ the sets of states increase monotonically, $V_i \sqsubseteq V_{i+1}$ for all $i\in [1..m-1]$. Here, $\sqsubseteq$ denotes the componentwise inclusion. In the suffix $V_m\rightarrow _G^* V_n$, the sets of states decrease monotonically, $V_i\sqsupseteq V_{i+1}$ for all $i\in [m..n-1]$. The following lemma states that if there is a path in the graph, then there is also a path in normal form. The intuition is that the variants of the transitions that decrease the sets of states can be postponed towards the end of the computation.

Lemma 4

There is a path from $V_1$ to $V_2$ in G if and only if there is a path in normal form from $V_1$ to $V_2$.

Proof

If $V_1 \rightarrow ^*_G V_2$ is a path in normal form, there is nothing to prove. For the other direction, let $\sigma = V_1 \rightarrow ^*_G V_2$ be an arbitrary path. To get a path in normal form, we first simulate the edges of $\sigma$ in such a way that no states are deleted. In a second step, we erase the states that should have been deleted. We have to respect a particular deletion order ensuring that we construct a valid path.

Let $\sigma = U_1 \rightarrow _G U_2 \rightarrow _G \dots \rightarrow _G U_\ell$ with $U_1 = V_1$ and $U_\ell = V_2$. We inductively construct an increasing path with $U'_j \sqsupseteq U_i$ or all $i\le j$ by mimicking the edges of $\sigma$.

For the base case, we set $U'_1 = U_1$. Now assume has already been constructed up to vertex $U'_j$. There is an edge $e = U_j \rightarrow _G U_{j+1}$ in $\sigma$. Since $U'_j \sqsupseteq U_j$, we can simulate e on $U'_j$: all states needed to execute the edge are present in $U'_j$. Moreover, we can mimic e such that no state gets deleted. This is achieved by setting the corresponding Kill sets to be empty. Hence, we get an edge $U'_j \rightarrow U'_{j+1}$ with $U'_{j+1} \sqsupseteq U'_j$ (no deletion) and $U'_{j+1} \sqsupseteq U_{j+1}$ (simulation of e).

The states in $V'_2 = U'_\ell$ that are not in $V_2$ are those states that were deleted along $\sigma$. We construct a decreasing path , deleting all these states. To this end, let $V'_2 = (T_1, \dots , T_m)$ and $V_2 = (S_1, \dots , S_m)$. An edge in $\sigma$ deletes sets of states in each component $i \in [1..m]$. Hence, to mimic the deletion, we need to consider subsets of $Del = \bigcup _{i \in [1..m]} (T_i \setminus S_i) \times \lbrace i \rbrace$. Note that the index i in a tuple (s, i) displays the component the state s is in.

Consider the equivalence relation $\sim$ over $Del$ defined by $(x,i) \sim (y,t)$ if and only if the last occurrence of x in component i and y in component t in the path $\sigma$ coincide. Intuitively, two elements are equivalent if they get deleted at the same time and do not appear again in $\sigma$. We introduce an order on the equivalence classes: $[(x,i)]_{\sim } < [(y,t)]_{\sim }$ if and only if the last occurrence of (x, i) was before the last occurrence of (y, t). Since the order is total, we get a partition of $Del$ into equivalence classes $P_1, \dots , P_n$ such that $P_j < P_{j+1}$ for each $j \in [1..n-1]$.

We construct with $K_0 = V'_2$ and $K_n = V_2$ as follows. During each edge $K_{j-1} \rightarrow _G K_j$, we delete precisely the elements in $P_j$ and do not add further states. Deleting $P_j$ is due to an edge $e = U_{k} \rightarrow _G U_{k + 1}$ of $\sigma$. We mimic e in such a way that no state gets added and set the corresponding Gen sets to the empty set. Since we respect the order < with the deletions, the simulation of e is possible. Suppose, we need a state s in component t to simulate e but the state is not available in component t of $K_{j-1}$. Then it was deleted before, $(s,t) \in P_1 \cup \dots \cup P_{j-1}$. But this contradicts that s is present in $U_{k}$. Hence, all the needed states are available.

Since after the last edge of we have deleted all elements from $Del$, we get that $K_n = V_2$. This concludes the proof.    $\square$

Using the normal-form result in Lemma 4, we now give a polynomial-time algorithm to check whether $(\{s_1\}, \dots , \{s_m\}) \rightarrow ^+_G (\{s_1\}, \dots , \{s_m\})$. The idea is to mimic the monotonically increasing prefix of the computation by a suitable post operator, the monotonically decreasing suffix by a suitable pre operator, and intersect the two. The difficulty in computing an appropriate post operator is to ensure that the receive operations are enabled by sends leading to a state in the intersection, and similar for the pre. The solution is to use a greatest fixed-point computation. In a first Kleene iteration step, we determine the ordinary $post ^+$ of $(\{s_1\}, \dots , \{s_m\})$ and intersect it with the $pre ^*$. In the next step, we constrain the $post ^+$ and the $pre ^*$ computations to visiting only states in the previous intersection. The results are intersected again, which may remove further states. Hence, the computation is repeated relative to the new intersection. The thing to note is that we do not work with standard post and pre operators but with operators that are constrained by (tuples of) sets of states.

For the definition of the operators, consider $C = (C_1,\dots ,C_m)\in {\mathcal {P}(Q)}^m$ for an $m \le |Q|$. Given a sequence of sets of states $X_1,\dots ,X_m$ where each $X_i \subseteq C_i$, we define $post _C(X_1,\dots ,X_m)=(X'_1,\dots ,X'_m)$ with

$$\begin{aligned} X'_i\; =&\; \lbrace s'\in Q \mid \exists s \in X_i: s \xrightarrow {! a}_{P\downarrow _{C_i}} s' \rbrace \\ \cup&\; \lbrace s'\in Q \mid \exists s_1,s_2 \in X_\ell : \exists s \in X_i: s_1 \xrightarrow {! a}_{P\downarrow _{C_\ell }} s_2\wedge s \xrightarrow {? a}_{P\downarrow _{C_i}} s' \rbrace \;. \end{aligned}$$

Here, $P\!\downarrow _{C_{i}}$ denotes the automaton obtained from $P$ by restricting it to the states $C_{i}$. Similarly, we define $pre _C(X_1,\dots ,X_m)=(X'_1,\dots ,X'_m)$ with

$$\begin{aligned} X'_i\; =&\; \lbrace s\in Q \mid \exists s' \in X_i: s \xrightarrow {! a}_{P\downarrow _{C_i}} s' \rbrace \\ \cup&\; \lbrace s\in Q \mid \exists s_1,s_2 \in X_\ell : \exists s' \in X_i: s_1 \xrightarrow {! a}_{P\downarrow _{C_\ell }} s_2 \wedge s \xrightarrow {? a}_{P\downarrow _{C_i}} s' \rbrace . \end{aligned}$$

The next lemma shows that the (reflexive) transitive closures of these operators can be computed in polynomial time.

Lemma 5

The closures $post ^+_C(X_1,\dots ,X_m)$ and $pre ^*_C(X_1,\dots ,X_m)$ can be computed in polynomial time.

Proof

Both closures can be computed by a saturation. For $post ^+_C(X_1, \dots , X_m)$, we keep m sets $R_1, \dots , R_m$, each being the post of a component. Initially, we set $R_i = X_i$. The defining equation of $X'_i$ in $post ^+_C(X_1, \dots , X_m)$ gives the saturation. One just needs to substitute $X_i$ by $R_i$ and $X_\ell$ by $R_\ell$ on the right hand side. The resulting set of states is added to $R_i$. This process is applied consecutively to each component and then repeated until the sets $R_i$ do not change anymore, the fixed point is reached.

The saturation terminates in polynomial time. After updating $R_i$ in each component, we either already terminated or added at least one new state to a set $R_i$. Since there are $m \le |Q|$ of these sets and each one is a subset of Q, we need to update the sets $R_i$ at most $|Q|^2$ many times. For a single of these updates, the dominant time factor comes from finding appropriate send and receive transitions. This can be achieved in $\mathcal {O}(|\delta |^2)$ time.

Computing the closure $pre ^*_C(X_1,\dots ,X_m)$ is similar. One can apply the above saturation and only needs to reverse the transitions in the client.    $\square$

As argued above, the existence of a cycle reduces to finding a fixed point. The following lemma shows that it can be computed efficiently.

Lemma 6

There is a cycle $(\{s_1\}, \dots , \{s_m\}) \rightarrow ^+_G (\{s_1\}, \dots , \{s_m\})$ if and only if there is a non-trivial solution to the equation

$$\begin{aligned} C = post ^+_C (\{s_1\}, \dots , \{s_m\}) \cap pre ^*_C (\{s_1\}, \dots , \{s_m\})\;. \end{aligned}$$

Such a solution can be found in polynomial time.

Proof

We use a Kleene iteration to compute the greatest fixed point. It invokes Lemma 5 as a subroutine. Every step of the Kleene iteration reduces the number of states in C by at least one, and initially there are at most $|Q|$ entries with $|Q|$ states each. Hence, we terminate after quadratically many iteration steps.

It is left to prove correctness. Let $( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ be a cycle in G. By Lemma 4 we can assume it to be in normal form. Let $( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G C$ be the increasing part and $C \rightarrow ^*_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ the decreasing part. Then, C is a solution to the equation.

For the other direction, let a solution C be given. Since C is contained in $post ^+_C ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$ we can construct a monotonically increasing path $( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace ) \rightarrow ^+_G C$. Similarly, since $C \subseteq pre ^*_C ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$, we get a decreasing path $C \rightarrow ^*_G ( \lbrace s_1 \rbrace , \dots , \lbrace s_m \rbrace )$. Hence, we get the desired cycle.    $\square$

What is yet open is the question on which states $s_1$ to $s_m$ to perform the search for a cycle. After all, we need that the corresponding configuration is reachable from an initial configuration. The idea is to use the set of all states reachable from an initial state in the client. Note that there is a live computation if and only if there is a live computation involving all those states. Indeed, if a state is not active during the cycle, the corresponding clients will stop moving after an initial set-up phase. Since the states reachable from an initial state can be computed in polynomial time [11], the proof of Theorem 1 is completed.

The liveness verification problem does not take fairness into account. A client may contribute to the live computation (and help the distinguished client reach a final state) without ever making progress towards its own final state.

4 Fair Liveness

We study the fair liveness verification problem that strengthens the requirement on the computation sought. Given a broadcast network $\mathcal {N}= (D, P)$ with clients $P= (Q, I, \delta )$ and a set of final states $F \subseteq Q$, the problem asks whether there is an infinite initialized computation $\pi$ in which clients that send or receive messages infinitely often also visit their final states infinitely often, . This requirement is also known as compassion or strong fairness [33].

We solve the problem by applying the cycle finding algorithm from Sect. 3 to an instrumentation of the given broadcast network. Formally, given an instance $(\mathcal {N}, F)$ of fair liveness, we construct a new broadcast network $\mathcal {N}_F$, containing several copies of Q. Recall that Q is the set of client states in $\mathcal {N}$. The construction ensures that cycles over Q in $\mathcal {N}_F$ correspond to cycles in $\mathcal {N}$ where each participating client sees a final state. Such cycles make up a fair computation. The main result is the following.

Theorem 7

Fair liveness verification is in $\mathsf{P}$.

To explain the instrumentation, we need the notion of a good computation, where good means the computation respects fairness. Computation $c_1 \rightarrow ^+ c_n$ is good for F, denoted $c_1 \Rightarrow _F c_n$, if every client i that makes a move during the computation, $i \in idx (c_j \rightarrow c_{j+1})$ for some j, also sees a final state in the computation, $c_k[i]\in F$ for some k. The following strengthens Lemma 2.

Lemma 8

There is a fair computation from $c_0$ if and only if $c_0\rightarrow ^*c\Rightarrow _F c$.

The broadcast network $\mathcal {N}_F$ is designed to detect good cycles $c \Rightarrow _F c$. The idea is to let the clients compute in phases. The original state space Q is the first phase. As soon as a client participates in the computation, it moves to a second phase given by a copy $\hat{Q}$ of Q. From this copy it enters a third phase $\tilde{Q}$ upon seeing a final state. From $\tilde{Q}$ it may return to Q.

Let the given broadcast network be $\mathcal {N}=(D, P)$ with $P=(Q, I, \delta )$. We define $\mathcal {N}_F = (D\cup \lbrace n \rbrace , P_F)$ with fresh symbol $n\notin D$ and extended client

$$\begin{aligned} P_F = (\bar{Q}, \tilde{I}, \bar{\delta })\quad \text {where}\quad \bar{Q}=Q\cup \hat{Q} \cup \tilde{Q}. \end{aligned}$$

For every transition $(q,a,q') \in \delta$, we have $(q,a,\hat{q}'), (\hat{q},a,\hat{q}'), (\tilde{q},a,\tilde{q}')\in \bar{\delta }$. For every final state $q \in F$ we have $(\hat{q},! n,\tilde{q})\in \bar{\delta }$. For every state $q\in Q$ we have $(\tilde{q}, ! n, q)\in \bar{\delta }$. Configuration c admits a good cycle if and only if there is a cycle at c in the instrumented broadcast network. Even more, also an initial prefix can be mimicked by computations in the third phase.

Lemma 9

$c_0\rightarrow ^*c\Rightarrow _F c$ in $\mathcal {N}$ if and only if $\tilde{c}_0\rightarrow ^*c\rightarrow ^+ c$ in $\mathcal {N}_F$.

We argue that the cycle can be mimicked, the reasoning for the prefix is simpler. A good cycle entails a cycle in the instrumented broadcast network. For the reverse direction, note that in c all clients are in states from Q. As soon as a client participates in the computation, it will move to $\hat{Q}$. To return to Q, the client will have to see a final state. This makes the computation good.

For the proof of Theorem 7, it is left to state the algorithm for finding a computation $\tilde{c}_0\rightarrow ^*c \rightarrow ^+ c$ in $\mathcal {N}_F$. We compute the states reachable from an initial state in $\mathcal {N}_F$. As we are interested in a configuration c over Q, we intersect this set with Q. Both steps can be done in polynomial time. Let $s_1$ up to $s_m$ be the states in the intersection. To these states we apply the fixed-point iteration from Lemma 6. By Lemma 3, the iteration witnesses the existence of a cycle over a configuration c of $\mathcal {N}_F$ that involves only the states $s_1$ up to $s_m$.