Keywords

1 Introduction

The SIFT [1] key-point plays an important role in computer vision and pattern recognition tasks such as structure from motion, object matching, object recognition, and texture analysis [2,3,4,5,6]. Though many other key-points have been proposed [7,8,9,10,11], the SIFT key-point is still favored by many applications especially for those with high accuracy needed [12]. However, the SIFT key-point has also been criticized for the drawback of its heavy computational burden, thus many variational methods have been proposed to accelerate the computational speed, but at the cost of insufficient accuracy or degraded repeatability of the key-points. To efficiently compute the SIFT key-point while preserving the accuracy and repeatability is the goal of this paper. The SIFT key-point is obtained by the DOG blob detector which is an approximation of LOG detector. There are also some other blob detectors such as [13,14,15], but their performance is inferior to SIFT in terms of accuracy and repeatability, as the scale space theory[16, 17] proved that the Gaussian kernel is the only smoothing kernel that could be used to create the image scale space. Based on the center limit theorem, repeated averaging filtering can be used to approximate Gaussian filtering. We propose a bank of averaging filters that accurately approximate the Gaussian filter in the SIFT algorithm, and the averaging filters are implemented via integral images. Because integral image is computed in our method, a combined method for eliminating key-points on the edge is also presented by reusing the integral images, which is more efficient than the original one in SIFT algorithm.

2 A Brief Review of SIFT Scale Space Construction and Key-Point Detection

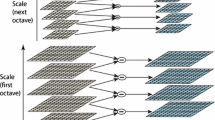
The SIFT scale space consists of two pyramids, the Gaussian pyramid and the DOG(difference of Gaussian) pyramid. The Gaussian pyramid consists of M octaves and each octave consists of N layers. Suppose L(a, b) denotes the ath layer in octave b, it is produced by the convolution of a Gaussian function with the input image I(x, y)

$$\displaystyle \begin{aligned} L(a,b)=G(x,y,\sigma)*I(x,y) \end{aligned} $$
(1)

where ∗ stands for the convolution operation and

$$\displaystyle \begin{aligned} G(x,y,\sigma)=\frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2} \end{aligned} $$
(2)

where σ is determined by a, b and the scale of the first layer σ 0

$$\displaystyle \begin{aligned} \sigma=2^{a+\frac{b}{N-3}}\cdot\sigma_{0} \end{aligned} $$
(3)

Since the computation complexity of Eq. (1) is proportion to σ 2, in practical implementation, smaller σ can be used due to the property of the Gaussian convolution that the convolution of two Gaussian functions is also a Gaussian with variance being the sum of the original variances. That is,

$$\displaystyle \begin{aligned} I(x,y)*G(x,y,\sigma_{1})*G(x,y,\sigma_{2})=I(x,y)*G(x,y,\sigma_{3}) \end{aligned} $$
(4)

where \(\sigma _{1}^{2}+\sigma _{2}^{2}=\sigma _{3}^2\). So, if b ≠ 0, L(a, b) is computed as

$$\displaystyle \begin{aligned} L(a,b)=G(x,y,\sigma_{\text{gap}})*L(a,b-1) \end{aligned} $$
(5)

where

$$\displaystyle \begin{aligned} \sigma_{\text{gap}}=\sqrt{\sigma(0,b)^{2}-\sigma(0,b-1)^{2}} \end{aligned} $$
(6)
Fig. 1
figure 1

The process to construct the SIFT scale space

Full size image

It can be seen from Eq. (6) that each octave shares the same group of σ to generate a successive layer, this is because when b = 0 and a ≠ 0, the L(a, b) is obtained by down sampling the layer L(a − 1, b + N − 2). Once the Gaussian pyramid is computed, the difference of Gaussian pyramid is obtained via the subtraction of two successive layers in the Gaussian pyramid. Figure 1 shows the SIFT scale space construction processes. The SIFT key-point is detected by finding the extrema in the DOG pyramid, after that interpolation is performed to get sub-pixel precision if the key-point is not on the edge.

3 Approximation of Gaussian Smoothing Using Repeated Averaging Filter

In this section, we introduce the quantitative relationship between repeated averaging filtering and Gaussian filtering for a given image. The coefficients of an averaging filter can be viewed as the probability density of a random variable X which is uniformly distributed in a square area centered at the origin. Given an image I(x, y) and an averaging filter A(x, y, w), where w is the window width of the averaging filter, repeated averaging filtering of the image can be mathematically expressed as:

$$\displaystyle \begin{aligned} I(x,y,n)=I(x,y)*\underbrace{A(x,y,w)*A(x,y,w)\ldots A(x,y,w)}_{n} \end{aligned} $$
(7)

Based on the center limit theorem, when n approaches to infinity,

$$\displaystyle \begin{aligned} \begin{aligned} \lim\limits_{n \to \infty }{I(x,y,n)} &=I(x,y)*\lim\limits_{n \to \infty }\underbrace{A(x,y,w)*A(x,y,w)\ldots A(x,y,w)}_{n} \\&=I(x,y)*G(x,y,\sigma_{\text{gau}}) \end{aligned} \end{aligned} $$
(8)

where G(x, y, σ gau) is the Gaussian function with the variance \(\sigma _{\text{gau}}^2\). Suppose the window width of an averaging filter is w, the variance of its corresponding discrete random variable is

$$\displaystyle \begin{aligned} \sigma_{\text{av}}^2=\frac{w^2-1}{12} \end{aligned} $$
(9)

the relation of σ av, σ gau, w and n can be deduced:

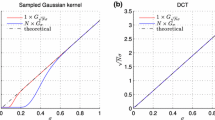
$$\displaystyle \begin{aligned} \sigma_{\text{gau}}=\sqrt{n\sigma_{\text{av}}^2}=\sqrt{\frac{nw^2-n}{12}} \end{aligned} $$
(10)

For discrete averaging filter and discrete Gaussian filter, the two sides of the first equal sign of Eq. (10) are very close to each other when n ≮ 3, which indicates no less than 3 times repeated averaging filtering can well approximate a specified Gaussian filter. Figure 2 shows the two curves are close to each other.

Fig. 2
figure 2

Two similar curves: the red one is the Gaussian kernel with \(\sigma =2 \sqrt {2}\), the blue one is its approximation resulted by 4 times convolution of an averaging filter with the window width w = 5

Full size image

4 Scale Space Construction via Repeated Averaging Filtering

To create the scale space introduced in Sect. 1, the key problem is to seek the initial scale σ 0, a group of Gaussian filters used to construct next layer from current layer and a group of averaging filters to approximate these Gaussian filters. Given a Gaussian kernel, it is not hard to find an optimal averaging filter A(x, y, w) and the times n needed to approximate the Gaussian kernel based on Eq. (10). However, there are more difficulties to get the optimal averaging filter and filtering times in real applications. Here we mainly focus on finding optimal averaging filters to construct the scale space introduced in Sect. 1.

The constraint of Eq. (10) is that n is a positive integer not smaller than 3 and not bigger than 10, because if n < 3 it is not enough to approximate the Gaussian kernel and if n > 10 the computational complexity will have no advantage over the original Gaussian filtering. The variable w should be a positive odd number not smaller than 3, in order to satisfy that there could always be a center pixel the filtering result can be assigned to. Suppose the initial scale of the Gaussian pyramid is σ 0, as most key-points lie in the first several layer of the scale space, thus σ 0 should not be large. According to the original SIFT algorithm where σ 0 = 1.6, here we set σ 0 < 2.0. The number of layers N in each octave depends on the sampling frequency F, and F = N − 3. In [1] the sampling frequency is set to 2, 3, or 4, which gains an acceptable balance between key-point repeatability and computational time. Constraints to σ i under SIFT scale space is that \(\sigma _{i} = \sigma _{0}\sqrt {2^{\frac {2(i+1)}{F}}-2^{\frac {2i}{F}}}\). Besides, \(\sigma _{i} = \sqrt {\frac {n_{i}w_{i}^2-n_{i}}{12}}\) is needed for discrete averaging filters and discrete Gaussian filters. These constraints can be formulated as:

$$\displaystyle \begin{aligned} \sigma_{i} = \sigma_{0}\sqrt{2^{\frac{2(i+1)}{F}}-2^{\frac{2i}{F}}} = \sqrt{\frac{n_{i}w_{i}^2-n_{i}}{12}} \end{aligned} $$
(11)

where i = 1, 2, 3, …, F + 2, σ 0 < 2, n i ∈{3, 4, 5, …, 10}, w i ∈{3, 5, 7, …}. It can be verified that the only solution to Eq. (11) is

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} \sigma_{0} & = \sqrt{2}, \sigma_{1}=2, \sigma_{2}=2\sqrt{2}, \sigma_{3}=4, \sigma_{4}=4\sqrt{2} \\ n_{1}&=3, n_{2}=6, n_{3}=4, n_{4}=4\\ w_{1}&=3, w_{2}=3, w_{3}=5, w_{4}=7\\ F&=2 \end{aligned} \right. \end{aligned} $$
(12)

The approximated SIFT scale space is constructed in the same procedure as it is in the original SIFT algorithm, the Gaussian filters are replaced by averaging filters, and their quantitative relation is given in Eq. (12). Note that the key-point detector in SIFT is actually the DOG detector obtained from subtraction of two Gaussian kernels, Fig. 3 shows the approximated DOG and DOG curves in one octave of the DOG pyramid.

Fig. 3
figure 3

Approximated DOG detector for SIFT key-point detection

Full size image

5 Key-Point Detection

The key-points are detected by searching the local extrema in a 3 × 3 region of the approximated DOG pyramid. However, the DOG detector is sensitive to image edges, and the key-point on the edge should be removed since it is unstable. As integral image is computed in our method (depicted in Fig. 4a), we propose to use fast Hessian measure to reject key-points on the edge. The principal curvature is used to determine whether a point is on the edge, which is computed by the eigenvalues of scale adapted Hessian matrix:

$$\displaystyle \begin{aligned} H(X,\sigma)=\left[\begin{array}{cc} L_{xx}(X,\sigma), &\;\; L_{xy}(X,\sigma) \\ L_{xy}(X,\sigma), &\;\; L_{yy}(X,\sigma) \end{array}\right], \end{aligned} $$
(13)

The partial derivatives in Eq. (13) are computed by integral image and a group of box filters as illustrated in Fig. 4. The images of before and after filtering out the key-point on the edge are shown in Fig. 5. After filtering out the key-points on edge, the scale space quadratic interpolation is performed for every key-point to get a sub-pixel accurate location (Fig. 5).

Fig. 4
figure 4

Using integral image and box filters to compute the partial derivatives of Hessian matrix. (a) The integral image: SUM = A + D − B − C. (b) Box filters to compute the partial derivatives of the Hessian matrix

Full size image
Fig. 5
figure 5

Before-and-after filtering out the edge key-points. (a) Before filtering out the edge key-points. (b) After filtering out the edge key-points

Full size image

6 Experimental Results

The accuracy of our method is validated by the performance comparison of the approximated SIFT detector, SIFT detector, SURF detector, and FAST detector. The SIFT code implemented by Rob Hess [18] is used in our experiment. For the SURF algorithm, we use the original implementation released by its authors. The FAST detector in our experiment is implemented in OpenCV 3.2.0. The datasets proposed by Mikolajczyk and Schmid [19] are used for the evaluation. There are totally 8 datasets, and each dataset has six images with increasing amount of deformation from a reference image. The deformations, covering zoom and rotation (Boat and Bark sequences), view-point change (Wall and Graffiti sequences), brightness changes (Leuven sequence), blur (Trees and Bikes sequence) as well as JPEG compression (UBC sequence), are provided with known ground truth which can be used to identify the correspondence. The repeatability score introduced in [19] is used to measure the reliability of the detectors on detecting the same feature point under different deformations of the same scene. The repeatability score is defined as the ratio between the number of corresponding features and the smaller number of features in one image in the image pair. To give a fair comparison, the thresholds of these detectors are adjusted to give approximately equal number of feature points as SURF detector detected. The results in Fig. 6 show that the SIFT detector has the best performance in most cases, and the proposed method is close to SIFT and better than SURF and FAST detector.

Fig. 6
figure 6

The repeatability of several key-point detectors

Full size image

The efficiency of the proposed method is also compared to SIFT, SURF, and FAST. The times of detection of the key-points in the first image of the wall sequence is shown in Table 1, where we can see that the FAST detector is most efficient among all methods, but it merely detects key-points in one scale, while others detect them in more than 10 scales. The proposed method is about 3 times faster than SURF and 10 times faster than SIFT. Real-world image matching using the approximated SIFT detector with SURF descriptor is shown in Fig. 7.

Table 1 Timing results of SIFT, SURF, FAST and our method for key-point detection on the first image of the Wall sequence (size: 1000 × 700 pixels)
Full size table
Fig. 7
figure 7

Real-world image matching using the approximated SIFT detector with SURF descriptor

Full size image

7 Conclusion

In this paper we have proposed a framework to efficiently and accurately approximate the SIFT scale space for key-point detection. The quantitative relation between repeated averaging filtering and Gaussian filtering has been analyzed, and a group of averaging filters has been found to accurately approximate the DOG detector. Experimental results demonstrate that the proposed method is about 10 times faster than SIFT detector, while preserving the high accuracy and high repeatability of the SIFT detector.