Keywords

1 Introduction

Image segmentation is a fundamental task in many image processing and computer vision applications. However, due to the presence of noise, complex background, low contrast, and intensity inhomogeneity, image segmentation is still a challenging problem. In the past decades, a variety of algorithms for image segmentation have been introduced. Among them, active contour models have attracted considerable interest. The basic idea of the active contour models is to evolve the initial contour towards the object boundaries by minimizing a given energy functional. Although the energy functionals of the active contour models are diverse, they can be divided into two kinds: edge-based methods and region-based methods. Edge-based methods [1,2,3,4] guide a given contour to the object boundaries based on image gradients. The geodesic active contour model [5] is one of the most commonly used models. It utilizes the gradient information to construct an edge stopping function to stop the evolving contours on the object boundaries. Generally, edge-based approaches can provide stable segmentation results when segmenting images with strong object boundaries. However, these models suffer from the leakage problem when segmenting objects with weak boundaries. Moreover, the performance is dependent on the presence of noise as well as the position of initial contours. To overcome these problems, region-based active models have been widely studied. They use intensities or statistics like mean and standard deviation in the energy minimization frameworks. Thus, they are less sensitive to noise and initializations and perform better than edge-based active contour models for the segmentation of images with noise, intensity inhomogeneities, weak and missing boundaries. Specifically, Chan and Vese [6] simplified the Mumford–Shah [7] energy functional by using the variational level set [8] formulation and apply it to image segmentation. Suppose I : Ω → R is the input image, C is a closed contour which can be represented by the level set function ϕ(x), x ∈ Ω . The region inside/outside the contour C can be represented as Ω in = {x ∈ Ω|ϕ(x)〉0} and Ω out = {x ∈ Ω| ϕ(x) < 0}, respectively. Then the energy functional of the C-V model becomes:

$$ \begin{aligned}{E}^{\mathrm{cv}}\left(\phi, {u}_1,{u}_2\right)&={\lambda}_1{\int}_{\!\!\Omega }{\left(I{-}{u}_1\right)}^2{H}_{\epsilon}\left(\phi (x)\right) dx{+}{\lambda}_2{\int}_{\!\!\Omega }{\left(I{-}{u}_2\right)}^2\left(1{-}{H}_{\epsilon}\left(\phi (x)\right)\right) dx\nonumber\\ &\quad+\mu {\int}_{\!\!\Omega }{\delta}_{\varepsilon}\left(\phi (x)\right)\left|\nabla \phi (x)\right| dx,\end{aligned} $$

where μ, λ 1, λ 2 are positive constants. u 1 and u 2 are two constants that represent the average intensities inside and outside the contour. H ε(ϕ(x)) is the regularized approximation of the Heaviside function defined in [8]:

$$ {\displaystyle \begin{array}{l}{H}_{\varepsilon}\left(\phi (x)\right)=\left\{\begin{array}{ll}1& \phi (x)>\varepsilon, \\ {}0& \phi (x)<-\varepsilon, \\ {}\frac{1}{2}\left\{1+\frac{\phi }{\varepsilon }+\frac{1}{\pi}\sin \left(\frac{\pi \phi (x)}{\varepsilon}\right)\right\}& \mathrm{otherwise}.\end{array}\right.\\ {}\end{array}} $$

The derivative of H ε(ϕ(x)) is:

$$ {\delta}_{\varepsilon}\left(\phi (x)\right)=\left\{\begin{array}{ll}0& \left|\phi (x)\right|>\varepsilon, \\ {}\frac{1}{2\varepsilon}\left\{1+\cos \left(\frac{\pi \phi (x)}{\varepsilon}\right)\right\}& \left|\phi (x)\right|<\varepsilon .\end{array}\right. $$

The C-V model assumes that the image intensity is homogeneous. However, when the image intensity is inhomogeneous, the C-V model fails to produce acceptablesegmentation results. To solve the problem of segmenting intensity inhomogeneous images, a popular way is to treat the image information in local region. Li et al. proposed the active contour models: the region-scalable fitting (RSF) [9] model and the local binary fitting (LBF) [10] model which utilize the local intensity information instead of global average intensities inside and outside the contour. The energy functional of the RSF model is defined as:

$$ {\begin{aligned} &{E}^{\mathrm{rsf}}\left(\phi, {u}_1(x),{u}_2(x)\right)=\mu \vphantom{\frac{5}{5_{5_{5}}}}\int_{\varOmega }{\delta}_{\varepsilon}\left(\phi (x)\right)\left|\nabla \phi (x)\right| dx +{\lambda}_1\\&{\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(y)-{u}_1(x)\right)}^2{H}_{\varepsilon}\left(\phi (x)\right) dydx +{\lambda}_2\\&{\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(y)-{u}_2(x)\right)}^2\left(1-{H}_{\varepsilon}\left(\phi (x)\right)\right) dydx\end{aligned}} $$

where μ, λ 1, λ 2 are weights of each term, u 1(x), u 2(x) are smooth functions to approximate the local image intensities inside and outside the contour C. K σ(y − x) is the Gaussian kernel function with variance σ 2 defined as:

$$ {K}_{\sigma}\left(y-x\right)=\frac{1}{2{\pi \sigma}^2}{\mathrm{e}}^{\frac{-{\left|y-x\right|}^2}{2{\sigma}^2}}. $$

K σ has the localization property that it decreases and approaches 0 as |y − x| increases. Due to the usage of local image information, these models can achieve better segmentation results than the C-V model when segmenting images with inhomogeneous intensities. Various kinds of operators that utilize local image information have been proposed to correct or reduce the effect of inhomogeneity. Zhang et al. [11] introduced a local image fitting (LIF) energy and incorporated it into the variational level set framework for the segmentation of images with intensity inhomogeneity. Wang et al. [12] proposed a local Chan–Vese model that utilizes the Gaussian convolution of the original image to describe the local image statistics. Lankton et al. [13] proposed a localized region-based active contour model, which can extract the local image information in a narrow band region. Zhang et al. [14] proposed a level set method for the segmentation of images with intensity inhomogeneity. The inhomogeneous objects are modeled as Gaussian distribution with different means and variances. Wang et al. [15] proposed an improved region-based active contour model which is based on the combination of both global and local image information (LGIF). A hybrid energy functional is defined based on a local intensity fitting term used in the RSF model and a global intensity fitting term in the C-V model. In most of the methods that can deal with intensity inhomogeneous images, the original image is modeled as a multiplicative of the bias or shading which accounts for the intensity inhomogeneity and a true image. These methods seem to produce promising segmentation results when the intensity inhomogeneity varies smoothly [16,17,18,19,20,21,22,23]. However, when the intensity inhomogeneity varies sharply (e.g., the image of a cheetah), they still cannot yield correct segmentation results. Recently, more algorithms are proposed to solve this by employing more features. Qi et al. [24] proposed an anisotropic data fitting term based on local intensity information along the evolving contours to differentiate the sub-regions. A structured gradient vector flow is incorporated into the regularization term to penalize the length of the active contour. Kim et al. [25] proposed a hybrid active contour model which incorporates the salient edge energy defined by higher order statistics on the diffusion space. Zhi et al. [26] proposed a level set based method which utilizes both saliency information and color intensity as region external energy. These models were reported effective for the segmentation of image with intensity inhomogeneity. But these kinds of features seem not powerful enough to handle images with significantly inhomogeneous intensities. More related works can be found in [27,28,29,30,31,32].

In this chapter, we propose a level set framework which can make use of the intensity inhomogeneity in images to accomplish the segmentation. Self-similarity [33] is firstly used to measure and quantify the degree of the intensity inhomogeneity in images. Then a region intensity inhomogeneity energy term is constructed based on the quantified inhomogeneity and incorporated into a variational level set framework. The total energy functional of the proposed algorithm consists of three terms: a local region fitting term, an intensity inhomogeneity energy term, and a regularization term. By integrating these three terms, the intensity inhomogeneity is converted into useful information to improve the segmentation accuracy. The proposed method has been tested on various images and the experimental results show that the proposed model effectively drives the contours to the object boundary compared to the state-of-the-art methods.

2 Model and Algorithm

Image intensity inhomogeneity exists in both medical images and natural images. Intensity inhomogeneity occurs when the intensity between adjacent pixels is different. It is observed that the pattern of intensity inhomogeneity in the same object may be similar. In other words, the intensity difference may have some continuity or consistency in the same object. That is, the quantification of intensity inhomogeneity in the same object may be homogeneous to some extent. Inspired by this, we use the self-similarity to quantify it and then incorporate it into the level set framework. In this way, the intensity inhomogeneity which is often treated as a negative effect is converted to positive effect that can help accomplish the segmentation. Figure 1 shows the flowchart of the proposed algorithm.

Fig. 1
figure 1

The flowchart of the proposed model

Full size image

Firstly, we give the definition of self-similarity. For a given M × M window W centered at x in an input image I, W can be divided into N nonoverlap small n × n patches. We denote the set of features (e.g., image intensity) in the ith small patch as \( {F}_n^i,\kern0.5em i=1,\dots, N \), then the difference between each small patch inside the window W can be defined as:

$$ {D}_{W_x}:= {\left\{{d}_{i,j}\right\}}_{N\times N}={\left\{\mathrm{Diff}\left({F}_n^i,{F}_n^j\right)\right\}}_{N\times N}. $$

Here the \( \mathrm{Diff}\left({F}_n^i,{F}_n^j\right) \) can be calculated as follows:

$$ \mathrm{Diff}\left({F}_n^i,{F}_n^j\right)=\sqrt{\sum {\left({f}_n^i-{f}_n^j\right)}^2}. $$

Here \( {f}_n^i \) is the image intensity value in the ith patch. \( {D}_{W_x} \) evaluates the structure similarity inside W. It is a symmetric positive semi-definite matrix with zero-valued diagonal. If one patch is similar with the other patches inside W, then its corresponding element in \( {D}_{W_x} \) will be small; on the other hand, if one patch is dissimilar with the other patches, then its corresponding element in \( {D}_{W_x} \) will be large. Figure 2 shows the details of computing \( {D}_{W_x} \). After getting the difference inside W, we can define the self-similarity measure. For a given pixel p, t p is a template window region centered at p. The self-similarity measure (SSM) can be obtained by comparing the similarity of the \( {D}_{t_p} \) to \( {D}_{W_x} \) which is the difference of M × M window centered at x in the image. The sum of the squares differences is used to measure the similarity.

$$ \mathrm{SSM}\left({t}_p,{W}_x\right)=\sqrt{\sum \limits_{i=1}^N\sum \limits_{j=1}^N{\left({D}_{t_p}\left(i,j\right)-{D}_{W_x}\left(i,j\right)\right)}^2} $$
Fig. 2
figure 2

The details of the computation of \( {D}_{W_x} \). The \( {D}_{W_x} \) is a symmetric positive semi-definite matrix with zero-valued diagonal

Full size image

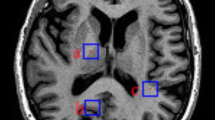
In Fig. 3, we show an example of computing the self-similarity measure. A template region on the object is first selected. From Fig. 3, we can see that, for the region with similar intensity structure with the template region, the SSM of this region is approximately 0, and for the region with the intensity structure significantly different from the template region, the SSM of this region is bigger than 0.

Fig. 3
figure 3

One example of the SSM. Yellow point is the center of the template. Blue point and red point are two center points of the 9 × 9 region selected from object and background, respectively (The center pixels are marked as the same color in the original image). We also show the D w inside each region and the SSM value around the center points, respectively

Full size image

In Fig. 4, more images and their corresponding SSMs are shown. We found that one can use the SSM to define a new image that describes the inhomogeneity of the original image. In this chapter, we call this image intensity inhomogeneity image. Locations with small SSM values are regarded as the same texture as the template. After we get the intensity inhomogeneity image, we can define the intensity inhomogeneity energy under the framework of C-V model:

$$ {\begin{aligned} &{E}_{\mathrm{IIH}}\left(\phi, {Ih}_1,{Ih}_2\right)={\int}_{\!\!\!\varOmega_1}{\left(\mathrm{IIH}-{Ih}_1\right)}^2 dx+{\int}_{\!\!\!\varOmega_2}{\left(\mathrm{IIH}-{Ih}_2\right)}^2 dx\\ &{}={\int}_{\!\!\!\varOmega}{\left(\mathrm{IIH}-{Ih}_1\right)}^2{H}_{\varepsilon}\left(\phi (x)\right) dx+{\int}_{\!\!\varOmega}{\left(\mathrm{IIH}-{Ih}_2\right)}^2\left(1-{H}_{\varepsilon}\left(\phi (x)\right)\right) dx\end{aligned}} $$

where IIH denotes the intensity inhomogeneity image. Ω 1 and Ω 2 denote the regions inside and outside the contour, respectively. and Ih 2 are the average intensities of the IIH image inside and outside the contour.

Fig. 4
figure 4

The intensity inhomogeneity images (SSM) and the original images. W is a 9 × 9 region and it is divided into 9 nonoverlapping 3 × 3 small patches

Full size image

Due to the complexity of natural images, the intensity inhomogeneity image is not powerful enough to yield an accurate result. It is necessary to also consider the intensity information of the original images. In this chapter, we use the region-scalable fitting energy in [8] to utilize the information of the original images:

$$ {\begin{aligned}&{E}_{\mathrm{RSF}}\left(\phi, {u}_1(x),{u}_2(x)\right)={\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(y)-{u}_1(x)\right)}^2{H}_{\varepsilon}\left(\phi (x)\right) dydx\\& {}\kern1em +{\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(y)-{u}_2(x)\right)}^2\left(1-{H}_{\varepsilon}\left(\phi (x)\right)\right) dydx.\end{aligned}} $$

I is the original image. u 1(x), u 2(x) are smooth functions to approximate the local image intensities inside and outside the contour C. K σ(y − x) is the Gaussian kernel function with variation σ 2:

$$ {K}_{\sigma}\left(x-y\right)=\frac{1}{2{\pi \sigma}^2}{\mathrm{e}}^{\frac{-{\left|x-y\right|}^2}{2{\sigma}^2}}. $$

By combining these energies together, we can get the following energy functional:

$$ E={\lambda}_1{E}_{\mathrm{IIH}}+{\lambda}_2{E}_{\mathrm{RSF}}+{\lambda}_3R. $$

Here λ 1, λ 2 and λ 3 are positive constants to balance each energy term. R is the level set regularization term defined as:

$$ R\left(\phi \right)={\int}_{\!\!\!\varOmega}\mid \nabla {H}_{\varepsilon}\left(\phi \right)\mid dx. $$

Then the total energy functional becomes:

$$ { {\begin{aligned}&E\left(\phi, {Ih}_1,{Ih}_2,{u}_1,{u}_2\right)={\lambda}_1\left({\int}_{\!\!\varOmega}{\left(\mathrm{IIH}-{Ih}_1\right)}^2{H}_{\varepsilon}\left(\phi (x)\right) dx\right.\\ &\left.+{\int}_{\!\!\varOmega}{\left(\mathrm{IIH}-{Ih}_2\right)}^2\left(1-{H}_{\varepsilon}\left(\phi (x)\right)\right) dx\right)+{\lambda}_2\left({\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(x)-{u}_1(y)\right)}^2\right.\\ &\left. {H}_{\varepsilon}\left(\phi (x)\right) dydx +{\int}_{\!\!\varOmega}{\int}_{\!\!\varOmega}{K}_{\sigma}\left(x-y\right){\left(I(x)-{u}_2(y)\right)}^2\left(1-{H}_{\varepsilon}\left(\phi (x)\right)\right) dydx\right)\\&{}+{\lambda}_3{\int}_{\!\!\varOmega}\left|\nabla {H}_{\varepsilon}\left(\phi \right)\right| dx.\end{aligned} }}$$

Here Ih 1, Ih 2, u 1, u 2 have the following form:

$$ {Ih}_1=\frac{\int_{\varOmega_{\mathrm{in}}}\mathrm{IIH}\; dx}{\int_{\varOmega_{\mathrm{in}}} dx},\kern1em {Ih}_2=\frac{\int_{\varOmega_{\mathrm{out}}}\mathrm{IIH}\; dx}{\int_{\varOmega_{\mathrm{out}}} dx} $$
$$ {u}_1=\frac{\int_{\varOmega_{\mathrm{in}}}{K}_{\sigma}\left(x-y\right)I(y) dy}{\int_{\varOmega_{\mathrm{in}}}{K}_{\sigma}\left(x-y\right) dy},\kern1em {u}_2=\frac{\int_{\varOmega_{\mathrm{out}}}{K}_{\sigma}\left(x-y\right)I(y) dy}{\int_{\varOmega_{\mathrm{out}}}{K}_{\sigma}\left(x-y\right) dy} $$

By taking the irst variation of the energy functional with respect to ϕ, we can get the following updating equation of ϕ:

$$ { {\begin{aligned}&\frac{\partial \phi }{\partial t}={\delta}_{\varepsilon}\left(\phi (x)\right)\Big({\lambda}_1\left(-{\left(\mathrm{IIH}-{Ih}_1\right)}^2+{\left(\mathrm{IIH}-{Ih}_2\right)}^2\right)\\ &{}{+}{\lambda}_2\left({-}\Big({\int}_{\!\!\varOmega}{K}_{\sigma}\left(y{-}x\right){\left(I(x){-}{u}_1(y)\right)}^2 dy{+}\left({\int}_{\!\!\varOmega}{K}_{\sigma}\left(y{-}x\right){\left(I(x){-}{u}_2(y)\right)}^2 dy\right)\right)\Big)\\&{}+{\lambda}_3\operatorname{div}\left(\frac{\nabla \phi (x)}{\left|\nabla \phi (x)\right|}\right).\end{aligned}}} $$

Different SSMs may be obtained by choosing different template regions. For example, in Fig. 5, we show different SSMs computed by using different templates. Comparing the SSMs of (b) and (c), we can see that the SSMs of (c) are more suitable to assist the segmentation. In other words, an appropriate template is very important for segmentation. In order to automatically choose the optimal position of the template, we use the following strategy: L pixels are randomly selected in the whole image and L templates can be obtained. Then we can get L SSMs by using these templates. The optimal position of the template can be selected by:

$$ \underset{i\in L}{\min }{\left(\frac{1}{L}\sum \limits_{j=1}^L{\left(\mathrm{SSM}\left({T}_i,{T}_j\right)-\mathrm{mean}\left(\mathrm{SSM}\left({T}_i,L\right)\right)\right)}^2\right)}^{\frac{1}{2}}, $$

where \( \mathrm{mean}\left(\mathrm{SSM}\left({T}_i,L\right)\right)=\frac{1}{L}\sum \limits_{j=1}^L\mathrm{SSM}\left({T}_i,{T}_j\right) \). This means that the template region is selected on the pixel whose standard deviation of SSM is the minimum.

Fig. 5
figure 5

(a) The original image. (b, c) The SSM computed by using different template. The red dots are the center points of the template region

Full size image

3 Experimental Results

In this section, we evaluate and compare the proposed model with the C-V model [5], the RSF [9] model, the LGIF model [15], and the LSM model [14]. In these comparisons, for the C-V model, λ 1 = λ 2 = 1, Δt = 0.1, μ which is the weight of the regularization term is set to 6500. For the RSF model, λ 1 = λ 2 = 1, Δt = 0.1, σ = 3, μ is set to 5400. The LGIF model, λ 1 = 0.5, λ 2 = 0.95, they are the weights of the C-V data force and the RSF data force. Δt = 0.1, σ = 3, and the weight for the regularization term is set as μ = 6500. For the LSM model, σ = 3, , the weight for the regularization term is set to 0.2. For the proposed algorithm, N = 9, W = 9, n = 3, σ = 3, λ 1 = 4, λ 2 = 0.1, λ 3 = 5. All the experiments are implemented with Matlab R2017b on a PC of CPU 2.8 GHz, RAM 16G.

We test the segmentation performance of the proposed model on 40 natural images with extremely inhomogeneous intensities which are collected from MSRA dataset [34] and the ECSSD dataset [35]. For quantitative analysis, we compute the F 1-measure given as:

$$ {F}_1=\frac{2\times \mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}. $$

Here \( \mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}\ } \). TP is the number of true positive pixels, FP is the number of false positive pixels, and the FN is the number of false negative pixels. In Fig. 6, we show the comparison results. Results of the quantitative evaluation of these methods are shown in Table 1. In Fig. 6, the original images are shown in the first column, and the ground truths are shown in the second column. The segmentation results of the C-V, RSF, LGIF, LSM, and the proposed algorithm are shown in the other columns, respectively. In the first three images, the extremely inhomogeneous intensities are mainly in the objects and in the last three images, the backgrounds are extreme intensity inhomogeneity. It is shown that the LGIF model and the LSM model perform better than the C-V and the RSF models. In the LGIF model, the author proposed a hybrid model that combines the advantages of both global information (C-V data force) and the local intensity information (RSF data force). For the proposed algorithm, the global information is replaced by the region intensity inhomogeneity term. From the segmentation results, we can see that the proposed algorithm has the overall best performance, which further illustrates that the intensity inhomogeneity in the images can be useful information to assist the segmentation.

Fig. 6
figure 6

Segmentation performance of each algorithm

Full size image
Table 1 F 1-measure of the images in Fig. 3 and the average F 1-measure of the 40 images
Full size table

4 Conclusion

In this chapter, a novel active contour model is proposed for the segmentation of images with intensity inhomogeneity. We use self-similarity to quantify the intensity inhomogeneity in the images. Based on the quantified inhomogeneity, we design a region intensity inhomogeneity energy term and then incorporate it into the level set framework. The proposed model can get promising segmentation results on images with extreme intensity inhomogeneity. The experimental results show that, compared with traditional methods, the proposed segmentation model is more effective.