Keywords

1 Introduction

Clustering analysis is different from classifying analysis that is an unsupervised analysis process. Before the analysis, it does not know the characteristics of all attributes and the importance of all kinds of attributes for the clustering analysis process [1]. The paper [2] introduces the information entropy theory to analyze the attributes of data objects and obtains the importance of each attribute, so as to dynamically adjust the analysis process. The paper [3] introduces the idea of C4.5 algorithm, uses the information gain for the continuous attributes and category attributes, so as to help the category analysis. Although the above papers dynamically analyze the importance of each attribute, they fail to effectively combine the fuzzy theory and the rough theory to deal with nonlinear problems. Fuzzy theory and rough set theory describe problems from the two different aspects: the fuzziness and the uncertainty. Therefore, a lot of papers combine fuzzy theory or rough set theory with clustering analysis algorithm to analyze problems. These papers [4,5,6] use fuzzy clustering algorithm to analyze medical image problem, social service problem, and carbonate fluid detection problem. These papers [7,8,9] use rough clustering algorithm to analyze fault detection in rotating machinery equipment, gene expression problems, and psychological anxiety problems of students. The paper [10] tries to combine the fuzzy theory and rough set theory and applies the algorithm to analyze hydrological engineering. In the process of combination, FCM algorithm is firstly adopted to obtain the mean points of fuzzy clustering, and then the rough set is calculated to obtain the upper and lower approximation of clusters. In the process, the two theories are not combined well, instead there are separated. In the paper [11], data object sets are preprocessed by using support vector machine, then introduces fuzzy clustering and rough set respectively, so the two steps are also independent. In the paper [12], fuzzy rough clustering is applied to the image analysis of brain MRI. In the process of analysis, the difference of membership degree is used to determine the rough boundary, but for calculating the mean point, only using the same method in the FCM algorithm. There are the same defect likely papers [10, 11].

In this paper, a new algorithm is provided. The reduction algorithm in rough set theory is used to obtain the importance of each attribute, dynamically adjust the weight values of each attribute in the iteration calculate process, so as to optimize the value of important attributes. In the clustering analysis, to combine the fuzzy and rough set theories, firstly it gets the fuzzy membership degree of each data object, and then gets fuzzy lower approximations and upper approximations of these clusters. The process effectively combines fuzzy and rough theory by calculating cluster mean points. This method more approximately describes the real world. The new algorithm presented in this paper is proved to have better analysis performance by several related experiments.

Chapter 2 introduces rough set theory and attribute reduction algorithm. This chapter introduces fuzzy clustering and rough clustering. In Chap. 4, fuzzy rough clustering based on reduction is introduced. In Chap. 5, a new algorithm is adopted to analyze multiple data sets. Chapter 6 is the conclusion and expectation.

2 Rough Set Theory and Reduction Algorithm

Rough set theory is a common method to analyze uncertain problems. In this theory, the most important concepts include lower approximation, upper approximation, bound and approximation quality.

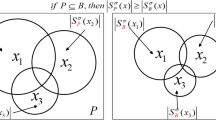
Definition 1 for Low approximation, Upper approximation, and Bound. For an information system IS = (U, A, V, F), B ⊆ A, there exists equivalent relation R B, 〈U, R B〉 is defined as approximate space. For any set X, X ⊆ U, the low approximation of X for 〈U, R B〉 is defined as:

$$ \underline {R_B}X=\left\{x\in U|{\left[x\right]}_B\subseteq X\right\} $$
(1)

The upper approximation of X for 〈U, R B〉 is defined as:

$$ \overline{R_B}X=\left\{x\in U|{\left[x\right]}_B\cap X\ne \phi \right\} $$
(2)

The bound of X for 〈U, R B〉 is defined as:

$$ {BN}_B=\overline{R_B}X-\underline {R_B}X $$
(3)

In formula (1), U is a finite object set for analysis, A is an attribute set for objects. V is a domain set for A, f : U × A → V is an information function. By definition, \( \underline {R_B}X \) is looked as the set composed by objects that certainly belong to X, \( \overline{R_B}X \) is looked as the set composed by objects that probably belong to X, BN B is looked as the set composed by objects that probably belong or not belong to X.

Definition 2, Approximate quality. r B(X) is the rough degree of set X for B, it is defined as:

$$ {r}_B(X)=\mid \underline {R_B}X\mid /\mid X\mid $$
(4)

In formula (4), ∣ • ∣ is the number of elements contained in the set. If r B(X) = 1, it means the bound does not exist, BN B = Φ. If r B(X) < 1, it means that X is rough referring to B.

In the analysis of actual data, there is a lot of redundant information, and the importance of each attribute is different. In order to deal with problems effectively, the attribute reduction of rough set theory can be used to find the importance of attributes and eliminate the irrelevant or redundant attributes, so as to improve the correctness of clustering.

Definition 3, Attribute importance. For the decision table DT = (U, C ∪ D), if B ⊆ C and a ∈ C − B, sigr(a, B, D) is the importance of attribute a referring to attribute set B, sigr(a, B, D) is defined as:

$$ {\mathrm{sig}}_r\left(a,B,D\right)={r}_{B\cup \left\{a\right\}}(D)-{r}_B(D) $$
(5)

In formula (5), r B(D) is the dependent degree of decision attribute D referring to conditional attribute.

According to formula (5), sigr(a, B, D)can be seen as the analysis contribution of attribute a in attribute set B. If the figure of sigr(a, B, D) is bigger, the attribute a is more important for decision. According to this reason, we can get an attribute reduction algorithm. The reduction algorithm starts from an empty attribute set, and then iteratively selects the attribute with the maximum importance. In order to avoid the influence of noise, the algorithm imports a stop threshold ε.

The reduction algorithm is described as follows:

  • Input: decision table DT = (U, C ∪ D), stop threshold ε

  • Output: set B that is arelative reduction of set C for set D

Steps:

 Calculate the reliance of decision attributes on conditional attributes, r C(D);

 B ← ϕ;

  while B ⊂ C do

  begin

   for every a ∈ C − B do

    Calculate sigr(a, B, D);

    Select the attribute a having biggest sigr(a, B, D), if many attributes meet this condition, then select the attribute a that has least number of combinations with attribute set B;

    B ← B ∪ {a};

    if r C(D) − r B(D) ≤ ε

     break;

    end if

   end for

   for every a ∈ B do

    if r C(D) − r B − {a}(D) ≤ ε

    B ← B − {a};

    End if

    output B;

   end for

  end while

3 Fuzzy Clustering and Rough Clustering

3.1 Fuzzy Clustering

Fuzzy c-mean clustering (FCM) is using fuzzy theory into clustering analysis process. In this algorithm, membership degree is used to indicate the possibility of object belonging to a certain cluster. The membership degree u ik is described as how much degree of data object x k belonged to the No. i cluster, u ik ∈ [0, 1], \( {\sum}_{i=1}^C{u}_{ik}=1 \).

The objective function of FCM algorithm is:

$$ {J}_m\left(U,V\right)=\sum \limits_{i=1}^C\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m{d}_{ik}^2 $$
(6)

In formula (6), d ik is described as the distance between the object x k and the mean v i, it is defined as follows:

$$ {d}_{ik}^2={\left\Vert {x}_k-{v}_i\right\Vert}^2 $$
(7)

In formula (6), m is the fuzzy factor, m ∈ [1, ∞]. Usually, m = 2. Through many iterative calculations, the mean point is obtained by the following formula:

$$ \underset{\begin{array}{l}1\le i\le c\\ {}1\le k\le n\end{array}}{\forall }{u}_{ik}=\left\{\begin{array}{ll}{\left({d}_{ik}\right)}^{2/\left(1-m\right)}\left/\left[\sum \limits_{j=1}^c{\left({d}_{jk}\right)}^{2/\left(1-m\right)}\right]\right.,& \mathrm{if}\kern1em {v}_i\ne {x}_k;\\ {}1,& \mathrm{if}\kern1em {v}_i={x}_k;\\ {}0,& \mathrm{if}\kern1em {v}_{\mathrm{l}}={x}_k,l\ne i;\end{array}\right. $$
(8)

and

\( \underset{1\le i\le c}{\forall }{v}_i=\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m{x}_k/\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m \) (9)

3.2 Rough Clustering

Rough c-mean clustering (RCM) is using rough theory into clustering analysis process. In the algorithm, it is agreed that an object can only belong to the lower approximation of one cluster mostly. When calculating the distance between the data object and each mean point, if the difference between these distances is less than a certain threshold value, the object will be divided into the upper approximation of each corresponding cluster. Otherwise, it is divided into the lower approximation of nearest cluster.

According to the definition of lower approximation, upper approximation, and bound in formula (1)–(3), the new definition of mean point in RCM is obtained as follows:

$$ \begin{aligned}&\underset{1\le i\le c}{\forall }{v}_i=\left\{\begin{array}{ll}{w}_l\frac{\sum\limits_{x_k\in {\underline{C}}_i}{\!\!\!\!x}_k}{\mid \underline {C_i}\mid }+{w}_{bn}\frac{\sum \limits_{x_k\in {C}_i^{BN}}{\!\!\!\!\!\!x}_k}{\mid {C}_i^{BN}\mid },& \mathrm{if}\kern1em \underline {C_i}\ne \phi \wedge {C}_i^{BN}\ne \phi; \\[8pt] {}\frac{\sum \limits_{x_k\in {\underline{C}}_i}{\!\!\!\!x}_k}{\mid \underline {C_i}\mid },& \mathrm{if}\kern1em \underline {C_i}\ne \phi \wedge {C}_i^{BN}=\phi; \\[8pt] {}\frac{\sum \limits_{x_k\in {C}_i^{BN}}{\!\!\!\!\!\!x}_k}{\mid {C}_i^{BN}\mid },& \mathrm{if}\kern1em \underline {C_i}=\phi \wedge {C}_i^{BN}\ne \phi; \end{array}\right.\end{aligned} $$
(10)

In the above formula, w l is the weight of lower approximation, w bn is the weight of bound. Then w l + w bn = 1. If w bn is larger, the prior knowledge is less complete, and the information set is rougher.

4 Fuzzy Rough Clustering Based on Attribute Reduction

4.1 Fuzzy Rough Clustering

In practical application scenarios, there are many problems often lacking prior knowledge that are fuzzy description. In this case, if only fuzzy clustering or rough clustering is used, it will inevitably lead to one-sidedness of the analysis process. In this paper, the fuzzy theory and rough set theory are applied to clustering analysis, and a new fuzzy clustering algorithm is designed. In the algorithm, two equivalent classes can be obtained for the set U: they are upper approximation and non-upper approximation; upper approximation can be divided continually into lower approximation and bound; this process is defined in formula (11). However, the definition of mean point is combined with the fuzzy theory and the rough theory. In the analysis, it is believed that the fuzzy degree of data objects belong to the lower approximation, boundary or non-upper approximation of each cluster is different, and the calculation method of fuzzy membership degree is shown in formula (12).

$$ {\displaystyle \begin{array}{rcl}\displaystyle \underset{1\le i\le c}{U}&=&\displaystyle \left\{{x}_k|{x}_k\in \overline{C_i}(X)\right\}\cup \left\{{x}_k|{x}_k\notin \overline{C_i}(X)\right\}\\ {}&=&\displaystyle \left\{{x}_k|{x}_k\in \underline {C_i}\right\}\cup \left\{{x}_k|{x}_k\in {C}_i^{BN}\right\}\cup \left\{{x}_k|{x}_k\notin \overline{C_i}(X)\right\}\end{array}} $$
(11)
$$ \underset{1\le i\le c}{\forall }{v}_i=\left\{\begin{array}{l}\left.\left(\begin{array}{l}{w}_l\frac{\sum \limits_{x_k\in {\underline{C}}_i}{\left({u}_{ik}\right)}^m{x}_k}{\mid \underline {C_i}\mid }+{w}_{bn}\frac{\sum \limits_{x_k\in {C}_i^{BN}}{\left({u}_{ik}\right)}^m{x}_k}{\mid {C}_i^{BN}\mid}\\ {}+\sum \limits_{x_k\notin \overline{C_i}}{\left({u}_{ik}\right)}^m{x}_k\end{array}\right)\right/\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m,\\[8pt] {}\mathrm{if}\kern1em \underline {C_i}\ne \phi \wedge {C}_i^{BN}\ne \phi; \\[8pt] {}\left.\left(\frac{\sum \limits_{x_k\in {\underline{C}}_i}{\left({u}_{ik}\right)}^m{x}_k}{\mid \underline {C_i}\mid }+\sum \limits_{x_k\notin \overline{C_i}}{\left({u}_{ik}\right)}^m{x}_k\right)\right/\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m,\\[8pt] {}\mathrm{if}\kern1em \underline {C_i}\ne \phi \wedge {C}_i^{BN}=\phi; \\[8pt] {}\left.\left(\frac{\sum \limits_{x_k\in {C}_i^{BN}}{\left({u}_{ik}\right)}^m{x}_k}{\mid {C}_i^{BN}\mid }+\sum \limits_{x_k\notin \overline{C_i}}{\left({u}_{ik}\right)}^m{x}_k\right)\right/\sum \limits_{k=1}^n{\left({u}_{ik}\right)}^m,\\ {}\mathrm{if}\kern1em \underline {C_i}=\phi \wedge {C}_i^{BN}\ne \phi; \end{array}\right. $$
(12)

In the formula (12), u ik is got in formula (8).

When analyzing, the fuzzy rough clustering algorithm needs to comply with the following three rules:

  1. (a)

    A data object can only belong to the lower approximation of a cluster.

  2. (b)

    If the data object belongs to the lower approximation of a cluster, it must also belong to the upper approximation of the cluster.

  3. (c)

    When the difference between the maximum fuzzy membership of a cluster (it is u Max) and the fuzzy membership of other cluster (it is u i) is less than a certain threshold value, the data object can belong to the upper approximation of two or more clusters.

In this paper, the threshold in point C above is called the fuzzy rough threshold, which is denoted as δ.

4.2 Fuzzy Rough Clustering Based on Attribute Reduction

In the paper, a fuzzy rough clustering based on attribute reduction (FRCMbR) is proposed. In the calculation process, the algorithm obtains the importance of each attribute by the reduction algorithm. Then it gives different weight value to each attribute according to the importance. At last, it makes corresponding adjustments for the distance between data object and cluster by different weight value. The new difference is calculated as shown in formula (13).

$$ {d}_{ik}^2=\sum \limits_{p=1}^{\mathrm{cond}}{r}_p{\left({x}_{kp}-{v}_{ip}\right)}^2 $$
(13)

where r p is the weight of the No. p attribute of the object, cond is the count of the attributes, and

$$ 1=\sum \limits_{p=1}^{\mathrm{cond}}{r}_p $$
(14)

Fuzzy rough theory is introduced in clustering analysis.

The fuzzy rough clustering algorithm is described as follows:

  • Input: Set U has n data objects; number of clusters (c); lower approximate weight (w l); bound weight (w bn); fuzzy rough threshold (δ); algorithm stop threshold (ε).

  • Output: c clusters

Steps:

 Initialize the weight of each attribute of a data object: r p ← 1/n;

 Randomly generate the c mean points of each cluster,

 The number of iterations: j ← 0;

 do

  Running the reduction algorithm to get the weight of each attribute;

  Using formula (13) calculate the difference between data objects and each cluster;

  Using formula (8) get the membership degree of each object (u ik) in the No. j iteration calculation;

  if ∣u ik − u mk ∣  ≤ δ && i ≠ m

   \( \overline{C_i}\leftarrow \overline{C_i}\cup \left\{{x}_k\right\} \);

   \( \overline{C_m}\leftarrow \overline{C_m}\cup \left\{{x}_k\right\} \);

  else

   \( \underline {C_i}\leftarrow \underline {C_i}\cup \left\{{x}_k\right\} \)

  end if-else

  Using formula (12) get the mean points of each cluster again;

  The number of iterations: j ← j + 1;

 while \( \left(\max \left\{|{u}_{ik}^{(j)}-{u}_{ik}^{\left(j-1\right)}|\right\}>\varepsilon \right) \);

 end do-while;

5 Experiments of FRCMbR Algorithm

5.1 Experimental Setting

The computer configuration for testing the algorithm: CPU is 2.93 GHz dual–core, and the memory is 4 GB. Software configuration: Window 7, Matlab2007. The experimental UCI data sets are Iris, Nursery, Ionosophere, and Isolet5, respectively. The characteristics of the data sets are shown in Table 1.

Table 1 Characterization of four UCI sets
Full size table

The definition of accuracy in the experiment is as follows:

$$ \mathrm{accurate}(U)=\frac{\sum_{k=1}^c{\mathrm{correct}}_i}{\mid U\mid }\vspace*{-3pt} $$
(15)

In formula (15), ∣U∣ is the number of data sets, and correcti is the number of data objects correctly divided into corresponding clusters.

5.1.1 Comparison of the Accuracy of Each Algorithm

Tables 2, 3, 4, and 5 shows the accuracy of different algorithm after analysis of the above four data sets. For the four experiments of FRCMbR algorithm, the stooping threshold ε = 0.00001, the lower approximate weight w l = 0.9, and the bound weight w bn = 0.1.

Table 2 Comparison of correction for Iris set
Full size table
Table 3 Comparison of correction for Nursery set
Full size table
Table 4 Comparison of correction for Ionosophere set
Full size table
Table 5 Comparison of correction for Isolet5 set
Full size table

According to the analysis results in Tables 2, 3, 4, and 5, the traditional FRCM algorithm combines the fuzzy theory with the rough theory, which makes the analysis more robust. Compared with FCM and RCM, it is more capable of analyzing nonlinear problems, so its analysis results are more accurate. The FRCMbR algorithm proposed in this paper is superior to the other four algorithms because it not only recombines the fuzzy and rough theory, but also conforms to the concept of fuzzy roughness and is close to the real world. In the process of analysis, the weights of each attribute are dynamically adjusted according to the analysis results, so as to optimize the analysis results. From the perspective of Iris and Nursery data sets, if the attribute dimension of the data set is small, the FRCMbR algorithm is superior to the FRCM algorithm, but its advantages are not particularly obvious. When the attribute dimension increases, the FRCMbR algorithm’s analytical capability gradually shows that it is superior to the FRCM algorithm in a word, FRCMbR algorithm has two advantages:

  1. (a)

    FRCMbR algorithm combines the characteristics of fuzzy theory and rough theory, making it better able to deal with nonlinear problems, especially when the background knowledge is not clear, fuzzy, and incomplete, it has more advantages.

  2. (b)

    FRCMbR algorithm introduces reduction algorithm, which can dynamically adjust the weight of attributes according to the actual importance in the analysis, so as to strengthen the major attributes on final analysis results.

5.2 Parameter Experiments of FRCMbR Algorithm

The important parameters to be adjusted in FRCMbR analysis include: lower approximate weight w l, bound weight w bn, fuzzy rough threshold δ, algorithm stop threshold ε. Where the algorithm stop threshold ε generally selects a minimum value approaching 0. The approximate weight w l, bound weight w bn, and fuzzy rough threshold δ are directly related to rough calculation. Therefore, this paper conducts experiments on these three parameters to further verify the validity of FRCMbR algorithm. Among the three parameters, w l and w bn are correlated, w l + w bn = 1, so when analyzing these two parameters, only one of them needs to be set, and the other one can be determined.

In order to test the w l and w bn, it sets δ = 0.1. The algorithm deals with data set Iris, Nursery, Ionosophere, and Isolet5, respectively, 20 times each for each data set, and then average the results. These test results are shown in Fig. 1.

Fig. 1
figure 1

Influence of boundary weight for correction

Full size image

As can be seen in Fig. 1, when it deals with Iris data set, it sets w bn = 0.1, the analysis accuracy 92.7% is the highest; when it deals with Nursery data set, it sets w bn = 0.15, the analysis accuracy 82.7% is the highest; when it deals with Ionosophere data set, it sets w bn = 0.15, the analysis accuracy 85.9% is the highest; when it deals with Isolet5data set, it sets w bn = 0.2, the analysis accuracy 88.4% is the highest. Conclusion can be drawn from the above analysis:

  1. (a)

    When w bn is within the [0.1, 0.2] range, the accuracy is highest. This is because only a small part of the data object that clusters in the whole problem domain is uncertain, but the overall information is uncertain. The impact of these uncertain data objects on the overall analysis results can be small.

  2. (b)

    At that time w bn = 0, FRCMbR algorithm is focused only on the data objects determined by prior knowledge, completely ignoring the bound objects in rough set. And the algorithm is reduced to a fuzzy clustering, that only dealt with lower approximation of each cluster.

  3. (c)

    At that time w bn > 0.25, the analytical capability of FRCMbR algorithm is gradually declined. This is because, in the process, the algorithm will only pay more attention to these objects whose prior knowledge is uncertain, but easing to ignore the objects of the low approximation.

In the fuzzy rough threshold δ test, this paper sets the boundary weight w bn = 0.1, and the algorithm tests the four data sets, respectively. The test results are shown in Fig. 2.

Fig. 2
figure 2

Influence of fuzzy rough threshold for correction

Full size image

As can be seen from Fig. 2 when δ = 0.1 in the test for Iris data set, the highest accuracy rate is 92.7%; when δ = 0.08 in the test for Nursery data set, the highest accuracy rate is 87.7%; when δ = 0.06 in the test for Ionosophere data set, the highest accuracy rate is 84.1%; when δ = 0.06 in the test for Isolet5 data set, the highest accuracy rate is 86.0%. The conclusion is drawn from the above analysis:

  1. (a)

    When the δ value range within the [0.06, 0.1], the accuracy is the highest. This is because most of the data is not fuzzy and uncertainty, only the data of bound that is fuzzy.

  2. (b)

    Comparing with the bound weight w bn, the fuzzy rough threshold δ is a smaller values The reason is that the δ is a difference of fuzzy membership degrees for the data object belonging to different clusters. (e.g., | u ik − u ij| is the difference of fuzzy membership degree for the No. i data object belonging to the No. k or the No. j cluster). The fuzzy membership degree value is small and it is in [0, 1], so the δ is more smaller.

  3. (c)

    At that time δ = 0, the FRCMbR algorithm is no longer capable of rough analysis, and the algorithm is degraded to fuzzy clustering algorithm.

  4. (d)

    At that time δ > 0.1, the analysis capability of FRCMbR algorithm is also declining. This is because as δ increases, the algorithm divides more data objects into the bound, believing that the whole analysis object is more rough, which is inconsistent with the actual situation.

6 Conclusion

Fuzzy theory and rough set theory helps to understand the real world from different angles. When combined with K-Means algorithm, the two theories can be selected according to different scenarios. Fuzzy K-Means is better at the ambiguous and paradoxical problems, while rough K-Means is better at the problems of incomplete prior knowledge or incomplete prerequisite knowledge. The FRCMbR algorithm proposed in this paper combines fuzzy theory and rough set theory and deals with problems from two aspects at the same time. FRCMbR algorithm also introduces the reduction algorithm in rough set theory, in order to obtain the important degree of each attribute, then, dynamically adjust their weight, and further optimize the important attribute. The FRCMbR algorithm is verified through several experiments on UCI data sets. However, in the process of algorithm calculation, the parameter setting will affect the final analysis results. Therefore, it is necessary to further improve the algorithm in future research to reduce the influence of experience factors on the algorithm.