Keywords

1 Introduction

In constraint programming, each problem class is defined by a problem specification; many different specifications are possible for the same problem class. A problem specification identifies a class of combinatorial structures, and lists constraints that these structures must satisfy. A solution is a structure satisfying all constraints. Problem specifications usually also have formal parameters, which are variables for which the specification does not assign values but are not intended to be part of the search for solutions. Values for such formal parameters are provided separately, and the specification together with a particular choice of values for these formal parameters defines a problem instance.

Instance generation is the task of choosing particular values for the formal parameters of a problem instance, and is often a key component of published work when existing benchmarks are inadequate or missing. Our goal is to automate instance generation. We aim to automatically create parameter files containing definitions of the formal parameters of a problem specification, from the high level problem specification itself, and without human intervention.

We automate instance generation by rewriting a high level constraint specification in the Essence language [7] into a sequence of generator instances for the problem class. Values for the parameters of the generator specification are chosen based on the high level types in the problem specification. A solution to a generator instance is a valid parameter file defining a problem instance. We use irace  [15], a popular tool for the automatic configuration of algorithms, to search the space of generator parameters for regions where “graded instances” exist. Graded instances have specific properties; in this work they are satisfiable, and neither too trivial nor too difficult to be solved. However, our methodology does not depend on a specific definition of grading, and can be applied more generally. We first prove the soundness of our rewriting scheme. The system is then empirically evaluated over 5 different problem classes that contain different combinations of integers, functions, matrices, relations and sets of sets. We show the viability of our system and the efficacy of the parameter tuning against randomised search over all problem classes.

2 Related Work

In combinatorial optimisation a wide variety of custom instance generators have been described. These are used to construct synthetic instances for problem classes where too few benchmarks are available. In just the constraint programming literature generators have been proposed for many problem classes, including quasigroup completion [4], curriculum planning [17], graph isomorphism [26], realtime scheduling [11], and bike sharing [6]. Different evolutionary methods have also been proposed to find instances for binary CSPs [18], Quadratic Knapsack [13], and TSP [23]. In particular, Ullrich et al. specified problem classes with a formal language, and used this system to evolve instances for TSP, MaxSAT, and Load Allocation [24]. Efforts have also been made to extend existing repositories of classification problems via automated instance generation [19].

Instance generators are typically built to support other parts of the research, such as verifying robustness of models. However, a generator often requires significant effort to develop, and it cannot be applied to new problem classes without major modifications [24]. A generator is typically controlled by means of parameters, and a further challenge of instance generation is to find regions of parameter values where an instance generator can reliably create interesting instances.

Gent et al. developed parametric generators of instances for several problem classes [8]. They developed a semi-automated prototype to produce instances for discriminating among potential models for a given high-level specification. Their system requires manual rewriting of the domains when there are dependencies between parameters, and does not support all of Essence. In contrast, our system works in a completely automated fashion, for all Essence types, and supports dependencies between formal parameters.

We use the irace system to sample intelligently from the space of instances. irace is a general-purpose tool for automatic configuration of an algorithm’s parameters, and its effectiveness has been shown in a wide range of applications [5, 12, 14, 15]. Our system uses irace to find values of the generator parameters covering graded instances.

Our generator instance method could be applied to many constraint modelling languages such as MiniZinc [20], Zinc [16], Essence Prime [22], or OPL [25]. In this paper we focus on the Essence language [7] because of its support for high level types, and since the open-source Conjure system [1,2,3] provides a convenient basis on which to build an automated instance generation system. We exploit the high level types of Essence to guide the rewriting process.

3 Background

We now introduce notation used in the remainder of the paper.

A problem class is the set of problem instances of interest. A problem specification is a description of a problem class in a constraint specification language. A problem specification defines the types but not the values of several formal parameter variables. An assignment of specific values to the formal parameters is called an input, and a parameter file contains an input. A variable that occurs in the problem specification, but which neither occurs within the scope of a quantifier over that variable, nor is a formal parameter, is called a decision variable. We refer to a specification together with an input as an instance. A solution to an instance is an assignment of values to the decision variables in the instance. An instance is satisfiable if it has a solution. If all input values are of the correct type for the corresponding formal parameters, then the input is valid. An valid instance consists of a specification and a valid input for that specification. Valid instances may have many, one, or no solutions. For optimisation problems, we further wish to search among satisfying solutions to find those of high quality, where quality is determined by an expression to be optimised.

We use the abstract constraint specification language Essence  [7]. This comprises formal parameters ( ), which may themselves be constrained ( ); the combinatorial objects to be found ( ); constraints the objects must satisfy ( ); identifiers declared ( ); and an optional objective function ( ). Essence supports abstract decision variables, such as multiset, relation and function, as well as nested types, such as multiset of sets.

We seek graded instances. With this we mean instances that satisfy pre-defined criteria. The criteria should be tailored to the use to which the instances will be put. In this work, we require graded instances to be neither too easy nor too difficult. To ensure an instance is not too easy, we require that the back-end solver (in our case, Minion [9]) takes at least 10 s to decide the instance. To ensure an instance is not too difficult, we exclude instances for which the solver has not returned a solution in 5 min. Our choices of grading criteria were guided by our computational budget and available resources, and so in this work we have chosen to accept only satisfiable instances as graded. We do not advocate a specific definition of grading, and other criteria for grading would be reasonable, such as “the instance is decided or solved to optimality by at least one solver from a portfolio of solvers in a reasonable amount of time”.

A key step of our method is a process of automatic rewriting, discussed in more detail in Sect. 4.1. Briefly, the rewriting steps are:

  1. 1.

    remove all constraints ( statements) and decision variables ( statements),

  2. 2.

    replace all input parameters ( statements) with decision variables ( statements) and type specific constraints, and

  3. 3.

    promote parameter constraints ( statements) to constraints.

We call the result of this process a generator specification.

Definition 1

A generator instance consists of a generator specification together with a particular choice of generator parameters, which restrict the domains of decision variables appearing in the generator instance.

Rewriting is one step in an iterative process. The choice of generator parameters is performed automatically using the parameter tuning tool irace. Solutions to the generator instance are then filtered according to our grading criteria, retaining graded instances. We want the rewriting procedure to have the following two properties: soundness (the solutions of the generator instance should always be valid inputs for the instance), and completeness (every valid instance should be obtainable as a possible solution of the generator instance). We now discuss the semantics of generator instances and our approach.

Variables may represent tuples, and for clarity of presentation we take some liberties with the corresponding Essence syntax. When referring to a specification s with variables v, we omit the variables that occur within the scope of a quantifier, and partition the remaining variables so that \(s(x\mid y)\) denotes a specification s with formal parameters x and decision variables y, both of which are generally tuples. With \(s(x:=a\mid y)\) we denote the specification \(s'(\mid y)\) (with no formal parameters and only decision variables) which is obtained from s by substituting the tuple of formal parameters x by a fixed tuple of values a.

Start with an Essence specification of the form

where the specification has formal parameters x and decision variables y. We are interested in valid inputs a, such that \(s(x:=a\mid y)\) is a valid instance. Here domain D may be a product of component domains, of arbitrarily nested types as allowed in the Essence language. Now let

be a specification obtained from s(x) by our rewriting process, which drops the original constraints f(x, y), replaces the by a , and modifies statements into statements, leaving a specification with no formal parameters but only decision variables (Note that many possible but equivalent specifications are possible for \(s'\)). In principle we could search for a solution \(x:=a\) to this specification \(s'(\mid x)\), as this would be a valid input for \(s(x\mid y)\), yielding the instance \(s(x:=a\mid y)\). Such search seldom finds graded instances in a reasonable amount of time, unless more guidance is provided.

Thus, we want to introduce a new parameter p with domain P to structure our search for instances. We then rewrite the specification \(s(x\mid y)\) differently, as

so that as the values assigned to the formal parameters p vary, the solutions to the instance \(s''(p:=q\mid x)\) form valid inputs to \(s(x\mid y)\). The specification \(s''(p\mid x)\) will be our generator specification, instead of \(s'(\mid x)\). We can then treat P as a space of parameters, and explore this space with a parameter tuning tool.

The types or domain expressions of the formal parameters x with domain D in the specification \(s'(\mid x)\) may have a lot of structure and be quite complex. Exploring such parameter spaces successfully is a challenging problem. We therefore aim to simplify our task of instance generation by replacing these structured domains by the usually smaller domains D(p) in the new specification \(s''(p\mid x)\), and automatically incorporate this structural information into the constraints c(p, x) instead; the constraints c(p, x) include both the constraints h(x) and also the additional constraints to capture structural information. Like D, the parameter domain P is usually a product of domains, but for P these are usually just intervals of reals, ranges of integers, or Booleans.

4 Methodology

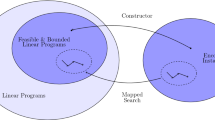
In Fig. 1 we show how our system turns an abstract problem specification into concrete problem instances with the use of rewriting rules and an iterated sequence of tuned generator instances. The steps of the automated process are:

  1. 1.

    Start with a specification of a problem in the Essence language.

  2. 2.

    Rewrite the problem specification into a generator specification (Sect. 4.1).

  3. 3.

    Create a configuration file for the parameter tuner irace.

  4. 4.

    irace searches for promising values of the generator parameters (Sect. 4.3).

  5. 5.

    At each iteration the current generator instance is used to create multiple problem instances which are solved by Savile Row [21].

  6. 6.

    The time to solve an instance and its satisfiability are used as feedback to irace about the quality of the current parameters.

  7. 7.

    At the end of the process several problem instances are generated.

The rest of this section describes the details of this process, correctness of the rewriting procedure, how we use tuning based on instance difficulty, the problem classes we studied, and our experimental setup.

Fig. 1.
figure 1

Essence specifications (top-left) are fed to the Conjure parameter generator (left-red). Here they are rewritten into a generator specification and a configuration file for irace (bottom-green), which selects parameter values to generate a synthetic instance (centre-purple). Solution meta-data are used to inform the tuner. (Color figure online)

Full size image

4.1 Rewriting Rules

For each Essence type we deploy a set of rules that transform a statement into a different Essence statement or set of statements that captures the problem of finding valid input parameters for the initial . Whenever a given type is nested inside other types, such as an input parameter, the rewriting rules are applied recursively until an explicit numerical value is obtained.

4.1.1 Rewriting int   

For every integer domain, we generate two configurator parameters, and . The domains of these configurator parameters are identical to that of the original integer domain. If the original domain is not finite, we use and values as bounds, which are to be provided to Conjure. Default values for and are 0 and 50, respectively. For an integer decision variable we generate the following constraints to relate it to the corresponding and parameters: and .

figure ac

is rewritten as:

figure ad

4.1.2 Rewriting function   

For every parameter with a domain, we produce a decision variable that has a finite function domain and additional constraints to ensure it can only be assigned to the allowed values. Total function domains are rewritten as (without the attribute) and add an extra constraint to ensure the function is defined (NB returns the set of elements of the range of function that have an image) up to the value required.

figure aj

is rewritten as:

figure ak

4.1.3 Rewriting matrix   

Each is rewritten into a and the rewriting rules for functions are utilised.

4.1.4 Rewriting relation

For relations we generate two configurator parameters that bound the cardinality of the relations, two that bound the left-hand side values of the relation ( ), and another two for the right-hand side values ( ).

figure ap

is rewritten as:

figure aq

4.1.5 Rewriting set

We discuss the case of a . Here we generate a pair of configurator parameters for the cardinality of the outer set with the usual bounds, then for the cardinality of the inner set we use a much smaller and use the size of the set as . Finally another pair of parameters bounds the size of the innermost set. The outer cardinality and the innermost bounds parameters are omitted as they are equivalent to the ones for and , respectively.

figure aw

is rewritten as:

figure ax

4.2 Correctness of Instance Generation via Generator Instances

We need to prove that the rewriting that Conjure does to turn an Essence specification into a generator instance is sound, in that rewriting should always produce an instance that is a valid input to the specification. We show soundness by means of a decomposition based on types; we illustrate the proof for the case of total functions and leave the remaining cases to the full version of the paper. We also wish rewriting to be complete, in that every possible instance for the specification should be an output of the instance generator specification as long as it is given the right parameter file as input, but this is only possible for instances that satisfy some additional assumptions.

We illustrate the rewriting process with the following example, which demonstrates the rewriting of the type for a restricted instance. Given the specification as in the example Sect. 4.1.2 our system rewrites this into the generator specification

 

We have built our system to ensure soundness by design.

Proposition 1

The semantics of our rewriting rule for types is sound.

Proof

Consider a solution of the generator instance

where the values u, v, r, s are provided in a parameter file, created by our system. This solution consists of an integer in the range and a function with domain and codomain . The constraints force to be defined over the entire range , and for its values to be in the range

Moreover must hold as a consequence of the choices made by the system for and . Similarly the system ensures that . Hence is a total function with domain and codomain . Therefore together with a solution of the generator instance is a valid instance.    \(\square \)

The other types can be dealt with similarly; in particular, proofs for nested types follow a standard compositional style.

In contrast, it seems challenging to ensure completeness. One issue is infinite domains: when a formal parameter of a specification has a type that allows an infinite domain, then any restriction of this domain to a finite set means that the rewriting process cannot be complete. However, our current system is built on Conjure and requires finite domains for all decision variables. Our generator specifications therefore restrict all domains to be finite, and in such cases completeness is necessarily lost. For specifications where the domains of the formal parameters are all finite, it seems possible to guarantee completeness. Parameters that are dependent can be another obstacle to achieving completeness. To avoid this issue the generator parameters must all be sampled independently and the rewriting process must ensure that no dependencies between parameters are introduced. We leave issues of completeness to further work.

4.3 Tuning Instance Difficulty

Posing the problem of finding valid instances as Essence statements is a fundamental step but not sufficient for the reliable creation of problem instances. Efficient and effective searching in the instance space for graded instances is not a trivial task. We solve this problem by utilising the tuning tool irace. In this section, we first describe the tuning procedure of irace. We then explain how we have applied irace, including details of the input to irace and the feedback provided by each generator’s evaluation to guide the search of irace.

4.3.1 The Tuning Procedure of irace

We give a brief summary of the specific tuning procedure implemented by irace and explain why such an automatic algorithm configurator is a good choice for our system in the next section. For a detailed description of irace and its applications, readers are referred to [15].

The algorithm configuration problem irace tackles is as follows: given a parameterised algorithm A and a problem instance set I, we want to find algorithm configurations of A that optimise a performance metric defined on I, such as minimising the average solving time of A across all instances in I. The main idea of irace is using racing, a machine learning technique, in an iterated fashion to efficiently use the tuning budget. Each iteration of irace is a race. At the first iteration, a set of configurations is randomly generated and these are evaluated on a number of instances. A statistical test is then applied to eliminate the statistically significantly worse configurations. The remaining configurations continue to be tested on more instances before the statistical test is applied again. At the end of the race, the surviving configurations are used to update a sampling model. This model is then used to generate a set of new configurations for the next iteration (race). This process repeats until the tuning budget is exhausted. The search mechanism of irace allows it to focus more on the regions of promising configurations: the more promising a configuration is, the more instances it is evaluated on and the more accurate the estimate of its performance over the whole instance set I will be. This is particularly useful when I is a large set and/or A is a stochastic algorithm.

4.3.2 Using irace to Find Graded Instances

In our instance generation context, the parameterised algorithm A is our generator instance. Each input for the generator instance, which we call a generator configuration, will cover a part of the instance space. The instance set I in our context is a set of random seeds. The search procedure of irace enables efficient usage of the tuning budget, as the more promising an instance region covered by a configuration proves, the more instances will be generated from it.

Paired with each Essence generator specification there is a configuration file that is utilised by irace to tune the parameters of the generator specification. The configuration file is automatically created by Conjure and defines a generator configuration.

Given a random seed, an evaluation of a generator configuration involves two steps. First, a problem instance is generated by solving the generator instance using Conjure, Savile Row, and Minion. The generator configuration normally covers several instances, and the random seed is passed to Minion for deciding which instance is to be returned.

Second, the generated instance is solved by Minion, and its satisfaction property and the solving time are recorded. We use these values to assign a score to the generator configuration. The highest score is given if the instance satisfies our grading criteria, so that irace is guided to move towards the generator’s configuration spaces where graded instances lie. The assignment of scores depends on the specific definition of instance grading. In our case, we define graded instances as satisfiable (SAT) and solvable by Minion within [10, 300] seconds. We also place a time limit of 5 min on Savile Row for the translation from the Essence instance parameter to Minion input format. A score of 0 is given if the generated instance is either UNSAT, or too difficult (Minion times out), or too large (Savile Row times out). If the instance is SAT but too easy (solvable by Minion in less than 10 s), the Minion solving time is returned as the score. If the instance satisfies our grading criteria, a score of 10 is returned. The scale of the scores is not important, as the default choice for the statistical test used in irace is the Friedman test, a non-parametric test where scores are converted to ranks before being compared. Following tuning, we collect the set of graded instances generated. irace also returns a number of promising generator configurations. These configurations can be kept for when we want to sample more graded instances that are similar to the ones produced by the tuning procedure.

4.4 Problem Classes

CSPlib is a diverse collection of combinatorial search problems, covering ancient puzzles, operational research, and group theory [10]. Most of these problems have Essence specifications. To test our system we have selected representative problems that span most of the Essence types used for formal parameters in CSPlib. We now briefly describe each of these problems (with CSPlib problem numbers).

Template Design (2): The objective is to minimise the wastage in a printing process where the number of templates, the number of design variations and the number of slots are given, while satisfying the demand. The formal parameters are 3 integers and 1 total function.

The Rehearsal Problem (39): The objective is to produce a schedule for a set of musicians that have to practice pieces with specified durations in groups. The goal is to minimise the total amount of time the musicians are waiting to play. The formal parameters are 2 integers, 1 total bijective function and 1 relation.

A Distribution Problem with Wagner-Whitin Costs (40): The objective is to find an ordering policy minimising overall cost, given the number of products, their cost, maximum stock available, their demand, holding costs, and the distribution hierarchy. The formal parameters are 4 integers and 4 matrices.

Synchronous Optical Networking (SONET) Problem (56): Consider a set of nodes and a demand value for each pair of nodes. A ring connects nodes and a node can be installed into the ring using an add-drop multiplexer (ADM). Network traffic can be routed between two nodes only if they are on the same ring. The objective is to minimise the number of ADMs to install while satisfying all demands. The formal parameters are 3 integers and 1 set of sets of integers.

Van der Waerden Numbers (135): The goal is to decide if a given number n is smaller than the Van der Waerden number predefined by a number of colors and an arithmetic length. The problem has 3 formal integer parameters.

4.5 Experimental Setup

We demonstrate our methodology on the five problem classes described in Sect. 4.4. A budget of 1000 generator configuration evaluations is given to the tuning. To illustrate the tuning’s efficiency, we also run the same experiment with uniformly randomly sampling using the same budget.

The system parameter defines the maximum value for any unbounded integer parameters. Here we set it to 50. We leave for future work the questions about the impact of this parameter and the tuning budget on the effectiveness of the system, and how to set them properly given a specific problem class.

We also consider two options for sampling each generator parameter’s values, both of which are supported by irace. The first is linear-scale sampling, where all values in the domain are treated equally at the start of tuning (or during the whole random search). The second is logarithmic-scale sampling, where the logarithms of the lower and upper bounds of the parameter domains are calculated first, and a value is sampled from this new domain before being converted back into the original range. The logarithmic scale makes smaller ranges finer-grained and vice versa, and can potentially help search in scenarios where larger parameter values tend to make instances become either too large or too difficult. This will be demonstrated in our experimental results in the next section.

Table 1. Number of graded instances produced for each problem class and parameter search method within a budget of 1000 evaluations.
Full size table

Each generated instance is solved using Minion for 5 random seeds. During an evaluation of a generator configuration, as soon as the generated instance violates the criteria on one of the seeds, the evaluation is stopped, and the violated run is used as a result for scoring the generator configuration. We use this early-stopping mechanism to maximise the information gained per CPU-hour, as little information is gained from multiple runs on an uninteresting instance.

Experiments were run on two servers, one with 40-core Intel Xeon E5-2640 2.4 GHz, and one with 64-core AMD Opteron 6376 2.3 GHz. All experiments for the same problem class were performed on the same server. Each experiment used between 7 and 95 CPU core hours, depending on problem class and search variants. The experiments we report here used 700 CPU core hours in total.

Table 2. Progress of the four search variants for each problem class, with a budget of 1000 evaluations. Each plot shows how the number of graded instances found grows as the number of evaluations increases. The table displays the number of instances for each problem class, instance category, and search variant. (SR refers to Savile Row.)
Full size table

5 Results and Analysis

In Table 1 we report the number of graded instances found by the four search variants: irace or random search in combination with linear or logarithmic scale-sampling. Across the five problem classes, the winner is always an irace tuning variant. irace with linear-scale sampling works best on Template Design and Van der Waerden Numbers, while irace with logarithmic-scale sampling is able to find more graded instances for Rehearsal, Wagner-Whitin Distribution, and SONET.

In Table 2 we juxtapose plots of the progress over time with the total numbers of instances produced during the process for each problem class, divided into categories. It can be seen that irace vastly outperforms randomised search. In all cases, during the first half of the tuning budget, the difference in performance between irace and random search is not always clearly visible as irace is still in its exploration mode (the few first iterations/races where the sampling model of irace was still initialised). However, by the second half of the budget the tuning has gained some knowledge about the promising regions of the generator configuration space, and irace starts showing a significant boost in the number of graded instances found compared with random search.

In the case of the Rehearsal Problem, where we generate relatively fewer instances compared with other classes, the plot shows that by the end of the tuning budget the system is just picking up pace and it is fair to expect that with more iterations it would produce significantly more instances.

Looking at the category results in Table 2, we can infer some knowledge about the instance space of a specific problem class based on those statistics and the difference in performance between the two scales for sampling (linear vs logarithmic). For example, in the Template Design case, most generated instances are SAT, and are either too easy or graded. The larger number of too easy instances found by the logarithmic scale sampling suggests a strong correlation between the domains of the generator parameters and easiness of the instances generated. Smaller generator configuration values mostly cover SAT and easy-to-solve instances, while larger configurations cover more difficult instances. Since we prefer sufficiently difficult instances to too easy instances, this explains why linear sampling works better than log-scale for this particular problem. A similar explanation can be applied for the Van der Waerden case. However, the large number of too-difficult instances suggests that is probably too large for this problem, and reducing this parameter value could potentially boost performance of the search within our limited budget. Another example is Rehearsal where the statistics indicate a strong correlation between the numbers of UNSAT and too-difficult instances, and between the number of too easy instances and infeasible generator configurations. These suggest that a smaller value combined with linear sampling could potentially improve search performance.

6 Conclusions and Future Work

We have developed a system that automates the production of graded instances for combinatorial optimisation and decision problems. Our system creates a generator specification from an abstract problem specification. Generator parameters are explored using the irace parameter tuning system. We demonstrated the soundness of our approach and performed an empirical evaluation over several problem classes. The experiments showed that automated tuning of generator parameters outperforms random sampling for all problem classes under study, and is able to discover significant numbers of graded instances automatically. The system and all data produced by this work is publicly available as a github repository https://github.com/stacs-cp/CP2019-InstanceGen.

Much future work remains. We first would like to extend our approach to generate instances for every problem class in CSPlib, or at least the ones for which exhibiting a valid instance does not involve first solving long-standing open problems. Many of the classes in CSPlib only have trivially easy instances, or have none, and we would like to remedy this situation. We further seek to automate creation of balanced and heterogeneous sets of instances, by refining our system’s notion of a graded instance, and by further investigating the diversity of the generated instances. We believe much work also remains in investigating grading of instances more generally. As we saw in Sect. 5, some problem classes are especially amenable to automatic discovery of their features; in particular, we plan to automate the choice of sampling regime based on performance of tuning in its early stages. A comparison with existing hand-crafted instances/instance-generators will also be considered. Furthermore the system can be adapted to find instances that are easy for one solver but challenging for other solvers; we believe automating the generation of such instances would greatly assist those researchers who build solvers to improve performance of their solvers. Another application is to find instances with certain structures that reflect real-world instances. Finally, we intend to work toward automatic instance generation for specifications involving infinite domains.