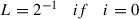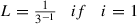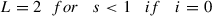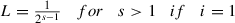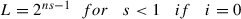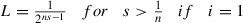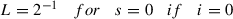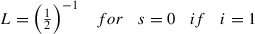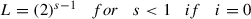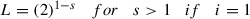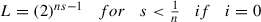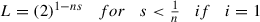Abstract
In this paper, the authors investigate the general solution of a new additive functional equation
where n is a positive integer with \(\mathbb {N}-\{1,2,3,4 \}\) and discuss its generalized Hyers–Ulam stability in Banach spaces and stability in fuzzy normed spaces using two different methods.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
In 1940, Ulam [26] raised the following question. Under what conditions does there exist an additive mapping near an approximately addition mapping? The case of approximately additive functions was solved by Hyers [11] under the assumption that for 𝜖 > 0 and f : E 1 → E 2 be such that ∥f(x + y) − f(x) − f(y)∥≤ 𝜖 for all x, y ∈ E 1 then there exists a unique additive mapping T : E 1 → E 2 such that ∥f(x) − T(x)∥≤ 𝜖 for all x ∈ E 1.
In 1978, a generalized version of the theorem of Hyers for approximately linear mapping was given by Rassias [20]. He proved that for a mapping f : E 1 → E 2 be such that f(tx) is continuous in \(t \in \mathbb {R}\) and for each fixed x ∈ E 1 assume that there exist constant 𝜖 > 0 and p ∈ [0, 1) with
for all x, y ∈ E 1 then there exists a unique R-Linear mapping T : E 1 → E 2 such that
for all x ∈ E 1.
A number of mathematicians were attracted by the result of Rassias. The stability concept that was introduced and investigated by Rassias is called the Hyers–Ulam–Rassias stability.
During the last decades, the stability problems of several functional equations have been extensively investigated by a number of authors [1, 5, 8, 12, 23, 24].
In 1982–1989, Rassias [21, 22] replaced the sum appeared in the right-hand side of the Eq. (1) by the product of powers of norms. In modelling applied problems only partial information may be known (or) there may be a degree of uncertainty in the parameters used in the model or some measurements may be imprecise. Due to such features, we are tempted to consider the study of functional equations in the fuzzy setting.
For the last 40 years, fuzzy theory has become a very active area of research and a lot of development has been made in the theory of fuzzy sets to find the fuzzy analogues of the classical set theory. This branch finds a wide range of applications in the field of science and engineering.
Katsaras [13] introduced an idea of fuzzy norm on a linear space in 1984, in the same year Wu and Fang [27] introduced a notion of fuzzy normed space to give a generalization of the Kolmogoroff normalized theorem for fuzzy topological linear spaces. In 1991, Biswas [4] defined and studied fuzzy inner product spaces in linear space. In 1991, Felbin [7] introduced an alternative definition of a fuzzy norm on a linear topological structures of a fuzzy normed linear spaces. In 1994, Cheng and Mordeson [6] introduced a definition of fuzzy norm on a linear space in such a manner that the corresponding induced fuzzy metric is of Kramosil and Michalek [14]. In 2003, Bag and Samanta [2] modified the definition of Cheng and Mordeson [6] by removing a regular condition. Recently various results have been investigated by numerous authors, one can refer to [3, 9, 10, 15,16,17,18,19, 25].
Before we proceed to the main theorems, we will introduce some definitions and an example to illustrate the idea of fuzzy norm.
Definition 1
Let X be a real linear space. A function \(N:X\times \mathbb {R}\longrightarrow [0,1]\) is said to be fuzzy norm on X if for all x, y ∈ X and \(a,b\in \mathbb {R}.\)
- (N 1 ):
-
N(x, a) = 0 for a ≤ 0;
- (N 2 ):
-
x = 0 iff N(x, a) = 1 for all a > 0;
- (N 3 ):
-
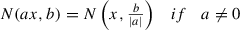 ;
; - (N 4 ):
-
N(x + y, a + b) ≥ min{N(x, a), N(y, b)};
- (N 5 ):
-
N(x, .) is a non-decreasing function on \(\mathbb {R}\) and lim a→∞N(x, a) = 1.
- (N 6 ):
-
For x ≠ 0, N(x, .) is continuous on \(\mathbb {R}\).
The pair (X, N) is called a fuzzy normed linear space. One may regard N(x, a) as the truth value of the statement the norm of x is less than or equal to the real number a.
Definition 2
Let \(\left (X, N\right )\) be a fuzzy normed linear space. Let x n be a sequence in X. Then x n is said to be convergent if there exists x ∈ X such that \( lim_{n \rightarrow \infty } N\left (x_{n}-x,t\right )=1\) for all t > 0. In that case, x is called the limit of the sequence x n and we denote it by N − lim n→∞x n = x.
Definition 3
A sequence x n in X is called Cauchy if for each 𝜖 > 0 and each t > 0 there exists n 0 such that for all n ≥ n 0 and all p > 0, we have \(N\left (x_{n+p}-x_{n},t\right )>1-\epsilon \).
Definition 4
Every convergent sequence in a fuzzy normed space is Cauchy. If each Cauchy sequence is convergent, then the fuzzy norm is said to be complete and the fuzzy normed space is called a fuzzy Banach space.
Definition 5
A mapping f : X → Y between fuzzy normed spaces X and Y is continuous at a point x 0 if for each sequence {x n} converging to x 0 in X, the sequence f{x n} converges to f{x 0}. If f is continuous at each point of x 0 ∈ X, then f is said to be continuous on X.
Example
Let (X, ∥.∥) be a normed linear space. Then
is a fuzzy norm on X.
In the following we will suppose that N(x, .) is left continuous for every x. A fuzzy normed linear space is a pair(X, N), where X is a real linear space and N is a fuzzy norm on X. Let (X, N) be a fuzzy normed linear space. A sequence {x n} in X is said to be convergent if there exist x ∈ X such that limn→∞N(x n − x, t) = 1 (t > 0). In that case, x is called the limit of the sequence {x n} and we write N −limn→∞x n = x. A sequence {x n} in fuzzy normed space (X, N) is called cauchy if for each 𝜖 > 0 and δ > 0, there exist n 0 ∈ N such that
If each cauchy sequence is convergent, then the fuzzy norm is said to be complete and the fuzzy normed space is called a fuzzy Banach space.
In this paper, the authors investigate the general solution and generalized Hyers–Ulam stability of a new type of n-dimensional functional equation of the form
where n is a positive integer with \(\mathbb {N}-\{1,2,3,4 \}\), in the setting of Banach space and fuzzy normed space using direct and fixed point methods.
Theorem 1 (Banach’s Contraction Principle)
Let (X, d) be a complete metric space and consider a mapping T : X→X which is strictly contractive mapping, that is
- (A1):
-
d(Tx, Ty) ≤ Ld(x, y) for some (Lipschitz constant) L < 1, then
-
(i)
The mapping T has one and only fixed point x ∗ = T(x ∗);
-
(ii)
The fixed point for each given element x ∗is globally attractive that is
-
(i)
- (A2):
-
lim n→∞T nx = x ∗, for any starting point x ∈ X;
-
(iii)
One has the following estimation inequalities:
-
(iii)
- (A3):
-
\((T^n x,x^* )\leq \frac {1}{1-L} d(T^n x,T^{n+1} x)\) , for all n ≥ 0, x ∈ X.
- (A4):
-
\((x,x^* )\leq \frac {1}{1-L} d(x,x^* ) , \forall x\in X\).
Theorem 2 (The Alternative of Fixed Point)
Suppose that for a complete generalized metric space (X, d) and a strictly contractive mapping T : X→Y with Lipschitz constant L. Then, for each given element x ∈ X either
- (B1):
-
(T nx, T n+1x) = +∞, for all n ≥ 0, or
- (B2):
-
there exists natural number n 0 such that:
-
(i)
d(T nx, T n+1x) < ∞ for all n ≥ n 0;
-
(ii)
The sequence (T nx) is convergent to a fixed point y ∗ of T;
-
(iii)
y ∗ is the unique fixed point of T in the set \(Y{=}\left \{y\in X;d(T^{n_{0}} x,y){<}\infty \right \}\);
-
iv)
\(d(y^*,y)\leq \frac {1}{1-L}d(y,Ty)\) for all y ∈ L.
-
(i)
2 General Solution of the Functional Equation (3)
In this section, we obtain the general solution of the functional equation (3). Throughout this section , let X and Y be real vector spaces.
Theorem 3
A function f : X→Y satisfies the functional equation (3) then f : X→Y satisfies the functional equation (1).
Proof
Let f : X→Y satisfy the functional equation (3). Replacing (x 1, x 2, x 3, …, x n) by (0, 0, …, 0), (x, 0, …, 0) and (x, x, 0…, 0) in (3) we obtain
for all x ∈ X. It is easy to verify from (3) that
for all x ∈ X. Setting (x 1, x 2, x 3, …, x n) by (x, y, 0, …, 0) in (3) and using oddness of f, we obtain the result of (1).
Define a mapping f : X → Y by
for allx 1, x 2, …, x n ∈ X.
2.1 Stability Result for (3) in Banach Space Using Direct Method
In this section, we consider X to be a real vector space and Y to be a Banach space, we present the Hyers–Ulam stability of the functional equation (3).
Theorem 4
Let ψ : X n→[0, ∞) be a function such that \(\sum _{k=0}^{\infty } \frac {\psi (2^{kj} x,2^{kj} x,0,\dots ,0) }{2^{kj}}\) converges in \(\mathbb {R}\) and
for all x 1, x 2, …, x n ∈ X. If a function f : X→Y satisfies
for all x 1, x 2, …, x n ∈ X, then there exists a unique additive function A : X→Y which satisfies the functional equation (3) and
for all x ∈ X. The function A is given by
for all x ∈ X.
Proof
Setting (x 1, x 2, x 3, …, x n) by (x, x, 0, …, 0) in (7), we obtain
for all x ∈ X. It follows from (10) that
for all x ∈ X. Setting x by 2x in (11), we obtain
for all x ∈ X. It follows from (12) we get
for all x ∈ X. It follows from (11) and (13) that
for all x ∈ X. Generalizing, we get
for all x ∈ X. Now we have to prove that the sequence \(\left \{\frac {f(2^k x)}{2^k}\right \}\) is a cauchy sequence for all x ∈ X. For every positive integer n, m and for all x ∈ X, consider
for all x ∈ X. By condition (6), the right-hand side approaches 0 as n →∞. Thus, the sequence is a cauchy sequence due to the completeness of the Banach space Y
is well-defined. We can see that (9) holds. To show that A satisfies (3), we set (x, y) = (2nx 1, 2nx 2, …, 2nx n) in (7) and divide the resulting equation by 2n, we obtain
Taking the limit as n →∞, using (6) and (9), A satisfies (3). To prove the uniqueness of A, suppose that there exist another cubic function B : X → Y such that B satisfies (3) and (8), we have
By condition (6), the right-hand side approaches 0 as n →∞, and it follows that A(x) = B(x) for all x ∈ X. Hence, A is unique. This completes the proof of the theorem.
The following corollary is an immediate consequence of Theorem 4, concerning the stability of (3).
Corollary 1
Let λ and s be a non-negative real numbers. Let f : X→Y be a function satisfying the inequality
for all x 1, x 2, …, x n ∈ X. Then there exists a unique additive function A : X→Y such that

2.1.1 Stability Result for (3) in Banach Space Using Fixed Point Method
In this segment, the authors presented the generalized Ulam–Hyers stability of the functional equation (3) in Banach space and using fixed point method.
Theorem 5
Let f : X→Y be a mapping for which there exists a function ψ : X n→[0, ∞) with the condition
where

such that the functional inequality
for all x 1, x 2, …, x n ∈ W. If there exists L = L(i) such that the function
has the property,
for all x ∈ X. Then there exists a unique additive function A : X→Y satisfying the functional equation (3) and
holds for all x ∈ X.
Proof
Consider the set d = {u∕u : X→Y, u(0) = 0)} and introduce the generalized metric on M. \(d(u,v)=inf\left \{k\in (0,\infty ):||u(x)-v(x)||\leq k\beta (x), x\in X\right \}.\)It is easy to see that (M, d) is complete. Define T : M→M by
for all x ∈ M. Now u, v ∈ M,



This implies d(Tu, Tv) ≤ Ld(u, v) for all u, v ∈ M. (i.e.,) T is strictly contractive mapping on with Lipschitz constant L. Replacing (x 1, x 2, x 3, …, x n) by (x, x, 0, …, 0) in (18), we obtain
for all x ∈ X. It follows from (21) that
for all x ∈ X. Using (19) for the case i = 0, it reduces to
for all x ∈ X.
Again replacing \(x=\frac {x}{2}\) in (21) and (22), we get
and
for all x ∈ X. Using (19) for the case i = 0, it reduces to
for all x ∈ X. (i.e.,) d(f, Tf) ≤ 2 ⇒ d(f, Tf) ≤ 2 = L 0 < ∞. In the above case, we arrive
Therefore (B 2(i))holds. By (B 2(ii)), it follows that there exists a fixed point A of T in X, such that
for all x ∈ X. In order to prove A : X→Y is additive. Replacing (x 1, x 2, …, x n) by \((\eta _{i}^{k} x_1,\eta _{i}^{k} x_2,\ldots ,\eta _{i}^{k} x_n )\) in (18) and dividing by \(\eta _{i}^{k},\) it follows from (17) and (25), we see that A satisfies (3) for all x 1, x 2, …, x n ∈ X. Hence A satisfies the functional equation (3). By (B 2(iii)), A is the unique fixed point of T in the set, Y = {f ∈ M;d(Tf, A) < ∞}. Using the fixed point alternative result, A is the unique function such that
for all x ∈ W and k > 0.Finally by (B 2(iv)), we obtain
Hence, we conclude that
for all x ∈ X. This completes the proof of the theorem.
The following corollary is an immediate consequence of Theorem 5 concerning the stability of (3).
Corollary 2
Let f : X→Y be a mapping and there exist real numbers λ and s such that
for all x 1, x 2, …, x n ∈ X. Then there exists a unique additive function A : X→Y such that

for all x ∈ X.
Proof
Setting
for all x 1, x 2, …, x n ∈ X. Now

i.e., (21) holds. But we have \(\beta (x)=\frac {2}{(n^2-5n+6)}\psi (\frac {x}{2},\frac {x}{2},0,\ldots ,0)\).
Hence

for all x ∈ X. Hence the inequality (3) holds for
Now, from (21) we prove the following cases:
- Case1: :
-
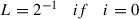
\(||f(x)-A(x)|\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {(2^{-1)}}{1-2^{-1}}\frac {2\lambda }{(n^2-5n+6)}=\frac {2\lambda }{(n^2-5n+6)}\)
- Case2: :
-
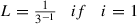
\(||f(x)-A(x)||\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {1}{1-2}\frac {2\lambda }{(n^2-5n+6)}=\frac {-2\lambda }{(n^2-5n+6)}\)
- Case3: :
-
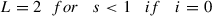
\(||f(x)-A(x)||\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {2^{s-1}}{1-2^{s-1}}\frac {4\lambda ||x||{ }^s}{(n^2-5n+6)2^{s}}=\frac {4\lambda ||x||{ }^s}{(n^2-5n+6)(2-2^{s})}\)
- Case4: :
-
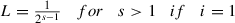
\(||f(x)-A(x)||\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {1}{1-\frac {1}{2^{s-1}}}\frac {4\lambda ||x||{ }^s}{(n^2-5n+6)2^{s}}=\frac {4\lambda ||x||{ }^s}{(n^2-5n+6)(2^{s}-2)}\)
- Case5: :
-
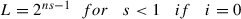
\(||f(x)-A(x)||\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {2^{ns-1}}{1-2^{ns-1}}\frac {4\lambda ||x||{ }^{ns}}{(n^2-5n+6)2^{ns}}=\frac {4\lambda ||x||{ }^{ns}}{(n^2-5n+6)(2-2^{ns})}\)
- Case6: :
-
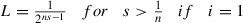
\(||f(x)-A(x)||\leq \frac {L^{1-i}}{1-L}\beta (x)=\frac {1}{1-\frac {1}{2^{ns-1}}}\frac {4\lambda ||x||{ }^{ns}}{(n^2-5n+6)2^{ns}}=\frac {4\lambda ||x||{ }^{ns}}{(n^2-5n+6)(2^{ns}-2)}.\)
3 Stability Result for (3) in Fuzzy Normed Space Using Direct Method
Throughout this section, assume that X, \(\left (Z,N^{\prime }\right )\), \( \left (Y, N\right )\) are linear space, Banach space, and fuzzy normed space, respectively, we now investigate the fuzzy stability of the functional equation (3).
Theorem 6
Let β ∈{1, −1} be fixed and let ψ : X n→Z be a mapping such that for some d > 0 with \(0<\left (\frac {d}{2}\right )^{\beta }<1.\)
for all x ∈ X and all r > 0, d > 0, and
for all x 1, x 2, …, x n ∈ X and all r > 0. Suppose an odd mapping f : X→Y with f(0) = 0 satisfies the inequality
for all r > 0 and all x 1, x 2, …, x n ∈ X. Then the limit
exists for all x ∈ X and the mapping A : X→Y is the unique additive mapping such that
for all x ∈ X and for all r > 0.
Proof
Let β = 1. Replacing (x 1, x 2, x 3, …, x n) by (x, x, 0, …, 0) in (28), we get
for all x ∈ X and all r > 0. Replacing x by 2kx in (31), we obtain
for all x ∈ X and for all r > 0. Using (26), we get
for all x ∈ X and for all r > 0. It is easy to verify from (33) that
holds for all x ∈ X and for all r > 0. Replacing r by d kr in (34),we get
for all x ∈ X and for all r > 0. It follows from
and (35) that
for all x ∈ X and for all r > 0. Replacing x by 2mx in (37), we get
for all x ∈ X and for all r > 0 and all m, k ≥ 0. Replacing r by d mr in (38), we get
for all x ∈ X and for all r > 0 and all m, k ≥ 0. Using (N 3) in (38), we obtain
for all x ∈ X, r > 0 and all m, k ≥ 0. Since 0 < d < 2 and \(\sum _{i=0}^{k}\left (\frac {d}{2}\right )^{i}<\infty \), the Cauchy criterion for convergence and (N 5) implies that \(\left \{\frac {f(2^{k}x)}{2^k}\right \}\) is a Cauchy sequence in (Y, N). Since (Y, N) is a fuzzy Banach space, this sequence converges to some point A(x) ∈ Y. So one can define the mapping A : X→Y by
for all x ∈ X. Letting m = 0 in (40), we get
for all x ∈ X. Taking the limits as k→∞ and using (N 6), we arrive
for all x ∈ X and for all r > 0. Now, we claim that A is additive. Replacing (x 1, x 2, x 3, …, x n) by (2kx 1, 2kx 2, …, 2kx n) in (28), respectively, we get
for all r > 0 and for all x 1, x 2, …, x n ∈ X. Since
A satisfies the additive functional equation (3). Hence A : X → Y is additive. To prove the uniqueness of A, let A′ be another additive mapping satisfying (30). Fix x ∈ X, clearly A(2nx) = 2nA(x) and A ′(2nx) = 2nA ′(x) for all x ∈ X and all n ∈ N. It follows from (30) that \(N(A(x)-A'(x),r)=N\left (\frac {A(2^k x)}{2^k}-\frac {A'(2^k x)}{2^k},r\right )\)

for all x ∈ X and r > 0. Since \(lim_{k\longrightarrow \infty }\frac {r(n^2-5n+6) 2^k (2-d)}{2d^k}=\infty ,\) we obtain
Thus N(A(x) − A′(x), r) = 1 for all x ∈ X and r > 0 and so A(x) = A′(x). For β = −1, we can prove the result by a similar method.
The following corollary is an immediate consequence of Theorem 6, concerning the stability for the functional equation (3).
Corollary 3
Suppose that the function f : X→Y satisfies the inequality
for all x 1, x 2, …, x n ∈ X and all r > 0, where θ, s are constants then there exists a unique additive mapping A : X → Y such that

3.1 Stability Result for (3) in Fuzzy Normed Space Using Fixed Point Method
Throughout this section, the authors investigated the generalized Ulam–Hyers stability of the functional equation (3) in fuzzy normed space using fixed point method.
To prove the stability result, we define the following μ i is a constant such that

and Ω is the set such that \(\Omega =\left \{t/t:W\longrightarrow B,t(0)=0\right \}.\)
Theorem 7
Let f : X→Y be a mapping for which there exists a function ψ : X n→Z with condition
for all x 1, x 2, …, x n ∈ X and all r > 0 and satisfying the inequality
for all x ∈ X and r > 0. If there exist L = L[i] such that the function \(x\longrightarrow \beta (x)=\frac {1}{\left (n^{2}-5n+6\right )} \psi \left ( \frac {x}{2}, \frac {x}{2},0,\ldots ,0\right )\) has the property
for all x ∈ X and r > 0, then there exists a unique additive function A : X→Y satisfying the functional equation (3) and
for all x ∈ X and r > 0.
Proof
Let d be a general metric on Ω such that
It is easy to see that ( Ω, d) is complete. Define T : Ω→ Ω by \(Tt (x)=\frac {1}{\eta _i} t(\eta _i x)\) for all x ∈ X, for t, u ∈ Ω, we have

for all t, u ∈ Ω.Therefore T is strictly contractive mapping on Ω with Lipschitz constant L, replacing (x 1, x 2, x 3, …, x n) by (x, x, 0, …, 0) in (44), we get
for all x ∈ X and r > 0. Using (N 3) in (47), we arrive
for all x ∈ X and r > 0 with the help of (45) when i = 0, it follows from (48) that
Replacing x by \(\frac {x}{2}\) in (47), we obtain
for all x ∈ X and r > 0, when i = 1, it follows from (49), we get
Then from (49) and (50), we can conclude
Now from the fixed point alternative in both cases, it follows that there exists a fixed point A of T in Ω such that
for all x ∈ W and r > 0. Replacing (x 1, x 2, …, x n) by \((\eta _{i}^{k} x_1,\eta _{i}^{k} x_2,\ldots ,\eta _{i}^{k} x_n )\) in (44), we arrive
for all r > 0 and all x 1, x 2, …, x n ∈ X. By proceeding the same procedure of the Theorem 5.1 , we can prove the function A : X→Y is additive and it satisfies the functional equation (3). By a fixed point alternative, since A is a unique fixed point of T in the set
Therefore A is a unique function such that
for all x ∈ W and r > 0. Again using the fixed point alternative, we obtain
for all x ∈ X and r > 0. This completes the proof of the theorem.
The following corollary is an immediate consequence of Theorem 7 concerning the stability of (3).
Corollary 4
Suppose a function f : X→Y satisfies the inequality
for all x 1, x 2, …, x n ∈ X and r > 0, where θ, s are constants with θ > 0. Then there exists a unique additive mapping A : X→Y such that

for all x ∈ X and r > 0.
Proof
Setting
for all x 1, x 2, …, x n ∈ X. Then

Thus, (6) holds. But we have
has the property
for all x ∈ X and r > 0. Hence

Now,
Now from the following cases for the conditions (i) and (ii)
- Case(i): :
-
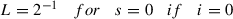
\(N(f(x)-A(x),r)\geq N'\left (\frac {L^{1-i}}{1-L}\beta (x),r\right )\geq N'\left (\frac {2^{-1}}{1-2^{-1}}\frac {2\theta }{(n^2-5n+6)},r\right )\geq N'\left (\theta ,\frac {r(n^2-5n+6)}{2}\right )\)
- Case(ii): :
-
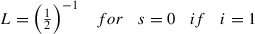
\(N(f(x)-A(x),r)\geq N'\left (\frac {L^{1-i}}{1-L}\beta (x),r\right )\geq N'\left (\frac {1}{1-\left (\frac {1}{2}\right )^{-1}}\frac {2\theta }{(n^2-5n+6)},r\right )\geq N'\left (\theta ,\frac {-r(n^2-5n+6)}{2}\right )\)
- Case(iii): :
-
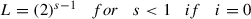 $$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{s-1}}{1-2^{s-1}}\frac{2\theta||x||{}^{s}}{(n^2-5n+6)2^{s}},r\right)\\ &\geq N'\left(2\theta||x||{}^{s},\frac{r(n^2-5n+6)(2-2^{s})}{2}\right) \end{aligned} \end{aligned}$$
$$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{s-1}}{1-2^{s-1}}\frac{2\theta||x||{}^{s}}{(n^2-5n+6)2^{s}},r\right)\\ &\geq N'\left(2\theta||x||{}^{s},\frac{r(n^2-5n+6)(2-2^{s})}{2}\right) \end{aligned} \end{aligned}$$ - Case(iv): :
-
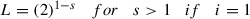 $$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{1-s}}{1-2^{1-s}}\frac{2\theta||x||{}^{s}}{(n^2-5n+6)2^{s}},r\right)\\ &\geq N'\left(2\theta||x||{}^{s},\frac{r(n^2-5n+6)(2^{s}-2)}{2}\right) \end{aligned} \end{aligned}$$
$$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{1-s}}{1-2^{1-s}}\frac{2\theta||x||{}^{s}}{(n^2-5n+6)2^{s}},r\right)\\ &\geq N'\left(2\theta||x||{}^{s},\frac{r(n^2-5n+6)(2^{s}-2)}{2}\right) \end{aligned} \end{aligned}$$ - Case(v): :
-
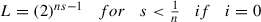 $$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{ns-1}}{1-2^{ns-1}}\frac{2\theta||x||{}^{ns}}{(n^2-5n+6)2^{ns}},r\right)\\ &\geq N'\left(2\theta||x||{}^{ns},\frac{r(n^2-5n+6)(2-2^{ns})}{2}\right) \end{aligned} \end{aligned}$$
$$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{ns-1}}{1-2^{ns-1}}\frac{2\theta||x||{}^{ns}}{(n^2-5n+6)2^{ns}},r\right)\\ &\geq N'\left(2\theta||x||{}^{ns},\frac{r(n^2-5n+6)(2-2^{ns})}{2}\right) \end{aligned} \end{aligned}$$ - Case(vi): :
-
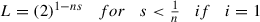 $$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{1-ns}}{1-2^{1-ns}}\frac{2\theta||x||{}^{ns}}{(n^2-5n+6)2^{ns}},r\right)\\ &\geq N'\left(2\theta||x||{}^{ns},\frac{r(n^2-5n+6)(2^{ns}-2)}{2}\right) \end{aligned} \end{aligned}$$
$$\displaystyle \begin{aligned} \begin{aligned} N(f(x)-A(x),r)&\geq N'\left(\frac{L^{1-i}}{1-L}\beta(x),r\right)\\ &\geq N'\left(\frac{2^{1-ns}}{1-2^{1-ns}}\frac{2\theta||x||{}^{ns}}{(n^2-5n+6)2^{ns}},r\right)\\ &\geq N'\left(2\theta||x||{}^{ns},\frac{r(n^2-5n+6)(2^{ns}-2)}{2}\right) \end{aligned} \end{aligned}$$Hence the proof is completed.
References
T. Aoki, On the stability of the linear transformation in Banach space. Int. J. Math. Soc. 2(1–2), 64–66 (1950)
T. Bag, S.K. Samanta, Finite dimensional fuzzy normed linear spaces. J. Fuzzy Math. 11(3), 687–705 (2003)
T. Bag, S.K. Samanta, Fuzzy bounded linear operators. Fuzzy Sets Syst. 151, 513–547 (2005)
R. Biswas, Fuzzy inner product space and fuzzy norm functions. Inf. Sci. 53, 185–190 (1991)
I.S. Chang, H.M. Kim, On the Hyers-Ulam stability of quadratic functional equations. J. Inequal. Pure Appl. Math. 3, 33 (2002)
S.C. Cheng, J.N. Mordeson, Fuzzy linear operator and fuzzy normed linear spaces. Bull. Calcuta Math. Soc. 86, 429–436 (1994)
C. Felbin, Finite dimensional fuzzy normed space. Fuzzy Sets Syst. 48, 239–248 (1992)
P. Gavruta, A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. J. Math. Anal. Appl. 184, 431–436 (1992)
V. Govindan, K. Tamilvanan, Stability of functional equation in Banach space: using two different methods. Int. J. Math. Appl. 6(1-C), 527–536 (2018)
V. Govindan, S. Murthy, M. Saravanan, Solution and stability of New type of (aaq,bbq,caq,daq) mixed type functional equation in various normed spaces: using two different methods. Int. J. Math. Appl. 5(1-B), 187–211 (2017)
D.H. Hyers, On the stability of the linear functional equation. Proc. Natl. Acad. Sci. 27, 222–224 (1941)
P. L. Kannappan, Quadratic functional equation and inner product spaces. Results Math. 27, 368–372 (1995)
A.K. Katsaras, Fuzzy topological vector spaces II. Fuzzy Sets Syst. 12, 143–154 (1984)
I. Kramosil, J. Michalek, Fuzzy metric and statistical metric spaces. Kybernetica 11, 326–334 (1975)
A.K. Mirmostafee, M.S. Moslehian, Fuzzy versions of Hyers-Ulam-Rassias theorem. Fuzzy Sets Syst. 159, 720–729 (2008)
A.K. Mirmostafee, M.S. Moslehian, Fuzzy almost quadratic functions. Results Math. https://doi.org/10.1007/s00025-007-0278-9
S. Murthy, V. Govindhan, General solution and generalized HU (Hyers-Ulam) stability of new dimension cubic functional equation in Fuzzy ternary Banach algebras: using two different methods. Int. J. Pure Appl. Math. 113( 6), 394–403 (2017)
S. Pinelas, V. Govindan, K. Tamilvanan, Stability of a quartic functional equation. J. Fixed Point Theory Appl. 20(148), 10pp. (2018). https://doi.org/10.007/s11784-018-0629-z
S. Pinelas, V. Govindan, K. Tamilvanan, Stability of non- additive functional equation. IOSR J. Math. 14( 2 - I), 60–78 (2018)
T.M. Rassias, On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 72, 297–300 (1978)
J.M. Rassias, On approximation of approximately linear mappings by linear mapping. J. Funct. Anal. 46(1), 126–130 (1982)
J.M. Rassias, On approximation of approximately linear mappings by linear mappings. Bull. Sci. Math. 108(4), 445–446 (1984)
K. Ravi, P. Narasimman, R. Kishore Kumar, Generalized Hyers-Ulam-Rassias stability and J. M. Rassias stability of a quadratic functional equation. Int. J. Math. Sci. Eng. Appl. 3(2), 79–94 (2009)
K. Ravi, R. Kodandan, P. Narasimman, Ulam stability of a quadratic functional equation. Int. J. Pure Appl. Math. 51(1), 87–101 (2009)
B. Shieh, Infinite fuzzy relation equations with continuous t-norms. Inf. Sci. 178, 1961–1967 (2008)
S.M. Ulam, A Collection of the Mathematical Problems (Interscience, New York, 1960).
C. Wu, J. Fang, Fuzzy generalization of Klomogoroffs theorem. J. Harbin Inst. Technol. 1, 1–7 (1984)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Pinelas, S., Govindan, V., Tamilvanan, K. (2019). Stability of an n-Dimensional Functional Equation in Banach Space and Fuzzy Normed Space. In: Anastassiou, G., Rassias, J. (eds) Frontiers in Functional Equations and Analytic Inequalities. Springer, Cham. https://doi.org/10.1007/978-3-030-28950-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-28950-8_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-28949-2
Online ISBN: 978-3-030-28950-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




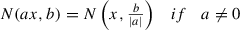 ;
;