Abstract
Due to the increasing demands for modeling large-scale and complex systems, designing optimal controls, and conducting optimization tasks, many real-world applications require sophisticated models. Geometric methods are designed to capture the underlying structure of the system at hand and to preserve the global qualitative or geometric properties of the flow, such as symplecticity, volume preservation and symmetry. A survey on three of such structure preserving numerical methods is proposed in the present article. Testing the validity of such simulations is achieved by exhibiting analytically solvable models and comparing the result of simulations with their exact behavior.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
It is today well established that geometrical methods connected to powerful numerical tools (i.e. Runge-Kutta, Butcher series) can be applied to equations on the Lie algebra to design high order methods and determine their numerical convergence. Beyond these structure preservations, approaches for integration algorithms based on variational principles give a unified treatment of many symplectic numerical schemes. In this context, the Noether theorem [10] allows for a numerical formulation that preserves symmetries and conservation laws.
In the case of homogeneous spaces (smooth manifold on which a Lie group acts transitively), the so-called Lie group integrators, comprising Runge-Kutta-Munthe-Kaas [12] methods is presented shortly in Sect. 2. The main preoccupation is to ensure that discrete solutions are guaranteed to stay on the given manifold. However in this case no particular preservation of symmetries is obtained without further constraints. This is why variational methods are revisited in Sect. 3 to be compared to Lie-Poisson Hamilton-Jacobi algorithm based on generating function for which higher order designs are also available (Sect. 4).
2 Lie Group Integrators, Runge-Kutta-Munthe-Kaas Methods
The Runge-Kutta-Munhe-Kaas methods (RKMK) developed in a serie of articles [12], are an example of Lie group methods. Let Y(t) be a curve in a matrix Lie group G verifying
where \(A(t,Y)\in \mathfrak g\) for all \(t,Y\in \mathbb R\times G\). The starting point is to describe the solution of (1) as \(Y(t)=\exp (\varOmega (t))Y_0\) and to deduce an ODE on \(\varOmega \). Computing the derivative of Y we get

where the right trivialized derivative  is introduced. Using this expression in (1) and invertingFootnote 1
is introduced. Using this expression in (1) and invertingFootnote 1  a differential equation is obtained for \(\varOmega \) lying on the Lie algebra \(\mathfrak {g}\)
a differential equation is obtained for \(\varOmega \) lying on the Lie algebra \(\mathfrak {g}\)

The advantage is that the non linear invariants defining the Lie group become linear invariants on the Lie algebra, and will be preserved by any numerical method [7]. This ensures that the solution stays on the Lie group.
The idea behind RKMK methods is to approximate the solution Y of Eq. (1) with a discrete solution \((Y_n)\) by approximately solving Eq. (2) with a general Runge-Kutta method \(\dot{\varOmega }=f(\varOmega )\) with  and updating the position via the exponential map. Knowing that
and updating the position via the exponential map. Knowing that  where \(B_k\) are Bernouilli numbers, a truncated sum up to order q is used in Eq. (2). If the Runke-Kutta method is order p and the truncature order is such that \(q\ge p-2\), then the associated RKMK method is order p [12].
where \(B_k\) are Bernouilli numbers, a truncated sum up to order q is used in Eq. (2). If the Runke-Kutta method is order p and the truncature order is such that \(q\ge p-2\), then the associated RKMK method is order p [12].
Application to the Rigid Body Problem. We consider here the free rigid body problem. Let  be the angular momentum in the body frame and
be the angular momentum in the body frame and  the inertia tensor, it verifies the Euler-Poincaré equation \(\dot{\pi }=\pi \wedge \xi ,\,\pi (0)=\pi _0\) where
the inertia tensor, it verifies the Euler-Poincaré equation \(\dot{\pi }=\pi \wedge \xi ,\,\pi (0)=\pi _0\) where  and \(\pi _0\) is the initial angular momentum. In terms of matrix product, this yields
and \(\pi _0\) is the initial angular momentum. In terms of matrix product, this yields
This is in the form of Eq. (1), hence \(\pi \) can be approximately solved using a RKMK method where SO(3) is the acting group. The Lie group SO(3) leaves the vector space  invariant, reflecting the conservation of \(\Vert \pi (t)\Vert \) in time. Applying a Lie group method guarantees the preservation of that constraint, ensuring that the angular momentum \(\pi (t)\) lies on the sphere of radius \(\Vert \pi _0\Vert \) for all t.
invariant, reflecting the conservation of \(\Vert \pi (t)\Vert \) in time. Applying a Lie group method guarantees the preservation of that constraint, ensuring that the angular momentum \(\pi (t)\) lies on the sphere of radius \(\Vert \pi _0\Vert \) for all t.
Defining \(\varOmega \) with \(\pi (t)=\exp (\varOmega (t))\pi _0\), the following expression is obtained for Eq. (2)

We build an order 4 RKMK method by truncating the sum (4) up to order 2 and a applying a classical order 4 RK method. The results shown in Fig. 1, outputting the expected behaviour, have been computed for the following parameters:

3 Covariant Variational Methods
Here we build a covariant variational method based on the Hamilton principle associated to a discrete Lagrangian following a similar approach to [5]. We take the case where the configuration space of the system is a Lie group G together with a reduced Lagrangian \(\ell :\mathfrak g\rightarrow \mathbb R\).
Let a time step h divide equally the time interval, the set of discrete paths is defined by \(\mathcal C_d(G)=\left\{ g_d:\left\{ t_k\right\} _{0\le k\le N}\rightarrow G\right\} \) where \(\forall k,\,t_k=kh\). To determine an approximate trajectory \(g_d\in \mathcal C_d(G)\) such that \(g_k:=g_d(k)\approx g(t_k)\), we define a discrete reduced Lagrangian \(\ell _d\) approximating the action

where \(\xi (0)=\xi _0\) and \(\xi =g^{-1}\dot{g}\) such that g is an action extremum on \([t_0,t_1]\). To discretize the relation \(\xi =g^{-1}\dot{g}\) we introduce a local diffeomorphism \(\tau :\mathfrak g\rightarrow G\) defined on an open set containing the identity and such that \(\tau (0)=e_G\) (the exponential map is an example of such a diffeomorphism). Starting from the reconstruction formula
we define \(\xi _i:=\frac{1}{h}\tau ^{-1}(g_i^{-1}g_{i+1})\)
The discrete action is approximated from the classical action by the sum \(S_d(g_d)=\sum _{i=0}^{N-1}\ell _d(\xi _i)\). Applying the Hamilton principle on \(S_d\) evaluated on a discrete path \(g_d\) yields \(\delta S_d(g_d)= \sum _{i=0}^{N-1}\left\langle \frac{\partial \ell _d}{\partial \xi }(\xi _i),\delta \xi _i\right\rangle \). The variation \(\delta \xi _i\) is expressed using (5) as

where \(\zeta _i=g_i^{-1}\delta g_i\). Here the right trivialized differential  defined by
defined by  is introduced, allowing us to write
is introduced, allowing us to write

Using the definition of the adjoint \(\left\langle \pi ,A\xi \right\rangle =\left\langle A^*\pi ,\xi \right\rangle \) where \(\pi \in \mathfrak g^*\) and \(\xi \in \mathfrak g\), the variation of the action functional now reads

Introducting the momentum \(\mu _i\) associated to \(\xi _i\) via the formula

and changing the indexes in the sum (discrete integration by part), we finally get, by the independence of \(\zeta _i\) for all \(i\in \{1,\ldots ,N-1\}\), the discrete Euler-Poincaré equations

This allows us to define the general formulation of a covariant method in Algorithm 1 for given boundary conditions \(g_0\) et \(\xi _0\). The momentum \(\mu _i\) is computed from (7), and the associated \(\xi _i\in \mathfrak {g}\) is then deduced from (6). This equation being implicit, it is typically solved using a numerical solver such as a Newton method. Finally, the position is updated via the reconstruction formula (5).

Application to the Rigid Body Problem. A rigid body is represented by an element of the rotation group SO(3). The reduced Lagrangian for this system is defined for  as the rotation kinetic energy \(\ell (\xi ):=1/2\left\langle \mathbb J\xi ,\xi \right\rangle \). We chose to approximate this Lagrangian with \(\ell _d\) defined by \(\ell _d(\xi _0):=h\ell (\xi _0)=\frac{h}{2}\left\langle \mathbb J\xi _0,\xi _0\right\rangle \) and choose the local diffeomorphism \(\tau \) to be defined as the Cayley map
as the rotation kinetic energy \(\ell (\xi ):=1/2\left\langle \mathbb J\xi ,\xi \right\rangle \). We chose to approximate this Lagrangian with \(\ell _d\) defined by \(\ell _d(\xi _0):=h\ell (\xi _0)=\frac{h}{2}\left\langle \mathbb J\xi _0,\xi _0\right\rangle \) and choose the local diffeomorphism \(\tau \) to be defined as the Cayley map  (details can be found in [4]).
(details can be found in [4]).
The results of the application of Algorithm 1 for the parameters given in Sect. 2 are also plotted on Fig. 1 for comparison.
4 Methods Based on Generating Functions, Hamilton-Jacobi Equation
4.1 Classical Case
The Hamilton Jacobi equation plays an important role in the development of numerical integrators that preserve the symplectic structure. In this section Hamilton-Jacobi theory is approached from the point of view of extended phase space as it is presented by Marsden [11] (p 206) and Arnold [1] (chapter 9). A link between Hamilton-Jacobi integrators and variational integrators could also be find in ([10]).
By definition, canonical transformations preserve the (pre)-symplectic 2-form, which can be deduced from the differential of the Poincaré-Cartan form. Let us consider a canonical transformation in the extended phase space \((t,q,p)\mapsto (T,Q,P)\) depicted in Fig. 2. Let (t, q, p) be coordinate functions in some chart of extended phase space considered as a manifold M. The Poincaré-Cartan form  is a differential 1-form on M for which H(t, q, p) is a Hamiltonian function. The coordinates (t, Q, P) can be considered as giving another chart on M associated to the 1-form
is a differential 1-form on M for which H(t, q, p) is a Hamiltonian function. The coordinates (t, Q, P) can be considered as giving another chart on M associated to the 1-form  with a corresponding Hamiltonian function K(T, Q, P).
with a corresponding Hamiltonian function K(T, Q, P).
As it is well-know, it is possible to find fourFootnote 2 generating functions depending of all mixes of old and new variables: (q, Q), (q, P), (p, Q), or (p, P). It appears that the second kind (q, P) of generating function is easily used to generate an infinitesimal transformation closed to the identity. And in turn, defines, by construction, a structure preserving numerical method. The mixed coordinates system (t, q, P) may be related to the previous ones through two mappings h and f: such that
If each the (pre-)symplectic forms  and
and  are invariantly associated to one another, their pull-back should agree: \(h^*\omega _\theta =f^*\varOmega _\varTheta \). Since the operator
are invariantly associated to one another, their pull-back should agree: \(h^*\omega _\theta =f^*\varOmega _\varTheta \). Since the operator  and \((\,^*)\) commute, that means
and \((\,^*)\) commute, that means  . Consequently, \(h^*\theta \) and \(f^*\varTheta \) differ from a closed form \(dS=h^*\theta -f^*\varTheta \) which is
. Consequently, \(h^*\theta \) and \(f^*\varTheta \) differ from a closed form \(dS=h^*\theta -f^*\varTheta \) which is

Replacing  and introducing \(G=(f^*Q) P+S\), one computes
and introducing \(G=(f^*Q) P+S\), one computes

and obtains
Now suppose that G(t, q, P) satisfies the so-called Hamilton-Jacobi equation,
for a given time dependent Hamiltonian H. This equation is obtained by taking \(K\equiv 0\) in (8-a). The generating function G generates a time dependent canonical transformation \(\psi \) that transforms the Hamiltonian vector fields \(X_H\) to equilibrium: \(\psi _{*}X_H=X_{K=0}\). That means that the integral curves of \(X_K\) are represented by straight lines in the image space. The vector field has been "integrated" by the transformation (see Fig. 2).
The choice of the second kind of generating function is convenient to easily generate the identity transformation. Choosing \(G=qP\) in (8b) and (8c) reads \(Q=\frac{\partial G}{\partial P}=q\) and \(p=\frac{\partial G}{\partial q}=P\). So, a canonical (infinitesimal) transformation is obtained by plugging the ansatz
into the Hamilton-Jacobi Eq. (9). Equating coefficients of equal powers of t gives
A numerical method of the order k is obtained by truncating the serie (10) to a certain order k (see also [2]). The remaining variables (p, Q) are computed using the generating function G in (8b) and (8c): \(Q=\frac{\partial G}{\partial P}\) and \(p=\frac{\partial G}{\partial q}\). Putting (q, p) in the left-hand size, the numerical algorithm is finally
As it can be seen, the first step may be implicit for the variable q. But when it is solved, the second step is explicit for p. The symplectic Euler method is an example of such methods of order 1 with \(G_1=-H(q,P)\) given by
for which the “discrete Hamiltonian structure” is easily recognizable.
4.2 Lie-Poisson Hamilton-Jacobi Integrators
Following the same approach as the preceding section, the Hamilton-Jacobi theory is reduced from \(T^*G\) to \(\mathfrak {g}^*\), the dual Lie algebra. Let \((t,q_0,\pi _0)\) be coordinate functions in some chart of extended phase space considered as a manifold \(M=\mathbb {R} \times G\times \mathfrak {g}^*\) (see Fig. 3). The 1-form

is the reduced Poincaré-Cartan for which the Maurer-Cartan form is defined by \(\lambda _{q_0}(v)=(L_{q_0^{-1}})_{*}(v)\). The coordinates \((t, q_1, \pi _1)\) can be considered as giving another chart in M associated to the 1-form  with \(\lambda _{q_1}(v)=(L_{q_1^{-1}})_{*}(v)\). The mixed coordinates system \((t, q_0,q_1)\) may be related to the previous ones through two mappings \(h: (t, q_0,q_1)\mapsto \pi _0(t, q_0,q_1)\) and \(f(t, q_0,q_1)\mapsto \pi _1(t, q_0,q_1)\).
with \(\lambda _{q_1}(v)=(L_{q_1^{-1}})_{*}(v)\). The mixed coordinates system \((t, q_0,q_1)\) may be related to the previous ones through two mappings \(h: (t, q_0,q_1)\mapsto \pi _0(t, q_0,q_1)\) and \(f(t, q_0,q_1)\mapsto \pi _1(t, q_0,q_1)\).
For the left invariant system, the Hamiltonian function is left invariant. It is then natural to seek for left invariant generating functions satisfying \(S_t(q_0,q_1)=S_t(hq_0,hq_1)\), \(\forall h\in G\). Choosing \(h=q_0^{-1}\) we can construct a left invariant function \(\bar{S}_t\) given by
The invariance of the (pre-)symplectic forms  and
and  gives now rise to a function \(\bar{S}_t(g)\) such that
gives now rise to a function \(\bar{S}_t(g)\) such that

So computing  , it appears that
, it appears that  must also be computed in term of \(\lambda _{q_0}\) and \(\lambda _{q}\),
must also be computed in term of \(\lambda _{q_0}\) and \(\lambda _{q}\),

So, comparing the expression  with (11), one obtains
with (11), one obtains
For \(H\equiv 0\), this yields the Lie-Poisson Hamilton-Jacobi equation
So Eq. (12c)
plugged into Eq. (12b) gives
Marsden [6, 9], Li [8] and de Degio [3] obtained a slightly different result using the convention \(g=q_1^{-1}q_0\). Nevertheless, one can obtain a Lie-Poisson integrator by approximately solving the Lie-Poisson Hamilton-Jacobi Eq. (13) and then using (14) and (15) to generate the algorithm. This last Eq. (15) manifestly preserves the co-adjoint orbit \(\mathcal {O}_{\pi _0}=\{\pi \in \mathfrak {g}^* | \pi =Ad^*_{g}\pi _0, \forall g \in G\}\). As in the classical case, one can generate algorithms of arbitrary accuracy by approximating the generative function by an ansatz such as the one given by (10), i.e \(\bar{S}_t(g)=S_0(g)+\sum _{m=1}^\infty \frac{t^m}{m!}S_m(g)\) The main difficulty is to determine \(S_0\) that can generate the identity map. Marsden propose to use in [6] the function \(S_0=trace(Ad^*_g)\) and astoundingly, de Diego [3], approximating the solution by taking the Taylor series in t of S up to order k, mention \(S_0=0\).
Li [8] propose to reformulate the above theory of a generating function on \(TG*\) by the exponential mapping in terms of algebra variable. For \(g\in G\), choose \(\xi \in \mathfrak {g}\) so that \(g=\exp {\xi }\). He use Channel and Scovel’s [2] results for which \(S_0=(\xi ,\xi )/2)\).
4.3 Conclusions and Future Research
In our case, our perspective is to relate the Lie-Poisson Hamilton-Jacobi algorithm to the Euler-Poincaré algorithm developed in Sect. 3 based on the Cayley map. In particular, since Eqs. (15) and (7) are the same in both algorithm, it will be instructive to compare the approximation of the Lie-Poisson Hamilton-Jacobi Eq. (13) to the relationship between \(\mu \) and \(\xi \) given by Eq. (6).
Notes
- 1.
Here we made the assumption that
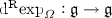 is invertible, which is the case for SO(3) whenever \(\Vert \varOmega \Vert <\pi \).
is invertible, which is the case for SO(3) whenever \(\Vert \varOmega \Vert <\pi \). - 2.
At least four since many generating functions can be constructed.
References
Arnol’d, V.I.: Mathematical Methods of Classical Mechanics, vol. 60. Springer, New York (2013)
Channell, P.J., Scovel, C.: Symplectic integration of hamiltonian systems. Nonlinearity 3(2), 231 (1990)
de Diego, D.M.: Lie-Poisson integrators. arXiv e-prints arXiv:1803.01427, March 2018
Demoures, F., Gay-Balmaz, F., Kobilarov, M., Ratiu, T.S.: Multisymplectic lie group variational integrator for a geometrically exact beam in R3. Commun. Nonlinear Sci. Numer. Simul. 19(10), 3492–3512 (2014)
Demoures, F., Gay-Balmaz, F., Ratiu, T.S.: Multisymplectic variational integrators and space/time symplecticity. Anal. Appl. 14(03), 341–391 (2016)
Ge, Z., Marsden, J.E.: Lie-Poisson Hamilton-Jacobi theory and Lie-Poisson integrators. Phys. Lett. A 133(3), 134–139 (1988)
Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, vol. 31. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-30666-8
Li, S.T., Qin, M.: A note for Lie-Poisson Hamilton-Jacobi equation and Lie-Poisson integrator. Comput. Math. Appl. 30(7), 67–74 (1995)
Marsden, J.E., Pekarsky, S., Shkoller, S.: Discrete Euler-Poincaré and Lie-Poisson equations. Nonlinearity 12(6), 1647–1662 (1999)
Marsden, J.E., West, M.: Discrete mechanics and variational integrators. Acta Numerica 10, 357–514 (2001)
Marsen, J., Ratiu, T.: Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Texts in Applied Mathematics, vol. 17. Springer, New York (1994). https://doi.org/10.1007/978-0-387-21792-5
Munthe-Kaas, H.: High order Runge-Kutta methods on manifolds. Appl. Numer. Math. 29(1), 115–127 (1999)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Bensoam, J., Carré, P. (2019). Geometric Numerical Methods with Lie Groups. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2019. Lecture Notes in Computer Science(), vol 11712. Springer, Cham. https://doi.org/10.1007/978-3-030-26980-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-26980-7_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26979-1
Online ISBN: 978-3-030-26980-7
eBook Packages: Computer ScienceComputer Science (R0)








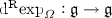 is invertible, which is the case for SO(3) whenever
is invertible, which is the case for SO(3) whenever