When Geometry Meets Psycho-Physics and Quantum Mechanics: Modern Perspectives on the Space of Perceived Colors

Abstract

We discuss some modern perspectives about the mathematical formalization of colorimetry, motivated by the analysis of a groundbreaking, yet poorly known, model of the color space proposed by H.L. Resnikoff and based on differential geometry. In particular, we will underline two facts: the first is the need of novel, carefully implemented, psycho-physical experiments and the second is the role that Jordan algebras may have in the development of a more rigorously founded colorimetry.

1 Introduction

In 1974, H.L. Resnikoff published a revolutionary paper about the geometry of the space of perceived colors $\mathcal P$ [12]. Starting from the axiomatic set for colorimetry provided by Schrödinger [15], he added a new axiom, the homogeneity of $\mathcal P$ with respect to a suitable group of transformations, and proved that only two geometrical structures were coherent with the new set of axioms: the first is isomorphic to the well-known tristimulus flat space $\mathbb {R} ^+\times \mathbb {R} ^+\times \mathbb {R} ^+\equiv \mathcal{P}_1$, while the second, totally new, is isomorphic to $\mathbb {R} ^+\times SL(2, \mathbb {R} )/SO(2)\equiv \mathcal{P}_2$, thus confirming the interest about hyperbolic geometry in colorimetry, already pointed out by Yilmaz in [21].

Resnikoff was also able to single out a unique Riemannian metric on the two geometrical structures by requiring it to be invariant with respect to the group transformations: the resulting metric on $\mathcal{P}_1$ coincides with the well-known Helmholtz-Stiles flat metric [20], while that on $\mathcal{P}_2$ is constant negative curvature Rao-Siegel metric, which is analogous to the Fisher metric in the geometric theory of information [1].

Finally, Resnikoff provided an elegant framework to treat the two cases $\mathcal{P}_1$ and $\mathcal{P}_2$ as special instances of a unique theory based on Jordan algebras. In spite of its elegance and innovative character, Resnikoff’s and Yilmaz’s paper remained practically ignored until today, receiving only a few quotation since their publication.

With this contribution, we would like to share our ideas about the influence that these pioneers might have for the development of a modern, geometry-based, colorimetry. The aim is both to overcome the lack of mathematical rigor that affects the foundation of this discipline and to create a theory more suited for color image processing applications.

2 Description of Resnikoff’s Model of Color Space

As we said in the introduction, in the paper [12], Resnikoff analyzed the geometrical properties of the space of perceived colors $\mathcal{P}$ with a high level mathematical rigor. He started from Schrödinger’s axioms [15] for $\mathcal{P}$:

• Axiom 1 (Newton 1704): if $x\in \mathcal{P}$ and $\alpha \in \mathbb {R} ^+$, then $\alpha x \in \mathcal{P}$.

• Axiom 2: if $x \in \mathcal{P}$ then it does not exist any $y \in \mathcal{P}$ such that $x+y=0$.

• Axiom 3 (Grassmann 1853, Helmholtz 1866): for every $x,y \in \mathcal{P}$ and for every $\alpha \in [0,1]$, $\alpha x+(1-\alpha )y \in \mathcal{P}$.

• Axiom 4 (Grassmann 1853): every collection of more than three perceived colors is a linear dependent family in the vector space V spanned by the elements of $\mathcal{P}$.

The axioms imply that $\mathcal{P}$ is a convex cone embedded in a vector space V of dimension 3, for standard observers non affected by color blindness, as it will be implicitly assumed in the following part of the paper.

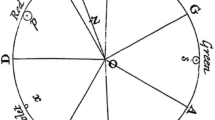
Resnikoff added another axiom, that of local homogeneity of $\mathcal{P}$ with respect to changes of background. To correctly introduce this axiom, it is worthwhile showing the observational arrangement that he considered, which is depicted in Fig. 1: a standard observer is watching a simple color stimulus embedded in a uniform background.

Fig. 1.

The observational arrangement considered by Resnikoff.

When the background of the color stimulus is modified, our perception of the stimulus changes. Resnikoff identified the change of background transformations B with the following group:

$$ GL_+( \mathcal{P} ):=\{B\in GL(V) \; : \;\text {det}(B)>0, \text { and } B(x)\in \mathcal{P} \; \; \forall x\in \mathcal{P} \}, $$

where GL(V) is the group of invertible linear operators on V, the requirements det$(B)>0$ and $B(x)\in \mathcal{P}$ guarantee that these transformations preserve the orientation of the cone and that $\mathcal{P}$ is stable under their action.

The previous observation about how a change of background modifies the perception of the colors stimulus can thus be formalized by saying that $\mathcal{P}$ is locally homogeneous with respect to $GL_+( \mathcal{P} )$. However, thanks to the convex nature of $\mathcal{P}$, it is clear that local homogeneity implies global homogeneity.

For this reason, Resnikoff postulates a fifth axiom on the structure of the color space:

• Axiom 5 (Resnikoff 1974): $\mathcal{P}$ is globally homogeneous with respect to the group of background transformations $GL_+( \mathcal{P} )$.

Starting from the set of axioms 1–5 and by using standard results from the theory of Lie groups and algebras, Resnikoff managed to show that the only two geometrical structures compatible with these axioms are:

$$\begin{aligned} \mathcal{P} _1 \simeq \mathbb {R} ^+ \times \mathbb {R} ^+ \times \mathbb {R} ^+, \end{aligned}$$

(1)

or

$$\begin{aligned} \mathcal{P} _2 \simeq \mathbb {R} ^+ \times SL(2, \mathbb {R} )/SO(2), \end{aligned}$$

(2)

where $SL(2, \mathbb {R} )$ is the group of $2\times 2$ matrices with real entries and determinant $+1$ and SO(2) is the group of matrices that perform rotations in the plane $\mathbb {R} ^2$.

The first geometrical structure, $\mathcal{P} _1$ agrees with the usual trichromatic space, such as RGB, XYZ, and so on. The second one, $\mathcal{P} _2$, on the contrary, is a totally new geometrical structure for the space $\mathcal{P}$.

If a Riemannian metric on $\mathcal{P}$ existed, then the difference between the perceived colors $x,y\in \mathcal{P}$ would be calculated with the integral

$$\begin{aligned} d(x,y)=\int _\gamma ds, \qquad \gamma (0)=x, \, \gamma (1)=y, \end{aligned}$$

(3)

where $\gamma$ is the unique geodesic arc between x and y.

Resnikoff proved that the only Riemannian $GL_+( \mathcal{P} )$-invariant metric on $\mathcal{P} _1$ is precisely the Helmholtz-Stiles metric (obtained with a totally different method), i.e.,

$$\begin{aligned} ds^2=\alpha _1 \left( \frac{dx_1}{x_1} \right) ^2 + \alpha _2 \left( \frac{dx_2}{x_2} \right) ^2 + \alpha _3 \left( \frac{dx_3}{x_3} \right) ^2, \end{aligned}$$

(4)

where $x_j \in \mathbb {R} ^+$ and $\alpha _j$ are positive real constants for $j=1,2,3$.

Turning his attention to $\mathcal{P} _2$, he showed that the only Riemannian $GL_+( \mathcal{P} )$-invariant metric on it can be written like this:

$$\begin{aligned} ds^2 = \text {tr}(x^{-1} dx x^{-1} dx), \end{aligned}$$

(5)

which is equivalent to the Rao-Siegel metric [4, 17].

Resnikoff concluded his paper by showing that the models $\mathcal{P} _1$ and $\mathcal{P} _2$ are particular instances of a unified framework based on the use of Jordan algebras. We recall that a Jordan algebra $\mathcal A$ is an algebra over a field whose multiplication $\circ$ is commutative but non-associative and it satisfies the so-called Jordan’s identity:

$$\begin{aligned} (x\circ y)\circ x^2 = x\circ (y\circ x^2), \end{aligned}$$

(6)

for all x and y in $\mathcal A$. Such an algebra is power-associative in the sense that the sub-algebra generated by any of its element is associative.

In the Sect. 3 we will underline some problems that remained opened since the appearance of Resnikoff’s paper, while in Sect. 4 we will discuss how Resnikoff’s use of Jordan algebras was ahead of his time and it can be rescued from oblivion and used to define the colorimetric attributes of a color.

3 Missing Pieces in Resnikoff’s Model from the Viewpoint of Modern Colorimetry

Resnikoff’s paper remains, after more than 40 years since its publication, an example of elegance, originality and independent research. However, in the light of nowadays knowledge about color perception, there are three issues that must be discussed carefully.

The first, and more delicate, one is the hypothesis of linearity for the background transformations $B\in GL_+( \mathcal{P} )$. Resnikoff himself, in a subsequent paper [13] recognized that this hypothesis is a very strong one with the sentence: ‘the least verified aspect of Axiom 5 is its assertion of the linearity of transitive group of changes of background’.

Without linearity, the whole mathematical structure built by Resnikoff to arrive to the identification of $\mathcal{P} _1$ and $\mathcal{P} _2$ as the only two possible geometrical representations of $\mathcal{P}$ loses its foundation. Thus, a carefully developed psycho-physical experiment based on color matching [6] is needed to check the linearity of background transformations $B\in GL_+( \mathcal{P} )$.

An original experiment to check additivity, i.e. the fact that $B(x+y)$ color matches $B(x)+B(y)$, would be the following: on one side, we superpose the lights $\mathbf x$ and $\mathbf y$ which generate the perceived colors x and y, respectively, with respect to the same background b, then we perform a change of background with the transformation B and we call $b'$ the new background. Finally, we color match what we obtain, this will give us the perceived color $B(x+y)\in \mathcal{P}$ which represents $\mathbf {x}+\mathbf {y}$ in the context $b'$.

On the other side, we separately perform the change of context B on x and y and we color match the results, obtaining $B(x)\in \mathcal{P}$ and $B(y)\in \mathcal{P}$, respectively. We then match B(x) with the physical light $\mathbf{x}'$ and B(y) with the physical light $\mathbf{y}'$. If the color sensations produced by $x+y$ in the background $b'$ matches that of $\mathbf{x}'+\mathbf{y}'$ in the same background, then the change of context is additive.

To test homogeneity, i.e. the fact that $B(\alpha x)$ color matches $\alpha B(x)$, we must use a similar procedure for at least a sufficiently large range of coefficients $\alpha \in \mathbb {R}$.

The question about how large this range of coefficients must be leads us directly to the second issue, which is shared by any model of visual perception. We are referring to the fact that Axiom 1, i.e. the fact that $\mathcal{P}$ is an infinite cone, is only an idealization: for any $x\in \mathcal{P}$ and very large $\alpha$, $\alpha x$ will cease to be perceived, and this it will not belong to $\mathcal{P}$ anymore, because the retinal photoreceptors will be firstly saturated and then permanently damaged [16]. Similarly, for $\alpha \ne 0$, but $\alpha \simeq 0$, $\alpha x$ will firstly switch the human visual system to mesopic and then scotopic vision via the Purkinje effect [8], and then it will fall below the threshold limit to be perceived. Thus, more than an infinite cone, $\mathcal{P}$ has the structure of a truncated cone. In classical colorimetry, one bypasses this last observation by working far from these limits, however, in order to build a modern theory of colorimetry we must start taking into account more seriously the lower and upper perceptual bound.

The third issue about Resnikoff’s model is the lack of locality, i.e. the fact the observational configuration considered, that of Fig. 1 is a over-simplified version of a real-world visual condition. Everyday vision deals with what is commonly called ‘color in context’, i.e. the fact that a non-uniform background strongly influences color perception, this phenomenon is referred to as color induction [18]. Actually, many papers has been emphasized the role of context for color vision to the point that a standalone definition of the color of a surface, without the specification of the context in which the surface is embedded does not make sense anymore: color is color in context [7, 10, 11, 14].

This observation implies that the Resnikoff model, and any other color perception model based on the observational configuration of Fig. 1, can only be viewed as a first step towards a local theory of color, mathematically similar to a field theory. A more thorough understanding of the color induction phenomenon and properties as color constancy, i.e. the robustness of color perception with respect to changes of illumination [10] or the invariance of saturation perception for monochromatic light stimuli [21], are likely to play a fundamental role in the construction of this kind of color field theory.

4 On the Role of Jordan Algebras in Colorimetry

The second part of [12] devoted to Jordan algebras may suggest that Resnikoff had already a quantum interpretation of his new hyperbolic model. Jordan algebras are non-associative commutative algebras that have been classified by Jordan, Von Neumann and Wigner [9] under the assumptions that they are of finite dimension and formally real. They are considered as a fitting alternative to the usual associative non-commutative framework for the geometrization of quantum mechanics. One of the main motivation to introduce Jordan algebras in our context is Koecher-Vinberg theorem which states that every open convex regular homogeneous and self-dual cone is the interior of the positive domain of a Jordan algebra [5]. From a quantum viewpoint, this means that such a cone is the set of positive observables of a quantum system.

Contrary to Resnikoff, one may postulate at first that $\mathcal P$ can be described from the state space of a quantum system characterized by a formally real Jordan algebra $\mathcal A$ of real dimension 3, according to the dimension of $\mathcal P$. Such an algebra $\mathcal A$ is necessarily isomorphic to one of the following two: either $\mathbb R\oplus \mathbb R\oplus \mathbb R$ or $\mathcal H(2,\mathbb R)$, which is the algebra of real symmetric $2\times 2$ matrices, with Jordan product given by

$$\begin{aligned} x\circ y={1\over 2}(xy+yx). \end{aligned}$$

(7)

The classification by Resnikoff can be simply recovered by taking the symmetric cone of the positive elements of $\mathcal A$ [5].

Let us, in particular, concentrate on the geometrical structure $\mathcal P_2$ of the color space: the algebra $\mathcal H(2,\mathbb R)$ is isomorphic to the so-called spin factor $\mathbb R\oplus \mathbb R^2$ via the transformation defined by

$$\begin{aligned} (\alpha +v)\longmapsto \left( \begin{array}{cc}\alpha +v_1 &{} v_2 \\ v_2 &{} \alpha -v_1\end{array}\right) , \end{aligned}$$

(8)

with $\alpha \in \mathbb R$ and $v=(v_1,v_2)\in \mathbb {R} ^2$, where $v_1$ and $v_2$ are the components of v with respect to the canonical basis of $\mathbb R^2$. One may consider the spin factor $\mathbb R\oplus \mathbb R^2$ as a 3-dimensional Minkowski space-time equipped with the metric

$$\begin{aligned} (\alpha +v)\cdot (\beta +w)=\alpha \beta -\langle v,w\rangle , \end{aligned}$$

(9)

where $\alpha$ and $\beta$ are reals and v and w are vectors of $\mathbb R^2$. Let us also recall that the light-cone $\mathcal C$ of $\mathbb R\oplus \mathbb R^2$ is the set of elements $x=(\alpha +v)$ that satisfy

$$\begin{aligned} x\cdot x=0, \end{aligned}$$

(10)

and that a light ray is a 1-dimensional subspace of $\mathbb R\oplus \mathbb R^2$ spanned by an element of $\mathcal C$. It is clear that every light ray is spanned by a unique element of the form $(1+v)$ with v a unit vector of $\mathbb R^2$ and, therefore, that the space of light rays coincides with the projective real space $\mathbb P_1(\mathbb R)$. In other words, we have the following result.

Proposition 1

There is a one to one correspondence between the light rays of the spin factor $\mathbb R\oplus \mathbb R^2$ and the rank 1 projections of the Jordan algebra $\mathcal H(2,\mathbb R)$.

The correspondance is given by

$$\begin{aligned} (1+v)\longmapsto {1\over 2}\left( \begin{array}{cc}1+v_{1} &{} v_{2}\\ v_{2} &{} 1-v_{1}\end{array}\right) . \end{aligned}$$

(11)

This correspondence has a meaningful interpretation: the light rays of the spin factor $\mathbb R\oplus \mathbb R^2$, as a Minkowski space-time of dimension 3, are precisely the pure states of the algebra $\mathcal H(2,\mathbb R)$, as a quantum system over $\mathbb R^2$.

A state of $\mathcal A$ is a linear functional $\langle \cdot \rangle :\mathcal A\longrightarrow \mathbb R$ that is nonnegative and normalized, i.e. $\langle 1\rangle =1$. It can be shown that the states of $\mathcal A$ are given by density matrices, namely by the elements of $\mathcal H(2,\mathbb R)$ that are non-negative and have trace 1 [2]. They correspond precisely to the elements $x=(1+v)/2$ of the spin factor with $\Vert v\Vert \le 1$. The pure states, i.e those which can be characterized as projections, form the boundary of this disk since, for pure states, it holds that $\Vert v\Vert =1$. It is clear that this boundary can be identified with $\mathbb P_1(\mathbb R)$. Contrary to the usual context of quantum mechanics, the system that we consider is real, i.e. the algebra $\mathcal H(2,\mathbb C)$ is replaced by $\mathcal H(2,\mathbb R)$.

This system is a so-called rebit, a real qubit [2], that has no classic physical interpretation because there is no space with a rotation group of dimension two. As explained in the sequel, it appears that this kind of system is relevant to explain color perception. We refer also to [19] for information on real-vector-space quantum theory and its consistency regarding optimal information transfer.

An element $\rho$ of $\mathcal H(2,\mathbb R)$ is a state density matrix if and only if it can be written as:

$$\begin{aligned} \rho (v_1,v_2)={1\over 2}(Id_2+v\cdot \sigma ) , \end{aligned}$$

(12)

where $\sigma =(\sigma _1,\sigma _2)$ with:

$$\begin{aligned} \sigma _1=\left( \begin{array}{cc}1 &{} 0 \\ 0 &{} -1\end{array}\right) \,\, \,\, \sigma _2=\left( \begin{array}{cc}0 &{} 1 \\ 1 &{} 0\end{array}\right) , \end{aligned}$$

(13)

and $v=v_1e_1+v_2e_2$ is a vector of $\mathbb R^2$ with $\Vert v\Vert \le 1.$ The matrices $\sigma _1$ and $\sigma _2$ are Pauli-like matrices. In the usual framework of quantum mechanics, the Bloch body [2], is the unit Bloch ball in $\mathbb R^3$. It represents the states of the two-level quantum system of a spin-${1\over 2}$ particle, also called a qubit. In the present context, the Bloch body is the unit disk of $\mathbb R^2$ associated to a rebit.

More precisely, let us consider the four state vectors:

$$\begin{aligned} |u_1\rangle =\left( \begin{array}{c}1\\ 0\end{array}\right) ,\ |d_1\rangle =\left( \begin{array}{c}0\\ 1\end{array}\right) ,\ |u_2\rangle ={1\over \sqrt{2}}\left( \begin{array}{c}1\\ 1\end{array}\right) ,\ |d_2\rangle ={1\over \sqrt{2}}\left( \begin{array}{c}-1\\ 1\end{array}\right) . \end{aligned}$$

(14)

We have:

$$\begin{aligned} \sigma _1= |u_1\rangle \langle u_1|-|d_1\rangle \langle d_1| ,\ \sigma _2=|u_2\rangle \langle u_2|-|d_2\rangle \langle d_2| . \end{aligned}$$

(15)

The state vectors $|u_1\rangle$ and $|d_1\rangle$, resp. $|u_2\rangle$ and $|d_2\rangle$, are eigenstates of $\sigma _1$, resp. $\sigma _2$, with eigenvalues 1 and $-1$. Using polar coordinates $v_1=r\cos \theta$, $v_2=r\sin \theta$, we can write $\rho (v_1,v_2)$ as:

$$\begin{aligned} \begin{aligned} \rho (r,\theta )&={1\over 2}\left( \begin{array}{cc}1+r\cos \theta &{} r\sin \theta \\ r\sin \theta &{} 1-r\cos \theta \end{array}\right) \\&={1\over 2}\left\{ (1+r\cos \theta )|u_1\rangle \langle u_1|+(1-r\cos \theta )|d_1\rangle \langle d_1| \right. \\&\left. \quad +\, (r\sin \theta )|u_2\rangle \langle u_2| -(r\sin \theta )|d_2\rangle \langle d_2|\right\} . \end{aligned} \end{aligned}$$

(16)

In particular, every pure state density matrix can be written as:

$$\begin{aligned} \rho (1,\theta )=|(1,\theta )\rangle \langle (1,\theta )| , \end{aligned}$$

(17)

with:

$$\begin{aligned} |(1,\theta )\rangle =\cos (\theta /2)|u_1\rangle +\sin (\theta /2)|d_1\rangle . \end{aligned}$$

(18)

This means that we can identify the pure state density matrices $\rho (1,\theta )$ with the state vectors $|(1,\theta )\rangle$ and also with the points of the unit disk boundary of coordinate $\theta$. More generally, every state density matrix can be written as a mixture:

$$\begin{aligned} \rho (r,\theta )=\rho _0+{r\cos \theta \over 2}\left( \rho (1,0)-\rho (1,\pi )\right) +{r\sin \theta \over 2}\left( \rho (1,\pi /2)-\rho (1,3\pi /2)\right) , \end{aligned}$$

(19)

with:

$$\begin{aligned} \rho _0={1\over 2}\left( \begin{array}{cc} 1 &{} 0\\ 0 &{} 1\end{array} \right) . \end{aligned}$$

(20)

Such a mixture is given by the point of the unit disk of polar coordinates $(r,\theta )$.

It is important to notice that the four state density matrices $\rho (1,0)$, $\rho (1,\pi )$, $\rho (1,\pi /2)$ and $\rho (1,3\pi /2)$ correspond to two pairs of state vectors $(|u_1\rangle ,|d_1\rangle )$, $(|u_2\rangle ,|d_2\rangle )$, the state vectors $|u_i\rangle$ and $|d_i\rangle$, for $i=1,2$, being linked by the “up and down” Pauli-like matrix $\sigma _i$. It can be shown that this Bloch disk coincides with Hering’s disk given by the color opponency mechanism. Details will appear elsewhere [3].

Among all the states, the normalized identity $\rho _0=(1+0)/2=1/2I_2$ plays a significant role: it is the state of maximal von Neumann entropy. It is characterized by:

$$\begin{aligned} \rho _0=\underset{\rho }{\mathrm {argmax}} ({\mathrm {-Trace}}(\rho \log \rho )). \end{aligned}$$

(21)

Actually, ${\mathrm {-Trace}}(\rho _0\log \rho _0)=\log 2$ and ${\mathrm {-Trace}}(\rho \log \rho )=0$ for a pure state $\rho$.

This quantum interpretation allows us to define the three main attributes of a color, without any reference to physical colors or even to an observer. In fact, we can define a perceived color as a non-negative normalized element $(\alpha +v)/2$ of the spin factor $\mathbb R\oplus \mathbb R^2$. Nonnegativity is equivalent to $\alpha ^2\ge \Vert v\Vert ^2$, so that a perceived color can be identified with a time-like element of the 3-dimensional Minkowski space-time.

The real value $\alpha$ is naturally interpreted as the ‘luminance’ of the perceived color, so that $(\alpha +v)/2\alpha$ is a ‘chromatic’ state. Pure ‘chromatic’ states are primary, monochromatic, colors and form the ‘hue’ circle $\mathbb P_1(\mathbb R)$ equipped with the projective metric. Finally, since $0\le \mathrm {-Trace}(\rho \log \rho )\le \log 2$, for all states $\rho$, the entropy measure $\mathrm {-Trace}(x\log x)$ provides the description of the ‘saturation’, the state of maximal entropy $\rho _0$ being perceived as ‘achromatic’.

5 Conclusions

A critical analysis of the mathematically elegant and theoretically avant-garde model of Resnikoff for the space of perceived colors led us to propose a psycho-physical experiment to verify one of the fundamental hypothesis on which the model is based.

We have also underlined that the finite threshold and saturation limit of retinal photoreceptors should be taken into account in a moder rigorous description of the color space geometry.

Moreover, we have motivated through the very important (and often undervalued) phenomenon of color induction, why a color theory should be constructed with the building blocks of local field theories.

Finally, we have sketched our ideas about how Jordan algebras can be used to define the colorimetric attributes by pointing out the similarities to the formalism of quantum mechanics. The quantum description that we propose creates a deep connection between the pioneering works of Yilmaz and Resnikoff. A more detailed study shows that the above mentioned rebit makes it possible to recover Hering’s disk and thus to obtain a mathematical justification of the coherence between trichromatic and color opponency theories [3].