Abstract
This paper develops Sobolev variants of the non-parametric statistical manifolds appearing in [10] and [11]. The manifolds are modelled on a particular class of weighted, mixed-norm Sobolev spaces, including a Hilbert-Sobolev space. Densities are expressed in terms of a deformed exponential function having linear growth, which lifts to a continuous nonlinear superposition (Nemytskii) operator. This property is used in the construction of finite-dimensional mixture and exponential submanifolds, on which approximations can be based. The manifolds of probability measures are developed in their natural setting, as embedded submanifolds of those of finite measures.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
This paper develops non-parametric statistical manifolds modelled on spaces of Sobolev type. It applies some of the results of [12] to a particular class of manifolds, and develops smoothly embedded finite-dimensional exponential submanifolds. The non-parametric manifolds are natural refinements of those in [10] and [11]; they employ charts that are “balanced” between the density function and its log. The inverses of the charts are expressed in terms of a deformed exponential function having linear growth, a property shared by other deformed exponentials (notably the Kaniadakis exponential with parameter \(\kappa =1\)). (See [8] and the discussion in [12]). The linear growth property is highly advantageous in the Sobolev context because the deformed exponential then “lifts” to a nonlinear superposition (Nemytskii) operator that acts continuously on particular classes of model spaces.
For some  , let \(\mathcal{X}\) be the \(\sigma \)-algebra of Lebesgue measurable subsets of
, let \(\mathcal{X}\) be the \(\sigma \)-algebra of Lebesgue measurable subsets of  , and let \(\mu \) be a probability measure on \(\mathcal{X}\) that is mutually absolutely continuous with respect to Lebesgue (volume) measure. \(\mathcal{X}\) is a very rich collection of subsets,
, and let \(\mu \) be a probability measure on \(\mathcal{X}\) that is mutually absolutely continuous with respect to Lebesgue (volume) measure. \(\mathcal{X}\) is a very rich collection of subsets,  , for which the Lebesgue measure dx(A) is well defined. Each \(A\in \mathcal{X}\) has a well-defined probability \(\mu (A)\), which can be expressed in terms of the probability density function
, for which the Lebesgue measure dx(A) is well defined. Each \(A\in \mathcal{X}\) has a well-defined probability \(\mu (A)\), which can be expressed in terms of the probability density function  as follows:
as follows:
The simplest example of a statistical manifold over the sample space  is the finite-dimensional exponential model [1, 3]. This is based on a finite set of linearly independent random variables \(\eta _1,\ldots \eta _n\) defined on
is the finite-dimensional exponential model [1, 3]. This is based on a finite set of linearly independent random variables \(\eta _1,\ldots \eta _n\) defined on  . Let B be an open subset of
. Let B be an open subset of  such that, for any \(y\in B\), \({{\mathbf{E}_\mu }\exp (\sum _i y_i\eta _i)<\infty }\), where \({\mathbf{E}_\mu }\) is expectation (integration) with respect to \(\mu \). Any \(y\in B\) represents the probability measure \(P_y\), defined by
such that, for any \(y\in B\), \({{\mathbf{E}_\mu }\exp (\sum _i y_i\eta _i)<\infty }\), where \({\mathbf{E}_\mu }\) is expectation (integration) with respect to \(\mu \). Any \(y\in B\) represents the probability measure \(P_y\), defined by
where \({c=\log {\mathbf{E}_\mu }\exp (\sum _i y_i\eta _i)}\). The set \(N:=\{P_y: y\in B\}\) is a manifold of probability measures, with a differentiable structure in terms of which the important statistical divergences of estimation theory are suitably smooth.
The first fully successful infinite-dimensional (non-parametric) statistical manifold was constructed in [14], and further developed in [2, 5, 13]. This is the natural extension of exponential models such as N to the non-parametric setting. The chart is a centred version of the log of the probability density function \(p:=dP/d\mu \), and so, as in (2), p is represented in terms of the exponential of the model space variable. The model space used is the exponential Orlicz space, which has a stronger topology than the Lebesgue \(L^\lambda (\mu )\) spaces for \(1\le \lambda <\infty \).
A central requirement of a chart in a statistical manifold is that it should induce a topology with respect to which statistical divergences, such as the Kullback-Leibler (KL)-divergence, are appropriately smooth. The KL-divergence between finite measures P and Q on \(\mathcal{X}\) is defined as follows [1, 3]:

It is of class \(C^\infty \) on the exponential Orlicz manifold. As (3) shows, the KL-divergence is bilinear in the density p and its log, and so its smoothness properties are closely connected with those of p and \(\log p\) considered as elements of dual function spaces. This is why the following deformed logarithm  was introduced in the Hilbert setting of [10]:
was introduced in the Hilbert setting of [10]:
This is composed with probability density functions to realise a chart on a manifold of finite measures that maps into the Lebesgue space \(L^\lambda (\mu )\), for any \(2\le \lambda <\infty \) [10, 11]. A centred version of this can be used as a chart on the submanifold of probability measures. The inverse of \(\log _d\) can be thought of as a deformed exponential function. It has linear growth, as a result of which the density, p, and its log both belong to the same space as \(\log _d(p)\) (i.e. the model space \(L^\lambda (\mu )\)). This property is not shared by the exponential Orlicz manifold. Reference [12] shows that it is retained when the sample space is  and the model space \(L^\lambda (\mu )\) is replaced by particular spaces of Sobolev type.
and the model space \(L^\lambda (\mu )\) is replaced by particular spaces of Sobolev type.
The natural domain of statistical divergences, such as the KL-divergence, is a space of measures defined on an abstract measurable space \((\varOmega ,\mathcal{F})\). Since the primary concern of “raw” information geometry is the smoothness of these divergences, the exponential Orlicz and \(L^\lambda (\mu )\) manifolds of [14] and [11], in their general form, make no reference to any other structures that the sample space \(\varOmega \) may possess. However, in the special case that  , the topology and linear structure of
, the topology and linear structure of  play important roles in many applications. For example, the Fokker-Planck equation makes direct reference to the linear structure of
play important roles in many applications. For example, the Fokker-Planck equation makes direct reference to the linear structure of  through a differential operator. For this reason, it is of interest to develop “hybrid” information manifolds, in which the topology of the sample space is somehow incorporated into the model space. One way of achieving this is to use model spaces of Sobolev type. This approach is taken here, in the context of the \(L^\lambda (\mu )\) manifolds of [10, 11]. For the development of Sobolev variants of the exponential Orlicz manifold, the reader is referred to [7].
through a differential operator. For this reason, it is of interest to develop “hybrid” information manifolds, in which the topology of the sample space is somehow incorporated into the model space. One way of achieving this is to use model spaces of Sobolev type. This approach is taken here, in the context of the \(L^\lambda (\mu )\) manifolds of [10, 11]. For the development of Sobolev variants of the exponential Orlicz manifold, the reader is referred to [7].
The paper is structured as follows. Section 2 introduces the spaces on which the manifolds are modelled. Section 3 presents the principal results on the non-parametric manifolds constructed from these spaces; it discusses both manifolds of finite measures and submanifolds of probability measures. Finally Sect. 4 develops a class of smoothly embedded finite-dimensional exponential manifolds that are of potential use in applications.
2 The Model Spaces
For some \(t\in (1,2]\), let \(\theta _t:[0,\infty )\rightarrow [0,\infty )\) be a strictly increasing, convex function that is twice continuously differentiable on \((0,\infty )\), such that \(-\sqrt{\theta _t}\) is convex, \(\lim _{z\downarrow 0}\theta _t^\prime (z)<\infty \), and

Examples, including some for which  is of class \(C^2\) are given in [12], which also develops variants for which \(t\in (0,1]\). (The restriction \(t\in (1,2]\), used here, simplifies the presentation in what follows while retaining a useful subset of the manifolds developed in [12]). For each \(t\in (1,2]\), we define a reference probability measure, \(\mu =\mu _t\), as follows.
is of class \(C^2\) are given in [12], which also develops variants for which \(t\in (0,1]\). (The restriction \(t\in (1,2]\), used here, simplifies the presentation in what follows while retaining a useful subset of the manifolds developed in [12]). For each \(t\in (1,2]\), we define a reference probability measure, \(\mu =\mu _t\), as follows.
and  is such that \(\int \exp (C_t-\theta _t(|z|))dz=1\). For any \(1\le \lambda <\infty \), let \(L^\lambda (\mu )\) be the Banach space of (equivalence classes of) measurable functions
is such that \(\int \exp (C_t-\theta _t(|z|))dz=1\). For any \(1\le \lambda <\infty \), let \(L^\lambda (\mu )\) be the Banach space of (equivalence classes of) measurable functions  for which \(\Vert u\Vert _{L^\lambda (\mu )}:=(\int |u|^\lambda d\mu )^{1/\lambda }<\infty \).
for which \(\Vert u\Vert _{L^\lambda (\mu )}:=(\int |u|^\lambda d\mu )^{1/\lambda }<\infty \).
For  , let \(S:=\{0,\ldots , k\}^d\) be the set of d-tuples of integers in the range \(0\le s_i\le k\). For \(s\in S\), we define \(|s|=\sum _is_i\), and denote by 0 the d-tuple for which \(|s|=0\). For any \(0\le i\le k\), \(S_i:=\{s\in S:i\le |s|\le k\}\) is the set of d-tuples of weight at least i and at most k. Let \(\varLambda =(\lambda _0,\lambda _1,\ldots ,\lambda _k)\), where \(\lambda _i\in [1,\infty )\) for \(0\le i\le k\), and let \(W^{k,\varLambda }(\mu )\) be the mixed-norm, weighted Sobolev space comprising functions \(a\in L^{\lambda _0}(\mu )\) that have weak partial derivatives \(D^sa\in L^{\lambda _{|s|}}(\mu )\), for all \(s\in S_1\). For \(a\in W^{k,\varLambda }(\mu )\) we define the mixed norm
, let \(S:=\{0,\ldots , k\}^d\) be the set of d-tuples of integers in the range \(0\le s_i\le k\). For \(s\in S\), we define \(|s|=\sum _is_i\), and denote by 0 the d-tuple for which \(|s|=0\). For any \(0\le i\le k\), \(S_i:=\{s\in S:i\le |s|\le k\}\) is the set of d-tuples of weight at least i and at most k. Let \(\varLambda =(\lambda _0,\lambda _1,\ldots ,\lambda _k)\), where \(\lambda _i\in [1,\infty )\) for \(0\le i\le k\), and let \(W^{k,\varLambda }(\mu )\) be the mixed-norm, weighted Sobolev space comprising functions \(a\in L^{\lambda _0}(\mu )\) that have weak partial derivatives \(D^sa\in L^{\lambda _{|s|}}(\mu )\), for all \(s\in S_1\). For \(a\in W^{k,\varLambda }(\mu )\) we define the mixed norm
\(W^{k,\varLambda }(\mu )\) is a Banach space with respect to this norm. (See Theorem 2.1 in [12]).
We shall confine our attention here to the following special class of model spaces, parametrised by  and \(\lambda \in [k,\infty )\):
and \(\lambda \in [k,\infty )\):

This includes the Hilbert-Sobolev space \(G_m^{1,2}\). Let  be the inverse of the deformed logarithm of (4). The following is proved as part of Proposition 2 in [12].
be the inverse of the deformed logarithm of (4). The following is proved as part of Proposition 2 in [12].
Proposition 1
- (i):
-
For any \(a\in G_m^{k,\lambda }\), \(\psi (a)\in G_m^{k,\lambda }\).
- (ii):
-
The nonlinear superposition (Nemytskii) operator \(\varPsi _m^{k,\lambda }:G_m^{k,\lambda }\rightarrow G_m^{k,\lambda }\), defined by \(\varPsi _m^{k,\lambda }(a)(x)=\psi (a(x))\), is continuous.
This is rare property in the theory of nonlinear maps between Sobolev spaces, and has its origins in the boundedness of the derivatives of \(\psi \). It is useful in the construction of finite-dimensional mixture or exponential submanifolds. Normally the Sobolev space forming the domain of a continuous nonlinear superposition operator would need a stronger topology than that forming its range [15]. This would require it to have larger Lebesgue exponents, or to control a greater number of derivatives.
Remark 1
It is shown in [12] that the continuity of \(\varPsi \) between identical Sobolev spaces is also true of the fixed-norm space \(W^{2,(1,1,1)}(\mu )\), but of no other fixed-norm spaces (except for \(G_m^{1,\lambda }\) with \(\lambda \in [1,\infty )\)).
3 The Nonparametric Manifolds
Let \(G=G_m^{k,\lambda }\) be the mixed-norm Sobolev space as defined in (8). Let \(\varPsi :=\varPsi _m^{k,\lambda }\) be as defined in Proposition 1. We consider the set M of finite measures on \(\mathcal{X}\) satisfying the following:
- (M1):
-
P is mutually absolutely continuous with respect to \(\mu \);
- (M2):
-
\(p, \log p\in G\), where \(p=dP/d\mu \).
This is equipped with the global chart \(\phi :M\rightarrow G\), defined by
In view of Proposition 1, it is not difficult to show that \(\phi \) is a bijection onto G. (See Proposition 1 in [12]). For any \(P\in M\), let \({\tilde{P}}_a\in M\) have density \(d{\tilde{P}}_a/d\mu =\psi ^{(1)}(a)\), where \(a=\phi (P)\) and \(\psi ^{(1)}=\psi /(1+\psi )\) is the first derivative of \(\psi \). We define a tangent vector, U at \(P\in M\), to be a signed measure on \(\mathcal{X}\) of finite total variation such that
- (T1):
-
U is mutually absolutely continuous with respect to \({\tilde{P}}_a\);
- (T2):
-
\(dU/d{\tilde{P}}_a\in G\), where \(a=\phi (P)\).
The tangent space \(T_PM\) is the linear space of all such signed measures, and the tangent bundle is the disjoint union \(TM=\cup _{P\in M}(P,T_PM)\). This admits the global chart \(\varPhi :TM\rightarrow G\times G\), defined by
The derivative of a (Fréchet) differentiable, Banach-space-valued map  (at P and in the “direction” U) is defined as follows: (clearly \(u=U\phi \)).
(at P and in the “direction” U) is defined as follows: (clearly \(u=U\phi \)).
Let \(m_\lambda ,e_\lambda :M\rightarrow L^\lambda (\mu )\) be the nonlinear superposition operators defined by
The map \(m_\lambda \) is the composition of \(\varPsi _m^{k,\lambda }-1\) with the inclusion map \(\imath :G\rightarrow L^\lambda (\mu )\). It is smoother than \(\varPsi _m^{k,\lambda }\) since its range has a weaker topology. The following is a corollary of Lemma 4 in [12].
Lemma 1
\(m_\lambda ,e_\lambda \in C^1(M;L^\lambda (\mu ))\).
The smoothness properties of the KL-divergence on manifolds modelled on \(L^\lambda (\mu )\) is investigated in detail in [11]. Its derivatives can be used to construct the Fisher-Rao metric and Amari-Chentsov tensor on M by the Eguchi method [4]. The Fisher-Rao metric is the covariant 2-tensor field defined, for \(\lambda \ge 2\), by
The Amari-Chentsov tensor is the covariant 3-tensor field defined, for \(\lambda \ge 3\), by
Corollary 1
- (i):
-
If \(\lambda \ge 2\) then the Fisher-Rao metric is a continuous covariant 2-tensor field on M.
- (ii):
-
If \(\lambda \ge 3\) then the Amari-Chentsov tensor is a continuous covariant 3-tensor field on M.
Proof
Both parts follows from the first representations in (13) and (14), Lemma 1 and the chain rule of Fréchet derivatives. \(\square \)
In the raw (non-Sobolev) Hilbert manifold of [10], the composition map  is continuous for all continuous vector fields \(\mathbf{U}\), \(\mathbf{V}\). However, the metric is not continuous in the stronger “operator topology” of Corollary 1(i). The extra regularity here arises from the log-Sobolev embedding theorem, and is not retained if \(t\in (0,1]\). (See Lemma 4 in [12]). Similarly, in the raw Banach manifold of [11] with \(\lambda \ge 3\), the composition map
is continuous for all continuous vector fields \(\mathbf{U}\), \(\mathbf{V}\). However, the metric is not continuous in the stronger “operator topology” of Corollary 1(i). The extra regularity here arises from the log-Sobolev embedding theorem, and is not retained if \(t\in (0,1]\). (See Lemma 4 in [12]). Similarly, in the raw Banach manifold of [11] with \(\lambda \ge 3\), the composition map  is continuous for all continuous vector fields \(\mathbf{U}\), \(\mathbf{V}\), \(\mathbf{W}\), but not continuous in the sense of Corollary 1(ii) unless \(\lambda >3\).
is continuous for all continuous vector fields \(\mathbf{U}\), \(\mathbf{V}\), \(\mathbf{W}\), but not continuous in the sense of Corollary 1(ii) unless \(\lambda >3\).
Let \(M_0\subset M\) be the subset of M whose members are probability measures. These satisfy the additional hypothesis:
- (M3):
-
\({\mathbf{E}_\mu }p = 1\).
The co-dimension 1 subspace of G whose members, a, satisfy \({\mathbf{E}_\mu }a=0\) will be denoted \(G_0\). Let \(\phi _0:M_0\rightarrow G_0\) be defined by
The following is a special case of parts of Propositions 5 and 6 in [12].
Proposition 2
- (i):
-
\((M_0,G_0,\phi _0)\) is a \(C^{\lfloor \lambda \rfloor }\)-embedded submanifold of \((M,G,\phi )\).
- (ii):
-
In terms of the charts \(\phi _0\) and \(\phi \), the inclusion map \(\rho :G_0\rightarrow G\) has the following form
$$\begin{aligned} \rho (a) = a + Z(a), \end{aligned}$$(16)where
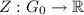 is an (implicitly defined) normalisation function.
is an (implicitly defined) normalisation function. - (iii):
-
The first and (if \(\lambda \ge 2\)) second derivatives of \(\rho \) are as follows:
 (17)
(17)where
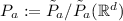 , \({\tilde{P}}_a\) is the finite measure defined after (9) and \(\psi ^{(i)}\) is the ith derivative of \(\psi \).
, \({\tilde{P}}_a\) is the finite measure defined after (9) and \(\psi ^{(i)}\) is the ith derivative of \(\psi \).
For any \(P\in M_0\), tangent vectors \(U\in T_PM_0\) are distinguished from those only in \(T_PM\) by the fact that  . The pushforward of the inclusion map \(\imath :M_0\rightarrow M\) splits \(T_PM\) into \(T_PM_0\) and the complementary subspace of signed measures
. The pushforward of the inclusion map \(\imath :M_0\rightarrow M\) splits \(T_PM\) into \(T_PM_0\) and the complementary subspace of signed measures  .
.
Remark 2
The probability measure \(P_a\) in (17) is the escort probability in the interpretation of \(M_0\) as a deformed exponential model [9].
4 Finite-Dimensional Exponential Models
The \(\alpha \)-divergences (and their derivatives such as the Fisher-Rao metric) are at least as smooth on the Sobolev manifolds of Sect. 3 as they are on their non-Sobolev counterparts (as developed in [10, 11]) because the Sobolev manifolds have stronger topologies. When it comes to embedded submanifolds, however, this benefit is reversed. Theorem 5.1 in [10] shows that any finite dimensional exponential manifold that is contained in the raw Hilbert manifold of [10] is smoothly embedded in that manifold. That this is not so of the Hilbert-Sobolev manifold M modelled on \(G_m^{1,2}\) is demonstrated by the following example.
Example 1
Let \(d=1\), let \(\mu \) be the standard Gaussian measure, \(k=1\) and \(\lambda =2\). For \(i=0,1\), let \(p_i:=\exp (\eta _i)\) where \(\eta _0=3x^2/16\) and \(\eta _1=\sin (\exp (3x^2/16))\). Then \(P_0\) and \(P_1\) are both in M, but the measure with density \(\exp ((\eta _0+\eta _1)/2)\) is not, since its derivative is not square integrable.
Nevertheless, the smooth embedding property can be recovered under additional hypotheses. Let \(G=G_m^{k,\lambda }\) be the general mixed-norm space of Sect. 2, and let M be the associated manifold of finite measures. Since the Fisher-Rao metric is positive definite on M, it is a (strong) Riemannian metric on any finite-dimensional, smoothly embedded submanifold, N, and the full geometry of dual \(\pm \alpha \)-covariant derivatives (for \(\alpha \in [-1,1]\)) is realised on N.
For some  , let \(1,\eta _1,\ldots ,\eta _n\) be linearly independent members of G, and for any
, let \(1,\eta _1,\ldots ,\eta _n\) be linearly independent members of G, and for any  let P(y) be the measure on \(\mathcal{X}\) with density
let P(y) be the measure on \(\mathcal{X}\) with density
The function  is clearly injective. Let
is clearly injective. Let  be open and such that \(P(y)\in M\) for every
be open and such that \(P(y)\in M\) for every  , and let
, and let  . As well as being a subset of M, N is a finite-dimensional exponential model with chart
. As well as being a subset of M, N is a finite-dimensional exponential model with chart  , defined by \(\theta =\gamma ^{-1}\circ e_\lambda \circ \imath \), where \(e_\lambda \) is as defined in (12) and \(\imath :N\rightarrow M\) is the inclusion map.
, defined by \(\theta =\gamma ^{-1}\circ e_\lambda \circ \imath \), where \(e_\lambda \) is as defined in (12) and \(\imath :N\rightarrow M\) is the inclusion map.
Theorem 1
Suppose that \(\lambda \ge \max \{2,k\}\) and that, for every \(y\in B\), \(1\le j\le n\) and \(s\in S_1\),
then N is a \(C^\infty \)-embedded submanifold of M.
Proof
A partition of \(s\in S_1\) is a set \(\pi =\{\sigma _1,\ldots ,\sigma _n\in S_1\}\) such that \(\sum _i\sigma _i=s\). Let \(\varPi (s)\) denote the set of partitions of s. According to the Faá di Bruno formula, for any \(s\in S_1\),
where the \(K_\pi <\infty \) are combinatoric constants, and x is made explicit in \(D_x^s\) for the sake of clarity.
As in the proof of Theorem 5.1 in [10], we define a local coordinate system around a generic  . Let \(\epsilon >0\) be such that the ball of centre y and radius \(\epsilon \) is contained in
. Let \(\epsilon >0\) be such that the ball of centre y and radius \(\epsilon \) is contained in  , and let B(y, r) be the ball of centre y and radius r. For any \({\tilde{y}}\in B(y,\epsilon /2n)\) let \(\zeta \in (1/4,3/4)^{n+1}\) be defined by \(\zeta _j=(1+(n+1)\epsilon ^{-1}({\tilde{y}}-y)_j)/2\); then
, and let B(y, r) be the ball of centre y and radius r. For any \({\tilde{y}}\in B(y,\epsilon /2n)\) let \(\zeta \in (1/4,3/4)^{n+1}\) be defined by \(\zeta _j=(1+(n+1)\epsilon ^{-1}({\tilde{y}}-y)_j)/2\); then
where  is the coordinate orthonormal basis. Differentiating p with respect to y, for any
is the coordinate orthonormal basis. Differentiating p with respect to y, for any  ,
,
where \(p_{j\pm }=p(y\pm \epsilon \mathbf{e}_j)\). The product rule now shows that, for any \({\tilde{y}}\in B(y,\epsilon /2n)\),
where the \(K_\beta <\infty \) are combinatoric constants. For any  there is a \(K_m<\infty \) such that, for all \(q,r\in (0,\infty )\) and all \(\delta \in (1/4,3/4)\),
there is a \(K_m<\infty \) such that, for all \(q,r\in (0,\infty )\) and all \(\delta \in (1/4,3/4)\),
Applying this to (21) and (22), we obtain the bound
for some \(K<\infty \). It follows from (19) and Hölder’s inequality that the term, whose absolute value is taken on the right-hand side here, belongs to \(L^{\lambda /|s|}(\mu )\), and a further application of Hölder’s inequality shows that
A Taylor expansion of \(D_y^\alpha D_x^s p_y\) about y, in the direction \(\mathbf{e}_j\), yields
for some \(\delta =\delta (y,t,j,x)\in [0,1]\). Together with (23) and the dominated convergence theorem, this shows that \((-\epsilon /2n,\epsilon /2n)\ni t\mapsto D_y^\alpha D_x^s p(y+t\mathbf{e}_j)\in L^{\lambda _{|s|}}(\mu )\) is differentiable at \(t=0\), with derivative \(D_y^{\alpha +\mathbf{e}_j}D_x^s p(y)\). An inductive argument thus establishes the infinite differentiability of  . The same is clearly true of
. The same is clearly true of  , and so we have shown that the inclusion map \(\imath \) is of class \(C^\infty \).
, and so we have shown that the inclusion map \(\imath \) is of class \(C^\infty \).
Expressed in terms of the charts, \(\imath \) takes the form \(f=\phi \circ e_\lambda ^{-1}\circ \gamma \). Let  be defined by \(g=\pi \circ e_\lambda \circ \phi ^{-1}\), where
be defined by \(g=\pi \circ e_\lambda \circ \phi ^{-1}\), where  is the \(L^2(\mu )\)-projection onto the subspace spanned by \((1,\eta _1,\ldots ,\eta _n)\). It follows from Lemma 1 that g is of class \(C^1\). Now \(g\circ f\) is the identity function of
is the \(L^2(\mu )\)-projection onto the subspace spanned by \((1,\eta _1,\ldots ,\eta _n)\). It follows from Lemma 1 that g is of class \(C^1\). Now \(g\circ f\) is the identity function of  , and so f is a homeomorphism onto its image (endowed with the subspace topology), and its derivative, \(f^{(1)}\), is a toplinear isomorphism onto its image. So
, and so f is a homeomorphism onto its image (endowed with the subspace topology), and its derivative, \(f^{(1)}\), is a toplinear isomorphism onto its image. So  is a finite-dimensional closed linear subspace of both G and \(L^2(\mu )\). Let \(H^c\) be its orthogonal complement in \(L^2(\mu )\); then \(f^{(1)}\) splits G into the components
is a finite-dimensional closed linear subspace of both G and \(L^2(\mu )\). Let \(H^c\) be its orthogonal complement in \(L^2(\mu )\); then \(f^{(1)}\) splits G into the components  and \(G\cap H^c\). So f is an immersion and an embedding. (See Proposition 2.3 in [6]). This completes the proof. \(\square \)
and \(G\cap H^c\). So f is an immersion and an embedding. (See Proposition 2.3 in [6]). This completes the proof. \(\square \)
Condition (19) is clearly satisfied if \(p(y)\in L^\infty (\mu )\) for all  ; this is so, for example, if N is the exponential manifold of all non-singular (scaled) Gaussian measures on \(\mathcal{X}\), and \(t<2\). However, there are other possibilities, for example that in which \(\gamma (y)\), p(y) and their x derivatives have sub-exponential growth in x for all \(y\in B\).
; this is so, for example, if N is the exponential manifold of all non-singular (scaled) Gaussian measures on \(\mathcal{X}\), and \(t<2\). However, there are other possibilities, for example that in which \(\gamma (y)\), p(y) and their x derivatives have sub-exponential growth in x for all \(y\in B\).
Let \(N_0:=M_0\cap N\) be the subset of probability measures. This is, itself, a finite dimensional exponential manifold with chart \(\theta _0:N\rightarrow B\) defined by \(\theta _0(P)=(\theta (P)_1,\ldots ,\theta (P)_n)\).
Corollary 2
Under the hypotheses of Theorem 1:
- (i):
-
\(N_0\) is a \(C^\infty \)-embedded submanifold of N;
- (ii):
-
\(N_0\) is a \(C^\infty \)-embedded submanifold of \(M_0\).
Proof
The map  was shown, in the proof of Theorem 1, to be of class \(C^\infty \). Its first derivative with respect to \(y_0\) is \({\mathbf{E}_\mu }p(y)\). Since this is strictly positive on
was shown, in the proof of Theorem 1, to be of class \(C^\infty \). Its first derivative with respect to \(y_0\) is \({\mathbf{E}_\mu }p(y)\). Since this is strictly positive on  , the implicit function theorem shows that
, the implicit function theorem shows that  , defined by \(\exp (f(z)+\sum _{j=1}^nz_j\eta _j)=1\), is of class \(C^\infty \). In terms of the charts \(\theta \) and \(\theta _0\), the inclusion map \(\imath :N_0\rightarrow N\) takes the form \(\varphi (z)=(f(z),z)\). This is clearly a \(C^\infty \)-embedding, which proves part (i).
, defined by \(\exp (f(z)+\sum _{j=1}^nz_j\eta _j)=1\), is of class \(C^\infty \). In terms of the charts \(\theta \) and \(\theta _0\), the inclusion map \(\imath :N_0\rightarrow N\) takes the form \(\varphi (z)=(f(z),z)\). This is clearly a \(C^\infty \)-embedding, which proves part (i).
Let \(\tau :G\rightarrow G_0\) be defined by \(\tau (a)=a-{\mathbf{E}_\mu }a\). This is of class \(C^\infty \), and so the same is true of the map \(g:=\tau \circ \phi \circ \imath \circ \theta _0^{-1}:B\rightarrow G_0\), where \(\imath :N_0\rightarrow M\) is the inclusion map. Now g is injective and, since \(\tau ^{(1)}\rho ^{(1)}\) is the identity map of \(G_0\), the same is true of its first derivative, at all points in B. The latter clearly splits \(G_0\), and so the inclusion map \(\imath :N_0\rightarrow M_0\) (which is expressed in charts by g) is an embedding. This completes the proof of part (ii). \(\square \)
References
Amari, S.-I., Nagaoka, H.: Methods of Information Geometry. American Mathematical Society, Providence (2000)
Cena, A., Pistone, G.: Exponential statistical manifold. Ann. Inst. Stat. Math. 59, 27–56 (2007)
Chentsov, N.N.: Optimal Decision Rules and Optimal Inference. American Mathematical Society, Providence (1982)
Eguchi, S.: Second order efficiency of minimum contrast estimators in a curved exponential family. Ann. Stat. 11, 793–803 (1983)
Gibilisco, P., Pistone, G.: Connections on non-parametric statistical manifolds by Orlicz space geometry. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 1, 325–347 (1998)
Lang, S.: Fundamentals of Differential Geometry. Springer, New York (2001)
Lods, B., Pistone, G.: Information geometry formalism for the spatially homogeneous Boltzmann equation. Entropy 17, 4323–4363 (2015)
Montrucchio, L., Pistone, G.: A class of non-parametric deformed exponential statistical models, arXiv:1709.01430 (2018)
Naudts, J.: Generalised Thermostatistics. Springer, London (2011). https://doi.org/10.1007/978-0-85729-355-8
Newton, N.J.: An infinite-dimensional statistical manifold modelled on Hilbert space. J. Funct. Anal. 263, 1661–1681 (2012)
Newton, N.J.: Infinite-dimensional statistical manifolds based on a balanced chart. Bernoulli 22, 711–731 (2016)
Newton, N.J.: A class of non-parametric statistical manifolds modelled on Sobolev space, arXiv:1808.06451 (2018)
Pistone, G., Rogantin, M.P.: The exponential statistical manifold: mean parameters, orthogonality and space transformaions. Bernoulli 5, 721–760 (1999)
Pistone, G., Sempi, C.: An infinite-dimensional geometric structure on the space of all the probability measures equivalent to a given one. Ann. Stat. 23, 1543–1561 (1995)
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations. de Gruyter, Berlin (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Newton, N.J. (2019). Sobolev Statistical Manifolds and Exponential Models. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2019. Lecture Notes in Computer Science(), vol 11712. Springer, Cham. https://doi.org/10.1007/978-3-030-26980-7_46
Download citation
DOI: https://doi.org/10.1007/978-3-030-26980-7_46
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26979-1
Online ISBN: 978-3-030-26980-7
eBook Packages: Computer ScienceComputer Science (R0)




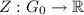 is an (implicitly defined) normalisation function.
is an (implicitly defined) normalisation function.
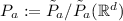 ,
,