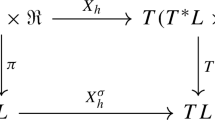Keywords

1 Port-Thermodynamic Systems

It was argued in [2] that the phase space of thermodynamic systems can be defined as the projectivization of a symplectic manifold, and that reversible and irreversible thermodynamic processes can be expressed as Hamiltonian dynamics with respect to a Hamiltonian that is homogeneous of degree one in the generalized momentum variables. In this section, we will recall the recently proposed generalization of this framework to non-isolated thermodynamic systems, summarizing the definition of homogeneous Hamiltonian control systems and port-thermodynamic systems as given in [13, 22, 23].

1.1 Homogeneous Hamiltonian Control Systems

Consider an \((n+1)\)-dimensional manifold \(Q^{e}\), with elements denoted by \(q^{e}\) (the vector of extensive variables in thermodynamics). Consider its cotangent bundle, denoted by \(T^{*}Q^{e}\), with generalized momentum variables \(p^{e}\in T_{q^{e}}^{*}Q^{e}\), equipped with the canonically defined Liouville one-form \(\alpha \) and symplectic form \(\omega =d\alpha \). In natural cotangent bundle coordinates \((q^e,p^e)=\left( q_{0}^{e},\,\ldots \,,\,q_{n}^{e},\,p_{0}^{e},\,\ldots \,,\,p_{n}^{e}\right) \) for \(T^{*}Q^{e}\) the Liouville form \(\alpha \) has the expression

$$\begin{aligned} \alpha =\sum _{i=0}^{n}p_{i}^{e}\,dq_{i}^{e}, \end{aligned}$$
(1)

while the symplectic form \(\omega \) is given as \(\omega =\sum _{i=0}^{n}dp_{i}^{e}\wedge dq_{i}^{e}\). On the symplectic manifold \(T^{*}Q^{e}\) we consider Hamiltonian vector fields which are generated by Hamiltonian functions that are homogeneous of degree 1 in the momentum variables \(p^{e}\). Such vector fields are characterized in the following proposition.

Proposition 1

[22, Prop. A.1] If the function \(h:T^{*}Q^{e}\rightarrow \mathbb {R}\) is homogeneous of degree 1 in \(p^{e}\), then the Hamiltonian vector field \(X=X_{h}\) satisfies

$$\begin{aligned} \mathbb {L}_{X}\alpha =0, \end{aligned}$$
(2)

where \(\mathbb {L}_{X}\) denotes the Lie derivative with respect to the vector field X. Conversely, if a vector field X satisfies (2) then \(X=X_{h}\) for some locally defined Hamiltonian h that is homogeneous of degree 1 in \(p^{e}\).Footnote 1

Hamiltonian vector fields \(X_{h}\) with h homogeneous of degree 1 in \(p^e\) will be referred to as homogeneous Hamiltonian vector fields.

By Gibbs’ relation the state properties of any thermodynamic system are specified by a Lagrangian submanifold of the cotangent bundle \(T^{*}Q^{e}\) with the following additional homogeneity property [22].

Definition 1

A homogeneous Lagrangian submanifold \(\mathcal {L}\subset T^{*}Q^{e}\) is a Lagrangian submanifold \(\mathcal {L}\subset T^{*}Q^{e}\) (i.e., \(\left. \omega \right| _{\mathcal {L}}=0\) and \(\mathcal {L}\) is maximal with respect to this property) satisfying \((q^{e},p^{e})\in \mathcal {L}\Rightarrow (q^{e},\lambda p^{e})\in \mathcal {L}, \text{ for } \text{ every } \lambda \in \mathbb {R}^{*}\).

Equivalently, in [22] homogeneous Lagrangian submanifolds are geometrically characterized as maximal submanifolds satisfying \(\left. \alpha \right| _{\mathcal {L}}=0\).

Motivated by thermodynamics we require that the dynamics specified by a homogeneous Hamiltonian vector field is compatible with the state properties defined by a homogeneous Lagrangian submanifold, in the sense of leaving this submanifold invariant. This is characterized as follows.

Proposition 2

[11, 23] A homogeneous Hamiltonian vector field \(X_{h}\) leaves invariant the homogeneous Lagrangian submanifold \(\mathcal {L}\subset T^{*}Q^{e}\) if and only if \(\left. h\right| _{\mathcal {L}}=0\).

This leads to the following definition of a class of Hamiltonian control systems.

Definition 2

[23] Consider an \((n+1)\)-dimensional manifold \(Q^{e}\). A homogeneous Hamiltonian control system on \(T^{*}Q^{e}\) is defined as a pair \((\mathcal {L},\,K)\), composed of a homogeneous Lagrangian submanifold \(\mathcal {L}\subset T^{*}Q^{e}\) and a nonlinear control system

$$\begin{aligned} \dot{x} =X_{K^{a}}(x)+ X_{K^{c}}(x)\, u, \quad x= \left( \begin{array}{c} q^{e}\\ p^{e} \end{array}\right) , \end{aligned}$$
(3)

generated by the control dependent Hamiltonian function \(K:=K^{a}+K^{c}u:T^{*}Q^{e}\rightarrow \mathbb {R},\,u\in \mathbb {R}^{m}\), where \(K^a\) and the elements of the m-dimensional row vector \(K^{c}\) are functions which are homogeneous of degree 1 in \(p^{e}\), and satisfy the invariance conditions \(\left. K^{a}\right| _{\mathcal {L}}=\left. K^{c}\right| _{\mathcal {L}}=0\).

Hence homogeneous Hamiltonian control systems leave invariant the homogeneous Lagrangian submanifold \(\mathcal {L}\) characterizing the state properties of the system; in particular energy-storage. In the control-theoretic sense, this homogeneous Lagrangian submanifold is the actual state space of the system and only the restriction of the homogeneous Hamiltonian control system to this submanifold is relevant. Thus the state space is defined as a submanifold of a covering manifold, similarly to approaches to differential-algebraic equation systems such as described in [3, 4, 21].

1.2 Relation with Irreversible Thermodynamic Systems

The Thermodynamic Phase Space.

In the thermodynamic case the \((n+1)\)-dimensional manifold \(Q^{e}\) consists of the space of all extensive variables. For simple thermodynamic systems, the extensive variables are volume, number of moles of chemical species, as well as entropy and internal energy. Following [2], the thermodynamic phase space is the \((2n+1)\)-dimensional manifold \(\mathbb {P}\left( T^{*}Q^{e}\right) \), called the projectivization of \(\mathcal {T}^{*}Q^{e}\), the \((2n+2)\)-dimensional cotangent bundle \(T^{*}Q^{e}\) without its zero-section. The projectivization \(\mathbb {P}\left( T^{*}Q^{e}\right) \) is defined as the fiber bundle over \(Q^{e}\) with fiber at any point \(q^{e}\in Q^{e}\) given by the projective space \(\mathbb {P}\left( T_{q^{e}}^{*}Q^{e}\right) \), with projection map \(\pi :\mathcal {\,T}^{*}Q^{e}\rightarrow \mathbb {P}\left( T_{q^{e}}^{*}Q^{e}\right) \).

It is a classical result, see e.g. [11, chap. V], [1, Appendix 4], that the \((2n+1)\)-dimensional manifold \(\mathbb {P}\left( T^{*}Q^{e}\right) \) is a contact manifold, endowed with a locally defined canonical contact form, denoted by \(\theta \). In fact, in a neighborhood where \(p_{0}\ne 0\), the contact form \(\theta \) is given as

$$ \theta =dq_{0}^{e}-\sum _{i=1}^{n}\gamma _{i}dq_{i}^{e}, $$

where \(\gamma _{i}=-\frac{p_{i}}{p_{0}}\,,\,i=1,\,\ldots \,,\,n,\) are the homogeneous coordinates corresponding to the condition \(p_{0}\ne 0\). For a thermodynamic system, the n coordinates \(\gamma _{i}\,,\,i=1,\,\ldots \,,\,n,\) are called the intensive variables. Whenever \(p_{1}\ne 0\) we may define different homogeneous coordinates \(\hat{\gamma }_{i}=-\frac{p_{i}}{p_{1}}\,,\,i=0,2,\,\ldots \,,\,n\), corresponding to the contact form \(\hat{\theta }=dq_{1}^{e}-\hat{\gamma }_0dq^0 -\sum _{i=2}^{n}\hat{\gamma }_{i}dq_{i}^{e}\), and so on for \(p_{2}\ne 0, p_{3}\ne 0,\ldots \). In thermodynamics this reflects the choice of different intensive variables corresponding to, e.g., the energy or entropy representation of the thermodynamic system.

The formulation of the thermodynamic phase space as a contact manifold is well-known [1, 9, 15]. The covering symplectization of the contact manifold \(\mathbb {P}\left( T^{*}Q^{e}\right) \) by the symplectic manifold \(\mathcal {T}^{*}Q^{e}\), together with the resulting different choices of intensive variables, unifies the different representations of the thermodynamic phase space; in particular, the energy and entropy representations [2, 22, 23]. In the same vein, the description of the state properties of the thermodynamic system by a Legendre submanifold of the thermodynamic phase space, see e.g. [15], is extended to a covering homogeneous Lagrangian submanifold. In this way, the formulation of reversible and irreversible processes of thermodynamic systems using contact vector fields as given before in [7, 8, 16, 17], and for open thermodynamic systems as control contact systems in [5, 6, 14, 19], is now replaced by ordinary, but homogeneous, Hamiltonian dynamics on the symplectization \(\mathcal {T}^{*}Q^{e}\) of the thermodynamic phase space \(\mathbb {P}\left( T^{*}Q^{e}\right) \). Apart from unifying different representations as mentioned above, this covering has other advantages as well. From a computational point of view, Hamiltonian dynamics is more easy than contact dynamics. More importantly, as we will see in the next subsection, the homogeneous Hamiltonian formulation admits to define in a natural way the outputs of the thermodynamic system. For further details on the mathematical relation between the symplectic, but homogeneous, and the contact representations we refer to [22].

Port-Thermodynamic Systems. In order to ensure the compatibility with the First and Second Law of thermodynamics, and to define natural outputs which are conjugate to the inputs, we first recall Euler’s theorem for homogeneous functions. Since the Hamiltonian functions \(K^a\) and the elements of the row vector \(K^c\) are homogeneous of degree 1 in the momenta \(p^{e}\), Euler’s theorem yields the identities

$$\begin{aligned} K^{a}=p^{e^{T}}\frac{\partial K^{a}}{\partial p^{e}}\quad \text {and}\quad K^{c}=p^{e^{T}}\frac{\partial K^{c}}{\partial p^{e}}, \end{aligned}$$
(4)

where \(\frac{\partial K^{a}}{\partial p^{e}}\) and \(\frac{\partial K^{c}}{\partial p^{e}}\) are homogeneous of degree 0 in the \(p^e\) variables, and thus project to well-defined functions on the thermodynamic phase space \(\mathbb {P}\left( T^{*}Q^{e}\right) \). Furthermore, by definition of Hamiltonian vector fields, \(\frac{\partial K^{a}}{\partial p^{e}}\) equals the autonomous drift dynamics, and \(\frac{\partial K^{c}}{\partial p^{e}}\) the input-dependent dynamics, of the extensive variables \(q^{e}\in \mathcal {T}^{*}Q^{e}\). In view of the First and Second Law of thermodynamics this leads to the following additional requirements on the autonomous Hamiltonian function \(K^a\), and to the following definition of natural outputs, which combined with the previous definition of homogeneous Hamiltonian control systems culminates in the definition of port-thermodynamic systems.

Definition 3

[22] Port-thermodynamic systems are homogeneous Hamiltonian control systems \((\mathcal {L},K)\) (as in Definition 2) for which the set of extensive variables contains a coordinate \(q_{0}^{e}\) corresponding to the total energy of the system and \(q_{1}^{e}\) corresponding to the total entropy of the system, and the autonomous Hamiltonian \(K^a\) satisfies the following additional conditions in relation to the homogeneous Lagrangian submanifold

$$\begin{aligned} \left. \frac{\partial K^{a}}{\partial p_{0}^{e}}\right| _{\mathcal {L}}=0, \qquad \left. \frac{\partial K^{a}}{\partial p_{1}^{e}}\right| _{\mathcal {L}}\ge 0 \end{aligned}$$
(5)

Furthermore, the power-conjugate outputs of the thermodynamic system are defined by the row vector

$$\begin{aligned} y_{p}=\left. \frac{\partial K^{c}}{\partial p_{0}^{e}}\right| _{\mathcal {L}} \end{aligned}$$
(6)

while the entropy flow-conjugate outputs are defined as the row vector

$$\begin{aligned} y_{e}=\left. \frac{\partial K^{c}}{\partial p_{1}^{e}}\right| _{\mathcal {L}} \end{aligned}$$
(7)

The above definition of the outputs \(y_p\) and \(y_e\) of a port-thermodynamic system, together with the conditions (5) , imply the following balance laws for the dynamics restricted to the invariant manifold \(\mathcal {L}\):

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt}E &{} = &{} y_pu \\[3mm] \frac{d}{dt}S &{}\ge &{} y_eu \end{array} \end{aligned}$$
(8)

As an illustrative example we discuss the gas-piston-damper system. (Compare with the treatment of this example in a contact geometry setting in [5].)

Example 1

(Actuated gas-piston-damper system). Consider extensive variables V (volume of the gas), \(\pi \) (momentum of the piston with mass m), entropy S and total energy E. The state properties of the system are described by the homogeneous Lagrangian submanifold \(\mathcal {L}\) with generating function (in energy representation) \(-p_E \left( U(V,S) + \frac{\pi ^2}{2m}\right) \), where U(V, S) is the internal energy of the gas (expressed as a function of volume and entropy):

$$\begin{aligned} \begin{array}{rcl} \mathcal {L}&{} = &{}\{(V,\pi ,S,E,p_V,p_{\pi },p_S,p_E) \mid E= U(V,S) + \frac{\pi ^2}{2m}, \\[2mm] &{}&{} p_V=-p_E{\frac{\partial U}{\partial V}} , p_{\pi }= -p_E \frac{\pi }{m},p_S=-p_E{\frac{\partial U}{\partial S}} \} \end{array} \end{aligned}$$
(9)

The dynamics of the system is defined by the homogeneous Hamiltonian

$$\begin{aligned} \begin{array}{rcl} K &{}= &{} K^a + K^cu \\[2mm] &{}= &{} \left[ p_V A\frac{\pi }{m} +p_{\pi }\left( -\frac{\partial U}{\partial V} -d\frac{\pi }{m}\right) +p_S \frac{d (\frac{\pi }{m})^2}{\frac{\partial U}{\partial S}}\right] + \left( p_{\pi } + p_E \frac{\pi }{m}\right) u, \end{array} \end{aligned}$$
(10)

where A is the area of the piston, and u the external force applied to the piston. The power-conjugate output \(y_p=\frac{\pi }{m}\) is the velocity of the piston. The entropy-conjugate output \(y_e\) is identically zero, implying \(\frac{d}{dt}S \ge 0\) for every u.

2 System-Theoretic Properties of Port-Thermodynamic Systems

In the first part of this section we make some observations regarding the passivity properties of port-thermodynamic systems, while in the second part we study their observability in relation with the controllability properties as treated before in [22].

2.1 Passivity Properties of Port-Thermodynamic systems

Throughout this subsection we will denote \(q^e=(q,S,E)\), with E the energy, S the entropy (previously denoted by, respectively, \(q_{0}^{e}\) and \(q_{1}^{e}\)), and q the remaining extensive variables.

Following passivity theory [20, 24] the equations (8) imply that port-thermo-dynamic systems restricted to their invariant Lagrangian submanifold \(\mathcal {L}\) are cyclo-lossless with respect to the supply rate \(y_{p}u\) and the storage function E (expressed as a function of the extensive variables (q, S)), and cyclo-passive with respect to the supply rate \(-y_{e}u\) and the storage function \(-S\) (expressed as a function of the extensive variables (q, E)). Here, ’cyclo’ [20, 24] refers to the fact that in general the storage function E need not be bounded from below, nor S is bounded from above.

Let us in particular concentrate on the dissipation inequality \(\frac{d}{dt}(-S) \le -y_{e}u\) corresponding to the Second Law of thermodynamics. If the entropy S happens to be bounded from above, and thus \(-S\) is bounded from below, then the port-thermodynamic system is truly passive with respect to the supply rate \(-y_{e}u\). Furthermore, see [20, 24], in this case the available storage given as

$$\begin{aligned} V(q,E):= \sup _{\tau \ge 0, u:[0,\tau ] \rightarrow \mathbb {R}^m} \int _0^{\tau } y_{e}(t)u(t) dt, \end{aligned}$$
(11)

where \(y_{e}(t)\) is the output time-function corresponding to an input time-function u(t) and initial condition (q, E) at time 0, is well-defined (i.e., finite for all (q, E)), while obviously \(V\ge 0\). Furthermore, V is itself a storage function, and actually the minimal one among all other non-negative storage functions.

Interpreting minus the entropy as ’information’, it follows that V as defined in (11) can be interpreted as the maximally extractable information of the system, where \(y_{e}(t)u(t)\) is the rate of extracted information from the system at time t.

Alternatively, \(-V\) is maximal among all functions \(S\le 0\) satisfying the inequality

$$\begin{aligned} \frac{d}{dt}S \ge y_eu \end{aligned}$$
(12)

In this sense, \(-V\) can be interpreted as the maximal entropy function for the thermodynamic system. (Obviously, this relates to the question of identifying the entropy function from the external behavior of the system.)

However, as mentioned before, in general the entropy function S need not be bounded from above. A possible approach to resolve this problem, as already discussed in [25], is to consider an exergy function

$$\begin{aligned} \mathcal {E}(q,S) := E(q,S) -T_0S, \end{aligned}$$
(13)

with \(T_0\) a constant temperature. Indeed, by combining the energy and entropy balance laws (8) one obtains

$$\begin{aligned} \frac{d}{dt} \left( E-T_0S \right) \le y_pu - T_0y_eu = \left( y_p - T_0y_e \right) u, \end{aligned}$$
(14)

showing that for every \(T_0 \ge 0\) the system is cyclo-passive with respect to the output \(y_p - T_0y_e\), with storage function \(\mathcal {E}(q,S)\) given by (13).

Furthermore, in monophase thermodynamic systems E is a convex function of S. This implies that under additional conditions the exergy function is actually bounded from below; in this case yielding true passivity. For example, if E(q, S) only depends on S then convexity yields that for any constant \(S_0\) the function

$$\begin{aligned} A(S):= E(S) - E'(S_0)(S-S_0) - E(S_0) \end{aligned}$$
(15)

is non-negative. This function is known as the Bregman divergence in convex analysis, or availability function [10] in thermodynamics. Denoting the temperature \(T_0:= E'(S_0) \ge 0\) this function equals the exergy function (13) modulo a constant, implying that the exergy is bounded from below.

2.2 Controllability and Observability Properties

First we recall from [22], with some extensions, how the controllability properties of a port-thermodynamic system \((\mathcal {L},K)\) can be directly studied in terms of the homogeneous Hamiltonians \(K^a\) and \(K^c_j,\, j=1, \cdots ,m,\) and their Poisson brackets. First note the following property proved in [22].

Proposition 3

Consider the Poisson bracket \(\{h_1,h_2\}\) of functions \(h_1,h_2\) on \(T^*Q^e\) defined with respect to the symplectic form \(\omega =d\alpha \). Then

  1. (a)

    If \(h_1,h_2\) are both homogeneous of degree 1 in \(p^e\), then also \(\{h_1,h_2\}\) is homogeneous of degree 1 in \(p^e\).

  2. (b)

    If \(h_1\) is homogeneous of degree 1 in \(p^e\), and \(h_2\) is homogeneous of degree 0 in \(p^e\), then \(\{h_1,h_2\}\) is homogeneous of degree 0 in \(p^e\).

  3. (c)

    If \(h_1,h_2\) are both homogeneous of degree 0 in \(p^e\), then \(\{h_1,h_2\}\) is zero.

In particular, Poisson brackets of the homogeneous (degree 1 in \(p^e\)) Hamiltonians \(K^a\) and \(K^c_j,\, j=1, \cdots ,m,\) are again homogeneous of degree 1 in \(p^e\). Secondly, we recall the well-known correspondence [11] between Poisson brackets of Hamiltonians \(h_1,h_2\), and Lie brackets of their corresponding Hamiltonian vector fields

$$\begin{aligned}{}[X_{h_1},X_{h_2}] =X_{\{h_1,h_2\}} \end{aligned}$$
(16)

In particular, this property implies that if the homogeneous Hamiltonians \(h_1,h_2\) are zero on the homogeneous Lagrangian submanifold \(\mathcal {L}\), and thus the homogeneous Hamiltonian vector fields \(X_{h_1},X_{h_2}\) are tangent to \(\mathcal {L}\), then also \([X_{h_1},X_{h_2}]\) is tangent to \(\mathcal {L}\), and therefore the Poisson bracket \(\{h_1,h_2\}\) is also zero on \(\mathcal {L}\). Furthermore, with respect to the projection to the corresponding Legendre submanifold L, we note the following property of homogeneous Hamiltonians

$$\begin{aligned} \widehat{\{h_1,h_2\}}= \{\widehat{h}_1,\widehat{h}_2\} \end{aligned}$$
(17)

where \(\widehat{h}\) is the contact Hamiltonian of the contact vector field obtained by projection of the Hamiltonian vector field \(X_h\) corresponding to a homogeneous Hamiltonian h. This leads to the following characterization of the accessibility algebra of a port-thermodynamic system characterizing controllability, cf. [22].

Proposition 4

Consider a port-thermodynamic system \((\mathcal {L},K)\) on \(\mathbb {P}(T^*Q^e)\) with homogeneous \(K:= K^a + \sum _{j=1}^mK_j^cu_j : \mathcal {T}^*Q^e \rightarrow \mathbb {R}\), zero on \(\mathcal {L}\). Consider the algebra \(\mathcal {P}\) (with respect to the Poisson bracket) generated by \(K^a, K_j^c, \; j=1, \cdots ,m\), consisting of homogeneous functions that are zero on \(\mathcal {L}\), and the corresponding algebra \(\widehat{\mathcal {P}}\) generated by \(\widehat{K}^a, \widehat{K}_j^c, \; j=1, \cdots ,m,\) on the corresponding Legendre submanifold L. The accessibility algebra [18] of the port-thermodynamic system is spanned by all contact vector fields \(X_{\widehat{h}}\) on L, with \(\widehat{h}\) in the algebra \(\widehat{\mathcal {P}}\).

It follows that the thermodynamic system \((\mathcal {L},K)\) is locally accessible [18] if the dimension of the co-distribution \(d\widehat{\mathcal {P}}\) on L defined by the differentials of \(\widehat{h}\), with h in the Poisson algebra \(\mathcal {P}\), is equal to the dimension of L. Conversely, if the system is locally accessible then the co-distribution \(d \widehat{\mathcal {P}}\) on L has dimension equal to the dimension of L on an open and dense subset of L.

Similar statements can be made with respect to local strong accessibility [18] of port-thermodynamic systems. In this case the same conditions need to be satisfied for the algebra \(\mathcal {P}_s\), which is equal to \(\mathcal {P}\) minus the drift Hamiltonian \(K^a\). (Thus, possibly repeated, Poisson brackets with \(K^a\) are taken into account, but not the function \(K^a\) itself.)

With regard to observability we proceed as follows. First, let us consider the observability properties with respect to the power-conjugate output \(y_{p}=\left. \frac{\partial K^{c}}{\partial p_{0}^{e}}\right| _{\mathcal {L}}\) as in (6), with \(q^e_0\) and \(p^e_0\) corresponding to the energy variable E. Note that

$$\begin{aligned} \frac{\partial K^{c}_j}{\partial p_{0}^{e}} = \{K^c_j,q_0^e \} \end{aligned}$$
(18)

Recall (cf. [18] for further information) the definition of the observation space \(\mathcal {O}\) as given by the linear span of functions of the form

$$\begin{aligned} \mathbb {L}_{X_1}\mathbb {L}_{X_2} \cdots \mathbb {L}_{X_k}\{K^c_j,q_0^e \}, \quad j=1, \cdots ,m, \end{aligned}$$
(19)

with \(X_i, i=1, \cdots ,k,\) taken from the set \(\{X_{K^a},X_{K^c_j}, j=1, \cdots ,m \}\). Using the equality \(\mathbb {L}_{X_h}K=\{h,K\}\) it follows that the observation space \(\mathcal {O}\) of the port-thermodynamic system with power-conjugate outputs \(y_p\) is given by the linear span of all expressions

$$\begin{aligned} \{h_1,\{h_2,\{\cdots , \{h_k,\{K^c_j,q_0^e \}\} \cdots \}\}\} ,\quad j=1, \cdots ,m, \end{aligned}$$
(20)

with \(h_i, i=1, \cdots ,k,\) taken from the set \(\{K^a,K^c_j, \; j=1, \cdots ,m \}\).

Furthermore, since by (5) \(\{K^a,q_0^e \}=0\) the following results.

Proposition 5

The observation space \(\mathcal {O}\) of a port-thermodynamic system \((\mathcal {L},K)\) with power-conjugate outputs \(y_p\) is equal to the linear span of all functions

$$\begin{aligned} \{h_1,\{h_2,\{\cdots , \{h_k,\{h_{k+1},q_0^e \}\} \cdots \}\}\} ,\quad j=1, \cdots ,m, \end{aligned}$$
(21)

with \(h_i, i=1, \cdots ,k +1,\) taken from the set \(\{K^a,K^c_j, \; j=1, \cdots ,m \}\).

Furthermore, analogously to [18, Proposition 3.8], \(\mathcal {O}\) is equal to the linear span of all functions (21) with \(h_i, i=1, \cdots ,k +1,\) taken from the accessibility algebra \(\mathcal {P}\).

Since the functions \(h_i\) in (21) are all homogeneous of degree 1 in \(p^e\), and clearly the function \(q_0^e\) is homogeneous of degree 0 in \(p^e\), it follows by Proposition 3 that all functions in \(\mathcal {O}\) are homogeneous of degree 0, and therefore project to functions \(\widehat{h}\) on the thermodynamic phase space \(\mathbb {P}\left( T^{*}Q^{e}\right) \). As a result, we obtain the following proposition.

Proposition 6

Consider the thermodynamic system with power-conjugate outputs \(y_{p}\). It is locally observable if \(\dim d\widehat{\mathcal {O}} = \dim L (\,=n+1)\), where \(\widehat{\mathcal {O}}\) is the set of all functions on \(L \subset \mathbb {P}\left( T^{*}Q^{e}\right) \) obtained by projection of the functions in \(\mathcal {O}\). Conversely, if the system is locally observable then \(\dim d\widehat{\mathcal {O}} = \dim L (\,=n+1)\) on an open and dense subset of L.

Comparing Proposition 6 with Proposition 4 we notice a close relation between the two conditions. In fact, the situation is similar to the relation between controllability and observability of lossless port-Hamiltonian systems as discussed in [12].

More or less the same story holds for the entropy flow-conjugate output \(y_{e}=\left. \frac{\partial K^{c}}{\partial p_{1}^{e}}\right| _{\mathcal {L}}\) as in (7), with the difference that in this case \(\{K^a,q_1^e \} \ne 0\), and hence in this case the observation space is slightly smaller than the linear span of all functions (21), with \(q_0^e\) replaced by \(q_1^e\).

3 Conclusion

In this paper we have considered homogenous Hamiltonian control systems, which are generated by Hamiltonian drift and control Hamiltonian functions that are all homogeneous of degree one in the momentum variables, and leave invariant a homogeneous Lagrangian submanifold representing the actual state space of the system. They represent open thermodynamic systems once additional conditions are satisfied corresponding to the First and Second Law of thermodynamics, leading to the definition of port-thermodynamic systems. The ’symplectization’ point of view also enables the definition of outputs which are conjugate in the sense of external energy or entropy flow, and leads to elegant results concerning controllability and observability. Furthermore, we have made some initial observations regarding the passivity properties of port-thermodynamic systems, and on the use of exergy functions; thus suggesting further research on passivity-based control of port-thermodynamic systems.