Abstract
Dirac structures are geometric objects that generalize Poisson structures and presymplectic structures on manifolds. They naturally appear in the formulation of constrained mechanical systems and play an essential role in the understanding of the interrelations between system elements in implicit dynamical systems. In this paper, we show how nonequilibrium thermodynamic systems can be naturally understood in the context of Dirac structures, by mainly focusing on the case of open systems, i.e., thermodynamic systems exchanging heat and matter with the exterior.
H. Yoshimura is partially supported by JSPS Grant-in-Aid for Scientific Research (S) 24224004, the MEXT Top Global University Project and Waseda University (SR 2019C-176 and SR 2019Q-020); F. Gay-Balmaz is partially supported by the ANR project GEOMFLUID, ANR-14-CE23-0002-01.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Nonequilibrium thermodynamics is a phenomenological theory which aims to identify and describe the relations among the observed macroscopic properties of a physical system and to determine the macroscopic dynamics of this system with the help of fundamental laws, see [15]. A novel Lagrangian variational approach for nonequilibrium thermodynamic has been proposed by the authors [4, 5] for both finite dimensional (discrete) and infinite dimensional (continuum) systems. This variational formulation was extended to the case of open systems as in [6]. The authors have also shown that, in the case of adiabatically closed systems, the variational formulation leads to an associated geometric formulation in terms of Dirac structures [7]. Recall that Dirac structures are geometric objects that extend both Poisson structures and presymplectic structures on manifolds [2]. Such structures play an essential role in formulating constrained systems such as electric circuits and nonholonomic mechanical systems (e.g., [16, 17]). On the other hand, for equilibrium thermodynamics, the geometric formulations have been mainly given by using contact geometry, see [1, 8, 9, 11,12,13]. In this geometric setting, the thermodynamic properties are encoded by Legendre submanifolds of the thermodynamic phase space. It was shown by [3] that a geometric formulation of irreversible processes can be made by lifting port-Hamiltonian systems to the thermodynamic phase space. The underlying geometric structure is again given in the context of contact geometry.
In this paper, we show that the equations of evolutions for an open system exchanging matter with the exterior can be geometrically formulated by using Dirac structures. This geometric formulation is associated to the variational formulation given in [6]. To achieve this goal, we first recall below the first and second laws as they apply to an open system. Then, we develop a general Dirac formulation for a class of systems with time-dependent nonlinear nonholonomic constraints. In particular, we introduce a time-dependent Dirac structure on the covariant Pontryagin bundle over a thermodynamic configuration manifold. Finally, we apply our Dirac formulation of systems with nonlinear time-dependent constraints to the case of open thermodynamic systems and we show that the system of evolution equations of the open system can be directly formulated as a Dirac dynamical system.
2 A Fundamental Setting for Open Systems
2.1 The First Law for Open Thermodynamic Systems
The first law of thermodynamics, following [15], asserts that for every system there exists an extensive state function, the energy, which satisfies
where t denotes time, \( P^\mathrm{ext}_W\) is the power associated to the work done on the system, \(P^\mathrm{ext}_H\) is the power associated to the transfer of heat into the system, and \(P^\mathrm{ext}_M\) is the power associated to the transfer of matter into the system. In particular, a system in which \(P^\mathrm{ext}_M \ne 0\) is called open. For such an open system, matter can flow into or out of the system through several ports, \(a=1,...,A\). We suppose, for simplicity, that the system involves only one chemical species and denote by N the number of moles of this species. In this case, the mole balance equation is

where  is the molar flow rate into the system through the a-th port, so that
is the molar flow rate into the system through the a-th port, so that  for flow into the system and
for flow into the system and  for flow out of the system.
for flow out of the system.
As matter enters or leaves the system, it carries its internal, potential, and kinetic energy. This energy flow rate at the a-th port is the product  of the energy per mole (or molar energy) \(\mathsf {E}^a\) and the molar flow rate
of the energy per mole (or molar energy) \(\mathsf {E}^a\) and the molar flow rate  at the a-th port. In addition, as matter enters or leaves the system it also exerts work on the system that is associated with pushing the species into or out of the system. The associated energy flow rate is given at the a-th port by
at the a-th port. In addition, as matter enters or leaves the system it also exerts work on the system that is associated with pushing the species into or out of the system. The associated energy flow rate is given at the a-th port by  , where \(p^a\) and \(\mathsf {V}^a\) are the pressure and the molar volume of the substance flowing through the a-th port. In this case, the power exchange due to the mass transfer is
, where \(p^a\) and \(\mathsf {V}^a\) are the pressure and the molar volume of the substance flowing through the a-th port. In this case, the power exchange due to the mass transfer is

A system is called adiabatically closed if \(P_H^\mathrm{ext}=P_M^\mathrm{ext}=0\).
2.2 The Second Law for Open Thermodynamic Systems
Following [15], the evolution part of the second law of thermodynamics asserts that for every adiabatically closed system, there exists an extensive state function, the entropy, which satisfies
where I is the entropy production of the system. Let us deduce the expression of the entropy production in an open system of one chemical component, with constant volume and an internal energy given by \(U=U(S,N)\). The balance of mole and the balance energy, i.e., the first law, are respectively given by

where \(\mathsf {H}^a=\mathsf {U}^a+ p^a\mathsf {V}^a\) is the molar enthalpy at the a-th port and where \(\mathsf {U}^a\), \( p^a\), and \(\mathsf {V}^a\) are respectively the molar internal energy, the pressure and the molar volume at the a-th port, see [10, 14]. From these equations and the second law, one obtains the equations for the rate of change of the entropy of the system as

where \(\mathsf {S}^a\) is the molar entropy at the a-th port and I is the rate of internal entropy production of the system given by

where \(T= \frac{\partial U}{\partial S}\) denotes the temperature and \(\mu =\frac{\partial U}{\partial N}\) the chemical potential. The entropy flow rate is given by  and we also have the relation \(\mathsf {H}^a=\mathsf {U}^a+ p^a\mathsf {V}^a= \mu ^a +T^a\mathsf {S}^a\). The thermodynamic quantities known at the ports are usually the pressure and the temperature \(p^a\), \(T^a\), from which the other thermodynamic quantities, such as \(\mu ^a=\mu ^a(p^a,T^a)\) or \(\mathsf {S}^a=\mathsf {S}^a(p^a,T^a)\) are deduced from the state equations of the gas.
and we also have the relation \(\mathsf {H}^a=\mathsf {U}^a+ p^a\mathsf {V}^a= \mu ^a +T^a\mathsf {S}^a\). The thermodynamic quantities known at the ports are usually the pressure and the temperature \(p^a\), \(T^a\), from which the other thermodynamic quantities, such as \(\mu ^a=\mu ^a(p^a,T^a)\) or \(\mathsf {S}^a=\mathsf {S}^a(p^a,T^a)\) are deduced from the state equations of the gas.
3 Dirac Formulation of Time-Dependent Nonlinear Nonholonomic Systems
3.1 Variational and Kinematic Time Dependent Constraints
In order to formulate an open thermodynamic system in the context of Dirac structures, we first introduce two different constraints \(C_V\) and \(C_K\) which depend explicitly on time t. For a thermodynamic configuration manifold  which is the space of the thermodynamic variables as well as the mechanical variables, we define the extended configuration manifold as
which is the space of the thermodynamic variables as well as the mechanical variables, we define the extended configuration manifold as  , which can be seen as a trivial vector bundle
, which can be seen as a trivial vector bundle  , \((t,x)\mapsto t\), over the space of time \(\mathbb {R}\). Consider the vector bundle
, \((t,x)\mapsto t\), over the space of time \(\mathbb {R}\). Consider the vector bundle  over Y, whose vector fiber at \(y=(t,x)\) is given by
over Y, whose vector fiber at \(y=(t,x)\) is given by  . An element in the fiber at (t, x) is denoted \((v,\delta {t},\delta {x})\). In general, by definition a variational constraint is a subset
. An element in the fiber at (t, x) is denoted \((v,\delta {t},\delta {x})\). In general, by definition a variational constraint is a subset  such that \(C_V(t,x,v)\), defined by \(C_V(t,x,v):=C_V\cap \left( \{(t,x,v)\}\times T_{(t,x)}Y\right) ,\) is a vector subspace of \(T_{(t,x)}Y\), for all
such that \(C_V(t,x,v)\), defined by \(C_V(t,x,v):=C_V\cap \left( \{(t,x,v)\}\times T_{(t,x)}Y\right) ,\) is a vector subspace of \(T_{(t,x)}Y\), for all  . In general, a kinematic constraint is a submanifold \(C_K\subset TY.\) More concretely, given functions
. In general, a kinematic constraint is a submanifold \(C_K\subset TY.\) More concretely, given functions  and
and  , \(r=1,...,m\), the variational constraint \(C_V\) is given by
, \(r=1,...,m\), the variational constraint \(C_V\) is given by

and the associated kinematic constraint \(C_K\) of thermodynamic type is
We will see later how \(C_V\) and \(C_K\) are concretely given in thermodynamics.
3.2 Covariant Pontryagin Bundles and the Generalized Energy
Associated to the extended configuration manifold  for the time-dependent system, we define the covariant Pontryagin bundle by
for the time-dependent system, we define the covariant Pontryagin bundle by

An element in the fiber at (t, x) is denoted \((v,\mathsf {p},p)\). Given the Lagrangian  , the covariant generalized energy is defined on
, the covariant generalized energy is defined on  as
as

3.3 Dirac Structures on the Covariant Pontryagin Bundle
Given a variational constraint  , we consider the distribution
, we consider the distribution  on the covariant Pontryagin bundle defined by
on the covariant Pontryagin bundle defined by

From the expression of \(C_V\) in (1), we get

Consider the canonical symplectic form on \(T^*Y\) given by \(\varOmega _{T^*Y}=-\mathbf {d}\varTheta _{T^*Y}\), where \(\varTheta _{T^*Y}\) is the canonical one-form on \(T^*Y\). In local coordinates, we have \(\varTheta _{T^*Y}=p_{i}dx^{i}+\mathsf {p}dt\) and \(\varOmega _{T^*Y}=dx^{i} \wedge dp_{i} + dt \wedge d\mathsf {p}.\) Using the projection  , \((t,x,v,\mathsf {p}, p)\mapsto (t,x,\mathsf {p}, p)\) onto \(T^{*}Y\), we get the presymplectic form on the covariant Pontryagin bundle given by
, \((t,x,v,\mathsf {p}, p)\mapsto (t,x,\mathsf {p}, p)\) onto \(T^{*}Y\), we get the presymplectic form on the covariant Pontryagin bundle given by  . The local expression is given by
. The local expression is given by  .
.
Given the distribution  in (4) and the presymplectic form
in (4) and the presymplectic form  , the Dirac structure
, the Dirac structure  on
on  is given by
is given by

for all  .
.
3.4 Dirac Dynamical Systems
Using the Dirac structure  on
on  in (5), we can define a Dirac dynamical system for a curve x(t) in
in (5), we can define a Dirac dynamical system for a curve x(t) in  as follows:
as follows:

Equivalently, condition (6) gives the equations of motion

Using coordinates, we can now explicitly express these equations as follows. The differential of  is given by
is given by

and the tangent vector \(\dot{\mathrm {x}}\) to  is given by \((t,x,\dot{t},\dot{x})\). We deduce that the Dirac dynamical system (7) gives the following conditions on the curve
is given by \((t,x,\dot{t},\dot{x})\). We deduce that the Dirac dynamical system (7) gives the following conditions on the curve  ,
,
In local expressions, these evolution Eq. (8) read
3.5 Energy Balance Equations
One immediately notices that the covariant generalized energy  defined in (3) is preserved along the solution curve \(\mathrm {x}(t)=(t,x(t),v(t),\mathsf {p}(t), p(t)) \) of the Dirac dynamical system (9),
defined in (3) is preserved along the solution curve \(\mathrm {x}(t)=(t,x(t),v(t),\mathsf {p}(t), p(t)) \) of the Dirac dynamical system (9),

Note that  does not represent the total energy of the system. The total energy is represented by the generalized energy
does not represent the total energy of the system. The total energy is represented by the generalized energy  defined as
defined as
and Eq. (10) yields
This is the balance of energy for the Dirac system. Note that \(\frac{d}{dt}\mathsf {p}\) is interpreted as the power flowing out of the system. The first term on the right hand side is essentially due to the explicit dependence of the Lagrangian on time. The second term is due to the affine character of the constraint and will be interpreted later as the energy flowing in or out of the systems through its ports.
4 Dirac Formulation of Open Thermodynamics
4.1 Geometric Setting
Consider a simple open finite dimensional system with a single entropy S and a single chemical species with number of moles N in a single compartment. The system has a constant volume \(V=V_{0}\), it has A external ports, through which matter can flow into or out of the system as well as B ports, through which heat can flow in or out of the system. Let U(S, N) be the internal energy of the system. Let  , \(\mathsf {S}^{a}(t)\), \(T ^{a}(t)\), \(\mu ^{a}(t)\) be given functions of time associated to the external flow of matter into the system through the a-port and define
, \(\mathsf {S}^{a}(t)\), \(T ^{a}(t)\), \(\mu ^{a}(t)\) be given functions of time associated to the external flow of matter into the system through the a-port and define  . We assume that there exist external heat sources at the b-port with entropy flow rate
. We assume that there exist external heat sources at the b-port with entropy flow rate  , molar entropy \(\mathsf {S}^{b}(t)\) and temperature \(T^b(t)\).
, molar entropy \(\mathsf {S}^{b}(t)\) and temperature \(T^b(t)\).
The thermodynamic configuration space is  , with \(\varGamma \), W, \(\varSigma \) the thermodynamic displacements, see [6]. As in Sect. 3.1, let
, with \(\varGamma \), W, \(\varSigma \) the thermodynamic displacements, see [6]. As in Sect. 3.1, let  be the trivial bundle over \(\mathbb {R}\) and consider the thermodynamic phase space
be the trivial bundle over \(\mathbb {R}\) and consider the thermodynamic phase space  over Y with coordinates
over Y with coordinates  , where
, where  . Let us employ the local coordinates for \((t,x,\delta {t},\delta {x}) \in TY\) and \((t,x,\mathsf {p},p) \in T^{*}Y\), where
. Let us employ the local coordinates for \((t,x,\delta {t},\delta {x}) \in TY\) and \((t,x,\mathsf {p},p) \in T^{*}Y\), where  and
and  .
.
4.2 Nonholonomic Constraints in Thermodynamics
For open thermodynamic systems, the constraint (1) reads

Hence the nonlinear kinematic constraint (2) becomes

where we have denoted \(\dot{x}=(\dot{S},\dot{N}, \dot{\varGamma },\dot{W}, \dot{\varSigma })\).
4.3 Dirac Structures on 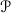 for Open Thermodynamic Systems
for Open Thermodynamic Systems
As in Sect. 3.2, let  be the covariant Pontryagin bundle over Y, whose coordinates are given by
be the covariant Pontryagin bundle over Y, whose coordinates are given by  . The canonical one form \(\varTheta _{T^{*}Y}\) and the canonical symplectic form \(\varOmega _{T^{*}Y}= - \mathbf {d}\varTheta _{T^{*}Y}\) are expressed as
. The canonical one form \(\varTheta _{T^{*}Y}\) and the canonical symplectic form \(\varOmega _{T^{*}Y}= - \mathbf {d}\varTheta _{T^{*}Y}\) are expressed as
Recall that the presymplectic form on  is defined by
is defined by  .
.
Associated with  , we have the natural projection
, we have the natural projection  , given by \((t,x,v,\mathsf {p}, p) \mapsto (t,x)\), and we can lift the constraint subspace \(C_{V}(t, x, v) \subset TY\) to get the constraint distribution
, given by \((t,x,v,\mathsf {p}, p) \mapsto (t,x)\), and we can lift the constraint subspace \(C_{V}(t, x, v) \subset TY\) to get the constraint distribution  on
on  defined as
defined as

As shown in (5), from the distribution  and the presymplectic form
and the presymplectic form  , we can define the induced Dirac structure
, we can define the induced Dirac structure  on
on  .
.
4.4 Dirac Thermodynamic Systems on 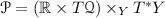
For each  , we write the vector and the covector in (5) as
, we write the vector and the covector in (5) as

where \(\dot{v}=( \dot{v}_{S},\dot{v}_{N} , \dot{v}_{\varGamma },\dot{v}_{W}, \dot{v}_{\varSigma }), \dot{p}=(\dot{p}_{S}, \dot{p}_{N}, \dot{p}_{\varGamma }, \dot{p}_{W}, \dot{p}_{\varSigma }), \alpha =(\alpha _{S},\alpha _{N}, \alpha _{\varGamma },\)\(\alpha _{W}, \alpha _{\varSigma })\), \(\beta =(\beta _{S},\beta _{N}, \beta _{\varGamma },\beta _{W}, \beta _{\varSigma })\), and \(w=(w_{S},w_{N}, w_{\varGamma },w_{W}, w_{\varSigma })\). From (6) the Dirac system reads

Using the definition of the Dirac structure in terms of \(C_V\), we get
Following [6], the Lagrangian is given by \(\mathcal {L}(t,x, v)=-U(S,N) + v_{W} N+ v_{\varGamma }( S- \varSigma )\). The covariant generalized energy is here given by

The differential of  is obtained as
is obtained as

where \(\pi =-\frac{\partial L}{\partial t}=0,\,\alpha =-\frac{\partial L}{\partial x}=\left( -v_\varGamma +\frac{\partial U}{\partial S},-v_W +\frac{\partial U}{\partial N}, 0, 0,v_\varGamma \right) ,\; \beta =p-\frac{\partial L}{\partial v}=\left( p_S, p_N, p_\varGamma +\varSigma -S, p_W-N, p_\varSigma \right) ,\;\; w=v=(v_S, v_N, v_\varGamma , v_W, v_\varSigma ).\)
By using this, the Dirac dynamical system

is equivalent to the following evolution equations:

Making arrangements, this system yields the equations of evolution as

where  and \(\frac{d_iS}{dt}:=I\ge 0\) denotes the internal entropy production due to the mixing of matter flowing into the system and \(\frac{d_eS}{dt}\) is the entropy flow. The system of equation also gives the definition of the thermodynamic displacement as
and \(\frac{d_iS}{dt}:=I\ge 0\) denotes the internal entropy production due to the mixing of matter flowing into the system and \(\frac{d_eS}{dt}\) is the entropy flow. The system of equation also gives the definition of the thermodynamic displacement as  ,
,  , and
, and  . The momentum \(\mathsf {p}\) represents the part of the energy associated to the interaction of the system with exterior through its ports. In fact, it follows
. The momentum \(\mathsf {p}\) represents the part of the energy associated to the interaction of the system with exterior through its ports. In fact, it follows

where E is the total energy of the system, defined by
Example: A Piston Device with Ports and Heat Sources. As illustrated in Fig. 1, we consider an open chamber containing a species with internal energy U(S, N), where we assume that the cylinder has two external heat sources with entropy flow rates  , \(i=1,2\), the volume of the chamber is constant \(V_0\) and two ports through which the species is injected into or flows out of the cylinder with molar flow rates
, \(i=1,2\), the volume of the chamber is constant \(V_0\) and two ports through which the species is injected into or flows out of the cylinder with molar flow rates  , \(i=1,2\). The entropy flow rates at the ports are given by
, \(i=1,2\). The entropy flow rates at the ports are given by  .
.
Recall that the Lagrangian is given by
The equations of evolution of the Dirac open thermodynamic system (11) read

where  is the internal entropy production given by
is the internal entropy production given by

The first term represents the entropy production associated to the mixing of gas flowing into the cylinder at the two ports \(a_1\), \(a_2\), and the third term denotes the entropy production due to the external heating. The second law requires that each of these terms is positive. The first law, i.e., the energy balance holds as

References
Carathéodory, C.: Untersuchungen über die Grundlagen der Thermodynamik. Math. Ann. 67, 355–386 (1909)
Courant, T.J.: Dirac manifolds. Trans. Am. Math. Soc. 319, 631–661 (1990)
Eberard, D., Maschke, B.M., van der Schaft, A.J.: An extension of Hamiltonian systems to the thermodynamic phase space: towards a geometry of nonreversible processes. Rep. Math. Phys. 60(2), 175–198 (2007)
Gay-Balmaz, F., Yoshimura, H.: A Lagrangian variational formulation for nonequilibrium thermodynamics. Part I: discrete systems. J. Geom. Phys. 111, 169–193 (2017a)
Gay-Balmaz, F., Yoshimura, H.: A Lagrangian variational formulation for nonequilibrium thermodynamics. Part II: continuum systems. J. Geom. Phys. 111, 194–212 (2017b)
Gay-Balmaz, F., Yoshimura, H.: A variational formulation of nonequilibrium thermodynamics for discrete open systems with mass and heat transfer. Entropy 20(3), 1–26 (2018a). https://doi.org/10.3390/e20030163
Gay-Balmaz, F., Yoshimura, H.: Dirac structures in nonequilibrium thermodynamics. J. Math. Phys. 59, 012701–29 (2018b)
Gibbs, J.W.: Graphical methods in the thermodynamics of fluids. Trans. Connecticus Acad. 2, 309–342 (1873)
Hermann, R.: Geometry, Physics and Systems. Dekker, New York (1973)
Klein, S., Nellis, G.: Thermodynamics. Cambridge University Press, Cambridge (2011)
Mrugala, R.: Geometrical formulation of equilibrium phenomenological thermodynamics. Rep. Math. Phys. 14, 419–427 (1978)
Mrugala, R.: A new representation of thermodynamic phase space. Bull. Polish Acad. Sci. 28, 13–18 (1980)
Mrugala, R., Nulton, J.D., Schon, J.C., Salamon, P.: Contact structure in thermodynamic theory. Rep. Math. Phys. 29, 109–121 (1991)
Sandler, S.I.: Chemical, Biochemical, and Engineering Thermodynamics. Wiley, Hoboken (2006)
Stueckelberg, E.C.G., Scheurer, P.B.: Thermocinétique Phénoménologique Galiléenne, Birkhäuser (1974)
Yoshimura, H., Marsden, J.E.: Dirac structures in Lagrangian mechanics. Part I: Implicit Lagrangian systems. J. Geom. Phys. 57, 133–156 (2006a)
Yoshimura, H., Marsden, J.E.: Dirac structures in Lagrangian mechanics. Part II: Variational structures. J. Geom. Phys. 57, 209–250 (2006b)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Yoshimura, H., Gay-Balmaz, F. (2019). Dirac Structures in Open Thermodynamics. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2019. Lecture Notes in Computer Science(), vol 11712. Springer, Cham. https://doi.org/10.1007/978-3-030-26980-7_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-26980-7_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26979-1
Online ISBN: 978-3-030-26980-7
eBook Packages: Computer ScienceComputer Science (R0)




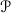 for Open Thermodynamic Systems
for Open Thermodynamic Systems