Subvector Commitments with Application to Succinct Arguments

Abstract

We put forward the notion of subvector commitments (SVC): An SVC allows one to open a committed vector at a set of positions, where the opening size is independent of length of the committed vector and the number of positions to be opened. We propose two constructions under variants of the root assumption and the CDH assumption, respectively. We further generalize SVC to a notion called linear map commitments (LMC), which allows one to open a committed vector to its images under linear maps with a single short message, and propose a construction over pairing groups.

Equipped with these newly developed tools, we revisit the “CS proofs” paradigm [Micali, FOCS 1994] which turns any arguments with public-coin verifiers into non-interactive arguments using the Fiat-Shamir transform in the random oracle model. We propose a compiler that turns any (linear, resp.) PCP into a non-interactive argument, using exclusively SVCs (LMCs, resp.). For an approximate 80 bits of soundness, we highlight the following new implications:

• 1. There exists a succinct non-interactive argument of knowledge (SNARK) with public-coin setup with proofs of size 5360 bits, under the adaptive root assumption over class groups of imaginary quadratic orders against adversaries with runtime $2^{128}$. At the time of writing, this is the shortest SNARK with public-coin setup.

• 2. There exists a non-interactive argument with private-coin setup, where proofs consist of 2 group elements and 3 field elements, in the generic bilinear group model.

G. Malavolta—Part of the work done while at Friedrich-Alexander-Universität Erlangen-Nürnberg.

1 Introduction

Commitment schemes are one of the fundamental building blocks and one of the most well-studied primitives in cryptography. Due to their pivotal importance in the design of cryptographic protocols, even small efficiency improvements have magnified repercussions in the field. In a recent work, Catalano and Fiore [27] put forth the notion of Vector Commitments (VC): A VC allows a prover to commit to a vector $\varvec{x}$ of $\ell$ messages, such that it can later open the commitment at any position $i \in [\ell ]$ of the vector, i.e., reveal a message and show that it equals to the i-th committed message. The distinguishing feature of VCs is that the size of the commitments and openings is independent of $\ell$. A VC scheme is required to be position binding, meaning that no efficient algorithm can open a commitment at some position i to two distinct messages $x_i \ne x'_i$. Catalano and Fiore [27] constructed two VC schemes based on the CDH assumption over pairing groups and the RSA assumption, respectively. In both schemes, a commitment and an opening both consist of a single group element (in the respective groups). Furthermore, the scheme based on the RSA assumption has public parameters whose size is independent of the length of the vectors to be committed.

This concept was later generalized by Libert et al. [48], who formalized the notion of functional commitment (FC). Intuitively, an FC allows the prover to commit to a vector $\varvec{x}$, and to open the commitment to function-value tuples (f, y) such that $y = f(\varvec{x})$. Libert et al. [48] proposed a construction for linear forms¹ based on the Diffie-Hellman exponent assumption over pairing groups, where a commitment and an opening both consist of a single group element. VCs and FCs for linear forms are very versatile tools and turned out to be useful for a variety of applications, such a zero-knowledge sets [54], polynomial commitments [44], accumulators, and credentials, to mention a few.

While a short commitment is certainly an appealing feature, there are contexts where there is still a lot to be desired. For example, in case the prover wants to reveal multiple locations of the committed vector (resp. multiple function outputs) the best known solution is to repeat the above protocol in parallel. This means that the size of the openings grows linearly with the amount of revealed locations (resp. function outputs).

1.1 Commitments with Even Shorter Openings

We introduce the notion of subvector commitments (SVCs). An SVC allows one to commit to a vector $\varvec{x}$ of length $\ell$ and later open to a subvector of an arbitrary length $\le \ell$. Given an ordered index set $I \subseteq [\ell ]$, we define the I-subvector of $\varvec{x}$ as the vector formed by collecting the i-th component of $\varvec{x}$ for all $i \in I$. While a VC is required to be succinct, namely the commitment size and the size of the proof of the opening are independent of the length of the committed vector, an SVC has a stronger compactness² property which additionally requires that these sizes do not depend on the length of the subvector to be opened. This difference is going to be critical for our applications (explained later). Improving upon the VC constructions of Catalano and Fiore [27], we propose two constructions of SVCs based on the CDH assumption over pairing groups and the RSA assumption, respectively. We further generalize the RSA-based scheme to work over modules over Euclidean rings [51], where variants of the root assumption are conjectured to hold. Loosely speaking, the root assumption states that it is hard to find the e-th root of a random ring element, for any non-trivial e. In these settings we obtain public-coin-setup instantiations of SVCs using class groups of imaginary quadratic orders.

We then generalize the notion of SVCs to allow the prover to reveal arbitrary linear maps computed over the committed vector. We call such class of schemes linear map commitments (LMC). As in SVC, it is important to require an LMC to be compact, meaning that both the commitment and the proofs are of size independent of $\ell$ and q, whereas succinctness only requires their size to be independent of $\ell$. Note that an SVC can be viewed as an LMC restricted to the class of linear maps whose matrix representation has exactly one 1 in each row and 0 everywhere else.

Table 1. Comparison of subvector and linear map commitments for messages of length $\ell$, with binding against adversaries of runtime . All constants are omitted. $\mathsf {pp}$: public parameters, C: commitment, $\varLambda$: proof, Pub: public-coin, Pri: private-coin, CRH: collision-resistant hash, Root: strong or adaptive root, SD: subgroup decision, GGM: generic bilinear group model.

Naively, one may attempt to generalize position binding for LMC by requiring that the prover cannot open a commitment to $(f, \varvec{y})$ and $(f, \varvec{y} ')$ with $\varvec{y} \ne \varvec{y} '$, where f is a linear map and are now vectors. This turns out to be insufficient for our applications: This is because the prover may be able to open to $(f, \varvec{y})$ and $(f', \varvec{y} ')$ where $f \ne f'$ and $\varvec{y} \ne \varvec{y} '$ such that they form an inconsistent system of linear equations, yet the attack is not captured by the definition. We tackle this issue by defining a more general function binding notion which requires that no efficient algorithm can produce openings for Q function-value tuples $\{(f_k,\varvec{y} _k)\}_{k \in [Q]}$ for any , such that there does not exist $\varvec{x}$ with $f_k(\varvec{x}) = \varvec{y} _k$ for all $k \in [Q]$.

We then modify the construction of Libert et al. [48] to support batch openings to linear forms or, equivalently opening to a linear map. Since the verification equation of their construction is linear, a natural way to support batch openings is to define the new verification equation as a random linear combination of previous ones. With this observation, we embed a secret linear combination in the public parameters, and show that the resulting construction is function binding in the generic bilinear group model. In Table 1 we compare our SVC and LMC constructions with existing schemes.

1.2 The Quest of Constructing Ever Shorter Arguments

In addition to enabling batching in the original applications of VCs and FCs for linear forms mentioned above, the compactness of SVCs and LMCs opens the new possibilities of application in constructing succinct argument systems.

Background. An argument system for an NP language $\mathcal {L}$ allows a prover, with a witness w, to convince a verifier that a certain statement x is in $\mathcal {L}$. In contrast with proof systems, argument systems are only required to be computationally sound. Due to this relaxation, it is possible that the interaction between the prover and the verifier is succinct, i.e., the communication complexity is bounded by some polynomial in the security parameter and is independent of the size of w. Other desirable properties of an argument system are:

• “of knowledge”: a successful prover implies an extractor that can recover the witness;

• non-interactive: the protocol consists of a single message from the prover;

• (verifier) public-coin: messages from the verifier are sampled from public domains.

Recently, much progress has been made both in theory and practice to construct succinct non-interactive arguments of knowledge (SNARK) for general NP languages. We distinguish between SNARKs in the public-coin-setup model and the pre-processing model. In the public-coin-setup model, the prover and the verifier do not share any input other than the statement x to be proven. In the pre-processing model, they share a common reference string, generated by a trusted third party, which may depend on the language $\mathcal {L}$ and the statement x. In general, existing SNARKs in the pre-processing model are more efficient, in terms of both communication and computation, than those in the public-coin-setup model. This reflects the intuition that pushing the majority of the verifier’s workload to the offline pre-processing phase reduces its workload in the online phase. On the other hand, in some applications, such as cryptocurrencies, it is crucial to have a public-coin setup, which can be publicly initialized via, e.g., a random oracle [8].

Public-Coin-Setup SNARKs. While it is known that public-coin-setup non-interactive arguments for NP do not exists in the standard model [15], one can circumvent this impossibility by working in the random oracle model [8]. A common way to obtain public-coin-setup SNARKs is through the “CS proofs” paradigm [45, 53] based on probabilistically checkable proofs (PCP) [3]. To recall, a q-query $2^{-\sigma }$-soundness PCP scheme allows the prover to efficiently compute a PCP string which encodes the witness of the statement to be proven. The verifier can then decide whether the statement is true with probability close to $1 - 2^{-\sigma }$ by inspecting q entries of the PCP string. Given a PCP, a SNARK under the CS proofs paradigm are constructed in two steps. First, the PCP is turned into an interactive argument system: The prover first commits to the PCP string, typically using a Merkle-tree commitment. The verifier then sends the indices of the entries to be inspected. Next, the prover opens the commitment at these entries. Finally, by inspecting the revealed entries, the verifier can decide whether the statement is valid. Typically, an argument system constructed this way has a public-coin verifier and can be made non-interactive using the Fiat-Shamir transform [35].

Under the CS proofs paradigm, a proof (e.g., in the scheme by Micali [53]) consists of a -bit Merkle-tree commitment of a $\ell$-bit PCP string, q bits of the PCP string, and q openings of the commitment, each of size bits. For concreteness, assuming a 3-query PCP and $\ell = 2^{30}$, for $2^{-80}$-soundness against a $2^{128}$-time adversary, the proof size is around 113 KB. Despite having linear verification time (hence not being a SNARK) Bulletproof [21, 26] is arguably the most practically efficient non-interactive argument to date. A proof in [26] consists of $2 \log n + 13$ (group and field) elements, where n is the number of multiplication gates in the arithmetic circuit representation of the verification algorithm of $\mathcal {L}$. In their instantiation over the curve secp256k1, each of the group elements and integers can be represented by $\sim$256 bits, thus a proof consists of roughly $512 \log n+3328$ bits.

Pre-Processing SNARKs. In the pre-processing model, there exist plenty of SNARK constructions originated by [37] based on pairings and linear interactive proofs (LIP), where the latter can be constructed from linear PCPs. To recall, linear PCPs [42] generalizes traditional PCPs in the sense that the PCP string now encodes a linear form. In a q-query linear PCP, the verifier, who is given oracle access to the linear form, can decide the veracity of the statement with overwhelming probability by making only q queries. SNARK constructions in this category typically have a computationally expensive statement-dependent pre-processing phase, meaning that one set of public parameters has to be generated per statement to be proven.

In this setting, the scheme with the shortest proofs (4 group elements) in the standard model is due to Danezis et al. [32]. In the generic bilinear group model, Groth [40] proposed a scheme [60] with only 3 group elements, and showed that proofs constructed from LIP must consist of at least 2 group elements. These schemes can be instantiated over pairing-friendly elliptic curves. A popular choice is the 256-bit Barreto-Naehrig curve [7], in which a group element can be represented using 256 bits.

Our Approach. Equipped with our newly developed tools, we revisit the CS proofs paradigm. In previous schemes following this paradigm, the proof size is dominated by the factor $q \log \ell$ due to the q Merkle-tree commitment openings. Moreover, due to the lack of structure of a Merkle-tree commitment, prior schemes do not work with linear PCPs. The main idea is thus to replace the Merkle-tree commitment with an SVC/LMC, so that the q openings can be compressed into a single one which has size independent of $\ell$ and q. By doing so, we obtain a compiler which compiles any (resp. linear) PCP into an interactive argument using an SVC (resp. LMC).

We highlight two interesting instantiations of our construction. The first instantiation is with classical PCPs and our public-coin-setup SVC based on $Cl(\varDelta )$, the class group of imaginary quadratic order with discriminant $\varDelta$.

Instantiation 1

If the adaptive root assumption holds in $Cl(\varDelta )$, then there exist public-coin-setup SNARKs for NP with soundness error $2^{-\sigma }$ in which a proof consists of 2 $Cl(\varDelta )$ elements and q bits in the random oracle model, using any q-query $2^{-\sigma }$-soundness PCP.

If one aims for an extremely short proof and is willing to accept expensive prover computation, then a 3-query $2^{-1}$-soundness PCP can be amplified into a $3\sigma$-query $2^{-\sigma }$-soundness PCP and gives the shortest SNARK. Based on the best known attacks on the root problem in class groups [41], for a soundness error of $2^{-80}$ against a $2^{128}$-time adversary, we obtain a proof size of 5360 bits, which is shorter than that of Bulletproof [26] for $n > 16$, i.e., the verification circuit has more than 16 multiplication gates. We view this instantiation as a feasibility for extremely succinct proofs and a step forward towards optimal ($O(\lambda )$-sized) public-coin-setup SNARKs. Next we turn our attention to the instantiation with linear PCPs and our pairing-based LMCs.

Table 2. Comparison of SNARKs with -soundness against adversaries of runtime $2^{128}$. All constants are omitted. $\mathsf {pp}$: public parameters, $\pi$: proof, n: size of circuit, $\ell _{\mathsf {PCP}}$: length of PCP proof, $\ell _{\mathsf {LPCP}}$: length of linear PCP proof, Pub: public-coin, Pri: private-coin, Pre-Proc: pre-processing, Root: strong or adaptive root assumption, GGM: generic group model.

Instantiation 2

In the generic bilinear group and random oracle model, there exist pre-processing non-interactive arguments for NP in which a proof consists of 2 elements and q field elements, using any q-query linear PCP.

Using a 3-query linear PCP (e.g. [17]) and instantiating the pairing group over the 256-bit Barreto-Naehrig curve yields a proof consisting of 5 elements or 1280 bits. Compared to other pairing-based compilers from linear PCPs to preprocessing SNARKs (e.g., [40]), our compiler has the advantages that it supports any linear PCPs, but not only those where the verifier is restricted to only evaluate quadratic polynomials. Moreover the setup phase is independent of the statements to be proven, and thus the same public parameters can be reused for proving many statements.

A comparison with the shortest succinct arguments from the literature is given in Table 2. To summarize, our approach yields extremely short proofs in exchange for a higher prover complexity and the usage of public-key cryptography. We also stress that our compiler is compatible with a broader class of PCPs, when compared with schemes under the CS proofs paradigm and pairing-based schemes. Being a very active area of research, we expect significant advancements in the design of more efficient PCPs, which are going to benefit from the generality of our approach.

Other Applications. Catalano and Fiore [27] suggested a number of applications of VC, including verifiable databases with efficient updates, updatable zero-knowledge elementary databases, and universal dynamic accumulators. In all of these applications, one can gain efficiency by replacing the VC scheme with an SVC scheme which allows for batch opening and updating. When instantiated with our first construction of SVC, one can further avoid the private-coin setup, which is especially beneficial to database applications as trusted third parties are no longer required.

The notion of SVC has already attracted the attention of the community. A follow up work by Boneh et al. [20] shows how SVCs can be used as a drop-in replacement for Merkle-trees in SNARKs based on interactive oracle proofs (IOPs) which generalizes PCPs. They leverage the structure of class group-based SVCs to reduce the proof size to $(r + 1)$ group elements and r integers, where r is the number of iterations of the underlying IOP. They also propose a technique to improve the efficiency of the verification algorithm and they estimate a decrease in verification time of ${\sim }80\%$. Finally, they discuss how to use SVCs to improve the current design of blockchain-based transaction ledger in such a way that no user has to store the entire state of the ledger in memory.

1.3 Related Work

Succinct arguments were introduced by Kilian [45, 46] and later improved, in terms of round complexity, by Lipmaa and Di Crescenzo [34]. Succinct non-interactive arguments, or computationally sound proofs, were first proposed by Micali [53]. These early approaches rely on PCP and have been recently extended [9] to handle interactive oracle proofs [13] (also known as probabilistic checkable interactive proofs [57]), largely improving the efficiency of the prover. A recent manuscript by Ben-Sasson et al. [10] improves the concrete efficiency of interactive oracle proofs. The first usage of knowledge assumptions to construct SNARKs appeared in the work of Mie [55]. Later, Groth [39] and Lipmaa [50] upgraded this approach to non-interactive proofs.

Ishai, Kushilevitz, and Ostrovsky [42] observed that linear PCPs can be combined with a linearly homomorphic encryption to construct more efficient arguments, with pre-processing. The also introduced a new (interactive) commitment scheme with private-coin verifier for linear functions. However, in contrast with LMC, their binding definition does not ensure that the committed function is actually linear. Gennaro et al. [37] presented a very elegant linear PCP that gave rise to a large body of work to improve the practical efficiency of non-interactive arguments [5, 11, 14, 28, 29, 33]. All of these constructions assume a highly structured and honestly generated common reference string (of size proportional to the circuit to be evaluated) and rely on some variant of the knowledge of exponent assumption. Recently, Ames et al. [2] proposed an argument based on the MPC-in-the-head [43] paradigm to prove satisfiability of a circuit C with proofs of size . Zhang et al. [64] show how to combine interactive proofs and verifiable polynomial delegation schemes to construct succinct interactive arguments. The scheme requires a private-coin pre-processing and the communication complexity is . A recent result by Whaby et al. [62] introduces a prover-efficient construction with proofs of size . Recent works [1, 36] investigate on the resilience of SNARKs against a subverted setup. Libert, Ramanna, and Yung [48] constructed an accumulator for subset queries. Although similar in spirit to SVC, the critical difference is that accumulators are not position binding, which is crucial for the soundness of our argument system.

2 Preliminaries

Throughout this work we denote by the security parameter, and by and the sets of polynomials and negligible functions in , respectively. We say that a Turing machine is probabilistic polynomial time (PPT) if its running time is bounded by some polynomial function . An interactive protocol $\varPi$ between two machines A and B is referred to as $(A,B)_\varPi$. Given a set S, we denote sampling a random element from S as and the output of an algorithm A on input x is written as $z \leftarrow A(x)$. Let , the set $[\ell ]$ is defined as $[\ell ] := \{1,\ldots , \ell \}$. Vectors are written vertically.

2.1 Subvectors

We define the notion of subvectors. Roughly speaking, a subvector $(x_{i_1}, \ldots , x_{i_{|I|}})^T$ is an ordered subset (indexed by I) of the entries of a given vector $(x_1, \ldots , x_\ell )^T$.

Definition 1

(Subvectors). Let , $\mathcal {X}$ be a set, and $(x_1,\ldots ,x_\ell )^T \in \mathcal {X} ^\ell$ be a vector. Let $I = (i_1,\ldots ,i_{|I|}) \subseteq [q]$ be an ordered index set. The I-subvector of $\varvec{x}$ is defined as $\varvec{x} _I := (x_{i_1}, \ldots , x_{i_{|I|}})^T$.

2.2 Arguments of Knowledge

Let $\mathcal {R}: \{0,1\}^* \times \{0,1\}^* \rightarrow \{0,1\}$ be an NP-relation with corresponding NP-language $\mathcal {L}:= \{ x : \exists w \ { s.t.}\ \mathcal {R} (x,w) =1 \}$. We define arguments of knowledge [22] for interactive Turing machines [38]. To be as general as possible, we define an additional setup algorithm $\mathcal {S}$, which is executed once and for all by a possibly trusted party. If the argument is secure without a setup, then such an algorithm can be omitted.

Definition 2

(Arguments of knowledge). A tuple is a $2^{-\sigma }$-sound (succinct) argument of knowledge for $\mathcal {R}$ if the following conditions hold.

• (Completeness). If $\mathcal {R} (x,w)=1$ then

• (Soundness). For any adversary , all $x \notin \mathcal {L}$, and all

• (Argument of Knowledge). For any adversary , there exists a PPT extractor , such that for all $x,z \in \{0,1\}^*$, , then

• (Succinctness). The communication between and is at most .

2.3 Probabilistically Checkable Proofs

One of the principal tools in the construction of argument systems is probabilistic checkable proofs ($\text {PCP}$) [3]. It is known that any witness w for an NP-statement can be encoded into a $\text {PCP}$ of length bits such that it is sufficient to probabilistically test O(1) bits of the encoded witness.

Definition 3

(Probabilistically Checkable Proofs). A pair of machines is a $\ell$-long q-query $2^{-\sigma }$-sound $\text {PCP}$ for an NP-relation $\mathcal {R}$ if the following hold.

(Completeness). If $\mathcal {R} (x,w) = 1$, then

(Soundness). For all $x \notin \mathcal {L}$,

(Proof Length). If $\mathcal {R} (x,w) = 1$, then for all , $|\varvec{\pi } | \le \ell$.

(Query Complexity). For all $x, \varvec{\pi } \in \{0,1\}^{*}$, queries at most q locations of $\varvec{\pi }$.

The notation means that does not read the entire string $\varvec{\pi }$ directly, but is given oracle access to the string. On input a position $i \in [|\varvec{\pi } |]$, the oracle returns the value $\pi _i$. It is well known that one can diminish the soundness error to a negligible function by repetition. We additionally require that the witness can be efficiently recovered from the encoding of the witness $\varvec{\pi }$ [61].

Definition 4

(Proof of Knowledge). A $\text {PCP}$ is of knowledge if there exists a PPT algorithm such that, given any strings x and $\varvec{\pi }$ with , extracts an NP witness w for x.

Linear PCPs. Ishai et al. [42] considered the notion of linear PCP, where the string $\varvec{\pi }$ is instead a vector in for some finite field $\mathbb {F}$ (or in general a ring) and positive integer $\ell$. The oracle given to the verifier is modified, such that on input , it returns the inner product $\langle \varvec{f}, \varvec{\pi } \rangle$. Note that this generalizes the classical notion of PCP as one can recover the original definition by restricting the queries $\varvec{f}$ to be unit vectors. In this paper we are interested in the notion of linear PCP where soundness is only guaranteed to hold against linear functions (same as considered in [17]).

3 Mathematical Background and Assumptions

To capture the minimal mathematical structure required for one of our constructions, we follow the module-based cryptography framework of Lipmaa [51].

Background. A (left) R-module $R_D$ over the ring R (with identity) consists of an Abelian group $(D,+)$ and an operation $\circ : R \times D \rightarrow D$, denoted $r \circ A$ for $r \in R$ and $A \in D$, such that for all $r, s \in R$ and $A, B \in D$, we have

• $r \circ (A + B) = r \circ A + r \circ B$,

• $(r+s) \circ A = r \circ A + s \circ A$,

• $(r \cdot s) \circ A = r \circ (s \circ A)$, and

• $1_R \circ r = r$, where $1_R$ is the multiplicative identity of R.

Let be an ordered set, and $\varvec{r} = (r_{s_1}, \ldots , r_{s_\ell })^T \in R^\ell$ and $\varvec{A} = (A_{s_1}, \ldots , A_{s_\ell })^T \in D^\ell$ be vectors of ring and group elements respectively. For notational convenience, we denote $\sum _{i \in S} r_i \circ A_i$ by $\langle \varvec{r}, \varvec{A} \rangle$.

A commutative ring R with identity is called an integral domain if for all $r, s \in R$, $rs = 0_R$ implies $r = 0_R$ or $s = 0_R$, where $0_R$ is the additive identity of R. A ring R is Euclidean if it is an integral domain and there exists a function , called the Euclidean degree, such that (i) if $r, s \in R$, then there exist $q,k \in R$ such that $r = qs + k$ with either $k = 0_R$, $k \ne 0_R$ and $\deg (k) < \deg (q)$, and (ii) if $r, s \in R$ with $rs \ne 0_R$ and $r \ne 0_R$, then $\deg (r) < \deg (rs)$. The set of units $U(R) := \{u \in R: \exists v \ { s.t.}\ uv = vu = 1_R\}$ contains all invertible elements in R. An element $r \in R \setminus (\{0_R \}\cup U(R))$ is said to be irreducible if there are no elements $s, t \in R \setminus \{1_R\}$ such that $r = st$. The set of all irreducible elements of R is denoted by $\mathrm {IRR}(R)$. An element $r \in R \setminus (\{0_R \}\cup U(R))$ is said to be prime if for all $s,t \in R$, whenever r divides st, then r divides s or r divides t. If R is Euclidean, then an element is irreducible if and only if it is prime.

Adaptive Root. The adaptive root assumption (over unknown order groups, and in particular over class groups of imaginary quadratic orders) was introduced by Wesolowski [63] and re-formulated by Boneh et al. [19] to establish the security of the verifiable delay function scheme of Wesolowski [63]. Here we state the same assumption over modules in two variants – with private and public coins. Note that Wesolowski [63] and Boneh et al. [19] implicitly considered the public-coin-setup variant.

Definition 5

((Public-Coin) Adaptive Root). Let I be some ordered set. Let $\mathcal {R}_{\mathcal {D}} = \left( (R_i)_{D_i} \right) _{i \in I}$ be a family of modules. Let be a deterministic algorithm which picks some $i \in I$ (hence some $R_D = (R_i)_{D_i} \in \mathcal {R}_{\mathcal {D}}$) and some element $A \in D$. For a ring R, let be some set of prime elements in R of size . The adaptive root assumption is said to hold over the family of modules $\mathcal {R}_{\mathcal {D}}$ with respect to , if for any adversary there exists such that

where is not given $\omega$ (highlighted by the dashed box). If the inequality holds even if is given $\omega$, then we say that the assumption is public-coin.

Strong Distinct-Prime-Product Root. We define the following variant of the “strong root assumption” [30] over modules over Euclidean rings, which is a generalization of the strong RSA assumption. Let $R_D$ be a module over some Euclidean ring R, and A be an element of D. The strong distinct-prime-product root problem with respect to A asks to find a set of distinct prime elements $\{e_i\}_{i \in S}$ in R and an element Y in D such that $\left( \prod _{i \in S} e_i \right) \circ Y = A$. We define the assumption in two variants depending on whether $R_D$ and A are sampled with public coins.

Definition 6

((Public-Coin) Strong Distinct-Prime-Product Root). Let I be an ordered set, $\mathcal {R}_{\mathcal {D}} = \left( (R_i)_{D_i} \right) _{i \in I}$ be a family of modules, and be a deterministic algorithm which picks some $i \in I$ (hence some $R_D = (R_i)_{D_i} \in \mathcal {R}_{\mathcal {D}}$) and some element $A \in D$. The strong distinct-prime-product root assumption is said to hold over the family $\mathcal {R}_{\mathcal {D}}$, if for any adversary there exists such that

where is not given $\omega$ (highlighted by the dashed box). If the inequality holds even if is given $\omega$, then we say that the assumption is public-coin.

Lipmaa [51] defined several variants of the (strong) root assumption with respect to a random element in D sampled with private coin, given the description of the module $R_D$ sampled with public coin. Note that the (resp. public-coin) strong distinct-prime-product root assumption is weaker than the (resp. public-coin) strong root assumption, where the latter requires the adversary to simply output (e, Y) such that $e \ne 1_R$ and $e \circ Y = A$. It is apparent that the strong distinct-prime-product root assumption over RSA groups is implied by the strong RSA assumption.

4 Subvector Commitments

In the following we define the main object of interest for our work. Subvector commitments are a generalization of vector commitments [27], where the opening is performed with respect to subvectors.

Definition 7

(Subvector Commitments (SVC)). A subvector commitment scheme $\mathsf {SVC}$ over $\mathcal {X}$ consists of the following algorithms :

• The deterministic setup algorithm inputs the security parameter , the vector size $1^\ell$, and a random tape $\omega$. It outputs a public parameter $\mathsf {pp}$. We assume that all other algorithms input $\mathsf {pp}$ which we omit.

• The committing algorithm inputs a vector $\varvec{x} \in \mathcal {X} ^\ell$. It outputs a commitment string C and some auxiliary information $\mathsf {aux}$.

• The opening algorithm inputs an index set I, an I-subvector $\varvec{x} _I'$, and some auxiliary information $\mathsf {aux}$. It outputs a proof $\varLambda _I$ that $\varvec{x} _I'$ is the I-subvector of the committed vector.

• The verification algorithm inputs a commitment string C, an index set I, an I-subvector $\varvec{x} _I'$, and a proof $\varLambda _I$. It accepts (i.e., it outputs 1) if and only if C is a commitment to $\varvec{x}$ and $\varvec{x} _I'$ is the I-subvector of $\varvec{x}$.

The definition of correctness is given as follows.

Definition 8

(Correctness). A subvector commitment $\mathsf {SVC}$ over $\mathcal {X}$ is said to be correct if, for any security parameter , random tape , public parameters , $\varvec{x} \in \mathcal {X} ^\ell$, index set $I \in [\ell ]$, $(C, \mathsf {aux}) \in \mathsf {Com}(\varvec{x})$, $\varLambda _I \in \mathsf {Open} (I, \varvec{x} _I, \mathsf {aux})$, there exists such that

The distinguishing property for SVCs is compactness. Loosely speaking it says that the size of the commitment strings C and the proofs $\varLambda _I$ are not only independent of the length of the committed vector $\varvec{x}$, but also that of $\varvec{x} _I$.

Definition 9

(Compactness). A subvector commitment $\mathsf {SVC}$ over $\mathcal {X}$ is compact if there exists a universal polynomial such that for any , random tape , public parameters , vector $\varvec{x} \in \mathcal {X} ^\ell$, index set $I \in [\ell ]$, $(C, \mathsf {aux}) \in \mathsf {Com}(\varvec{x})$, $\varLambda _I \in \mathsf {Open} (I, \varvec{x} _I, \mathsf {aux})$, it holds that and .

We consider the notion of position binding for subvector commitments with public-coin setup. Recall that position binding for vector commitments requires that it is infeasible to open a commitment with respect to some position i to two distinct messages $\varvec{x} _i$ and $\varvec{x} _i'$. We extend this notion to subvector commitments, by requiring that it is infeasible to open a commitment with respect to some index sets I and J to subvectors $\varvec{x} _I$ and $\varvec{x} _J'$, respectively, such that there exists an index $i \in I \cap J$ where $x_i \ne x'_i$. Furthermore, we require this property to hold even if the setup algorithm is public coin.

Definition 10

((Public-Coin) Position Binding). A subvector commitment $\mathsf {SVC}$ over $\mathcal {X}$ is position binding if for any adversary , there exists a negligible function such that

where is not given $\omega$ (highlighted by the dashed box). If the inequality holds even if is given $\omega$, then we say that $\mathsf {SVC}$ is function binding with public coins.

We do not define hiding as it is not needed for our purpose. However, as discussed in [27], one can construct a hiding VC generically by committing to (normal) commitments using VC. This naturally extends to SVC as well.

4.1 Linear Map Commitments

Functional commitments for linear functions, specifically for linear forms $f : \mathbb {F}^\ell \rightarrow \mathbb {F}$ for some field , were introduced by Libert, Ramanna and Yung [48] and is a generalization of vector commitments (VC) introduced by Catalano and Fiore [27]. Here we refine the notion to capture a more general class of function families, which allows the prover to open a commitment to the output of multiple linear forms or, equivalently, to the output of a linear map . Note that any linear map from to can be represented by a matrix .

Definition 11

(Linear Map Commitments (LMC)). A linear map commitment scheme $\mathsf {LMC}$ over consists of the following algorithms :

• Let be positive integers, and be a family of linear maps. The deterministic setup algorithm inputs the security parameter 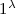, the description of the family $\mathcal {F}$, and a random tape $\omega$. It outputs a public parameter . We assume that all other algorithms input $\mathsf {pp}$ which we omit.

• The committing algorithm inputs a vector . It outputs a commitment string C and some auxiliary information $\mathsf {aux}$.

• The opening algorithm inputs an $f \in \mathcal {F}$, an image , and some auxiliary information $\mathsf {aux}$. It outputs a proof $\varLambda$ that $\varvec{y} = f(\varvec{x})$.

• The verification algorithm inputs a commitment string C, an $f \in \mathcal {F}$, an image $\varvec{y}$, and a proof $\varLambda$. It accepts (i.e., it outputs 1) if and only if C is a commitment to $\varvec{x}$ and $\varvec{y} = f(\varvec{x})$.

In the following we define correctness and compactness for LMCs.

Definition 12

(Correctness). A linear map commitment scheme $\mathsf {LMC}$ over is said to be correct if, for any security parameter and length , random tape , linear map family , public parameters , , linear map $f \in \mathcal {F}$, $(C, \mathsf {aux}) \in \mathsf {Com}(\varvec{x})$, $\varLambda \in \mathsf {Open} (f, f(\varvec{x}), \mathsf {aux})$, there exists such that

Definition 13

(Compactness). A linear map commitment $\mathsf {LMC}$ over is compact if there exists a universal polynomial , such that for any , family of linear maps , random tape , public parameters , vector , linear map $f \in \mathcal {F}$, $(C, \mathsf {aux}) \in \mathsf {Com}(\varvec{x})$, $\varLambda \in \mathsf {Open} (f, f(\varvec{x}), \mathsf {aux})$, it holds that and .

We next generalize the notion of function binding for linear maps. The original definition, as considered by Libert, Ramanna and Yung [48], requires that it is hard to open a commitment to (f, y) and $(f, y')$ where $y \ne y'$. When considering broader classes of functions, such as linear maps where the target space is multidimensional, each opening defines a system of equations. Note that in this case one might be able to generate an inconsistent system with just a single opening, or generate openings to (f, y) and $(f', y')$ with $f \ne f'$ but the systems defined by the tuples are inconsistent. Therefore, our definition explicitly forbids the adversary to generate inconsistent equations.

Definition 14

((Public-Coin) Function Binding). A linear map commitment $\mathsf {LMC}$ over is function binding if for any adversary , positive integers , and family of linear maps , there exists a negligible function such that

where is not given $\omega$ (highlighted by the dashed box). If the inequality holds even if is given $\omega$, then we say that $\mathsf {LMC}$ is function binding with public coins.

As for SVC, we omit the hiding definition as it is not needed for our purpose.

5 Constructions for SVCs

We propose two direct constructions of SVC, one from modules over Euclidean rings where certain variants of the root assumption hold, and one from pairing groups where the CDH assumption holds. Both schemes allow one to commit to binary strings (i.e., we consider the field ). Our constructions are inspired by the work of Catalano and Fiore [27] and extend the opening algorithms of their vector commitment schemes to simultaneously handle multiple positions. These modifications introduce several complications in the security proofs that require a careful manipulation of the exponents.

5.1 SVC from Modules over Euclidean Rings

Our first SVC scheme relies on modules over Euclidean rings where some variants of the root problem (the natural generalization of the RSA problem) is hard. Let be a positive integer. Let $\mathsf {MGen}$ be an efficient module sampling algorithm as defined in Sect. 3 and let R be an Euclidean ring sampled by $\mathsf {MGen}$. Let be a set of prime elements in R of size . Let be a prime-valued function which maps finite bit strings to tuples of $\ell$ distinct elements in . That is, for all string $s \in \{0,1\}^{*}$, if $(e_1,\ldots ,e_\ell ) = H(s)$, then $e_i \ne e_j$ for all $i, j \in [q]$ where $i \ne j$. Let $\mathcal {X}:= \{0_R, 1_R\}$³ where $0_R$ and $1_R$ are the additive and multiplicative identity elements of R respectively. We construct our first subvector commitment scheme in Fig. 1. Note that in the opening algorithm, it is required to compute

$$\begin{aligned} \varLambda _I := \left( \prod _{i \in I} e_i \right) ^{-1} \circ \langle \varvec{x} _{[\ell ] \setminus I}, \varvec{S} _{[\ell ] \setminus I} \rangle . \end{aligned}$$

Fig. 1.

SVC from the root assumption.

Although multiplicative inverses of ring elements do not exist in general, and if so, they may be hard to compute, the above are efficiently computable because, for all $i \in [\ell ] \setminus I$ and hence for all $i \in J \setminus I$, we have

$$\begin{aligned} S_i := \left( \prod _{j \in [\ell ] \setminus \{i\}} e_j \right) \circ X = \left( \prod _{j \in I} e_j \prod _{j \in [\ell ] \setminus (I \cup \{i\})} e_j \right) \circ X. \end{aligned}$$

The correctness of the construction follows straightforwardly by inspection. Depending on the instantiation of H, we can prove our scheme secure against different assumptions:

• H is a (non-cryptographic) hash: Our construction is secure if the strong distinct-prime-product root assumption (introduced in Sect. 3) holds over the module family $\mathcal {R}_{\mathcal {D}}$. This is shown in Theorem 1.

• H is a random oracle: Our construction is secure if the adaptive root problem (introduced in [19]) is hard over the module family. This is shown in Theorem 2.

Theorem 1

If the (resp. public-coin) strong distinct-prime-product root assumption holds over the module family $\mathcal {R}_{\mathcal {D}}$, then the scheme in Fig. 1 is (resp. public-coin) position binding.

Proof

Suppose not, let be a adversary such that

for some polynomial , where gets $\omega$ as input (highlighted by the dashed box) only in the public-coin variant. We construct an algorithm as follows, whose existence contracts the fact that $\mathcal {R}_{\mathcal {D}}$ is a (public-coin) strong distinct-prime-product root modules family.

In the private-coin setting, receives as input $(R_D, A)$ generated by for some . It sets $X := A$, and computes $(e_1, \ldots , e_\ell ) \leftarrow H(R_D, X)$. It then sets $S_i := \left( \textstyle \prod _{j \in [\ell ] \setminus \{i\}} e_j \right) \circ X$ for all $i \in [\ell ]$, $\varvec{S} := (S_1, \ldots , S_q)^T$, and $\varvec{e} := (e_1, \ldots , e_\ell )$. It sets $\mathsf {pp}:= (R_D, X, \varvec{S}, \varvec{e})$ and runs on input . In the public-coin setting, receives additionally $\omega$ and runs on instead. In any case, it is clear that $\mathsf {pp}$ and $\omega$ obtained above distribute identically as

Hence, with probability at least , obtains $(C, I, J, \varvec{x} _I, \varvec{x} '_J, \varLambda _I, \varLambda '_J)$ such that

which implies

$$\begin{aligned} \langle \varvec{x} _{I \setminus J}, \varvec{S} _{I \setminus J} \rangle - \langle \varvec{x} '_{J \setminus I}, \varvec{S} _{J \setminus I} \rangle + \langle \varvec{x} _{I \cap J} - \varvec{x} '_{I \cap J}, \varvec{S} _{I \cap J} \rangle \\ = \left( \prod _{i \in I \cap J} e_i \right) \left( \left( \prod _{i \in J \setminus I} e_i \right) \circ \varLambda '_J - \left( \prod _{i \in I \setminus J} e_i \right) \circ \varLambda _I \right) . \end{aligned}$$

Recall that $S_i = \left( \prod _{j \in [\ell ] \setminus \{i\}} e_j \right) \circ A$. Define $\delta _i := {\left\{ \begin{array}{ll} x_i &{} i \in I \setminus J \\ -x'_i &{} i \in J \setminus I \\ x_i - x'_i &{} i \in I \cap J \end{array}\right. }$ and

$\varLambda := \left( \left( \prod _{i \in J \setminus I} e_i \right) \circ \varLambda '_J - \left( \prod _{i \in I \setminus J} e_i \right) \circ \varLambda _I \right)$. obtains

$$\begin{aligned} \left( \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j \right) \circ A = \left( \prod _{i \in I \cap J} e_i \right) \circ \varLambda . \end{aligned}$$

Let $K_0 := \{i \in I \cap J: \delta _i = 0_R \}$ and $K_1 := \{i \in I \cup J: \delta _i \ne 0_R \}$. Next, we show that $d := \gcd \left( \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j, \prod _{i \in I \cap J} e_i\right) = \prod _{j \in K_0} e_j$. Furthermore, suppose that this is the case, we have $(I \cap J) \setminus K_0 \ne \emptyset$ since there exists $i \in I \cap J$ such that $\delta _i = x_i - x'_i \ne 0_R$. To prove the above, we first note that

$$\begin{aligned} \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j = \sum _{i \in K_1} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j = \prod _{j \in [\ell ] \setminus (I \cup J)} e_j \left( \sum _{i \in K_1} \delta _i \prod _{j \in (I \cup J) \setminus \{i\}} e_j \right) . \end{aligned}$$

Hence

$$\begin{aligned} d&= \gcd \left( \sum _{i \in K_1} \delta _i \prod _{j \in (I \cup J) \setminus \{i\}} e_j, \prod _{i \in I \cap J} e_i\right) \\&= \prod _{j \in K_0} e_j \cdot \gcd \left( \sum _{i \in K_1} \delta _i \prod _{j \in (I \cup J) \setminus (K_0 \cup \{i\})} e_j, \prod _{i \in (I \cap J)\setminus K_0} e_i\right) . \end{aligned}$$

It remains to show that $d' := \gcd \left( \sum _{i \in K_1} \delta _i \prod _{j \in (I \cup J) \setminus (K_0 \cup \{i\})} e_j, \prod _{i \in (I \cap J)\setminus K_0} e_i\right)$ $= 1_R$. Suppose not, let $d' = \prod _{i \in L} e_i$ for some $L \subseteq (I \cap J)\setminus K_0$. Suppose $\ell \in L \ne \emptyset$. This means $\delta _\ell \ne 0_R$ and hence $\ell \in K_1$. Then there exists $r \in R$ such that

$$\begin{aligned} e_{\ell } \cdot r =&\sum _{i \in K_1} \delta _i \prod _{j \in (I \cup J) \setminus (K_0 \cup \{i\})} e_j \\ =\,&\delta _{\ell } \prod _{j \in (I \cup J) \setminus (K_0 \cup \{ \ell \})} e_j + e_{\ell } \sum _{i \in K_1 \setminus \{ \ell \}} \delta _i \prod _{j \in (I \cup J) \setminus (K_0 \cup \{i\})} e_j. \end{aligned}$$

Let $r' := r - \sum _{i \in K_1 \setminus \{ \ell \}} \delta _i \prod _{j \in (I \cup J) \setminus (K_0 \cup \{i\})} e_j$. We have

$$\begin{aligned} e_{\ell } \cdot r' = \delta _{\ell } \prod _{j \in (I \cup J) \setminus (K_0 \cup \{ \ell \})} e_j. \end{aligned}$$

Since $\delta _{\ell } \ne 0_R$, i.e., $\delta _{\ell } \in \{-1_R, 1_R\}$, the above contradicts the fact that $e_{\ell }$ is a prime element. Thus we must have $L = \emptyset$ and hence $d' = 1_R$.

Now that we have concluded $d = \gcd \left( \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j, \prod _{i \in I \cap J} e_i\right) = \prod _{j \in K_0} e_j$, can use the extended Euclidean algorithm to find $a, b \in R$ such that

$$\begin{aligned} a \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j + b \prod _{i \in I \cap J} e_i = \prod _{j \in K_0} e_j. \end{aligned}$$

Multiplying this to A, it gets

$$\begin{aligned} \left( \prod _{j \in K_0} e_j\right) \circ A&= \left( a \sum _{i \in I \cup J} \delta _i \prod _{j \in [\ell ] \setminus \{i\}} e_j + b \prod _{i \in I \cap J} e_i = \prod _{j \in K_0} e_j \right) \circ A \\&= \left( a \prod _{i \in I \cap J} e_i \right) \circ \varLambda + \left( b \prod _{i \in I \cap J} e_i \right) \circ A \\&= \left( \prod _{i \in I \cap J} e_i \right) \left( a \circ \varLambda + b \circ A \right) . \\ \end{aligned}$$

Since $(I \cap J) \setminus K_0 \ne \emptyset$, can set $S := (I \cap J) \setminus K_0$ and $Y := \left( a \circ \varLambda + b \circ A \right)$, and output $(\{e_i\}_{i \in S},Y)$ as a solution to the strong distinct-prime-product root problem.    $\square$

Theorem 2

If the (resp. public-coin) adaptive root assumption holds over the module family $\mathcal {R}_{\mathcal {D}}$ with respect to , then the scheme in Fig. 1 is (resp. public-coin) position binding in the random oracle model.

Due to space constraints, we refer to [47] for a full proof.

Efficiency and Optimizations. Our construction admits two complementary instantiations, discussed in the following.

• Efficient Verifier (assuming random access to public parameters): The vectors $\varvec{S}$ and $\varvec{e}$ are explicitly included in the public parameters (as it is currently described). In this case, and suppose the verifier has random access to each $e_i$ and $S_i$, the computational effort of the verifier is only proportional to |I|, the size of the subvector. The shortcoming of this scheme is that the size of the public parameters is linear in $\ell$, which can be very large depending on the application.

• Short Public Parameters: One can reduce the size of the public parameters to a constant by including only the module description $(R_D, X)$ and letting each algorithm recompute the terms of $\varvec{S}$ needed for the computations. This however increases the computational complexity of the verifier, since the computation needed for each element of $\varvec{S}$ is linear in the vector length $\ell$. This can be partially amortized by observing that the values $(S_1, \ldots , S_\ell )$ do not depend on the committed vector and can be precomputed by both parties.

Another possible tradeoff is given by the assumption that one is willing to rely on: Note that the main workload for the verifier (in the verifier-optimized variant) is to compute the term $\left( \textstyle \prod _{i \in I} e_i \right) \circ \varLambda _I$. Assuming and the term is computed by repeated squaring, the complexity of the computation depends on the bit-length of the primes $e_i$. In the adaptive root assumption, the primes $(e_1, \ldots , e_\ell )$ are sampled randomly from a set of primes of size , therefore representing each prime requires at least bits. On the other hand, under the strong distinct-prime-product root assumption we can set $(e_1, \ldots , e_\ell )$ to be the smallest $\ell$ primes. Since , each prime can be represented by bits. This greatly reduces the computational effort of the verifier.

Fig. 2.

SVC from CDH.

5.2 SVC from the Computational Diffie-Hellman Assumption

Next we present our SVC construction from pairing groups. In favor of a simpler presentation and a more general result we describe our scheme assuming symmetric pairings. However, we stress that the scheme can be easily adapted to work over the more efficient asymmetric (type III) bilinear groups without affecting computational efficiency nor opening size by, e.g., replicating all public parameters in both source groups.

The public parameters consist of a set of random elements $\{G_i = G^{z_i}\}_{i \in [q]}$ and their pairwise “Diffie-Hellman products” $H_{i,i'} = G^{z_i z_{i'}}$ with $i \ne i'$. To commit to a vector $\varvec{x}$ one computes $C := \prod _{i} G_i^{x_i}$. The opening of a subvector $\varvec{x} _I$ is then $\prod _{i\in I} \prod _{i' \notin I} H_{i,i'}^{x_{i'}}$. Note that since $i \in I$ and $i' \notin I$, it is always true that $i \ne i'$. Therefore the product is efficiently computable for an honest prover. Assuming that the verifier has random access to each $G_i$ in the public parameters, it can check the relation by accessing |I| entries in the public parameters, and computing $2\cdot |I|$ group operations and 2 pairings (which are independent of $\ell$). Since the public parameters are highly structured, this scheme does not admit an instantiation with short public parameters, which grow quadratically with the vector size $\ell$.

Let $\mathsf {GGen}$ be an efficient bilinear group sampling algorithm. Let be a group description output by $\mathsf {GGen}$. Let . Our second subvector commitment scheme is shown in Fig. 2. In the following we show that our SVC scheme is position binding with a private-coin setup.

Theorem 3

If the computational Diffie-Hellman (CDH) assumption holds with respect to $\mathsf {GGen}$, then the scheme in Fig. 2 is position binding.

Proof

Suppose not, let be a adversary such that

for some . We construct a square-DH solver , which implies a CDH solver [6], as follows.

receives as input , where and $H = G^z$ for some random , and must output $G^{z^2}$. It picks an index and set $G_{i^*} := H$. Symbolically, let $z_{i^*} := z$, which is not known by . For the other indices $i, i' \in [\ell ] \setminus \{i^*\}$, it samples and sets $G_i := G^{z_i}$ and $H_{i,i'} := G^{z_i z_{i'}}$. It also sets $H_{i^*,i} = H_{i,i^*} = G^{z z_i}$ for each $i \in [\ell ] \setminus \{i^*\}$. It then sets , which is identically distributed as $\mathsf {pp}$ output by $\mathsf {Setup}$. runs on input . With probability at least , it obtains such that , , and $\exists i \in I \cap J \ { s.t.}\ x_i \ne x'_i$. Conditioning on the above, with probability $1/\ell$, it holds that $i^* \in I \cap J$ and $x_{i^*} \ne x'_{i^*}$. By examining the verification equations, we have

$$\begin{aligned} e \left( \prod _{i \in I} G_i^{x_i}, \prod _{i \in I} G_i \right) \cdot e(\varLambda _I, G)&= e \left( \prod _{i \in J} G_i^{x'_i}, \prod _{i \in J} G_i \right) \cdot e(\varLambda _J, G) \\ e \left( \prod _{i \in J} G_i^{x'_i}, \prod _{i \in J} G_i \right) \cdot e \left( \prod _{i \in I} G_i^{-m_i}, \prod _{i \in I} G_i \right)&= e(\varLambda , G),~\text {where}\ \varLambda := \varLambda _I/\varLambda _J \\ \left( \sum _{i \in J} z_i x'_i \right) \left( \sum _{i \in J} z_i\right) - \left( \sum _{i \in I} z_i x_i \right) \left( \sum _{i \in I} z_i\right)&= \log _G \varLambda \\ \alpha z_{i^*}^2 + \beta z_{i^*} + \gamma&= \log _G\varLambda \end{aligned}$$

where

$$\begin{aligned} \alpha := (x'_{i^*} - x_{i^*}) \quad \quad \quad \beta := \sum _{i \in J \setminus \{i^*\}} z_i (x'_i + x'_{i^*}) - \sum _{i \in I \setminus \{i^*\}} z_i (x_i + x_{i^*}) \\ \gamma := \left( \sum _{i \in J\setminus \{i^*\}} z_i x'_i \right) \left( \sum _{i \in J\setminus \{i^*\}} z_i \right) - \left( \sum _{i \in I\setminus \{i^*\}} z_i x_i \right) \left( \sum _{i \in I\setminus \{i^*\}} z_i \right) \end{aligned}$$

are computable by since they do not depend on $z = z_{i^*}$. then outputs $G^{z^2} = \left( \frac{\varLambda }{H^{\beta } G^\gamma } \right) ^{1/\alpha }$ which is the solution to the square-DH instance.    $\square$

Fig. 3.

LMC from bilinear pairings.

6 Construction for LMC

Our LMC construction is inspired by the scheme presented in [48] and it is based upon the following observations. First, when the vectors for some field are encoded as the polynomials $p_{\varvec{f}}(\alpha ) := \sum _{j \in [\ell ]} f_j \alpha ^{\ell +1-j}$ and $p_{\varvec{x}}(\alpha ):=\sum _{j \in [\ell ]} x_j \alpha ^j$ with variable $\alpha$ respectively, their inner product is the coefficient of the monomial $\alpha ^{\ell +1}$ in the polynomial product $p_{\varvec{f}}(\alpha ) p_{\varvec{x}}(\alpha )$. Second, due to linearity of polynomial multiplication, if a matrix is encoded in the polynomial $p_{F}(\alpha ) := \sum _{\begin{array}{c} i \in [q], j \in [\ell ] \end{array}} f_{i,j} z_i\alpha ^{\ell +1-j}$ with variables $(\alpha , z_1, \ldots , z_q)$, then the matrix-vector product $F \varvec{x}$ is given in the coefficients of the monomials $z_i \alpha ^{\ell +1}$ for $i \in [q]$ in the polynomial $p_{F}(\alpha ) p_{\varvec{x}}(\alpha )$.

With the above observations, we give an overview of our construction. We let the commitment C to $\varvec{x}$ be $G^{p_{\varvec{x}}(\alpha )}$, which is computable by combining elements of the form $G^{\alpha ^j}$ given in the public parameters. Given $(F, \varvec{y})$, to verify that $F \varvec{x} = \varvec{y}$, the verifier computes via pairing $e(G^{p_{F}(\alpha ,z_1,\ldots ,z_q)},G^{p_{\varvec{x}}(\alpha )})$, where the left-input is computable by combining elements of the form $G^{z_i \alpha ^j}$ given in the public parameters. If the relation $F \varvec{x} = \varvec{y}$ indeed holds, then the coefficients of $\varvec{y}$ must be encoded as the coefficients of the (lifted) monomials $G^{z_i \alpha ^{\ell +1}}$. To convince the verifier that this is the case, it suffices for the prover to provide the remaining terms of the product polynomial.

Let $\mathsf {GGen}$ be an efficient bilinear group sampling algorithm. Let be a group description output by $\mathsf {GGen}$. Let , , and $\mathcal {F}$ be the set of all linear maps from to . Our LMC for is given in Fig. 3. For full generality we present the construction over symmetric pairings, however one can easily convert it to the more efficient asymmetric pairing groups via standard techniques, without affecting the size of the openings. Although we do not aim to achieve the hiding property, our construction can be easily modified to be hiding, by introducing randomness similar to that in Pedersen commitment [56]. Indeed this is how the FC of [48] achieves hiding. We show that our construction is function binding (in the generic bilinear group model) in the following.

Theorem 4

Let and . The scheme in Fig. 3 is function binding in the generic bilinear group model.

Proof

The proof uses the generic group model abstraction of Shoup [59] and we refer the reader to [18] for a comprehensive introduction to the bilinear group model. Here we state the central lemma useful for proving facts about generic attackers.

Lemma 1

(Schwartz-Zippel). Let $F(X_1, \ldots , X_m)$ be a non-zero polynomial of degree $d \ge 0$ over a field . Then the probability that $F(x_1, \ldots , x_m) = 0$ for randomly chosen values $(x_1, \ldots , x_m)$ in is bounded from above by .

Fix . Suppose there exists an adversary , who only performs generic bilinear group operations, such that there exists a polynomial with

Since is generic, and C and each of $\varLambda _k$ are elements, we can write $\log _G C$ and each $\log _G \varLambda _k$ in the following form:

$$\begin{aligned} \log _G C&= \gamma _0 + \sum _{j \in [\ell ]} \gamma _j \alpha ^j + \sum _{\begin{array}{c} i \in [q] \\ j \in [2\ell ]\setminus \{\ell +1\} \end{array}} \gamma _{i,j} z_i \alpha ^j \\ \log _G \varLambda _k&= \lambda _{k,0} + \sum _{j \in [\ell ]} \lambda _{k,j} \alpha ^j + \sum _{\begin{array}{c} i \in [q] \\ j \in [2\ell ]\setminus \{\ell +1\} \end{array}} \lambda _{k,i,j} z_i \alpha ^j \end{aligned}$$

for some integer coefficients $\gamma _j$, $\gamma _{i,j}$, $\lambda _{k,j}$, and $\lambda _{k,i,j}$ for i, j, and k in the appropriate ranges. Since for each , the following relations hold:

$$\begin{aligned} \left( \log _G C \right) \left( \sum _{i \in [q]} \sum _{j \in [\ell ]} f_{k,i,j} z_i \alpha ^{\ell +1-j}\right)&= \sum _{i \in [q]} y_{k,i} z_i \alpha ^{\ell +1} + \log _G \varLambda _k. \end{aligned}$$

Note that the above defines a $(n+1)$-variate polynomial of degree $3\ell +2$ which evaluates to zero at a random point $(\alpha , z_1,\ldots ,z_q)$. Suppose that the polynomial is non-zero. By the Schwartz-Zippel lemma, the probability that the above happens is bounded by $\frac{3\ell +2}{p}$ which is negligible as and . We can therefore assume that the polynomial is always zero. In particular, the coefficients of the monomials $z_i \alpha ^{\ell +1}$ are zero for all $i \in [q]$. Thus, we have the following relations for all $k \in [Q]$ and $i \in [q]$:

$$\begin{aligned} \sum _{j \in [\ell ]} f_{k,i,j} \gamma _j = y_{k,i}. \end{aligned}$$

In other words, there exists such that $F_k(\varvec{x}) = \varvec{y} _k$, for all $k \in [Q]$, which contradicts the assumption about . We thus conclude that such adversaries exist only with negligible probability. Since the above holds for any , we conclude that the construction is function binding.    $\square$

Fig. 4.

Succinct argument of knowledge for NP from SVC/LMC

7 Succinct Arguments of Knowledge from SVC/LMC

We present our compiler for constructing interactive arguments of knowledge either from traditional PCPs and subvector commitments (Sect. 5), or from linear PCPs [42] and linear map commitments (Sect. 6). The constructions for both cases are in fact identical and we present only the latter since it is strictly more general (an traditional PCP can be seen as a linear PCP where queries are restricted to unit vectors).

Let be an $\ell$-long q-query (linear) $\text {PCP}$ over some field for NP with r being the length of the random coins of the possibly adaptive verifier. Let be a pseudo-random generator and let be a linear map commitment for the set of all linear maps $\mathcal {F}$ from to , possibly with public-coin setup. We present a 4-move interactive argument of knowledge in Fig. 4.

7.1 Protocol Description

We first describe some subroutines to be used in the protocol. We construct polynomial time algorithms $\mathsf {Record}$, $\mathsf {Reconstruct}$, and $\mathsf {Decide}$ which perform the following:

• $\mathsf {Record}$: On input a statement x, a proof $\varvec{\pi }$, a randomness $\rho$, it runs and records the queries made by . It outputs a query matrix .

• $\mathsf {Reconstruct}$: On input a statement x, a response vector , and a randomness $\rho$, it runs by simulating the oracle $\varvec{\pi }$ using the response vector $\varvec{y}$. That is, when makes the i-th query $\varvec{f} _i$ for $i \in [q]$, it responds by returning the value $y_i$. It outputs a query matrix .

• $\mathsf {Decide}$: On input a statement x, a response vector , it runs by simulating the oracle $\varvec{\pi }$ as in $\mathsf {Reconstruct}$, and outputs whatever outputs.

It is clear that for any strings x and $\varvec{\pi }$ and randomness $\rho$, if $\varvec{y}$ is formed in such a way that $y_i$ is the response to the i-th query made by , then $\mathsf {Record}(x,\varvec{\pi }, \rho ) = \mathsf {Reconstruct}(x, \varvec{y}, \rho )$, and .

We now describe the protocol. The setup algorithm samples a random string $\omega$ and computes the public parameters $\mathsf {pp}$ of $\mathsf {LMC}$ using $\omega$. It outputs $\mathsf {pp}$ if an LMC with private-coin setup is used, which results in an argument system with private-coin setup. Alternatively, if an LMC with public-coin setup is used, it outputs additionally $\omega$ (as highlighted in the dashed box). This results in a public-coin setup.

In the rest of the protocol, the verifier is entirely public-coin. On input the public parameter $\mathsf {pp}$, the statement x and the witness w, the prover produces $\varvec{\pi }$ as the $\text {PCP}$ encoding of the witness w, then it commits to $\varvec{\pi }$ and sends its commitment C to the verifier . Upon receiving the commitment C, responds with a random string $\alpha$. The prover stretches $\alpha$ with a into $\rho$ and executes on $\rho$. Here the is used to compress the (possibly large) randomness of the verifier, which is strictly needed only for linear PCPs (standard PCPs typically have low randomness complexity and therefore the random coins can be sent in plain).

The prover then records the sets of queries $F = \mathsf {Record}(x, \varvec{\pi }, \rho )$ of using randomness $\rho$ to $\varvec{\pi }$, and computes the responses $\varvec{y} = F \varvec{\pi }$. Next, it computes the opening $\varLambda$ of the commitment C to the tuple $(F, \varvec{y})$. The opening $\varLambda$ along with the response $\varvec{y}$ are sent to the verifier . The verifier runs $\mathsf {Reconstruct}(x, \varvec{y}, \rho )$ to reconstruct the query matrix F. It then checks if $\varLambda$ is a valid opening of C to $(F, \varvec{y})$. Finally, it checks if $\mathsf {Decide}(x,\varvec{y},\rho )$ returns 1. If all checks are passed, it outputs 1. Otherwise, it outputs 0.

7.2 Analysis

Clearly, if is a complete linear PCP, and $\mathsf {LMC}$ is a correct LMC, then the argument system is complete. Alternatively, if is a complete (traditional) PCP, and $\mathsf {LMC}$ is a correct SVC, then the system is also complete. The succinctness of the system follows directly from the compactness of $\mathsf {LMC}$. Next, we show that the argument system is of knowledge by the following theorem. Due to space constraints, we refer to [47] for a full proof.

Theorem 5

Let be a $2^{-\sigma }$-sound linear $\text {PCP}$ of knowledge for NP, be a pseudo-random generator, and be (resp. public-coin) function binding. Then the protocol in Fig. 4 is a $2^{-\sigma }$-sound (resp. public-coin) argument of knowledge.

7.3 Instantiations and Efficiency

Since our argument system has a public-coin verifier, we can apply the Fiat-Shamir transformation to turn it into a non-interactive argument and sometimes a SNARK.⁴ We highlight some interesting instantiations of our compiler: Regardless of the specific root assumption used, we can instantiate our first SVC construction over $Cl(\varDelta )$, the class group of an imaginary quadratic order with discriminant $\varDelta$. Considering the current best attacks, we can assume that root problems for a -bit $\varDelta$ are hard for a -time adversary. Concretely, with a 2560-bit $\varDelta$, which roughly offers security against a $2^{128}$-time adversary, each element in $Cl(\varDelta )$ can be represented by at most 2560 bits (see Sect. 8 for more details). Using a 240-query $2^{-80}$-sound PCP, the resulting proof size is $2 \cdot 2560 + 240 = 5360$ bits. When using the verifier-optimized SVC (see Sect. 5.1) the workload of the verifier is dominated by 240 exponentiations, regardless of the witness size. However the public parameters grow linearly with the length of the PCP encoding. One can reduce the size of the public parameters to constant at the cost of having an inefficient verifier. We stress that class groups of imaginary quadratic orders have a public-coin setup and so does the resulting SNARK.

Alternatively, we can use our second SVC construction over the pairing-friendly 256-bit Barreto-Naehrig curve [7], which roughly offers security against $2^{128}$-time adversaries. In such a curve, each group element can be represented by 256 bits. Therefore the resulting proof size is $2 \cdot 256 + 240 = 752$ bits. This marginally improves over the shortest proofs known [40]. A shortcoming of this approach is that the public parameters of the resulting SNARK grow quadratically in the length of the PCP proof.

An unsatisfactory aspect of the instantiations above is that PCPs with such short queries have typically a very high prover complexity and are therefore very expensive to compute, which means that our arguments described above have a high prover complexity. One approach to address this issue is to leverage the large body of work on linear PCPs [17, 42], which significantly improve the complexity of the prover. Any of these schemes can be used in combination with an LMC (such as the construction of Sect. 6) to obtain a non-interactive argument with slightly larger proofs (by a constant factor) but with a more efficient prover. We stress that our compiler supports any linear PCP, whereas existing compilers only support those with a verifier who only evaluates quadratic polynomials. Moreover, although our pairing-based instantiations inherit the private-coin setup from underlying SVC/LMC, the setup is statement-independent. In contrast, the setup in existing pairing-based schemes such as [40] depends on the statement to be proven. We shall mention however that our LMC has a linear verifier complexity and therefore it yields an argument with verifier computation linear in the length of the PCP.

For the efficiency of the verifier, there are several techniques to reduce its computational overhead: As an example, one could compose our scheme with a verifier-optimized SNARK to prove the validity of the verification equation, instead of having the verifier computing it. Very recently, Boneh et al. [20] presented a special-purpose proof of knowledge of co-prime roots (PoKCR) that drastically reduces the running time of the verifier in class group-based SVCs (see Sect. 5) by trading group operations for modular multiplications and additions, which are orders of magnitude more efficient. We refer the reader to [20] for a detailed analysis of the concrete costs.

8 Candidate Module Families

In the following we suggest some candidate instantiations for modules (specifically groups) where the strong distinct-prime-root assumption and/or the adaptive root assumption are believed to hold.

8.1 Class Groups of Imaginary Quadratic Orders

The use of class groups in cryptography was first proposed by Buchmann and Williams [25]. We refer to, e.g., [23, 24], for more detailed discussions. We recall the basic properties of class groups necessary for our purpose. Let $\varDelta$ be a negative integer such that $\varDelta \equiv 0$ or $1 \pmod 4$. The ring is called an imaginary quadratic order of discriminant $\varDelta$. Its field of fractions is . The discriminant is fundamental if $\varDelta /4$ (resp. $\varDelta$) is square-free in the case of $\varDelta \equiv 0 \pmod 4$ (resp. $\varDelta \equiv 1 \pmod 4$). If $\varDelta$ is fundamental, then $\mathcal {O}_\varDelta$ is a maximal order. The fractional ideals of $\mathcal {O}_\varDelta$ are of the form with , and , subject to the constraint that there exists such that $\varDelta = b^2 - 4ac$ and $\gcd (a,b,c) = 1$. A fractional ideal can therefore be represented by a tuple (q, a, b). If $q = 1$, then the ideal is called integral and can be represented by a tuple (a, b). An integral ideal (a, b) is reduced if it satisfies $-a < b \le a \le c$ and $b > 0$ if $a = c$. It is known that if an ideal (a, b) is reduced, then $a \le \sqrt{|\varDelta |/3}$. Two ideals $\mathfrak {a}, \mathfrak {b} \subseteq \mathcal {O}_\varDelta$ are equivalent if there exists such that $\mathfrak {b} = \alpha \mathfrak {a}$. It is known that, for each equivalence class of ideals, there exists exactly one reduced ideal which serves as the representative of the equivalence class. The set of equivalence classes of ideals equipped with ideal multiplication forms an Abelian group $Cl(\varDelta )$ known as a class group.

Properties Useful in Cryptography. Since for all reduced ideals, $|b| \le a \le \sqrt{|\varDelta |/3}$, $Cl(\varDelta )$ is finite. For sufficiently large $|\varDelta |$, no efficient algorithm is known for finding the cardinality of $Cl(\varDelta )$, also known as the class number. Group operations can be performed efficiently, as there exist efficient algorithms for ideal multiplication and computing reduced ideals [23]. Assuming the extended Riemann hypothesis, $Cl(\varDelta )$ is generated by the classes of all invertible prime ideals of norm smaller than $12(\log |\varDelta |)^2$ [4], where the norm of a fractional ideal (q, a, b) is defined as $q^2a$ ($=a$ for integral ideals). Since these ideals have norms logarithmic in $|\varDelta |$, they can be found in polynomial time through exhaustive search. A random element can then be sampled by computing a power product of the elements in the generating set, with exponents randomly chosen from $[|\varDelta |]$.

(Strong) Root Problem and its Variants in $\varvec{Cl}(\varvec{\varDelta })$. To recall, the strong root problem in $Cl(\varDelta )$ is to find a prime and a group element $Y \in Cl(\varDelta )$ such that $Y^e = X$, for some given element $X \in Cl(\varDelta )$. It is widely believed that root problems in $Cl(\varDelta )$ for a large enough $\varDelta$ are hard if the problem instances are sampled randomly with private coin [25]. Although the strong root problem in $Cl(\varDelta )$ is not as well studied, it is shown to be hard for generic group algorithms [31]. The best attacks currently known are the ones for the root problem which runs in time proportional to $L_{|\varDelta |}(\frac{1}{2},1)$ [41], where $L_{x}(d,c) := \exp (c (\log x)^d (\log \log x)^{1-d})$. As discussed in [41], using a 2560-bit $\varDelta$ offers approximately 128 bits of computational security.

The (resp. public-coin setup) position binding property of our first construction of SVC can be proven under either the (resp. public-coin setup) strong distinct-prime-product root assumption or the (resp. public-coin setup) adaptive root assumption. Note that these two assumptions are somewhat “dual” to each other, in the sense that the former allows the adversary to choose which root it is going to compute, while the latter allows the adversary to choose the element whose root is to be found.

In the private-coin setup setting, it is clear that the strong distinct-prime-product root assumption is implied by the standard strong root assumption. In the public-coin setup setting, it is conjectured [19, 63] that the adaptive root assumption holds in $Cl(\varDelta )$. In the following, we first propose a simple candidate sampling algorithm $\mathsf {MGen}$ for sampling $Cl(\varDelta )$ and random elements in $Cl(\varDelta )$ with public coin, and then elaborate more about the strong distinct-prime-product root assumption with respect to $\mathsf {MGen}$.

The sampling algorithm $\mathsf {MGen}$ first samples random integers of the appropriate length until it finds a fundamental discriminant $\varDelta$. Let $\{G_1,\ldots ,G_k\}$ be a generating set of $Cl(\varDelta )$. Our sampling algorithm samples random primes $c_1, \ldots , c_k \in [|\varDelta |]$ subject to the constraint that the $c_i$’s are pairwise coprime⁵. That is $\gcd (c_i,c_j) = 1$ for all $i, j \in [k]$ with $i \ne j$. The algorithm then outputs $\varDelta$ along with $A = \prod _{i \in [k]} G_i^{c_i}$.

With the above restriction in place, it seems that the best strategy of finding an e-th root of A is to find an e-th root of $G_i$ for all $i \in [k]$ simultaneously. On the other hand, the additional constraint seems necessary for the strong distinct-prime-product root problem with respect to A to be hard. Suppose that (1) there exists a subset $I = \{c_{i_1}, \ldots , c_{i_\ell }\} \subseteq [k]$ such that $\gcd (c_{i_1}, \ldots , c_{i_\ell }) = d \ne 1$; (2) d can be efficiently factorized into $\{e_i\}_{i \in S}$ such that $d = \prod _{i \in S} e_i$ for distinct primes $e_i \ne 1$; and (3) for all $j \in [k] \setminus I$, $G_j$ can be efficiently represented as a product $G_j = \prod _{i \in I} G_i^{a_{i,j}}$ for some $a_{i,j}$. Then one can efficiently find a d-th root of A, say Y, and output $(\{e_i\}_{i \in S}, Y)$ as a solution to the strong distinct-prime-product root problem. Since it seems unreasonable to assume that d cannot be efficiently factorized into a product of distinct primes (see also the discussion of RSA-UFO below), nor is it sound to assume that none of the $G_j$ can be represented with a power product of the $G_i$’s where $i \ne j$, we impose the more reasonable restriction that the $c_i$’s are pairwise coprime.

8.2 RSA Groups

RSA-based cryptosystems operate over , the group of positive integers smaller and coprime with N, equipped with modular multiplication, where N is an integer with at least two distinct large prime factors. The security of these systems relies on the hardness of the (strong) root problem over , known as the (strong) RSA assumption. Typically, N is chosen as a product of two secret distinct large primes p, q. However, the (strong) root problem over is easy if p and q are known. In other words, for N generated this way, the (strong) root assumption with public-coin setup does not hold over .

RSA-UFOs. The problem of constructing RSA-based accumulators without trapdoors was considered by Sander [58], who proposed a way to generate $(k,\epsilon )$-“generalized RSA moduli of unknown complete factionization (RSA-UFOs)” N which has at least two distinct k-bit prime factors with probability $1 - \epsilon$, summarized as follows. Let $N_1,\ldots ,N_r$ be random 3k-bit integers with $r = O(\log 1/\epsilon )$. It is known that with constant probability $N_i$ has at least two distinct k-bit prime factors [58]. It then follows that $N := \prod _{i \in [r]} N_i$ has at least two distinct k-bit prime factors. An important observation is that N can be generated with public coin, e.g., using a random oracle. However, since N is a 3kr-bit integer, any cryptosystem based on seems impractical. Nevertheless, one can show that strong RSA over RSA-UFO groups is implied by the standard strong RSA assumption in the presence of a random oracle. This result is implicitly shown by Sander [58] and a proof sketch is given in [47].