Abstract
In this article we first review some by-now classical results about the geometry of ℓ p-balls \(\mathbb {B}_p^n\) in \(\mathbb {R}^n\) and provide modern probabilistic arguments for them. We also present some more recent developments including a central limit theorem and a large deviations principle for the q-norm of a random point in \(\mathbb {B}_p^n\). We discuss their relation to the classical results and give hints to various extensions that are available in the existing literature.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Asymptotic geometric analysis
- \(\ell _p^n\text{-Balls}\)
- Central limit theorem
- Law of large numbers
- Large deviations
- Polar integration formula
2010 Mathematics Subject Classification
9.1 Introduction
The geometry of the classical ℓ p sequence spaces and their finite-dimensional versions is nowadays quite well understood. It has turned out that it is often a probabilistic point of view that shed (new) light on various geometric aspects and characteristics of these spaces and, in particular, their unit balls. In this survey we want to take a fresh look at some of the classical results and also on some more recent developments. The probabilistic approach to study the geometry of \(\ell _p^n\)-balls will be an asymptotic one. In particular, our aim is to demonstrate the usage of various limit theorems from probability theory, such as laws of large numbers, central limit theorems or large deviation principles. While the law of large numbers and the central limit theorem are already part of the—by now—classical theory (see, e.g., [21, 23, 24]), the latter approach via large deviation principles was introduced only recently in the theory of asymptotic geometric analysis by Gantert et al. in [9]. Most of the results we present below are not new and we shall always give precise references to the original papers. On the other hand, we provide detailed arguments at those places where we present generalizations of existing results that cannot be found somewhere else. For some of the other results the arguments are occasionally sketched as well.
Our text is structured as follows. In Sect. 9.2 we collect some preliminary material. In particular, we introduce our notation (Sect. 9.2.1), the class of \(\ell _p^n\)-balls (Sect. 9.2.2), and also rephrase some background material on Grassmannian manifolds (Sect. 9.2.3) and large deviation theory (Sect. 9.2.4). In Sect. 9.3 we introduce a number of probability measures that can be considered in connection with a convex body. We do this for the case of \(\ell _p^n\)-balls (Sect. 9.3.1), but also more generally for symmetric convex bodies (Sect. 9.3.2). The usage of the central limit theorem and the law of large numbers in the context of \(\ell _p^n\)-balls is demonstrated in Sect. 9.4. We rephrase there some more classical results of Schechtman and Schmuckenschläger (Sect. 9.4.1) and also consider some more recent developments (Sect. 9.4.2) including applications of the multivariate central limit theorem. We also take there an outlook to the matrix-valued set-up. The final Sect. 9.5 is concerned with various aspects of large deviations. We start with the classical concentration inequalities of Schechtman and Zinn (Sect. 9.5.1) and then describe large deviation principles for random projections of \(\ell _p^n\)-balls (Sect. 9.5.2).
9.2 Preliminaries
In this section we shall provide the basics from both asymptotic geometric analysis and probability theory that are used throughout this survey article. The reader may also consult [3, 5,6,7, 14] for detailed expositions and additional explanations when necessary.
9.2.1 Notation
We shall denote with \(\mathbb {N}=\{1,2,\ldots \} \), \(\mathbb {R}\) and \(\mathbb {R}^+ \) the set of natural, real and real non-negative numbers, respectively. Given \(n\in \mathbb {N} \), let \(\mathbb {R}^n\) be the n-dimensional vector space on the real numbers, equipped with the standard inner product denoted by 〈⋅ , ⋅〉. We write \(\mathcal {B}(\mathbb {R}^n) \) for the σ-field of all Borel subsets of \(\mathbb {R}^n \). Analogously, for a subset \(S\subseteq \mathbb {R}^n\), we denote by \(\mathcal {B}(S)\mathrel{\mathop:}= \{A\cap S:A\in \mathcal {B}(\mathbb {R}^n)\}\) the corresponding trace σ-field of \(\mathcal {B}(\mathbb {R}^n)\). Given a set A, we write #A for its cardinality. For a set \(A\subseteq \mathbb {R}^n\), we shall write \(\boldsymbol {1}_A\colon \mathbb {R}^n\to \{0,1\} \) for the indicator function of A. Given \(A\in \mathcal {B}(\mathbb {R}^n)\), we write  for its n-dimensional Lebesgue measure and frequently refer to this as the volume of A.
for its n-dimensional Lebesgue measure and frequently refer to this as the volume of A.
Given sets \(I\subseteq \mathbb {R}^+\) and \(A\subseteq \mathbb {R}^n\), we define the set IA as follows,
If I = {r}, we also write rA instead of {r}A. Note that \(\mathbb {R}^+ A\) is usually called the cone spanned by A.
We say that \(K\subseteq \mathbb {R}^n\) is a convex body if it is a convex, compact set with non-empty interior. We indicate with ∂K its boundary.
Fix now a probability space \((\Omega ,\mathcal {F},\mathbf {P}) \). We will always assume that our random variables live in this probability space. Given a random variable \(X\colon \Omega \to \mathbb {R}^n\) and a probability measure Q on \(\mathbb {R}^n\), we write X ∼ Q to indicate that Q is the probability distribution of X, namely, for any \(A\in \mathcal {B}(\mathbb {R}^n)\),
We write \( \operatorname {\mathrm {\mathbf {E}}} \) and \( \operatorname {\mathrm {\mathbf {Var}}} \) to denote the expectation and the variance with respect to the probability P, respectively.
Given a sequence of random variables \((X_n)_{n\in \mathbb {N}}\) and a random variable Y we write

to indicate that \((X_n)_{n\in \mathbb {N}}\) converges to Y in distribution, probability or almost surely, respectively, as n →∞.
We write \(N\sim \mathcal {N}(0,\Sigma )\) and say that N is a centred Gaussian random vector in \(\mathbb {R}^n\) with covariance matrix Σ, i.e., its density function w.r.t. the Lebesgue measure is given by
For α, θ > 0, we write X ∼ Γ(α, 𝜗) (resp. X ∼ β(α, 𝜗)) and say that X has a Gamma distribution (resp. a Beta distribution) with parameters α and 𝜗 if the probability density function of X w.r.t. to the Lebesgue measure is proportional to x↦x α−1e −𝜗x1 [0,∞)(x) (resp. x↦x α−1(1 − x)𝜗−11 [0,1](x)). We also say that X has a uniform distribution on [0, 1] if X ∼Unif([0, 1]): = β(1, 1) or an exponential distribution with parameter 1 if \(X\sim \exp (\vartheta )\mathrel{\mathop:}= \Gamma (1,\vartheta )\).
The following properties of the aforementioned distributions are of interest and easy to verify by direct computation:
for any \(\alpha ,\tilde \alpha ,\vartheta ,k\in (0,\infty ) \).
Given a real sequence \((a_n)_{n\in \mathbb {N}}\), we write a
n ≡ a if a
n = a for every \(n\in \mathbb {N}\). If \((b_n)_{n\in \mathbb {N}}\) is a positive sequence, we write \(a_n=\mathcal {O}(b_n)\) if there exists C ∈ (0, ∞) such that  for every \(n\in \mathbb {N}\), and a
n = o(b
n) if limn→∞(a
n∕b
n) = 0.
for every \(n\in \mathbb {N}\), and a
n = o(b
n) if limn→∞(a
n∕b
n) = 0.
9.2.2 The \(\ell _p^n\)-Balls
For \(n\in \mathbb {N}\), let \(x=(x_1,\ldots ,x_n)\in \mathbb {R}^n\) and define the p-norm of x via

The unit ball \(\mathbb {B}_p^n\) and sphere \(\mathbb {S}_p^{n-1}\) with respect to this norm are defined as

As usual, we shall write \(\ell _p^n\) for the Banach space  . The exact value of
. The exact value of  is known since Dirichlet [8] and is given by
is known since Dirichlet [8] and is given by

The interested reader may consult [19] for a modern computation. The volume-normalized ball shall be denoted by \(\mathbb D_p^n\) and is given by

For convenience, in what follows we will use the convention that in the case p = ∞, 1∕p: = 0. It is worth noticing that the restriction on the domain of p is due to the fact that an analogous definition of  for p < 1 does only result in a quasi-norm, meaning that the triangle inequality does not hold. As a consequence, \(\mathbb {B}_p^n\) is convex if and only if p ≥ 1. Although a priori many arguments of this survey do not rely on
for p < 1 does only result in a quasi-norm, meaning that the triangle inequality does not hold. As a consequence, \(\mathbb {B}_p^n\) is convex if and only if p ≥ 1. Although a priori many arguments of this survey do not rely on  being a norm, we restrict our presentation to the case p ≥ 1, since it is necessary in some of the theorems.
being a norm, we restrict our presentation to the case p ≥ 1, since it is necessary in some of the theorems.
9.2.3 Grassmannian Manifolds
The group of (n × n)-orthogonal matrices is denoted by \(\mathbb O(n)\) and we let \(\mathbb {S}\mathbb {O}(n)\) be the subgroup of orthogonal n × n matrices with determinant 1. As subsets of \(\mathbb {R}^{n^2}\), \(\mathbb {O}(n)\) and \(\mathbb {S}\mathbb {O}(n)\) can be equipped with the trace σ-field of \(\mathcal {B}(\mathbb {R}^{n^2})\). Moreover, both compact groups \(\mathbb O(n)\) and \(\mathbb {S}\mathbb {O}(n)\) carry a unique Haar probability measure which we denote by η and \(\tilde {\eta }\), respectively. Since \(\mathbb {O}(n)\) consists of two copies of \(\mathbb {S}\mathbb {O}(n)\), the measure η can easily be derived from \(\tilde {\eta }\) and vice versa. Given k ∈{0, 1, …, n}, we use the symbol \(\mathbb {G}^n_k\) to denote the Grassmannian of k-dimensional linear subspaces of \(\mathbb {R}^n\). We supply \(\mathbb {G}_{k}^n\) with the metric

where B E and B F stand for the Euclidean unit balls in E and F, respectively. The Borel σ-field on \(\mathbb {G}_k^n\) induced by this metric is denoted by \(\mathcal {B}(\mathbb {G}_k^{n})\) and we supply the arising measurable space \(\mathbb {G}_k^n\) with the unique Haar probability measure \(\eta _k^n\). It can be identified with the image measure of the Haar probability measure \(\tilde {\eta }\) on \(\mathbb {S}\mathbb {O}(n)\) under the mapping \(\mathbb {S}\mathbb {O}(n)\to \mathbb {G}_k^n,\, T\mapsto TE_0\) with E 0: = span({e 1, …, e k}). Here, we write \(e_1\mathrel{\mathop:}= (1,0,\ldots ,0),e_2\mathrel{\mathop:}= (0,1,0,\ldots ,0),\ldots ,e_n\mathrel{\mathop:}= (0,\ldots ,0,1)\in \mathbb {R}^n\) for the standard orthonormal basis in \(\mathbb {R}^n\) and \(\mathrm {span}(\{e_1,\ldots ,e_k\})\in \mathbb {G}_k^n\), k ∈{1, …, n}, for the k-dimensional linear subspace spanned by the first k vectors of this basis.
9.2.4 Large Deviation Principles
Consider a sequence \((X_n)_{n\in \mathbb {N}}\) of i.i.d. integrable real random variables and let
be the empirical average of the first n random variables of the sequence. It is well known that the law of large numbers provides the asymptotic behaviour of S n, as n tends to infinity. In particular, the strong law of large numbers says that

If X 1 has also positive and finite variance, then the classical central limit theorem states that the fluctuations of S n around \( \operatorname {\mathrm {\mathbf {E}}}[X_1]\) are normal and of scale \(1/\sqrt {n}\). More precisely,

One of the important features of the central limit theorem is its universality, i.e., that the limiting distribution is normal independently of the precise distribution of the summands X 1, X 2, …. This allows to have a good estimate for probabilities of the kind
when n is large, but fixed. However, such estimate can be quite imprecise if x is much larger than \( \operatorname {\mathrm {\mathbf {E}}}[X_1]\). Moreover, it does not provide any rate of convergence for such tail probabilities as n tends to infinity for fixed x.
In typical situations, if S n arises as a sum of n independent random variables X 1, …, X n with finite exponential moments, say, one has that
if n →∞, where \(\mathcal {I}\) is the so-called rate function. Here ≈ expresses an asymptotic equivalence up to sub-exponential functions of n. For concreteness, let us consider two examples. If P(X 1 = 1) = P(X 1 = 0) = 1∕2, then
which describes the upper large deviations. If on the other hand \(X_1\sim \mathcal N(0,\sigma ^2)\), then the rate function is given by
Contrarily to the universality shown in the central limit theorem, these two examples already underline that the function \(\mathcal {I}\) and thus the decay of the tail probabilities is much more sensitive and specific to the distribution of X 1.
The study of the atypical situations (in contrast to the typical ones described in the laws of large numbers and the central limit theorem) is called Large Deviations Theory. The concept expressed heuristically in the examples above can be made formal in the following way. Let \(\mathbf {X}\mathrel{\mathop:}= (X_n)_{n\in \mathbb {N}}\) be a sequence of random vectors taking values in \(\mathbb {R}^d\). Further, let \(s\colon \mathbb {N}\to [0,\infty ]\) be a non-negative sequence such that s(n) ↑∞ and assume that \(\mathcal {I}\colon \mathbb {R}^d\to [0,\infty ]\) is a lower semi-continuous function, i.e., all of its lower level sets \(\{x\in \mathbb {R}^d:\mathcal {I}(x) \leq \ell \}\), ℓ ∈ [0, ∞], are closed. We say that X satisfies a large deviation principle (or simply LDP) with speed s(n) and rate function \(\mathcal {I}\) if and only if
for all \(A\in \mathcal {B}(\mathbb {R}^d)\). Moreover, \(\mathcal {I}\) is said to be a good rate function if all of its lower level sets are compact. The latter property is essential to guarantee the so-called exponential tightness of the sequence of measures.
The following result, known as Cramér’s Theorem, guarantees an LDP for the empirical average of a sequence of i.i.d. random vectors, provided that their common distribution is sufficiently nice (see, e.g. [14, Theorem 27.5]).
Theorem 9.2.1 (Cramér’s Theorem)
Let \((X_n)_{n\in \mathbb {N}}\) be a sequence of i.i.d. random vectors in \(\mathbb {R}^d\) such that the cumulant generating function of X 1 ,
is finite in a neighbourhood of \(0\in \mathbb {R}^d\) . Let \(\mathbf {S}\mathrel{\mathop:}= (\frac {1}{n}\sum _{i=1}^n X_i)_{n\in \mathbb {N}}\) be the sequence of the sample means. Then S satisfies an LDP with speed n and good rate function \(\mathcal {I}=\Lambda ^*\) , where
is the Fenchel-Legendre transform of Λ.
Cramér’s Theorem is a fundamental tool that allows to prove an LDP if the random variables of interest can be transformed into a sum of independent random variables.
Sometimes there is the need to ‘transport’ a large deviation principle from one space to another by means of a continuous function. This can be done with a device known as the contraction principle and we refer to [6, Theorem 4.2.1] or [14, Theorem 27.11(i)].
Proposition 9.2.2 (Contraction Principle)
Let \(d_1,d_2\in \mathbb {N}\) and let \(F:\mathbb {R}^{d_1}\to \mathbb {R}^{d_2}\) be a continuous function. Further, let \(\mathbf {X}\mathrel{\mathop:}= (X_n)_{n\in \mathbb {N}}\) be a sequence of \(\mathbb {R}^{d_1}\mathit{\text{-valued}}\) random vectors that satisfies an LDP with speed s(n) and rate function \(\mathcal {I}_{\mathbf {X}}\). Then the sequence \(\mathbf {Y}\mathrel{\mathop:}= (F(X_n))_{n\in \mathbb {N}}\) of \(\mathbb {R}^{d_2}\mathit{\text{-valued}}\) random vectors satisfies an LDP with the same speed and with good rate function \(\mathcal {I}_{\mathbf {Y}}=\mathcal {I}_{\mathbf {X}}\circ F^{-1}\), i.e., \(\mathcal {I}_{\mathbf {Y}}(y)\mathrel{\mathop:}= \inf \{\mathcal {I}_{\mathbf {X}}(x):F(x)=y\}\) , \(y\in \mathbb {R}^{d_2}\), with the convention that \(\mathcal {I}_{\mathbf {Y}}(y)=+\infty \) if F −1({y}) = ∅.
While this form of the contraction principle is sufficient to analyse the large deviation behavior for one-dimensional random projections of \(\ell _p^n\)-balls, a refinement to treat the higher-dimensional cases is needed. To handle this situation, the classical contraction principle can be extended to allow a dependency on n of the continuous function F. We refer the interested reader to [6, Corollary 4.2.21] for the precise statement.
9.3 Probability Measures on Convex Bodies
There is a variety of probability measures that can be defined on the family of \(\ell _p^n\)-balls or spheres. We shall present some of them and their key properties below.
9.3.1 Probability Measures on an \(\ell _p^n\,\text{-Ball}\)
One can endow \(\mathbb {B}_p^n\) with a natural volume probability measure. This is defined as follows,

for any \(A\in \mathcal {B}(\mathbb {R}^n)\). We also refer to \(\nu _p^n\) as the uniform distribution on \(\mathbb {B}_p^n \).
As far as \(\mathbb {S}_p^{n-1}\) is concerned, there are two probability measures that are of particular interest. The first is the so-called surface measure, which we denote by \(\sigma _p^n\), and which is defined as the normalised (n − 1)-dimensional Hausdorff measure. The second, \(\mu _p^n\), is the so-called cone (probability) measure and is defined via

In other words, \(\mu _p^n(A)\) is the normalised volume of the cone that intersects \(\mathbb {S}_p^{n-1} \) in A, intersected with \(\mathbb {B}_p^n \). The cone measure is known to be the unique measure that satisfies the following polar integration formula for any integrable function f on \(\mathbb {R}^n\) (see, e.g., [18, Proposition 1])

In particular, whenever f is p-radial, i.e., there exists a function g defined on \(\mathbb {R}^+\) such that  , then
, then

The relation between \(\sigma _p^n\) and \(\mu _p^n\) has been deeply investigated. It is known, for example, that they coincide whenever p ∈{1, 2, ∞} (see, e.g., [20]). In the other cases, Naor [17] provided a bound on the total variation distance of these two measures.
Proposition 9.3.1
Let \(\sigma _p^n\) and \(\mu _p^n\) be the surface probability and cone probability measure on \(\mathbb {S}_p^{n-1} \) , respectively. Then

where C ∈ (0, ∞) is an absolute constant.
In particular, the above proposition ensures that for p fixed, such a distance decreases to 0 not slower than n −1∕2.
An important feature of the cone measure is described by the following probabilistic representation, due to Schechtman and Zinn [22] (independently discovered by Rachev and Rüschendorf [20]). We will below present a proof in a more general set-up.
Theorem 9.3.2
Let \(n\in \mathbb {N}\) and p ∈ [1, ∞]. Let \((Z_i)_{i\in \mathbb {N}}\) be independent and p-generalized Gaussian random variables, meaning absolutely continuous w.r.t. to the Lebesgue measure on \(\mathbb {R}\) with density

Consider the random vector \(Z\mathrel{\mathop:}= (Z_1,\ldots ,Z_n)\in \mathbb {R}^n\) and let U ∼Unif([0, 1]) be independent of Z 1, …, Z n. Then

Moreover,  is independent of
is independent of  .
.
It is worth noticing that in [22] the density used by the authors for Z
1 is actually proportional to  . As will become clear later, this difference is irrelevant as far as the conclusion of the theorem is concerned.
. As will become clear later, this difference is irrelevant as far as the conclusion of the theorem is concerned.
Indeed, although the statement of Theorem 9.3.2 reflects the focus of this survey on the \(\ell _p^n\text{-balls} \) and the literature on the topic, its result is not strictly dependent on the particular choice of f p in Eq. (9.7). In fact, it is not even a prerogative of the \(\ell _p^n\text{-balls} \), as subsequently explained in Proposition 9.3.3.
9.3.2 The Cone Measure on a Symmetric Convex Body
Consider a symmetric convex body \(K\subseteq \mathbb {R}^n\), meaning that if x ∈ K then also − x ∈ K. Define the functional  by
by

The functional  is known as the Minkowski functional associated with K and, under the aforementioned conditions on K, defines a norm on \(\mathbb {R}^n \). We will also say that
is known as the Minkowski functional associated with K and, under the aforementioned conditions on K, defines a norm on \(\mathbb {R}^n \). We will also say that  is the K-norm of the vector \(x\in \mathbb {R}^n\). Whenever a function on \(\mathbb {R}^n\) is dependent only on
is the K-norm of the vector \(x\in \mathbb {R}^n\). Whenever a function on \(\mathbb {R}^n\) is dependent only on  , we say that it is a K-radial function. Analogously, we call a probability measure K-radial when its distribution function is K-radial. We will also write p-radial meaning \(\mathbb {B}_p^n\text{-radial} \).
, we say that it is a K-radial function. Analogously, we call a probability measure K-radial when its distribution function is K-radial. We will also write p-radial meaning \(\mathbb {B}_p^n\text{-radial} \).
In analogy with Eqs. (9.3) and (9.4), it is possible to define a uniform probability measure ν K on K and a cone measure μ K on ∂K, respectively, as

for any \(A\in \mathcal {B}(\mathbb {R}^n)\) and \(B\in \mathcal {B}(\partial K)\).
Note that μ
K, as a ratio of volumes, is invariant under a simultaneous transformation of both the numerator and the denominator. In particular, for any \(I\in \mathcal {B}(\mathbb {R}^+)\), such that  , it holds
, it holds

for any \(B\in \mathcal {B}(\partial K)\) (note that K = [0, 1]∂K). This fact will be used in the proof of the following generalization of Theorem 9.3.2 to arbitrary symmetric convex bodies.
Proposition 9.3.3
Let \(K\subseteq \mathbb {R}^n\) be a symmetric convex body. Suppose that there exists a continuous function f : [0, ∞) → [0, ∞) with the property  such that the distribution of a random vector Z on \(\mathbb {R}^n\) is given by
such that the distribution of a random vector Z on \(\mathbb {R}^n\) is given by

for any \(A\in \mathcal {B}(\mathbb {R}^n)\). Also, let U ∼Unif([0, 1]) be independent of Z. Then,

In addition,  is independent of
is independent of  .
.
The proof of Proposition 9.3.3 is based on the following polar integration formula, which generalizes Eq. (9.5). It says that for measurable functions \(h:\mathbb {R}^n\to [0,\infty )\),

By the usual measure-theoretic standard procedure to prove Eq. (9.10) it is sufficient to consider functions h of the form h(x) = 1
A(x), where A = (a, b)E with 0 < a < b < ∞ and E a Borel subset of ∂K. However, in this case, the left-hand side is just  , while for the right-hand side we obtain, by definition of the cone measure μ
K,
, while for the right-hand side we obtain, by definition of the cone measure μ
K,

which is clearly also equal to  .
.
Proof of Proposition 9.3.3
Let \(\varphi :\mathbb {R}^n\to \mathbb {R}\) and \(\psi :\mathbb {R}\to \mathbb {R}\) be non-negative measurable functions. Applying the polar integration formula, Eq. (9.10), yields

By the product structure of the last expression this first shows the independence of  and
and  . Moreover, choosing ψ ≡ 1 we see that
. Moreover, choosing ψ ≡ 1 we see that

by definition of f. This proves that  . That
. That  finally follows from the fact that U
1∕n ∼ β(n, 1), which has density r↦nr
n−1 for r ∈ (0, 1). □
finally follows from the fact that U
1∕n ∼ β(n, 1), which has density r↦nr
n−1 for r ∈ (0, 1). □
The main reason why the theory treated in this survey is restricted to \(\ell _p^n\text{-balls} \), and not to more general convex bodies K, is that \(\ell _p^n\text{-balls} \) are a class of convex bodies whose Minkowski functional is of the form

for certain functions f 1, …, f n and invertible positive function F. This is necessary for Z to have independent coordinates. Indeed, in this case one can assign a joint density on Z that factorizes into its components, like for example (omitting the normalizing constant),

which ensures the independence of the coordinates Z i of Z.
Already for slightly more complicated convex bodies than \(\ell _p^n\text{-balls} \), Eq. (9.11) no longer holds. For example, considering the convex body defined as

It can be computed that  , which is not of the form (9.11).
, which is not of the form (9.11).
On the other hand, the coordinate-wise representation of the density of Z in the precise form given by Eq. (9.7), is also convenient to explicitly compute the distribution of some functionals of Z, as we will see in the following section.
9.3.3 A Different Probabilistic Representation for p-Radial Probability Measures
Another probabilistic representation for a p-symmetric probability measure on \(\mathbb {B}_p^n\) has been given by Barthe et al. [4] in the following way,
Theorem 9.3.4
Let Z be a random vector in \(\mathbb {R}^n\) defined as in Theorem 9.3.2 . Let W be a non-negative random variable with probability distribution P W and independent of Z. Then
where \(\mathrm {H}_W\colon \mathbb {B}_p^n\to \mathbb {R}\) , HW(x) = h(x), with
Remark
Note that all the distributions obtainable from Theorem 9.3.4 are p-radial, especially the p-norm of Z∕(Z p + W)1∕p is
Moreover, some particular choices of W in Theorem 9.3.4 lead to interesting distributions:
-
1.
When W ≡ 0 we recover the cone measure of Theorem 9.3.2;
-
2.
For α > 0, choosing W ∼ Γ(α, 1) results in the density proportional to x↦(1 − x p)α−1 for x ≤ 1.
-
3.
As a particular case of the previous one, when \(W\sim \exp (1)=\Gamma (1,1) \), then H W ≡ 1 and

This is not in contrast with Theorem 9.3.2. Indeed, it is easy to compute that

In view of the properties (9.1) and (9.2), this implies

As a consequence of this fact, the orthogonal projection of the cone measure \(\mu _p^{n+p}\) on \(\partial \mathbb {B}_p^{n+p}\) onto the first n coordinates is \(\nu _p^n \). Indeed, if
 , then \(W\sim \exp (1)\), while
, then \(W\sim \exp (1)\), while 
is the required projection. We refer to [4, Corollaries 3-4] for more details in this direction.
9.4 Central Limit Theorems and Laws of Large Numbers
The law of large numbers and the central limit theorem are arguably among the most prominent limit theorems in probability theory. Thanks to the probabilistic representation for the various geometric measures on \(\ell _p^n\)-balls described in Sect. 9.3.1, both of these limit theorems can successfully applied to deduce information about the geometry of \(\ell _p^n\)-balls. This—by now classical—approach will be described here, but we will also consider some more recent developments in this direction as well as several generalizations of known results.
9.4.1 Classical Results: Limit Theorems à la Schechtman-Schmuckenschläger
The following result on the absolute moments of a p-generalized Gaussian random variable is easy to derive by direct computation, and therefore we omit its proof, which the reader can find in [13, Lemma 4.1]
Lemma 9.4.1
Let p ∈ (0, ∞] and let Z 0 be a p-generalized Gaussian random variable (i.e., its density is given by Eq.(9.7)). Then, for any q ∈ [0, ∞],

For convenience, we will also indicate m p,q: = M p(q)1∕q and

We use the convention that M ∞(∞) = C ∞(∞, ∞) = C ∞(∞, q) = 0. The next theorem is a version of the central limit theorem in [24, Proposition 2.4].
Theorem 9.4.2
Let 0 < p, q < ∞, p ≠ q and \(X\sim \nu _p^n\). Then

where \(N\sim \mathcal {N}\bigl (0,\sigma ^2_{p,q}\bigr )\) and
Note that, since M p(p) = 1, then \( \sigma ^2_{p,p}=0\). In fact, in such a case

and a different normalization than \(\sqrt {n} \) is needed to obtain a non-degenerate limit distribution. Moreover, \(\sigma _{p,q}^2>0 \) whenever p ≠ q.
For our purposes, it is convenient to define the following quantities

and
It is easy to verify with Sterling’s approximation that, for any p, q > 0, \(A_{p,q,n}=A_{p,q}+\mathcal {O}(1/n)\) for A p,q ∈ (0, ∞), as n →∞.
With this definition in mind, we exploit Theorem 9.4.2 to prove a result on the volume of the intersection of \(\ell _p^n\text{-Balls}\). This can be regarded as a generalization of the main results in Schechtman and Schmuckenschläger [21], and Schmuckenschläger [23, 24].
Corollary 9.4.3
Let 0 < p, q < ∞ and p ≠ q. Let r ∈ [0, 1] and \((t_n)_{n\in \mathbb {N}}\subseteq \mathbb {R}^+\) be such that
where Φ p,q : [−∞, +∞] → [0, 1] is the distribution function of \(N\sim \mathcal {N}(0,\sigma ^2_{p,q})\) and \(\sigma ^2_{p,q}\) is defined in Theorem 9.4.2, i.e.,
Then

In particular, when t n ≡ t, then

Proof
First of all, note that, since \(A_{p,q,n}=A_{p,q}+\mathcal {O}(1/n)\), then
provided that the latter exists in [−∞, ∞], as per assumption. In particular, taking the limit on both sides of the following equality,

we get, because of Theorem 9.4.2,

On the other hand, it is true that the following chain of equalities hold:

which concludes the main part of proof. For the last observation, note that for any t constant, either \(\sqrt {n}(t A_{p,q}-1)\equiv 0\) or it diverges. □
9.4.2 Recent Developments
9.4.2.1 The Multivariate CLT
We present here a multivariate central limit theorem that recently appeared in [13]. It constitutes the multivariate generalization of Theorem 9.4.2. Similar to the classical results of Schechtman and Schmuckenschläger [21], and Schmuckenschläger [23, 24] this was used to study intersections of (this time multiple) \(\ell _p^n\)-balls. In part 1, we replace the original assumption \(X\sim \nu _p^n\) of [13] to a more general one, that appears naturally from the proof. Part 2 is substantially different and cannot be generalized with the same assumption.
Theorem 9.4.4
Let \(n,k\in \mathbb {N}\) and p ∈ [1, ∞].
-
1.
Let X be a continuous p-radial random vector in \(\mathbb {R}^n\) such that
 (9.12)
(9.12)Fix a k-tuple (q 1, …, q k) ∈ ([1, ∞) ∖{p})k. We have the multivariate central limit theorem

where \(N=(N_1,\ldots ,N_k)\sim \mathcal {N}(0,\Sigma )\), with covariance matrix \(\Sigma =(c_{i,j})_{i,j=1}^k \) whose entries are given by
$$\displaystyle \begin{aligned} c_{i,j}\mathrel{\mathop:}= \begin{cases} \frac{1}{q_iq_j}\biggl( \frac{\Gamma(\frac{1}{p})\Gamma(\frac{q_i+q_j+1}{p})}{\Gamma(\frac{q_i+1}{p})\Gamma(\frac{q_j+1}{p})}-1\biggr)-\frac{1}{p}&\quad \mathit{\text{if }}\, p<\infty,\\ \frac{1}{q_i+q_j+1}&\quad \mathit{\text{if }}\, p=\infty. \end{cases} \end{aligned} $$(9.13) -
2.
Let \(X\sim \nu _p^n\). If p < ∞, then we have the non-central limit theorem

where
$$\displaystyle \begin{aligned} A_n^{(p)}\mathrel{\mathop:}= p\log n -\frac{1-p}{p}\log (p\log n)+\log(p^{1/p}\Gamma(1+1/p)) \end{aligned}$$and G is a Gumbel random variable with distribution function \(\mathbb {R}\ni t\mapsto e^{-e^{-t}}\).
Remark
Note that the assumptions of Theorem 9.4.4 include the cases \(X\sim \nu _p^n\) and \( X\sim \mu _p^n\). In fact, condition (9.12) is just the quantitative version of the following concept: to have Gaussian fluctuations it is necessary that the bigger n gets, the more the distribution of X is concentrated in near \(\partial \mathbb {B}_p^n\). It is relevant to note that (9.12) also keeps open the possibility for a non-trivial limit distribution when rescaling  with a sequence that grows faster than \(\sqrt {n}\). This would yield a limit-theorem for
with a sequence that grows faster than \(\sqrt {n}\). This would yield a limit-theorem for  . For example, when \(X\sim \nu _p^n\), we already noted that
. For example, when \(X\sim \nu _p^n\), we already noted that  , so that
, so that

On the other hand, when \(X\sim \mu _p^n\), then  .
.
Proof
We only give a proof for the first part of the theorem, the second one can be found in [13].
Let first p ∈ [1, ∞). Consider a sequence of independent p-generalized Gaussian random variables \((Z_j)_{j\in \mathbb {N}}\), also independent from every X. Set Z = (Z 1, …, Z n). For any \(n\in \mathbb {N}\) and i ∈{1, …, k}, consider the random variables

According to the classical multivariate central limit theorem, we get

with covariance matrix given by
Using Theorem 9.3.2 and the aforementioned definitions we can write, for i ∈{1, …, k},

where we defined the function \(F_i\colon \mathbb {R}\times (\mathbb {R}\setminus \{-1\} )\to \mathbb {R} \) as
Note that F i is continuously differentiable around (0, 0) with Taylor expansion given by
Since, for the law of large numbers,  and
and  , the previous equation means that there exists a random variable C, independent of n, such that
, the previous equation means that there exists a random variable C, independent of n, such that

In particular,

Note that the first summand of both bounding expressions tends to 0 in distribution by assumption (9.12), while the second converges in distribution to \(\frac {1}{q_iM_p(q_i)}\xi ^{(i)}-\frac {1}{p}\eta \). This implies that

where N i is a centered Gaussian random variable. To obtain the final multivariate central limit theorem, we only have to compute the covariance matrix Σ. For {i, j}⊆{1, …, k}, its entries are given by
and this can be made explicit to get Eq. (9.13). The remaining case of p = ∞ can be repeated using the aforementioned conventions on the quantities M ∞ and C ∞. □
Remark
From the proof is evident that in the case when \(\sqrt {n}({X}-1)\) converges in distribution to a random variable F, independence yields, for every i ∈{1, …, k}, the convergence in distribution

in which case the limiting random variable is not normal in general. Analogously, if there exists a sequence \((a_n)_{n\in \mathbb {N}}\), \(a_n=o(\sqrt {n})\) and a random variable F such that

then the previous proof, with just a change of normalization, yields the limit theorem

for every q ∈ [1, ∞), as n →∞.
In analogy to Corollary 9.4.3, one can prove in a similar way the following result concerning the simultaneous intersection of several dilated ℓ p-balls. In particular, we emphasize that the volume of the simultaneous intersection of three balls \(\mathbb {D}_p^n\cap t_1\mathbb {D}_{q_1}^n\cap t_2\mathbb {D}_{q_2}\) is not equal to 1∕4 if these balls are in ‘critical’ position, as one might conjecture in view of Corollary 9.4.3.
Corollary 9.4.5
Let \(n,k\in \mathbb {N}\) and p ∈ [1, ∞]. Fix a k-uple (q 1, …, q k) ∈ ([1, ∞) ∖{p})k. Let t 1, …, t k be positive constants and define the sets \(I_\star \mathrel{\mathop:}= \{i\in \{1,\ldots ,k\}:A_{p,q_i}t_i\star 1\}\), where ⋆ is one of the symbols > , = or < . Then,

where N = (N 1, …, N k) is as in Theorem 9.4.4.
9.4.2.2 Outlook: The Non-commutative Setting
Very recently, Kabluchko et al. obtained in [11] a non-commutative analogue of the classical result by Schechtman and Schmuckenschläger [21]. Instead of considering the family of \(\ell _p^n\)-balls, they studied the volumetric properties of unit balls in classes of classical matrix ensembles.
More precisely, we let β ∈{1, 2, 4} and consider the collection \(\mathscr H_n(\mathbb {F}_\beta )\) of all self-adjoint n × n matrices with entries from the (skew) field \(\mathbb {F}_\beta \), where \(\mathbb {F}_1=\mathbb {R}\), \(\mathbb {F}_2=\mathbb C\) or \(\mathbb {F}_4=\mathbb H\) (the set of Hamiltonian quaternions). By λ 1(A), …, λ n(A) we denote the (real) eigenvalues of a matrix A from \(\mathscr H_n(\mathbb {F}_\beta )\) and consider the following matrix analogues of the classical \(\ell _p^n\)-balls discussed above:

where we interpret the sum in brackets as \(\max \{\lambda _j(A):j=1,\ldots ,n\}\) if p = ∞. As in the case of the classical \(\ell _p^n\)-balls we denote by \(\mathbb D_{p,\beta }^n\), β ∈{1, 2, 4} the volume normalized versions of these matrix unit balls. Here the volume can be identified with the \((\beta \frac {n(n-1)}{2}+\beta n)\)-dimensional Hausdorff measure on \(\mathscr H_n(\mathbb {F}_\beta )\).
Theorem 9.4.6
Let 1 ≤ p, q < ∞ with p ≠ q and β ∈{1, 2, 4}. Then

To obtain this result, one first needs to study the asymptotic volume of the unit balls of \(\mathscr H_n(\mathbb {F}_\beta )\). This is done by resorting to ideas from the theory of logarithmic potentials with external fields. The second ingredient is a weak law of large numbers for the eigenvalues of a matrix chosen uniformly at random from \(\mathbb B_{p,\beta }^n\). For details we refer the interested reader to [11].
9.5 Large Deviations vs. Large Deviation Principles
The final section is devoted to large deviations and large deviation principles for geometric characteristics of \(\ell _p^n\)-balls. We start by presenting some classical results on large deviations related to the geometry of \(\ell _p^n\)-balls due to Schechtman and Zinn. Its LDP counterpart has entered the stage of asymptotic geometry analysis only recently in [13]. We then continue by presenting a large deviation principle for one-dimensional random projections of \(\ell _p^n\)-balls of Gantert et al. [9]. Finally, we present a similar result for higher-dimensional projections as well.
9.5.1 Classical Results: Large Deviations à la Schechtman-Zinn
We start by rephrasing the large deviation inequality of Schechtman and Zinn [22]. It is concerned with the ℓ q-norm of a random vector in an \(\ell _p^n\)-balls. The proof that we present follows the argument of [17].
Theorem 9.5.1
Let 1 ≤ p < q ≤∞ and \(X\sim \nu _p^n\) or \(X\sim \mu _p^n\). Then there exists a constant c ∈ (0, ∞), depending only on p and q, such that

for every z > 1∕c.
Proof
We sketch the proof for the case that \(X\sim \mu _p^n\). Let Z
1, …, Z
n be p-generalized Gaussian random variables and put  for r ≥ 1. Now observe that by the exponential Markov inequality and Theorem 9.3.2, for t > 0,
for r ≥ 1. Now observe that by the exponential Markov inequality and Theorem 9.3.2, for t > 0,

where we also used the independence property in Theorem 9.3.2 in the last step. Next, we observe that \( \operatorname {\mathrm {\mathbf {E}}} S_p=n\) by Lemma 9.4.1. Moreover from [17, Corollary 3] it is known that there exists a constant c ∈ (0, ∞) only depending on p and q such that
as long as 0 < t < 1∕c. Thus, choosing \(t=\frac {n}{c}-\frac {n}{z^p}\) we arrive at

This implies the result. □
9.5.2 Recent Developments
9.5.2.1 The LDP Counterpart to Schechtman-Zinn
After having presented the classical Schechtman-Zinn large deviation inequality, we turn now to a LDP counterpart. The next result is a summary of the results presented in from [13, Theorems from 1.2 to 1.5]. The speed and the rate function in its part 4 resembles the right hand side of the inequality in Theorem 9.5.1.
Theorem 9.5.2
Let \(n\in \mathbb {N}\), p ∈ [1, ∞], q ∈ [1, ∞) and \(X\sim \nu _p^n\). Define the sequence

-
1.
If q < p < ∞, then
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 
Here
$$\displaystyle \begin{aligned} \mathcal{I}_1(x)=\begin{cases} -\log(x)&\quad \mathit{\text{if }}\, x\in(0,1],\\ +\infty&\quad \mathit{\text{otherwise}}, \end{cases} \end{aligned} $$(9.14)and
$$\displaystyle \begin{aligned} \mathcal{I}_2(x)=\begin{cases} \inf\{\Lambda^*(y,z):x=y^{1/q}z^{-1/p}, y\ge 0, z\ge 0 \}&\quad \mathit{\text{if }}\, x\ge 0\\ +\infty&\quad \mathit{\text{otherwise}}, \end{cases} \end{aligned}$$where Λ ∗ is the Fenchel-Legendre transform of the function
$$\displaystyle \begin{aligned} \Lambda(t_1,t_2)\mathrel{\mathop:}=\log\int_0^{+\infty} \frac{1}{p^{1/p}\Gamma(1+1/p)}e^{t_1 s^q+(t_2-1/p) s^p }{}\mathrm{d} s,\qquad (t_1,t_2)\in\mathbb{R}\times\Bigl(-\infty,\frac{1}{p}\Bigr). \end{aligned}$$ -
2.
If q < p = ∞, then
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 
where Ψ ∗ is the Fenchel-Legendre transform of the function
$$\displaystyle \begin{aligned} \Psi(t)\mathrel{\mathop:}=\int_0^1 e^{t s^q}{}\mathrm{d} s,\qquad t\in\mathbb{R}. \end{aligned}$$ -
3.
If p = q, then
 satisfies an LDP with speed n and good rate function \(\mathcal {I}_1 \) defined in Eq.(9.14).
satisfies an LDP with speed n and good rate function \(\mathcal {I}_1 \) defined in Eq.(9.14). -
4.
If p < q, then
 satisfies an LDP with speed n
p∕q and good rate function
satisfies an LDP with speed n
p∕q and good rate function 
9.5.2.2 LDPs for Projections of \(\ell _p^n\)-Balls: One-Dimensional Projections
We turn now to a different type of large deviation principles. More precisely, we consider random projections of points uniformly distributed in an \(\ell _p^n\)-ball or distributed according to the corresponding cone probability measure onto a uniform random direction. The following result is a summary of from [9, Theorems 2.2,2.3]. The proof of the first part follows rather directly from Cramér’s theorem (Theorem 9.2.1) and the contraction principle (Proposition 9.2.2), the second part is based on large deviation theory for sums of stretched exponentials.
Theorem 9.5.3
Let \(n\in \mathbb {N}\) and p ∈ [1, ∞). Let \(X\sim \nu _p^n \) or \(X\sim \mu _p^n \) and \(\Theta \sim \sigma _2^n \) be independent random vectors. Consider the sequence
-
1.
If p ≥ 2, then W satisfies an LDP with speed n and good rate function

where Φ ∗ is the Fenchel-Legendre transform of

-
2.
If p < 2, then W satisfies an LDP with speed n 2p∕(2+p) and good rate function
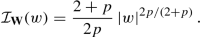
Proof
Let us sketch the proof for the case that p > 2, by leaving out any technical details. For this, let Z 1, …, Z n be p-generalized Gaussian random variables, G 1, …, G n be Gaussian random variables and U be a uniform random variable over [0, 1]. Also assume that all the aforementioned random variables are independent. Also put Z: = (Z 1, …, Z n) and G: = (G 1, …, G n). When \(X\sim \mu _p^n\), by Theorem 9.3.2, we can state that for each \(n\in \mathbb {N}\) the target random variable n 1∕p−1∕2X Θ has the same distribution as

Note that Φ is finite whenever p < 2, t 0 < 1∕2, \(t_1\in \mathbb {R}\) and t 2 < 1∕p. Then, Cramér’s theorem (Theorem 9.2.1) shows that the \(\mathbb {R}^3\text{-valued}\) sum

satisfies an LDP with speed n and rate function Φ∗. Applying the contraction principle (Proposition 9.2.2) to the function F(x, y, z) = x −1∕2yz −1∕p yields the LDP for W with speed n and the desired rate function \(\mathcal {I}_{\mathbf {W}}\). Once the LDP is proven for the cone measure, it can be pushed to the case of the uniform measure. By Theorem 9.3.2, multiplying the expression in Eq. (9.15) by U 1∕n, we obtain a random variable distributed according to \( \nu _p^n\). It is proven in [9, Lemma 3.2] that multiplying by U 1∕n every element of the sequence W, we obtain a new sequence of random variables that also satisfies an LDP with the same speed and the same rate function as W. On the other hand, when p < 2, Φ(t 0, t 1, t 2) = ∞ for any t 1 ≠ 0, hence suggesting that in this case the LDP could only occur at a lower speed than n. □
9.5.2.3 LDPs for Projections of \(\ell _p^n\)-Balls: The Grassmannian Setting
Finally, let us discuss projections to higher dimensional subspaces, generalizing thereby the set-up from the previous section. We adopt the Grassmannian setting and consider the 2-norm of the projection to a uniformly distributed random subspace in the Grassmannian \(\mathbb {G}_n^k\) of k-dimensional subspaces of \(\mathbb {R}^n\) of a point uniformly distributed in the \(\ell _p^n\)-unit ball. Since we are interested in the asymptotic regime where n →∞, we also allow the subspace dimension k to vary with n. However, in order to keep our notation transparent, we shall nevertheless write k instead of k(n). The next result is the collection of [1, Theorems 1.1,1.2].
Theorem 9.5.4
Let \(n\in \mathbb {N}\). Fix p ∈ [1, ∞] and a sequence k = k(n) ∈{1, …, n − 1} such that the limit λ: =limn→∞(k∕n) exists. Let P EX be the orthogonal projection of a random vector \(X\sim \nu _p^n\) onto a random independent linear subspace \(E\sim \eta _k^n\). Consider the sequence

-
1.
If p ≥ 2, then
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 
where we use the convention \(0\log 0\mathrel{\mathop:}= 0\) and for p ≠ ∞ we have
$$\displaystyle \begin{aligned} \mathcal{J}_p(y)\mathrel{\mathop:}=\inf_{\substack{x_1, x_2>0\\ x_1^{1/2}x_2^{-1/p}=y}}\mathcal{I}_p^*(x_1,x_2),\qquad y\in\mathbb{R}\,, \end{aligned}$$and \(\mathcal {I}_p^*(x_1,x_2)\) is the Fenchel-Legendre transform of

For p = ∞, we write \(\mathcal {J}_\infty (y)\mathrel{\mathop:}= \mathcal {I}_\infty ^*(y^2)\) with \(\mathcal {I}_\infty ^*\) being the Fenchel-Legendre transform of \(\mathcal {I}_\infty (t)\mathrel{\mathop:}= \log \int _0^1e^{tx^2}{}\mathrm {d} x\).
-
2.
If p < 2 and λ > 0, then
 satisfies and LDP with speed n
p∕2 and good rate function
satisfies and LDP with speed n
p∕2 and good rate function 
where m p: = p p∕2 Γ(1 + 3∕p)∕(3 Γ(1 + 1∕p)).
Let us emphasize that the proof of this theorem is in some sense similar to its one-dimensional counterpart that we have discussed in the previous section. However, there are a number of technicalities that need to be overcome when projections to high-dimensional subspaces are considered. Among others, one needs a new probabilistic representation of the target random variables. In fact, the previous theorem heavily relies on the following probabilistic representation, proved in [1, Theorem 3.1] for the case \(X\sim \nu _n^p\). We shall give a proof here for a more general set-up, which might be of independent interest.
Theorem 9.5.5
Let \(n\in \mathbb {N}\), k ∈{1, …, n} and p ∈ [1, ∞]. Let X be a continuous p-radial random vector in \(\mathbb {R}^n\) and \(E\sim \eta _k^n\) be a random k-dimensional linear subspace. Let Z = (Z 1, …, Z n) and G = (G 1, …, G n) having i.i.d. coordinates, distributed according to the densities f p and f 2, respectively. Moreover, let X, E, Z and G be independent. Then

Proof
Fix a vector \(x\in \mathbb {R}^n\). By construction of the Haar measure \(\eta _k^n\) on \(\mathbb {G}_k^n\) and uniqueness of the Haar measure η on \(\mathbb {O}(n)\), we have that, for any \(t\in \mathbb {R}\) ,

where E
0: = span({e
1, …, e
k}). Again, by the uniqueness of the Haar measure \(\sigma _2^n\) on \(\mathbb {S}_2^{n-1}\)
,  , provided that \(T\in \mathbb {O}(n)\) has distribution η. Thus,
, provided that \(T\in \mathbb {O}(n)\) has distribution η. Thus,

By Theorem 9.3.2
,  . Thus,
. Thus,

Therefore, if \(E\in \mathbb {G}^n_k\) is a random subspace independent of X having distribution \(\eta _k^n\) , and G is a standard Gaussian random vector in \(\mathbb {R}^n\) that is independent of X and E, we have that

Here, P (X,E) denotes the joint distribution of the random vector \((X,E)\in \mathbb {R}^n\times \mathbb {G}_{k}^n\), while P (X,G) stands for that of \((X,G)\in \mathbb {R}^n\times \mathbb {R}^n\). By Proposition 9.3.3, X has the same distribution as XZ∕Z. Therefore,

with P
(X,Z,G) being the joint distribution of the random vector \((X,Z,G)\in \mathbb {R}^n\times \mathbb {R}^n\times \mathbb {R}^n\). Consequently, we conclude that the two random variables  and
and  have the same distribution. □
have the same distribution. □
Remark
Let us remark that in his PhD thesis, Kim [15] was recently able to extend the results from [1] and [9] to more general classes of random vectors under an asymptotic thin-shell-type condition in the spirit of [2] (see [15, Assumption 5.1.2]). For instance, this condition is satisfied by random vectors chosen uniformly at random from an Orlicz ball.
9.5.2.4 Outlook: The Non-commutative Setting
The body of research on large deviation principles in asymptotic geometric analysis, which we have just described above, is complemented by another paper of Kim and Ramanan [16], in which they proved an LDP for the empirical measure of an n 1∕p multiple of a point drawn from an \(\ell _p^n\)-sphere with respect to the cone or surface measure. The rate function identified is essentially the so-called relative entropy perturbed by some p-th moment penalty (see [16, Equation (3.4)]).
While this result is again in the commutative setting of the \(\ell _p^n\)-balls, Kabluchko et al. [12] recently studied principles of large deviations in the non-commutative framework of self-adjoint and classical Schatten p-classes. The self-adjoint setting is the one of the classical matrix ensembles which has already been introduced in Sect. 9.4.2.2 (to avoid introducing further notation, for the case of Schatten trace classes we refer the reader to [12] directly). In the spirit of [16], they proved a so-called Sanov-type large deviations principles for the spectral measure of n 1∕p multiples of random matrices chosen uniformly (or with respect to the cone measure on the boundary) from the unit balls of self-adjoint and non self-adjoint Schatten p-classes where 0 < p ≤ +∞. The good rate function identified and the speed are quite different in the non-commutative setting and the rate is essentially given by the logarithmic energy (which is the negative of Voiculescu’s free entropy introduced in [25]). Interestingly also a perturbation by a constant connected to the famous Ullman distribution appears. This constant already made an appearance in the recent works [10, 11], where the precise asymptotic volume of unit balls in classical matrix ensembles and Schatten trace classes were computed using ideas from the theory of logarithmic potentials with external fields.
The main result of [12] for the self-adjoint case is the following theorem, where we denote by \(\mathcal M(\mathbb {R})\) the space of Borel probability measures on \(\mathbb {R}\) equipped with the topology of weak convergence. On this topological space we consider the Borel σ-algebra, denoted by \(\mathcal B(\mathcal M(\mathbb {R}))\).
Theorem 9.5.6
Fix p ∈ (0, ∞) and β ∈{1, 2, 4}. For every \(n\in \mathbb {N}\), let Z n be a random matrix chosen according to the uniform distribution on \(\mathbb {B}_{p,\beta }^n\) or the cone measure on its boundary. Then the sequence of random probability measures
satisfies an LDP on \(\mathcal M(\mathbb {R})\) with speed n 2 and good rate function \(\mathcal I:\mathcal M(\mathbb {R}) \to [0,+\infty ]\) defined by

Let us note that the case p = +∞ as well as the case of Schatten trace classes is also covered in that paper (see [12, Theorems 1.3 and 1.5]). The proof of Theorem 9.5.6 requires to control simultaneously the deviations of the empirical measures and their p-th moments towards arbitrary small balls in the product topology of the weak topology on the space of probability measures and the standard topology on \(\mathbb {R}\). It is then completed by proving exponential tightness. Moreover, they also use the probabilistic representation for random points in the unit balls of classical matrix ensembles which they have recently obtained in [10]. We close this survey by saying that as a consequence of the LDP in Theorem 9.5.6, they obtained that the spectral measure of n 1∕pZ n converges weakly almost surely to a non-random limiting measure given by the Ullman distribution, as n →∞ (see [12, Corollary 1.4] for the self-adjoint case and [12, Corollary 1.6] for the non-self-adjoint case).
References
D. Alonso-Gutiérrez, J. Prochno, C. Thäle, Large deviations for high-dimensional random projections of \(\ell _{p}^{n}\)-balls. Adv. Appl. Math. 99, 1–35 (2018)
M. Anttila, K. Ball, I. Perissinaki, The central limit problem for convex bodies. English. Trans. Am. Math. Soc. 355(12), 4723–4735 (2003)
S. Artstein-Avidan, A. Giannopoulos, V. Milman, Asymptotic Geometric Analysis. Part I. Mathematical Surveys and Monographs, vol. 202 (American Mathematical Society, Providence, 2015), pp. xx+451
F. Barthe, O. Guédon, S. Mendelson, A. Naor, A probabilistic approach to the geometry of the \(l_{p}^{n}\)-ball. Ann. Probab. 33(2), 480–513 (2005)
S. Brazitikos, A. Giannopoulos, P. Valettas, B.-H. Vritsiou, Geometry of Isotropic Convex Bodies. Mathematical Surveys and Monographs, vol. 196 (American Mathematical Society, Providence, 2014), pp. xx+594
A. Dembo, O. Zeitouni, Large Deviations. Techniques and Applications. Stochastic Modelling and Applied Probability, vol. 38. Corrected reprint of the second (1998) edition (Springer, Berlin, 2010), pp. xvi+396
F. den Hollander, Large Deviations. Fields Institute Monographs, vol. 14 (American Mathematical Society, Providence, 2000), pp. x+143
P. Dirichlet, Sur une nouvelle méthode pour la détermination des intégrales multiples. J. Math. Pures Appl. 4, 164–168 (1839)
N. Gantert, S. Kim, K. Ramanan, Large deviations for random projections of ℓ p balls. Ann. Probab. 45(6B), 4419–4476 (2017)
Z. Kabluchko, J. Prochno, C. Thäle, Exact asymptotic volume and volume ratio of Schatten unit balls. ArXiv e-prints (Apr. 2018). arXiv: 1804.03467 [math.FA]
Z. Kabluchko, J. Prochno, C. Thäle, Intersection of unit balls in classical matrix ensembles. Israel J. Math. (to appear). ArXiv e-prints (Apr. 2018). arXiv: 1804.03466 [math.FA]
Z. Kabluchko, J. Prochno, C. Thäle, Sanov-type large deviations in Schatten classes. Ann. Inst. H. Poincaré Probab. Statist. (to appear). ArXiv e-prints (Aug. 2018). arXiv: 1808.04862 [math.PR]
Z. Kabluchko, J. Prochno, C. Thäle, High-dimensional limit theorems for random vectors in \(\ell _{p}^{n}\)-balls. Commun. Contemp. Math. 21, 1750092 (2019)
O. Kallenberg, Foundations of Modern Probability, Second. Probability and Its Applications (Springer, New York, 2002), pp. xx+638
S. Kim, Problems at the interface of probability and convex geometry: random projections and constrained processes. Ph.D. thesis. Brown University, 2017
S. Kim, K. Ramanan, A conditional limit theorem for high-dimensional ℓ p spheres. ArXiv e-prints (Sept. 2015). arXiv: 1509.05442 [math.PR]
A. Naor, The surface measure and cone measure on the sphere of \(\ell _{p}^{n}\). Trans. Am. Math. Soc. 359(3), 1045–1079 (2007)
A. Naor, D. Romik, Projecting the surface measure of the sphere of \(\ell _{p}^{n}\). English. Ann. Inst. Henri Poincaré, Probab. Stat. 39(2), 241–261 (2003)
G. Pisier, The Volume of Convex Bodies and Banach Space Geometry (Cambridge University Press, Cambridge, 1999)
S. Rachev, L. Rüschendorf, Approximate independence of distributions on spheres and their stability properties. Ann. Probab. 19(3), 1311–1337 (1991)
G. Schechtman, M. Schmuckenschläger, Another remark on the volume of the inter-section of two \(l_{p}^{n}\) balls, in Geometric Aspects of Functional Analysis (1989–90), vol. 1469. Lecture Notes in Mathematics (Springer, Berlin, 1991), pp. 174–178
G. Schechtman, J. Zinn, On the volume of the intersection of two \(l_{p}^{n}\)balls. Proc. Am. Math. Soc. 110(1), 217–224 (1990)
M. Schmuckenschläger, Volume of intersections and sections of the unit ball of \(\ell _{p}^{n}\). Proc. Am. Math. Soc. 126(5), 1527–1530 (1998)
M. Schmuckenschläger, CLT and the volume of intersections of \(\ell _{p}^{n}\)-balls. English. Geom. Dedicata 85(1–3), 189–195 (2001)
D. Voiculescu, The analogues of entropy and of Fisher’s information measure in free probability theory. I. Commun. Math. Phys. 155(1), 71–92 (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Prochno, J., Thäle, C., Turchi, N. (2019). Geometry of \(\ell _p^n\,\text{-Balls}\): Classical Results and Recent Developments. In: Gozlan, N., Latała, R., Lounici, K., Madiman, M. (eds) High Dimensional Probability VIII. Progress in Probability, vol 74. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-26391-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-26391-1_9
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-26390-4
Online ISBN: 978-3-030-26391-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)







 , then
, then 



 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function  satisfies an LDP with speed n
p∕q and good rate function
satisfies an LDP with speed n
p∕q and good rate function 


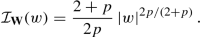
 satisfies an LDP with speed n and good rate function
satisfies an LDP with speed n and good rate function 

 satisfies and LDP with speed n
p∕2 and good rate function
satisfies and LDP with speed n
p∕2 and good rate function 