Static Case of the Golden Rule

Abstract

In this chapter, the concept of Berge equilibrium is introduced as a mathematical model of the Golden Rule. This concept was suggested by the Russian mathematician K. Vaisman in 1994. The Berge–Pareto equilibrium is formalized and sufficient conditions for the existence of such an equilibrium are established. As an application, the existence in the class of mixed strategies is proved.

Celui qui croit pouvoir trouver en soi-même

de quoi se passer de tout le monde se trompe

fort; mais celui qui croit qu’on ne peut se

passer de lui se trompe encore davantage.

—La Rochefoucauld¹

In this chapter, the concept of Berge equilibrium is introduced as a mathematical model of the Golden Rule. This concept was suggested by the Russian mathematician K. Vaisman in 1994. The Berge–Pareto equilibrium is formalized and sufficient conditions for the existence of such an equilibrium are established. As an application, the existence in the class of mixed strategies is proved.

2.1 What is the Content of the Golden Rule?

Virtue is its own reward.

—English proverb

In the religious-ethical foundations, most nations are guided by the same strategy of behavior, embodied in the demands of the so-called Golden Rule (see Chap. 1). It will hopefully become an established ethical rule for the behavior of the mankind. The well-known statement of the Golden Rule declares, “Behave to others as you would like them to behave to you” (from a lecture delivered by Academician A. Guseinov, Director of RAS Institute of Philosophy, during The IX Moscow Science Festival on October 10, 2014 at Moscow State University). It originates from the New Testament, see the Gospel of Luke, Chapter 6:31, precepting that “And as ye would that men should do to you, do ye also to them likewise.”

Prior to formalizing the concept of Berge equilibrium that matches the Golden Rule, we will present the concept of Nash equilibrium as a standard approach to resolve conflicts. In fact, a critical discussion of the latter has led to the Berge equilibrium, the new solution of noncooperative games that is cultivated in this book.

2.2 Main Notions

Suum cuique.²

Nowadays, when the world shudders at the possibility of escalating military conflicts, the Golden Rule becomes more relevant than ever. Indeed, the Golden Rule is a possible way to avoid wars and blood-letting. The modern science of warfare relies mostly on the concept of Nash equilibrium. In this section, the definition of a Nash equilibrium is given, preceded by background material from mathematical theory of noncooperative games.

2.2.1 Preliminaries

Non multa sed multum.³

Some general notions from the mathematical theory of noncooperative games that will be needed in the text are presented.

Which mythical means were used by Pygmalion to revivify Galatea? We do not know the true answer, but Pygmalion surely was an operations researcher by vocation: at some moment of time his creation became alive. This idea underlines creative activities in any field, including mathematical modeling. To build an integral entity from a set of odd parts means “to revivify” it in an appropriate sense:

$$\displaystyle \begin{aligned}\begin{array}{l} \mbox{``She has not yet been born:} \\ \mbox{ she is music and word,} \\ \mbox{ and therefore the un-torn,} \\ \mbox{ fabric of what is stirred.'' (Mandelshtam{${}^{4}$})} \end{array} \end{aligned}$$

This section is devoted to the revivification of a conflict.

⁴

What is a conflict? Looking beyond the common (somewhat criminal) meaning of this word, we will use the following notion from [189, p. 333]: “conceptually a conflict is any phenomenon that can be considered in terms of its participants, their actions, the outcomes yielded by these actions as well as in terms of parties interested in one way or another in these outcomes, including the nature of these interests.” As a matter of fact, game theory suggests mathematical models of optimal decision-making under conflict. The logical foundation of game theory is a formalization of three fundamental ingredients, namely, the features of a conflict, decision-making rules and the optimality of solutions. In this book, we study “rigid” conflicts only, in which each party is guided by his own reasons according to his perception and hence pursues individual goals, l’esprit les intérêst du clocher.⁵

The branch of game theory dealing with such rigid conflicts is known as the theory of noncooperative games. The noncooperative games described in Chap. 2 possess a series of peculiarities. Let us illustrate them using two simple examples.

Example 2.1.1

Imagine several competing companies (firms) that supply the same product in the market. Product price (hence, the profit of each firm) depends on the total quantity of products supplied in the market. The goal of each firm is to maximize its profit by choosing an appropriate quantity of supply.

Example 2.1.2

The economic potential of an individual country can be assessed by a special indicator—a function that depends on controllable factors (taxation, financial and economic policy, industrial and agricultural development, foreign supplies, investments, credits, etc.) and also on uncontrollable factors (climate changes and environmental disasters, anthropogenic accidents, suddenly sparked wars, etc.). Each country seeks to achieve a maximal economic potential through a reasonable choice of the controllable factors with a proper consideration of the existing economic relations with other countries.

These examples elucidate well the character of noncooperative games.

The differentia specifica ⁶ of such games are the following.

First, the decision-making process involves several parties (decision makers, e.g., sellers or governments), which are often called players in game theory. Note that a priori they are competitors: quilibet (quisque) fortunae suae faber.⁷

Second, each player has an individual goal (profit or economic potential maximization) and the goals are bound to each other: tout s’enchaine, tout se lie dans ce monde.⁸ A dazzling success of one party may turn out to be a disaster for another party.

Third, each player uses his own tools for achieving his goal (for sellers, the quantity of products supplied; for a country, the controllable factors in Example 2.1.2); in game theory, the controllable factors of each player are called his strategies, while a specific strategy chosen by a player is his decision or action in a noncooperative game.

Let us list three important circumstances.

First, quantitative analysis in any field requires an appropriate mathematical model; this fully applies to noncooperative games. In the course of mathematical modeling, a researcher inevitably faces the risks of going too deep into details (“not see the wood for the trees”) and presenting the phenomenon under study in a rough outline (“throwing out the baby with the bathwater”). The mathematical model of a noncooperative game often includes the following elements:

• the set of players;

• for each player, the set of his strategies;

• for each player, a scalar functional defined on the set of players’ strategies. The value of this functional is the degree to which a given player achieves his goal under given strategies. In game theory, the functional is called the payoff function (or utility function) of a given player.

Second, “many intricate phenomena become clear naturally if treated in terms of game theory.” [21, p. 97]. Following these ex cathedra ⁹ pronouncements by Russian game theory maître N. Vorobiev, we are employing the framework of noncooperative games in this book.

A series of conventional requirements have been established for a game-theoretic model (of course, including a sufficient adequacy to the conflict under consideration) as follows.

First, the model must incorporate all interested parties of the conflict (players).

Second, the model must specify possible actions of all parties (the strategies of players).

Third, the model must describe the interests of all parties (for each player and each admissible collection of actions chosen by all players, the model must assign a value called the payoff of that player).

The main challenges of game theory [24] are

• (1∘) the design of optimality principles;

• (2∘) the proof of existence of optimal actions for players;

• (3∘) the calculation of optimal actions.

Different game-theoretic concepts of optimality often reflect intuitive ideas of profitability, stability and equitability, rarely with an appropriate axiomatic characterization. Therefore, in most cases the notion of optimality in game theory (an optimal solution of a game) is not unique, prior or absolute.

We will make the normative ¹⁰ approach to noncooperative games the cornerstone of this book: it will be established which behavior of the players should be considered optimal (rational or reasonable) [47, 48].

Depending on the feasibility of joint actions among the players (coordination of their individual actions), the games are classified as noncooperative, cooperative, and coalitional [50].

In the noncooperative setup of a game (simply called a noncooperative game, see above), each player chooses his action (strategy) in order to achieve the best individual result for himself without any coordination with other players: chacun pour soi, chacun chez soi.¹¹

The cooperative setup of a game (cooperative game) is opposite to the noncooperative one. Here all players jointly choose their strategies in a coordinate way and, in some cases, even share the results (their payoffs). Alle für einen, einer für alle.¹²

Finally, in the coalitional setup of a game (coalitional game), all players are partitioned into pairwise disjoint groups (coalitions) so that the members of each coalition act cooperatively while all coalitions play a noncooperative game with each other.

2.2.2 Elements of the Mathematical Model

Ad Disputandum

Consider several subsystems that are interconnected with each other. In economics, these can be industrial enterprises or sectors, countries, sellers in a market, producers of every sort and kind with the same type of products, and other economic systems (called firms in [124, p. 28]). In ecology, industrial enterprises with the same purification and treatment facilities, competing populations of different species (e.g., predators and preys), epidemics propagation and control. In the mechanics of controlled systems, a group of controlled objects (aircrafts, missiles) that attempt to approach each other or to capture an evader.

Each subsystem is controlled by a supervisor (henceforth called a player), who undertakes certain actions for achieving his goal based on available information. In social and economic systems, the role of players is assigned to the general managers of industrial enterprises and business companies, the heads of states, sellers (suppliers) and buyers (customers). In mechanical control systems, this role is played by the captains of ships or aircrafts and the chiefs of control centers.

Assume that, due to a priori conditions, the players have to follow the “Help yourself” slogan. This leads to the noncooperative setup of their interaction.

As an example, consider a simplified mathematical model of competition among N firms in a market.

Example 2.2.3

There are $N \geqslant 2$ competing firms (players) that supply an infinitely divisible good of the same type (flour, sugar, etc.) in a market. The cost of one unit of good for firm i is $c_i>0,\; i \in \mathbb {N}=\{1,\ldots ,N\}$. Suppose the number of market participants is sufficiently small so that the prices for goods depend directly on the quantity supplied by each firm. More specifically, denote by K the total supply of goods in the market; then the price p of one good can be calculated as $p=\max \{a-Kb,0\}$, where a > 0 gives the constant price of one good without any supply in the market, while b > 0 is the elasticity coefficient that characterizes the price drop in response to the supply of one unit of good. Here a natural assumption is that $c_i<a, \; i \in \mathbb {N}$, since otherwise the activity of firms makes no economic sense. In addition, the production capacities of the players are unlimited and they sell the goods at the price p.

Suppose the firms operate in stable (not extreme) conditions and hence their behavior is aimed at increasing profits. Denote by x _i the quantity of goods supplied by firm i $(i\in \mathbb {N})$. Then the total supply of goods in the market is given by

$$\displaystyle \begin{aligned}K=\sum_{i=1}^N x_i, \end{aligned}$$

while the profit of firm i is described by the function

$$\displaystyle \begin{aligned}f_i(x) =p x_i-c_i x_i \;\;\;\; ( i \in \mathbb{N} ), \end{aligned}$$

where (as before) p is the unit price.

Another reasonable hypothesis is that a − Kb > 0, since otherwise p = 0 and production yields no benefit for all firms (the profits become negative, f _i(x) = −c _ix _i < 0, i ∈N). In this case, the function

$$\displaystyle \begin{aligned}f_i(x) =\left[a-b \sum_{k = 1}^N x_k \right] x_i-c_i x_i \;\;\;\; ( i \in \mathbb{N} ) \end{aligned}$$

is the profit of firm i.

Therefore, in Example 2.2.3 the players are the competing firms and the action (strategy) of each player $i \in \mathbb {N}$ consists in choosing the quantity $x _i\in X_i= \left [ 0,+\infty \right )$ of its goods supplied in the market. Making its choice, each player i seeks to maximize its profit f _i(x) (payoff) given the supplied quantities x = (x ₁, …, x _N) of all players.

Idée Générale

Now, let us clarify the framework of the noncooperative games studied in this chapter.

For this purpose, we will answer Quintilian’s questions “Quis? Quid? Ubi? Quibus auxiliis? Cur? Quomodo? Quando?”¹³

Quis?

(Who?) In fact, a leading part in noncooperative games is assigned to the players. As mentioned earlier, players can be general managers of industrial enterprises and business companies, heads of states, sellers (suppliers) and buyers (customers), captains of ships or aircrafts and so on, i.e., those who have the right or authority to make decisions, give instructions and control their implementation (interestingly, some people considering themselves to be (fairly!) serious strongly object to such a game-theoretic interpretation of their activity). Each player has a corresponding serial number: 1, 2, …, i, …, N. Denote by $\mathbb {N}=\{1,2,\ldots ,N\}$ the set of all players and let the set $\mathbb {N}$ be finite. Note that games with an infinite number of players (called non-atomic games) are also studied in game theory [160, 171]. Players may form groups, i.e., coalitions $\mathbb {K} \subseteq \mathbb {N}$. A coalition is any subset $\mathbb {K}=\{i_1,\ldots ,i_k\}$of the player set $\mathbb {N}$. In particular, possible coalitions are singletons (the noncoalitional setup of the game) and the whole set $\mathbb {N}$ (the cooperative setup of the game). A partition of the set $\mathbb {N}$ into pairwise disjoint subsets forming N in union is a coalitional structure of the game:

$$\displaystyle \begin{aligned}\mathcal{P}= \{ \mathbb{K}_1, \mathbb{K}_2,\ldots,\mathbb{K}_l \;|\;\mathbb{K}_i \cap \mathbb{K}_j = \varnothing \; (i,j=1,\ldots,l;i \ne j), \; \bigcup\limits_{i=1}^l \mathbb{K}_i= \mathbb{N} \} . \end{aligned}$$

For example, in the noncooperative three-player game $(\mathbb {N}=\{1,2,3\})$, there exist five possible coalitional structures, given by $\mathcal {P}_1=\{\{1\},\{2\},\{3\}\}$, $\mathcal {P}_2=\{\{1,2\},\{3\}\}$, $\mathcal {P}_3=\{\{1\},\{2,3\}\}$, $\mathcal {P}_4=\{\{1,3\},\{2\}\}$, $\mathcal {P}_5=\{\{1,2,3\}\}$.

For a compact notation, we will sometimes consider only two-player games, letting $\mathbb {N} =\{1,2\}$.

In Example 2.2.3, the players are the general managers of competing firms.

Quid?

(What?) Each player chooses and then uses his strategy. A strategy is understood as a rule that associates each state of the player’s awareness with a certain action (behavior) from a set of admissible actions (behaviors) given this awareness. For the head of a state, this is a direction of strategic development. In a sector composed of several industrial enterprises, a strategy of a general manager is the output of his enterprise, the price of products, the amount of raw materials and equipment purchased, supply contracts, investments, innovations and implementation of new technologies, payroll redistribution, penalties, bonuses and other incentive and punishment mechanisms. For a seller, a strategy is the price of one good; for the captain of a ship, own course (rudder angle, the direction and magnitude of reactive force).

Thus, the action of each player consists in choosing and using his individual strategy, which gives an answer to the question Quid? Speaking formally, the strategy of player i in the game Γ₃ is x _i while the strategy set of this player is denoted by X_i.

Ubi?

(Where?) Here the answer is short: in the conflict, more precisely put, in its mathematical model described by the noncooperative game. In Example 2.2.3, this is the market of goods.

Quibus Auxiliis? Quomodo?

(Who helped? How?) Actually the players affect the conflict using their strategies, which is the answer to both questions.

In Example 2.2.3, the firms choose the quantities of their goods supplied in the market as their strategies. The resulting situation in the market is the strategy profile in the corresponding noncooperative game.

Cur?

(Why?) The answer is: in order to assess the performance of each player. The noncooperative game (the mathematical model of a conflict adopted in our book) incorporates the payoff function of player i ($i\in \mathbb {N}$). The value of this function (called payoff or outcome in game theory) is a numerical assessment of the desired performance. In Example 2.2.3, the payoff function of player i has the form

$$\displaystyle \begin{aligned}f_i(x,y) =\left[a-b\sum_{ k \in \mathbb{N} } x_k\right]x_i-c_ix_i. \end{aligned}$$

It measures the profit of firm i in the single-stage game. The following circumstances should be taken into account while assessing the performance of each player in a noncooperative game.

First, the design of payoff functions (performance assessment criteria) is a rather difficult and at times subjective task: “Nous ne désirerions guére de choses avec ardeur, si nous connaissions parfaitement ce que nous dèsirons.”¹⁴ [119, p. 55].

Sometimes, the goal consists in higher profit or lower cost; in other cases, in smaller environmental impact. Other goals are possible as well. As a rule, in a noncooperative game these criteria represent scalar functions defined on the set of all admissible strategy profiles. For the sake of definiteness, assume each player seeks to increase his payoff function as much as possible.

Second, in accordance with the noncoalitional setup of the game, the players act in an isolated way and do not form coalitions. Being guided by the Suum cuique slogan,¹⁵ each player chooses his strategy by maximizing his own payoff.

As a result, each player endeavors to implement his cherished goal: “Chacun produit selon ses facultés et recoit selon ses besoins.”¹⁶

Third, the decision-making process in the noncooperative game is organized as follows. Each player chooses and then uses his strategy, which yields a strategy profile of the game. The payoff function of each player is defined on the set of all admissible strategy profiles. The value of this function (payoff) is a numerical assessment of the player’s performance.

In game theory, both terms are equivalent and widespread! Person = player.

At a conceptual level, during the decision-making process in the noncoalitional game player i chooses his strategy x _i ∈X_i so that

• first, this choice occurs simultaneously for all N players;

• second, no agreements or coalitions among the players and no information exchange are allowed during the game [178, p. 1].

Quando?

(When?) The answer to the last question of Quantilian’s system is the shortest: at the time of decision-making in the conflict (within its mathematical model—the noncoalitional game) through an appropriate choice of strategies by the players.

In principle, a conflict can be treated as a certain controlled system, a “black box” in which the players input their strategies and receive their payoffs at the output. This is a standard approach to “instantaneous, single-period, static” noncooperative games in general game theory [23]. However, in most applications (particularly, in economics and the mechanics of controlled systems), the controlled system itself undergoes some changes with time, and the players are able to vary their strategies during the whole conflict. The games whose state evolves in time are called dynamic. Hopefully, our next book will be focused on the analysis of dynamic games.

2.2.3 Nash Equilibrium

Politica del campanile.¹⁷

A generally accepted solution concept for noncooperative games is the so-called Nash equilibrium.¹⁸ Nash equilibrium is widely used in economics, military science, policy and sociology. Almost each issue of modern journals on operations research, systems analysis or game theory contains papers involving the concept of Nash equilibrium.

Thus, let us consider a noncooperative three-player game described by

$$\displaystyle \begin{aligned}\Gamma_3 = \left\langle \; \{ 1,2,3 \}, \{ \mathrm{X}_i \}_{i=1,2,3}, \{ f_i(x) \}_{i=1,2,3} \; \right\rangle , \end{aligned}$$

where each player i  =  {1,  2,  3} chooses an individual strategy $x_i \!\in \!\mathrm {X}_i \!\subseteq \mathbb {R}^{n_i}$ in order to increase his performance $f_i(x\!=(x_1,\!x_2,\!x_3)\!)$, i.e., his payoff f _i(x) in a current strategy profile x = (x ₁, x ₂, x ₃) ∈ ∈X₁ ×X₂ ×X₃ = X.

A Nash equilibrium is a pair $(x^{\mathrm {e}},f^{\mathrm {e}} = (f_1(x^{\mathrm {e}}),f_2(x^{\mathrm {e}}),f_3(x^{\mathrm {e}})) \in \mathrm {X} \times \mathbb {R}^{3}$ defined by the three equalities

$$\displaystyle \begin{aligned}\begin{array}{c} f_1(x^{\mathrm{e}}) = \max\limits_{x_1 \in \mathrm{X}_1} f_1\left(x_1,x^{\mathrm{e}}_2,x^{\mathrm{e}}_3\right), \\ f_2(x^{\mathrm{e}}) = \max\limits_{x_2 \in \mathrm{X}_2} f_2\left(x^{\mathrm{e}}_1,x_2,x^{\mathrm{e}}_3\right), \\ f_3(x^{\mathrm{e}}) = \max\limits_{x_3 \in \mathrm{X}_3} f_3\left(x^{\mathrm{e}}_1,x^{\mathrm{e}}_2,x_3\right). \end{array} \end{aligned} $$

(2.2.1)

Each player therefore acts selfishly, seeking to satisfy his individual ambitions regardless of the interests of the other players. As repeatedly mentioned earlier, this concept of equilibrium was suggested in 1949 by J. Nash, a Princeton University graduate at that time and a famous American mathematician and economist as we know him today. Moreover, 45 years later J. Nash, J. Harsanyi and R. Selten were awarded the Nobel Prize in Economic Sciences “for the pioneering analysis of equilibria in the theory of non-cooperative games.” Let us note two important aspects. First, owing to his research in the field of game theory, by the end of the twentieth century J. Nash became a leading American apologist of the Cold War. Second, the Nash equilibrium had been so widely used in economics, sociology, and military science that during the period 1994–2012 the Nobel Committee awarded seven Nobel Prizes for different investigations that to a large degree stemmed from the concept of Nash equilibrium. However, the selfish character of NE prevents it from “paving the way” towards a peaceful resolution of conflicts.

2.2.4 Berge Equilibrium

Que jamais le mérite avec lui ne

perd rien, Et que, mieux que du

mal, il se souvient du bien.¹⁹

Almost all notions in the modern theory of measure

and integral go back to Lebesgue’s works,

and introduction of these notions was in some sense

a turning point of transition from the mathematics of

the 19th century to the science of the 20th century.

—Vilenkin²⁰

A peaceful resolution of conflicts can be achieved using Berge equilibrium (BE). This concept appeared in 1994 in Russia, following a critical analysis of C. Berge’s book [202]. Interestingly, Berge wrote his book as a visiting professor at Princeton University, simultaneously with Nash, who also worked there under support of the Alfred P. Sloan Foundation.

A Berge equilibrium is a pair (x ^B, f ^B = (f ₁(x ^B), f ₂(x ^B), f ₃(x ^B))) defined by the equalities

$$\displaystyle \begin{aligned}\begin{array}{c} f_1\left(x^{\mathrm{B}}\right) = \max\limits_{(x_2,x_3) \in \mathrm{X}_2 \times \mathrm{X}_3} f_1\left(x^{\mathrm{B}}_1,x_2,x_3\right), \\ f_2\left(x^{\mathrm{B}}\right) = \max\limits_{(x_1,x_3) \in \mathrm{X}_1 \times \mathrm{X}_3} f_2\left(x_1,x^{\mathrm{B}}_2,x_3\right), \\ f_3\left(x^{\mathrm{B}}\right) = \max\limits_{(x_1,x_2) \in \mathrm{X}_1 \times \mathrm{X}_2} f_1\left(x_1,x_2,x^{\mathrm{B}}_3\right). \end{array} \end{aligned} $$

(2.2.2)

Equilibria (2.2.2) and (2.2.1) exhibit the following fundamental difference. In (2.2.1), each player directs all efforts to increase his individual payoff (the value of his payoff function) as much as possible. The antipode of (2.2.1) is (2.2.2), where each player strives to maximize the payoffs of the other players, ignoring his individual interests. Such an altruistic approach is intrinsic to kindred relations and occurs in religious communities. The elements of such altruism can be found in charity, sponsorship, and so on. The concept of Berge equilibrium also provides a solution to the Tucker problem in the well-known Prisoner’s Dilemma (see Example 2.6.1 below). Due to (2.2.2), an application of this equilibrium concept eliminates armed clashes and murderous wars. This is an absolute advantage of Berge equilibrium.

As a matter of fact, the Berge equilibrium had an unenviable fate. The publication of the book [202] in 1957 initiated a sharp response of Shubik [269, p. 821] (“…no attention has been paid to applications to economics…the book will be of a little direct interest to economists…”). Most likely, such a negative review in combination with Shubik’s authority in scientific community pushed away the Western experts in game theory and economics from the book [202]. In Russia, after its translation in 1961, the book was analyzed in depth (Russian researchers were not acquainted with Shubik’s review!) and the concept of Berge equilibrium was suggested on the basis of an appropriate modification of the notion of Nash equilibrium. The difference between Berge equilibrium and Nash equilibrium is that the former postulates stable payoffs against the deviations of all players and also reassigns the “ownership” of the payoff function (in the definition of a Nash equilibrium, the strategies of a separate player and all other players are interchanged). Note that the book [202] did not actually introduce the definition of Berge equilibrium, but it inevitably comes to mind while studying the results of Chaps. 1 and 5 of [202].

Subsequently, the Berge equilibrium was rigorously defined in 1994–1995 by K. Vaisman in his papers and dissertation [11, 13, 302], under the scientific supervision of V. Zhukovskiy. This concept was immediately applied in [280, 281] for noncooperative linear-quadratic positional games under uncertainty. Unfortunately, Vaisman’s sudden death at the age of 35 suspended further research on Berge equilibrium in Russia. At that time, however, the concept of Berge equilibrium was “exported from Russia” by Algerian postgraduates of V. Zhukovskiy Radjef [266] and Larbani [248]. Later on, it was actively used by Western researchers (e.g., see the survey [255] with over 50 references and also the recent review [131, pp. 53–56] published in Ukraine). As shown by these and more than 100 subsequent publications, most of research works are dedicated to the properties of Berge equilibrium, the specific features and modifications of this concept, and relations to Nash equilibrium. It seems that an incipient theory of Berge equilibrium will soon emerge as a rigorous mathematical theory. Hopefully, an intensive accumulation of facts will be replaced by the stage of evolutionary internal development.

This chapter reveals the internal instability of the set of Berge equilibria. To eliminate this negative feature, we suggest a method to construct a Berge equilibrium that is Pareto-maximal with respect to all other Berge equilibria. The method reduces to a saddle point calculation for an auxiliary zero-sum two-player game that is effectively designed using the original noncooperative game. As a supplement, we prove the existence of such a (Pareto refined) Berge equilibrium in mixed strategies under standard assumptions of mathematical game theory, i.e., compact strategy sets and continuous payoff functions of the players.

2.3 Compactness of the Set X^B

The notion of infinity is our greatest friend;

it is also the greatest enemy of our peace in mind.

—Pierpont²¹

It is shown that the set of Berge equilibria is closed and bounded.

Thus, we consider the mathematical model of a conflict in the form of a noncooperative N-player game, $N \geqslant 2$, described by an ordered triplet

$$\displaystyle \begin{aligned}\Gamma = \langle \{ \mathbb{N} \}, \{ \mathrm{X}_i \}_{i \in \mathbb{N} }, \{ f_i(x) \}_{i \in\mathbb{N} } \rangle. \end{aligned} $$

(2.3.1)

Here $\mathbb {N} = \{ 1,2,\ldots ,N \}$ denotes the set of players; each of the N players, forming no coalitions with other players, chooses his strategy (action) $x_i \in \mathrm {X}_i \subseteq \mathbb {R}^{n_i}$ (throughout the book, the symbol $\mathbb {R}^{k}, \; k \geqslant 1$, stands for the k-dimensional Euclidean space whose elements are ordered sets of k real numbers in the form of columns, with the standard scalar product and the Euclidean norm); such a choice yields a strategy profile $x\!=(x_1,\ldots ,x_N) \!\in \! \mathrm {X}\! =\!\prod _{i \in \mathbb {N}}\!\mathrm {X}_i \!\subseteq \!\mathbb {R}^{n}$ ($n\! = \!\sum _{i \!\in \mathbb {N}}\! n_i$); a payoff function f _i(x) defined on the set X numerically assesses the performance of player i $(i \in \mathbb {N})$; let (x∥z _i) = (x ₁, …, x _i−1, z _i, x _i+1, …, x _N) and f = (f ₁, …, f _N).

A pair $(x^{\mathrm {B}},f^{\mathrm {B}}) = ((x^{\mathrm {B}}_1,\ldots ,x^{\mathrm {B}}_N),(f_1(x^{\mathrm {B}}),\ldots ,f_N(x^{\mathrm {B}}))) \in \mathrm {X} \times \mathbb {R}^{N}$ is called a Berge equilibrium in game (2.3.1) if

$$\displaystyle \begin{aligned}\max\limits_{x \in \mathrm{X}} f_i\left(x\|x^{\mathrm{B}}_i\right) = f_i\left(x^{\mathrm{B}}\right) \;\;\; (i \in \mathbb{N}). \end{aligned} $$

(2.3.2)

In the sequel, we will consider mostly the strategy profiles x ^B from such pairs, also calling them Berge equilibria in game (2.3.1).

Property 2.3.1

If in the game Γ the sets X_i are closed and bounded, i.e., $\mathrm {X}_i \in \mathrm {comp} \:\mathbb {R}^{n_i}$, and the payoff functions f _i(⋅) are continuous, f _i(⋅) ∈ ∈ C(X) $(i \in \mathbb {N})$, then the set X^B of all Berge equilibria in the game Γ is compact in X (possibly, empty) and $f(\mathrm {X}^B) \in \mathrm {comp} \:\mathbb {R}^{N}$.

Proof

Since X^B ⊆X and $\mathrm {X} \in \mathrm {comp} \:\mathbb {R}^{n}$, then X^B is bounded. Thus, if we can show that X^B is closed, then $\mathrm {X}^B \in \mathrm {comp} \:\mathbb {R}^{n}$. Let us prove the closedness of X^B by contradiction. Assume that, for a infinite sequence $\{ x^{(k)} \}_{k=0}^{\infty }$, x ^(k) ∈X^B, there exist a subsequence $\{ x^{(k_r)} \}_{r=0}^{\infty }$ and a strategy profile x ^∗∈X such that, first, $\lim _{r \rightarrow \infty } x^{(k_r)} = x^{*}$ and, second, x ^∗∉X^B.

Since x ^∗∉X^B, there exist a strategy profile $\bar {x} \in \mathrm {X}$ and a number $j \in \mathbb {N}$ such that $f_j( \bar {x}\|x^{*}_j)\! >\! f_j(x^{*})$, where $x^{*}\!=(\!x^{*}_1,\ldots ,x^{*}_j,\ldots ,x^{*}_N\!)$ and, as before, $(\bar {x}\|x^{*}_j ) = (\bar {x}_1,\ldots ,\bar {x}_{j-1},x^{*}_j,\bar {x}_{j+1},\ldots ,\bar {x}_N)$.

Owing to the continuity of $f_j( \bar {x}\|x_j )$ and f _j(x) in x ∈X and the convergence $\lim _{r \rightarrow \infty } x^{(k_r)} = x^{*}$, there exists an integer M > 0 such that, for $r \geqslant M$, $f_j( \bar {x}\| x^{(k_r)}_j ) > f_i(x^{(k_r)})$. This strict inequality contradicts $f_j( x\| x^{\mathrm {B}}_j ) \leqslant f_j( x^{\mathrm {B}})$ ∀x ∈X, and the conclusion follows. $\blacksquare$

Corollary 2.3.1

Let the hypotheses of Property 2.3.1 be valid and the set X^B ≠ ∅ in the game Γ. Then there exists a Berge equilibrium that is Pareto-maximal with respect to all other equilibria x ^B ∈X^B in this game.

Indeed, since the set X^B is compact, f _i(⋅) ∈ C(X) $(i \in \mathbb {N})$ and the hypotheses of Property 2.3.1 hold, the N-criteria choice problem

$$\displaystyle \begin{aligned}\left\langle \mathrm{X}^B, \{ f_i(x) \}_{i \in \mathbb{N}} \right\rangle\end{aligned} $$

has a Pareto-maximal alternative x ^B ∈X^B [152, p. 149]. In other words, for every x ∈X^B, the system of N inequalities

$$\displaystyle \begin{aligned}f_i(x) \geqslant f_i(x^{\mathrm{B}}) \quad (i \in \mathbb{N}),\end{aligned} $$

with at least one strict inequality, is inconsistent.

2.4 Internal Instability of the Set X^B

It is easier to stop the Sun and move the Earth

than to decrease the sum of angles in a triangle,

to make parallels converge, and to drop perpendiculars

to the same line from a far distance.

—Kagan²²

It is found that there may exist two Berge equilibria, in one of which each player has a strictly greater payoff than in the other.

Property 2.4.1

The set X^B of all Berge equilibria can be internally unstable, i.e., in the game Γ there may exist two Berge equilibria x ⁽¹⁾ and x ⁽²⁾ such that, for all $i \in \mathbb {N}$,

$$\displaystyle \begin{aligned}f_i\left(x^{(1)}\right) > f_i\left(x^{(2)}\right). \end{aligned}$$

Example 2.4.1

Consider a noncooperative two-player game (N = 2) of the form

$$\displaystyle \begin{aligned} \Gamma_{2} \!\!=\!\! \left\langle \{ 1,2 \},\ \{ \mathrm{X}_i \!=\! [-1,\!+1] \}_{i =1,2 },\ \left\{ f_1(x)\!=\! -x^2_2 + 2x_1 x_2,\ f_2(x)\!=\! -x^2_1 + 2x_1 x_2 \right\} \right\rangle . \end{aligned}$$

In this game, the strategy profiles are x = (x ₁, x ₂) ∈ [−1, +1]², the strategy sets of both players coincide, X_i = [−1,  +1] (i = 1,  2), while the Berge equilibrium $x^{\mathrm {B}}=(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ is defined by the inequalities

$$\displaystyle \begin{aligned}\begin{array}{l} -x^2_2 + 2x^{\mathrm{B}}_1 x_2 \leqslant -\left(x^{\mathrm{B}}_2\right)^2 + 2x^{\mathrm{B}}_1 x^{\mathrm{B}}_2, \\ -x^2_1 + 2x_1 x^{\mathrm{B}}_2 \leqslant -\left(x^{\mathrm{B}}_1\right)^2 + 2x^{\mathrm{B}}_1 x^{\mathrm{B}}_2 \;\;\;\;\; \forall \: x_i \!\in\! [-1,+1] \quad (i=1,2), \end{array} \end{aligned}$$

or

$$\displaystyle \begin{aligned}-\left(x_2-x^{\mathrm{B}}_1\right)^2 \!\!\leqslant\! -\left(x^{\mathrm{B}}_2-x^{\mathrm{B}}_1\right)^2, \; -\left(x_1-x^{\mathrm{B}}_2\right)^2 \!\!\leqslant\! -(x^{\mathrm{B}}_1-x^{\mathrm{B}}_2)^2 \;\;\;\;\: \forall \: x_1,x_2 \!\in\! [-1,\!+1]\end{aligned} $$

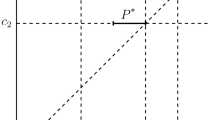
(these inequalities follow from (2.3.2)). Hence, $x^{\mathrm {B}}_1 =x^{\mathrm {B}}_2 = \alpha$ for all α = const ∈ [−1,  +1] (see Fig. 2.1a), and then $f^{\mathrm {B}}_i = f_i(x^{\mathrm {B}}) = \alpha ^2$ for all α = const ∈ [−1,  +1] (see Fig. 2.1b).

Fig. 2.1

(a) Set of Berge equilibria. (b) Payoffs in Berge equilibria

Thus, we have established that, first, there may exist a continuum of Berge equilibria (in Example 2.4.1, the set X^B = AB as illustrated by Fig. 2.1a) and, second, the set X^B is internally unstable, since f _i(0,  0) = 0 < f _i(1,  1) = 1 (i = 1,  2) (see Fig. 2.1b).

Hence, in the game Γ the players should use the Berge equilibrium that is Pareto-maximal with respect to all other Berge equilibria. We introduce the following definition for further exposition.

Definition 2.4.1

A strategy profile x ^∗∈X is called a Berge–Pareto equilibrium (BPE) in the game Γ if

• (1) x ^∗ is a Berge equilibrium in Γ (x ^∗ satisfies conditions (2.3.2));

• (2) x ^∗ is a Pareto-maximal alternative in the N-criteria choice problem

$$\displaystyle \begin{aligned}\Gamma_{\mathrm{c}} = \left\langle \mathrm{X}^{\mathrm{B}}, \{f_i(x)\}_{i \in \mathbb{N}} \right\rangle,\end{aligned} $$

i.e., for any alternatives x ∈X^B, the system of inequalities

$$\displaystyle \begin{aligned}f_i(x) \geqslant f_i(x^{*}) \;\; (i \in \mathbb{N}),\end{aligned} $$

with at least one strict inequality, is inconsistent.

In Example 2.4.1, we have two BPE, x ⁽¹⁾ = (−1; −1) and x ⁽²⁾ = (+1; +1), with the same payoffs f _i(x ⁽¹⁾) = f _i(x ⁽²⁾) = 1 (i = 1,  2).

Remark 2.4.1

If X^B ≠ ∅, $\mathrm {X}_i \in \mathrm {comp} \:\mathbb {R}^{n_i}$, and f _i(⋅) ∈ C(X) $(i \in \mathbb {N})$, then Definition 2.4.1 relies on Corollary 2.3.1, stating that the set of BPE is nonempty under the two requirements above.

Interestingly, the set of Nash equilibria in the game Γ is also internally unstable (this is demonstrated by Example 2.4.1 with the change x ₁ ↔ x ₂).

In the forthcoming sections, we will establish sufficient conditions for the existence of a BPE, which are reduced to a saddle point calculation for an auxiliary zero-sum two-player game that is effectively designed using the original noncooperative game.

2.5 No Guaranteed Individual Rationality of the Set X^B

Among the splendid generalizations effected by modern mathematics,

there is none more brilliant or more inspiring or more fruitful,

and none more commensurate with the limitless immensity of being itself,

than that which produced the great concept designated …

hyperspace or multidimensional space.

—Keyser²³

A Nash equilibrium has the property of individual rationality, whereas a Berge equilibrium generally does not, as illustrated by an example in this section. It is also established that there may exist a Berge equilibrium in which at least one player obtains a smaller payoff than the maximin.

Another negative property of a Berge equilibrium is the following.

Property 2.5.1

A Berge equilibrium may not satisfy the individual rationality conditions, as opposed to the Nash equilibrium x ^e in the game Γ₂ (under the assumptions $\mathrm {X}_i \in \mathrm {comp}\:\mathbb {R}^{n_i}$ and f _i(⋅) ∈ C(X) $(i \in \mathbb {N})$, the game Γ₂ (the game Γ with $\mathbb {N} = \{1,2\}$) satisfies the inequalities

$$\displaystyle \begin{aligned}f_1(x^{\mathrm{e}}) \geqslant \max\limits_{x_1 \in \mathrm{X}_1} \min\limits_{x_2 \in \mathrm{X}_2} f_1(x_1,x_2), \;\;\; f_2(x^{\mathrm{e}}) \geqslant \max\limits_{x_2 \in \mathrm{X}_2} \min\limits_{x_1 \in \mathrm{X}_1} f_2(x_1,x_2), \end{aligned}$$

known as the individual rationality conditions).

Example 2.5.1

Consider a noncooperative two-player game of the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Gamma_2^{\prime} &\displaystyle =&\displaystyle \langle \{1,2\}, \{ \mathrm{X}_1 = (-\infty,+\infty), \mathrm{X}_2 = [-1,+1] \}, \{ f_1(x)= \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; &\displaystyle =&\displaystyle -4x^2_1 + 2x_1 x_2 + x^2_2, f_2(x)= -(x_1 - 1)^2 +5 \} \rangle, \end{array} \end{aligned} $$

where x = (x ₁, x ₂). A Berge equilibrium $x^{\mathrm {B}}=(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ in the game $\Gamma _2^{\prime }$ is defined by the two equalities

$$\displaystyle \begin{aligned}\max\limits_{x_2 \in \mathrm{X}_2} f_1\left(x^{\mathrm{B}}_1,x_2\right) = f_1\left(x^{\mathrm{B}}\right), \;\;\; \max\limits_{x_1 \in \mathrm{X}_1} f_2\left(x_1,x^{\mathrm{B}}_2\right) = f_2\left(x^{\mathrm{B}}\right).\end{aligned} $$

The second equality holds only for the strategy $x^{\mathrm {B}}_1=1$. Due to the strong convexity of f ₁(x) in x ₂ (which follows from the fact that $\left . \frac {\partial ^2 f_1(x^{\mathrm {B}}_1 ,x_2)}{\partial x^2_2}\right |{ }_{x_2} = 2 > 0$), the maximum of the function

$$\displaystyle \begin{aligned}f_1\left(x^{\mathrm{B}}_1,x_2\right) = - 4 + 2x_2 + x^2_2\end{aligned} $$

is achieved on the boundary of X₂, more specifically, at the point $x^{\mathrm {B}}_2 = 1$. Thus, the game $\Gamma _2^{\prime }$ has the Berge equilibrium x ^B = (1,  1), and the corresponding payoff is f ₁(x ^B) = f ₁(1,  1) = −1.

Now, find $\max \limits _{x_1 \in \mathrm {X}_1} \min \limits _{x_2 \in \mathrm {X}_2} f_1(x_1,x_2)$ in two steps as follows. In the first step, construct a scalar function x ₂(x ₁) that implements the inner minimum:

$$\displaystyle \begin{aligned}\min\limits_{x_2 \in \mathrm{X}_2} f_1(x_1,x_2)=f_1(x_1,x_2(x_1)) \;\;\; \forall x_1 \in {\mathbf{X}}_1 .\end{aligned} $$

By the strong convexity of f ₁(x ₁, x ₂) in x ₂,

$$\displaystyle \begin{aligned}\left. \frac{\partial f_1(x_1,x_2)}{\partial x_2} \right|{}_{x_2(x_1)} = 2x_1 + 2x_2(x_1) = 0,\end{aligned} $$

yielding the unique solution x ₂(x ₁) = −x ₁ and $f_1[x_1]=f_1(x_1,x_2(x_1))=- 5 x^2_1$.

In the second step, construct the outer maximum, i.e., find

$$\displaystyle \begin{aligned}\max\limits_{x_1 \in \mathrm{X}_1} f_1[x_1] = \max\limits_{x_1 \in \mathbb{R}} f_1(x_1,x_2(x_1)) = \max\limits_{x_1 \in \mathbb{R}} \left[-5x^2_1\right] = 0.\end{aligned} $$

Consequently,

$$\displaystyle \begin{aligned}f_1(x^B) = -1 < 0 = \max\limits_{x_1 \in \mathbb{R}} f_1(x_1,x_2(x_1)) = \max\limits_{x_1 \in \mathbb{R}} \min\limits_{x_2 \in [-1,+1]} f_1(x_1,x_2),\end{aligned} $$

which shows that the individual rationality property may fail for a Berge equilibrium.

Remark 2.5.1

Individual rationality is a requirement for a “good” solution in both noncooperative and cooperative games: each player can guarantee the maximin individually, i.e., by his own maximin strategy, regardless of the behavior of the other players [173]. However, in a series of applications (especially for the linear-quadratic setups of the game), the maximin often does not exist. Such games were studied in the books [52, pp. 95–97, 110–116, 120] and [93, pp. 124–131].

In the case where game (2.3.1) has maximins, Vaisman suggested to incorporate the individual rationality property into the definition of a Berge equilibrium. Such equilibria are called Berge–Vaisman equilibria.

2.6 Two-Player Game

You don’t have to be a mathematician

to have a feel for numbers.

—Nash²⁴

The specific features of Berge equilibria in two-player games are identified.

Non-antagonistic Case

Consider a special case of game (2.3.1) with two players, i.e., the game Γ in which $\mathbb {N} = \{ 1,2 \}$. Then a Berge equilibrium $x^{\mathrm {B}}=(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ is defined by the equalities

$$\displaystyle \begin{aligned}f_1\left(x^{\mathrm{B}}\right) = \max\limits_{x_2 \in \mathrm{X}_2} f_1\left(x^{\mathrm{B}}_1,x_2\right), \quad f_2\left(x^{\mathrm{B}}\right) = \max\limits_{x_1 \in \mathrm{X}_1} f_2\left(x_1,x^{\mathrm{B}}_2\right).\end{aligned} $$

Recall that a Nash equilibrium x ^e in this two-player game is given by the conditions

$$\displaystyle \begin{aligned}f_1\left(x^{\mathrm{e}}\right) = \max\limits_{x_1 \in \mathrm{X}_1} f_1\left(x_1,x^{\mathrm{e}}_2\right), \quad f_2\left(x^{\mathrm{e}}\right) = \max\limits_{x_2 \in \mathrm{X}_2} f_2\left(x^{\mathrm{e}}_1,x_2\right).\end{aligned} $$

A direct comparison of these independent formulas leads to the following result.

Property 2.6.1

A Berge equilibrium in game (2.3.1) with $\mathbb {N} = \{ 1,2 \}$ coincides with a Nash equilibrium if both players interchange their payoff functions and then apply the concept of Nash equilibrium to solve the modified game.

Remark 2.6.1

In view of Property 2.6.1, a special theoretical study of Berge equilibrium in game (2.3.1) with $\mathbb {N} = \{ 1,2 \}$ seems unreasonable, despite careful attempts by a number of researchers. In fact, all results concerning Nash equilibrium in a two-player game are automatically transferred to the Berge equilibrium setting (of course, with an appropriate “interchange” of the payoff functions, as described by Property 2.6.1).

Let us proceed with an example of a two-player matrix game in which the players have higher payoffs in a Berge equilibrium than in a Nash equilibrium (in the setting of game, this is an analog of the Prisoner’s Dilemma).

Also note the following interesting fact for game (2.3.1) with $\mathbb {N} = \{ 1,2 \}$, $f_i(x)=x^T_1 A_i x_1 +x^T_2 B_i x_2$, the strategies $x_1 \in \mathbb {R}^{n_1}$ and $x_2 \in \mathbb {R}^{n_2}$, where the matrices A _i and B _i of compatible dimensions are square, constant and symmetric, A ₁ > 0, B ₁ < 0, A ₂ < 0, and B ₂ > 0 (the notation A > 0 (<) stands for the positive (negative) definiteness of the quadratic form x ^TAx): in this game, there exist no Nash equilibria, while the strategy profile $(0_{n_1},0_{n_2})$ forms a Berge equilibrium (as before, 0_k denotes the zero vector of dimension k).

Example 2.6.1

Consider the bimatrix game in which player 1 has two strategies, i.e., chooses between rows 1 and 2. Accordingly, the strategies of player 2 are represented by columns 1 and 2. For example, the choice of the strategy profile (1,  2) means that the payoffs of players 1 and 2 are 4 and 7, respectively.

According to the above definitions, in this bimatrix game the strategy profiles (2,  2) and (1,  1) are a Nash and Berge equilibrium, respectively. As 6 > 5, the payoffs of both players in the Berge equilibrium are strictly greater than their counterparts in the Nash equilibrium. The same result occurs in the Prisoner’s Dilemma, a well-known bimatrix game. Note that the paper [255] gave some examples of 2 × 2 bimatrix games in which the payoffs in a Nash equilibrium are greater than or equal to those in a Berge equilibrium.

Antagonistic Case

To conclude this section, consider the antagonistic case of game (2.3.1), which arises for Γ with $\mathbb {N} = \{ 1,2 \}$ and f ₂(x) = −f ₁(x) = f(x). In other words, consider an ordered triplet

$$\displaystyle \begin{aligned}\Gamma_{\mathrm{a}} = \left\langle \{1,2\}, \{ \mathrm{X}_i \}_{i=1,2}, f(x) \right\rangle.\end{aligned} $$

A conventional solution of the game Γ_a is the saddle point $x^0 = (x^0_1,x^0_2) \in \mathrm {X}_1 \times \mathrm {X}_2$, which is formalized here by the chain of inequalities

$$\displaystyle \begin{aligned}f\left(x^0_1,x_2\right) \leqslant f\left(x^0\right) \leqslant f\left(x_1,x^0_2\right) \;\;\; \forall \: x_i \in \mathrm{X}_i \; (i=1,2).\end{aligned} $$

(2.6.1)

Property 2.6.2

For the antagonistic case Γ_a of the game Γ, the Berge equilibrium $(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ matches the saddle point $(x^0_1,x^0_2)$ defined by (2.6.1).

The proof of this property follows immediately from the inequalities

$$\displaystyle \begin{aligned}f_1\left(x^{\mathrm{B}}_1,x_2\right) \leqslant f_1\left(x^{\mathrm{B}}\right), \quad f_2\left(x_1,x^{\mathrm{B}}_2\right) \leqslant f_2\left(x^{\mathrm{B}}\right) \;\;\; \forall \: x_i \in \mathrm{X}_i \; (i=1,2)\end{aligned} $$

and the identity f(x) = f ₂(x) = −f ₁(x) ∀ x ∈X. $\blacksquare$

2.7 Comparison of Nash and Berge Equilibria

There are only two kinds of certain knowledge:

Awareness of our own existence and the truths of mathematics.

—d’Alembert²⁵

A detailed comparison of Berge and Nash equilibria is made.

NE	BE
Stability
against a unilateral deviation of a single player, since the inequality $f_i (\!x^{\mathrm {e}}_1,\ldots ,x^{\mathrm {e}}_{i\!-\!1},x_i,x^{\mathrm {e}}_{i\!+\!1},\ldots ,x^{\mathrm {e}}_N \!) \!\! \leqslant \!\! f_i (\!x^{\mathrm {e}})$ holding ∀x i  ∈ Xi $(i\!\in \! \mathbb {N})$ implies that the payoff of the deviating player i is not greater than in the NE.	against the deviations of the coalition of all players except player i, since the inequality $f_i (x_1,\ldots ,x_{i\!-\!1},\! x^{\mathrm {B}}_i \!\! ,x_{i\!+\!1},\ldots ,\! x_N \!) \!\! \leqslant \!\! f_i (x^{\mathrm {B}} \!)$ holding ∀x j  ∈ Xj $(j \!\in \! \mathbb {N} \!\setminus \! \{i\}$, $i\!\in \! \mathbb {N})$ implies that the payoff of each player i under such a deviation of the coalition of the other N − 1 players from the BE is not greater than in the BE.
Individual rationality (IR)
Here and in the sequel, $x_{\mathbb {N} \setminus \! \{i\}} \!\!=\!\! (x_1,\ldots ,x_{i\!-\!1},$ $x_{i+1},\ldots ,x_N) \in {\mathbf {X}}_{\mathbb {N} \setminus \{i\}} = \prod \limits _{j \in \mathbb {N} \setminus \{i\}}\!\!\! {\mathbf {X}}_j.$ If x e exists and	Generally speaking, fails (see Property 2.5.1, Example 2.5.1, and Remark 2.5.1).
$f^{\mathrm {g}}_i = \max \limits _{x_i \!\in \! {\mathbf {X}}_i} \min \limits _{x_{\mathbb {N} \setminus \! \{i\}} \!\in \! {\mathbf {X}}_{\mathbb {N} \setminus \{i\}}} f(x\|x_i) =$ $= \min \limits _{x_{\mathbb {N} \setminus \! \{i\}} \!\in \! {\mathbf {X}}_{\mathbb {N} \setminus \{i\}}} f_i(x\|x^{\mathrm {g}}_i)$ $(i\in \mathbb {N})$, then $f_i(x^{\mathrm {e}}) \!\!\geqslant \!\! f^{\mathrm {g}}_i$ $(i \!\!\in \!\! \mathbb {N})$, i.e., NE satisfies the IR condition.
Internal instability
The set of NE is internally unstable (see proof in [54]).	The set of BE is internally unstable (see Property 2.4.1 and Example 2.4.1).
To eliminate this drawback both for the NE and BE ,
Pareto maximality with respect to
the other equilibria of a given type is required.
Saddle point (SP) in the game
$\Gamma _{a} = \left \langle \{1,2\}, \{ {\mathbf {X}}_i \}_{i=1,2}, \{ f_1(x_1,x_2),f_2(x_1,x_2)=-f_1(x_1,x_2) \} \right \rangle$
is a special case of NE and BE.
NE coincides with the SP $(x^{\mathrm {e}}_1,x^{\mathrm {e}}_2)$ of the form $\max \limits _{x_1 \in {\mathbf {X}}_1} f_1(x_1,x^{\mathrm {e}}_2)\!\! =$ $=f_1(x^{\mathrm {e}}_1,x^{\mathrm {e}}_2) = \min \limits _{x_2 \in {\mathbf {X}}_2} f_1(x^{\mathrm {e}}_1,x_2)$.	The BE coincides with the SP $(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ of the form $\max \limits _{x_2 \in {\mathbf {X}}_2} f_1(x^{\mathrm {B}}_1,x_2) =$ $=f_1(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2) = \min \limits _{x_1 \in {\mathbf {X}}_1} f_1(x_1,x^{\mathrm {B}}_2)$.

Conclusions

The main difficulty in many modern developments of mathematics

is not to learn new ideas but to forget old ones.

—Sawyer²⁶

Nash equilibria have three undisputable advantages, namely, they are stable, coincide with the saddle point (containing this generally accepted concept as a special case), and satisfy the individual rationality condition. The first and second advantages are shared also by the Berge equilibria.

At the same time, Nash equilibria suffer from several drawbacks, namely, the internal instability of the set of NE and selfishness (each player seeks to increase his individual payoff, as by definition $\forall i \in \mathbb {N}$: $f_i(x^{\mathrm {e}})=\max \limits _{x_i \in \mathrm {X}_i} f_i(x^{\mathrm {e}}\|x_i)$).

Internal instability is intrinsic to the set of BE too. This negative feature can be eliminated by requiring Pareto maximality for the NE and BE. The selfish nature of NE is eliminated using the altruistic orientation of BE (“help the others if you seek for their help”). This constitutes a clear merit of BE as a way of benevolent conflict resolution.

2.8 Sufficient Conditions

Mathematics as an expression of the human mind reflects the active will,

the contemplative reason, and the desire for aesthetic perfection.

Its basic elements are logic and intuition, analysis and construction,

generality and individuality. Though different traditions may emphasize

different aspects, it is only the interplay of these antithetic forces

and the struggle for their synthesis that constitute the life, usefulness,

and supreme value of mathematical science.

—Courant²⁷

2.8.1 Continuity of the Maximum Function of a Finite Number of Continuous Functions

I turn with terror and horror from this lamentable scourge

of continuous functions with no derivatives.²⁸

An auxiliary result from operations research is described, which will prove fruitful for the ensuing theoretical developments.

Consider N + 1 scalar functions φ _i(x, z) = f _i(x∥z _i) − f _i(z) $(i \in \mathbb {N})$ and $\varphi _{N+1} (x,z) = \sum \limits _{i \in \mathbb {N}} \left [ f_i(x) - f_i(z) \right ]$ that are defined on the Cartesian product X ×Z; from this point on, all strategy profiles $x=(x_1,\ldots ,x_N) \in \mathrm {X} = \prod _{i \in \mathbb {N}} \mathrm {X}_i \subset \mathbb {R}^{n}$ $(n = \sum _{i \in \mathbb {N}} n_i)$, and also x _i, z _i ∈X_i $(i \in \mathbb {N})$, $z=(z_1,\ldots ,z_N) \in \mathrm {Z} = \mathrm {X} \subset \mathbb {R}^{n}$ (recall that (x∥z _i) = (x ₁, …, x _i−1, z _i, x _i+1, …, x _N)).

Lemma 2.8.1

If the N + 1 scalar functions φ _j(x, z) $(j\!=\!1,\ldots ,N,N\!+\!1\!)$ are continuous on X ×Z while the sets X and Z are compact $(\mathrm {X},\mathrm {Z} \in \mathrm {comp} \: \mathbb {R}^{n})$, then the function

$$\displaystyle \begin{aligned}\varphi (x,z) = \max\limits_{j\!=\!1,\ldots,N\!+\!1} \varphi_j (z,z) \end{aligned} $$

(2.8.1)

is also continuous on X ×Z.

The proof of a more general result can be found in many textbooks on operations research, e.g., [136, p. 54]; it was included even in textbooks on convex analysis [46, p. 146]. Note that function (2.8.1) is called the Germeier convolution of the functions φ _j(x, z) $(j\!=\!1,\ldots , N\!+\!1\!).$

Finally, note that our choice of Hermite’s quote on “terror and horror” refers to the fact that although each of the functions φ _j(x, z) can be differentiable, in general this is not necessarily true for the function φ(x, z) defined by (2.8.1).

2.8.2 Reduction to Saddle Point Design

The result presented in this section is the pinnacle of our book.

Thus, using the payoff functions f _i(x) of game (2.3.1), construct the Germeier convolution

$$\displaystyle \begin{aligned}\varphi (x,z) \!= \max \!\left\{ \! [f_i(x\|z_i) \!-\! f_i(z) \; (i \in \mathbb{N})], \!\left( \sum_{j \in \mathbb{N}} f_j(x) \!-\!\! \sum_{j \in \mathbb{N}} f_j(z) \right) \! \right\}, \end{aligned} $$

(2.8.2)

with the domain of definition X × (Z = X).

A saddle point (x ⁰, z ^B) ∈X ×Z of the scalar function φ(x, z) in the zero-sum two-player game

$$\displaystyle \begin{aligned}\Gamma^{\mathrm{a}} = \langle \mathrm{X}, \mathrm{Z}=\mathrm{X}, \varphi (x,z) \rangle \end{aligned}$$

is defined by the chain of inequalities

$$\displaystyle \begin{aligned}\varphi \left(x,z^{\mathrm{B}}\right) \leqslant \varphi \left(x^0,z^{\mathrm{B}}\right) \leqslant \varphi \left(x^0,z\right) \;\;\; \forall \: x,z \in \mathrm{X}. \end{aligned} $$

(2.8.3)

Theorem 2.8.1

If in the zero-sum two-player game Γ ^a, there exists a saddle point (x ⁰, z ^B), then the minimax strategy z ^B is a Berge–Pareto equilibrium in noncooperative game (2.3.1).

Proof

In view of (2.8.2), the first inequality in (2.8.3) with z = x ⁰ shows that φ(x ⁰, x ⁰) = 0. By (2.8.3) and transitivity, for all x ∈X,

$$\displaystyle \begin{aligned}\varphi \left(x,z^{\mathrm{B}}\right) \! = \! \max \! \left\{ \! \left(f_i\left(x\|z^{\mathrm{B}}_i\right) \!-\! f_i\left(z^{\mathrm{B}}\right)\right) \: (i \in \mathbb{N}), \!\left( \! \sum_{j \in \mathbb{N}} f_j(x) \!-\!\!\! \sum_{j \in \mathbb{N}} f_j\left(z^{\mathrm{B}}\right) \!\right) \!\! \right\} \!\leqslant\! 0.\end{aligned} $$

Hence, for each $i \in \mathbb {N}$ and all x ∈X,

$$\displaystyle \begin{aligned}f_i\left(x\|z^{\mathrm{B}}_i\right) - f_i\left(z^{\mathrm{B}}\right) \leqslant 0, \quad \sum_{j \in \mathbb{N}} f_j(x) \leqslant \sum_{j \in \mathbb{N}} f_j\left(z^{\mathrm{B}}\right).\end{aligned} $$

Hence, for all x ∈X we have

$$\displaystyle \begin{aligned} f_i\left(x\|z^{\mathrm{B}}_i\right) \leqslant f_i\left(z^{\mathrm{B}}\right) \;\; (i \in \mathbb{N}), \;\;\; \max\limits_{x \in \mathrm{X}^B} \sum_{j \in \mathbb{N}} f_j(x) = \sum_{j \in \mathbb{N}} f_j\left(z^{\mathrm{B}}\right).\end{aligned} $$

(2.8.4)

Since the first N inequalities in (2.8.4) hold for all x ∈X, the strategy profile x ^B = z ^B satisfies the Berge equilibrium requirements (2.3.2) in the game Γ. The last equality in (2.8.4) where x ∈X^B (the set of Berge equilibria) is a sufficient condition [152, p. 71] for x ^B = z ^B to be a Pareto-maximal alternative in the N-criteria choice problem $\langle \mathrm {X}^{\mathrm {B}}, \{f_i(x)\}_{i \in \mathbb {N}} \rangle$. Thus, by Definition 2.4.1, the resulting strategy profile z ^B ∈X is a Berge–Pareto equilibrium in game (2.3.1). $\blacksquare$

Remark 2.8.1

Theorem 2.8.1 suggests the following design method of a Berge–Pareto equilibrium in the noncooperative game (2.3.1):

first, construct the function φ(x, z) using formula (2.8.2);

second, find the saddle point (x ⁰, z ^B) of the function φ(x, z) from the chain of inequalities (2.8.3).

Then the resulting strategy profile z ^B ∈X is a Berge–Pareto equilibrium in game (2.3.1).

2.8.3 Germeier Convolution

The world of curves has a richer texture than the world of points.

It has been left for the twentieth century to penetrate into this full richness.

—Wiener²⁹

Let us associate with game (2.3.1) the N-criteria choice problem

$$\displaystyle \begin{aligned}\Gamma_\nu = \langle \mathrm{X}, \{ f_i(x) \}_{i \in\mathbb{N} } \rangle , \end{aligned}$$

where $\mathrm {X} =\prod _{i\in \mathbb {N}}\mathrm {X}_i$ is the set of all admissible alternatives and f(x) = (f ₁(x), …, f _N(x)) is the N-dimensional vector criterion. In the problem Γ_ν, a decision maker (DM) seeks to choose an alternative x ∈X in order to maximize the values of all N criteria (objective functions) f ₁(x), …, f _N(x).

2.8.3.1 Necessary and Sufficient Conditions

In Definition 2.4.1 we have used the following notion of a vector optimum for the problem Γ_ν.

Definition 2.8.1

An alternative x ^P ∈X is called Pareto-maximal in the problem Γ_ν if, for any x ∈X, the combined inequalities

$$\displaystyle \begin{aligned}f_i(x) \geqslant f_i(x^{\mathrm{P}}) \;\;\; (i\in\mathbb{N}), \end{aligned}$$

with at least one strict inequality, are inconsistent. An alternative x ^S ∈X is called Slater-maximal in the problem Γ_ν if, for any x ∈X, the combined strict inequalities

$$\displaystyle \begin{aligned}f_i(x) > f_i(x^{\mathrm{S}}) \;\;\; (i\in\mathbb{N}) \end{aligned}$$

are inconsistent.

In this section, we are dealing with the Germeier convolution

$$\displaystyle \begin{aligned} \max\limits_{i\in\mathbb{N}} \mu_i f_i(x) = \varphi(x), \end{aligned} $$

(2.8.5)

where the constants μ _i belong to the set M of positive vectors from $\mathbb {R}^N$ (sometimes, with the unit sum of their components).

Note that if f _i(x) = −ψ _i(x), then formula (2.8.5) yields the standard Germeier convolution (with φ(x) = −ψ(x)) given by

$$\displaystyle \begin{aligned} \psi(x) = \min\limits_{i\in\mathbb{N}} \mu_i \psi_i(x), \end{aligned} $$

(2.8.6)

since

$$\displaystyle \begin{aligned}\max\limits_{i\in\mathbb{N}} \mu_i f_i(x) = - \min\limits_{i\in\mathbb{N}} \mu_i \psi_i(x). \end{aligned}$$

Most applications employ Germeier convolutions of two types:

$$\displaystyle \begin{aligned}\psi(x) = \min\limits_{i\in\mathbb{N}} \frac{\psi_i(x)}{a_i}, \end{aligned}$$

where a _i = const > 0 are convolution parameters, i = 1, …, N, and

$$\displaystyle \begin{aligned}\psi(x) = \min\limits_{i\in\mathbb{N}} \mu_i \psi_i(x), \end{aligned}$$

where μ _i = const > 0 are convolution parameters, i = 1, …, N. Clearly, the transition from the first form to the second can be performed by the change of variables $\mu _i = \frac {1}{a_i}$.

The following results were obtained in multicriteria choice theory.

Germeier’s theorem ([152, p. 66])

. Consider the N-criteria choice problem

$$\displaystyle \begin{aligned}\Gamma_\nu = \langle \mathrm{X}, \{ f_i(x) \}_{i \in\mathbb{N} } \rangle, \end{aligned}$$

and assume that the objective functions f _i(x) are positive for all x ∈X and $i\in \mathbb {N}$.

An alternative x ^S ∈X is Slater-maximal in Γ _ν if and only if there exists a vector μ = (μ ₁, …, μ _N) ∈M such that

$$\displaystyle \begin{aligned} \max\limits_{x \in \mathrm{X}} \min\limits_{i\in\mathbb{N}} \mu_i f_i(x) = \min\limits_{i\in\mathbb{N}} \mu_i f_i(x^{\mathrm{S}}). \end{aligned} $$

(2.8.7)

For the Slater-maximal alternatives x ^S ∈X, let $\mu = \mu ^{\mathrm {S}} = (\mu _1^{\mathrm {S}},\ldots ,\mu _N^{\mathrm {S}})$, where

$$\displaystyle \begin{aligned}\mu_i^{\mathrm{S}} = \frac{\lambda^0}{f_i(x^S)} \;\;\; (i\in\mathbb{N}), \;\;\; \lambda^0 = \frac{1}{ \sum_{i\in\mathbb{N} }\frac{1}{f_i(x^{\mathrm{S}})}}, \end{aligned}$$

which leads to

$$\displaystyle \begin{aligned}\max\limits_{x \in \mathrm{X}}\min\limits_{i\in\mathbb{N}}\mu_i^{\mathrm{S}} f_i(x^S) = \lambda^0. \end{aligned}$$

Recall that M is the set of positive vectors $\mu = (\mu _1,\ldots ,\mu _N) \in \mathbb {R}^N$ (possibly with the unit sum of components). The next result is a useful generalization of Germeier’s theorem.

Corollary 2.8.1 ([152, p. 67])

. Suppose x ^S ∈X and ζ _i(y) $(i\in \mathbb {N})$ are increasing functions of the variable $y \in \mathbb {R}$ that satisfy

$$\displaystyle \begin{aligned}\zeta_1(f_1(x^{\mathrm{S}}))=\zeta_2(f_2(x^{\mathrm{S}}))= \cdots = \zeta_N(f_N(x^{\mathrm{S}})). \end{aligned}$$

An alternative x ^S is Slater-maximal in the multicriteria choice problem Γ _ν if and only if

$$\displaystyle \begin{aligned}\zeta_1(f_1(x^{\mathrm{S}})) = \max\limits_{x \in \mathrm{X}} \min\limits_{i\in\mathbb{N}} \zeta_i(f_i(x)). \end{aligned}$$

Corollary 2.8.2 ([152, p. 68])

. An alternative x ^S is Slater-maximal in the multicriteria choice problem Γ _ν if and only if

$$\displaystyle \begin{aligned}\max\limits_{x \in \mathrm{X}} \min\limits_{i\in\mathbb{N}} \left[ f_i(x) - f_i(x^{\mathrm{S}}) \right] = 0. \end{aligned}$$

Finally, a Pareto-maximal alternative x ^P in the problem Γ _ν has the following property.

Proposition 2.8.1 ([152, p. 72])

. Let x ^P  ∈ X and f _i(x ^P) > 0 $(i\in \mathbb {N})$. An alternative x ^P is Pareto-maximal in the multicriteria choice problem Γ _ν if and only if there exists a vector

$$\displaystyle \begin{aligned}\mu = (\mu_1,\ldots,\mu_N) \in M =\{ \mu \: | \: \mu_i = \mathrm{const} > 0 \; (i\in\mathbb{N}), \; \sum_{i\in\mathbb{N}} \mu_i = 1 \} \end{aligned}$$

such that f(x ^P) yields the maximum point of the function $\sum _{i\in \mathbb {N}} f_i(x)$ on the set

$$\displaystyle \begin{aligned}\left\{ f(\mathrm{X}) = \bigcup\limits_{x\in\mathrm{X}} f(x) \mid \min\limits_{i\in\mathbb{N}} \mu_i f_i(x^{\mathrm{P}}) \geqslant \max\limits_{x \in \mathrm{X}} \min\limits_{i\in\mathbb{N}} \mu_i f_i(x) \right\} .\end{aligned} $$

2.8.3.2 Geometrical Interpretation

Consider the Germeier convolution in the case of two criteria in the choice problem Γ_ν, i.e., f(x) = (f ₁(x), f ₂(x)). Assume that at some point A = (f ₁(x ^A), f ₂(x ^A)) one has

$$\displaystyle \begin{aligned}\mu_1 f_1(x^A) = \mu_2 f_2(x^A) = 1 \end{aligned}$$

for some parameter values, i.e., $f_1(x^A) = \frac {1}{\mu _1}$ and $f_2(x^A) = \frac {1}{\mu _2}$ (see Fig. 2.2). Then the Germeier convolution takes the form

$$\displaystyle \begin{aligned}\min\limits_{i=1,2} f_i(x^A) = 1. \end{aligned}$$

Then the following relations hold on the rays originating from the point A parallel to the coordinate axes:

• 1. $\mu _1 f_1(x) \geqslant 1$ and μ ₁f ₂(x) = 1 on the horizontal ray, or

  Fig. 2.2

  

  Contour lines of the function $\min \limits _{i\in \{1,2\}}\mu _i f_i(x)$

• 2. μ ₁f ₁(x) = 1 and $\mu _1 f_2(x) \geqslant 1$ on the vertical ray.

Hence, $\min _{i\in \mathbb {N}} \mu _i f_i(x) = 1$ on these rays. Consequently, the contour lines of the Germeier convolution coincide with the boundaries of the cone $\{ f(x^A) + \mathbb {R}^2_{+} \}$, where $\mathbb {R}^2_{+} = \{ f=(f_1,f_2) \mid f_i \geqslant 0 \: (i=1,2) \}$. In the same way, the contour lines of min_{i ∈{1;2}}μ _if _i(x) = γ are defined by the vertical and horizontal rays originating from the point $f(\widetilde {x}) =(f_1(\widetilde {x}),f_2(\widetilde {x}))$, where $\mu _1 f_1(\widetilde {x}) = \mu _2 f_2(\widetilde {x}) = \gamma$. In other words, the contour lines of the Germeier convolution min_{i ∈{1;2}}μ _if _i(x) = γ form the boundaries of the cone $\{ f(\widetilde {x}) + \mathbb {R}^2_{+} \}$, where $f(\widetilde {x}) = \gamma f(x^A)$.

In the general case of N criteria, the level surfaces form the boundaries of the cone $\{ f(\widetilde {x}) + \mathbb {R}^N_{+} \}$, where $f(\widetilde {x})$ is any point satisfying the relation $\min _{i \in \mathbb {N}} \mu _i f_i(x) = \gamma = \mathrm {const} > 0$ $(i\in \mathbb {N})$. Therefore, the level surfaces of the Germeier convolution are the boundaries of the cone of points that dominate its vertex.

It is geometrically obvious that x ^S is a Slater-maximal alternative in the bi-criteria choice problem Γ_ν (N = 2) if and only if the interior of the orthant $\mathbb {R}^N_{+}$ shifted to the point f(x ^S) does not intersect f(X) (see Fig. 2.3).

Fig. 2.3

Geometrical interpretation of Germeier’s theorem

2.9 Mixed Extension of a Noncooperative Game

The value of pure existence proofs consists precisely in that

the individual construction is eliminated by them and that

many different constructions are subsumed under one fundamental idea,

so that only what is essential to the proof stands out clearly;

brevity and economy of thought are the raison d’être

of existence proofs…To prohibit existence proofs…

is tantamount to relinquishing the science of mathematics altogether.

—Hilbert³⁰

2.9.1 Mixed Strategies and Mixed Extension of a Game

The theory of probabilities is at bottom nothing but common sense

reduced to calculus; it enables us to appreciate with exactness that

which accurate minds feel with a sort of instinct for which ofttimes

they are unable to account…It teaches us to avoid the illusions

which often mislead us; …there is no science more worthy of

our contemplations nor a more useful one for admission to our system of

public education.

—Laplace³¹

The mixed extension of a game that includes mixed strategies and profiles as well as expected payoffs is formalized.

Let us, consider the noncooperative N-player game (2.3.1). For each compact set $\mathrm {X}_i \subset \mathbb {R}^{n_i}$ $(i \in \mathbb {N})$, consider the Borel σ-algebra $\mathcal {B}(\mathrm {X}_i)$, i.e., the minimal σ-algebra that contains all closed subsets of the compact set X_i (recall that a σ-algebra is closed under taking complements and unions of countable collections of sets).

Assuming that there exist no Berge–Pareto equilibria x ^B (see Definition 2.4.1) in the class of pure strategies x _i ∈X_i $(i \in \mathbb {N})$, we will extend the set X_i of pure strategies x _i to the mixed ones, using the approach of Borel [204], von Neumann [261], and Nash [257] and their followers [192, 194, 195, 197, 198]. Next, the idea is to establish the existence of (properly formalized) mixed strategy profiles in game (2.3.1) that satisfy the requirements of a Berge–Pareto equilibrium (an analog of Definition 2.4.1).

Thus, we use the Borel σ-algebras $\mathcal {B}(\mathrm {X}_i)$ for the compact sets X_i $(i \in \mathbb {N})$ and the Borel σ-algebra $\mathcal {B}(\mathrm {X})$ for the set of strategy profiles $\mathrm {X}= \prod _{i \in \mathbb {N}}\mathrm {X}_i$, so that $\mathcal {B}(\mathrm {X})$ contains all Cartesian products of arbitrary elements of the Borel σ-algebras $\mathcal {B}(\mathrm {X}_i)$ $(i \in \mathbb {N})$.

In accordance with mathematical game theory, a mixed strategy ν _i(⋅) of player i will be identified with a probability measure on the compact set X_i. By the definition in [122, p. 271] and notations in [108, p. 284], a probability measure is a nonnegative scalar function ν _i(⋅) defined on the Borel σ-algebra $\mathcal {B}(\mathrm {X}_i)$ of all subsets of the compact set $\mathrm {X}_i \subset \mathbb {R}^{n_i}$ that satisfies the following conditions:

• 1. $\nu _i(\bigcup \nolimits _k Q^{(i)}_k) = \bigcup \nolimits _k \nu _i(Q^{(i)}_k)$ for any sequence $\{Q^{(i)}_k\}_{k=1}^{\infty }$ of pairwise disjoint elements from $\mathcal {B}(\mathrm {X}_i)$ (countable additivity);

• 2. ν _i(X_i) = 1 (normalization), which yields $\nu _i(Q^{(i)}) \leqslant 1$ for all $Q^{(i)} \in \mathcal {B}(\mathrm {X}_i)$.

Let {ν _i} denote the set of all mixed strategies of player i $(i \in \mathbb {N})$.

Also note that the product measures ν(dx)  =  ν ₁(dx ₁) ⋯ ν _N(dx _N), see the definitions in [122, p. 370] (and the notations in [108, p. 123]), are probability measures on the strategy profile set X. Let {ν} be the set of such probability measures (strategy profiles). Once again, we emphasize that in the design of the product measure ν(dx) the role of a σ-algebra of subsets of the set X₁ ×⋯ ×X_N = X is played by the smallest σ-algebra $\mathcal {B}(\mathrm {X})$ that contains all Cartesian products Q ⁽¹⁾ ×⋯ × Q ^(N), where $Q^{(i)} \in \mathcal {B}(\mathrm {X_i})$ $(i \in \mathbb {N})$. The well-known properties of probability measures [41, p. 288], [122, p. 254] imply that the sets of all possible measures ν _i(dx _i) $(i \in \mathbb {N})$ and ν(dx) are weakly closed and weakly compact ([122, pp. 212, 254], [180, pp. 48, 49]). As applied, e.g., to {ν}, this means that from any infinite sequence {ν ^(k)} (k = 1,  2, …) one can extract a subsequence $\{\nu ^{(k_j)}\}$ (j = 1,  2, …) that weakly converges to a measure ν ⁽⁰⁾(⋅) ∈{ν}. In other words, for any continuous scalar function φ(x) on X, we have

$$\displaystyle \begin{aligned}\lim_{j\rightarrow\infty} \int\limits_{\mathrm{X}} \varphi(x)\nu^{(k_j)}(dx) = \int\limits_{\mathrm{X}} \varphi(x)\nu^{(0)}(dx) \end{aligned}$$

and ν ⁽⁰⁾(⋅) ∈{ν}. Owing to the continuity of φ(x), the integrals $\int \limits _{\mathrm {X}} \varphi (x)\nu (dx)$ (the expectations) are well-defined; by Fubini’s theorem,

$$\displaystyle \begin{aligned}\int\limits_{\mathrm{X}} \varphi(x)\nu(dx) = \int\limits_{\mathrm{X}_1} \cdots \int\limits_{\mathrm{X}_N} \varphi(x)\nu_N(dx_N) \cdots \nu_1(dx_1), \end{aligned}$$

and the order of integration can be interchanged.

Let us associate with game (2.3.1) in pure strategies its mixed extension

$$\displaystyle \begin{aligned} \langle \mathbb{N}, \{\nu_i\}_{i \in \mathbb{N}}, \{ f_i[\nu] = \int\limits_{\mathrm{X}} f_i[x]\nu(dx) \}_{i \in \mathbb{N}} \rangle, \end{aligned} $$

(2.9.1)

where, like in (2.3.1), $\mathbb {N}$ is the set of players while {ν _i} is the set of mixed strategies ν _i(⋅) of player i. In game (2.9.1), each conflicting party $i \in \mathbb {N}$ chooses its mixed strategy ν _i(⋅) ∈{ν _i}, thereby forming a mixed strategy profile ν(⋅) ∈{ν}; the payoff function of each player i, i.e., the expectation

$$\displaystyle \begin{aligned}f_i[\nu] = \int\limits_{\mathrm{X}} f_i[x]\nu(dx), \end{aligned}$$

is defined on the set {ν}.

For game (2.9.1), the notion of a Berge–Pareto equilibrium x ^∗ (see Definition 2.4.1) has the following analog.

Definition 2.9.1

A mixed strategy profile ν ^∗(⋅) ∈{ν} is called a Berge–Pareto equilibrium in the mixed extension (2.9.1) (equivalently, a Berge–Pareto equilibrium in mixed strategies in game (2.3.1)) if

first, the profile ν ^∗(⋅) is a Berge equilibrium in game (2.9.1), i.e.,

$$\displaystyle \begin{aligned} \max\limits_{\nu_{\mathbb{N} \setminus \{i\}}(\cdot) \in \{ \nu_{\mathbb{N} \setminus \{i\}} \}} f_i\left(\nu\|\nu^{*}_i\right) = f_i(\nu^{*}) \;\;\; (i \in \mathbb{N}), \end{aligned} $$

(2.9.2)

and second, ν ^∗(⋅) is a Pareto-maximal alternative in the N-criteria choice problem

$$\displaystyle \begin{aligned}\langle \{\nu^{\mathrm{B}}\}, \{f_i(\nu)\}_{i \in \mathbb{N}} \rangle, \end{aligned}$$

i.e., for all ν(⋅) ∈{ν ^B}, the system of inequalities

$$\displaystyle \begin{aligned}f_i(\nu) \geqslant f_i(\nu^{*}) \;\;\; (i \in \mathbb{N}), \end{aligned}$$

with at least one strict inequality, is inconsistent.

Here and in the sequel,

$\nu _{\mathbb {N} \setminus \{i\}}(dx_{\mathbb {N} \setminus \{i\}}) = \nu _1(dx_1) \cdots \nu _{i-1}(dx_{i-1}) \nu _{i+1}(dx_{i+1}) \cdots \nu _{N}(dx_{N})$, $(\nu \|\nu ^{*}_i)=(\nu _1(dx_1) \cdots \nu _{i-1}(dx_{i-1}) \nu ^{*}_{i}(dx_{i}) \nu _{i+1}(dx_{i+1}) \cdots \nu _{N}(dx_{N}))$, $\nu ^{*}(dx)=\nu ^{*}_1(dx_1)\cdots \nu ^{*}_N(dx_N)$, $\{ \nu _{\mathbb {N} \setminus \{i\}} \} = \{ \nu _{\mathbb {N} \setminus \{i\}} (\cdot ) \}$; in addition, {ν ^B(⋅)} denotes the set of Berge equilibria ν ^B(⋅), i.e., the strategy profiles that satisfy (2.9.2) with ν ^∗ replaced by ν ^B. Let {ν ^∗} be the set of mixed strategy profiles in game (2.9.1) that are given by the two requirements of Definition 2.9.1.

The following sufficient condition for Pareto maximality is obvious, see the statement below.

Remark 2.9.1

A mixed strategy profile ν ^∗(⋅) ∈{ν} is Pareto-maximal in the game $\tilde {\Gamma }_\nu = \langle \{\nu ^{\mathrm {B}}\}, \{f_i(\nu )\}_{i \in \mathbb {N}}\rangle$ if

$$\displaystyle \begin{aligned}\max\limits_{\nu(\cdot)\in\{\nu^{\mathrm{B}}\}} \sum_{i \in \mathbb{N}} f_i(\nu) = \sum_{i \in \mathbb{N}} f_i(\nu^{*}). \end{aligned}$$

2.9.2 Préambule

Proposition 2.9.1

In game (2.3.1), suppose the sets X_i are compact, the payoff functions f _i(x) are continuous on X = X₁ ×⋯ ×X_N, and the set of mixed strategy Berge equilibria {ν ^B} that satisfy (2.9.2) with ν ^∗ replaced by ν ^B is nonempty.

Then {ν ^B} is a weakly compact subset of the set of mixed strategy profiles {ν} in game (2.9.1).

Proof

To establish the weak compactness of the set {ν ^B}, take an arbitrary scalar function ψ(x) that is continuous on the compact set X and an infinite sequence of mixed strategy profiles

$$\displaystyle \begin{aligned} \nu^{(k)} (\cdot) \in \{\nu^{\mathrm{B}}\} \;\;\; (k=1,2,\ldots) \end{aligned} $$

(2.9.3)

in game (2.9.1). Inclusion (2.9.3) (hence, {ν ^B}⊂{ν}) implies {ν ^(k)(⋅)}⊂{ν}. As mentioned earlier, the set {ν} is weakly compact; hence, there exist a subsequence $\{\nu ^{(k_j)} (\cdot )\}$ and a measure ν ⁽⁰⁾(⋅) ∈{ν} such that

$$\displaystyle \begin{aligned}\lim_{j\rightarrow\infty} \int\limits_{\mathrm{X}} \psi(x)\nu^{(k_j)}(dx) = \int\limits_{\mathrm{X}} \psi(x)\nu^{(0)}(dx). \end{aligned}$$

We will show that ν ⁽⁰⁾(⋅) ∈{ν ^B(⋅)}by contradiction. Assume that ν ⁽⁰⁾(⋅) does not belong to {ν ^B}. Then for sufficiently large j, one can find a number $i \in \mathbb {N}$ and a strategy profile $\bar {\nu } (\cdot ) \in \{\nu \}$ such that

$$\displaystyle \begin{aligned}f_i\left[\bar{\nu}\|\nu^{(k_j)}_{i}\right] > f_i\left[\nu^{(k_j)}\right], \end{aligned}$$

which clearly contradicts the inclusion $\{\nu ^{(k_j)} (\cdot )\} \in \{\nu ^{\mathrm {B}}\}$.

Thus, we have proved the requisite weak compactness. $\blacksquare$

Corollary 2.9.1

In a similar fashion, one can prove the compactness (closedness and boundedness) of the set

$$\displaystyle \begin{aligned}f\left[\left\{\nu^B\right\}\right] = \bigcup\limits_{\nu(\cdot) \in \{\nu^B\}} f[\nu], \mathit{\text{ where }} f=(f_1,\ldots,f_N), \end{aligned}$$

in the criteria space $\mathbb {R}^{N}$.

Proposition 2.9.2

If in game (2.9.1) the sets $\mathrm {X}_i \in \mathrm {comp}\:\mathbb {R}^{n_i}$ and f _i(⋅) ∈ C(X) $(i \in \mathbb {N})$, then the function

$$\displaystyle \begin{aligned} \varphi(x,z) = \!\!\!\!\! \max\limits_{r=1,\ldots,N+1} \varphi_r(x,z) \end{aligned} $$

(2.9.4)

satisfies the inequality

$$\displaystyle \begin{aligned} \max\limits_{r=1,\ldots,N+1} \int\limits_{\mathrm{X}\times\mathrm{X}} \varphi_r(x,z) \mu(dx)\nu(dz) \leqslant \int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{r=1,\ldots,N+1} \varphi_r(x,z) \mu(dx) \nu(dz)\end{aligned} $$

(2.9.5)

for any μ(⋅) ∈{ν}, ν(⋅) ∈{ν}; recall that

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \varphi_i(x,z) &\displaystyle =&\displaystyle f_i(x\|z_i) - f_i(z) \;\;\;\; (i \in \mathbb{N}), \\ \varphi_{N+1}(x,z) &\displaystyle =&\displaystyle \sum_{i \in \mathbb{N}} \left[f_i(x) - f_i(z)\right]. \end{array} \end{aligned} $$

(2.9.6)

Proof

Indeed, from (2.9.4) we have $N\!+\!1$ inequalities of the form

$$\displaystyle \begin{aligned}\varphi_r(x,z) \leqslant \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \;\;\;\; (r=1,\ldots,N+1)\end{aligned} $$

for each x, z  ∈ X. Integrating both sides of these inequalities with respect to an arbitrary product measure μ(dx)ν(dz) yields

$$\displaystyle \begin{aligned}\varphi_r(\mu,\nu) = \!\!\!\! \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \varphi_r(x,z) \mu(dx)\nu(dz) \leqslant \!\!\!\!\! \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu(dx) \nu(dz)\end{aligned} $$

for all μ(⋅)  ∈ {ν}, ν(⋅)  ∈ {ν} and each $r\!=1,\ldots ,N\!+\!1$. Consequently,

$$\displaystyle \begin{aligned}\max\limits_{r=1,\ldots,N+1} \varphi_r(\mu,\nu) = \max\limits_{r=1,\ldots,N+1} \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \varphi_r(x,z) \mu(dx)\nu(dz) \leqslant \end{aligned}$$

$$\displaystyle \begin{aligned}\;\;\;\;\;\;\;\;\;\;\;\;\;\; \leqslant \!\!\!\!\! \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu(dx) \nu(dz) \;\;\;\;\; \forall \: \mu(\cdot) \in \{\nu\}, \: \nu(\cdot) \in \{\nu\},\end{aligned} $$

which proves (2.9.5). $\blacksquare$

Remark 2.9.2

In fact, formula (2.9.5) generalizes the well-known property of maximization: the maximum of a sum does not exceed the sum of the maxima.

2.9.3 Existence Theorem

Good mathematicians see analogies.

Great mathematicians see analogies between analogies.

—Banach³²

The central result of Chap. 2—the existence of a Berge–Pareto equilibrium in mixed strategies—is established.

Theorem 2.9.1

If in game (2.3.1) the sets $\mathrm {X}_i \in \mathrm {cocomp}\:\mathbb {R}^{n_i}$ and f _i(⋅) ∈ C(X) $(i \in \mathbb {N})$, then there exists a Berge–Pareto equilibrium in mixed strategies.

Proof

Consider the auxiliary zero-sum two-player game

$$\displaystyle \begin{aligned}\Gamma^{\mathrm{a}} = \langle \: \{ 1,2 \}, \{ \mathrm{X}, \mathrm{Z}=\mathrm{X} \}, \varphi(x,z) \: \rangle. \end{aligned}$$

In the game Γ^a, the set X of strategies x chosen by player 1 (which seeks to maximize φ(x, z)) coincides with the set of strategy profiles of game (2.3.1); the set Z of strategies z chosen by player 2 (which seeks to minimize φ(x, z)) coincides with the same set X. A solution of the game Γ^a is a saddle point (x ⁰, z ^B) ∈X ×X; for all x ∈X and each z ∈X, it satisfies the chain of inequalities

$$\displaystyle \begin{aligned}\varphi\left(x,z^{\mathrm{B}}\right) \leqslant \varphi\left(x^0,z^{\mathrm{B}}\right) \leqslant \varphi\left(x^0,z\right). \end{aligned}$$

Now, associate with the game Γ^a its mixed extension

$$\displaystyle \begin{aligned}\tilde{\Gamma}^{\mathrm{a}} = \langle \: \{ 1,2 \}, \{\mu\}, \{\nu\}, \varphi(\mu,\nu) \: \rangle , \end{aligned}$$

where {ν} and {μ} = {ν} denote the sets of mixed strategies ν(⋅) and μ(⋅) of players 1 and 2, respectively. The payoff function of player 1 is the expectation

$$\displaystyle \begin{aligned}\varphi(\mu,\nu) = \int\limits_{\mathrm{X}\times\mathrm{X}} \varphi(x,y) \mu(dx) \nu(dz). \end{aligned}$$

The solution of the game $\tilde {\Gamma }^{\mathrm {a}}$ (the mixed extension of the game Γ^a) is also a saddle point (μ ⁰, ν ^∗) defined by the two inequalities

$$\displaystyle \begin{aligned} \varphi \left(\mu,\nu^{*}\right) \leqslant \varphi \left(\mu^0,\nu^{*}\right) \leqslant \varphi \left(\mu^0,\nu\right) \end{aligned} $$

(2.9.7)

for any ν(⋅) ∈{ν} and μ(⋅) ∈{ν}.

Sometimes, this pair (μ ⁰, ν ^∗) is called the solution of the game Γ^a in mixed strategies.

In 1952, Gliksberg [30] established the existence of a mixed strategy Nash equilibrium for a noncooperative game of $N \geqslant 2$ players. Applying this existence result to the zero-sum two-player game Γ^a as a special case, we obtain the following statement. In the game Γ^a, let the set $\mathrm {X} \!\subset \! \mathbb {R}^{n}$ be nonempty and compact and let the payoff function φ(x, z) of player 1 be continuous on X ×X (note that the continuity of φ(x, z) is assumed in Lemma 2.8.1). Then the game Γ^a has a solution (μ ⁰, ν ^∗) defined by (2.9.7), i.e., there exists a saddle point in mixed strategies.

In view of (2.9.4), inequalities (2.9.7) can be written as

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle\int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu(dx) \nu^{*}(dz) \\ \quad \leqslant \displaystyle\int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu^0(dx) \nu^{*}(dz) \\ \quad \leqslant \displaystyle\int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu^0(dx) \nu(dz) \end{array} \end{aligned} $$

(2.9.8)

for all ν(⋅) ∈{ν} and μ(⋅) ∈{ν}. Using the measure $\nu _i(dz_i) = \mu ^0_i(dx_i)$ $(i \!\in \! \mathbb {N})$ (so that ν(dz) = μ ⁰(dx)) in the expression

$$\displaystyle \begin{aligned}\varphi(\mu^0,\nu) = \int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu^0(dx) \nu(dz), \end{aligned}$$

we obtain φ(μ ⁰, μ ⁰) = 0 due to (2.9.6). Similarly, φ(ν ^∗, ν ^∗) = 0, and it follows from (2.9.7) that

$$\displaystyle \begin{aligned} \varphi(\mu^{0},\nu^{*})=0. \end{aligned} $$

(2.9.9)

The condition φ(μ ⁰, μ ⁰) = 0 and the chain of inequalities (2.9.7) give, by transitivity,

$$\displaystyle \begin{aligned}\varphi(\mu,\nu^{*}) = \int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu(dx) \nu^{*}(dz) \leqslant 0 \;\;\;\; \forall \: \mu(\cdot) \in \{\nu\}. \end{aligned}$$

In accordance with Proposition 2.9.2, then we have

$$\displaystyle \begin{aligned}0 \geqslant \int\limits_{\mathrm{X}\times\mathrm{X}} \max\limits_{j=1,\ldots,N+1} \varphi_j(x,z) \mu(dx) \nu^{*}(dz) \geqslant \max\limits_{j=1,\ldots,N+1} \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \varphi_j(x,z) \mu(dx) \nu^{*}(dz). \end{aligned}$$

Therefore, for all j = 1, …, N  +  1,

$$\displaystyle \begin{aligned} \int\limits_{\mathrm{X}\times\mathrm{X}} \varphi_j(x,z) \mu(dx) \nu^{*}(dz) \leqslant 0 \;\;\;\;\; \forall \: \mu(\cdot) \! \in \! \{\nu\}. \end{aligned} $$

(2.9.10)

Consider two cases as follows.

Case I (j = 1, …, N). Here, by (2.9.10), (2.9.6) and the normalization of ν(⋅), we arrive at

$$\displaystyle \begin{aligned} \begin{array}{rcl} 0 &\displaystyle \geqslant&\displaystyle \int\limits_{\mathrm{X}\times\mathrm{X}} \!\!\!\! \varphi_i(x,z) \mu(dx) \nu^{*}(dz) = \int\limits_{\mathrm{X}\times\mathrm{X}}[f_i(x\|z_i) - f_i(z)] \mu(dx) \nu^{*}(dz) \\ &\displaystyle =&\displaystyle \!\!\!\!\! \int\limits_{\mathrm{X}\times\mathrm{X}_i} \!\!\!\! f_i(x\|z_i) \mu(dx) \nu^{*}_i(dz) - \int\limits_{\mathrm{X}} f_i(z)\mu(dz) \cdot \int\limits_{\mathrm{X}} \nu^{*}(dz) \\ &\displaystyle =&\displaystyle f_i(\mu\|\nu^{*}_i) - f_i(\nu^{*}) \;\;\;\; \forall \: \mu(\cdot) \! \in \! \{\nu\}, \; i \in \mathbb{N}. \end{array} \end{aligned} $$

By Definition 2.9.1, ν ^∗(⋅) is a Berge equilibrium in mixed strategies in game (2.3.1).

Case II (j = N + 1). Again, using (2.9.10), (2.9.6) and the normalization of ν(⋅) and μ(⋅), we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} 0 &\displaystyle \geqslant&\displaystyle \!\!\!\!\! \int\limits_{\mathrm{X}\times\mathrm{X}} \!\! \left[ \sum_{r \in \mathbb{N}} f_r(x) - \!\! \sum_{r \in \mathbb{N}} f_r(z) \right] \!\! \mu(dx) \nu^{*}(dz) \!\! = \!\!\! \int\limits_{\mathrm{X}} \!\! \sum_{r \in \mathbb{N}} f_r(x) \mu(dx) \!\cdot\! \int\limits_{\mathrm{X}} \!\! \nu^{*}(dz) \\ &\displaystyle &\displaystyle - \int\limits_{\mathrm{X}} \!\! \mu(dx) \int\limits_{\mathrm{X}} \!\! \sum_{r \in \mathbb{N}} f_r(z) \nu^{*}(dz) = \sum_{r \in \mathbb{N}} f_r(\mu) - \sum_{r \in \mathbb{N}} f_r(\nu^{*}) \;\;\;\; \forall \: \mu(\cdot) \! \in \! \{\nu^B\}. \end{array} \end{aligned} $$

In accordance with Remark 2.9.1, the mixed strategy profile ν ^∗(⋅)  ∈ {ν} of game (2.3.1) is a Pareto-maximal alternative in the multicriteria choice problem

$$\displaystyle \begin{aligned}\tilde{\Gamma}_\nu = \left\langle \left\{\nu^{\mathrm{B}}\right\}, \{f_i(\nu)\}_{i \in \mathbb{N}} \right\rangle . \end{aligned}$$

Thus, we have proved that the mixed strategy profile ν ^∗(⋅) in game (2.3.1) is a Berge equilibrium that satisfies Pareto maximality. Hence, by Definition 2.9.1, the mixed strategy profile ν ^∗(⋅) is a Berge–Pareto equilibrium in game (2.3.1). $\blacksquare$

2.10 Linear-Quadratic Two-Player Game

Verba docent, exempla trahunt.³³

Readers who studied Lyapunov’s stability theory surely remember algebraic coefficient criteria. The whole idea of such criteria is to establish the stability of unperturbed motion without solving a system of differential equations, by using the signs of coefficients and/or their relationships. In this section of the book, we are endeavoring to propose a similar approach to equilibrium choice in noncooperative linear-quadratic two-player games. More specifically, our approach allows one to decide about the existence of a Nash equilibrium and/or a Berge equilibrium in these games based on the sign of quadratic forms in the payoff functions of players.

2.10.1 Preliminaries

Consider a noncooperative linear-quadratic two-player game described by

$$\displaystyle \begin{aligned}\Gamma_2 = \langle \{ 1,2 \}, \{ \mathrm{X}_i = \mathbb{R}^{n_i} \}_{i =1,2}, \{ f_i(x_1,x_2) \}_{i =1,2 } \rangle. \end{aligned}$$

A distinctive feature of Γ₂ is the absence of constraints on the strategy sets X_i: the strategies of player i can be any column vectors of dimension n _i, i.e., elements of the n _i-dimensional Euclidean space $\mathbb {R}^{n_i}$ with the standard Euclidean norm ∥⋅∥ and the scalar product. Let the payoff function of player i (i = 1,  2) have the form

$$\displaystyle \begin{aligned} f_i(x_1,x_2) = x^{\prime}_1 A_i x_1 + 2x^{\prime}_1 B_i x_2 + x^{\prime}_2 C_i x_2 + 2a^{\prime}_i x_1 + 2c^{\prime}_i x_2, \end{aligned} $$

(2.10.1)

where A _i and C _i are constant symmetric matrices, B _i is a constant rectangular matrix, and a _i and c _i are constant vectors, all of compatible dimensions; ′ denotes transposition; det A denotes, the determinant of a matrix A. Henceforth, A < 0 $(>, \: \geqslant )$ means that the quadratic form z′Az is negative definite (positive definite, positive semidefinite, respectively). We will adopt the following rules of differentiation of bilinear quadratic forms with respect to the vector argument [19, 27]:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \left[\frac{\partial}{\partial x_{1}}\left[x^{\prime}_{1} B_{i} x_{2} \right]= B_{i} x_{2}\right]&\displaystyle \Rightarrow&\displaystyle \left[\frac{\partial}{\partial x_{2}}\left[ x^{\prime}_{1} B_{i} x_{2} \right] = B^{\prime}_{i} x_{1} \wedge\frac{\partial}{\partial x_{1}} \left[ x^{\prime}_{1} A_{i} x_{1} \right]\right.\\ &\displaystyle &\displaystyle \hspace{-12pt}\left. = 2A_{i} x_{1} \wedge \frac{\partial}{\partial {x}_{1}} \left[a^{\prime}_{1} x_{1} \right] = a_{1} \right], \\ \frac{\partial^2}{\partial x^2_{i}} \left[ x^{\prime}_{1} A_{i} x_{1} \right] &\displaystyle =&\displaystyle 2 A_{i}. \end{array} \end{aligned} $$

(2.10.2)

For a scalar function Ψ(x) of a k-dimensional vector argument x, sufficient conditions for

$$\displaystyle \begin{aligned}\max\limits_{x \in \mathbb{R}^k} \Psi (x) = \Psi (x^{*}) \end{aligned}$$

are

$$\displaystyle \begin{aligned} \begin{array}{l} \left( 1 \right) \; \left. \displaystyle\frac{\partial \Psi (x)}{\partial x} \right|{}_{x=x^{*}} = \left. \mathrm{grad}\ \Psi (x) \right|{}_{x=x^{*}} = 0_k, \\ \; \\ \left( 2 \right) \; \left. \displaystyle\frac{\partial^2 \Psi (x)}{\partial x^2} \right|{}_{x=x^{*}} < 0, \end{array} \end{aligned} $$

(2.10.3)

where 0_k denotes a zero column vector of dimension k.

2.10.2 Berge Equilibrium

For the payoff functions (2.10.1), relations (2.10.3) yield the following sufficient condition for the existence of a Berge equilibrium in the game Γ₂.

Proposition 2.10.1

Assume that in the game Γ ₂

$$\displaystyle \begin{aligned} A_2 < 0, \;\; C_1 < 0, \end{aligned} $$

(2.10.4)

and

$$\displaystyle \begin{aligned} \mathrm{det} \left[ C_1 - B^{\prime}_1A^{-1}_2B_2 \right] \neq 0. \end{aligned} $$

(2.10.5)

Then the Berge equilibrium $x^{\mathrm {B}} =(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ is given by

$$\displaystyle \begin{aligned} \begin{array}{l} x^{\mathrm{B}}_1 = - A^{-1}_2 B_2 \left[ C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right]^{-1} \left( B^{\prime}_1 A^{-1}_2 a_2 - c_1 \right) - A^{-1}_2 a_2, \\ x^{\mathrm{B}}_2 = \left[ C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right]^{-1} \left( B^{\prime}_1 A^{-1}_2 a_2 - c_1 \right). \end{array} \end{aligned} $$

(2.10.6)

Proof

By definition, a strategy profile $(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)=x^{\mathrm {B}}$ is a Berge equilibrium in the game Γ₂ if and only if

$$\displaystyle \begin{aligned} \begin{array}{l} \max\limits_{x_2 \in \mathbb{R}^{n_2}} f_1\left(x_1^{\mathrm{B}},x_2\right) = f_1\left(x^{\mathrm{B}}\right), \\ \max\limits_{x_1 \in \mathbb{R}^{n_1}} f_2\left(x_1,x^{\mathrm{B}}_2\right) = f_2\left(x^{\mathrm{B}}\right). \end{array} \end{aligned} $$

(2.10.7)

In view of (2.10.3) and(2.10.1), sufficient conditions for the first equality in (2.10.7) to hold can be written as

$$\displaystyle \begin{aligned} \left. \displaystyle\frac{\partial f_1\left(x^{\mathrm{B}}_1,x_2\right)}{\partial x_2} \right|{}_{x_2=x^{\mathrm{B}}_2} &= 2B^{\prime}_1x^{\mathrm{B}}_1 +2C_1x^{\mathrm{B}}_2 + 2c_1 = 0_{n_2}, \\ \left. \displaystyle\frac{\partial^2 f_1\left(x^{\mathrm{B}}_1,x_2\right)}{\partial x^2_2} \right|{}_{x_2=x^{\mathrm{B}}_2} &= 2 C_1. \end{aligned} $$

Similarly, for the second equality in (2.10.7) we obtain

$$\displaystyle \begin{aligned}\begin{array}{l} \left. \displaystyle\frac{\partial f_2\left(x_1,x^{\mathrm{B}}_2\right)}{\partial x_1} \right|{}_{x_1=x^{\mathrm{B}}_1} = 2A_2 x^{\mathrm{B}}_1 +2 B_2 x^{\mathrm{B}}_2 + 2a_1 = 0_{n_1}, \\ {} \left. \displaystyle\frac{\partial^2 f_2\left(x_1,x^{\mathrm{B}}_2\right)}{\partial x^2_1} \right|{}_{x_1=x^{\mathrm{B}}_1} = 2 A_2. \end{array} \end{aligned}$$

In accordance with (2.10.4), the matrices C ₁ and A ₂ are negative definite and hence the Berge equilibrium $(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ in the game Γ₂ satisfies the linear nonhomogeneous system of matrix equations

$$\displaystyle \begin{aligned} \left\{ \begin{array}{c} A_2 x^{\mathrm{B}}_1 + B_2 x^{\mathrm{B}}_2 = - a_2, \\ B^{\prime}_1 x^{\mathrm{B}}_1 + C_1 x^{\mathrm{B}}_2 = - c_1. \end{array} \right. \end{aligned} $$

(2.10.8)

Using the chain of implications $\left [ A_2 < 0 \right ] \; \Rightarrow \; \left [ \mathrm {det} A_2 \neq 0 \right ] \; \Rightarrow \; \left [ \exists A^{-1}_2\right ]$, we multiply the first equation in (2.10.8) on the left by $A^{-1}_2$ to get

$$\displaystyle \begin{aligned} x^{\mathrm{B}}_1 = - A^{-1}_2 B_2 x^{\mathrm{B}}_2 - A^{-1}_2 a_2. \end{aligned} $$

(2.10.9)

Substituting this expression into the second equation of system (2.10.8), one obtains

$$\displaystyle \begin{aligned} \left[ C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right] x^{\mathrm{B}}_2= - c_1 + B^{\prime}_1 A^{-1}_2 a_2, \end{aligned} $$

(2.10.10)

or

$$\displaystyle \begin{aligned} x^{\mathrm{B}}_2 = \left[ C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right]^{-1} \left( B^{\prime}_1 A^{-1}_2 a_2 - c_1 \right). \end{aligned} $$

(2.10.11)

Here we used the fact that

$$\displaystyle \begin{aligned}\left[ \mathrm{det} \left[ C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right] \neq 0 \right] \; \Rightarrow \; \left[ \exists \left( C_1 - B^{\prime}_1 A^{-1}_2 B_2 \right)^{-1} \right]; \end{aligned}$$

formula (2.10.11) is easily derived upon multiplying both sides of (2.10.10) on the left by the matrix $\left [ C_1 - B^{\prime }_1 A^{-1}_2 B_2 \right ]^{-1}.$ Finally, using the resulting expression for $x^B_2$ in (2.10.9), we arrive at the first equality of system (2.10.6).

In the same fashion, it is possible to solve system (2.10.8) by multiplying the second equation by $C^{-1}_1\!\!$. This leads to

Proposition 2.10.2

Assume inequalities (2.10.4) and

$$\displaystyle \begin{aligned} \mathrm{det} \left[ A_2 - B_2C^{-1}_1B^{\prime}_1 \right] \neq 0\end{aligned} $$

(2.10.12)

hold in the game Γ ₂ . Then the Berge equilibrium $x^{\mathrm {B}} =(x^{\mathrm {B}}_1,x^{\mathrm {B}}_2)$ has the form

$$\displaystyle \begin{aligned}\begin{array}{l} x^{\mathrm{B}}_1 = \left[ A_2 - B_2C^{-1}_1B^{\prime}_1 \right]^{-1} ( B_2 C^{-1}_1 c_1 - a_2 ), \\ x^{\mathrm{B}}_2 = - C^{-1}_1B^{\prime}_1 \left[ A_2 - B_2C^{-1}_1B^{\prime}_1 \right]^{-1} \left( B_2 C^{-1}_1 c_1 - a_2 \right) - C^{-1}_1 c_1. \end{array}\end{aligned} $$

Remark 2.10.1

System (2.10.8) has a unique solution for A ₂ < 0 and C ₁ < 0. The two explicit forms of this solution presented above are equivalent and can be reduced to each other.

2.10.3 Nash Equilibrium

In this section, we derive similar results for the Nash equilibrium in the game Γ₂. Instead of (2.10.7), we consider a Nash equilibrium $x^{\mathrm {e}}=(x^{\mathrm {e}}_1,x^{\mathrm {e}}_2)$ defined by the two equalities

$$\displaystyle \begin{aligned} \max\limits_{x_1 \in \mathbb{R}^{n_1}} f_1\left(x_1,x^{\mathrm{e}}_2\right) = f_1\left(x^{\mathrm{e}}\right), \;\;\;\; \max\limits_{x_2 \in \mathbb{R}^{n_2}} f_2\left(x^{\mathrm{e}}_1,x_2\right) = f_2\left(x^{\mathrm{e}}\right).\end{aligned} $$

(2.10.13)

The sufficient conditions for implementing (2.10.13) take the form

$$\displaystyle \begin{aligned} \left. \mathrm{grad}_{x_1} f_1\left(x_1,x^{\mathrm{e}}_2\right) \right|{}_{x_1=x^{\mathrm{e}}_1} = \left. \displaystyle\frac{\partial f_1\left(x_1,x^{\mathrm{e}}_2\right)}{\partial x_1} \right|{}_{x_1=x^{\mathrm{e}}_1} &= 2A_1 x^{\mathrm{e}}_1 +2 B_1 x^{\mathrm{e}}_2 + 2a_1 = 0_{n_1}, \\ \left. \mathrm{grad}_{x_2} f_2\left(x^{\mathrm{e}}_1,x_2\right) \right|{}_{x_2=x^{\mathrm{e}}_2} = \left. \displaystyle\frac{\partial f_2\left(x^{\mathrm{e}}_1,x_2\right)}{\partial x_2} \right|{}_{x_2=x^{\mathrm{e}}_2} &= 2B^{\prime}_2 x^{\mathrm{e}}_1 +2 C_2 x^{\mathrm{e}}_2 + 2c_2 = 0_{n_2}, \\ \left. \displaystyle\frac{\partial^2 f_1\left(x_1,x^{\mathrm{e}}_2\right)}{\partial x^2_1} \right|{}_{x_1=x^{\mathrm{e}}_1} &= 2 A_1 <0, \\ \left. \displaystyle\frac{\partial^2 f_2\left(x^{\mathrm{e}}_1,x_2\right)}{\partial x^2_2} \right|{}_{x_2=x^{\mathrm{e}}_2} &= 2 C_2 <0. \end{aligned} $$

The first two conditions give the linear nonhomogeneous system of matrix equations

$$\displaystyle \begin{aligned}\left\{ \begin{array}{c} A_1 x^{\mathrm{e}}_1 + B_1 x^{\mathrm{e}}_2 = - a_1, \\ B^{\prime}_2 x^{\mathrm{e}}_1 + C_2 x^{\mathrm{e}}B_2 = - c_2. \end{array} \right. \end{aligned}$$

As in Propositions 2.10.1 and 2.10.2, the conditions A ₁ < 0 and C ₂ < 0 allow us to establish the following results. The onus probandi ³⁴ is left to the reader.

Proposition 2.10.3

Assume the inequalities

$$\displaystyle \begin{aligned} A_1 < 0, \;\;\; C_2 < 0, \end{aligned} $$

(2.10.14)

and

$$\displaystyle \begin{aligned} \mathrm{det} \left[ C_2 - B^{\prime}_2 A^{-1}_1 B_1 \right] \neq 0 \end{aligned} $$

(2.10.15)

hold in the game Γ ₂ . Then the Nash equilibrium $x^{\mathrm {e}}=(x^{\mathrm {e}}_1,x^{\mathrm {e}}_2)$ has the form

$$\displaystyle \begin{aligned}\begin{array}{l} x^{\mathrm{e}}_1 = - A^{-1}_1 B_1 \left[ C_2 - B^{\prime}_2 A^{-1}_1 B_1 \right]^{-1} ( B^{\prime}_2 A^{-1}_1 a_1 - c_2 ) - A^{-1}_1 a_1, \\ x^{\mathrm{e}}_2 = \left[ C_2 - B^{\prime}_2 A^{-1}_1 B_1 \right]^{-1} ( B^{\prime}_2 A^{-1}_1 a_1 - c_2 ). \end{array} \end{aligned}$$

Proposition 2.10.4

Assume inequalities (2.10.14) and

$$\displaystyle \begin{aligned} \mathrm{det} \left[ A_1 - B_1 C^{-1}_2 B^{\prime}_2 \right] \neq 0 \end{aligned} $$

(2.10.16)

are satisfied in the game Γ ₂ . Then the Nash equilibrium $x^{\mathrm {e}}=(x^{\mathrm {e}}_1,x^{\mathrm {e}}_2)$ has the form

$$\displaystyle \begin{aligned}\begin{array}{l} x^{\mathrm{e}}_1 = \left[ A_1 - B_1 C^{-1}_2 B^{\prime}_2 \right]^{-1} \left( B_1 C^{-1}_2 c_2 - a_1 \right), \\ x^{\mathrm{e}}_2 = - C^{-1}_2 B^{\prime}_2 \left[ A_1 - B_1 C^{-1}_2 B^{\prime}_2 \right]^{-1} \left( B_1 C^{-1}_2 c_2 - a_1\right) - C^{-1}_2 c_2. \end{array} \end{aligned}$$

2.10.4 Auxiliary Lemma

Despite the negativa non probantur ³⁵ principle of Roman law, we will rigorously obtain a result useful for discarding the games without any Berge and/or Nash equilibria.

Lemma 2.10.1

In the game Γ ₂ with A ₁ > 0, there exists no $\bar {x}_1$ such that, for each fixed x ₂,

$$\displaystyle \begin{aligned} \max\limits_{x_1 \in \mathbb{R}^{n_1}} f_1(x_1,x_2) = f_1(\bar{x}_1,x_2).\end{aligned} $$

(2.10.17)

In other words, the payoff function f ₁ of the first player is not maximized in this game.

Proof

Let us “freeze” a certain strategy $x_2 \in \mathbb {R}^{n_2}$ of the second player. Then the payoff function of the first player can be written in the form

$$\displaystyle \begin{aligned}f_1(x_1,x_2) = x^{\prime}_1 A_1 x_1 + 2 x^{\prime}_1 \varphi (x_2) + \psi (x_2),\end{aligned} $$

where the column vector φ(x ₂) of dimension n ₁ and the scalar function ψ(x ₂) depend on the frozen value x ₂ only.

By the hypothesis of Lemma 2.10.1, the symmetric matrix A ₁ is positive definite. In this case, the characteristic equation $\mathrm {det} [A_1 - E_{n_1}\lambda ] = 0$ (where $E_{n_1}$ denotes an identity matrix of dimensions n ₁ × n ₁) has n ₁ positive real roots owing to symmetry and, in addition,

$$\displaystyle \begin{aligned} x^{\prime}_1 A_1 x_1 \geqslant \lambda^{*} \|x_1\|{}^2 \;\;\; \forall x_1 \in \mathbb{R}^{n_1},\end{aligned} $$

(2.10.18)

where λ ^∗ > 0 is the smallest root among them. Thus, maximum (2.10.17) is not achieved if, for any large value m > 0, there exists a strategy $x_1(m,x_2 )\in \mathbb {R}^{n_1}$ such that

$$\displaystyle \begin{aligned}f_1(x_1(m,x_2 ),x_2) > m.\end{aligned} $$

Under (2.10.18), this inequality holds if

$$\displaystyle \begin{aligned} \lambda^{*} \|x_1(m,x_2 )\|{}^2 + 2 x^{\prime}_1(m,x_2 ) \varphi (x_2) + \psi (x_2) > m.\end{aligned} $$

(2.10.19)

Let us construct a solution x ₁(m, x ₂) of inequality (2.10.19) in the form

$$\displaystyle \begin{aligned} x_1(m,x_2 ) = \beta e_{n_1},\end{aligned} $$

(2.10.20)

where the constant β > 0 will be specified below and e ₁’s the n ₁-dimensional vector with all components equal to 1.

Substituting (2.10.20) into (2.10.19) yields the following inequality for β:

$$\displaystyle \begin{aligned}\lambda^{*} \beta^2 n_1 +2 \beta \left( e_{n_1}, \varphi (x_2) \right) + \psi (x_2) - m > 0.\end{aligned} $$

Hence, for any constant

$$\displaystyle \begin{aligned}\beta > \beta_{+} = \frac{\left| \left( e_{n_1}, \varphi (x_2) \right) \right| + \sqrt{\left( e_{n_1}, \varphi (x_2) \right)^2 + \lambda^{*} n_1 | \psi (x_2) - m |}}{\lambda^{*} n_1} \end{aligned}$$

and corresponding strategy $x_1(m,x_2 ) = \beta e_{n_1}$ of the first player, we have

$$\displaystyle \begin{aligned}f_1(x_1(m,x_2 ),x_2)>m. \end{aligned}$$

Thus, maximum (2.10.17) does not exist. $\blacksquare$

Remark 2.10.2

In this case, the game Γ₂ with a matrix A ₁ > 0 admits no Nash equilibria. In combination with Proposition 2.10.1, this shows that

• 1. the game Γ₂ with matrices $A_1\!>\!0$ or (and) $C_2\! >\!0$ and also $A_2\!<\!0$, $C_1\!<\!0$ that satisfies condition (2.10.5) has no Nash equilibria, but does have a Berge equilibrium defined by (2.10.6).

  In a similar way, it is easy to obtain the following.

• 2. If $A_2\!<\!0$, $C_1\! <\!0$, condition (2.10.5) or (2.10.12) holds and also $A_1\!>\!0$ or (and) $C_2\! >\!0$, then the game Γ₂ has a Berge equilibrium only.

• 3. If $A_1\!<\!0$, $C_2\! <\!0$, condition (2.10.15) or (2.10.16) holds and also $A_2\!>\!0$ or (and) $C_1\! >\!0$, then the game Γ₂ has a Nash equilibrium only.

• 4. If $A_1\!>\!0$ or (and) $C_2\! >\!0$ and also $A_2\!>\!0$ or (and) $C_1\! >\!0$, then the game Γ₂ has none of these equilibria.

• 5. If A ₂ < 0, C ₁ < 0, A ₁ < 0, C ₂ < 0 and also conditions (2.10.5) or (2.10.12) and (2.10.15) or (2.10.16) hold, then the game Γ₂ has both types of equilibrium.

2.10.5 Concluding Remarks

Thus, we have considered the noncooperative linear-quadratic two-player game without constraints $(\mathrm {X}_i = \mathbb {R}^{n_i}, i=1,2)$ and with the payoff functions

$$\displaystyle \begin{aligned}\begin{array}{c} f_1(x_1,x_2) = x^{\prime}_1 A_1 x_1 + 2x^{\prime}_1 B_1 x_2 + x^{\prime}_2 C_1 x_2 + 2a^{\prime}_1 x_1 + 2c^{\prime}_1 x_2, \\ f_2(x_1,x_2) = x^{\prime}_1 A_2 x_1 + 2x^{\prime}_1 B_2 x_2 + x^{\prime}_2 C_2 x_2 + 2a^{\prime}_2 x_1 + 2c^{\prime}_2 x_2. \end{array} \end{aligned}$$

Here ′ denotes transposition; A _i and C _i are constant symmetric matrices of dimensions n ₁ × n ₁ and n ₂ × n ₂, respectively; B _i is a constant rectangular matrix of dimensions n ₁ × n ₂; finally, a _i and c _i are constant vectors of dimensions n ₁ and n ₂, respectively (i = 1,  2).

Based on Propositions 2.10.1–2.10.4, we introduce the following coefficient criteria for the existence of Nash and Berge equilibria in the game Γ₂. Par acquit de conscience, ³⁶ they are presented in form of Table 2.1.

Table 2.1 Coefficient criteria of equilibria

How should one use Table 2.1? Just follow the three simple steps indicated below.

• Step1. First, check the signs of the quadratic forms with the matrices A ₁, A ₂, C ₁, and C ₂. For example, suppose A ₁ < 0, C ₂ < 0 (both matrices are negative definite), while A ₂ > 0 (i.e., A ₂ is positive definite).

• Step2. Find the corresponding row in Table 2.1 (in our case, the conditions A ₁ < 0, C ₂ < 0 and A ₂ > 0 are in row 3); then verify the nondegeneracy of the matrix (2.10.15) in column 5, i.e., the condition $\mathrm {det} \left [ C_2 - B^{\prime }_2 A^{-1}_1 B_1 \right ] \neq 0.$

• Step3. As shown in columns 6 and 7 of Table 2.1, the game Γ₂ with these matrices has no Berge equilibria, but has a Nash equilibrium for any matrices C ₁, B _i and any vectors a _i, b _i of compatible dimensions. The explicit form of this Nash equilibrium is given in Proposition 2.10.3.