The Two-Scale Periodic Unfolding Technique

Abstract

In this paper, the definitions of the periodic unfolding and averaging operators are extended to the case of two sub-domains separated by a thin interface. Their properties are introduced and illustrative examples of these operators are given.

1 Introduction

This paper is devoted to a useful tool in the homogenization procedure for models defined in a two-phase domain, which is the two-phase periodic unfolding technique.

The periodic unfolding technique was introduced in continuous and perforated domains, see, e.g., [1, 3] and it is based on the periodic unfolding and the averaging operators. The paper [2] suggests an extension of the definition of the unfolding operator on a boundary. Our specific interest concerns the Poisson–Nernst–Planck system in a two-phase domain with an interface, see our works [4, 5]. For this reason, we extend the definitions to the case of two phases and their interface. We describe a two-phase medium with a microstructure consisting of solid and pore phases, which are separated by a thin interface. The corresponding geometry is represented by a disconnected domain. A special interest of our consideration is the interface between the two phases because of electrochemical reactions which occur here.

The paper has the following structure. In Sect. 2, the definitions of the periodic unfolding and the averaging operators in the two-phase domain are introduced. Section 3 is devoted to clarifying examples of these operators.

2 Definitions

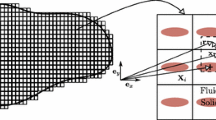
We start with the two-phase geometry. A unit cell $Y = (0,1)^d$, $d \in \mathbb {N}$, consists of two open, connected sub-domains: a solid part $\omega$ and a pore part $\Pi$, separated by a thin interface $\partial \omega$ which is assumed to be Lipschitz continuous, see Fig. 1. By scaling a unit cell Y with a small parameter $\varepsilon > 0$, we introduce a local cell $Y_\varepsilon ^l$ with some index l. Its solid part is denoted by $\omega _\varepsilon ^l$ and its pore part by $\Pi _\varepsilon ^l$.

Every spacial point $x \in \mathbb {R}^d$ can be decomposed as the following sum:

$$\begin{aligned} x = \varepsilon \lfloor \frac{x}{\varepsilon } \rfloor + \varepsilon \{\frac{x}{\varepsilon }\}, \end{aligned}$$

(1)

where $\left\lfloor x/\varepsilon \right\rfloor \in \mathbb {Z}^d$ is the floor part and $\left\{ x/\varepsilon \right\} \in Y = (0,1)^d$ is the fractional part of $x/\varepsilon$.

We consider a domain $\Omega \subset \mathbb {R}^d$ with a Lipschitz boundary $\partial \Omega$. Based on the decomposition (1), it is covered by repeating periodically local cells $Y_\varepsilon ^l$ in such a way that all local cells lay inside of $\Omega$. The union of these periodic local cells is denoted by $\Omega _\varepsilon := \bigcup _{l\in I^\varepsilon } Y_\varepsilon ^l$ with the solid part $\omega _\varepsilon = \bigcup _{l\in I^\varepsilon } \omega _\varepsilon ^l$, and the pore part $\Pi _\varepsilon = \bigcup _{l\in I^\varepsilon } \Pi _\varepsilon ^l$. The interface $\partial \omega _\varepsilon := \bigcup _{l\in I^\varepsilon } \partial \omega _\varepsilon ^l$ is the union of local interfaces in each local cell. A thin boundary layer attaching the external boundary $\partial \Omega$ is called $\Omega \setminus \Omega _\varepsilon$, see Fig. 2. Summarizing, the two-phase domain $\Omega$ consists of the pore phase $Q_\varepsilon = (\Omega \setminus \Omega _\varepsilon ) \cup \Pi _\varepsilon$, the solid phase $\omega _\varepsilon$, and the interface $\partial \omega _\varepsilon$.

Fig. 1

A unit cell Y

Fig. 2

The domain $\Omega = Q_\varepsilon \cup \omega _\varepsilon$

In the prescribed geometry, we define the periodic unfolding and the averaging operators in the two-phase domain and at the interface.

Definition 1

(two-phase unfolding operator) The linear continuous operator $f(x) \mapsto T_\varepsilon :H^1 (Q_\varepsilon ) \times H^1(\omega _\varepsilon ) \mapsto L^2(\Omega ; H^1(\Pi ) \times H^1(\omega ))$ is defined as

$$\begin{aligned} (T_\varepsilon f) (x,y) = {\left\{ \begin{array}{ll} f\bigl (\varepsilon \lfloor \frac{x}{\varepsilon }\rfloor + \varepsilon y\bigr ),&{}\text {for a.e. }x \in \Omega _\varepsilon \text { and }y \in \Pi \cup \omega ,\\ f(x),&{}\text {for a.e. }x \in \Omega \setminus \Omega _\varepsilon \text { and } y \in \Pi \cup \omega . \end{array}\right. } \end{aligned}$$

(2)

Definition 2

(two-phase averaging operator) The left-inverse operator to $T_\varepsilon$ (linear and continuous) is defined as $u(x,y) \mapsto T_\varepsilon ^{-1}:L^2(\Omega ; H^1(\Pi ) \times H^1(\omega )) \mapsto H^1(\bigcup _{l\in I^\varepsilon } \Pi _\varepsilon ^l) \times H^1(\Omega \setminus \Omega _\varepsilon ) \times H^1(\omega _\varepsilon )$:

$$\begin{aligned} (T_\varepsilon ^{-1} u) (x) = {\left\{ \begin{array}{ll} \displaystyle \frac{1}{|Y|}\displaystyle \int _{\Pi \cup \omega } u \bigl (\varepsilon \lfloor \frac{x}{\varepsilon }\rfloor + \varepsilon z, \bigl \{\frac{x}{\varepsilon }\bigr \}\bigr )\, dz,&{}\text {for a.e. }x \in \Pi _\varepsilon \cup \omega _\varepsilon ,\\ \displaystyle \frac{1}{|Y|}\displaystyle \int _{\Pi \cup \omega } u(x,y) \, dy,&{}\text {for a.e. }x \in \Omega \setminus \Omega _\varepsilon . \end{array}\right. } \end{aligned}$$

(3)

The operators satisfy the following properties:

Lemma 3

(Properties of the operators $T_\varepsilon$ and $T_\varepsilon ^{-1}$ in the domain) For arbitrary $f,g,h \in H^1(Q_\varepsilon ) \times H^1(\omega _\varepsilon )$, the following equalities hold:

• (i) $(T_\varepsilon ^{-1} T_\varepsilon ) f(x) = f(x)$, and $(T_\varepsilon T_\varepsilon ^{-1} u) (x,y) = u (y)$, when u is constant for $x \in Q_\varepsilon \cup \omega _\varepsilon$, or a periodic function u(y) of $y \in \Pi \cup \omega$ for $x \in \Pi _\varepsilon \cup \omega _\varepsilon$;

• (ii) composition rule: $T_\varepsilon (\mathcal {F}(f)) = \mathcal {F}(T_\varepsilon f)$ for any elementary function $\mathcal {F}$;

• (iii) integration rules:

  $\displaystyle \int _{\Pi _\varepsilon \cup \omega _\varepsilon } f(x) g(x)\, dx = \displaystyle \frac{1}{|Y|} \int _{\Omega _\varepsilon } \int _{\Pi \cup \omega } (T_\varepsilon f)(x,y) \cdot (T_\varepsilon g)(x,y)\, dy\, dx$,

  $\displaystyle \int _{\Omega \setminus \Omega _\varepsilon } f(x) g(x)\, dx = \displaystyle \frac{1}{|Y|} \int _{\Omega \setminus \Omega _\varepsilon } \int _{\Pi \cup \omega } (T_\varepsilon f)(x,y) \cdot (T_\varepsilon g)(x,y)\, dy\, dx$;

• (iv) boundedness of $T_\varepsilon$:

  $\displaystyle \int _{Q_\varepsilon \cup \omega _\varepsilon } h^2(x) \, dx = \frac{1}{|Y|} \int _{\Omega } \int _{\Pi \cup \omega } (T_\varepsilon h)^2(x,y) \, dy\, dx$,

  $\displaystyle \int _{Q_\varepsilon \cup \omega _\varepsilon } |\nabla _x h|^2(x)\, dx= \frac{1}{{\varepsilon ^{2}} |Y|} \int _{\Omega } \int _{\Pi \cup \omega } |\nabla _y (T_\varepsilon h)|^2(x,y) \, dy\, dx$.

2.1 Restriction of the Operators to the Interface

The definitions (2) and (3) are extended to the interface in a natural way:

Definition 4

The restriction of the two-phase unfolding operator $T_\varepsilon$ to the interface $\partial \omega _\varepsilon$ is well defined as follows: $f(x) \mapsto T_\varepsilon :L^2 (\partial \omega _\varepsilon ) \mapsto L^2(\Omega _\varepsilon ) \times L^2(\partial \omega )$,

$$\begin{aligned} (T_\varepsilon f) (x,y) = f\bigl (\varepsilon \lfloor \frac{x}{\varepsilon }\rfloor + \varepsilon y\bigr ), \quad \text {for a.e. } x \in \Omega _\varepsilon \text { and } y \in \partial \omega . \end{aligned}$$

(4)

The corresponding averaging operator $u(x,y) \mapsto T_\varepsilon ^{-1}:L^2(\Omega _\varepsilon ) \times L^2(\partial \omega ) \mapsto L^2 (\partial \omega _\varepsilon )$,

$$\begin{aligned} (T_\varepsilon ^{-1} u) (x) = \frac{1}{|Y|}\int _{\Pi \cup \omega } u \bigl (\varepsilon \lfloor \frac{x}{\varepsilon }\rfloor + \varepsilon z, \bigl \{\frac{x}{\varepsilon }\bigr \}\bigr )\, dz, \quad \text {for a.e. } x \in \Omega _\varepsilon . \end{aligned}$$

(5)

Analogously, the following properties at the interface hold:

Lemma 5

(Properties of the operators $T_\varepsilon$ and $T_\varepsilon ^{-1}$ at the interface) For arbitrary $f,g \in L^2(\partial \omega _\varepsilon )$, the following equalities hold.

• (i) $(T_\varepsilon ^{-1} T_\varepsilon ) f(x) = f(x)$;

• (ii) composition rule: $T_\varepsilon (\mathcal {F}(f)) = \mathcal {F}(T_\varepsilon f)$ for any elementary function $\mathcal {F}$;

• (iii) integration rule:

  $\displaystyle \int _{\partial \omega _\varepsilon } f(x) g(x)\, dS_x =\frac{1}{{\varepsilon }|Y|} \int _{\Omega _\varepsilon } \int _{\partial \omega } (T_\varepsilon f)(x,y) \cdot (T_\varepsilon g)(x,y)\, dS_y\, dx$;

• (iv) boundedness of $T_\varepsilon$:

  $\displaystyle \int _{\partial \omega _\varepsilon } f^2 (x) \, dS_x = \frac{1}{{\varepsilon }|Y|} \int _{\Omega _\varepsilon }\int _{\partial \omega } (T_\varepsilon f)^2(x,y) \, dS_y \, dx$.

3 Examples

In this section, two examples representing the behavior of the periodic unfolding operator is given.

Example 6

In the one-dimensional domain $\Omega = (-2\pi ,2\pi )$, we consider the function $f(x)=\sin x$ and the small parameter $\varepsilon = 2 \pi$, which coincides with the period of the function f. We consider a unit cell $Y = (0,1)$, therefore, the number of local cells is 2 which are the intervals $Y_\varepsilon ^1 = (-2\pi , 0)$ and $Y_\varepsilon ^2 = (0, 2\pi )$. On the first graph in Fig. 3, the red curve is the function f and the blue line represents the projection of the mapping $T_\varepsilon f$ for $y=0$. On the second graph, both functions are presented on the two-dimensional (x, y)-plane, where the interval $Y = (0,1)$ in y-axis is a unit cell and the intervals $(-2\pi , 0)$, $(0, 2\pi )$ in x-axis are local cells $Y_\varepsilon ^1$ and $Y_\varepsilon ^2$, and the point $\{x = 0\}$ is a part of the cell boundary $\partial Y_\varepsilon ^1$. We note that in the case of periodic functions $f \in H^1(\Omega _\varepsilon )$ with respect to a small parameter $\varepsilon$, the mapping $T_\varepsilon f$ is continuous across the boundary $\partial Y_\varepsilon ^l$.

Fig. 3

$\varepsilon = 2 \pi$

Fig. 4

$\varepsilon = \pi$

Example 7

We consider the same setting as in Example 6 but with $\varepsilon =\pi$, which does not coincide now with the period of the function f or, in other words, the function f is not periodic with respect to $\varepsilon$. Comparing with the Example 6, the mapping $T_\varepsilon f (x,y)$ is discontinuous along the x-variable, see Fig. 4. This example illustrates that for nonperiodic functions, the averaging mapping $(T_\varepsilon ^{-1} T_\varepsilon ) f$ does not belong to the space $H^1(\Omega _\varepsilon )$ but only to $L^2(\Omega _\varepsilon )$ even for continuous functions f from the space $H^1(\Omega _\varepsilon )$. Such functions can be smoothed by the gradient folding operator, see, e.g., [6].