Critical Phenomena in a Dynamical System Under Random Perturbations

Abstract

The effect of Gaussian white noise on a canard cycle in dynamical model of an electrochemical reaction is analyzed. A critical noise intensity, at which the small-amplitude oscillations are transformed into mixed-mode oscillations, is obtained.

This work was funded by RFBR and Samara Region (project 16-41-630529-p) and the Ministry of Education and Science of the Russian Federation under the Competitiveness Enhancement Program of Samara University (2013–2020).

1 Introduction

It is well known that random perturbations can decisively affect the long-term behavior of dynamical systems. It should be noted that all realistic systems are subject to noise. For example, in a chemical system, the role of random perturbations can be played by various impurities, thermal vibrations, and many other external factors.

In this paper, we analyze the influence of an external noise on a canard cycle using an electrochemical reactor model as an example. The analysis is based on the stochastic sensitivity functions technique [1, 2]. We investigate the stochastic sensitivity of the equilibrium and the limit cycle of the model. We demonstrate transitions induced by the noise and find out the critical value of the noise intensity corresponding to the beginning of the transitions.

2 Stochastic Model of Electrochemical Reactor

Consider a model of an electrochemical reaction of the Koper–Sluyters type [6] with allowance for random perturbations. It is assumed that the system is affected by a Gaussian white noise of low intensity. In this case, the model can be represented by the following system:

$$\begin{aligned} \frac{du}{dt}=-k_ae^{\gamma \theta /2}u(1-\theta )+k_de^{-\gamma \theta /2}\theta +1-u + \epsilon w_1=f(u,\theta ), \end{aligned}$$

(1)

$$\begin{aligned} \beta \frac{d\theta }{dt}=k_ae^{\gamma \theta /2}u(1-\theta )-k_de^{-\gamma \theta /2}\theta -k_ee^{\alpha _0\zeta E}\theta + \epsilon w_2= g(u,\theta ), \end{aligned}$$

(2)

where u is the dimensionless interfacial concentration of electrolyte, $\theta$ is the dimensionless amount of electrolyte that is adsorbed on the electrode surface, E is the electrode potential, $\beta$ is the coverage ratio of the adsorbate, $\alpha _0$ is the symmetry factor for the electron transfer, $w_1$ and $w_2$ are (in)dependent Wiener processes, $\epsilon$ reflects the noise intensity, and the current density is given in dimensionless form by $J=k_ee^{\alpha _0\zeta E}\theta ; \zeta =F/(RT)$, where R is the universal gas constant, F is Faraday’s constant, and T is the temperature. The parameter $\gamma$ is interpreted an interaction parameter. Positive $\gamma$ signifies attractive and negative $\gamma$ signifies repulsive adsorbate interactions.

A detailed analysis of the deterministic model was carried out in [4, 7] using the theory of invariant manifolds. A critical regime corresponding to the canard cycle (see, for example, [8, 9] and references therein) was discovered. It was shown that the critical regime plays the role of a border between two main types of the reaction modes: a nonperiodic slow regime and relaxation oscillations.

In this paper, we investigate the influence of an external noise on the canard cycle [3, 5]. We start with the analysis of the stochastic sensitivity of the equilibrium of the system.

3 Theoretical Sensitivity to Random Perturbations

The stochastic sensitivity function method [1, 2] is applied to analyze the sensitivity of a stochastic equilibrium of a dynamical system to random perturbations. This method is based on the calculation of a stochastic sensitivity matrix W. The positively definite symmetric matrix W characterizes the spread of random trajectories of the system around the equilibrium position. The eigenvalues of W are the so-called theoretical characteristics of noise sensitivity.

The matrix W is found from the solution of the matrix equation

$$\begin{aligned} FW+WF^T+S=0, \end{aligned}$$

(3)

where

$$ F=\left( \begin{array}{ccccc} \frac{\partial f}{\partial u} &{} \frac{\partial f}{\partial \theta } \\ \frac{\partial g}{\partial u} &{} \frac{\partial g}{\partial \theta } \end{array}\right) _{(\bar{u}, \bar{\theta })} ,\quad S= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix},\quad W=\begin{pmatrix} w_{11} &{} w_{12} \\ w_{12} &{} w_{22}. \end{pmatrix}. $$

From (3), we can find the elements of the matrix W:

$$ w_{11} = \frac{-1-2f_{\theta }w_{12}}{2f_u}, ~~ w_{22} = \frac{-1-2g_uw_{12}}{2g_{\theta }}, ~~ w_{12} = \frac{f_u f_{\theta } +g_u g_{\theta }}{2(f^2_{\theta }g_{\theta }+g^2_{\theta }f_u - f_u f_{\theta }g_u - f_u g_u g_{\theta })}, $$

and the eigenvalues:

$$\begin{aligned} \lambda _{1,2} = \frac{w_{11}+w_{22} \pm \sqrt{(w_{11}+w_{22} )^2-4(w_{11}w_{22} -w^2_{12} )}}{2}. \end{aligned}$$

(4)

Here,

$$ f_u = \frac{\partial f}{\partial u} (\bar{u}, \bar{\theta }),\quad f_{\theta }= \frac{\partial f}{\partial \theta }(\bar{u}, \bar{\theta }),\quad g_u= \frac{\partial g}{\partial u}(\bar{u}, \bar{\theta }),\quad g_{\theta }=\frac{\partial g}{\partial \theta }(\bar{u}, \bar{\theta }). $$

Fig. 1

a Theoretical sensitivity to the random perturbations and b the critical noise intensity value as a function of the control parameter $k_e$

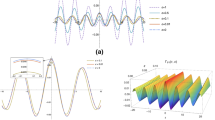
Figure 1a demonstrates the stochastic sensitivity of the equilibrium with respect to parameter $k_e$. Without loss of generality, the parameters’ values are chosen to be $\epsilon =0.2$, $\gamma = 8.99$, $k_a=10$, $k_d=100$, $\alpha _0=0.05$, $f=38.7$, $E=0.207564$ unless other values are specified in figure captions. Note that one of the eigenvalues (4) is sufficiently small (see the red curve), so the degree of stochastic sensitivity is determined by the highest eigenvalue. This figure shows that the equilibrium becomes more sensitive to random perturbations when the value of the control parameter $k_e$ is higher.

4 Noise-Induced Transitions

Qualitative changes are possible in the stochastic model under the noise influence: when a certain critical value of the noise intensity $\epsilon _{cr}$ is reached, a transition from one deterministic attractor (stable point) to another (limit cycle) occurs. Random trajectories leave the pool of attraction of the deterministic attractor and wind up the limit cycle. Such qualitative changes in the system are called noise-induced transitions. Consider the change in the stochastic phase portrait depending on the intensity of the noise.

For weak noise, the randomly forced system (1) and (2) exhibits the small-amplitude stochastic oscillations near its equilibrium. Rare transitions occur through the unstable cycle to the limit cycle and back with increasing noise intensity. In that case, the oscillations of mixed type are observed, see Fig. 2.

Fig. 2

Noise-induced transitions for $k_e=0.85$, $\epsilon = 0.0098$

Fig. 3

Noise-induced transitions for $k_e=0.85$, $\epsilon = 0.02$

However, as noise intensity increases, the large-amplitude stochastic oscillations appear, see Fig. 3. Transitions become more frequent with further increase of noise intensity. Thus, using the stochastic sensitivity function, we can predict the value of the noise intensity $\epsilon _{cr}$ corresponding to the beginning of the transitions.

We demonstrate transitions induced by noise for the control parameter $k_e=0.85$ and find out that the critical value of the noise intensity approximately equals to $\epsilon _{cr} \approx 0.009495$. After searching for the critical values of the noise intensity for the value of the parameter $k_e$ from the stable zone, we obtain the dependence of the $\epsilon _{cr}$ from the control parameter.

As it can be seen from Fig. 1b, the increase in control parameter value leads to the decrease in the noise intensity value, at which the transitions between attractors begin to appear.