Resonance-Based Mechanisms of Generation of Relaxation Oscillations in Networks of Non-oscillatory Neurons

Abstract

We investigate a minimal network model consisting of a 2D linear (non-oscillatory) resonator and a 1D linear cell, mutually inhibited with piecewise-linear graded synapses. We demonstrate that this network can produce oscillations in certain parameter regimes and the corresponding limit gradually transition from regular oscillations (of non-relaxation type) to relaxation oscillations as the levels of mutual inhibition increase.

This work was partially supported by the National Science Foundation grant DMS-1608077 (HGR), the NJIT Faculty Seed Grant 211278 (HGR) and the Universidad Nacional del Sur Grant PGI 24/L096. HGR is grateful to the Courant Institute of Mathematical Sciences at New York University and the Centre de Recerca Matemàtica, Barcelona. The authors are grateful to Antoni Guillamon for useful comments on an earlier version of this manuscript.

1 Introduction

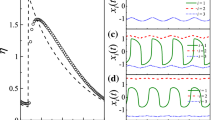
Membrane potential (subthreshold) resonance (MPR) refers to the ability of a neuron to exhibit a peak in their voltage amplitude response to oscillatory input currents at a preferred (resonant) input frequency ($f_{res}$); see [4,5,6,7] and Fig. 1a. MPR results from the interplay of an autocatalytic process (positive feedback) and a slower negative feedback effect. For neurons, these are provided by the participating currents. Neurons may also exhibit membrane potential (subthreshold) oscillations either damped or sustained in the absence of any time-dependent input. However, MPR and intrinsic oscillations are different phenomena governed by different mechanisms as demonstrated by the fact that 2D linear systems may exhibit MPR in the absence of damped oscillations [5,6,7]. We refer to the neurons that exhibit MPR as resonators. Here, we focus on resonators that are not damped oscillators.

MPR has been measured in a variety of neuron types and it has been investigated theoretically in [4,5,6, 9], and references therein. However, the role that MPR play in the generation of network oscillations is not well understood (but see [1, 3, 8]). In this paper, we demonstrate by means of a numerical simulation example that a minimal network model (Fig. 1b) consisting of a 2D linear resonator (e.g. Fig. 1a, blue) and 1D linear passive cell (e.g. Fig. 1a, red) mutually inhibited with piecewise-linear (PWL) graded synapses (Fig. 1c) can produce oscillations in certain parameter regimes. The corresponding limit cycles experience a transition from regular oscillations (of non-relaxation type) to relaxation oscillations as the levels of mutual inhibition increase.

Fig. 1

a   Representative impedance (Z) profiles for a band-pass (blue) and low-pass (red) filters. For linear systems receiving sinusoidal inputs with frequency f, the output is also a sinusoidal function with the same frequency and phase-shifted. b Network diagram of a mutually inhibited resonator (band-pass filter) and a non-resonator (low-pass filter). c Representative PWL connectivity function for the graded synapses

2 Model: Networks of Linearized Cells with Piecewise-Linear Graded Synapses

We used linearized biophysical (conductance based) models for the individual cells and piecewise-linear (PWL) graded synaptic connections. The linearization process for conductance-based models (around the resting potential for the voltage variable) for single cells has been previously described in [5, 7]. We refer the reader to these references for details.

The dynamics of a network of two mutually inhibitory cells are described by

$$\begin{aligned}&C_k\, \frac{dv_k}{dt} = -g_{L,k}\, v_k - g_{k}\, w_k - G_{in,jk}\, S_{\infty }(v_j) (v_k-E_{in}), \end{aligned}$$

(1)

$$\begin{aligned}&\tau _k\, \frac{dw_k}{dt} = v_k - w_k, \end{aligned}$$

(2)

for $k=1,2$, $j\ne k$. In Eqs. (1)–(2), t is time, $v_k$ represents the voltage (mV), $w_k$ represents the normalized gating variable for the resonant ionic current, $C_k = 1$ is the capacitance, $g_{L,k}$ is the linearized leak maximal conductance, $g_{k}$ is the ionic current linearized conductance, $\tau _k$ is the linearized time constant and the last term in Eq. (1) is the graded synaptic current modulated by the activity of the other cell where $G_{in,jk}$ is the maximal synaptic conductance, $E_{in} =-20$ is the synaptic reversal potential (referred to the resting potential) and $S_{\infty }(v)$ is a PWL function of sigmoid type (Fig. 1c) of the form

$$\begin{aligned} S_{\infty }(v) = \left\{ \begin{array}{lllll} 0 &{} &{} \text {if} &{} v< v_b \\ (v_a - v_b)^{-1}\, (v - v_b) &{} &{} \text {if} &{} v_b< v < v_a \\ 1 &{} &{} \text {if} &{} v > v_a, \\ \end{array} \right. \end{aligned}$$

(3)

where $v_a$ and $v_b$ are constants. In this paper we use $g_2 = 0$ (cell 2 is 1D), $v_b = -v_a$ and $G_{in} = G_{in,12} = G_{in,21}$.

We use the following units: mV for $v_k$ and $w_k$, ms for t, $\upmu$F/cm$^2$ for capacitance, $\upmu$A/cm$^2$ for current and mS/cm$^2$ for the maximal conductances.

The numerical solutions were computed by using the modified Euler method (Runge–Kutta, order 2) [2] with a time step $\Delta t = 0.1$ ms in MATLAB (The Mathworks, Natick, MA). Smaller values of $\Delta t$ have been used to check the accuracy of the results.

3 Results

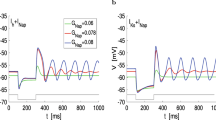
Figure 2 shows the results of our numerical simulations for representative values of $G_{in}$. Because the network is mutually inhibitory the two cells oscillate in antiphase. The network oscillations emerge for $G_{in} \sim 0.1296$. As $G_{in}$ increases the oscillation amplitude increases, first abruptly and then gradually (Fig. 3a). As this happens, the network oscillation frequency decreases (Fig. 3b). The network oscillations are terminated for $G_{in} \sim 0.176$ (not shown).

These oscillations (Fig. 2) are a network phenomena since for the parameter values we used, the resonator is not a damped oscillator and the passive cell is 1D. Sustained (limit cycle) oscillations require the interplay of a resonant (negative feedback) and amplifying (positive feedback) processes. For the network oscillations in Fig. 2, the resonant process is provided by the resonator and the amplifying process is provided by the network connectivity mediated by the passive cell [1].

Fig. 2

Representative voltage traces for the resonator/passive cell mutually inhibitory network (Fig. 1b). a $G_{in} = 0.1296$. b $G_{in} = 0.132$. c $G_{in} = 0.16$. The resonator has $f_{res} \sim 10.4$. We used the following parameter values: $C_1 = C_2 = 1$, $g_{L,1} = 0.25$, $g_1 = 0.25$, $\tau _1 = 100$, $g_{L,2} = 0.5$, $v_a = 3$, $v_b = -3$, $E_{in} = -20$, and $G_{in} = G_{in,12} = G_{in,21}$

The transition from regular oscillations (non-relaxation type) to relaxation oscillations as $G_{in}$ increases in Fig. 2 is a network phenomenon. There is a time scale separation between the activator ($v_1$) and the inhibitor ($w_1$) in the resonator ($\tau _1 = 100$). However, for this time scale separation at the individual cell level to be communicated to the network level to produce network relaxation oscillations the levels of mutual inhibition have to be relatively large.

Fig. 3

Dependence of the oscillations amplitude and frequency on the levels of mutual inhibition for the resonator/passive cell mutually inhibitory network (Fig. 1b). The parameter values are as in Fig. 2. a Amplitude versus $G_{in}$ curve. We plotted the amplitude of $v_1$. b Network oscillations frequency versus $G_{in}$

4 Discussion

We have demonstrated that a minimal network model (2D resonator, 1D linear cell and mutual inhibition) can produce sustained network oscillations in certain parameter regimes. These oscillations crucially depend on the negative feedback provided by the resonator. Mutual inhibition mediated by the passive cell is responsible for the amplification necessary to support the existence of a limit cycle. Our results provide an example of an oscillatory network of non-oscillatory cells, where resonance and amplification at different levels of organization interact to produce network oscillations. For high enough levels of mutual inhibition, the time scale between the two variables in the resonator is communicated to the network level to produce relaxation oscillations. If the levels of mutual inhibition are not high enough, this time scale separation remains occluded.

Our results highlight the role of MPR in isolated neurons for the generation of network oscillations, and have implications for neuronal network dynamics described either by conductance-based models or firing rate models with adaptation.