Call Admission Problems on Trees with Advice

Abstract

A well-studied problem in the online setting, where requests have to be answered immediately without knowledge of future requests, is the call admission problem. In this problem, we are given nodes in a communication network that request connections to other nodes in the network. A central authority may accept or reject such a request right away, and once a connection is established its duration is unbounded and its edges are blocked for other connections. This paper examines the admission problem in tree networks. The focus is on the quality of solutions achievable in an advice setting, that is, when the central authority has some information about the incoming requests. We show that $O(m \log d)$ bits of additional information are sufficient for an online algorithm run by the central authority to perform as well as an optimal offline algorithm, where m is the number of edges and d is the largest degree in the tree. In the case of a star tree network, we show that $\varOmega (m \log d)$ bits are also necessary (note that $d=m$). Additionally, we present a lower bound on the advice complexity for small constant competitive ratios and an algorithm whose competitive ratio gradually improves with added advice bits to $2 \lceil \log _{2} n \rceil$, where n is the number of nodes.

1 Introduction

A well-studied problem in the context of regulating the traffic in communication networks is the so-called call admission problem, where a central authority decides about which subset of communication requests can be routed. This is a typical example of an online problem: every request has to be routed or rejected immediately without the knowledge about whether some forthcoming, possibly more profitable, requests will be blocked by this decision.

We consider the call admission problem on trees (short CAT), which is an online maximization problem. An instance $I=(r_{1},\dots , r_{k})$ consists of requests $r=(v_{i}, v_{j})$ with $i,j\in \{0,\dots ,n-1\}$ and $v_{i}< v_{j}$, representing the unique path in a tree network that connects vertices $v_{i}$ and $v_{j}$. We require that all requests in I are pairwise distinct. The first request contains the network tree $T=(V,E)$, given to the algorithm in form of an adjacency list or matrix. In particular, we study the problem framework in which an accepted connection has an unbounded duration and each edge in the network may be used by at most one request, i.e., it has a capacity of 1. Thus, a valid solution $O=(y_{1}, \dots , y_{k}) \in \{0,1\}^{k}$ for I describes a set of edge-disjoint paths in T, where . Whenever I is clear from the context, we write $\mathchoice{ \mathrm {gain} \left( O\right) }{ \mathrm {gain} (O) }{ \mathrm {gain} (O) }{ \mathrm {gain} (O) }$ instead of $\mathchoice{ \mathrm {gain} \left( I,O\right) }{ \mathrm {gain} (I,O) }{ \mathrm {gain} (I,O) }{ \mathrm {gain} (I,O) }$.

An online algorithm $\textsc {Alg}$ for CAT computes the output sequence (solution) $\textsc {Alg} (I)=(y_{1},\dots , y_{k})$, where $y_{i}$ is computed from $x_{1},\dots , x_{i}$. The gain of $\textsc {Alg}$ ’s solution is given by $\mathchoice{ \mathrm {gain} \left( \textsc {Alg} (I)\right) }{ \mathrm {gain} (\textsc {Alg} (I)) }{ \mathrm {gain} (\textsc {Alg} (I)) }{ \mathrm {gain} (\textsc {Alg} (I)) }$. $\textsc {Alg}$ is c-competitive, for some $c\ge 1$, if there exists a constant $\gamma$ such that, for every input sequence I, $\mathchoice{ \mathrm {gain} \left( \textsc {Opt} (I)\right) }{ \mathrm {gain} (\textsc {Opt} (I)) }{ \mathrm {gain} (\textsc {Opt} (I)) }{ \mathrm {gain} (\textsc {Opt} (I)) } \le c \cdot \mathchoice{ \mathrm {gain} \left( \textsc {Alg} (I)\right) }{ \mathrm {gain} (\textsc {Alg} (I)) }{ \mathrm {gain} (\textsc {Alg} (I)) }{ \mathrm {gain} (\textsc {Alg} (I)) } + \gamma$, where $\textsc {Opt}$ is an optimal offline algorithm for the problem. This constitutes a measure of performance used to compare online algorithms based on the quality of their solutions, which was introduced by Sleator and Tarjan [18].

The downside of competitive analysis as a measurement of performance is that it seems rather unrealistic to compare the performance of an all-seeing offline algorithm to that of an online algorithm with no knowledge at all about future requests. This results in this method not really apprehending the hardness of online computation. Moreover, it cannot model information about the input that we may have outside the strictly defined setting of the problem. The advice model was introduced as an approach to investigate the amount of information about the future an online algorithm lacks [6, 7, 12, 13, 15]. It investigates how many bits of information are necessary and sufficient to achieve a certain output quality, which has interesting implications for, e.g., randomized online computation [5, 9, 16]. For lower bounds on this number in particular, we do not make any assumptions on the kind of information the advice consists of.

Let $\varPi$ be an online maximization problem, and consider an input sequence $I=(x_{1},\dots , x_{k})$ of $\varPi$. An online algorithm $\textsc {Alg}$ with advice computes the output sequence $\textsc {Alg} (I)^{\phi }=(y_{1},\dots , y_{k})$ such that $y_{i}$ is computed from $\phi ,x_{1},\dots , x_{i}$, where $\phi$ is the content of the advice tape, i.e., an infinite binary sequence. $\textsc {Alg}$ is c-competitive with advice complexity b(k) if there exists a constant $\gamma$ such that, for every k and for each input sequence I of length at most k, there exists some $\phi$ such that $\mathchoice{ \mathrm {gain} \left( \textsc {Opt} (I)\right) }{ \mathrm {gain} (\textsc {Opt} (I)) }{ \mathrm {gain} (\textsc {Opt} (I)) }{ \mathrm {gain} (\textsc {Opt} (I)) } \le c \cdot \mathchoice{ \mathrm {gain} \left( \textsc {Alg} ^{\phi }(I)\right) }{ \mathrm {gain} (\textsc {Alg} ^{\phi }(I)) }{ \mathrm {gain} (\textsc {Alg} ^{\phi }(I)) }{ \mathrm {gain} (\textsc {Alg} ^{\phi }(I)) } + \gamma$ and at most the first b(k) bits of $\phi$ have been read during the computation of $\textsc {Alg} ^{\phi }(I)$.

For a better understanding, consider the following example. A straightforward approach to an optimal online algorithm with advice for CAT is to have one bit of advice for each request in the given instance. This bit indicates whether the request should be accepted or not. Thus, $\textsc {Alg}$ reads |I| advice bits and accepts only requests in $\textsc {Opt} (I)$, i.e., $\textsc {Alg}$ is optimal.

This approach gives us a bound on the advice complexity that is linear in the size of the instance. Opposed to most other online problems however, call admission problems, like CAT, are usually analyzed with respect to the size of the communication network instead of the size of an instance as stated in the general definition. Thus, the advice complexity of this naive optimal algorithm on a tree with n vertices is of order $n^{2}$.

Related Work. The call admission problem is a well-studied online problem; for an overview of results regarding classical competitive analysis for this problem on various graph topologies, see Chapter 13 in the textbook by Borodin and El-Yaniv [3]. For the call admission problem on path networks (also called the disjoint path allocation problem, short DPA), Barhum et al. [2] showed that $l-1$ advice bits are both sufficient and necessary for an online algorithm to be optimal, where l is the length of the path. They also generalized the $\log _{2} l$-competitive randomized algorithm for DPA presented by Awerbuch et al. [1]. Gebauer et al. [14] proved that, with $l^{1-\varepsilon }$ bits of advice, no online algorithm for DPA is better than $(\delta \log _{2} l)/2$-competitive, where $0<\delta<\varepsilon <1$. The advice complexity of call admission problems on grids was investigated by Böckenhauer et al. [8].

When considering trees as network structure, we still have the property that the path between two nodes is unique in the network, thus all lower bounds on the advice complexity easily carry over by substituting the length l of the path network by the diameter D of the tree network. These lower bounds can be further improved as shown in Sect. 2. Concerning upper bounds, Borodin and El-Yaniv [3] presented two randomized online algorithms, a $2 \lceil \log _{2} n \rceil$-competitive algorithm, first introduced by Awerbuch et al. [1], and an $O(\log D)$-competitive algorithm. We will modify the former in Subsect. 3.2 to an online algorithm that reads $\lceil \log _{2} \log _{2} n - \log _{2} p\rceil$ advice bits and is $((2^{p+1}-2) \lceil \log _{2} n/p\rceil )$-competitive, for any integer $1\le p\le \log _2 n$.

Another problem closely related to DPA is the length-weighted disjoint path allocation problem on path networks, where instead of optimizing the number of accepted requests, one is interested in maximizing the combined length of all accepted requests. Burjons et al. [10] extensively study the advice complexity behavior of this problem.

Overview. In Sect. 2, we present the already mentioned lower bound for optimality, which even holds for star trees. We complement this with lower bounds for the trade-off between the competitive ratio and advice, based on reductions from the well-known string guessing problem [4]. Section 3 is devoted to the corresponding upper bounds. In Subsect. 3.1, we present algorithms for computing an optimal solution, both for general trees and for star trees and k-ary trees. As mentioned above, in Subsect. 3.2, we analyze the trade-off between the competitive ratio and advice and estimate how much the competitive ratio degrades by using less and less advice bits. Due to space restrictions, some of the proofs are omitted in this extended abstract.

Notation. Following common conventions, m is the number of edges in a graph and n the number of vertices. The degree of a vertex v is denoted by d(v). Let $v_{0}, \dots , v_{n-1}$ be the vertices of a tree T with some order $v_{0}<\dots <v_{n-1}$. This order can be arbitrarily chosen, but is fixed and used as order in the adjacency matrix or adjacency list of the tree. Hence, an algorithm knows the ordering on the vertices when given the network.

For the sake of simplicity, we sometimes do not enforce that $v<v'$, but regard $(v,v')$ and $(v',v)$ as the same request. For a request $r=(v,v')$, the function $\mathrm {edges}:V \times V \rightarrow \mathcal {P}(E)$ returns, for request r, the set of edges corresponding to the unique path in T that connects v and $v'$. Let ; we call l the length of request r. Note that all logarithms in this paper are of base 2, unless stated otherwise.

2 Lower Bounds

First we present lower bounds on the number of advice bits for the call admission problem on trees. We first look at optimal algorithms, then we focus on the connection between the competitive ratio and the advice complexity.

2.1 A Lower Bound for Optimality

Barhum et al. [2] proved that solving DPA optimally requires at least $l-1$ advice bits. As DPA is a subproblem of the call admission problem on trees, this bound also holds for CAT. We can improve on this by considering instances on trees of higher degree. We focus on the simplest tree of high degree, the star tree.

Theorem 1

There is no optimal online algorithm with advice for CAT that uses less than $\lceil (m/2) \log (m/\mathrm {e}) \rceil$ advice bits on trees of m edges.

Proof Sketch

This proof is based on the partition-tree method as introduced by Barhum et al. [2]. A partition tree of a set of instances $\mathcal {I}$ is defined as a labeled rooted tree such that (i) every of its vertices v is labeled by a set of input sequences $\mathcal {I}_v$ and a number $\varrho _v$ such that all input sequences in $\mathcal {I}_v$ have a common prefix of length at least $\varrho _v$, (ii) for every inner vertex v of the tree, the sets at its children form a partition of $\mathcal {I}_v$, and (iii) the root r satisfies $\mathcal {I}_r=\mathcal {I}$. If we consider two vertices $v_1$ and $v_2$ in a partition tree that are neither an ancestor of each other, with their lowest common ancestor v and any input instances $I_1\in \mathcal {I}_{v_1}$ and $I_2\in \mathcal {I}_{v_2}$ such that, for all optimal solutions for $I_1$ and $I_2$, their prefixes of length $\varrho _v$ differ, then any optimal online algorithm with advice needs a different advice string for each of the two input sequences $I_1$ and $I_2$. This particularly implies that any optimal online algorithm with advice requires at least $\log (w)$ advice bits, where w is the number of leaves of the partition tree. We sketch the construction of the instances that can be used for building such a partition tree.

Consider the star trees $S_{2k}$ for $k\ge 1$ with 2k edges. Let $v_{0}, v_{1}, \dots , v_{2k}$ be the vertices in $S_{2k}$, where $v_{0}$ denotes the center vertex. We construct a set $\mathcal {I}$ of input sequences for $S_{2k}$ so that any two input sequences share a common prefix of requests and each input $I\in \mathcal {I}$ has a unique optimal solution $\textsc {Opt} (I)$, which is only optimal for this particular instance.

Each input instance will be partitioned into k phases. At the end of each of these phases, one vertex will be blocked for all subsequent phases. We can uniquely describe each of our instances $I_{(j_{1}, \dots , j_{k})}$ by the sequence of these blocked vertices $(v_{j_{1}}, \dots , v_{j_{k}})$. Note that we will not use every possible vertex sequence for our construction. In phase i with $i\in \{1, \dots , k\}$, we request in ascending order all paths from the non-blocked vertex $v_{i}^{*}$ with the smallest index to all other non-blocked vertices, then we block $v_{i}^{*}$ and $v_{j_{i}}$ for all future phases. We note that, at the start of phase 1, all vertices are non-blocked. Let $\mathcal {I}_{(j_{1},\dots , j_{i})}$ denote the set of all input sequences whose tuples have prefix $(j_{1}, \dots , j_{i})$ with $i\le k$. Observe that, by definition, all input sequences in $\mathcal {I}_{(j_{1},\dots , j_{i})}$ have the same requests until phase i ends and that tuple $(j_{1}, \dots , j_{k})$ describes exactly one input sequence in $\mathcal {I}$, i.e., $|\mathcal {I}_{(j_{1},\dots , j_{k})} |=1$. Figure 1 shows an illustration of such an input sequence for the star $S_{6}$, i.e., for $k=3$.

Fig. 1.

Input sequence $I_{(3,5,6)}=(r_{1}, \dots , r_{9})$ on star graph $S_{6}$ partitioned into 3 phases. Red vertices are blocked, a red edge indicates the request is in the optimal solution $\textsc {Opt} (I_{(3,5,6)})$. For the sake of simplicity, the center vertex $v_{0}$ is omitted from the drawings; thus all lines represent paths of length 2 (Color figure online).

We can prove that, for each input sequence $I_{(j_{1}, \dots , j_{k})}$, the unique optimal solution is , where is the request accepted by $\textsc {Opt}$ in each phase i. The next step is to show that, for any two input sequences in $\mathcal {I}$, their unique optimal solution $\textsc {Opt}$ differs. Consider two input sequences $I, I'\in \mathcal {I}$ with $I\ne I'$ and let $(j_{1}, \dots , j_{k})$ and $(j'_{1}, \dots , j'_{k})$ be their identifying tuples, respectively. As the two input sequences are non-identical, there must exist some smallest index i so that $j_{i} \ne j'_{i}$. In particular, since i marks the first phase at whose end different vertices are blocked in I and $I'$, the requests in phase i must be identical in both input sequences. Let $v^{*}_{i}$ be the non-blocked vertex with the smallest index in phase i in both input sequences. By definition of $\textsc {Opt}$, request $(v^{*}_{i}, v_{j_{i}}) \in \textsc {Opt} (I)$ and request $(v^{*}_{i}, v_{j'_{i}}) \in \textsc {Opt} (I')$ with $j_{i} \ne j'_{i}$. It thus follows that $\textsc {Opt} (I)\ne \textsc {Opt} (I')$ as both requests share an edge.

Since the optimal solution for the common prefix differs between two instances, no online algorithm without advice can be optimal on this set, because, with no additional information on the given instance (i.e., based on the prefix alone) the two instances cannot be distinguished. It follows that the algorithm needs a unique advice string for each instance in the set. Thus, it only remains to bound the number of instances in $\mathcal {I}$. Each instance has a unique label $\mathcal {I}_{(j_{1}, \dots , j_{k})}$, so that the total number equals the number of tuples $(j_{1}, \dots , j_{k})$ of pairwise distinct vertex indices, that is,

$$\begin{aligned} (2k-1)\cdot (2k-3)\cdot (2k-5)\cdot \dots \cdot 1 = (2k-1)!!= \frac{(2k)!}{2^{k}\cdot k!}, \end{aligned}$$

which we can bound from below using Stirling’s inequalities, yielding

$$ \frac{(2k)!}{2^{k}\cdot k!} \ge \frac{(2k)!}{2^{k}\cdot \mathrm {e} \sqrt{k}\cdot (\frac{k}{\mathrm {e}})^{k}} \ge \frac{\sqrt{2 \pi 2k}\cdot (\frac{2k}{\mathrm {e}})^{2k}}{\mathrm {e} \sqrt{k}\cdot (\frac{2k}{\mathrm {e}})^{k}} \ge \frac{\sqrt{4 \pi }}{\mathrm {e} }\cdot \left( \frac{2k}{\mathrm {e}} \right) ^{k} \ge \left( \frac{2k}{\mathrm {e}} \right) ^{k}. $$

Using that $m=2k$, we conclude that at least $\lceil (m/2)\log (m/\mathrm {e}) \rceil$ advice bits are necessary for any online algorithm to be optimal on the tree $S_{m}$.    $\square$

This lower bound is asymptotically larger by a logarithmic factor than the DPA lower bound [2], which suggests that the advice complexity of CAT increases with the degree of the tree network and not only with its size.

2.2 A Lower Bound for Competitiveness

In this section, we present a reduction from an online problem called the string guessing problem to CAT. In the string guessing problem with unknown history (q-SGUH), an algorithm has to guess a string of specified length z over a given alphabet of size $q\ge 2$ character by character. After guessing all characters, the algorithm is informed of the correct answer. The cost of a solution $\textsc {Alg} (I)$ is the Hamming distance between the revealed string and $\textsc {Alg} (I)$. Böckenhauer et al. [4] presented a lower bound on the number of necessary advice bits depending on the achieved fraction of correct character guesses.

We will use this lower bound for our results, reducing the q-SGUH problem to CAT by assigning each element of the alphabet to an optimal solution for a family of instances on the star tree $S_{d}$ where $d=q$. The idea is to have a common prefix on all instances and the last requests specifying a unique optimal solution for the instance corresponding to the character in the string. For each character we have to guess, we insert such a star tree into our graph such that the graph is connected but the trees do not share edges. We can then look at each subtree independently and join the instances to an instance corresponding to the whole string. Let therefore, for some $z,d\in \mathbb {N}$, $\mathcal {T}_{z,d}$ be the set of trees that can be constructed from subtrees $S^{(i)}$ with $i\in \{1,\dots ,z\}$, such that any two subtrees share at most one vertex and the tree is fully connected. For each request of a d-SGUH instance of length z, where the optimal answer would be the string $s_1\ldots s_z$ we now construct a sequence of requests for $S^{(i)}$ such that choosing the optimal set of requests for $S^{(i)}$ corresponds to correctly guessing $s_i$. Then, any algorithm that solves a fraction $\alpha$ of all subtrees optimally can be used to achieve a fraction $\alpha$ of correct guesses on the d-SGUH instance.

Theorem 2

Every online algorithm with advice for CAT which achieves a competitive ratio of $c\le d/(d-1)$ on any tree $T\in \mathcal {T}_{z,d}$, for $d\ge 3$ and $z,d\in \mathbb {N}$, has to read at least

$$\begin{aligned} \left( 1-H_{d}\left( d-\frac{d-1}{c}-1\right) \right) \frac{m}{d} \log d \end{aligned}$$

advice bits, where $H_{d}$ is the d-ary entropy function.    $\square$

We can use the same tree structure to prove a better lower bound for small values of c by changing the reduction instance of CAT. This change increases the alphabet size of q-SGUH that we can reduce to instances on trees in $\mathcal {T}_{z,d}$ for $q=2^{d-1}$, and allows to prove the following theorem.

Theorem 3

Every online algorithm with advice for CAT which achieves a competitive ratio of $c\le d/(d-1\ +1/2^{d-1})$ on any tree $T\in \mathcal {T}_{z,d}$, for $d\ge 2$ and $z,d\in \mathbb {N}$, has to read at least

$$\begin{aligned} \left( 1-H_{2^{d-1}}\left( d-\frac{d}{c}\right) \right) m \cdot \frac{d-1}{d} \end{aligned}$$

advice bits, where $H_{d}$ is the d-ary entropy function.    $\square$

Fig. 2.

Lower bound on the number of advice bits stated in Theorem 2 (light green) and Theorem 3 (dark blue) divided by the number m of edges in $T\in \mathcal {T}_{z,d}$. (Color figure online)

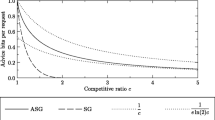
Figure 2 depicts the lower bounds of Theorems 2 and 3, respectively.

3 Upper Bounds

In the following, we present online algorithms with advice for the call admission problem on trees. In the first part, the focus will be on optimal algorithms with different advice complexities. In the second part, we discuss an algorithm whose competitiveness gradually improves with added advice bits.

3.1 Optimal Online Algorithms with Advice

The fundamental idea of the following algorithms is to encode the optimal solution using edge labels as advice. A straightforward approach is to give all requests in $\textsc {Opt} (I)$ an identifying number and label the edges of each request with this identifier. After communicating the labels of all edges, the algorithm will be able to distinguish which request is in $\textsc {Opt} (I)$ and which is not, by checking whether all the edges of the request have the same label and no other edges have this label. As a result, the algorithm can recognize and only accept requests that an optimal solution accepts.

As for the advice complexity, we need m labels each consisting of a number in $\{0, 1,\dots , |\textsc {Opt} (I)| \}$. Since, for any input sequence I, we have $|\textsc {Opt} (I) | \le m$, in total $m \lceil \log (m+1) \rceil$ advice bits suffice. If $|\textsc {Opt} (I)|$ is much smaller than m, we can communicate the size of a label using a self-delimiting encoding [17], using $m\, \lceil \log (| \textsc {Opt} (I)|+1) \rceil + 2\, \lceil \log \lceil \log (| \textsc {Opt} (I)|+1 )\rceil \rceil$ advice bits in total.

We will continue to use this idea of an identifier for the following algorithms in a more local manner. Instead of giving each request in $\textsc {Opt} (I)$ a global identifying number and labeling corresponding edges accordingly, we associate identifiers with an optimal request depending on the vertices incident to the request’s edges.

We can picture this labeling scheme with a request as a row of dominoes, where each edge of the request represents one domino and consecutive edges have the same identifying number at their common vertex. Knowing for all edges the incident edges that are part of the same request, we can reconstruct the paths belonging to all requests in $\textsc {Opt} (I)$ and since we only need local identifiers, this reduces the size of each label.

Theorem 4

There is an optimal online algorithm with advice for CAT that uses at most $2 m\, \lceil \log (d+1)\rceil$ advice bits, where d is the maximum degree of a vertex in T.

Proof Sketch

First, let us define such a local labeling formally. For some input sequence $I=(r_{1}, \dots , r_{l})$, let $\textsc {Opt} (I) \subseteq \{r_{1}, \dots , r_{l}\}$ be an arbitrary, but fixed optimal solution for I. Furthermore, for every vertex v, let $\textsc {Opt} _{v}(I)$ be the subset of requests in $\textsc {Opt} (I)$ which occupy an edge incident with v. Observe that $|\textsc {Opt} _{v}(I)|\le d(v)$ as there are d(v) edges incident with v. For all $v\in V$, let $g_{v}:\textsc {Opt} _{v}(I)\rightarrow \{1, \dots , d(v)\}$ be an injective function that assigns a number to each request in $\textsc {Opt} _{v}(I)$. These numbers serve as local identifiers of each request in $\textsc {Opt} _{v}(I)$. We define the label function lb as follows; for $e=\{v,v'\} \in E$, where $v<v'$, let

Thus, if an edge e is used by $r \in \textsc {Opt} (I)$, the local identifiers of r for the two vertices of e constitute the edge label; if unused, e is labeled (0, 0). Observe that, if $e=\{v,v'\} \in \mathrm {edges}(r)$ and $r\in \textsc {Opt} (I)$, it follows that $r\in \textsc {Opt} _{v}(I)$ and $r\in \textsc {Opt} _{v'}(I)$, so lb is well-defined. Figure 3 shows an example of a local and a global labeling side by side. Observe that, for vertex v, we have the label 4 for two edges, but no label 2. As $g_{v}$ may arbitrarily assign an identifier in $\{1, \dots , d_{v}\}$, the assigned number to a request does not have to be minimal. In the lb-labeled tree T, we call $p=(v'_{1}, \dots , v'_{l})$ a labeled path of length l if p is a path in T with $v'_{1}< v'_{l}$ and $lb_{v'_{j}}(\{v'_{j-1}, v'_{j}\}) = lb_{v'_{j}}(\{v'_{j}, v'_{j+1}\}) \ne 0$ for all $j\in \{2, \dots , l-1\}$.

We refer to p as a complete labeled path if further no other edges incident to $v'_{1}$ or $v'_{l}$ have label $lb_{v'_{1}}(\{v'_{1}, v'_{2}\})$ or $lb_{v'_{l}}(\{v'_{k-1}, v'_{l}\})$, respectively.

Fig. 3.

Examples of a global labeling (left) and a local labeling (right) for the same optimal solution.

Consider an algorithm $\textsc {Alg}'$ that reads the labels of all edges from the advice before starting to receive any request and then computes the set P of all complete labeled paths in T. $\textsc {Alg}'$ then accepts a request $r=(v,v')$ if and only if it coincides with a complete labeled path in P.

We can prove that $\textsc {Alg}'$ accepts all requests in $\textsc {Opt} (I)$, and thus is optimal, by showing that every request in $\textsc {Opt} (I)$ has a coinciding path in P and that all paths in P are pairwise edge-disjoint. It remains to bound the number of advice bits used. For an edge $\{v,v'\}$, we need $\lceil \log (d(v)+1) \rceil + \lceil \log (d(v')+1)\rceil$ advice bits to communicate the label $lb(\{v,v'\})$. Hence, per vertex w, we use $d(w) \cdot \lceil \log {(d(w)+1)} \rceil$ advice bits. Summing up over all vertices yields the claimed bound.    $\square$

We can further improve this bound by showing that pinpointing an endvertex of a request $r\in \textsc {Opt} (I)$ does not require a unique identifier.

Theorem 5

There is an optimal online algorithm with advice for CAT that uses at most $(m-1)\, \lceil \log ( \lfloor d/2\rfloor +1)\rceil$ advice bits, where d is the maximum degree of a vertex in T.

Proof Sketch

Consider a function $g_v:\textsc {Opt} _{v}(I)\rightarrow \{0,1, \dots , \lfloor d(v)/2 \rfloor \}$ that assigns a non-zero identifier only to requests in $\textsc {Opt} _{v}$ that occupy two incident edges to v, otherwise it assigns identifier 0. Observe that we halve the number of identifiers needed this way.

Let us now refer to a labeled path $p=(v'_{1},\dots , v'_{l})$ as complete if and only if

$$\begin{aligned} lb_{v'_{1}}(\{v'_{1}, v'_{2}\}) = lb_{v'_{l}}(\{v'_{l-1}, v'_{l}\}) =0. \end{aligned}$$

(1)

Again, we consider $\textsc {Alg}'$ that reads the advice $lb(e_{1}), \dots , lb(e_{m})$ for a tree T and computes the set P of all complete labeled paths in T according to Theorem 4. $\textsc {Alg}'$ then accepts a request $r=(v,v')$ if and only if it coincides with a complete labeled path in P.

We can show, analogously to the proof of Theorem 4, that all paths in P are pairwise edge-disjoint and that each request in $\textsc {Opt} (I)$ has a coinciding path in P (Fig. 4). Thus, as before, $\textsc {Alg}'$ accepts all requests in $\textsc {Opt} (I)$ and is therefore optimal. Finally, we note that not all labels have to be communicated. Consider a vertex v and its incident edges $e'_{1}, \dots , e'_{d(v)}$. Assuming that we have all labels $lb_{v}(e'_{1}), \dots , lb_{v}(e'_{d(v)-1})$, we can infer the last label $lb_{v}(e'_{d(v)})$ as follows. If there exists only one edge $e \in \{e'_{1}, \dots , e'_{d(v)}\}$ with non-zero label $lb_{v}(e)$, then $lb_{v}(e'_{d(v)})=lb_{v}(e)$, since by definition of $g_{v}(r)$ and lb there are exactly two edges with the same non-zero label. If there is no such edge, $lb_{v}(e'_{d(v)})=0$ for the same reason. Therefore, for each vertex we only need to communicate the advice for the first $d(v)-1$ edges and per edge only $\lceil \log (\lfloor d(v)/2\rfloor +1)\rceil$ advice bits. In total, $\textsc {Alg}'$ needs at most $\lceil \log (\lfloor d/2 \rfloor +1)\rceil \cdot (m-1)$ advice bits, where d is the maximum degree of a vertex in T.    $\square$

Note that the central idea behind the algorithms of Theorems 4 and 5 is to identify, for all inner vertices, which incident edges belong to the same request in some fixed optimal solution. We used edge labels as advice to convey this information. In what follows, we will discuss another technique to encode this information for some types of trees. First, let us examine the star tree $S_{d}$ of degree d; let $I_{d}=(r_{1}, \dots , r_{(d(d-1))/2})$ denote the instance with all possible requests in $S_{d}$ of length 2.

Fig. 4.

Example of a labeling as used in Theorem 4 (left) and the inferred full labeling (right) for the same optimal solution.

Lemma 1

For the instance $I_{d}$ of CAT on $S_{d}$, the size of the set of solutions $\mathcal {O}(I_{d})$ is at most

$$\begin{aligned} \sum _{j=0}^{\lfloor d/2 \rfloor } \frac{d\,!}{2^{j}\cdot j\,!\cdot (d-2j)\,!}. \end{aligned}$$

(2)

Proof

We construct a graph $G(I_{d})$, where the vertex set corresponds to the leaf vertices of $S_{d}$. For a request r of $I_{d}$, we insert an edge in $G(I_{d})$ between the respective vertices. Note that, since $I_{d}$ consists of all requests between leaf vertices in $S_{d}$, we have that $G(I_{d})$ is the complete graph $K_{d}$ on d vertices.

Any solution $O\in \mathcal {O}(I_{d})$ describes a set of edge-disjoint requests, and thus can be uniquely associated with a matching in $G(I_{d})$: In the tree $S_{d}$, with requests of length 2, this is equivalent to requests having pairwise different endpoints, i.e., their corresponding edges must form a matching in $G(I_{d})$. Thus, the size of the set $\mathcal {O}(I_{d})$ is the number of matchings in $G(I_{d})$, which is given by the Hosoya index¹ of $K_{d}$, that is, by (2).    $\square$

Now consider an arbitrary instance $I^{*}$ of CAT on $S_{d}$ and an optimal solution $\textsc {Opt} \in \mathcal {O}(I^{*})$. Any algorithm that knows the partial solution of $\textsc {Opt}$ for requests of length 2 is optimal on $I^{*}$, as it can allocate requests of length 2, such that the edges of length-1 requests in $\textsc {Opt}$ are not blocked. Furthermore, note that this partial solution can be described by a solution in the set $\mathcal {O}(I_{d})$ of instance $I_{d}$. Thus, enumerating the elements in the set $\mathcal {O}(I_{d})$ and using the index of the partial solution as advice yields an algorithm that is optimal on $I^{*}$.

Corollary 1

There exists an optimal online algorithm with advice for CAT on $S_{d}$ that uses at most

$$\begin{aligned} \left\lceil \log \left( \sum _{j=0}^{\lfloor d/2 \rfloor } \frac{d\,!}{2^{j}\cdot j\,!\cdot (d-2j)\,!} \right) \right\rceil \approx&\left\lceil \frac{d}{2} \log \left( \frac{d}{e}\right) + \log \left( \frac{e^{\sqrt{d}}}{(4e)^{1/4}} \right) \right\rceil \end{aligned}$$

advice bits.    $\square$

The asymptotical approximation is given by using Stirling’s inequality on the bound of Lemma 1 as shown by Chowla et al. [11]. Thus, the upper bound of Corollary 1 is asymptotically of the same order as the lower bound of Theorem 1 in the previous chapter, which is constructed on a star tree $S_{d}$.

We can use the set of solutions $\mathcal {O}(I_{d})$ to construct a similar algorithm as in Corollary 1 for k-ary trees of arbitrary height. The idea is to regard each inner vertex of a k-ary tree and its neighbors as a star tree with at most $k+1$ leaves. Since any k-ary tree has at most inner vertices, we get subtrees $S_{1}, \dots , S_{l}$ for which we can give advice as described before. Since the advice complexity of Theorem 5 is about twice that of Corollary 1 for a star tree $S_{k+1}$, this algorithm reduces the amount of advice used for each inner node, improving the upper bound for k-ary trees by a factor of about 2 when compared to Theroem 5.

Theorem 6

There exists an optimal online algorithm with advice for CAT on k-ary trees of height h that uses at most

$$\left\lceil \frac{k^{h}-1}{k-1} \cdot \log \left( \sum _{j=0}^{\lfloor (k+1)/2 \rfloor } \frac{(k+1)\,!}{2^{j}\cdot j\,!\cdot (k+1-2j)\,!} \right) \right\rceil $$

advice bits.    $\square$

3.2 Competitiveness and Advice

A popular approach to create competitive algorithms for online problems is to divide the requests into classes, and then randomly select a class. Within this class, requests are accepted greedily and requests of other classes are dismissed.

Awerbuch et al. [1] describe a version of the “classify and randomly select” algorithm for the CAT problem based on vertex separators as follows. Consider a tree with n vertices. There has to exist a vertex $v'_{1}$ whose removal results in disconnected subtrees with at most n / 2 vertices. Iteratively choose, in each new subtree created after the $(i-1)$-th round, a new vertex to remove and add it to the set $V_{i}$; vertices in this set are called level-i vertex separators. This creates disjoint vertex classes $V_{1}, V_{2}, \dots , V_{\lceil \log n\rceil }$. We can now separate incoming requests into levels. A request r is a level-$i_{V}$ request if $i_{V} = \min _{j}(V_{j} \cap V(r) \ne \emptyset )$ where V(r) is the set of vertices in the path of the request. The algorithm then chooses a level $i_{V}^{*}$ uniformly at random and accepts any level-$i_{V}^{*}$ request greedily, i.e., an incoming level-$i_{V}^{*}$ request is accepted if it does not conflict with previously accepted requests.

This randomized algorithm is $2 \lceil \log _{2} n \rceil$-competitive in expectation and can be easily adapted to the advice model by choosing the accepted class using advice. When we reduce the number of classes by a factor of 1 / p for some $p\in \{1, \dots , \lceil \log n\rceil \}$, the number of advice bits necessary to communicate the level index will decrease, but we can expect the greedy scheduling to perform worse.

Theorem 7

For any $p\in \{1,\dots , \lceil \log n\rceil \}$ there is an online algorithm with advice for CAT that uses $\left\lceil \log \log n - \log p\right\rceil$ advice bits and is

$$\begin{aligned} \left( (2^{p+1}-2) \cdot \left\lceil \frac{\log n}{p} \right\rceil \right) \text {-competitive}. \end{aligned}$$

Proof Sketch

We define the set $\mathrm {Join}(i_{V},p)$ to include all requests in I of levels $i_{V}, \dots , \min \{i_{V}+(p-1), \log n\}$. We say that request r is in a subtree S if all its edges are in S, and use “block” in the sense of two requests having at least one edge in common. Observe that requests of level $i_{V}$ or higher have all edges in a subtree created by removing vertices in $V_{1}, \dots , V_{i_{V}-1}$. We call such a subtree a level-$i_{V}$ subtree. Let $\textsc {Opt} (I)$ be an optimal solution to I; it can be proven by induction on p that for all $i_{V}\in \{1, \dots , \lceil \log n\rceil \}$, any request r in a subtree of level $i_{V}$ can block at most $2^{p+1}-2$ other requests in $\textsc {Opt} (I) \cap \mathrm {Join}(i_{V},p)$. We can conclude that, for a fixed $p\in \{1,\dots , \lceil \log n\rceil \}$, any greedy scheduler is $(2^{p+1}-2)$-competitive when requests are restricted to a level $i_{V'}$, for some $i_{V'}\in \{1, \dots , \left\lceil (\log n)/p \right\rceil \}$. This follows directly from the induction hypothesis. The competitive ratio and advice complexity are easily deduced from there on.

   $\square$

Corollary 2

There exists a $2\lceil \log n\rceil$-competitive algorithm for CAT that uses $\lceil \log \log n \rceil$ advice bits.    $\square$